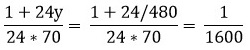В научно-популярной книге рассказывается о настольных играх и их связи с математикой от древних времен до настоящей поры; о первых попытках анализа различных игр и поиска выигрышных стратегий; о возникновении и развитии теории игр — науки, которая, несмотря на название, занимается не только играми, но и такими сложными областями человеческой деятельности, как экономика и организация сотрудничества.
Близкие по теме издания: Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью, Питер Бернстайн. Против богов. Укрощение риска, Авинаш Диксит, Барри Нейлбафф. Теория игр.
Николай Романецкий. Просто игра. — СПб.: ООО «Страта», 2015. — 216 с.
Скачать конспект (краткое содержание) в формате Word или pdf
ГЛАВА 1. МАТЕМАТИКА И ИГРА В ИСТОРИИ ЧЕЛОВЕЧЕСТВА
Джероламо Кардано создал один из первых трудов об играх и математике — «Книга об азартных играх» (Liber de Ludo Aleae), в которой впервые рассматривались проблемы, связанные с вероятностями при игре в кости, и давались оригинальные и остроумные, хотя временами и неправильные решения (подробнее см. Джироламо Кардано. О моей жизни; заключительный раздел конспекта). Эта книга была написана Кардано около 1564 года. Однако опубликовали ее посмертно, много позже. Эта книга должна считаться первой работой, в которой обсуждаются проблемы вероятностей, но она не оказала такого влияния на науку, как работы Паскаля и Ферма, чью переписку многие считают началом теории вероятностей (см. Альфред Реньи. Письма о вероятности: письма Паскаля к Ферма).
В работе «Всеобщая арифметика», опубликованной на латыни в 1707 году, Исаак Ньютон (1642–1727), наряду с идеями, ставшими большим вкладом в серьезную математику, представляет и развлекательные задачи. Самая знаменитая из них — задача, известная, как «луг, коровы и трава» или «задача Ньютона».
Вот она: «Трава на всём лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы ее за 24 дня, а 30 коров — за 60 дней. Сколько коров съели бы всю луговую траву за 96 дней?»
А вот ее решение: Введем вспомогательное неизвестное, которое будет обозначать суточный прирост травы в долях ее запаса на лугу. Пусть в сутки прирастает у, за 24 дня — 24y; если общий запас принять за 1, то в течение 24 дней коровы съедают 1 + 24у. В сутки всё стадо (из 70 коров) съедает (1 + 24y)/24, а одна корова съедает (1 +24 у)/(24×70). Аналогично для 30 коров, съевших траву того же луга за 60 суток, получаем, что одна корова съедает в сутки (1 +60у)/(30×60).
Однако количество травы, съедаемое коровой в сутки, для обоих стад одинаково. А значит,
Из этого уравнения получаем у = 1/480.
Теперь, найдя у (величину прироста), легко определить, какую долю первоначального запаса травы съедает одна корова в сутки:
Наконец, составляем уравнение для окончательного решения задачи: если искомое число коров х, то:
откуда х = 20. Итак, в течение 96 дней съели бы всю траву 20 коров.
Значительный вклад в анализ игр и математических головоломок в XIX в. внес французский математик Эдуард Люка, ставший автором отличного сборника «Занимательная математика». Среди игр, придуманных самим Люка, есть игра Ханойские башни (рис. 1).
Рис. 1. Исходная позиция «Ханойских башен». Цель— перенести все диски на другую башню, перекладывая только по одному за раз и никогда не помещая более крупный диск на более мелкий
В середине XX в. Роберт Эбботт изобретая игру Элевсин. В игре участвуют от 4 до 8 человек. Первый сдатчик («Творец») определяется жребием, далее игроки сдают карты по очереди. Колода тщательно тасуется, снимается, и карты с колоды сдаются поровну между всеми участниками игры, за исключением сдатчика. Последнюю карту с колоды «Творец» забирает себе. После этого сдатчик загадывает правило выкладывания карт на свою карту и кладет свою карту в открытом виде по центру стола. Первый ход принадлежит игроку слева от сдатчика. Игрок должен угадать правило выкладывания карт, которое загадал сдатчик, но вслух не должен произносить. После этого он кладет свою карту, следуя этому правилу. Если карта, которую положил игрок, следует этому правилу, то «Творец» говорит: «еще», и игрок кладет еще одну карту, если карта не соответствует задуманному правилу сдатчика, тот говорит: «нет», и ход переходит к следующему игроку по часовой стрелке. Игрок, который выложил не ту карту, забирает ее себе обратно. «Творец» может загадать, например, такое правило: выложить все карты колоды в восходящей последовательности, чередуя черные масти с красными.
Ближе к концу ошибающиеся игроки начинают выбывать из игры. Выигрывает тот, кто, угадав правило выкладывания карт, первым выложит все свои карты. Проводят столько партий, сколько игроков участвует в игре, дабы все побывали в роли «Творца».
После окончания Второй мировой войны много лет в области головоломок доминировал великий создатель и собиратель головоломок американец Мартин Гарднер (1914–2010), автор множества книг и статей, публиковавшихся на протяжении четверти века в популярном научном журнале Scientific American. Почти до самой смерти Гарднер продолжал издавать свои работы, выпустив более семи десятков книг (множество книг издано и на русском языке). В дополнение к собственным творениям он опубликовал некоторые из самых интересных головоломок других авторов, включая игру «Жизнь» (1970) Джона Конвея и Элевсин (1956) Роберта Эбботта.
Яков Исидорович Перельман (1882–1942), российский, советский учёный, популяризатор физики, математики и астрономии, один из основоположников жанра научно-популярной литературы и основоположник занимательной науки. Недавно издательство Альпина Паблишер выпустило классическую книгу Перельмана 5 минут на размышление (я помню, как в детстве зачитывался этой книгой). Одна из головоломок Якова Перельмана: четыре костяшки домино установлены квадратом таким образом, чтобы на каждой стороне получалась одна и та же сумма. Задача в том, чтобы, использовав все костяшки домино, создать по такому принципу семь квадратов (рис. 2).
Рис. 2. Два варианта «магического квадрата» Перельмана. На левом сумма равна четырем, на правом — двенадцати
Теория игр началась трудами Джона фон Неймана, в частности с его книги, опубликованной совместно с экономистом Оскаром Моргенштерном, Теория игр и экономическое поведение (1944). Авторы описали метод определения оптимальной стратегии для каждого игрока. Успех так называемой минимаксной стратегии фон Неймана и дополнений и приложений к ней, которые учитывают элементы случайности, — называемых «смешанными стратегиями», — привел к тому, что математики и экономисты стали использовать теорию игр для изучения более сложных и комплексных ситуаций. Развитие теории игр привело к созданию различных дилемм, концентрирующихся на необходимости выбора между конфликтом, риском и сотрудничеством. Это может быть применено в огромном количестве разнообразных ситуаций и составляет существенную часть этой теории.
ГЛАВА 2. ЛОГИЧЕСКИЕ ИГРЫ И РЕШЕНИЕ ЗАДАЧ
Термин «логические игры» используется для обозначения игр, где элемент случайности отсутствует напрочь. Течение игры зависит только от решений игроков при выборе ходов. Отсутствие случайности означает, что такие игры могут быть проанализированы с целью отыскать выигрышную стратегию. С математической точки зрения они делятся на два главных типа: конечные игры (те, где у каждого игрока имеется только конечное число альтернатив) и игры, в которых немалую роль играет случайность. Мы будем называть первую группу «логическими играми», а вторую — «играми с элементом случайности».
Рассмотрим пример логической игры. На столе размещаются двадцать фишек одного цвета. Каждый игрок по очереди забирает одну или две фишки. Игрок, который забирает последнюю фишку, считается победителем. У которого из двух игроков есть преимущество? Как обеспечить себе победу постоянно?
Читателю, незнакомому с игрой, чтобы ответить на поставленные выше вопросы, стоит найти партнера и несколько раз в нее сыграть. И он вскоре обнаружит, что игрок, оставляющий три фишки на столе, следующим ходом неизменно побеждает. Само по себе это знание полезно, но вовсе не оно определяет выигрыш, поскольку прежде необходимо понять, каким образом оставить эти три фишки.
Нам ясно, что игрок, забирающий 17-ю фишку, непременно выигрывает. Если продолжить анализ в обратном направлении, легко заметить, что выигрыш обеспечен и в случае, если на столе осталось 6 фишек. И вообще, если один из игроков постоянно оставляет количество фишек, кратное трем, то он всегда побеждает.
Этот вывод дает нам возможность определить выигрышную стратегию: если в исходном положении имеется 20 фишек, первый игрок всегда может выиграть, забрав 2 фишки при первом ходе, а затем всегда оставляя количество фишек, кратное 3 (если второй игрок забирает одну фишку, то первый забирает две и наоборот). Таким образом, в этой игре у первого игрока есть преимущество, поскольку для него всегда имеется выигрышная стратегия. Варьируя исходное количество фишек, можно частично изменить стратегию и даже поменять игрока, имеющего преимущество.
Мы уже определили, что выигрышная стратегия состоит из того, чтобы оставить на столе кратное трем количество фишек. Разделим исходное количество фишек на три и посмотрим на остаток деления. Если в остатке два (как в изначальном варианте), первый игрок выиграет, забрав 2 фишки при первом ходе, а затем оставляя на столе кратное трем (если оппонент забирает одну, то первый игрок должен брать две, и наоборот).
Если остаток деления — 1 (то есть игра начинается с 25, 199 или 2014 фишками), первый игрок также выигрывает, забирая во время первого хода всего одну фишку. Однако если остаток равен нулю (изначальное количество фишек делится на 3), то всегда будет выигрывать второй игрок, снимая две фишки, когда первый забирает одну, и наоборот. В этом случае первому игроку никогда не удастся оставить на столе количество фишек, кратное трем.
ГЛАВА 3. ИГРЫ С ЭЛЕМЕНТОМ СЛУЧАЙНОСТИ
Математическая формулировка теории случайностей основывается на концепции вероятности, которая появилась во Франции в середине XVII века, а именно в переписке между Блезом Паскалем и Пьером Ферма в 1654 году, связанной с проблемами, поставленными Антуаном Гомбо, известным как шевалье де Мере. Этот человек был алчным игроком, играл весьма азартно и хотел, чтобы Паскаль объяснил результаты определенных игр в кости.
Блез Паскаль (1623–1662), французский математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счетной техники, автор основного закона гидростатики.
Пьер Ферма (1601–1665), французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист. Блестящий полиглот. Главная заслуга Ферма — создание теории чисел. Самое знаменитое утверждение —Великая теорема Ферма: для любого натурального числа n > 2 уравнение xn + yn = zn не имеет натуральных решений x, y и z. Теорема была сформулирована им в 1637 году, на полях книги «Арифметика» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы привести его на полях.
Пьер Симон Лаплас (1749–1827), французский астроном, математик, физик. Автор классического сочинения «Аналитическая теория вероятностей» (1812), в котором ученый обобщил всё, что было сделано в теории вероятностей до него Паскалем, Ферма и Я.Бернулли. Благодаря ему теория вероятностей приобрела законченный вид. Лаплас был также приверженцем абсолютного детерминизма. Он постулировал, что, если бы какое-нибудь разумное существо смогло узнать положения и скорости всех частиц в мире в некий момент, оно могло бы совершенно точно предсказать все мировые события. Такое гипотетическое существо впоследствии было названо демоном Лапласа (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей).
Следует помнить: при расчете вероятности того, что событие произойдет, применяется следующее правило: Р (событие) = благоприятные случаи/возможные случаи, то есть определение количества раз, которые может произойти событие, и деление его на общее количество возможных случаев (здесь Р – вероятность события).
Что такое вероятность выигрыша? Рассмотрим три различных цветных кубика. У красного на гранях расположены числа 2, 4 и 9, причем каждое число использовано по два раза. На синем — числа 3, 5 и 7, и они также использованы дважды. На белом — числа 1, 6 и 8, и точно так же повторяются по два раза, как и на других кубиках. В игре участвуют двое, поочередно выбирающие и бросающие кубик. Выигрывает тот, кто наберет больше очков.
Это покажется удивительным, но второй игрок всегда может бросить кубик, который обеспечивает большую вероятность выигрыша. Как такое возможно? Какой кубик следует выбрать? Несмотря на то, что числа на всех кубиках при сложении дают одну и ту же сумму, здесь получается нечто странное. Синий кубик побеждает красный, белый побеждает синий, а красный побеждает белый. Во всех парах, при девяти бросках, в среднем в пяти из них победит тот, кто бросал кубик вторым.
Игровое шоу. Существует телевизионное игровое шоу, где одно из испытаний включает попытку найти спрятанный за дверью приз. Участнику показывают три двери и просят выбрать наугад одну (не открывая ее). Ведущий, который знает, за какой именно дверью спрятан приз, открывает одну из двух оставшихся дверей — ту, за которой приза точно нет. Затем игрока спрашивают, не хочет ли он поменять изначально выбранную дверь на оставшуюся. Если игрок соглашается поменять дверь, станет ли у него больше шансов на получение приза?
Когда участник выбирает одну из дверей, вероятность обнаружения приза составляет 1/3. Когда ведущий выбирает одну из двух оставшихся дверей (ту, за которой нет приза) и открывает ее, вероятность приза за первой дверью не меняется, поскольку уже известно, что за одной дверью приза нет. Однако вероятность в случае другой невыбранной двери (той, которая всё еще остается закрытой) меняется с 1/3 до 2/3 (вероятности в отношении двух остающихся закрытыми дверей должны складываться в единицу). Таким образом, участнику всегда следует менять двери, чтобы увеличить вероятность выигрыша до 2/3. (Любопытно, что описанный подход широко используется в карточной игре бридж. Там он известен как Принцип ограниченного выбора.)
Один из самых важных факторов для принятия решений в играх, где присутствует элемент случайности, — это то, что называют «математическим ожиданием». Пусть Е1, Е2, Е3 …En будут события, которые не могут произойти одновременно и которые возникают в игре с элементом случайности, каждое с вероятностью р1, р2, р3 … рn (где р1 + р2 + р3 + … + pn = 1), с соответствующими результатами r1, r2, r3, … rn. Ожидаемые выигрыши, или «математическое ожидание» (М) от игры (или случайного эксперимента), где результатом должно быть одно из событий Е1, Е2, Е3 …En, определяется как
М = p1 х г1 + p2 х r2 + p3 х r3 + … + pn x rn
Игра, где делаются ставки, считается сбалансированной, если математическое ожидание (средний выигрыш) равно сделанной на игру ставке.
ГЛАВА 4. ТЕОРИЯ ИГР
Теория игр — это область математики, которая, в основном, занимается принятием решений. Она применяется во всех ситуациях, где присутствует конфликт, где его участники должны принять наиболее благоприятные для себя решения, не зная решений, принятых оппонентами. Наука эта основывается на абстрактных играх (отсюда и происхождение названия), хотя на самом деле ее интересуют вовсе не игры. Просто теория игр применяет игровые идеи для анализа и решения всех видов задач.
Антагонистической (она же «игра с нулевой суммой») называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.
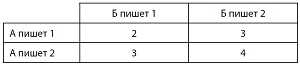
Чтобы ознакомиться с основами теории игр, давайте рассмотрим чрезвычайно простую ситуацию. Два человека, А и Б, должны одновременно написать или число один, или число два. Игрок Б должен заплатить игроку А сумму в рублях, полученную при сложении двух чисел, написанных каждым. Это очевидно не сбалансированная игра, так как А будет всегда выигрывать. Однако зададимся вопросом, как должен играть каждый из игроков в соответствии со своими интересами. Давайте представим игру как таблицу, известную под названием «матрица выигрыша» (платежная матрица), со следующими возможными результатами:
Рис. 3. Матрица выигрыша (1)
Числа в матрице показывают сумму в рублях, которую Б должен выплатить А, в зависимости от стратегии, выбранной каждым игроком (две возможности для каждого из игроков дают четыре результата в матрице). Учитывая простоту игры, становится очевидным, что если каждый игрок играет в своих собственных интересах, то А напишет два, а Б напишет 1. Это означает, что прибыль А составит три рубля.
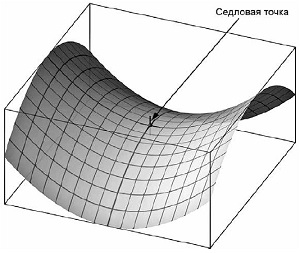
Учитывая, что А не знает шаг Б, он должен предположить, что Б будет играть так, чтобы свести к минимуму сумму, которую должен заплатить, то есть если А напишет один, то получит минимально два рубля, а если напишет два, то получит минимально три рубля. Говорят, что 3 (число в нижней левой ячейке) — это максимин (максимум минимумов). Точно также Б предполагает, что А будет играть так, чтобы получить максимальную прибыль, а это означает, что если Б напишет один, то потеряет максимально три рубля, а если напишет два, то потеряет максимально четыре рубля. Говорят, что 3 — это минимакс (минимум максимумов). Когда максимин и минимакс находятся в одной и той же ячейке для данной игры, говорят, что игра «строго детерминирована» (игра с полной информацией) и имеет «седловую точку» (рис. 4).
Рис. 4. Седловая точка
Значение, соответствующее этой седловой точке (в рассмотренном случае 3), — это «цена игры», и эта величина получается всегда, когда игрок выбирает оптимальную для себя стратегию.
Если один из двух игроков сделает другой ход (применит другую стратегию), то оппонент сможет увеличить цену игры, получить больше или потерять меньше, в зависимости от того, который это игрок, А или Б. Также говорят, что это детерминированная игра, для которой существует «чистая стратегия».
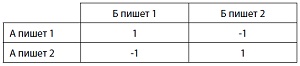
Давайте теперь рассмотрим похожую игру, но с другой матрицей выигрыша и несколько иными условиями: если оба написали одно и то же число, то А выигрывает рубль; если числа разные, то рубль в кармане у Б (рис. 5).
Рис. 5. Матрица выигрыша (2)
Теперь максимин А — это –1 (оба минимума составляют –1), в то время как минимакс Б — это 1 (оба максимума составляют 1). Разница означает, что в этой игре отсутствует седловая точка, а поэтому нет чистой стратегии. Если А выбирает определенную стратегию (например, всегда писать один) и это поймет Б, то он будет систематически писать два и всегда выигрывать рубль.
Учитывая простоту игры и ее симметрию, оптимальной стратегией должна быть та, которая включает пропорциональное количество единиц и двоек, чтобы оппонент не мог идентифицировать схему. По сути, оптимальная стратегия состоит в игре наугад, типа подбрасывания монетки (писать единицу, если выпадает орел, и двойку, если выпадает решка). При таких обстоятельствах невозможно говорить о чистых стратегиях, поскольку присутствующий элемент случайности означает, что игра не может быть детерминирована заранее. Когда оптимальная стратегия требует использования случайности и должна оставаться в секрете, говорят о «смешанных стратегиях».
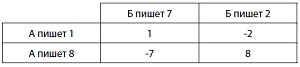
Определение оптимальной смешанной стратегии. Рассмотрим игру. Каждый игрок может написать одно из двух чисел: А может написать или 1, или 8; а Б — или 7, или 2. Если оба числа, написанные игроками, являются четными или оба являются нечетными, то А побеждает и получает сумму в рублях, равную своему написанному числу. Если же одно число четное, а второе нечетное, сумму, равную своему числу, получает Б (рис. 6).
Рис. 6. Матрица выигрыша (3)
Мы видим, что, как кажется, игра дает равные возможности обоим игрокам (А может выиграть рубль или восемь, а Б может выиграть два рубля или семь). Седловой точки нет: максимин составляет –2, а минимакс составляет 1.
Поэтому чистой стратегии для каждого игрока не существует. Давайте посмотрим, удастся ли нам установить смешанную стратегию, которая позволит определить цену игры. Смешанная стратегия требует внесения определенного элемента случайности в набор чистых стратегий. Она строится путем определения вероятности каждой чистой стратегии, которая связана с частотой, с которой используется каждая чистая стратегия.
Например, в нашем случае у А есть две чистые стратегии (написать 1 или написать 8) у Б их тоже две. Если знать шансы и выплаты по каждому случаю, это определит ожидаемую цену игры. Вначале нам надо определить вероятности, которые А должен приписать двум своим чистым стратегиям. Давайте решим, что р — это вероятность написать 8, поэтому 1–р — вероятность написать 1.
Таким образом, если Б выбирает стратегию написания 7, ожидаемая величина (V) для игрока А составит: V = 1 (1–p) + (–7)p = 1 – 8p. С другой стороны, если Б выбирает стратегию написания 2, ожидаемая величина для А получается: V = (–2)*(1 – p) + 8p = 10p – 2. Игрок А хочет определить р, чтобы получить самую высокую возможную ожидаемую величину, независимо от стратегии, выбранной игроком Б. Решение системы уравнений дает величину р и V для игрока А. В этом случае p = 1/6, а V = 1/3.
Мы можем рассчитать смешанную стратегию для игрока Б в той же манере. Пусть р будет вероятность написания 2, тогда вероятность написания 7 окажется (1 – р). Если А выбирает стратегию написания 1, ожидаемая величина для Б будет: V = 2p + (–1)*(1 – p) = 3p – 1. Точно так же, если А, выбирая другую стратегию, пишет 8, ожидаемая величина для Б составит: V = (–8)p + 7 (1 – p) = 7 – 15p. Игрок Б хочет определить р, чтобы получить самую высокую возможную ожидаемую величину, независимо от стратегии, выбранной игроком А. Используя эту систему, получаем величину р и V для игрока Б. В данном случае решение двух уравнений дает: p = 4/9 и V = 1/3.
Применяемый здесь метод может быть обобщен в матрице 2 х 2 и позволяет находить решение в играх, у которых нет седловой точки, используя смешанные стратегии.
Давайте теперь более подробно проанализируем значение результатов, которые были получены. Во-первых, можно заметить, что ожидаемая величина одна и та же для А и Б (V = 1/3), меняется только знак — для А величина отрицательная, а это означает, что А проиграет, в то время как для Б положительная, а это означает, что Б получит то, что проиграет А.
В целом цена игры (среднее равновесие для А) дается в выражении: (ad — bc)/(a + d — b — c), где a, b, c, d — это величины платежной матрицы (слева направо, сверху вниз). Таким образом, в нашем случае цена игры составит: (8 – 14)/18 = –6/18 = –1/3, что показывает, что, при условии, что оба игрока играют в соответствии с оптимальной для них стратегией, А, в среднем, каждые три игры будет терять рубль.
Смешанные стратегии для А и Б также можно определить и непосредственно по матрице выигрыша. Например, соотношение, используя которое, А должен выбирать ту или иную чистую стратегию, получается путем принятия в расчет его прибылей или убытков для каждой строки. Вот расчеты: 1 – (–2) = 3 (первая строка) и –7 – 8 = –15 (вторая строка). Из них становится ясно, что оптимальная стратегия для А — играть наугад с соотношением 15 к 3 или, в итоге, 5 к 1 в пользу написания 1. К примеру, бросать кубик, на пяти гранях которого стоит 1, а на одной 8. Обратите внимание, что этот результат согласуется с полученным путем решения системы уравнений и обнаружения, что вероятность написания 8 должна быть 1/6, и, таким образом, вероятность написания 1 должна быть 5/6.
Аналогично, игрок Б, на этот раз проведя расчеты по столбикам (первый столбик: 1 – (–7) = 8; второй столбик: –2 – 8 = –10), должен играть наугад с соотношением 10 к 8 или, в итоге, 5 к 4 в пользу написания 7 вместо 2. Этот результат согласуется с системой уравнений, решенных выше, что дает вероятность 4/9 для написания 2 и, соответственно, 5/9 для написания 7.
Теперь можно сформулировать оптимальную смешанную стратегию для каждого игрока: А придется наугад выбирать между написанием 1 (с вероятностью 5/6) или 8 (вероятность 1/6). Точно так же Б необходимо гадать между написанием 7 (с вероятностью 5/9) или 2 (вероятность 4/9).
Наконец, даже при отсутствии седловой точки, возможно, если каждый игрок выберет оптимальную для себя смешанную стратегию, обеспечить в среднем выигрыш Б в размере 33 копейки за игру. Если Б выберет другую стратегию, а А ничего не изменит, то прибыли Б уменьшатся. Однако если Б будет придерживаться своей оптимальной смешанной стратегии, а А изменит свою, потери А увеличатся.
ГЛАВА 5. ИГРА «ЖИЗНЬ»: ТЕОРИЯ И РЕАЛЬНЫЙ МИР
В предыдущей главе выигрыши одного игрока всегда были эквивалентны потерям другого, отсюда и термин «игра с нулевой суммой». Есть ситуации, где пользу обеим сторонам может принести сотрудничество. Это требует введения элементов коммуникации, связи и взаимного доверия, но также подразумевает и наличие угроз, которые проистекают из слепого исполнения всех заключенных договоров. Помните, что теория игр сконцентрирована на принятии решений, и этот аспект теперь становится более важным, чем когда-либо раньше. Во многих ситуациях, которые мы рассмотрим в этой главе, возникает необходимость выбора между соперничеством и совместной работой.
В целом, взаимное сотрудничество приведет к прибыли для обоих, и это лучший общий исход, в то время как взаимная конфронтация приведет к убыткам. Если бы имелись только эти две возможности, то не было бы и дилеммы. Однако возникает проблема, когда один из игроков пытается сотрудничать, а второй выбирает конфронтацию. Это приводит к увеличению прибыли для вероломного игрока, и она оказывается большей, чем можно было бы получить при взаимном сотрудничестве. В этом, собственно, и суть дилеммы. Сложность игр такого типа означает, что решения строго математическими не являются.
Впервые математические аспекты и приложения теории были изложены Джоном фон Нейманом и Оскаром Моргенштерном. Огромный вклад в развитие этой науки внес Джон Нэш (1928–2015). В 1949 году он пишет диссертацию по теории игр, за которую через сорок пять лет получает Нобелевскую премию по экономике. В 1998 году американская писательница и журналистка Сильвия Назар издала книгу о судьбе Джона Нэша, а в 2001 по мотивам книги был снят фильм «Игры разума». Большим вкладом в применение теории игр стала работа Томаса Шеллинга, нобелевского лауреата по экономике 2005 г., Стратегия конфликта. Понятие игры встречается в концепции Эрика Бёрна Игры, в которые играют люди, люди, которые играют в игры. Это сугубо психологические игры, основанные на трансакционном анализе.
В Советском Союзе игры использовались в семинарах Г. П. Щедровицкого, основоположника организационно-деятельностного подхода. Во время «Перестройки» Г. П. Щедровицкий провел множество игр с управленцами. По психологическому накалу ОДИ (организационно-деятельностные игры) были так сильны, что служили мощным катализатором изменений в СССР (см. Георгий Щедровицкий. Системное движение и перспективы развития системно-структурной методологии).
Ястребы и голуби. Джон Мейнард Смит (1920–2004) предложил так называемую дилемму «ястребы и голуби». Когда два зверя борются за добычу, для обоих нормально демонстрировать агрессивное отношение и использовать силу, чтобы победить противника. Если противостояние вот-вот должно перейти в драку, есть две возможности: бросить добычу и сбежать (голуби), то есть оставить добычу и остаться в живых; или сражаться (ястребы) с непредсказуемым исходом, который вполне может привести к смерти. Анализируя стратегию игры, Смит показал, что и популяция, состоящая исключительно из «ястребов», и популяция, состоящая только из «голубей», будут эволюционно нестабильны. Смешанная стратегия с 8/13 ястребов и 5/13 голубей даст эволюционно стабильное сообщество, то есть поможет избежать излишнего количественного увеличения, как ястребов, так и голубей.