Пожалуй, это наиболее известное произведение лорда Бертрана Артура Уильяма Рассела (1872–1970), оставившего яркий след в английской и мировой философии, логике, социологии, политической жизни. Вслед за Г.Фреге он вместе с А.Уайтхедом предпринял попытку логического обоснования математики (см. Принципы математики). Б.Рассел является основоположником английского неореализма, как разновидности неопозитивизма. Б.Рассел не признавал ни материализм, ни религию. Бертран Рассел очень широко цитируется, и когда я встретил не менее 10 ссылок в прочитанных мною книгах, я решил, что настал черед вгрызться в этот немаленький труд…
Бертран Рассел. Человеческое познание, его сферы и границы. – Киев: Ника-Центр, 2001. – 560 с. (На английском языке книга впервые вышла в 1948 г.)
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon (на момент публикации заметки книга отсутствовала в продажа)
ЧАСТЬ ПЕРВАЯ. МИР НАУКИ
ГЛАВА 1. ИНДИВИДУАЛЬНОЕ И ОБЩЕСТВЕННОЕ ПОЗНАНИЕ. Научное познание стремится стать абсолютно безличным и пытается утверждать то, что открыто коллективным разумом человечества.
Существует два способа узнать, что обозначает слово: один — путем определения значения слова при помощи других слов, что называется вербальным определением; другой — частое слышание слова в присутствии объекта, который оно обозначает, что называется наглядным определением. Вследствие этого значение, которое ребенок должен связать со словом, является продуктом его личного опыта и имеет различия в соответствии с обстоятельствами и его воспринимающей способностью. Ребенок, который часто видит мелкий моросящий дождь, свяжет со словом «дождь» другую идею, чем ребенок, который видел только тропические ливни.
Правда, образование ведет — и не без успеха — к обезличиванию языка.
ГЛАВА 2. ВСЕЛЕННАЯ АСТРОНОМИИ. Около конца пятого века до нашей эры пифагорейцы открыли, что Земля является сферическим телом; около сотни лет спустя Эратосфен определил диаметр Земли с точностью до пятидесяти миль (подробнее см. Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе).
Средневековый христианский космос скроен из некоторых элементов поэтической фантазии, которые язычество сохранило до конца. Как научные, так и поэтические элементы средневекового космоса получили выражение в Рае Данте. Именно против этой картины вселенной выступали пионеры новой астрономии. Интересно сопоставить шум, созданный вокруг Коперника, с почти полным забвением, которое выпало на долю Аристарха.
Теория Солнца и планет как законченная система была практически завершена Ньютоном. Вопреки Аристотелю и средневековым философам она показала, что Солнце, а не Земля является центром солнечной системы; что небесные тела, предоставленные самим себе, двигались бы по прямым линиям, а не по кругам; что фактически они движутся не по прямым линиям и не по кругам, а по эллипсам и что никакое действие извне не является необходимым для поддержания их движения. Но в отношении происхождения солнечной системы Ньютон не сказал ничего научного.
Общая теория относительности считает, что вселенная имеет конечные размеры — не в том смысле, что она имеет край, за которым находится нечто, что не является уже частью вселенной, но что она является сферой, имеющей три измерения, в которой самые прямые из возможных линий возвращаются со временем к исходному пункту, как на поверхности Земли. Теория предусматривает, что вселенная должна быть или сжимающейся, или расширяющейся; она использует наблюденные факты относительно туманностей для решения вопроса в пользу расширения. Согласно Эддингтону, вселенная удваивается в размерах каждые 1300 миллионов лет или около того. Если это так, то вселенная была некогда совсем маленькой, но будет со временем довольно большой (к моменту написания книги – 1948 г. – концепция Большого взрыва еще не стала доминирующей).
ГЛАВА 3. МИР ФИЗИКИ. Самой прогрессирующей наукой в наши дни, причем такой, которая, по-видимому, бросает больше всего света на структуру мира, является физика. Эта наука по-настоящему начинается с Галилея. Галилей и — в меньшей степени — Декарт ввели основные понятия и принципы, которые вполне удовлетворяли физику до настоящего столетия. Казалось, что законы движения одни и те же для всех видов мертвой материи, а, возможно, также и для живой. Декарт считал, что животные являются автоматами и что их движения могут быть теоретически вычислены с помощью тех же принципов, которые управляют падающим куском свинца. Научная ортодоксия сочла возможным согласиться со взглядом Лапласа, что вычислитель, обладающий достаточными математическими способностями и данными о положении, скорости и массе каждой частицы во вселенной в определенный момент времени, может вычислить все прошлое и будущее физического мира (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей).
Галилей ввел два принципа, которые содействовали возможности математической физики: закон инерции и закон параллелограмма. Аристотель думал, что планеты нуждаются в богах, которые двигали бы их по их орбитам, и что движения на земле могли самостоятельно начаться у животных. Движения в материи, согласно этому взгляду, могут быть объяснены только из нематериальных причин. Закон инерции изменил это воззрение и сделал возможным исчисление движений материи посредством одних только законов динамики. Закон параллелограмма в формулировке Ньютона касается того, что происходит с телом, когда на него действуют сразу две силы.
Со времени Ньютона и до конца XIX века прогресс физики не дал никаких существенно новых принципов. Первой революционной новостью было введение Планком квантовой постоянной h в 1900 году. Взгляд Ньютона касался аппарата динамики и имел, как он указывал, эмпирические основания для его предпочтения. Если вода в ведре вращается, она поднимается по стенкам ведра, а если вращается ведро, в то время как вода находится в покое, поверхность воды остается плоской. Мы можем поэтому различать вращение воды и вращение ведра, что мы не могли бы делать, если бы вращение было относительным. Эйнштейн показал, как можно избежать заключения Ньютона и сделать пространственно-временное положение чисто относительным.
Общая теория относительности содержит в своих уравнениях то, что называется «космической постоянной», которая определяет размер вселенной в любое время. Согласно этой теории, вселенная конечна, но безгранична, как в трехмерном пространстве поверхность сферы. Все это подразумевает неевклидову геометрию и может показаться загадочным тем, чье воображение связано с геометрией Евклида (подробнее см. Леонард Млодинов. Евклидово окно). Размер вселенной измеряется числом между 6000 и 60 000 миллионов световых лет, но размеры вселенной удваиваются приблизительно через каждые 1300 миллионов лет. Во всем этом, однако, вполне можно сомневаться.
Квантовые уравнения отличаются от уравнений классической физики в весьма важном отношении, а именно в том, что они «нелинейны». Это значит, что если вы открыли действие только одной причины, а затем действие только другой причины, то вы не можете найти действие их обеих посредством складывания двух определенных порознь действий. Получается очень странный результат.
Теория относительности и эксперименты показали, что масса не постоянна, как считалось раньше, а при быстром движении увеличивается; если бы частица могла двигаться со скоростью света, ее масса стала бы бесконечно большой. Квантовая теория осуществила еще большее посягательство на понятие «массы». Теперь оказывается, что везде, где энергия теряется в результате ее излучения, имеется также и соответствующая потеря массы. Считается, что Солнце теряет свою массу со скоростью четыре миллиона тонн в секунду.
ГЛАВА 4. БИОЛОГИЧЕСКАЯ ЭВОЛЮЦИЯ. Человечеству оказалось гораздо труднее встать на научную точку зрения в отношении жизни, чем в отношении небесных тел. Если то, что говорит Библия, понимать буквально, то мир был создан в 4004 году до нашей эры. Краткость времени, допускаемого книгой Бытия, была сначала самым серьезным препятствием для научной геологии. Все прежние битвы между наукой и теологией в этой области померкли перед лицом великой битвы по вопросу эволюции, которая началась с опубликования в 1859 году «Происхождения видов» Дарвина, и которая все еще не окончилась в Америке (с момента написания книги ситуация в США, наверное, только ухудшилась; см., например, Менее половины американцев верят в теорию Дарвина).
Благодаря теории Менделя процесс наследования стал более или менее понятным. Согласно этой теории, в яйце и в сперме имеется определенное, но очень небольшое число «генов», которые несут в себе наследственные черты (подробнее см. Ричард Докинз. Эгоистичный ген, Ричард Докинз. Слепой часовщик. Как эволюция доказывает отсутствие замысла во Вселенной). Учение об эволюции теперь пользуется общим признанием. Но особая движущая сила, допущенная Дарвином, именно борьба за существование и выживание наиболее приспособленного, сейчас не так популярна среди биологов, как пятьдесят лет назад. Теория Дарвина была распространением на жизнь в целом экономического принципа laisser-faire; теперь, когда этот вид экономики, как и соответствующий ей вид политики, вышел из моды, люди предпочитают другие способы объяснения биологических изменений.
Нет основания предполагать, что живая материя управляется другими законами, чем неживая материя, и имеются серьезные основания думать, что все в поведении живой материи может теоретически быть объяснено в терминах физики и химии (такой подход называется редукционизмом; его критику см. Даглас Хофштадтер, Дэниел Деннетт. Глаз разума).
ГЛАВА 5. ФИЗИОЛОГИЯ ОЩУЩЕНИЯ И ВОЛЕНИЯ. С точки зрения ортодоксальной психологии существуют две границы между миром психическим и физическим, именно — ощущение и воление. «Ощущение» может быть определено как первое психическое действие физической причины, «воление» — как последняя психическая причина физического действия.
Проблема отношения между сознанием и материей, относящаяся к области философии, касается перехода от явлений в мозгу к ощущению и от воления к другим явлениям в мозгу. Это, таким образом, двойная проблема: как материя воздействует на сознание в ощущении и как сознание воздействует на материю в волении?
Имеется два вида нервных волокон, одни проводящие раздражение к мозгу и другие — проводящие импульс от него. Первые связаны с физиологией ощущения.
Может ли процесс в мозгу, связывающий поступление сенсорного возбуждения с отправлением импульса к мускулам, быть полностью выражен в физических терминах? Или здесь необходимо прибегнуть к «психическим» посредникам — таким, как ощущение, размышление и воление?
Имеются рефлексы, в которых ответ является автоматическим и не контролируется волением. Условных рефлексов достаточно, чтобы объяснить большую часть человеческого поведения; имеется ли в нем остаток, который не может быть объяснен таким образом, — это вопрос, который в настоящее время остается открытым.
ГЛАВА 6. НАУКА О ДУХЕ. Психологии как науке повредило то, что ее связывали с философией. Различие между духом и материей, которое не проводилось резко досократиками, получило особое значение у Платона. Постепенно различение души и тела, которое сначала было неясной метафизической тонкостью, стало частью общепризнанного мировоззрения, и только немногие метафизики в наше время осмеливаются сомневаться в нем. Картезианцы усилили абсолютность этого различения путем отрицания всякого взаимодействия между мыслью и материей. Но за их дуализмом последовала монадология Лейбница, согласно которой все субстанции суть души. Во Франции в XVIII веке, появились материалисты, которые отрицали душу и утверждали существование только материальной субстанции. Среди великих философов один Юм отрицал всякую субстанцию вообще и тем самым указал путь для современных споров о различии между психическим и физическим.
Психологию можно определить, как науку о таких явлениях, которые по самой их природе могут наблюдаться только самим испытывающим их лицом. Часто бывает, однако, такое близкое сходство между одновременными восприятиями разных людей, что на ничтожные различия можно для многих целей не обращать внимания; в таких случаях мы говорим, что все эти люди воспринимают одно и то же явление, и мы относим такое явление к миру общественному, но не личному. Такие явления суть данные физики, тогда как явления, не имеющие такого общественного характера, являются (как я полагаю) данными психологии.
Это определение встречает серьезные возражения со стороны психологов, которые считают, что «самонаблюдение» не является настоящим научным методом и что ничто не может быть научным способом познано, за исключением того, что получено из общественных данных. «Общественные» данные — это такие, которые вызывают одинаковые ощущения у всех воспринимающих их лиц. Между общественными и личными данными трудно провести определенную границу. Я прихожу к выводу, что существует знание личных данных и что нет оснований отрицать существование науки о них.
Существуют ли какие-либо причинные законы, которые действуют только в сознании. Если такие законы существуют, то психология есть автономная наука. Например, психоанализ стремится к раскрытию чисто психических причинных законов. Но я не знаю ни одного психоаналитического закона, который претендовал бы на предсказание того, что будет происходить всегда при таких-то и таких-то обстоятельствах. Хотя в настоящее время трудно привести сколько-нибудь значительные примеры действительно точных психических причинных законов, все же кажется совершенно несомненным на основе обыденного здравого смысла, что такие законы существуют.
ЧАСТЬ ВТОРАЯ. ЯЗЫК
ГЛАВА 1. УПОТРЕБЛЕНИЕ ЯЗЫКА. Языком главным образом служит средством высказывания утверждений и передачи информации, но это только одна и, возможно, не самая основная его функция. Язык может служить для выражения эмоций или для того, чтобы влиять на поведение других. Каждая из этих функций; может быть выполнена, хотя и с меньшим успехом, при помощи доречевых средств.
Язык имеет две первичные функции: функцию выражения и функцию коммуникации. В обыкновенной речи обычно присутствуют оба элемента. Коммуникация состоит не только в передаче информации; в нее должны быть включены приказы и вопросы. Язык имеет два взаимосвязанных достоинства: первое — то, что он социален, и второе — что он является для общества средством выражения «мыслей», которые иначе остались бы личным достоянием.
Имеются два других очень важных употребления языка: он дает нам возможность вести наши дела с внешним миром посредством знаков (символов), которые имеют (1) определенную степень постоянства во времени и (2) значительную степень дискретности в пространстве. Каждое из этих достоинств больше проявляется в письме, чем в устной речи.
ГЛАВА 2. НАГЛЯДНОЕ ОПРЕДЕЛЕНИЕ может быть определено как «процесс, благодаря которому человек любым способом, исключая употребление других слов, научается понимать какое-либо слово». Имеются две ступени в процессе усвоения иностранного языка: первая — когда вы понимаете его только благодаря переводу на свой язык, и вторая — когда вы умеете уже «думать» на иностранном языке. Знание языка имеет два аспекта: пассивный — когда вы понимаете то, что слышите, активный — когда вы сами можете говорить. Пассивная сторона наглядного определения есть хорошо известный акт ассоциации, или условного рефлекса. Если определенный стимул А производит у ребенка определенную реакцию R и часто связывается со словом В, то со временем произойдет, что B будет производить реакцию R или какую-либо ее часть. Как только это произойдет, слово В приобретет для ребенка «значение»: оно уже будет «значить» А.
Активная сторона изучения языка требует других способностей. Для каждого ребенка является открытием, что существуют слова, то есть звуки со значением. Учиться произносить слова для ребенка является приносящей удовольствие игрой, особенно потому, что эта игра дает ему возможность сообщать свои желания более определенно, чем посредством криков и жестов. Именно благодаря этому удовольствию ребенок и проделывает ту умственную работу и мускульные движения, которые необходимы, чтобы научиться говорить.
ГЛАВА 3. СОБСТВЕННЫЕ ИМЕНА. Существует традиционное различение между «собственными» именами и именами «классов»; это различение объясняется тем, что собственные имена относятся только к одному объекту, тогда как имена классов относятся ко всем объектам определенного рода, как бы многочисленны они ни были. Так, «Наполеон» есть собственное имя, а «человек» — имя класса.
ГЛАВА 4. ЭГОЦЕНТРИЧЕСКИЕ СЛОВА. Я называю «эгоцентрическими словами» те слова, значение которых изменяется с переменой говорящего и его положения во времени и пространстве. Четырьмя основными словами этого рода являются «я», «это», «здесь» и «теперь».
ГЛАВА 5. ЗАДЕРЖАННЫЕ РЕАКЦИИ: ПОЗНАНИЕ И ВЕРА. Допустим, что вы собираетесь предпринять завтра железнодорожное путешествие, а сегодня ищете в расписании поездов ваш поезд; вы не предполагаете в этот момент как-либо использовать полученное вами знание, но, когда наступит время, вы будете действовать соответствующим образом. Познание в том смысле, в каком оно является не только регистрацией настоящих чувственных впечатлений, состоит главным образом из приготовлений для таких задержанных реакций. Такие приготовления во всех случаях могут быть названы «верой» и называются «знанием» только в том случае, когда они обещают успешные реакции или по крайней мере оказываются связанными с относящимися к ним фактами таким образом, что их можно отличить от приготовлений, которые можно было бы назвать «ошибками».
Другим примером является трудность, которую испытывают необразованные люди в отношении гипотез. Если вы им говорите: «Предположим то-то и то-то и посмотрим, что следует из этого предположения», — то такие люди или будут иметь тенденцию поверить в ваше предположение, или будут думать, что вы просто зря тратите ваше время. Поэтому reductio ad absurdum является непонятной формой аргументации для тех, кто не знаком с логикой или математикой; если доказывается ложность гипотезы, они оказываются не в состоянии условно принять гипотезу.
ГЛАВА 6. ПРЕДЛОЖЕНИЯ. Слова, которые обозначают объекты, можно назвать «изъявительными» словами. В число таких слов я включаю не только имена, но и слова, обозначающие качества, например: «белый», «твердый», теплый», а также слова, обозначающие воспринимаемые отношения, такие, как «до», «над», «в». Если бы единственным назначением языка было описание чувственных фактов, то мы довольствовались бы одними изъявительными словами. Но такие слова не достаточны для выражения сомнения, желания или неверия. Они также не достаточны для выражения логических связей, например: «Если это так, то я съем свою шляпу» или: «Если бы Вильсон был тактичнее, то Америка присоединилась бы к Лиге Наций».
ГЛАВА 7. ОТНОШЕНИЕ ИДЕЙ И ВЕРОВАНИЙ К ВНЕШНЕМУ. Отношение идеи или образа к чему-то внешнему заключается в вере, которая, будучи выявлена, может быть выражена в словах: «Это имеет прототип». При отсутствии такой веры, даже при наличии действительного прототипа, отношения к внешнему не бывает. Тогда это случай чистого воображения.
ГЛАВА 8. ИСТИНА И ЕЁ ЭЛЕМЕНТАРНЫЕ ФОРМЫ. Для того, чтобы определить «истину» и «ложь», мы должны выйти за пределы предложений и рассмотреть, что они «выражают» и что «изъявляют». Предложение обладает свойством, которое я буду называть «смыслом (значением)». То, что отличает истину от лжи, нужно искать не в самих предложениях, а в их значениях. Некоторые предложения, кажущиеся с первого взгляда вполне правильно построенными, являются на самом деле абсурдными в том смысле, что они не имеют смысла (значения). Например, «Нужда есть мать изобретения» и «Постоянное откладывание крадет время».
То, что утверждаемое предложение выражает, есть вера, то, что делает его истинным или ложным, есть факт, который в общем отличен от веры. Истина и ложь связаны с отношением к внешнему; это значит, что никакой анализ предложения или веры не скажет, истинно оно или ложно.
Предложение формы «Это есть A» называется «истинным», когда оно вызвано тем, что «A» обозначает. Мы можем сказать, кроме того, что предложение формы «это было A» или «Это будет A» «истинно», если предложение «Это есть A» было или будет истинно в указанном смысле. Это относится ко всем предложениям, утверждающим то, что есть, было или будет фактом восприятия, а также и к тем, в которых мы правильно выводим из восприятия его обычные сопутствующие обстоятельства посредством свойственной животным способности к выводу. По поводу нашего определения «значения» и «истины» можно высказать одно важное соображение, а именно то, что и то и другое зависит от понимания понятия «причины».
ГЛАВА 9. ЛОГИЧЕСКИЕ СЛОВА И ЛОЖЬ. Мы исследуем предложения тех видов, которые могут быть доказаны или опровергнуты, когда известны соответствующие данные, полученные из наблюдений. Когда речь идет о таких предложениях, мы больше не должны рассматривать отношение веры или предложений к чему-то, что не является в общем ни верой, ни предложением; вместо этого мы должны рассмотреть только синтаксические отношения между предложениями, в силу которых достоверная или вероятная истина, или ложь определенного предложения вытекает из истины или лжи определенных других предложений.
В таких выводах имеются определенные слова, из которых одно или больше всегда принимают участие в выводе и которые я буду называть «логическими» словами. Эти слова бывают двух видов, которые могут быть названы соответственно «союзами» и «общими словами», хотя и не совсем в обычном грамматическом смысле. Примерами союзов являются: «не», «или», «если — то». Примерами общих слов служат: «все» и «некоторые».
С помощью союзов мы можем делать различные простые выводы. Если «P» истинно, то «не — P» ложно, если «P» ложно, то «не — P» истинно. Если «P» истинно, то «P или q» истинно; если «q» истинно, то «P или q» истинно. Если «P» истинно и «q» истинно, то «P и q» истинно. И так далее. Предложения, содержащие союзы, я буду называть «молекулярными» предложениями; при этом соединяемые «P» и «q» понимаются как «атомы». При истинности или ложности атомарных предложений истинность или ложность каждого молекулярного предложения, составленного из этих атомарных предложений, следует по синтаксическим правилам и не требует нового наблюдения фактов. Мы здесь действительно находимся в царстве логики.
Когда высказывается изъявительное предложение, мы имеем дело с тремя моментами: во-первых, в рассмотренных случаях имеет место познавательное отношение утверждающего — вера, неверие и колебание; во-вторых, имеется содержание, обозначаемое предложением, и, в-третьих, имеется факт (или факты), в силу которого предложение является истинным или ложным, и который я называю «фактом-верификатором (verifier)» или «фактом-фальсификатором (falsifier)» предложения.
ГЛАВА 10. ОБЩЕЕ ПОЗНАНИЕ. Под «общим познанием» я имею в виду познание истинности или ложности предложений, содержащих слово «все», или слово «некоторые», или логические эквиваленты этих слов. Можно было бы думать, что слово «некоторые» означает меньшую степень общности, чем слово «все», но это было бы ошибкой. Это явствует из того, что отрицанием предложения со словом «некоторые» является предложение со словом «все», и наоборот. Отрицанием предложения: «Некоторые люди бессмертны» является предложение: «Все люди смертны», а отрицанием предложения: «Все люди смертны» является предложение: «Некоторые люди бессмертны». Из этого явствует, насколько трудно опровергать предложения со словом «некоторые» и, соответственно, доказывать предложения со словом «все».
ГЛАВА 11. ФАКТ, ВЕРА, ИСТИНА И ПОЗНАНИЕ. Факт, в моем понимании этого термина, может быть определен только наглядно. Все, что имеется во вселенной, я называю «фактом». Солнце — факт; переход Цезаря через Рубикон был фактом; если у меня болит зуб, то моя зубная боль есть факт. Большинство фактов не зависит от нашего воления, поэтому они называются «суровыми», «упрямыми», «неустранимыми».
Вся наша познавательная жизнь является с биологической точки зрения частью процесса приспособления к фактам. Этот процесс имеет место, в большей или меньшей степени, во всех формах жизни, но называется «познавательным» только тогда, когда достигает определенного уровня развития. Поскольку не существует резкой границы между низшим животным и самым выдающимся философом, постольку ясно, что мы не можем сказать точно, в каком именно пункте мы переходим из сферы простого поведения животного в сферу, заслуживающую по своему достоинству наименования «познание».
Вера проявляется в утверждении предложения. Понюхав воздух, вы восклицаете: «Боже! В доме пожар!» Или, когда затевается пикник, вы говорите: «Посмотрите на тучи. Будет дождь». Я склонен думать, что иногда чисто телесное состояние может заслуживать названия «веры». Например, если вы входите в темноте в вашу комнату, а кто-то поставил кресло на необычное место, вы можете наткнуться на кресло потому, что ваше тело верило, что в этом месте нет кресла.
Истинность есть свойство веры и, как производное, свойство предложений, выражающих веру. Истина заключается в определенном отношении между верой и одним или более фактами, иными, чем сама вера. Когда это отношение отсутствует, вера оказывается ложной. Нам нужно описание факта или фактов, которые, если они действительно существуют, делают веру истинной. Такой факт или факты я называю «фактом-верификатором (verifier) «веры.
Знание состоит, во-первых, из определенных фактических данных и определенных принципов вывода, причем ни то, ни другое не нуждается в постороннем свидетельстве, и, во-вторых, из всего того, что может утверждаться посредством применения принципов вывода к фактическим данным. По традиции считается, что фактические данные поставляются восприятием и памятью, а принципы вывода являются принципами дедуктивной и индуктивной логики.
В этой традиционной доктрине много неудовлетворительного. Во-первых, эта доктрина не дает содержательного определения «познания». Во-вторых, очень трудно сказать, что представляют собой факты восприятия. В-третьих, дедукция оказалась гораздо менее мощной, чем это считалось раньше; она не дает нового знания, кроме новых форм слов для установления истин, в некотором смысле уже известных. В-четвертых, методы вывода, которые можно назвать в широком смысле слова «индуктивными», никогда не были удовлетворительно сформулированы.
ЧАСТЬ ТРЕТЬЯ. НАУКА И ВОСПРИЯТИЕ
ГЛАВА 1. ПОЗНАНИЕ ФАКТОВ И ПОЗНАНИЕ ЗАКОНОВ. Когда мы исследуем нашу веру в фактические данные, мы находим, что иногда она основывается непосредственно на восприятии или воспоминании, а в других случаях — на выводе. Один и тот же внешний стимул, проникая в мозг двух людей с различным опытом, произведет различные результаты, и только то, что есть общего в этих различных результатах, может быть использовано для выводов о внешних причинах. Нет никаких оснований верить, что наши ощущения имеют внешние причины.
ГЛАВА 2. СОЛИПСИЗМ. Учение, называемое «солипсизм», обычно определяется как вера в то, что только один я существую. Мы можем различить две формы солипсизма. Догматический солипсизм говорит: «Ничего нет, кроме данных опыта», а скептический говорит: «Неизвестно, чтобы существовало что-нибудь ещё, кроме данных опыта». Солипсизм может быть и более и менее радикальным; когда он становится более радикальным, он становится и более логичным и в то же самое время более неправдоподобным.
Будда был доволен тем, что он мог размышлять, когда вокруг него рычали тигры; но, если бы он был последовательным солипсистом, он считал бы, что рычание тигров прекратилось, как только он перестал замечать его. В отношении воспоминаний результаты этой теории оказываются чрезвычайно странными. Вещи, которые я вспоминаю в один момент, оказываются совершенно отличными от тех, которые я вспоминаю в другой момент, но радикальный солипсист должен допустить только те, которые я вспоминаю сейчас.
ГЛАВА 3. ВЕРОЯТНЫЕ ВЫВОДЫ ОБЫДЕННОГО ЗДРАВОГО СМЫСЛА. «Вероятный» вывод – есть такой вывод, в котором предпосылки верны и построение правильно, а заключение тем не менее не достоверно, а только в большей или меньшей степени вероятно. В практике науки применяются два вида выводов: выводы чисто математические и выводы, которые можно назвать «субстанциальными». Вывод из законов Кеплера закона тяготения в его применении к планетам является математическим, а вывод законов Кеплера из отмеченных видимых движений планет является субстанциальным, так как законы Кеплера не являются единственными гипотезами, логически согласующимися с наблюденными фактами.
Донаучное познание выражается в выводах обыденного здравого смысла. Мы не должны забывать различия между выводом, как он понимается в логике, и тем выводом, который можно назвать «анимальным». Под «анимальным выводом» я имею в виду то, что происходит, когда некое событие А оказывается причиной веры В без какого-либо вмешательства сознания.
Если в жизни данного организма A часто сопровождалось B, то A будет одновременно или в быстрой последовательности сопровождаться «идеей» B, то есть импульсом к действиям, которые могли бы стимулироваться B. Если A и B эмоционально интересны для организма, то даже одного случая их связи может быть достаточно для образования привычки; если нет, то может понадобиться много случаев. Связь числа 54 с умножением 6 на 9 для большинства детей представляет ничтожный эмоциональный интерес; отсюда проистекает трудность изучения таблицы умножения.
Другой источник познания – словесное свидетельство, которое оказывается очень важным, именно в том, что оно помогает научиться отличать общественный мир чувств от личного мира мысли, который уже хорошо устанавливается, когда начинается научное мышление. Однажды я читал лекцию большой аудитории, когда какая-то кошка пробралась в помещение и улеглась у моих ног. Поведение аудитории убедило меня в том, что это не была моя галлюцинация.
ГЛАВА 4. ФИЗИКА И ОПЫТ. С самых ранних времен существует два типа теорий восприятия: один — эмпирический и другой — идеалистический.
Мы видим, что физические теории все время изменяются и что не найдется разумного представителя науки, который ожидал бы, что физическая теория останется неизменной в течение сотни лет. Но в силу того, что теории изменяются, это изменение обычно мало дает нового в отношении наблюдаемых явлений. Практическая разница между теориями тяготения Эйнштейна и Ньютона — ничтожна, хотя теоретическая разница между ними очень велика. Более того, в каждой новой теории имеются отдельные части, которые являются, по-видимому, вполне достоверными, тогда как другие остаются чисто умозрительными. Введение Эйнштейном пространства-времени вместо пространства и времени представляет собой изменение языка, основанием для которого, как и для коперниковского изменения языка, является его упрощение. Эта часть теории Эйнштейна может быть принята без всяких колебаний. Однако взгляд, что вселенная является трехмерной сферой и имеет конечный диаметр, остается умозрительным; никто не удивится, если найдутся основания, которые заставят астрономов отказаться от этого способа выражения.
Нашим основным вопросом является: если физика истинна, то как это можно установить и что, помимо физики, должны мы знать, чтобы её вывести? Эта проблема встает благодаря физическому причинению восприятия, которое делает вероятным допущение, что физические объекты значительно отличаются от восприятия; но если это действительно так, то как мы можем выводить физические объекты из восприятий? Более того, поскольку восприятие рассматривается как «психическое» событие, в то время как его причина считается «физической», мы сталкиваемся со старой проблемой отношения между духом и материей. Мое собственное мнение таково, что «психическое» и «физическое» не так отделены друг от друга, как обычно думают. Я определил бы «психическое» событие как такое, которое познается без помощи вывода; поэтому различие между «психическим» и «физическим» относится к теории познания, а не к метафизике.
Одной из трудностей, приведших к путанице, было неразличение перцептуального пространства и физического пространства. Перцептуальное пространство состоит из воспринимаемых отношений между частями восприятия, тогда как физическое пространство состоит из выведенных отношений между выведенными физическими вещами. То, что я вижу, может быть вне моего восприятия моего тела, но не вне моего тела как физической вещи.
Восприятия, рассматриваемые в причинном ряду, возникают между событиями, происходящими в центростремительных нервах (стимул) и событиями в центробежных нервах (реакция), их положение в причинных цепях то же самое, что и положение определенных событий в мозгу. Восприятия как источник познания физических объектов могут выполнять свое назначение только постольку, поскольку в физическом мире существуют отдельные, более или менее независимые друг от друга причинные цепи. Все это только приблизительно, и поэтому вывод от восприятий к физическим объектам не может быть вполне точным. Наука в значительной мере состоит из средств для преодоления этого первоначального недостатка точности на основе предположения, что восприятие дает первое приближение к истине.
ГЛАВА 5. ВРЕМЯ В ОПЫТЕ. Имеются два источника нашего познания времени. Одним из них является восприятие следования в течение одного являющегося настоящего, другим является воспоминание. Воспоминание может восприниматься и имеет качество большей или меньшей отдаленности, благодаря чему все мои настоящие воспоминания располагаются в хронологическом порядке. Но это — субъективное время, и его следует отличать от исторического времени. Историческое время имеет к настоящему отношение «предшествования», которое я знаю, как переживания изменения в течение одного являющегося настоящего. В историческом времени все мои настоящие воспоминания имеют место теперь. Но, если они правдивы, они указывают на события, имевшие место в историческом прошлом. Нет никаких логических оснований считать, что воспоминания должны быть правдивы; с логической точки зрения можно доказать, что все мои настоящие воспоминания могли бы быть совершенно таким же и в том случае, если бы никогда не было никакого исторического прошлого. Таким образом, наше познание прошедшего зависит от некоего постулата, который не может быть раскрыт простым анализом наших настоящих воспоминаний.
ГЛАВА 6. ПРОСТРАНСТВО В ПСИХОЛОГИИ. Когда я имею переживание, называемое «видением стола», видимый стол имеет прежде всего положение в пространстве моего мгновенного зрительного поля. Затем посредством имеющихся в опыте корреляций он получает положение в пространстве, — охватывающем все мои восприятия. Далее посредством физических законов он коррелятивно связывается с каким-либо местом в физическом пространстве-времени, именно с местом, занимаемым физическим столом. Наконец посредством физиологических законов он относится к другому месту в физическом пространстве-времени, именно к месту, занимаемому моим мозгом как физическим объектом. Если философия пространства хочет избежать безнадежной путаницы, она должна тщательно проводить грани между этими различными корреляциями. Следует заметить, что двойственное пространство, в котором заключаются восприятия, находится в отношении очень близкой аналогии к двойственному времени воспоминаний. В субъективном времени воспоминания относятся к прошедшему; в объективном времени они имеют место в настоящем. Подобным же образом в субъективном пространстве воспринимаемый мною стол находится там, а в физическом пространстве он находится здесь.
ГЛАВА 7. ДУХ И МАТЕРИЯ. Я утверждаю, что в то время, как психические явления и их качества могут быть познаны без выводов, физические явления познаются только в отношении их пространственно-временной структуры. Качества, присущие таким явлениям, непознаваемы, — настолько совершенно непознаваемы, что мы не может даже сказать, отличаются или не отличаются они от качеств, которые мы знаем, как принадлежащие психическим явлениям.
ЧАСТЬ ЧЕТВЕРТАЯ. НАУЧНЫЕ ПОНЯТИЯ
ГЛАВА 1. ИНТЕРПРЕТАЦИЯ. Часто случается, что мы имеем как будто достаточное основание верить в истинность какой-либо формулы, выраженной в математических символах, хотя и не можем дать ясного определения этик символов. В других случаях бывает также, что мы можем придать несколько различных значений символам, каждое из которых делает формулу истинной. В первом случае у нас нет даже и одной определенной интерпретации нашей формулы, тогда как во втором случае мы имеем много интерпретаций.
Пока мы остаемся в области арифметических формул, различные интерпретации «числа» равно хороши. И только тогда, когда мы начинаем эмпирическое употребление чисел в перечислении, мы находим основание для предпочтения одной интерпретации всем другим. Такая ситуация возникает всякий раз, когда математика применяется к эмпирическому материалу. Возьмем, например, геометрию. Если геометрия должна применяться к чувственно воспринимаемому миру, то мы должны найти определения точек, линий, плоскостей и так далее в терминах чувственных данных или же мы должны быть в состоянии вывести из чувственных данных существование невоспринимаемых сущностей, имеющих такие свойства, в которых нуждается геометрия. Нахождение путей или пути к выполнению того или другого является проблемой эмпирической интерпретации геометрии.
ГЛАВА 2. МИНИМАЛЬНЫЕ СЛОВАРИ. Как правило, существует несколько способов, с помощью которых слова, употребляемые в науке, могут быть определены небольшим числом терминов из числа этих слов. Эти немногие термины могут иметь или наглядные, или номинальные определения с помощью слов, не принадлежащих к данной науке. Такой набор начальных слов я называю «минимальным словарем» данной науки, если только (a) каждое иное слово, употребляемое в науке, имеет номинальное определение с помощью слов этого минимального словаря и (b) ни одно из этих начальных слов не имеет номинального определения с помощью других начальных слов.
В качестве примера возьмем географию. При этом я буду исходить из того, что словарь геометрии уже установлен; тогда нашей первой явно географической потребностью является метод установления широты и долготы. По-видимому, только два слова — «Гринвич» и «Северный полюс» необходимы для того, чтобы сделать географию наукой о поверхности Земли, а не какого-либо другого сфероида. Именно благодаря наличию этих двух слов (или двух других, служащих той же цели) география может рассказать об открытиях путешественников. Именно эти два слова участвуют везде, где упоминаются широта и долгота. Как показывает этот пример, наука, по мере того как она становится более систематической, нуждается во все меньшем и меньшем минимальном словаре.
ГЛАВА 3. СТРУКТУРА. Выявить структуру объекта — значит упомянуть его части и способы, с помощью которых они вступают во взаимоотношения. Структура всегда предполагает отношения: простой класс как таковой не имеет структуры. Из членов какого-либо данного класса может быть построено много структур, как множество различных видов домов может быть построено из какой-либо данной кучи кирпичей.
ГЛАВА 4. СТРУКТУРА И МИНИМАЛЬНЫЕ СЛОВАРИ. Каждое открытие структуры позволяет нам уменьшить минимальный словарь, необходимый для данного содержания предмета. Химия раньше нуждалась в именах для всех элементов, но теперь различные элементы могут быть определены в терминах атомной структуры с помощью двух слов: «электрон» и «протон».
ГЛАВА 6. ПРОСТРАНСТВО В КЛАССИЧЕСКОЙ ФИЗИКЕ. В элементарной геометрии прямые линии определяются в целом; их главной характеристикой является то, что прямая линия определена, если даны две ее точки. Возможность рассмотрения расстояния как прямолинейного отношения между двумя точками зависит от предположения, что существуют прямые линии. Но в современной геометрии, приспособившейся к нуждам физики, нет прямых линий в евклидовом смысле, и «расстояние» определяется двумя точками только тогда, когда они расположены очень близко друг к другу. Когда две точки расположены далеко друг от друга, мы должны сначала решить, по какому маршруту мы будем двигаться от одной к другой, и затем сложить много мелких отрезков этого маршрута. «Самой прямой» линией между этими двумя точками будет та, в которой сумма отрезков будет минимальной. Вместо прямых линий мы должны употреблять здесь «геодезические линии», которые являются более короткими маршрутами от одной точки к другой, чем любые другие отличающиеся от них маршруты. Это нарушает простоту измерения расстояний, которое становится зависимым от физических законов.
ГЛАВА 7. ПРОСТРАНСТВО-ВРЕМЯ. Эйнштейн вместо понятий пространства и времени ввел понятие пространства-времени. «Одновременность» оказывается неопределенным понятием, когда оно применяется к событиям, происходящим в разных местах. Эксперименты, особенно эксперимент Майкельсона-Морли, ведут к заключению, что скорость света является постоянной для всех наблюдателей, как бы они ни двигались. Имеется, однако, одно отношение между двумя событиями, которое оказывается одним и тем же для всех наблюдателей. Прежде было два таких отношения — расстояние в пространстве и промежуток времени; теперь же есть только одно, называемое «интервалом». Именно благодаря тому, что есть только одно это отношение интервала вместо расстояния и промежутка времени, мы должны вместо двух понятий — понятия пространства и понятия времени ввести одно понятие пространства-времени.
ГЛАВА 8. ПРИНЦИП ИНДИВИДУАЦИИ. Как определяем мы то различие, которое заставляет нас различать два объекта в перечне? По этому вопросу защищались с некоторым успехом три взгляда.
- Особенное образуется благодаря качествам; когда все его качества перечислены, оно полностью определено. Таков взгляд Лейбница.
- Особенное определяется его пространственно-временным положением. Это взгляд Фомы Аквинского в отношении материальных субстанций.
- Числовое различие является конечным и неопределимым, Таковы, как я думаю, были бы взгляды самых современных эмпириков, если бы они позаботились иметь по этому вопросу определенный взгляд.
Вторая из упомянутых трех теорий сводится или к первой, или к третьей в соответствии с тем, как она интерпретируется.
ГЛАВА 9. ПРИЧИННЫЕ ЗАКОНЫ. Практическая польза науки зависит от ее способности предвидеть будущее. «Причинный закон», как я буду употреблять этот термин, может быть определен как главный принцип, в силу которого — если имеются достаточные данные об определенной области пространства-времени — можно сделать какой-то вывод об определенной другой области пространства-времени. Вывод может быть только вероятным, но эта вероятность должна быть значительно больше половины, если интересующий нас принцип заслуживает названия «причинного закона».
Если закон устанавливает высокую степень вероятности, он может быть почти столь же удовлетворительным, как если бы он устанавливал достоверность. Например, статистические законы квантовой теории. Такие законы, даже если допустить, что они вполне истинны, делают выводимые на основе их события только вероятными, но это не мешает считать их причинными законами, согласно вышеприведенному определению.
Причинные законы бывают двух видов: одни, касающиеся постоянства, и другие, касающиеся изменений. Первые часто не рассматриваются как причинные, но это неверно. Хорошим примером закона постоянства является первый закон движения. Другим примером является закон постоянства материи.
Причинные законы, касающиеся изменения, были открыты Галилеем и Ньютоном и сформулированы с помощью ускорения, то есть изменения скорости по величине, или направлению, или по тому и другому. Величайшим триумфом этой точки зрения был закон тяготения, согласно которому каждая частица материи вызывает в каждой другой ускорение, прямо пропорциональное массе притягивающей частицы и обратно пропорциональное квадрату расстояния между ними. Основными законами изменения в современной физике являются законы квантовой теории, которые управляют переходом энергии из одной формы в другую. Атом может испускать энергию в форме света, который затем двигается без изменений, пока не встретится с другим атомом, который может поглотить энергию света. Все, что (как мы думаем) мы знаем о физическом мире, целиком зависит от допущения, что причинные законы существуют.
Научный метод состоит в изобретении гипотез, соответствующих данным опыта, которые являются настолько простыми, насколько это совместимо с требованием соответствия опыту, и которые делают возможным выведение заключений, подтверждаемых затем наблюдением.
Если не существует предела сложности возможных законов, то всякий воображаемый ход событий будет подчиняться законам, и тогда допущение о существовании законов станет тавтологией. Возьмем, например, номера всех такси, которые я нанимал в течение моей жизни, и моменты времени, когда я нанимал их. Мы получим конечный ряд целых чисел и конечное число соответствующих моментов времени. Если n есть номер такси, которое я нанял в момент времени t, то бесконечным числом способов безусловно можно найти такую функцию f, что формула n = f(t) будет истинной для всех значений n и f, которые до сего времени имели место. Бесконечное число этих формул окажется неверным в отношении следующего такси, которое я найму, но все еще будет бесконечное число таких, которые останутся истинными.
Достоинство этого примера для моей настоящей цели заключается в его явной абсурдности. В том смысле, в котором мы верим в естественные законы, мы сказали бы, что не существует закона, связывающего n и t вышеприведенной формулы, и что если какая-либо из предложенных формул окажется действенной, то это будет просто делом случая. Если бы мы нашли формулу, действенную для всех случаев, вплоть до настоящего времени, то мы не ждали бы, что она будет действенной в следующем случае. Только суеверный человек, действующий под влиянием эмоций, поверит в такого рода индукцию; игроки в Монте-Карло прибегают к индукциям, которые, однако, ни один ученый не одобрит.
ЧАСТЬ ПЯТАЯ. ВЕРОЯТНОСТЬ
ГЛАВА 1. ВИДЫ ВЕРОЯТНОСТИ. Попытки создать логику вероятности были многочисленны, но против большинства из них выдвигались роковые для них возражения. Одной из причин ошибочности этих теорий было то, что они не различали — или, скорее, намеренно смешивали — в корне различные понятия, которые в обычном словоупотреблении имеют одинаковое право называться словом «вероятность».
Первым весьма значительным фактом, который мы должны взять в расчет, является существование математической теории вероятности. Есть одно очень простое понятие, которое удовлетворяет требованиям аксиом теории вероятности. Если дан конечный класс В, имеющий n членов, и если известно, что количество m из них принадлежит к какому-то другому классу A, то мы говорим, что если выбрать наудачу какой-либо член класса В, то шанс, что он будет принадлежать к классу А, будет равен числу m/n.
Есть, однако, два афоризма, которые все мы склонны принимать без особой проверки, но которые, если их принять, предполагают такую интерпретацию «вероятности», которую, по-видимому, нельзя примирить с вышеприведенными определениями. Первым из этих афоризмов является изречение епископа Батлера, что «вероятность есть руководитель жизни». Вторым является положение, что все наше знание только вероятно, на чем особенно настаивал Рейхенбах.
Когда, как это обычно бывает, я не уверен в том, что должно произойти, но должен действовать в соответствии с той или иной гипотезой, мне обычно и вполне правильно советуют выбирать наиболее вероятную гипотезу и всегда правильно советуют учитывать степень вероятности при принятии решения.
Вероятность, являющаяся руководителем жизни, не относится к математическому виду вероятности не только потому, что она относится не к произвольным данным, а ко всем данным, которые с самого начала имеют отношение к вопросу, но также и потому, что она должна учитывать нечто целиком лежащее вне сферы математической вероятности, что можно назвать «внутренне присущей сомнительностью».
Если мы утверждаем, как это делает Рейхенбах, что все наше знание сомнительно, то мы не можем определить эту сомнительность математическим путем, ибо при составлении статистики уже предполагается, что мы знаем, что А есть или не есть В, что этот застрахованный человек умер или что он жив. Статистика строится на структуре предположенной достоверности прошедших случаев, и всеобщая сомнительность не может быть только статистической.
Я думаю поэтому, что все, во что мы склонны верить, имеет какую-то «степень сомнительности» или, наоборот, какую-то «степень правдоподобия». Иногда это бывает связано с математической вероятностью, а иногда нет; это более широкое и более неопределенное понятие.
Я думаю, что каждое из обоих различных понятий имеет на основе обычного употребления равное право называться «вероятностью». Первое из них является математической вероятностью, которая поддается числовому измерению и удовлетворяет требованиям аксиом исчисления вероятности.
Но существует и другой вид, который я называю «степенью правдоподобия». Этот вид применим к отдельным предложениям и всегда связан с учетом всех относящихся к делу свидетельств. Он применим даже в некоторых таких случаях, в которых нет никакого известного свидетельства. Именно этот вид, а не математическая вероятность подразумевается, когда говорят, что все наше познание только вероятно и что вероятность есть руководитель жизни.
ГЛАВА 2. ИСЧИСЛЕНИЕ ВЕРОЯТНОСТИ. Теорию вероятности как ветвь чистой математики, мы выводим из определенных аксиом, не стараясь приписать им ту или иную интерпретацию. Следуя Джонсону и Кейнсу, мы будем обозначать выражением p/h неопределенное понятие «вероятность p при данном h». Когда я говорю, что это понятие является неопределенным, я имею в виду, что оно определяется только с помощью аксиом или постулатов, которые должны быть перечислены. Все, что удовлетворяет требованиям этих аксиом, является «интерпретацией» исчисления вероятности, и следует думать, что здесь возможно множество интерпретаций.
Необходимые аксиомы:
- Если даны p и h, то существует только одно значение p/h. Мы поэтому можем говорить о «данной вероятности p при данном h».
- Возможные значения выражения p/h суть все действительные числа от 0 до 1, включая и то и другое.
- Если h имеет значение p, то p/h=1 (мы употребляем «1» для обозначения достоверности).
- Если h имеет значение не-p, то p/h=0 (мы употребляем «0» для обозначения невозможности).
- Вероятность p и q при данном h есть вероятность p при данном h, помноженная на вероятность q при данных p и h, и является также вероятностью q при данном h, помноженной на вероятность p при данных q и h. Эта аксиома называется «конъюнктивной».
- Вероятность p и q при данном h есть вероятность p при данном h плюс вероятность q при данном h минус вероятность p и q при данном h. Это называется «дизъюнктивной» аксиомой.
Важно иметь в виду, что наше основное понятие p/h является отношением двух предложений (или конъюнкцией предложений), а не свойством одного предложения p. Это отличает вероятность, каковой она является в математическом исчислении, от вероятности, которой руководствуются в практике, так как последняя должна относиться к предложению, взятому само по себе.
Аксиома V есть «конъюнктивная» аксиома. Она имеет дело с вероятностью того, что каждое из двух событий произойдет. Например, если я буду тянуть из колоды две карты, то каков шанс, что обе окажутся красными? Здесь «h» представляет собой данное, что колода состоит из 26 красных и 26 черных карт; «p» обозначает, что «первая карта красная», а «q» – что «вторая карта красная». Тогда (p и q)/h» есть шанс, что обе карты будут красные, «p/h «есть шанс, что первая — красная, «q / (p и h)» есть шанс, что вторая красная, при условии, что первая — красная. Ясно, что p/h =1/2, q (p и h) =25/51. Очевидно, согласно аксиоме, шанс, что обе карты будут красные, равен 1/2х25/51.
Аксиома VI есть «дизъюнктивная» аксиома. В вышеприведенном примере она дает шанс, что по крайней мере одна из карт будет красная. Она говорит, что шанс, что по крайней мере одна будет красная, есть шанс, что первая красная, плюс шанс, что вторая — красная (когда не дано, будет ли первая красной или не будет), минус шанс, что обе — красные. Это равняется 1/2+1/2 – 1/2х25/51.
Из конъюнктивной аксиомы следует, что
Это называется «принципом обратной вероятности». Ее полезность может быть иллюстрирована следующим образом. Пусть p будет какой-либо общей теорией, а q — экспериментальным данным, относящимся к p. Тогда p/h есть вероятность теории p в отношении ранее известных данных, q/h — вероятность q в отношении ранее известных данных и q (p и h) — вероятность q, если p истинно. Таким образом, вероятность теории p после того, как q установлено, получается посредством умножения прежней вероятности p на вероятность q при данном p и деления на прежнюю вероятность q. В самом благоприятном случае теория p будет предполагать q, так что q/(p и h) =1. В этом случае
Это значит, что новое данное q повышает вероятность p пропорционально предшествующей невероятности q. Другими словами, если наша теория предполагает нечто весьма неожиданное, а это неожиданное затем происходит, то это сильно повышает вероятность нашей теории.
Этот принцип может быть иллюстрирован открытием Нептуна, рассматриваемым как подтверждение закона тяготения. Здесь p — закон тяготения, h — все относящиеся к делу факты, известные до открытия Нептуна, q — факт обнаружения Нептуна в определенном месте. Тогда q/h было предварительной вероятностью, что до сего времени неизвестная планета будет найдена в определенной небольшой области неба. Пусть она была равна m/n. Тогда после открытия Нептуна вероятность закона тяготения стала в n/m раз большей, чем раньше. Ясно, что этот принцип имеет большое значение в оценке роли нового свидетельства в пользу вероятности научной теории.
Существует имеющее большое значение предложение, иногда называемое теоремой Бейеса, которая имеет следующий вид (подробнее см. Идеи Байеса для менеджеров). Пусть р1, р2, …, рn будут n взаимно исключающих друг друга возможностей, причем известно, что какая-то одна из них истинна; пусть h будет означать общие данные, а q — какой-либо относящийся к делу факт. Мы хотим узнать вероятность одной возможности p, при данном q, когда мы знаем вероятность каждого р1 до того, как стало известным q, a также вероятность q при данном р1 для каждого r. Мы имеем [1]
Это предложение позволяет нам решить, например, следующую задачу: дано n+1 сумок, из которых первая содержит n черных шаров и ни одного белого, вторая содержит n–1 черных шаров и один белый; r+1-я сумка содержит n–r черных шаров и r белых. Берется одна сумка, но неизвестно, какая именно; из нее вынимается m шаров, и оказывается, что все они белые; какова вероятность, что взята была сумка r? Исторически эта задача важна в связи с претензией Лапласа на доказательство индукции.
Возьмем, далее, закон больших чисел Бернулли. Этот закон устанавливает, что если на каждое число случаев шанс наступления определенного события есть p, то при данных любых двух сколько угодно малых числах δ и ε шанс, что, начиная с достаточно большого числа случаев, отношение случаев наступления события всегда будет отличаться от p больше, чем на величину ε, будет меньше, чем δ.
Поясним это с помощью примера с бросанием монеты. Допустим, что выпадение лицевой и оборотной сторон монеты одинаково вероятно. Это значит, что, по-видимому, после достаточно большого количества бросаний отношение выпадений лицевой стороной никогда не будет отличаться от 1/2 больше, чем на величину ε, как бы мала ни была эта величина ε; далее, как бы s не было мало, где бы то ни было после n бросаний, шанс такого отклонения от 1/2 будет меньше δ, если только n достаточно большое.
Так как это предложение имеет большое значение в приложениях теории вероятности, например, в статистике, постараемся получше освоиться с точным смыслом того, что утверждается в вышеприведенном примере с бросанием монеты. Прежде всего я утверждаю, что, начиная с определенного числа их выпадения процент выпадения монеты лицевой стороной всегда будет, скажем, между 49 и 51. Допустим, что вы оспариваете мое утверждение и мы решаем проверить его эмпирически насколько только возможно. Значит, теорема утверждает, что чем дольше мы будем продолжать проверку, тем больше будет казаться, что мое утверждение порождено фактами и что по мере того, как число бросаний будет увеличиваться, эта его вероятность будет приближаться к достоверности как к пределу. Предположим, что с помощью этого эксперимента вы убеждаетесь, что, начиная с некоторого числа бросаний процент выпадения лицевой стороной всегда остается между 49 и 51, но теперь я утверждаю, что, начиная с некоторого большего числа бросаний этот процент будет всегда оставаться между 49,9 и 50,1. Мы повторяем наш эксперимент, и спустя некоторое время вы снова в этом убеждаетесь, хотя на этот раз, возможно, спустя большее время, чем прежде. После любого данного числа бросаний останется шанс, что мое утверждение не подтвердится, но этот шанс все время будет уменьшаться по мере того, как число бросаний будет увеличиваться, и может стать меньше любой приписанной ему величины, если бросание будет продолжаться достаточно долго.
Вышеприведенные предложения являются основными предложениями чистой теории вероятности, имеющими большое значение в нашем исследовании. Я хочу, однако, сказать еще кое-что по вопросу о a+1 сумках, каждая из которых содержит n белых и черных шаров, причем r+1-я сумка содержит r белых шаров и n–r черных шаров. Мы исходим из следующих данных: я знаю, что сумки содержат разные количества белых и черных шаров, но при этом нет никакого способа отличить эти сумки друг от друга по внешним признакам. Я выбираю одну сумку наудачу и вынимаю из нее один за другим m шаров, причем, вынимая эти шары, я не кладу их обратно в сумку. Оказывается, что все вынутые шары белые. Учитывая этот факт, я хочу знать две вещи: во-первых, каков шанс того, что я выбрал сумку, содержащую одни только белые шары? Во-вторых, каков шанс того, что следующий шар, который я выну, окажется белым?
Мы рассуждаем следующим образом. Путь h будет тот факт, что сумки имеют вышеописанный вид и содержание, а q — тот факт, что было вынуто m белых шаров; пусть также рr будет гипотеза, что мы выбрали сумку, содержащую r белых шаров. Очевидно, что r должно быть по крайней мере таким же большим, как и m, то есть если r меньше, чем m, то pr/qh=0 и q/prh=0. После некоторых вычислений оказывается, что шанс, что мы выбрали сумку, в которой все шары белые, равен (m+1)/(n+1).
Теперь мы хотим знать шанс, что следующий шар будет белым. После некоторых дальнейших вычислений оказывается, что этот шанс равен (m+1)/(m+2). Заметьте, что он не зависит от n и что если m велико, то он очень близок к 1.
ГЛАВА 3. ИНТЕРПРЕТАЦИЯ С ПОМОЩЬЮ ПОНЯТИЯ КОНЕЧНОЙ ЧАСТОТЫ. В этой главе нас интересует одна интерпретация «вероятности», которую я буду называть «теорией конечной частоты». Пусть В будет любой конечный класс, а A — любой другой класс. Мы хотим определить шанс, что член класса В, выбранный наудачу, будет членом класса А, например, что первый человек, которого вы встретите на улице, будет иметь фамилию Смит. Мы определяем эту вероятность как число членов класса В, являющихся также членами класса А, деленное на полное число членов класса В. Мы обозначаем это знаком А/В. Ясно, что вероятность, определяемая таким образом, должна быть или рациональной дробью, или 0, или 1.
Несколько примеров сделают ясным смысл этого определения. Каков шанс, что какое-либо целое число меньше 10, выбранное наудачу, будет простым числом? Существует 9 целых чисел меньше 10, и 5 из них являются простыми; следовательно, этот шанс равен 5/9. Каков шанс, что в прошлом году в Кембридже в день моего рождения шел дождь, в предположении, что вы не знаете, когда бывает день моего рождения? Если m есть число дней, когда шел дождь, то шанс равен m/365. Каков шанс, что человек, фамилия которого содержится в лондонской телефонной книге, носит фамилию Смит? Для решения этой задачи вы должны сначала сосчитать все записи в этой книге с фамилией «Смит», а затем сосчитать вообще все записи и разделить первое число на второе. Каков шанс, что карта, вытащенная наудачу из колоды, окажется пиковой масти? Ясно, что этот шанс равен 13/52, то есть 1/4. Если вы вытянули карту пиковой масти, то каков шанс, что следующая карта, которую вы вытащите, будет тоже пика? Ответ: 12/51. Каков шанс, что в бросании двух костей выпадет сумма 8? Имеется 36 комбинаций выпадения костей, и в 5 из них сумма будет равна 8, так что шанс выпадения суммы 8 равен 5/36.
Рассмотрим предполагаемое Лапласом оправдание индукции. Имеется N+1 сумок, каждая из которых содержит N шаров. Из этих сумок r+1-я содержит г белых шаров и N–r черных шаров. Мы вытащили из одной сумки n шаров, причем все они оказались белыми.
Каков шанс
- что мы выбрали сумку с одними лишь белыми шарами?
- что следующий шар окажется тоже белым?
Лаплас говорит, что (a) есть (n+1)/(N+1) и (b) есть (n+1)/(n+2). Иллюстрируем это несколькими числовыми примерами. Во-первых, допустим, что всего имеется 8 шаров, из которых вытащено 4, все белые. Каковы шансы (a), что мы выбрали сумку, содержащую только белые шары, и (b) что следующий вытащенный шар тоже окажется белым?
Пусть pr представляет собой гипотезу, что мы выбрали сумку с r белыми шарами. Эти данные исключают р0, р1, р2, р3. Если мы имеем p4, то имеется только один случай, когда мы могли вытащить 4 белых, и остается 4 случая вытащить черный и ни одного — белый. Если мы имеем р5, то есть 5 случаев, когда мы могли бы вытащить 4 белых, и для каждого из них был 1 случай вытащить следующий белый и 3 — вытащить черный; таким образом, из р5 мы получаем 5 случаев, где следующий шар будет белым, и 15 случаев, где он будет черным. Если мы имеем p6, то есть 15 случаев выбора 4 белых, а когда они вытащены, остается 2 случая выбрать один белый и 2 случая выбрать черный; таким образом, из p6 мы имеем 30 случаев получения следующего белого и 30 случаев, когда следующий будет черным. Если мы имеем p7, то есть 35 случаев вытащить 4 белых, а после того, как они будут вытащены, останется 3 случая вытащить белый и один — вытащить черный; таким образом, мы получаем 105 случаев вытащить следующий белый и 35 — вытащить черный. Если мы имеем p8, то есть 70 случаев вытащить 4 белых, а когда они будут вытащены, то есть 4 случая вытащить следующий белый и ни одного — вытащить черный; таким образом, из p8 мы получаем 280 случаев вынуть пятый белый и ни одного — вынуть черный. Суммируя, мы имеем 5+30+105+280, то есть 420 случаев, когда пятый шар является белым, и 4+15+30+35, то есть 84 случая, когда пятый шар является черным. Следовательно, разница в пользу белого составляет отношение 420 к 84, то есть 5 к 1; это значит, что шанс, что пятый шар окажется белым, равен 5/6.
Шанс, что мы выбрали сумку, в которой все шары белые, есть отношение числа случаев получения 4 белых шаров из этой сумки ко всему числу случаев получения 4 белых шаров. Первых, как мы видели, 70; вторых 1+5+15+35+70, то есть 126. Следовательно, шанс равен 70/126, то есть 5/9. Оба эти результата согласуются с формулой Лапласа.
Возьмем теперь закон больших чисел Бернулли. Мы можем иллюстрировать его следующим образом. Допустим, что мы бросаем монету n раз и пишем 1 всякий раз, кода выпадает ее лицевая сторона, и 2 — всякий раз, когда она выпадает оборотной стороной, образуя, таким образом число из n-го количества однозначных чисел. Предположим, что каждая возможная последовательность выпадает только один раз. Таким образом, если n = 2, то мы получим четыре числа: 11, 12, 21, 22; если n =3, то мы получим 8 чисел: 111, 112, 121, 122, 211, 212, 221, 222; если n=4, мы получим 16 чисел: 1111, 1112, 1121, 1122, 1212, 1221, 1222, 2111, 2112, 2121, 2122, 2211, 2221, 2222 и так далее
Беря последнее из вышеприведенного перечня, мы находим: 1 число со всеми единицами, 4 числа с тремя единицами и одной двойкой, 6 чисел с двумя единицами и двумя двойками, 4 числа с одной единицей и тремя двойками, t число со всеми двойками.
Эти числа — 1, 4, 6, 4, 1 — являются коэффициентами в разложении бинома (а + b)4. Легко доказать, что для n однозначных чисел соответствующие числа являются коэффициентами в разложении бинома (a + b)n. Теорема Бернулли сводится к тому, что если n является большим, то сумма коэффициентов около середины будет почти равна сумме всех коэффициентов (которая равна 2n), Таким образом, если мы возьмем все возможные последовательности выпадения лицевой и оборотной сторон в большом числе бросаний, то огромное большинство их будет иметь почти одинаковое число у обеих (то есть у лицевой и оборотной сторон); это большинство и приближение к полному равенству будет, кроме того, неопределенно увеличиваться по мере того, как будет увеличиваться число бросаний.
Хотя теорема Бернулли и является более общей и более точной, чем вышеприведенные положения с равно вероятными альтернативами, на все-таки должна интерпретироваться, согласно нашему настоящему определению «вероятности», способом, аналогичным вышеприведенному. Является фактом, что если мы составим все числа, которые состоят из 100 знаков, каждый из которых есть или 1, или 2, то около четверти из них будут иметь 49, или 50, или 51 знак, равный 1, почти половина будет иметь 48, или 49, или 50, или 51, или-52 знака, равных 1, более половины будет иметь от 47 до 53 знаков, равных 1, и около трех четвертей будет иметь от 46 до 54 знаков. По мере того как число знаков будет увеличиваться, будет возрастать и преобладание случаев, в которых единицы и двойки будут почти полностью уравновешиваться.
Я хочу разъяснить мой собственный взгляд в отношении связи математической вероятности с естественным ходом вещей в природе. Возьмем в качестве примера закон больших чисел Бернулли, выбрав самый простой из возможных случаев. Мы видели, что если мы соберем все возможные целые числа, состоящие из n знаков, каждое из которых будет или 1, или 2, то, если n является большим скажем, не меньшим, чем 1000,- огромное большинство возможных целых чисел будет иметь приблизительно одинаковое число единиц и двоек. Это есть только применение того факта, что при разложении бинома (х + у)n, когда n большое, сумма биномиальных коэффициентов около середины будет мало отличаться от суммы всех коэффициентов, каковая равна 2n. Но какое это имеет отношение к утверждению, что если я буду достаточно много раз бросать монету, то я, вероятно, получу приблизительно одинаковое число выпадений лицевой и оборотной сторон? Первое есть логический факт, второе, очевидно, является эмпирическим фактом; какова же связь между ними?
При некоторых интерпретациях «вероятности» утверждение, содержащее слово «вероятный», никогда не может быть эмпирическим утверждением. Признается, что то, что не является вероятным, может произойти, а то, что считается вероятным, может не произойти. Из этого следует, что то, что на самом деле происходит, не показывает, что прежнее суждение о вероятности было или правильным, или ложным; любой воображаемый ход событий логически совместим с любой предшествующей оценкой вероятности, какую только можно вообразить. Это можно отрицать только в том случае, если мы будем считать, что то, что в высокой степени невероятно, не происходит, чего мы не имеем права думать. В частности, если индукция утверждает только вероятности, тогда все то, что может произойти, логически совместимо как с истинностью, так и с ложностью индукции. Следовательно, индуктивный принцип не имеет эмпирического содержания. Это есть reductio ad absurdum и показывает, что мы должны связывать вероятное с действительным теснее, чем это иногда делается.
ГЛАВА 5. ТЕОРИЯ ВЕРОЯТНОСТЕЙ КЕЙНСА. Сочинение Кейнса «Трактат о вероятности» [2] выдвигает теорию, которая в некотором смысле является антитезой теории частоты. Он считает, что отношение, применяемое в дедукции, именно «p имплицирует q», есть крайняя форма отношения, которое может быть названо «p более или менее имплицирует q». «Если знание h, — говорит он, оправдывает рациональную веру в а степени α, то мы говорим, что имеется отношение вероятности степени α между а и h». Мы записываем это: a/h=α. «Между двумя рядами предложений существует отношение, в силу которого, если мы знаем первый, мы можем приписать второму некоторую степень рациональной веры». Вероятность, по существу, есть отношение: «Так же бесполезно говорить «b вероятно», как и «b равно» или «b больше, чем». Из «a» и «a имплицирует b» мы можем вывести «b»; это значит, что мы можем опустить всякое упоминание посылки и просто утверждать заключение. Но если а так относится к b, что знание а превращает вероятную веру в b в рациональную, то мы не можем вообще ничего заключить о b, которое не имеет отношения к а; нет ничего соответствующего опусканию истинной посылки в доказательном выводе. [3]
Я прихожу к выводу, что главный формальный недостаток теории вероятности Кейнса состоит в том, что он рассматривает вероятность, скорее, как отношение между предложениями, чем как отношение между пропозициональными функциями. Я сказал бы, что применение ее к предложениям относится к приложению теории, а не к самой теории.
ГЛАВА 6. СТЕПЕНИ ПРАВДОПОДОБИЯ
Хотя любая часть того, что мы хотели бы рассматривать как «знание», может быть в некоторой степени сомнительной, ясно, что кое-что почти достоверно, в то время как кое-что иное является продуктом рискованных предположений. Для разумного человека существует шкала сомнительности от простых логических и арифметических предложений и суждений восприятия на одном конце до таких вопросов, как вопрос о том, на каком языке говорили микенцы или «какую песню пели сирены», на другом конце. Любое предложение, в отношении которого у нас есть разумные основания для какой-то степени веры или неверия, может теоретически быть помещено на шкале между достоверной истиной и достоверной ложью.
Существует определенная связь между математической вероятностью и степенями правдоподобности. Связь эта следующая: когда в отношении всех доступных нам свидетельств какое-либо предложение имеет определенную математическую вероятность, тогда это определяет и степень его правдоподобия. Например, если вы собираетесь бросить кости, то предложение «выпадет двойная шестерка» имеет только одну тридцать пятую правдоподобия, приписываемого предложению «двойная шестерка не выпадет». Таким образом, разумный человек, приписывающий каждому предложению правильную степень правдоподобия, будет руководствоваться математической теорией вероятности в тех случаях, когда она применима. Понятие «степень правдоподобия», однако, применяется гораздо более широко, чем понятие математической вероятности.
Предложение, которое не является чем-то данным, может получить правдоподобие из многих различных источников; человек, который хочет доказать свою невиновность в преступлении, может аргументировать и исходя из алиби и из своего прежнего хорошего поведения. Основания в пользу научной гипотезы практически всегда являются сложными. Если признается, что какое-то данное может не быть достоверным, степень его правдоподобия может быть повышена каким-либо аргументом или, напротив, может быть весьма снижена каким-либо контраргументом. Степень правдоподобия, сообщаемая доказательством, не поддается простой оценке.
Я намереваюсь обсудить правдоподобие, во-первых, в отношении к математической вероятности, затем в отношении данных, затем в отношении субъективной уверенности и, наконец, в отношении к рациональному поведению.
Правдоподобие и частота. Обыденному здравому смыслу, по-видимому, ясно, что в типичных случаях математической вероятности она равна степени правдоподобия. Если я вытаскиваю наудачу карту из колоды, то степень правдоподобия предложения «карта будет красная» будет в точности равна степени правдоподобия предложения «карта будет не красная», и, следовательно, степень правдоподобия каждого предложения равна 1/3, если 1 представляет собой достоверность. В отношении игральной кости степень правдоподобия предложения «выпадет 1» совершенно та же, что и предложения «выпадет 2», или 3, или 4, или 5, или 6. Отсюда все выведенные частоты математической теории могут быть интерпретированы как выведенные степени правдоподобия.
В этом переводе математических вероятностей в степени правдоподобия мы пользуемся принципом, в котором математическая теория не нуждается. Этот принцип требуется только тогда, когда математическая вероятность рассматривается как мера правдоподобия.
Правдоподобие данных. Я определяю «данное» как предложение, которое само по себе имеет некоторую степень разумного правдоподобия, независимо от какого-либо доказательства, полученного из других предложений. Традиционный взгляд принят Кейнсом и изложен им в его «Трактате о вероятности». Он говорит: «Для того чтобы мы могли иметь рациональную веру в p, обладающего не достоверностью, а только той или иной степенью вероятности, необходимо, чтобы мы знали ряд предложений h, а также знали какое-либо вторичное предложение q, утверждающее отношение вероятности между p и h».
Степени субъективной достоверности. Субъективная достоверность — это психологическое понятие, тогда как правдоподобие, по крайней мере отчасти, является логическим. Различим три вида достоверности.
- Пропозициональная функция достоверна в отношении другой функции, когда класс членов, удовлетворяющих второй функции, есть часть класса членов удовлетворяющих первой функции. Например, «x есть животное» достоверно по отношению к «х есть разумное животное». Это значение достоверности относится к математической вероятности. Мы будет называть этот вид достоверности «логической» достоверностью.
- Предложение достоверно, когда оно имеет наивысшую степень правдоподобия, которое или внутренне присуще этому предложению, или является результатом доказательства. Может быть, ни одно предложение не является достоверным в этом смысле, то есть, каким бы достоверным оно ни было по отношению к знанию данного лица, дальнейшее познание может повысить степень его правдоподобия. Мы будем называть этот вид достоверности «эпистемологической».
- Человек уверен в предложении, когда он не чувствует никакого сомнения в его истинности. Это чисто психологическое понятие, и мы будем называть его «психологической» достоверностью.
Вероятность и поведение. Большинство этических теорий относится к одному из двух видов. Согласно первому виду, хорошее поведение — это такое поведение, которое повинуется определенным правилам; согласно второму, — это такое поведение, которое направлено на достижение определенных целей. Первый тип теории представлен Кантом и десятью заповедями ветхого Завета. Когда этика рассматривается как совокупность правил поведения, тогда вероятность не играет в ней никакой роли. Она приобретает значение только во втором типе этической теории, согласно которому добродетель состоит в стремлении к определенным целям.
ГЛАВА 7. ВЕРОЯТНОСТЬ И ИНДУКЦИЯ. Проблема индукции сложна, имеет различные аспекты и ответвления.
Индукция через простое перечисление представляет собой следующий принцип: «Если дано некоторое число n случаев а, которые оказались p, и если при этом не оказалось ни одного а, которое не было бы p, тогда два утверждения: (а) «следующее а будет p» и (б) «все а суть p» — оба имеют вероятность, которая повышается по мере увеличения n и стремится к достоверности как к пределу, по мере того как n стремится к бесконечности».
Я буду называть (а) «частной индукцией» и (б) «общей индукцией». Таким образом, (а) утверждает на основании нашего знания о смертности людей в прошлом, что, вероятно, г-н такой-то умрет, тогда как (6) утверждает, что, вероятно, все люди смертны.
Со времени Лапласа делались различные попытки показать, что вероятная истинность индуктивного вывода вытекает из математической теории вероятности. Теперь всеми признается, что все эти попытки были безуспешными и что если индуктивные доказательства должны быть действенными, то это должно быть в силу какой-либо внелогической характеристики действительного мира в его противоположности различным логически возможным мирам, какие только могут представляться умственному взору логика.
Первое из таких доказательств принадлежит Лапласу. В своей истинной, чисто математической форме оно имеет следующий вид:
Имеется n+1 сумок, сходных друг с другом по внешнему виду, каждая из которых содержит n шаров. В первой — все шары черные; во второй — один белый и все остальные черные; r +1-й сумке r шаров белые и остальные черные. Из этих сумок выбирается одна, состав которой неизвестен, и из нее вынимается m шаров. Все они оказываются белыми. Какова вероятность, (а) что следующий вынутый шар будет белым, (б) что мы выбрали сумку, состоящую из одних белых шаров?
Ответ таков: (а) шанс, что следующий шар будет белым, равен (n+1)/(m +2), (б) шанс, что мы выбрали сумку, в которой все шары белые, равен (m+1)/(n +1). Этот правильный результат имеет непосредственную интерпретацию на основе конечно-частотной теории. Но Лаплас делает вывод, что если m членов А оказались членами В, то шанс, что следующий А будет равен В, равен (m+1)/(m+2), и что шанс, что все А суть В, равен (m +1)/(n +1). Он получает этот результат с помощью допущения, что при данном числе n объектов, о которых мы не знаем ничего, вероятности, что 0, 1, 2, …, n из этих объектов суть B, все равны. Это, конечно, является абсурдным допущением. Если мы заменим его несколько менее абсурдным допущением, что каждый из этих объектов имеет равный шанс быть или не быть В, то шанс, что следующий А будет В, остается равным 1/2, как бы много А ни оказались B.
Даже если бы его доказательство было принято, общая индукция остается невероятной, если n гораздо больше, чем m, хотя частная индукция может быть в высокой степени вероятной. В действительности же, однако, его доказательство является только историческим раритетом.
Индукция со времени Юма играла настолько большую роль в спорах о научном методе, что очень важно внести полную ясность в то, к чему — если я не ошибаюсь — приводят вышеприведенные доказательства.
Во-первых: в математической теории вероятности нет ничего, что оправдывало бы наше понимание как общей, так и частной индукции как вероятной, как бы при этом ни было велико установленное число благоприятных случаев.
Во-вторых: если не устанавливается никакое ограничение в отношении характера интенционального определения классов А и В, участвующих в индукции, то можно показать, что принцип индукции не только сомнителен, но и ложен. Это значит, что если дано, что n членов некоторого класса А принадлежит к некоторому другому классу В, то значения «В», для которых следующий член класса А не принадлежит к классу В, более многочисленны, чем значения, для которых следующий член принадлежит к В, если n не сильно отличается от полного числа вещей во вселенной.
В-третьих: то, что называется «гипотетической индукцией», в которой какая-либо общая теория рассматривается как вероятная, потому что все до сего времени наблюденные ее следствия подтверждались, не отличается сколько-нибудь существенно от индукции через простое перечисление. Ибо если p есть теория, о которой идет речь, А — класс относящихся к делу явлений и В — класс следствий р, тогда р эквивалентно утверждению ‘все А суть В», и свидетельство в пользу р получается с помощью простого перечисления.
В-четвертых: для того, чтобы индуктивное доказательство было действенным, индуктивный принцип должен быть сформулирован с каким-либо неизвестным до сего времени ограничением. Научный здравый смысл на практике избегает различных видов индукции, в чем он, по-моему, прав. Но пока еще не сформулировано то, что руководит научным здравым смыслом.
ЧАСТЬ ШЕСТАЯ. ПОСТУЛАТЫ НАУЧНОГО ВЫВОДА
ГЛАВА 1. ВИДЫ ПОЗНАНИЯ. То, что признается за познание, имеет две разновидности; во-первых, познание фактов, во-вторых, познание общих связей между фактами. С этим различием очень тесно связано другое, а именно существует познание, которое может быть описано как «отражение», и познание, которое состоит в способности к разумному действию. Монады Лейбница «отражают» вселенную и в этом смысле «познают» ее; но поскольку монады никогда не взаимодействуют, они не могут «действовать» на что-либо внешнее по отношению к ним. Это логическая крайность одной концепции «познания». Логической крайностью другой концепции является прагматизм, который был впервые провозглашен К. Марксом в его «Тезисах о Фейербахе» (1845): «Вопрос о том, обладает ли человеческое мышление предметной истинностью, — вовсе не вопрос теории, а практический вопрос. В практике должен доказать человек истинность, то есть действительность и мощь, посюсторонность своего мышления… Философы лишь различным образом объясняли мир, но дело заключается в том, чтобы изменить его».
В каком смысле можно говорить, что мы знаем необходимые постулаты научного вывода? Я считаю, что знание есть вопрос степени. Мы можем не знать, что, «конечно, за А всегда следует В», но мы можем знать, что, «вероятно, за А обычно следует В, где слово «вероятно» должно быть взято в смысле «степени правдоподобия». В каком-то смысле и до какой-то степени наши ожидания могут считаться «знанием».
Какое отношение имеют привычки животных к людям? Согласно традиционной концепции «знания» никакого. Согласно же концепции, которую я хочу защищать, — очень большое. По традиционной концепции, знание в своих лучших проявлениях есть интимный и почти мистический контакт между субъектом и объектом, в отношении которого некоторые могут в будущей жизни иметь полный опыт в блаженном видении. Кое-что из этого прямого контакта — как нас уверяют — существует в восприятии. Что же касается связей между фактами, то старые рационалисты приравнивали естественные законы к логическим принципам или непосредственно, или же обходным путем, с помощью божественной благости и мудрости. Все это устарело, за исключением того, что касается восприятия, которое многие все еще рассматривают как дающее непосредственное знание, а не как сложную и причудливую смесь ощущения, привычки и физического причинения, чем, как я доказывал, восприятие является. Вера в общее, как мы видели, имеет только довольно косвенное отношение к тому, во что, как утверждают, верят; когда я верю без слов, что скоро будет взрыв, совсем невозможно с точностью сказать, что совершается во мне. Вера в действительности имеет сложное и несколько неопределенное отношение к тому, во что верят, как и воспринимание к тому, что воспринимается.
Если животное имеет такую привычку, что при наличии конкретного А оно ведет себя так, как до приобретения привычки оно вело себя при наличии конкретного В, тогда я скажу, что животное верит в общее предложение: «Каждый (или почти каждый) конкретный случай А сопровождается (или за ним следует) случаем В’. Это значит, что животное верит в то, что эта форма слов обозначает. Если это так, то становится ясным, что привычка животного существенна для понимания психологии и биологического происхождения общих верований.
Возвращаясь к определению «знания», я скажу, что животное «знает» общее предложение: «За А обычно следует В, если выполняются следующие условия:
- Животное неоднократно испытывало, как за А следовало B.
- Этот опыт заставил животное вести себя при наличии А более или менее так же, как оно раньше вело себя при наличии В.
- За А действительно обычно следует B.
- A и B такого характера или так относятся друг к другу, что в большинстве случаев, где этот характер или отношение имеется, частота наблюдаемых следований является свидетельством вероятности общего, если не неизменного закона следования.
ГЛАВА 3. ПОСТУЛАТ ЕСТЕСТВЕННЫХ ВИДОВ ИЛИ ОГРАНИЧЕННОГО МНОГООБРАЗИЯ. Постулат Кейнса непосредственно возникает из его анализа индукции. Данная Кейнсом формулировка его постулата гласит следующее: «Следовательно, в качестве логического основания для аналогии мы, по-видимому, нуждаемся в каком-либо допущении, которое говорило бы, что количество многообразия во вселенной так ограниченно, что нет ни одного объекта настолько сложного, что его качества попадали бы в бесконечное число независимых групп (то есть групп, которые могли бы существовать как независимо, так и в соединении); или, скорее, что ни один из объектов, о котором мы делаем обобщение, не является таким сложным, как этот; или по крайней мере, что, хотя некоторые объекты и могут быть бесконечно сложными, мы иногда все же имеем конечную вероятность того, что объект, о котором мы стараемся сделать обобщение, не является бесконечно сложным».
В течение XVIII и XIX столетий было обнаружено, что колоссальное множество известных науке веществ можно объяснить с помощью предположения, что все они состоят из девяноста двух элементов (некоторые из которых еще были не известны). Каждый элемент, как считалось вплоть до нашего века, имеет некоторое число свойств, которые оказались сосуществующими, хотя и по неизвестной причине. Атомный вес, точка плавления, внешний вид и др. делали каждый элемент естественным видом столь же определенно, как в биологии до теории эволюции. Наконец, однако, оказалось, что различия между элементами являются различиями в структуре и следствиями законов, одних для всех элементов. Правда, есть еще естественные виды — в настоящее время это электроны, позитроны, нейтроны и протоны, — однако думают, что они не являются конечными и могут быть сведены к различиям в структуре. Уже в квантовой теории их существование несколько туманно и не столь существенно. Это наводит на мысль, что в физике, как и в биологии после Дарвина, может быть доказано, что учение о естественных видах было только временной фазой.
ГЛАВА 5. ПРИЧИННЫЕ ЛИНИИ. «Причина», как она встречается, например, у Джона Стюарта Милля, может быть определена следующим образом: все события могут быть разделены на классы таким образом, что за каждым событием некоторого класса А следует событие некоторого класса В, который может отличаться или может не отличаться от А. Если даны два таких события, то событие класса А называется «причиной», а событие класса В называется «действием».
Милль полагает, что этот закон всеобщей причинности в более или менее таком же виде, в каком мы его сформулировали, доказывается или по крайней мере делается чрезвычайно вероятным благодаря индукции. Его знаменитые четыре метода, которые предназначены в данном классе случаев открывать, что является причиной, а что действием, предполагают причинность и зависят от индукции только в том, что индукция — как предполагается — подтверждает это предположение. Но мы видели, что индукция не может доказать причинности, если причинность не является предварительно вероятной. Однако для индуктивного обобщения причинность, возможно, является гораздо более слабым основанием, чем это обычно думают.
Мы чувствуем, что можем представлять себе или иногда, может быть, даже воспринимать отношение «причина — действие», которое, когда оно имеет место, обеспечивает неизменное следствие. Единственное ослабление закона причинности, которое легко признать, говорит не то, что причинное отношение не является неизменным, а то, что в некоторых случаях может не быть никакого причинного отношения.
Вера в причинение — правильная или неправильная — глубоко укоренилась в языке. Вспомним, как Юм, несмотря на свое желание оставаться скептиком, с самого начала допускает употребление слова «впечатление». «Впечатление» должно быть результатом какого-то воздействия на кого-либо, что является чисто причинным пониманием. Различие между «впечатлением» и «идеен» должно заключаться в том, что первое (но не последнее) имеет ближайшую внешнюю причину. Правда, Юм заявляет, что он нашел и внутреннюю разницу: впечатления отличаются от идей своей большей «живостью». Но это не так: некоторые впечатления бывают слабыми, а некоторые идеи очень живыми. Что касается меня, то я определил бы «впечатление» или «ощущение» как психическое событие, ближайшая причина которого является физической, тогда как «идея» имеет ближайшую причину психическую.
«Причинная линия», как я собираюсь определить этот термин, есть временная последовательность событий, так относящихся друг к другу, что если даны некоторые из них, то что-то может быть выведено о других, что бы ни случилось в другом месте.
Большое значение статистической закономерности в физике начало сказываться с кинетической теории газов, которая сделала, например, температуру статистическим понятием. Квантовая теория в очень большой степени укрепила роль статистической закономерности в физике. Сейчас кажется вероятным, что основные закономерности физики являются статистическими и не могут сказать нам даже в теории, что будет делать индивидуальный атом. Более того, замена индивидуальных закономерностей статистическими оказалась необходимой только в отношении атомных явлений.
ГЛАВА 6. СТРУКТУРА И ПРИЧИННЫЕ ЗАКОНЫ. Индукция через простое перечисление не является принципом, посредством которого могут быть оправданы недоказательные выводы. Сам же я считаю, что концентрация внимания на индукции очень сильно помешала прогрессу всего исследования постулатов научного метода.
Мы имеем два разных случая тождественности структуры групп объектов: в одном случае структурными единицами являются материальные объекты, а в другом — события. Примеры первого случая: атомы одного элемента, молекулы одного соединения, кристаллы одного вещества, животные или растения одного вида. Примеры другого случая: то, что разные люди одновременно видят или слышат в одном месте, и то, что в одно и то же время отображают камеры и диски граммофонной записи, одновременные движения объекта и его тени, связь между разными исполнениями одной и той же музыки и так далее
Мы будем различать два вида структуры, а именно «структуру событий» и «материальную структуру». Дом имеет материальную структуру, а исполнение музыки — структуру событий. В качестве принципа вывода, неосознанно применяемого обыденным здравым смыслом, но сознательно — как в науке, так и в праве, я предлагаю следующий постулат: «Когда группа сложных событий, находящихся более или менее рядом друг с другом, имеет общую структуру и группируется, по-видимому, около какого-то центрального события, то вполне вероятно, что они имеют в качестве причины общего предшественника».
ГЛАВА 7. ВЗАИМОДЕЙСТВИЕ. Возьмем один исторически важный пример, а именно закон падения тел. Галилей с помощью небольшого числа довольно грубых измерений нашел, что расстояние, проходимое вертикально падающим телом, приблизительно пропорционально квадрату времени падения, другими словами, что ускорение приблизительно постоянно. Он предположил, что, если бы не сопротивление воздуха, оно было бы вполне постоянным, а когда спустя немного времени был изобретен воздушный насос, это предположение, казалось, подтвердилось. Но дальнейшие наблюдения навели на мысль, что ускорение незначительно изменяется с широтой, а последующая теория установила, что оно изменяется также и с высотой. Таким образом, элементарный закон оказался только приблизительным. Закон всемирного тяготения Ньютона, пришедший на смену этому, оказался более сложным законом, а закон тяготения Эйнштейна в свою очередь оказался еще более сложным, чем закон Ньютона. Подобная постепенная утрата элементарности характеризует историю большинства ранних открытий науки.
ГЛАВА 8. АНАЛОГИЯ. Вера в сознание других требует какого-то постулата, который не требуется в физике, поскольку физика может удовлетвориться познанием структуры. Мы должны обратиться к чему-то, что может быть довольно неопределенно названо «аналогией». Поведение других людей во многом аналогично нашему собственному, и мы предполагаем, что оно должно иметь аналогичные причины.
Из наблюдения за самими собой мы знаем причинный закон формы «А есть причина В’, где А есть «мысль», a B — физическое событие. Мы иногда наблюдаем В, когда не может наблюдать никакого А, тогда мы делаем вывод о ненаблюдаемом А. Например я знаю, что когда говорю: «Я хочу пить», я говорю это обычно потому, что я действительно хочу пить, и поэтому, когда я слышу фразу: «Я хочу пить», — в тот момент, когда сам я пить не хочу, я делаю предположение, что кто-то другой хочет пить.
Этот постулат, будучи принятым, оправдывает вывод о других сознаниях, как оправдывает и многие другие выводы, которые неосознанно делает обыденный здравый смысл.
ГЛАВА 9. СУММИРОВАНИЕ ПОСТУЛАТОВ. Я считаю, что постулаты, необходимые для признания научного метода, могут быть сведены к пяти:
- Постулат квазипостоянства.
- Постулат независимых причинных линий.
- Постулат пространственно-временной непрерывности в причинных линиях.
- Постулат общего причинного происхождения сходных структур, расположенных вокруг их центра, или, проще, структурный постулат.
- Постулат аналогии.
Все эти постулаты, взятые вместе, предназначаются для создания предварительной вероятности, необходимой для оправдания индуктивных обобщений.
Постулат квазипостоянства. Главным назначением этого постулата является такая замена понятий обыденного здравого смысла «вещь» и «личность», которая не предполагает понятия «субстанции». Этот постулат можно сформулировать следующим образом: Если дано какое-либо событие А, то очень часто случается, что в любое близкое время в каком-либо соседнем месте имеется событие, очень сходное с А. «Вещь» и есть последовательность таких событий. Именно потому, что такие последовательности событий обычны, «вещь» является практически удобным понятием. Имеется не очень большое сходство между трехмесячным зародышем и взрослым человеком, но они связаны постепенны ми переходами от одного состояния к следующему и поэтому рассматриваются как стадии в развитии одной «вещи».
Постулат независимых причинных линий. Этот постулат имеет много применений, но, возможно, наиболее важным из всех является его применение в связи с восприятием — например, при приписывании множественности наших зрительных ощущений (при взгляде на ночное небо) множеству звезд как их причине. Этот постулат может быть сформулирован следующим образом: Часто можно образовать такую последовательность событий, что из одного или двух членов этой последовательности можно вывести что-либо относящееся ко всем другим членам. Самым явным примером здесь является движение, особенно беспрепятственное движение, подобное движению фотона в межзвездном пространстве.
Между любыми двумя событиями, принадлежащими к одной причинной линии, как я сказал бы, имеется отношение, которое может быть названо отношением причины и действия. Но если мы назовем его так, то мы должны добавить, что причина не полностью определяет действие даже в наиболее благоприятных случаях.
Постулат пространственно-временной непрерывности. Задачей этого постулата является отрицание «действия на расстоянии» и утверждение того, что, когда имеется причинная связь между двумя событиями, не являющимися смежными, в причинной цепи должны быть такие промежуточные звенья, каждое из которых должно быть смежным со следующим, или же (альтернативно) такие, что получается процесс, непрерывный в математическом смысле. Этот постулат касается не свидетельства в пользу причинной связи, а вывода в тех случаях, когда причинная связь считается уже установленной. Он позволяет нам верить, что физические объекты существуют и тогда, когда они не воспринимаются.
Структурный постулат. Когда кокое-то число структурно сходных комплексов событий располагается около центра в относительно малой области, обычно бывает, что все эти комплексы принадлежат к причинным линиям, имеющим свой источник в событии той же структуры, находящемся в центре.
Постулат аналогии. Постулат аналогии может быть сформулирован следующим образом: Если даны два класса событий А и В и если дано, что, где бы оба эти класса А и В ни наблюдались, имеется основание верить, что А есть причина В, и тогда, если в каком-то данном случае наблюдается А, но нет никакого способа установить, имеется В или нет, то вероятно, что В все-таки имеется; и подобным же образом, если наблюдается В, а наличие или отсутствие А не может быть установлено.
ГЛАВА 10. ГРАНИЦЫ ЭМПИРИЗМА. Эмпиризм может быть определен как утверждение: «Всякое синтетическое знание основывается на опыте». «Знание» – есть термин, не поддающийся точному определению. Всякое знание является до некоторой степени сомнительным, и мы также не можем сказать, при какой степени сомнительности оно перестает быть знанием, как не можем сказать, сколько человек должен потерять волос, чтобы считаться лысым. Когда вера выражается в словах, мы должны иметь в виду, что все слова за пределами логики и математики неопределенны: имеются объекты, к которым они определенно применимы, и есть объекты, к которым они определенно неприменимы, но имеются (или по крайней мере могут быть) промежуточные объекты, в отношении которых мы не уверены, применимы эти слова к ним или нет. Знание отдельных фактов должно зависеть от восприятия, является одним из самых основных принципов эмпиризма.
[1] В книге, на мой взгляд, ошибка. Эта формула приведена не как частное, а как произведение.
[2] Похоже, что не издавался на русском языке. Надо отметить, что я не раз читал о теории вероятности, выдвинутой Кейнсом, и надеялся, что с помощью Рассела смогу в ней разобраться. Увы… пока это выше моего понимания.

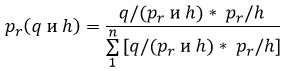
У Вас есть желание прочитать книгу ?
Сборник задач I и II открытых чемпионатов школ по экономике
выпишите 25 интересных задачек, все вместе будем думать.
ozon.ru/context/detail/id/19159931/