Писатель и популяризатор науки Джеймс Глик рассказывает о том, как наше отношение к информации изменило саму природу человеческого сознания. Его книга — увлекательное и напряженное путешествие по истории информации и связи от языка, на котором «говорили» африканские барабаны, к изобретению алфавитов, от первых попыток кодирования к электронным письмам и блогам, от древних времен к современности. На этом пути его сопровождают Чарльз Бэббидж, Ада Лавлейс, Клод Шеннон и другие великие ученые. «Информация» была признана лучшей научной книгой года по версии Los Angeles Times, получила множество призов и стала международным бестселлером. Мне книга очень понравилась.
Джеймс Глик. Информация. История. Теория. Поток. – М.: АСТ, Corpus, 2013. – 576 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon или Лабиринте
ПРОЛОГ
Так случилось, что 1948-й стал годом, когда Bell Telephone Laboratories объявили об изобретении полупроводника — «удивительно простого устройства», которое могло делать все то, что делала вакуумная лампа, но более эффективно. Благодаря появлению транзистора в электронике произошла революция, позволившая технологии пойти по пути широкого распространения уменьшившихся в размерах устройств, а трое главных изобретателей вскоре получили Нобелевскую премию. В Лаборатории по праву гордились транзистором, но на самом деле он оказался лишь вторым по важности изобретением того времени. Транзистор в конце концов был только оборудованием.
Изобретение более значимое и фундаментальное появилось в монографии, занимавшей в общей сложности семьдесят девять страниц июльского и октябрьского номеров The Bell System Technical Journal. Статья называлась Математическая теория связи. Она, как и транзистор, принесла с собой неологизм — слово «бит», выбранное автором, 32-летним Клодом Шенноном. Сегодня бит стоит в одном ряду с дюймом, фунтом, квартой и минутой, основными единицами измерения. Но что измерялось битами? «Единица измерения информации» — так определил бит Шеннон. Как будто существовала такая вещь, как измеримая и исчислимая информация!?
В двадцать два года Шеннон написал диссертацию, в которой применил логическую алгебру Джорджа Буля — идею родом из XIX века — к устройству электрических цепей. В 1943 году английский математик и криптоаналитик Алан Тьюринг посетил Bell Telephone Laboratories и как-то за обедом встретил Шеннона. Они обменялись взглядами на будущее искусственных думающих машин (о Тьюринге см. Эндрю Ходжес. Игра в имитацию).
Теория Шеннона перекинула мост между информацией и неопределенностью, между информацией и энтропией, между информацией и хаосом. Сегодня даже биология стала наукой об информации. Неудивительно, что генетика расцвела одновременно с теорией информации. ДНК — информационная молекула, самый совершенный процессор обработки сообщений, находящийся на клеточном уровне, — алфавит и код, 6 млрд бит информации для создания человеческого существа. «Коренная сущность каждого живого существа — не пламя, не теплое дыхание и не «искра жизни», — заявляет ученый Ричард Докинз, — но информация, слова, инструкции. Если вы хотите понять сущность жизни, не размышляйте о вибрирующих и трепещущих студнях и илах, а размышляйте об информационных технологиях». У гена есть и культурный аналог — мем. В эволюции культуры мем воспроизводит и распространяет идею (подробнее см. Ричард Докинз. Эгоистичный ген, Ричард Докинз. Слепой часовщик. Как эволюция доказывает отсутствие замысла во Вселенной).
Глава 1. ГОВОРЯЩИЕ БАРАБАНЫ
Язык барабанов не был легким и схематичным. Народам Африки удалось создать технологию коммуникации на расстоянии, передачи информации со скоростью большей, чем у любого гонца, пешего или конного. Ночью в безветренную погоду над рекой барабанная дробь разносится на 6 или 7 миль вокруг. Всего за час барабанные послания, передающиеся от деревни к деревне, могут преодолеть сотню миль.
К тому моменту, когда в 1841 году европейцы узнал о существовании говорящих барабанов, Сэмюэл Ф.Б. Морзе уже разрабатывал собственный ударный код — электромагнитный барабанный бой, пульсирующий по телеграфным линиям. За основу своей системы Морзе взял алфавит, который стал промежуточным звеном между речью и кодом. Точки и тире не были непосредственно связаны со звуками, они заменяли буквы, из которых состояли письменные слова, представлявшие в свою очередь слова сказанные. У барабанщиков не было такого промежуточного звена — они не могли строить систему на уровне символов, потому что африканские языки, как и почти 6 тыс. остальных языков, на которых говорят в современном мире (за исключением нескольких десятков), не имеют алфавита. Барабаны преобразовывали устную речь.
Это открытие сделал Джон Ф. Каррингтон. Он родился в 1914 году в Нортгемптоншире, в возрасте двадцати четырех лет уехал миссионером в Африку и прожил там до конца жизни. В 1949 году Каррингтон наконец опубликовал свои наблюдения о языке барабанов в небольшой книге, озаглавленной «Говорящие барабаны Африки» (The Talking Drums of Africa). При трансформации устной речи в язык барабанов терялась часть данных. Каррингтон обнаружил, что барабанщик всегда добавляет «небольшое выражение» к каждому короткому слову. Не просто «луна», а «луна, смотрящая вниз на землю». Не просто «курица», а «курица, которая говорит «коко». Язык барабанов занимался предоставление дополнительных битов для снятия многозначности и коррекции ошибок. Все естественные языки избыточны, вот почему люди могут понимать написанный с ошибками текст или разговор в шумной комнате.
После выхода своей книги Джон Каррингтон наткнулся на математический способ объяснения данного факта. Статья инженера телефониста из Bell Telephone Laboratories Ральфа Хартли даже содержала соответствующую формулу: Н = n*logS, где Н — количество информации, n — количество символов в сообщении, S — количество символов в языке. Младший коллега Хартли Клод Шеннон продолжил исследования в этой области и занялся измерением избыточности английского языка (о применении формулы Хартли для нахождения алгоритма игры см. Разработка оптимальной стратегии игры «Быки и коровы» на основе теории информации).
Глава 2. ПОСТОЯНСТВО СЛОВА
Письменность была нужна, чтобы сохранить информацию во времени и пространстве. До письменности коммуникация была недолговечной и локальной. Новый коммуникационный канал не просто расширил предыдущий. Он позволил появиться таким методам, как повторное использование и воспоминание. Возникли новые информационные системы. Среди них — история, право, бизнес, математика и логика. Причем и в виде данных, и в виде методик. Сила заключена не только в ценном самом по себе знании, сохраненном и переданном, но и в способах его получения и передачи — кодированная визуальная индикация, сам процесс передачи, знаки, заменяющие объекты.
По меньшей мере 30 тыс. лет назад люди эпохи палеолита начали выцарапывать и рисовать фигуры, напоминавшие изображения лошадей, рыб и охотников. Но историки не торопились называть их письменностью. Нужно было совершить еще один важный шаг от представления предметов к представлению слов языка, необходимо было представление второго порядка. Переход от пиктографии (записи изображения) к идеографии (записи идеи) и только потом к логографии (записи слова). Больше всего времени для развития потребовалось письменности, которая пошла по пути, противоположному китайскому, — по пути создания алфавита, где один символ соответствует одному минимальному звуку. Алфавитная — наиболее редуктивная, наиболее разрушительная из систем письма.
Во всех языках на Земле есть только одно слово для алфавита: alphabet, alfabet, alfabeto, αλφαβητο. Алфавит был изобретен лишь однажды. У всех известных алфавитов, которые используются в наши дни или были найдены на табличках и камнях, один и тот же предок. Он появился у восточного побережья Средиземного моря незадолго до 1500 года до н. э. в политически нестабильном регионе, на перекрестке культур, на земле Палестины, Финикии и Ассирии. Упрощенная система символов, всего 22 знака, была изобретением семитов Палестины или близлежащих местностей.
Алфавит распространялся как инфекция. Даже дети были в состоянии выучить небольшое количество легких, не несущих семантической нагрузки букв. Алфавит распространился в арабском мире и в Северной Африке, появились еврейский и финикийский алфавиты, затем он прошел через Среднюю Азию в Индию, где возник брахми и родственные ему письмена. Алфавит попал и в Грецию. Возникшая там новая цивилизация его сильно усовершенствовала. Среди прочих появились латинский и кириллический алфавиты.
Русский психолог Александр Романович Лурия проводил полевые исследования среди неграмотных жителей отдаленных областей Узбекистана и Киргизии в 1930-е. Он обнаружил, что неграмотные объекты его исследований серьезно отличаются не только от грамотных, но даже и от малограмотных, но не знаниями, а способом мышления. Логика напрямую связана с системой символов: вещи делятся на классы, они обладают отвлеченными и обобщенными свойствами. Люди, владевшие только устной речью, не имели представления о понятии категорий, ставшем естественным даже для неграмотных людей, живущих в культуре, у которой есть письменность, — например, такие люди знакомы с геометрическими фигурами. Рисунки кругов и квадратов объекты исследования называли «тарелка, решето, ведро, луна» и «зеркало, дверь, дом, доска для сушки абрикосов». Они не могли или не хотели принимать логические силлогизмы. Типичный вопрос: «На Крайнем Севере, где всегда лежит снег, все медведи белые. Новая Земля — на Крайнем Севере, и там всегда снег. Какого цвета там медведи?»
Типичный ответ: «Я не знаю. Я видел бурого медведя. И никогда не видел никаких других… В каждой местности свои животные». Напротив, человек, только что выучившийся читать и писать, отвечал: «Исходя из ваших слов они должны быть белыми». Словосочетание «исходя из ваших слов» свидетельствует о переходе на другой уровень. Информация отделяется от личности, от опыта говорящего.
Математика тоже родилась из изобретения письменности. Грецию часто считают истоком реки, ставшей современной математикой. Но сами греки ссылаются на другую древнюю для них традицию, которую они называют халдейской, а мы — вавилонской.
Систематизированный подход к записи чисел появился только во время правления Хаммурапи (1750 год до н. э.), когда Месопотамия объединилась вокруг великого города Вавилона. Хаммурапи был, наверное, первым грамотным королем, он сам писал клинописью, а не полагался на писарей, и устройство его империи говорит о наличии связи между письменностью и контролем над огромным государством (см., например, Законы Хаммурапи и проблема принципал – агент).
Маршалл Маклюэн говорит, что печать предлагает нам узкий канал коммуникации. Канал линейный и даже фрагментарный. Напротив, в речи в ее первозданном виде, разговоре людей лицом к лицу, оживленном жестами и прикосновениями, задействованы все чувства, а не только слух. Если идеал общения — это встреча двух душ, то письменный язык — это только жалкая тень идеала. Такой же критике подверглись другие ограниченные каналы коммуникации, созданные более поздними технологиями, — телеграф, телефон, радио, электронная почта. Джонатан Миллер перефразировал аргументы Маклюэна в квазитехнических терминах: «Чем больше число задействованных чувств, тем выше вероятность передачи точной копии ментального состояния посылающего».
Глава 3. ДBA СЛОВАРЯ
Роберт Кодри, деревенский школьный учитель и священник в 1604 году выпустил первый словарь английского языка (рис. 1).
Рис. 1. Титульная страница словаря Кодри
Из всех языков мира английский на тот момент уже был самым пестрым, самым полигенным. Его история свидетельствует о постоянных вторжениях и заимствованиях. Его самые старые слова, условно базовые, произошли из языков, на которых говорили англы, саксы и юты, германские племена, пересекшие Северное море, пришедшие в Англию в V веке и оттеснившие кельтов. Из кельтского языка в англосаксонскую речь проникло немного, но викинги-завоеватели принесли с собой норвежские и датские слова: egg, skyy anger, give, get. Латынь пришла с христианскими миссионерами — они пользовались римским алфавитом, который заменил руническое письмо, распространенное в Центральной и Северной Европе в начале первого тысячелетия. Затем началось французское влияние.
«Влияние» для Кодри означало «вливание». С лингвистической точки зрения норманнское завоевание больше походило на потоп. Английские крестьяне продолжали выращивать cows, pigs и oxen (коров, свиней и быков — германские слова), но во втором тысячелетии представители высшего сословия уже ели на обед beef, pork и mutton (говядину, свинину и баранину — французские слова).
Через 400 лет после появления книги Кодри путь ее автора повторил Джон Симпсон. В каком-то смысле Симпсон оказался естественным наследником Кодри — редактором грандиозной книги, «Оксфордского словаря английского языка». Симпсон был шестым в почетном ряду редакторов «Оксфордского словаря английского языка», чьи имена произносил без запинки — «Мюррей, Брэдли, Крейги, Оньонз, Берчфилд — как раз хватает пальцев», — и считал себя продолжателем их дела и традиций английской лексикографии, ведущей свою историю от Кодри и Сэмюеля Джонсона.
В античном мире списки, составленные по алфавиту, практически не встречались примерно до 250 года до н. э., когда появились александрийские тексты на папирусе. По-видимому, в великой Александрийской библиотеке алфавитизация использовалась хотя бы частично. Необходимость в такой искусственной схеме упорядочивания появилась лишь с увеличением количества данных, не организованных никаким иным способом.
Слово blog было внесено в Оксфордский словарь в 2003 году, dot-commer (тот, кто работает в интернет-компании) — в 2004-м, cyberpet (электронная игрушка, имитирующая домашнее животное) — в 2005-м, а глагол to Google (гуглить, искать информацию в поисковой системе Google) — в 2006-м.
Первый выпуск того, что потом стало «Оксфордским словарем английского языка», был одной из самых больших книг, когда-либо издававшихся. «Новый английский словарь, основанный на исторических принципах», 414 825 слов в десяти тяжелых томах, был представлен королю Георгу V и президенту США Калвину Кулиджу в 1928 году. Второе издание появилось лишь в 1989 году — 20 томов, 22 тыс. страниц, 62,5 кг. Третье издание отличается от первых двух: оно не имеет веса, потому что существует в цифровой реальности. С 2000 года результаты переработки по частям ежеквартально появляются в Сети, и каждый раз они включают несколько тысяч переработанных вхождений и сотни новых слов.
Глава 4. ПЕРЕВЕСТИ СИЛУ МЫСЛИ В ДВИЖЕНИЕ КОЛЕС
Цифровые таблицы были частью книжного дела еще до начала эры книгопечатания. В IX веке в Багдаде Абу Абдаллах Мухаммад ибн Муса аль-Хорезми, чье имя продолжает жить в слове «алгоритм», придумал таблицы тригонометрических функций, которые распространились на Запад — в Европу и на Восток — в Китай. Они были написаны от руки и копировались от руки еще сотни лет.
В XVII веке изобрели логарифмы. В современных терминах логарифм — это показатель степени. Логарифм 100 по основанию 10 равен 2, так как 100 = 102. Логарифм 1 000 000 равен 6, так как 6 является степенью в выражении 1 000 000 = 106. Чтобы перемножить два числа, можно найти их логарифмы и сложить. Например, 100 х 1 000 000 = 102 х 106 = 10(2 + 6). Найти и сложить проще, чем перемножить.
Богатый шотландец Джон Непер выразил свою идею иным образом — не в терминах степеней. Непер подошел к проблеме интуитивно, с помощью терминов «разница» и «отношение». Если разница между двумя соседними числами в числовой последовательности всегда одинакова, такую последовательность называют арифметической прогрессией: 0, 1, 2, 3, 4, 5, … Если между двумя соседними числами всегда одинаковое отношение, прогрессия становится геометрической: 1, 2, 4, 8, 16, 32, …
Поместим эти прогрессии одну под другой:
0 1 2 3 4 5… Логарифмы по основанию 2
1 2 4 8 16 32… Натуральные числа
То, что получилось, — таблица логарифмов в сыром виде. В сыром, потому что целые степени — это просто. Полезная таблица логарифмов должна была заполнить числа со многими знаками после запятой.
Герман Бригс, профессор геометрии пересмотрел и расширил необходимые последовательности чисел и опубликовал собственную книгу «Логарифмическая арифметика». С этого времени и до появления электронных машин большая часть вычислений выполнялась с помощью логарифмов. [1]
Чарльз Бэббидж родился 26 декабря 1791 года. В 1810 году он поступил в Тринити-колледж (Кембридж), вотчину Исаака Ньютона и математический центр Англии. Бэббидж был разочарован: он обнаружил, что по предмету знал больше, чем его преподаватели, и дополнительных знаний он здесь не получит, а возможно, не получит их и в Англии вообще. Он начал покупать иностранные книги, особенно из наполеоновской Франции, с которой Англия вела войну. У специализирующегося на предмете книготорговца в Лондоне он достал «Теорию аналитических функций» Лагранжа и «великую работу Лакруа «Дифференциальное и интегральное исчисление».
Рис. 2. Чарльз Бэббидж, 1860
Бэббидж задумал распространить великую силу для создания автоматической машины. В 1642 году Блез Паскаль уже сделал суммирующую машину с выстроенными в ряд вращающимися дисками, по одному на десятичную цифру. Однако по большому счету прототип Паскаля оставался ближе к счетам, чем к кинетической машине, потому что был пассивными счетчиком состояния памяти. С точки зрения Бэббиджа, она не была автоматической.
Бэббидж продолжал исследования: теперь его интересовали механические принципы чисел. Он заметил, что некоторые из них можно обнаружить, рассчитывая разницу между двумя последовательностями. «Исчисление конечных разниц» разрабатывалось математиками (особенно французскими) сотню лет. Его сила заключалась в упрощении вычислений высокого порядка до простого сложения, которое уже можно было превратить в рутину. Для Бэббиджа метод оказался столь важным, что математик сразу назвал свою машину разностной.
К 1820 году он выбрал конструкцию, купил токарный станок, работал на нем сам, наняв к тому же рабочих по металлу, и в 1822 году сумел представить Королевскому обществу маленькую действующую модель, блестящую и футуристическую. Разностная машина — ее реплика сегодня работает в Музее науки в Лондоне — стала важной вехой в развитии инженерии (рис. 3). В составе сплавов, четкости размеров, взаимозаменяемости частей ничто не превзошло этого блока незаконченной машины. Но она все равно была не более чем занятной вещицей. Дальше Бэббидж продвинуться не смог.
Рис. 3. Деревянная модель (1853) небольшой части разностной машины
Бэббиджа вдохновлял изобретенный Иосифом Марией Жаккардом ткацкий станок, управляемый инструкциями, закодированными и сохраненными с помощью отверстий в картоне. Внимание Бэббиджа привлекло кодирование узора, перенос его с одного носителя на другой.
Машина, задуманная Бэббиджем изначально, была машиной чисел. Теперь она стала машиной информации. Августа Ада Лавлейз ощущала это более отчетливо и представляла ее себе ярче, чем Бэббидж. Она рассказывала о будущем машины, о ее создании и устройстве так, будто та уже существовала: «Аналитическая машина — это не просто еще одна обыкновенная «вычислительная машина». Она занимает особое место… Разработан новый, обширный и мощный язык… овладение его истинами может сделать его практическое применение для задач человечества более быстрым и точным, чем до сих пор позволяли доступные средства. Таким образом, не только духовное и материальное, но и теоретическое и практическое в математическом мире получили более тесные и эффективные связи… Уместно сказать, что аналитическая машина ткет алгебраические узоры точно так же, как ткацкий станок Жаккарда — цветы и листья».
Ада описывает гипотетическую программу, выполняя которую гипотетическая машина могла бы рассчитывать знаменитые бесконечные последовательности — числа Бернулли. Ада придумала процесс, набор правил, последовательность операций. В другом веке это назвали бы алгоритмом, позже — компьютерной программой, но в то время концепция требовала мучительно сложных объяснений. Самым трудным было то, что ее алгоритм оказался рекурсивным. Он исполнялся циклически. Результат одной итерации становился исходными данными для следующей. Бэббидж описывал этот подход так: «Машина, пожирающая свой хвост». Ада программировала машину. Но она программировала в уме, потому что машины не было.
В те времена женщины в Англии не могли учиться в университете, но Ада очень хотела изучать математику. Огастес де Морган, математик и логик, друг Бэббиджа и леди Байрон (матери Ады), стал для Ады учителем по переписке. Однажды зимой она увлеклась модной головоломкой, известной как Solitaire (рис. 4). Тридцать две фишки расставлялись на доске с тридцатью тремя отверстиями. Правила просты: любая фишка могла перепрыгнуть через соседнюю, при этом та фишка, через которую перепрыгнули, убиралась с доски. Так продолжалось до тех пор, пока не оставалось возможных ходов. Цель — закончить с одной фишкой. «Люди могут пытаться тысячи раз и не добиться успеха», — с восторгом писала Ада Бэббиджу. – «Я добилась успеха путем экспериментов и наблюдений и теперь могу сделать это когда угодно, но мне интересно, можно ли эту задачу выразить и решить с помощью математической формулы… Тут должен быть определенный принцип, я думаю о комбинации цифровых и геометрических свойств, от которой зависит решение и которую можно выразить языком символов».
Рис. 4. Исходная позиция в игре Солитер; поиграть on-line можно здесь; а победный алгоритм подсмотреть здесь
Глава 5. НЕРВНАЯ СИСТЕМА ЗЕМЛИ
Изобретения телеграфа и телефона вызвали такой восторг, которого, казалось, не вызывало до этого ни одно открытие. «Электричество — поэзия науки», — заявил в 1852 году американский историк. Но никто не знал, что такое электричество. В XVII веке Томас Браун описывал электрическое излучение как «нити сиропа, растягивающиеся и сжимающиеся». В XVIII веке, запускавший воздушных змеев Бенджамин Франклин, доказал «похожесть молнии и электричества», объединив пугающие удары с неба со странными наземными искрами и токами (подробнее см. Уолтер Айзексон. Бенджамин Франклин).
Прошло совсем немного времени, и все увидели связь электричества с давнишней мечтой о коммуникации на большом расстоянии.
До того, как появился электрический телеграф, существовал просто телеграф — les telegraphes, изобретенный и названный так Клодом Шаппом во Франции во время Революции (рис. 5).
Рис. 5. Оптический телеграф Шаппа
Сэмюэл Морзе и Альфред Вейль в США и Вильям Кук и Чарльз Уитстоун в Англии сделали электрический телеграф реальностью и превратили его в бизнес. Выпускник Йельского колледжа, сын священника из Массачусетса, Морзе был художником, а не ученым. Большую часть 1820–1830-х он провел, путешествуя по Англии, Франции, Швейцарии и Италии и изучая живопись. В одной из таких поездок он и услышал об электрическом телеграфе.
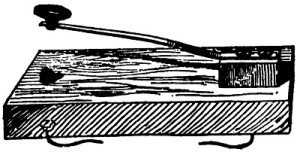
Морзе, ничего не зная о шариках, пузырьках или лакмусовой бумаге, понял, что знак можно создать на основе чего-то более простого, более фундаментального и менее осязаемого — минимального события, замыкания и размыкания цепи. И никаких стрелок. Электрический ток прерывался, и можно было придать этим прерываниям смысловое значение. Идея была проста, но первые устройства Морзе оказались сложными. Опытный механик Вейль справился с этим. Для передающего конца Вейль придумал то, что стало иконой пользовательского интерфейса: простой пружинный рычаг, с помощью которого оператор мог управлять цепью прикосновением пальца. Сначала Вейль назвал этот рычаг «корреспондентом», затем просто «ключом» (рис. 6).
Рис. 6. Телеграфный ключ Альфреда Вейля
В 1852 году знающие люди предупреждали: «Все идеи о связи Европы с Америкой линиями, проходящими напрямую через Атлантику, крайне непрактичны и абсурдны». Но невозможное было осуществлено в 1858м — королева Виктория и президент Бьюкенен обменялись любезностями.
Во многих смыслах использование телеграфа означало использование кода. Азбука Морзе из точек и тире не сразу стала называться кодом. Это был всего лишь алфавит — «телеграфная азбука Морзе», которая, по сути, не была алфавитом. Она не представляла звуки с помощью знаков. Азбука Морзе взяла алфавит за отправную точку и использовала его на новом уровне, заменив старые знаки новыми. Это был метаалфавит, алфавит следующей ступени абстракции. Переход от символов одного уровня к символам другого можно назвать кодированием.
В 1641 году, сразу после начала Английской революции, в одной маленькой анонимной книге были собраны многие известные методы того, что называлось криптографией. В конце концов автор открыл свое имя — это был Джон Уилкинс, викарий и математик, ставший впоследствии главой Тринити-колледжа (Кембридж) и основателем Королевского общества. Как математик он попробовал выяснить, как ограниченный набор символов, состоящий, например, из двух, трех или пяти, может представить целый алфавит. Символы тогда пришлось бы использовать в комбинациях.
Одним из примеров был двоичный код, неуклюже описанный словами: «Две буквы алфавита, будучи помещенными в пять различных позиций, принесут тридцать два отличия, что более чем достаточно для обозначения двадцати четырех букв» (рис. 7). В малопонятном «анонимном» трактате 1641 года основная идея теории информации прозвучала впервые и снова исчезла на целых четыре столетия.
Рис. 7. Двоичный код Уилкинса
С появлением телеграфа интерес публики к шифрованию вновь стал расти. Великим американским популяризатором криптографии был Эдгар Аллан По. В своих фантастических рассказах и журнальных статьях он описывал древнее искусство и хвастался собственными способностями к шифрованию. Также шифры использовали Жюль Верн и Оноре де Бальзак. Но самым передовым криптоаналитиком в викторианской Англии был Чарльз Бэббидж. Бэббидж поначалу увлекался созданием шифров, но позже перешел на сторону взломщиков. Он планировал написать «Философию взлома шифров», но не сумел ее закончить. Зато смог расшифровать полиалфавитный шифр, известный как шифр Виженера, считавшийся в Европе наиболее надежным. Как и в другой своей работе, он применил алгебраические методы, представив анализ шифра в форме уравнений.
Более молодые англичане Огастес де Морган и Джордж Буль заставили ту же методологию работать над еще более абстрактным материалом — логическими утверждениями. Де Морган был другом Бэббиджа, учителем Ады Байрон и профессором Университетского колледжа Лондона. Буль, сын сапожника из Линкольншира и горничной, к 1840м стал профессором Королевского колледжа Корка. В 1847 году ученые одновременно и независимо опубликовали труды, которые стали величайшими вехами в развитии логики со времен Аристотеля: «Математический анализ логики, или Опыт исчисления дедуктивных умозаключений» Буля и «Формальная логика, или Исчисление выводов, необходимых и возможных» де Моргана.
Буль представлял свою систему математикой без цифр. Он предложил единственными допустимыми цифрами сделать ноль и единицу. Все или ничего. Влияние Буля распространялось медленно и незаметно. Он совсем недолго переписывался с Бэббиджем, и они никогда не встречались. Одним из его кумиров был Льюис Кэрролл (подробнее см. Булева логика: критерии И, ИЛИ).
На рубеже веков Бертран Рассел сделал Джорджу Булю необычный комплимент: «Чистая математика была открыта Булем в работе, которую он назвал «Законы мышления». Его часто цитировали. Но у этой фразы есть неодобрительное продолжение, которое цитируют редко. А ведь именно оно делает комплимент Рассела столь необычным: «Он также ошибался, полагая, что имеет дело с законами мышления: вопрос, как люди на самом деле думают, не имел для него значения, и, если в его книге действительно содержатся законы мышления, забавно, что никто до этого не размышлял таким же образом». Судя по всему, Рассел любил парадоксы (подробнее см. Бертран Рассел. Человеческое познание, его сферы и границы).
Глава 6. НОВЫЕ ПРОВОДА, НОВАЯ ЛОГИКА
Клод Элвуд Шеннон 1916 года рождения был назван в честь своего уже немолодого отца — бизнесмена (он занимался мебелью, похоронным делом и недвижимостью) и судьи по наследственным делам. Они жили на Центральной улице, в нескольких кварталах к северу от Главной улицы. Население городка Гейлорд едва насчитывало 3 тыс. человек. Клод окончил среднюю школу Гейлорда за три года (вместо четырех) и в 1932 году поступил в Мичиганский университет, где изучал математику и электронную инженерию. Незадолго до выпуска, в 1936 году, он увидел объявление о работе для студентов-выпускников в Массачусетском технологическом институте. Вэнивар Буш, тогдашний декан инженерного факультета, искал помощника для работы на новой машине со странным названием «дифференциальный анализатор». Это была 100-тонная металлическая платформа с вращающимися стержнями и шестеренками (рис. 8). В годы Первой мировой войны в США было всего три места, в которых занимались научными приложениями к электронной инженерии; в эту тройку наряду с Bell Telephone Laboratories и General Electric входил и Массачусетский технологический.
Рис. 8. Дифференциальный анализатор Вэнивара Буша в МТИ
Как и машины Бэббиджа, анализатор был по своей сути механической машиной, хотя и использовал электродвигатели для привода тяжелого аппарата и по мере развития — все больше и больше электромеханических переключателей. Сегодня мы сказали бы, что она была аналоговой, а не цифровой, ее колеса и диски производили физический аналог дифференциальных уравнений. Клод Шеннон увлекся этим «компьютером», причем не только его грохочущей аналоговой частью, заполнявшей целую комнату, но и практически бесшумными (за исключением редких щелчков и стуков) электрическими системами контроля. Они были двух типов: обычные переключатели и специальные, называемые реле.
На последнем курсе колледжа Шеннон прослушал цикл лекций по символической логике и, попытавшись составить упорядоченный список возможных соединений переключающих цепей, обнаружил нечто знакомое. Оказалось, что, если взглянуть на эти проблемы максимально отвлеченно, они похожи. Странную искусственную систему обозначений, применяемую в символьной логике, — Булеву алгебру — можно было использовать и для описания цепей. Аналогия не была очевидной. Миры электричества и логики казались несовместимыми. Тем не менее Шеннон понял, что реле передает от одной цепи к другой скорее не электричество, а сообщение, замкнута цепь или разомкнута.
Глава 7. ТЕОРИЯ ИНФОРМАЦИИ
В начале 1943 года, в самый разгар войны, два похоже мыслящих человека, Клод Шеннон и Алан Тьюринг, ежедневно встречались за чаем в кафетерии Лабораторий Белла и ни слова не говорили о своей работе. Работа была засекречена — оба занимались криптоанализом. Они не обсуждали конкретные проекты, которыми занимались, однако Тьюринг показал Шеннону написанную семь лет назад статью «О вычислимых числах» о возможностях и ограничениях идеальной вычислительной машины. Они говорили на другую тему, которая также оказалась близка обоим, — о том, как научить машины думать.
Тьюринг был аспирантом и недавним выпускником Кингс-колледжа Кембриджа, когда в 1936 году представил статью о вычислимых числах своему профессору. Полное название заканчивалось причудливым немецким словом — оно звучало так: On Computable Numbers, with an Application to the Entscheidungsproblem («О вычислимых числах в применении к проблеме разрешимости»; подробнее см. Чарльз Петцольд. Читаем Тьюринга).
В статье описана универсальная вычислительная машина – Компьютер Тьюринга — фантастическая, абстрактная, целиком воображаемая машина. Тьюринг показал, что любая формальная система должна иметь неразрешимые утверждения. Математика неразрешима. Неполнота следует из невычислимости.
И Алан Тьюринг, и Клод Шеннон занимались кодами. Тьюринг кодировал инструкции числами, а десятичные числа — нулями и единицами. Шеннон придумал коды для генов и хромосом — реле и переключатели. Оба нашли способ описать одно множество объектов через другое.
В своей секретной статье 1945 г., едва ли не походя, Шеннон впервые употребил фразу «теория информации». Можно было дать несколько определений, и все они на первый взгляд казались парадоксальными. Информация есть неопределенность, неожиданность, трудность и энтропия.
- «Информация тесно связана с неопределенностью». Неопределенность в свою очередь можно измерить, сосчитав количество возможных сообщений. Если возможно лишь одно сообщение, неопределенности нет и, следовательно, нет информации.
- «Некоторые сообщения могут быть более вероятными, чем другие, и информация подразумевает неожиданность». Неожиданность есть способ выражать вероятности. Если буква, следующая за t (в английском языке), h, то передается не так много информации, потому что вероятность появления h сравнительно высока.
- «Имеет существенное значение трудность передачи сообщения из одной точки в другую». Это, наверное, покажется столь же тавтологичным, как определение массы в терминах силы, необходимой, чтобы сдвинуть объект. Но, с другой стороны, массу таким образом определить можно.
- «Информация есть энтропия». Это было самым странным и самым мощным определением из всех. Энтропия — само по себе трудное и плохо понимаемое понятие — есть мера неупорядоченности системы в термодинамике, науке о температурах и энергии.
Каждый инженер, если его просили передать больше информации по каналу, знал — надо увеличить мощность. Но на больших расстояниях этот подход не работал, потому что усиление сигнала снова и снова приводило к усилению шума. Шеннон обошел эту проблему, рассмотрев сигнал как цепочку дискретных символов. Теперь вместо увеличения мощности отправитель мог преодолеть шум, используя дополнительные символы для коррекции ошибок, точно так же как африканский барабанщик делает свою «речь» понятной на больших расстояниях не тем, что бьет в барабаны сильнее, а тем, что увеличивает количество слов в послании.
Формула Найквиста и Хартли – Н = nlogS Шеннон применил для измерения информации как функции вероятностей. Это логарифм невероятности сообщения, фактически мера неожиданности:
где рk есть вероятность каждого сообщения. Н обычно называется энтропией сообщения, энтропией Шеннона или просто информацией. Требовалась новая единица измерения. Шеннон утверждал: «Получившиеся единицы можно назвать двоичными цифрами или, более кратко, битами (сокращение от binary digit – англ., двоичная цифра).
Глава 8. ИНФОРМАЦИОННЫЙ ПОВОРОТ
Приблизительно теми же вопросами, что и Шеннон, занимался Нойберт Винер. Кибернетика была только что выдуманным им словом. Винер хотел, чтобы кибернетика стала наукой, которая бы объединила изучение способов коммуникации и управления, а также исследования человека и машины. Если определить поведение как «любое изменение сущности с учетом ее окружения», то это слово можно применять и к машинам, и к животным. Поведение, ориентированное на цель, является целесообразным, а цель иногда может быть введена в машину, а не передана оператору-человеку — например, если мы имеем дело с механизмом поиска цели: «Термин «сервомеханизмы» был придуман именно для обозначения машин со встроенным целесообразным поведением». Основной идеей было управление, или саморегуляция.
Чтобы как следует ее проанализировать, он позаимствовал туманный термин из электротехники — «обратная связь», возврат энергии из выхода цепи обратно на вход. Если обратная связь положительна, как в случае, когда звук из громкоговорителей усиливается через микрофон, она неудержимо растет и выходит из-под контроля. Но, если обратная связь отрицательна, как в механическом регуляторе паровых машин, впервые проанализированном Джеймсом Клерком Максвеллом, она может привести систему к равновесию; она служит источником стабильности (подробнее см. Обратная связь – основа поддержания и развития).
Первая книга Винера называлась «Кибернетика» и была опубликована осенью 1948 года сразу в США и во Франции с подзаголовком «Управление и связь в животном и машине». Книга была смесью определений и анализа и, к удивлению издателей, неожиданно стала бестселлером года. Заметная доля успеха трудной для понимания и неуклюжей книги Винера была связана с тем, что в центре внимания всегда оказывался человек, а не машина. Винер был заинтересован не в освещении развития вычислительной части теории, к которой он в любом случае имел отдаленное отношение, а скорее в том, как вычисления могут пролить свет на устройство человека.
Ученые-информатики хотели знать, на что способны их машины. Психологи хотели знать, является ли мозг компьютером или, скорее, только компьютером. В середине века информатика была новой наукой, и такой же новой была психология. К началу XX века в поисках строгости, проверяемости и, пожалуй, математизации исследователи разума разошлись по радикально противоположным путям, и путь Зигмунда Фрейда был лишь одним из многих. В США Уильям Джеймс почти в одиночку сконструировал дисциплину психологии: он стал профессором первого университетского курса и автором первого полного учебника и сдался, когда закончил его. Он писал, что его «Принципы психологии» были «противной, раздутой, опухшей, жирной, водянистой массой, не свидетельствующей ни о чем, кроме двух фактов: первый — что такой вещи, как наука психология, не существует и второй — что Уильям Джеймс некомпетентен».
В России новая разновидность психологии началась с физиолога Ивана Петровича Павлова, известного своим исследованием работы пищеварительной системы и получившим за нее Нобелевскую премию. Павлов отвергал и само слово «психология», и связанную с этой наукой терминологию. Единственное, что мог наблюдать ученый, — это поведение: его как минимум можно было записать и измерить. Бихевиористы, в частности Джон Б. Уотсон из США и затем Б. Ф. Скиннер, создали науку, которая основывалась на стимулах и реакции (см., например, Карен Прайор. Не рычите на собаку).
Но к середине столетия наступило разочарование. Чистота бихевиористов стала догмой, их отказ признавать существование психических состоянии — клеткой, а психологи все еще мечтали понять, что такое разум. Теория информации указала им путь. Ученые анализировали обработку информации и строили машины для этой обработки. У машин была память. Они воспроизводили способность к обучению и поиску цели.
Теория информации, сформулированная Шенноном, казалось, приглашает исследователей посмотреть в том направлении, о котором сам он и не помышлял. Он объявил: «Основополагающей проблемой связи является проблема воспроизведения, точно или приблизительно, в одной точке сообщения, выбранного в другой точке». Психолог вряд ли мог пропустить возможность рассмотреть ситуацию, когда отправителем сообщения был внешний мир, а получателем — человеческий разум.
Влиятельным коллегой Бродбента в США был Джордж Миллер, который в 1960 году помог создать Центр когнитивных исследований при Гарвардском университете. Это было началом движения, известного как когнитивная революция в психологии, и оно заложило основы дисциплины, названной когнитивной наукой (когнитивистикой), объединяющей психологию, информатику и философию. Некоторые философы впоследствии назвали этот момент информационным поворотом. Те, кто совершил информационный поворот, считают информацию основой, на которой построен мозг. Что касается кибернетики, то это слово стало угасать.
Глава 9. ЭНТРОПИЯ И ЕЕ ДЕМОНЫ
В начале своей истории слово энтропия обозначало обратное самому себе. И до сих пор ему мучительно трудно дать определение. Даже Oxford English Dictionary говорит об энтропии довольно туманно, что ему совершенно не свойственно: «Название одной из величин, с помощью которой определяется термодинамическое состояние части материи». Слово в 1865 году в процессе создания науки термодинамики придумал Рудольф Клаузиус. Ему нужно было как-то назвать определенное количество, которое он обнаружил, — количество, связанное с энергией, но не саму энергию.
Как заметил француз Николя Сади Карно, это похоже на водяное колесо: вода спускается сверху вниз, воды не становится больше или меньше, но во время своего движения она производит работу. Карно представлял себе тепло такой же субстанцией. Способность термодинамических систем производить работу зависит не столько от самого тепла, сколько от разницы температур горячего и холодного тела. Горячий камень, опущенный в холодную воду, способен производить работу — например, создавая пар, который вращает турбину, — но общее количество тепла в системе (камень плюс вода) остается постоянным. В конечном счете камень и вода достигнут одинаковых температур. Неважно, сколько энергии содержит замкнутая система: когда температура всех элементов одинакова, работа произведена не будет.
Именно эту недоступность энергии, ее бесполезность для работы Клаузиус и хотел измерить. Он придумал называть ее энтропией, взяв греческое слово, означающее «содержание преобразования». Энтропия не была видом энергии или ее количеством — это была, как сказал Клаузиус, недоступность энергии. Каким бы абстрактным ни было понятие, оказалось, что оно количественно измеримо, как температура, объем и давление.
Это понятие стало чрезвычайно важным. С энтропией законы термодинамики можно было выразить очень аккуратно:
- Закон первый: количество энергии во вселенной постоянно.
- Закон второй: энтропия вселенной всегда возрастает.
Максвелл первым начал внимательно изучать беспорядок как существенное свойство энтропии. Доступная энергия – есть энергия, которую мы можем направить в любой нужный нам канал. Рассеянная энергия есть энергия, которой мы не можем воспользоваться и распоряжаться по своему усмотрению, как энергия колебаний молекул, которую мы называем теплом.
Молекулы, каждая в отдельности, должны были подчиняться законам Ньютона — любое действие, любое столкновение измеряемо и вычислимо, по крайней мере в теории. Но слишком много нужно было измерять и вычислять отдельно. И на сцене появились вероятности. Новая наука статистической механики перекинула мост от микроскопических деталей к макроскопическому поведению. Предположим, что ящик с газом разделен перегородкой. Температура газа в половине А выше, чем в половине Б, то есть молекулы А движутся быстрее, с большей энергией. Как только перегородка убрана, молекулы начинают смешиваться, быстрые сталкиваются с медленными, энергия передается, и через некоторое время газ достигнет одинаковой температуры во всем объеме. Вопрос: почему этот процесс нельзя обратить? В уравнениях Ньютона для движения время может иметь как положительный, так и отрицательный знак, математика работает в обе стороны. Но в реальном мире прошлое и будущее нельзя просто поменять местами.
Такие процессы движутся только в одном направлении. Причина тому — вероятность. Примечательно, что физикам потребовалось много времени, чтобы принять то, что каждый необратимый процесс должен быть каким-то образом объяснен. Само время зависит от шанса, или «случайностей», как любил говорить Ричард Фейнман: «Ну, вы понимаете, что единственный вывод, к которому здесь можно прийти, заключается в том, что необратимость вызвана обычными случайностями» (подробнее см. Леонард Млодинов. Радуга Фейнмана. Поиск красоты в физике и в жизни). Физика не «запрещает» обратного разделения газа в коробке, просто вероятность этого события крайне мала. Поэтому второй закон попросту вероятностный: статистически все стремится к максимальной энтропии.
Вероятность (точнее, невероятность) того, что тепло перейдет от более холодного тела к более теплому (без помощи извне), идентична вероятности появления порядка из беспорядка (без помощи извне). На самом деле оба факта существуют лишь статистически. Если посчитать все возможные состояния системы, беспорядочных окажется гораздо больше упорядоченных. Существует множество способов организации или «состояний», в которых молекулы находятся в беспорядке, и очень немного таких, в которых они аккуратно вписаны в некую систему. Упорядоченные состояния имеют низкую вероятность и низкую энтропию.
Энтропия стала физическим эквивалентом вероятности: энтропия определенного макросостояния есть логарифм количества его возможных микросостояний. Значит, второй закон есть тенденция вселенной двигаться от менее вероятных (более упорядоченных) к более вероятным (беспорядочным) макросостояниям. Максвелл проиллюстрировал это мысленным экспериментом. Представим, предложил он, «существо», которое охраняет крохотную дырочку в перегородке, разделяющей сосуд с газом. Это создание может видеть приближающиеся молекулы, может определить, быстрые они или медленные, и может выбирать, пропускать их или нет. То есть способно изменить вероятность. Отсортировывая быстрые молекулы от медленных, оно может сделать сторону А горячее, а сторону Б холоднее, «и тем не менее никакой работы совершено не будет, задействованы только знания наблюдателя и сверхчувствительные пальцы существа».
Уильям Томсон (лорд Кельвин) назвал выдуманное существо демоном Максвелла. Демон видит то, чего не видим мы, потому что мы такие большие и медлительные, а именно то, что второй закон термодинамики является статистическим, а не механическим. На уровне молекул он по чистой случайности все время нарушается. Демон заменяет вероятность целью. Он использует информацию, чтобы исключить энтропию. Демон контролировал проход из мира физики в мир информации.
Через постоянно совершенствующиеся микроскопы ученые начала XX века изучали активный сортирующий процесс, выполняемый биологическими мембранами. Они обнаружили, что живые клетки работают как насосы, фильтры и фабрики. Целенаправленные процессы происходят в малых масштабах. Кто или что ими управляет?
Сама жизнь казалась организующей силой. Английский биолог Джеймс Джонстон в 1914 году писал: «Процессы земной жизни обратимы, следовательно, мы должны искать свидетельства того, что организм может управлять движением отдельных молекул». А Карл Эккарт утверждал: «Мышление порождает энтропию».
Для физика энтропия есть мера неопределенности состояния физической системы — одного из тех состояний, в которых может находиться система. Для ученого, занимающегося теорией информации, энтропия есть мера неопределенности сообщения — одного сообщения из тех сообщений, которые может произвести источник связи. Это не просто формальное совпадение: природа дает одинаковые ответы на одинаковые вопросы. Все это одна проблема. Чтобы уменьшить энтропию в сосуде с газом, выполнить полезную работу, приходится расплачиваться информацией. Аналогично, определенное сообщение сокращает энтропию.
Живые организмы не только борются с беспорядком вокруг себя, они сами по себе, их скелеты и плоть, везикулы и мембраны, панцири и раковины, листья и цветки, системы обращения и метаболические пути — чудеса структурирования и схематизации. Иногда кажется, что сдерживание энтропии является смыслом нашего существования во вселенной.
В 1943 году Эрвин Шредингер — первооткрыватель квантовой физики — выказал желание выступить с серией публичных лекций, решив, что пришло время ответить на один из самых великих безответных вопросов: «Что такое жизнь?» (см. Эрвин Шредингер. Что такое жизнь с точки зрения физика?). Шредингер начал с так называемой загадки биологической устойчивости. В противоположность сосуду с газом с его капризными вероятностями и флуктуациями, структуры живых существ проявляют замечательное постоянство. «Когда мы называем кусок материи живым?» — спросил он. — «Когда он продолжает «делать что-то», двигаться, обмениваться веществами с окружающей средой и т.д. в течение гораздо более длительного периода времени, чем мы ожидали бы от неодушевленного куска материи при схожих обстоятельствах».
Шредингер чувствовал, что живое существо «кажется таким загадочным» именно потому, что какое-то время избегает воздействия Второго закона. Способность организма симулировать вечное движение приводит к тому, что столько людей верят в специальную, сверхъестественную жизненную силу. Он посмеялся над этой идеей —vis viva. Нет, заявил он, организмы питаются отрицательной энтропией. Другими словами, организм высасывает порядок из окружающей среды.
Глава 10. СОБСТВЕННЫЙ КОД ЖИЗНИ
Коренная сущность каждого живого существа — не пламя, нетеплое дыхание и не «искра жизни», но информация, слова, инструкции. Если вы любите метафоры, то не представляйте себе огни, искры и дыхание, а представляйте себе миллиарды четких кодовых знаков, высеченных на гранях кристалла.
Ричард Докинз (1986)
В 1910 году датский ботаник Вильгельм Йохансон без особой шумихи придумал слово «ген». Ученый старался опровергнуть распространенную мифологию наследственности и думал, что новое слово сможет в этом помочь. Миф был таким: «личные качества» передаются от родителей к их потомству. Годы исследований Грегора Менделя с зеленым и желтым горохом показали, что штука, подобная гену, должна существовать. Мендель обнаружил ген, хотя и не назвал его. Ген был ему нужен скорее для алгебраического удобства, а не как физическая сущность.
Когда Шредингер размышлял о гене, перед ним встала проблема. Как могла такая «малюсенькая крупинка вещества» содержать весь сложнейший «план», зашифрованный сценарий, определяющий сложное развитие организма? Для разрешения этой проблемы Шредингер привел пример не из волновой механики или теоретической физики, а из телеграфии — из азбуки Морзе. Он заметил, что два знака, точка и тире, могут быть объединены в хорошо упорядоченные группы для передачи всего человеческого языка. Гены, предположил он, тоже должны использовать код: «Миниатюрный шифровальный код должен в точности соответствовать очень сложному и специфическому плану развития организма и каким-то образом содержать средства, способствующие его реализации».
Новая молекулярная биология начала изучать хранение и передачу информации. Джеймс Уотсон и Фрэнсис Крик нашли ген в 1953 г. То, что обнаружили ученые, стало иконой: двойная спираль ДНК. Их следующее замечание немедленно привлекло внимание по обе стороны Атлантики: «Таким образом, кажется вероятным, что точная последовательность оснований есть код, который несет генетическую информацию». Термины код и информация не были метафорами. Крик, который ради биологии ушел из физики, после того как прочитал книгу «Что такое жизнь?», послал Шредингеру копию их с Уотсоном статьи, но не получил ответа.
Код Геделя заменял математические выражения и операции обычными числами; генетический код использовал триплеты нуклеотидов для представления аминокислот. Даглас Хофштадтер был первым, кто обозначил эту связь понятным языком в 1980е: связь «между сложными процессами в живой клетке, которые позволяют молекуле ДНК воспроизводить самое себя, и умными машинами в математической системе, которые позволяют формуле сообщить нечто о самой себе». В обоих случаях он увидел петлю обратной связи. «Никто никогда ни в малейшей степени не подозревал, что один набор химических веществ может кодировать другой», — писал Хофштадтер (подробнее см. Даглас Хофштадтер. Гедель, Эшер, Бах. Эта бесконечная гирлянда).
Когда в начале 1960-х генетический код был расшифрован, некоторые единицы кода оказались избыточными; некоторые работают сигналами начала и конца. Избыточность дает устойчивость к ошибкам. Шум влияет на биологические сообщения так же, как и на любые другие. Ошибки в ДНК, опечатки, называются мутациями. Крик выразил фундаментальные принципы в утверждении, которое назвал центральной догмой: «Как только «информация» передана в белок, она не может снова попасть наружу. Более подробно, передача информации от нуклеиновой кислоты к нуклеиновой кислоте или от нуклеиновой кислоты к белку возможна, а передача от белка к белку или от белка к нуклеиновой кислоте — нет. Под информацией здесь понимается точное определение последовательности». Генетическое сообщение независимо и хорошо защищено: никакая информация, поступающая извне, не может его изменить.
Молодой зоолог из Оксфорда Ричард Докинз в своей первой книге, опубликованной в 1976 году, предназначенной для широкой аудитории, с провокационным названием «Эгоистичный ген» заявил: «Мы всего лишь машины для выживания, самоходные транспортные средства, слепо запрограммированные на сохранение эгоистичных молекул, известных под названием генов». Гены, а не организмы являются единицами естественного отбора. Они возникли как «репликаторы» — молекулы, случайно сформированные в первородном супе, обладающие необычным свойством создавать копии самих себя.
Докинз заявил: «Ген — это не несущая информацию макромолекула. Ген есть сама информация. Пары оснований ДНК не есть гены. Они кодируют гены. Сами гены состоят из битов».
Глава 11. В МЕМОФОН
Парижский биолог Жак Моно, лауреат Нобелевской премии в 1970 году предложил аналогию: точно так же, как биосфера находится выше мира неживой природы, «царство абстракции» поднимается над биосферой. Кто они, обитатели этого царства? Идеи. Идеи сохранили некоторые свойства организмов. Как и последние, они имеют тенденцию к сохранению структуры и размножению, они тоже могут сливаться, рекомбинировать, сегрегировать один из своих компонентов; разумеется, они тоже могут развиваться, и, без сомнения, в этом развитии естественный отбор должен играть важную роль.
Ричард Докинз по-своему связал эволюцию генов и идей: «Думаю, что на этой планете недавно появилась новая разновидность репликаторов… — объявил Докинз в конце своей первой книги в 1976 году. — Они бросаются в глаза. Они все еще на стадии младенчества, все еще неуклюже дрейфуют в своем первобытном супе, но уже добиваются эволюционных изменений с такой скоростью, которая оставляет старый ген пыхтеть далеко позади». Этот «суп» есть человеческая культура; вектор передачи есть язык; плодородная почва — мозг. Докинз предложил название для самого бесплотного репликатора. Он назвал его «мем».
Философ Дэниел Деннет заметил: «Фургон со спицевыми колесами перемещает не только зерно или груз с места на место, он также перемещает и гениальную идею фургона со спицевыми колесами от разума к разуму» (подробнее см. Дэниел Деннетт, Даглас Хофштадтер. Глаз разума).
Мы являемся переносчиками мемов и делаем возможным их существование. Мемы могли путешествовать не только посредством слов еще до появления языка. Простого подражания достаточно, чтобы передать знание. Среди животных шимпанзе и гориллы известны способностью перенимать поведение путем имитации. Несмотря на эти специальные случаи, большую часть истории человека мемы и язык шли рука об руку. Язык служит первым катализатором формирования культуры. Он намного мощнее простой имитации, поскольку распространяет знание через абстракцию и кодирование.
По мере того как кривая информации склоняется по направлению к все большим возможностям связи, мемы развиваются быстрее и распространяются дальше. Их присутствие чувствуется, если не наблюдается воочию, в проявлениях стадного чувства, в паническом изъятии вкладов из банков, кумулятивном эффекте при продвижении информации и финансовых пузырях. Ощутить присутствие мемов можно было в глобальном мировом дискурсе последнего года тысячелетия, когда доминировала уверенность в том, что все компьютеры мира начнут заикаться или поперхнутся, когда их внутренние часы достигнут некоторого особенно круглого числа.
Большая часть биосферы не может видеть инфосферу; она невидима, это параллельная вселенная, кишащая призрачными обитателями. Но для нас они не призраки, больше не призраки. Мы, люди, — единственные среди органических созданий на Земле, кто живет в обоих мирах сразу.
Глава 12. СМЫСЛ СЛУЧАЙНОСТИ
«Случай — это лишь мера нашего неведения, — сказал Анри Пуанкаре. — Феноменами случайности являются по определению те, законы которых мы не знаем» (см. также бестселлер Леонарда Млодинова (Не)совершенная случайность. Как случай управляет нашей жизнью).
Метод симуляции Монте-Карло для моделирования феноменов, не поддающихся аналитическим решениям, включал в себя случайную выборку (подробнее см. Использование метода Монте-Карло для расчета риска). Симуляция Монте-Карло была придумана польским математиком Станиславом Уламом в рамках проекта создания атомной бомбы командой фон Неймана, отчаянно пытавшейся сгенерировать случайные числа для расчета диффузии нейтронов (см. Станислав Улам. Приключения математика). Фон Нейман понимал, что механическая вычислительная машина с ее детерминированными алгоритмами и конечным объемом памяти никогда не сможет сгенерировать по-настоящему случайные числа. Ему придется довольствоваться псевдослучайными.
Число (как мы теперь понимаем) есть информация. Когда современные люди, наследники Шеннона, думают об информации в ее наивысшей, чистой форме, они могут представить себе строку из нулей и единиц, двоичное число. Вот два двоичных числа по пятьдесят знаков каждое:
А: 01010101010101010101010101010101010101010101010101
Б: 10001010111110101110100110101000011000100111101111
Если Алиса (А) и Боб (Б) говорят, что сгенерировали свои строки, подбрасывая монету, никто никогда не поверит Алисе. Строки, без всяких сомнений, не одинаково случайны. Классическая теория вероятностей не дает никаких оснований считать, что строка Б более случайна, чем строка А, потому что случайный процесс может дать любую из строк. Вероятность говорит о множествах, а не об отдельных событиях. Теория вероятностей рассматривает события статистически. Она не любит вопросов в форме «насколько вероятно, что это случится?». Что случилось, то случилось.
Шеннон рассматривал бы эти строки как сообщения. Он спросил бы: «Сколько информации содержит каждая из строк?» У оператора телеграфа, посылающего сообщение А, есть способ упростить работу: он может передать что-нибудь вроде «Повторить 01 двадцать пять раз». Для длинных сообщений с простыми закономерностями экономия нажатий на клавиши становится огромной. Как только понята закономерность, дополнительные знаки бесплатны. Оператору, передающему сообщение Б, придется передать каждый знак, потому что каждый знак в этом сообщении абсолютно непредсказуем; каждый знак несет один бит информации. Эта пара вопросов — насколько случайно и как много информации — оказывается одним и тем же вопросом.
Тьюринг назвал свою великую статью «О вычислимых числах», но, конечно, его внимание на самом деле было посвящено не вычислимым числам. Могут ли быть связаны невычислимые и случайные числа? В 1965 году Грегори Хайтин предположил: число не является случайным, если оно вычислимо — если определенная компьютерная программа его сгенерирует. Таким образом, вычислимость есть мера случайности (см. также Грегори Хайтин. Пределы доказуемости).
Хайтин применил алгоритмическую теорию информации к самому процессу научного познания. Предположим, в процессе эксперимента ученый получил последовательность:
0110101110…
которая продолжается еще несколько тысяч битов. Последовательность из 0 и 1 незакономерна, если только не существует лучшего способа вычислить ее, чем просто описать всю целиком из таблицы, где она представлена полностью. Но если ученый смог найти способ сгенерировать такую же последовательность с помощью алгоритма, компьютерной программы, существенно более короткой, чем сама последовательность, то тогда он с уверенностью может сказать, что события не были случайными. Он скажет, что наткнулся на теорию.
Хайтин послал свою статью в Journal of the Association for Computing Machinery. Там были рады ее опубликовать, но один из рецензентов упомянул, что до него доходили слухи об аналогичной работе из Советского Союза. И действительно, в начале 1966 года прибыл первый выпуск нового журнала «Проблемы передачи информации», и в нем была статья, озаглавленная Три подхода к определению понятия «количество информации» академика А. Н. Колмогорова. У Хайтина, который не читал по-русски, хватило времени только на то, чтобы добавить сноску.
Колмогоров описал три подхода: комбинаторный, вероятностный и алгоритмический. Он ввел новое слово для того, что он пытался измерить, — сложность. Сложность объекта он определил, как размер наименьшей компьютерной программы, необходимой для его создания. Колмогоров, анализируя динамические системы в терминах энтропии и информации, начал закладывать фундамент для возрождения теории хаоса, которая возникнет в 1970-е (см. Джеймс Глейк. [2] Хаос. Создание новой науки). Имело смысл сказать, что динамическая система производит информацию. Если она непредсказуема, она производит очень много информации.
Эйнштейн не хотел верить в то, что Господь играет в кости со Вселенной. Как сказал Хайтин, «Бог играет в кости не только в квантовой физике и нелинейной динамике, но даже в элементарной теории чисел». Среди его уроков были следующие.
- Большинство чисел случайно. Тем не менее доказать случайность можно для очень немногих из них.
- Хаотичный поток информации может скрывать простой алгоритм. Пройти путь назад от хаоса к алгоритму, скорее всего, невозможно.
- Сложность Колмогорова — Хайтина (КХ) в математике означает то же, что энтропия в термодинамике, — антидот совершенству. Точно так же, как не может быть вечного двигателя, не может существовать полной формальной аксиоматической системы.
- Некоторые математические факты истинны без причины. Они случайны, у них нет обоснования или более глубокого, скрытого значения.
Эпилог
МТИ учредил Центр коллективного разума, целью которого является поиск групповой мудрости и ее «использование». Все еще непонятно, насколько можно доверять мудрости толпы (заголовок книги Джеймса Шуровьески, выпущенной в 2004 году, не путать с безумством толпы, описанным в 1841 году Чарльзом Макеем, который объявил, что люди «сходят с ума толпами, а приходят в себя медленно и поодиночке»). Толпы очень быстро превращаются в группы с веками известным поведением — маниями, мыльными пузырями, линчующими бандами, флешмобами (подробнее см. Джеймс Шуровьески. Мудрость толпы).
В 2008 году Google создал систему раннего предупреждения регионального распространения гриппа, основанную всего лишь на частоте веб-поиска по слову «грипп». Система обнаруживала вспышки болезни на неделю раньше, чем Центры контроля и предотвращения заболеваний. Это был традиционно гугловский подход к решению классических трудных проблем искусственного интеллекта — машинный перевод и распознавание голоса, но не с помощью людей-экспертов или словарей и лингвистов, а с помощью собственной прожорливой системы сбора данных из триллионов слов на более чем трех сотнях языков. Если на то пошло, исходная стратегия интернет-поиска Google основывалась на привлечении коллективного знания.
Литература на русском языке
Айзексон. У. Бенджамин Франклин. – М.: Манн, Иванов и Фербер, 2015.
Винер Н. Кибернетика. – М.: Наука, 1983.
Витгенштейн Л. Избранные работы. – М.: Территория будущего, 2005.
Витгенштейн Л. Философские исследования. – М.: ACT; Астрель, 2011.
Глейк Дж. Хаос. Создание новой науки. – СПб.: Амфора, 2001.
Деннетт Д., Хофштадтер Д. Глаз разума. – Самара: Издательский дом «Бахрах-М», 2003.
Докинз Р. Расширенный фенотип. М.: ACT; Астрель; Corpus, 2010.
Докинз Д. Слепой часовщик. Как эволюция доказывает отсутствие замысла во Вселенной. – 2014.
Докинз Р. Эгоистичный ген. – М.: ACT; Corpus, 2013.
Колмогоров А. Н. Избранные труды: в 6 т. – М.: Наука, 2007.
Ланир Дж. ВЫ не гаджет. – М.: Астрель; Corpus, 2011.
Лонгфелло Г. Скачка Пола Ривера.
Маклюэн М. Галактика Гутенберга. Становление человека печатающего. – М.: Издательство: Академический Проект, 2015.
Млодинова Л. (Не)совершенная случайность. Как случай управляет нашей жизнью. – М.: Livebook/Гаятри, 2010.
Млодинов Л. Радуга Фейнмана. Поиск красоты в физике и в жизни. – М.: Лайвбук, 2014.
Нагель Э., Ньюмен Дж. Р. Теорема Гёделя. – М.: Красанд, 2010.
Петцольд Ч. Читаем Тьюринга. – М.: ДМК Пресс, 2014 г.
По Э. А. Полное собрание рассказов в одном томе. – М.: Эксмо, 2011.
По Э. А. Стихотворения, проза. – М.: Художественная литература, 1976.
Прайор К. Не рычите на собаку. – М.: Эксмо, 2009.
Рассел Б. Человеческое познание, его сферы и границы. – Киев: Ника-Центр, 2001.
Уилер Дж. А. Предвидение Эйнштейна. – М.: Мир, 1970.
Ходжес Э. Игра в имитацию. – М.: АСТ, 2015.
Хофштадтер Д. Гедель, Эшер, Бах. Эта бесконечная гирлянда. – Самара: Издательский дом «Бахрах-М», 2001.
Шеннон К. Работы по теории информации и кибернетике. – М.: Издательство иностранной литературы, 1963.
Шредингер Э. Что такое жизнь с точки зрения физика? – М.: Римис, 2009.
Шуровьески Дж. Мудрость толпы. – М: ООО «И. Д. Вильямс», 2007.
[1] Даже я в школе изучал логарифмическую линейку и таблицы Брадиса.
[2] «Хаос…» и «Информацию…» написал один и тот же человек – James Gleick. Только раньше его фамилию перевели, как Глейк, а сейчас, как Глик))