Казалось бы, термин «большие данные» понятен и доступен только специалистам. Но автор этой книги доказывает, что анализ данных можно организовать и в простом, понятном, очень эффективном и знакомом многим Excel. Причем не важно, насколько велик ваш массив данных. Техники, предложенные в этой книге, будут полезны и владельцу небольшого интернет-магазина, и аналитику крупной торговой компании. Вы перестанете бояться больших данных, научитесь видеть в них нужную вам информацию и сможете проанализировать предпочтения ваших клиентов и предложить им новые продукты, оптимизировать денежные потоки и складские запасы, другими словами, повысите эффективность работы вашей организации.
Джон Форман. Много цифр: Анализ больших данных при помощи Excel. – М.: Альпина Паблишер, 2016. – 464 с.
Скачать заметку в формате Word или pdf, примеры в формате Excel
Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon или Лабиринте
Содержание
Глава 1. Общие сведение о программе Excel
Глава 2. Кластерный анализ с использованием метода k-средних
Глава 3. Наивный байесовский классификатор документов
Глава 4. Линейное программирование
Глава 5. Кластерный анализ: сетевые графы и определение сообществ
Глава 6. Регрессия, как инструмент контролируемого искусственного интеллекта
Глава 7. Комплексное моделирование или бэггинг (bagging)
Глава 8. Прогнозирование на основе экспоненциального сглаживания
Глава 9. Определение выбросов
Глава 10. Использование R
См. Алексей Шипунов. Наглядная статистика. Используем R!
Введение. Я использую следующее определение: «Наука о данных — это трансформация данных методами математики и статистики в рабочие аналитические выводы, решения и продукты». Примеры (на английском языке) можно скачать на сайте издательства. Все примеры в книге приведены для английского Excel 2011 под управлением MacOS. В настоящей заметке – для русского Excel 2013 под Windows.
Глава 1. Все, что вы жаждали знать об электронных таблицах, но боялись спросить
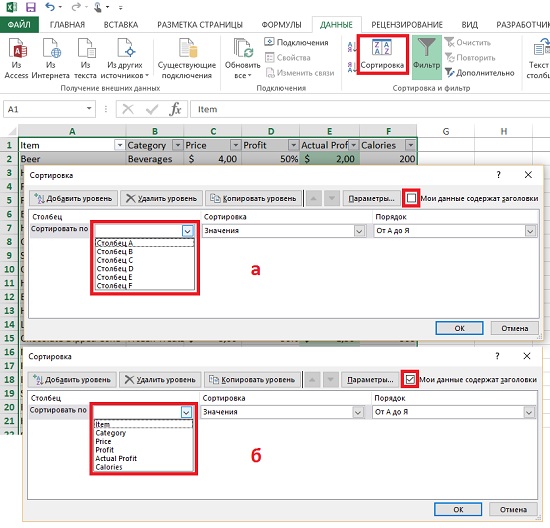
Сортировка. Опция содержит две редко используемые возможности. Выделите область, которую вы хотите отсортировать, пройдите по меню ДАННЫЕ –> Сортировка. В открывшемся окне Сортировка посмотрите, как реагирует выпадающее меню Сортировать по на наличие или отсутствие галки в позиции Мои данные содержат заголовки (рис. 1).
Рис. 1. Влияние опции Мои данные содержат заголовки на сортировку
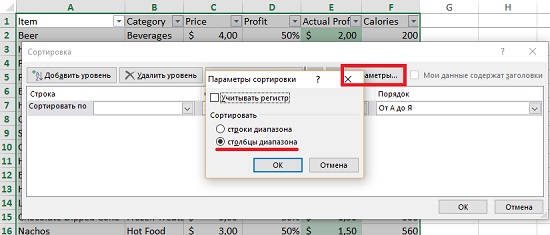
Теперь самая потрясающая часть этого интерфейса, скрытая под кнопкой Параметры. Нажмите ее, чтобы отсортировать данные слева направо вместо сортировки строк (рис. 2). В результате столбцы разместятся по алфавиту.
Рис. 2. Сортировка по столбцам
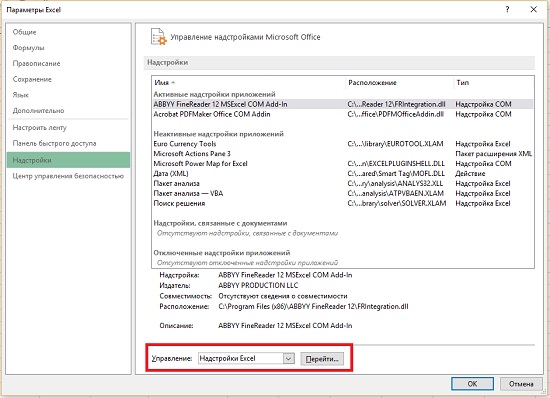
Решение задач с помощью надстройки Поиск решения. В Excel проблемы оптимизации решаются с помощью встроенного модуля под названием Поиск решения. Кнопка Поиск решения находится на вкладке ДАННЫЕ. Если вы не видите ее, пройдите по меню Файл –> Параметры –> Надстройки. В нижней части окна Параметры Excel в области Управление выберите Надстройки Excel и кликните Перейти (рис. 3).
Рис. 3. Параметры Excel
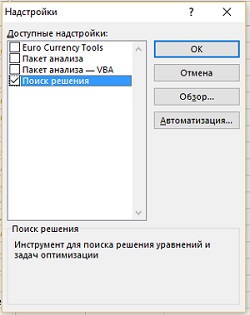
В открывшемся окне Надстройки поставьте галочку напротив Поиск решения и кликните Ok. Кнопка Поиск решения появится в разделе Анализ вкладки ДАННЫЕ.
Рис. 4. Инсталляция надстройки Поиск решения
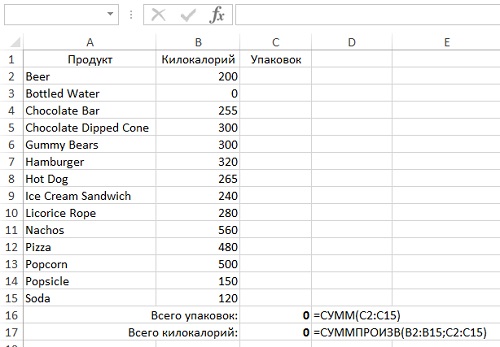
Чтобы заставить Поиск решения искать решение, нужно задать ему пределы ячеек, в которых следует вести поиск. Допустим мы хотим узнать минимальное число упаковок с различными продуктами, которые дают в точности 2400 ккал. Подготовьте лист Excel, как показано на рис. 5 (в ячейках D16 и D17 показаны формулы, вбитые в ячейки С16 и С17 соответственно). Во время работы надстройки Поиск решения Excel рассчитает значения всех ячеек в диапазоне С2:С15. А пока он считает их равными нулю, так что вам не нужно заполнять их перед началом работы.
Рис. 5. Настройка модели для работы оптимизационного алгоритма Поиск решения
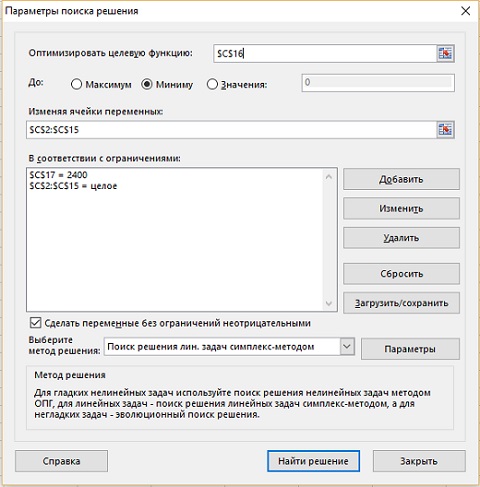
Теперь вы готовы к построению модели, так что кликайте на кнопке Поиск решения. В открывшемся окне Параметры поиска решения выберите ячейку, которая содержит целевую функцию (рис. 6). В нашем случае – $C$16. Мы хотим найти минимум, что отражено с помощью переключателя в следующей строке. Область, в которой можно изменять значения [для поиска оптимума] – $C$2:$C$15. Ограничений два: в сумме ровно 2400 ккал (это значение из ячейки $C$17); все изменяемые значения (переменные) – целые. Также проставлена галка, что все переменные должны быть неотрицательными. И последнее, выбран метод решения – линейный симплекс-метод (в окне Метод решения приведена подсказка, какой метод выбирать, в каких случаях).
Рис. 6. Окно модели Параметры поиска решения
Чтобы добавить ограничение, кликните справа Добавить. Чтобы отредактировать имеющееся ограничение, выберите его и кликните Изменить.
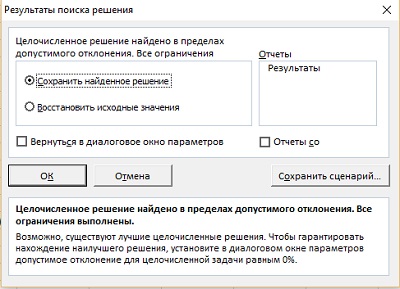
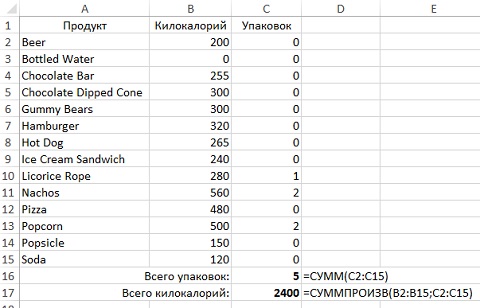
Нажмите Найти решение. Надстройка поработает некоторое время, и выдаст промежуточное окно Результаты поиска решения (рис. 7). Кликните Ok. Найденное решение в виде значений в диапазоне $C$2:$C$15 отразится на листе (рис. 8).
Рис. 7. Окно Результаты поиска решения
Рис. 8. Оптимизированный выбор покупок
OpenSolver – дополнительная бесплатная надстройка, которая может быть полезна для поиска решения в большом массиве данных. Работает быстрее, чем стандартная надстройка Excel, и обладает более широкими возможностями. Скачайте архив с сайта http://opensolver.org. Распакуйте всё содержимое в любую папку на локальном диске и дважды кликните на файле OpenSolver.xlam (нигде в пути к папке не должны содержаться символы unicode, в частности – русские буквы). Надстройка появится на вкладке ДАННЫЕ (рис. 9).
Рис. 9. Инсталляция надстройки OpenSolver
OpenSolver распознает ранее введенную в Поиск решения модель, и сразу же готова к работе с ней. Просто нажмите на кнопку Solve. Любопытно, что OpenSolver предложит иное решение – 5 упаковок пиццы по 480 ккал (сравни с решением на рис. 8).
Глава 2. Кластерный анализ, часть I: использование метода k-средних для сегментирования вашей клиентской базы
Когда вы имеете дело с множеством людей, трудно изучить каждого клиента в отдельности. Нужно взять клиентскую базу и найти золотую середину между «бомбардировкой» наобум и персонализированным маркетингом для каждого отдельного покупателя. Один из способов достичь такого баланса — использование кластеризации для сегментирования рынка. Кластеризация называется разведочной добычей данных, потому что эти техники помогают «вытянуть» информацию о связях в огромных наборах данных, которые не охватишь визуально. Самый простой способ кластеризации – метод k-средних.
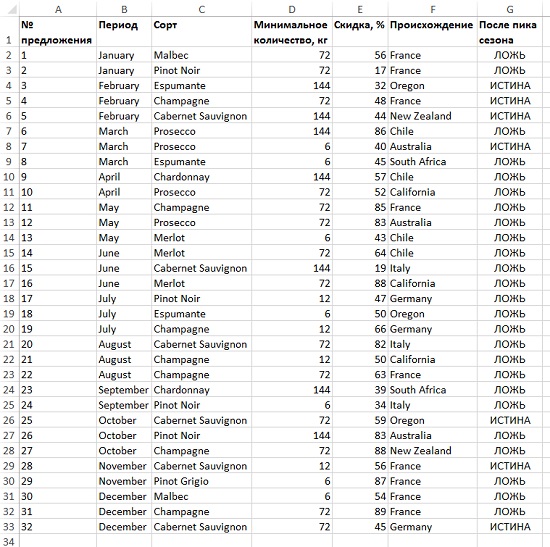
Рассмотрим пример. Вы продаете вина, и в течение года разослали 32 предложения (рис. 10).
Рис. 10. Детали последних 32 предложений
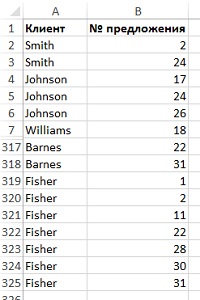
Ваши покупатели откликнулись на эти предложения различным образом, что нашло отражение в базе данных заказов (рис. 11).
Рис. 11. Список заказов в разрезе предложений и покупателей
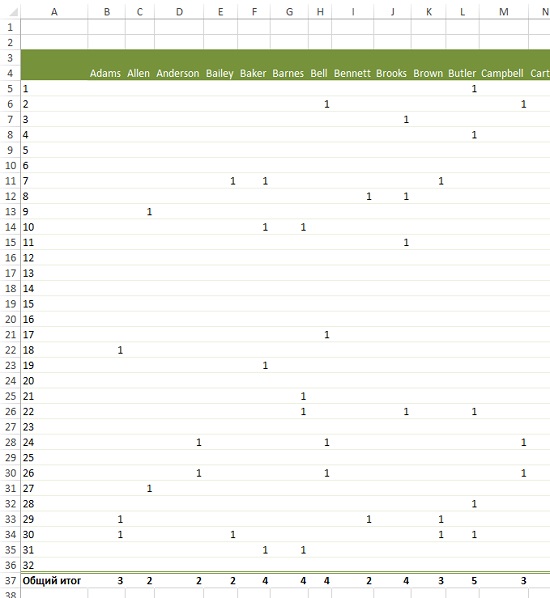
Начните обработку с создания матрицы «клиент – предложение». Для этого постройте сводную таблицу на основе списка заказов (см. рис. 11), расположив предложения по строкам, а покупателей – по столбцам (рис. 12). Если вы не использовали ранее сводные таблицы, рекомендую Билл Джелен, Майкл Александер. Сводные таблицы в Microsoft Excel 2013.
Рис. 12. Сводная таблица «клиент – предложение»
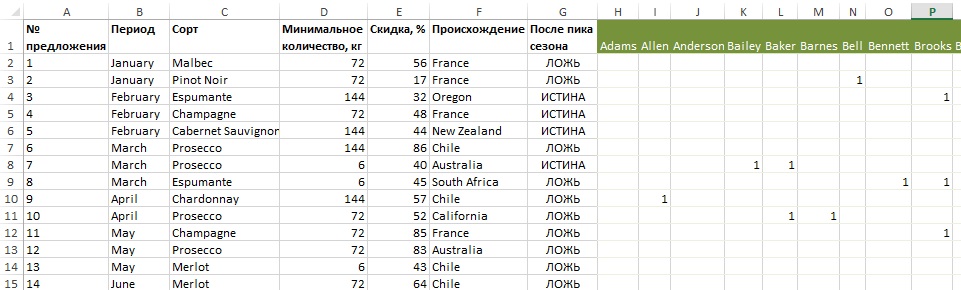
Соедините таблицу предложений (см. рис. 10) и матрицу «клиент – предложение» (см. рис. 12), как показано на рис. 13.
Рис. 13. Описание предложений и данные о заказах, слитые в единую таблицу (чтобы увеличить изображение, кликните на нем правой кнопкой мыши, и выберите Открыть картинку в новой вкладке)
Примечание. В настоящем примере каждое измерение данных представлено одинаково, в виде бинарной информации о заказах. Вообразите сценарий, в котором люди кластеризованы по росту, весу и зарплате. Эти три вида данных имеют разную размерность. Чтобы провести кластерный анализ данные сначала нужно стандартизовать. Для этого по каждому столбцу вычисляют среднее и среднеквадратичное отклонение. Далее из каждого значения вычитают среднее и затем делят поочередно на среднеквадратичное отклонение. Таким образом, все столбцы приводятся к единой безразмерной величине, варьируемой около 0.
Чтобы начать кластерный анализ, нужно выбрать k — количество кластеров в алгоритме k-средних. Позднее мы изучим, как выбирать значение k. Пока же просто допустим, что k = 4. Т.е., вы намерены разбить 100 ваших клиентов на 4 кластера.
Вставьте в таблицу (см. рис. 13) четыре столбца (от Н до К), которые будут кластерными центрами. Вы можете применить к ним условное форматирование, чтобы визуально увидеть, насколько они отличаются. Поскольку клиентские векторы бинарны (принимают лишь значения 0 и 1), то расстояния между каждым покупателем и его кластерным центром будут иметь значения от 0 до 1.
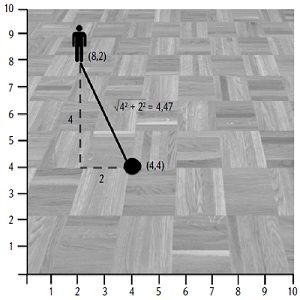
Но что означает «измерить расстояние между кластерным центром и покупателем»? В двумерном пространстве кратчайшее расстояние определяется на основе теоремы Пифагора: гипотенуза (кратчайшее расстояние) равна корню квадратному из суммы квадратов катетов (рис. 14).
Рис. 14. Кратчайшее расстояние равняется квадратному корню из суммы квадратов расстояний по каждой оси
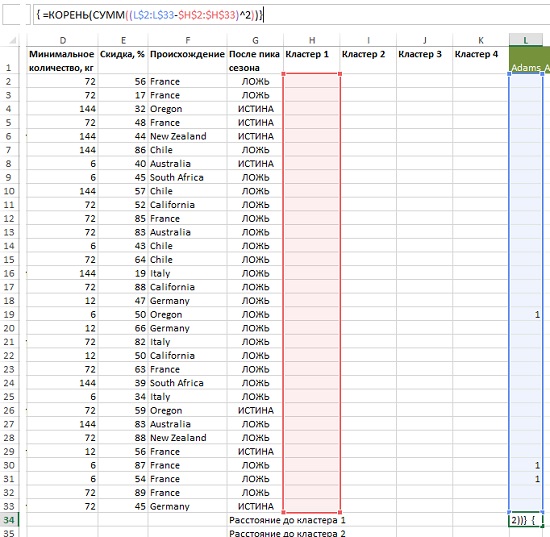
В нашем винном примере расстояние между покупателем и кластерным центром рассчитывается также, но для 32-мерного пространства (32 различных предложения) по формуле (рис. 15):
{=КОРЕНЬ(СУММ((L$2:L$33-$H$2:$H$33)^2))}
Рис. 15. Расстояние между центром кластера 1 и Адамсом
Фигурные скобки означают, что это формула массива. Не вводите эти скобки с клавиатуры, а наберите формулу =КОРЕНЬ(СУММ((L$2:L$33-$H$2:$H$33)^2)) и нажмите одновременно Ctrl+Shift+Enter. (Если ранее вы не использовали такие формулы, рекомендую Excel. Введение в формулы массива.) Обратите внимание на абсолютные и смешанные ссылки, подготавливающие формулу для копирования вправо или вниз без изменения ссылки на кластерный центр (подробнее см. Относительные, абсолютные и смешанные ссылки на ячейки в Excel).
Результат формулы в ячейке L34 – 1,732 – имеет следующий смысл: Адамс заключил три сделки, но так как изначальные кластерные центры (Н2:Н33) — нули, ответ будет равняться квадратному корню из 3, а именно 1,732.
Скопируем формулу из ячейки L34 вниз до L37. Заменим в ячейках L35:L37 ссылку на кластер 1 на ссылку на кластеры 2–4 соответственно. Скопируем формулы в ячейках L34:L37 вправо до ячеек DG34:DG37. Значения во всех этих ячейках пока просто равны корню квадратному из числа сделок. Например, Baker заключил 4 сделки, и значения в ячейках Р34:Р37 равны корню квадратному из 4, т.е., 2.
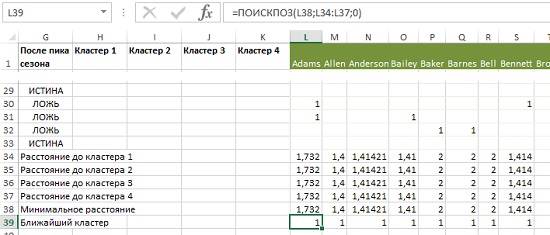
Добавьте еще одну строку – Минимальное расстояние, которое вычисляется по формуле =МИН(L34:L37). И, наконец, последняя строка – Ближайший кластер. Для расчета используем формулу =ПОИСКПОЗ(L38;L34:L37;0). В данном случае расстояние одинаково для всех четырех кластеров, так что формула выбирает первый (L34) и возвращает 1 (рис. 16). Скопируйте формулы в ячейках L38:L39 вправо до конца таблицы.
Рис. 16. Добавление в модель привязки к кластерам
Теперь, чтобы установить наилучшее положение кластерных центров, нужно найти такие значения в столбцах Н:К, которые минимизируют общее расстояние между покупателями и кластерными центрами, к которым они привязаны. Для этого в ячейке А36 введем формулу =СУММ(L38:DG38). Именно это значение в ячейке А36 мы и будем минимизировать с помощью Поиска решения. Поскольку расстояние со своими степенями и квадратными корнями — чудовищно нелинейная функция, для оптимизации используем эволюционный алгоритм. Надстройка OpenSolver не справится с задачей, так как она использует только симплексный алгоритм.
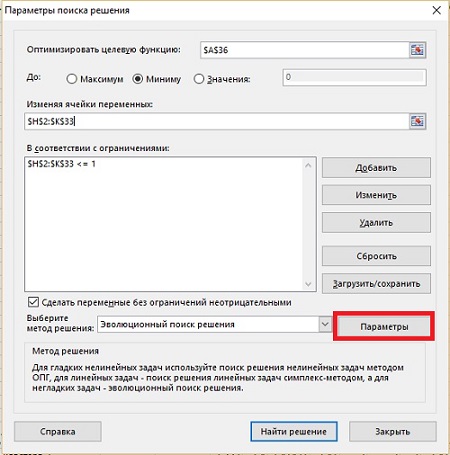
Кликаем кнопку ДАННЫЕ –> Поиск решения, и вводим параметры модели (рис. 17). В окне Параметры поиска решения кликните на кнопке Параметры, и настройте работу Эволюционного алгоритма (рис. 18). Нажмите Ok, и вернитесь в окно Параметры поиска решения.
Рис. 17. Параметры Поиска решения для 4-центровой кластеризации
Рис. 18. Параметры эволюционного алгоритма
Нажмите Найти решение и наблюдайте, как Excel делает свое дело, пока эволюционный алгоритм не сойдется (рис. 19). Десяти минут не хватило для завершения работы алгоритма, и, когда, появилось соответствующее оповещение, я кликнул Продолжить. В результате я получил значение целевой функции даже меньше, чем в книге: 140,3 против 140,7.
Рис. 19. Отображение промежуточных результатов во время работы эволюционного алгоритма
По окончанию работы алгоритма открывается окно Результаты поиска решения (рис. 20). Кликните Ok.
Рис. 20. Результаты поиска решения
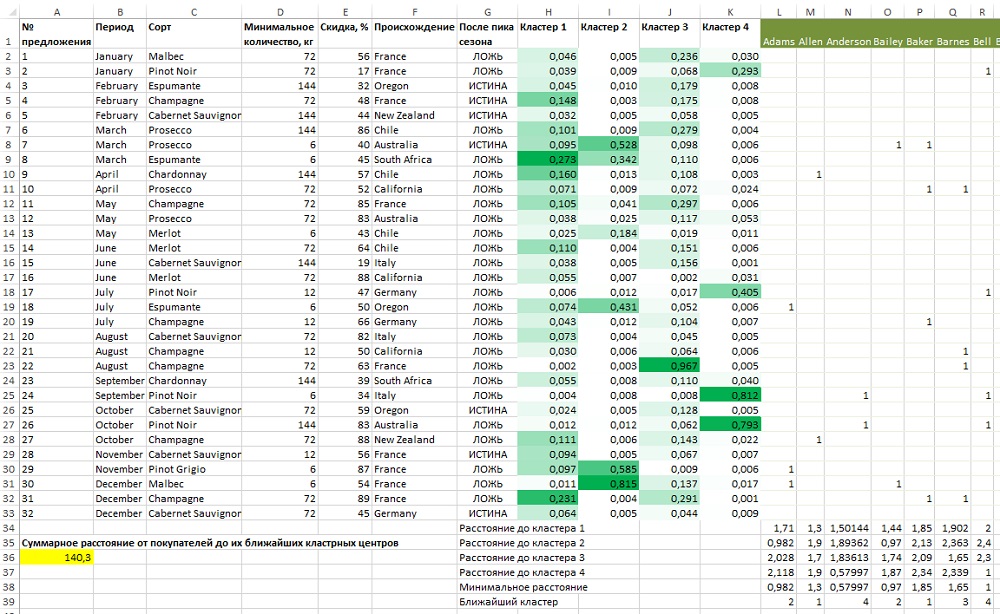
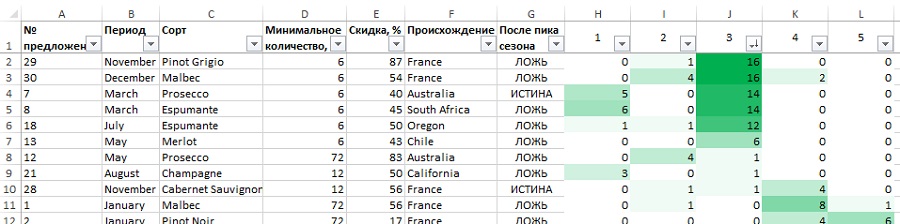
Завершив работу, Поиск решения выдает оптимальные кластерные центры (рис. 21), которые, благодаря условному форматированию выглядят совершенно по-разному. Имейте в виду, что ваши кластерные центры могут отличаться от представленных на рис. 21 и в моем Excel-файле с примерами, потому что эволюционный алгоритм использует случайные числа и ответ каждый раз получается разный. Кластеры могут быть совершенно другими или, что более вероятно, располагаться в другом порядке.
Для кластера 4 в столбце К условное форматирование выбирает предложения 24, 26 и, в меньшей степени, 2 и 17. Прочитав описание этих предложений, можно понять, что у них общего: они все касались сорта Pinot Noir. Взглянув на столбец I, видно, что во всех зеленых ячейках низкое минимальное количество – 6 кг. Это покупатели, которые не желают приобретать большие партии. А вот два остальных кластерных центра интерпретировать сложно. Вместо интерпретации кластерных центров, можно изучить самих покупателей в кластере и определить, какие предложения им нравятся.
Рис. 21. Четыре оптимальных кластерных центра
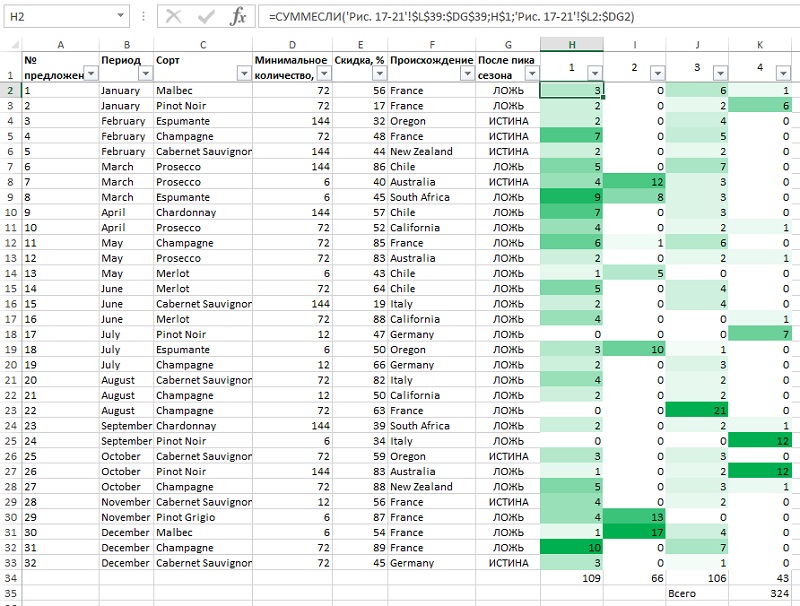
Сосчитаем предложения по кластерам с помощью формулы =СУММЕСЛИ(‘Рис. 17-21′!$L$39:$DG$39;H$1;’Рис. 17-21’!$L2:$DG2). Обратите внимание, что вид ссылок подобран таким образом, чтобы формулу можно было копировать по строкам и столбцам. Чтобы данные были более наглядными, примените к столбам Н:К условное форматирование (рис. 22).
Рис. 22. Общее количество сделок по каждому предложению, разбитое по кластерам
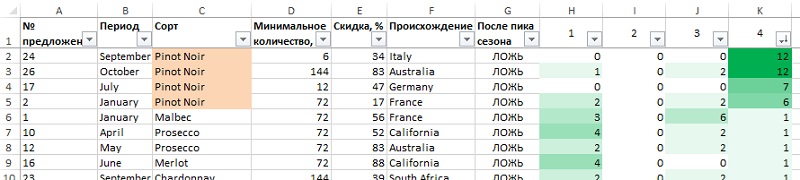
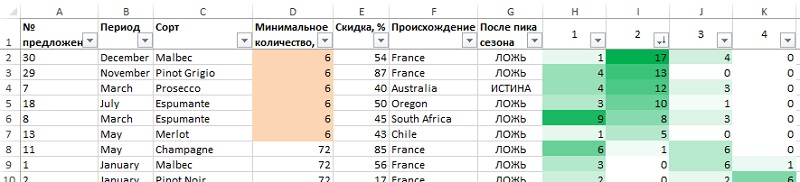
Выделите столбцы А:К и примените к ним автофильтрацию. Отсортировав от наибольшему к наименьшему по столбцу К, увидим, какие предложения наиболее популярны в кластере 4 (рис. 23). Если вы отсортируете кластер 2, то вам станет совершенно ясно, что это — мелкооптовые покупатели (рис. 24). Сортировка предложений по кластерам 1 и 3 не так показательна. Может быть, в информации о предложениях не хватает чего-то такого, что могло бы помочь понять кластеры лучше?
Рис. 23. Сортировка предложений в кластере 4. Любители Pinot Noir
Рис. 24. Сортировка предложений в кластере 2. Мелкооптовики
Как узнать, насколько хорошо подходит выбранное нами значение 4 для кластеризации по k-средним? Для этого используется показатель силуэт. Прелесть его в том, что он независим от значения k.
Вы можете сравнить среднее расстояние между каждым покупателем и его друзьями из его же кластера и покупателями из соседних кластеров. Если я немного ближе к членам своего кластера, чем соседнего, то это говорит об удачной кластеризации. Вот, как это можно записать формально:
Силуэт = (Среднее расстояние до членов ближайшего соседнего кластера – Среднее расстояние до членов своего кластера)/Максимум из этих двух средних
Значение силуэта изменяется от –1 до +1. Чем дальше от вас находящиеся в соседнем кластере (и чем менее они вам подходят), тем ближе к +1 значение силуэта. А если два средних расстояния почти одинаковы, то силуэт стремится к 0. Вы можете сравнить силуэты для различных значений k, чтобы увидеть, какое из них лучше.
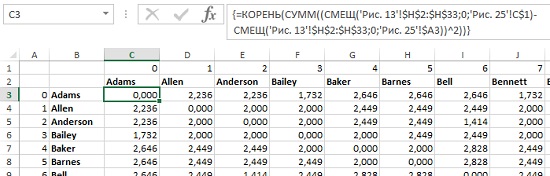
Для начала создайте матрицу расстояний между покупателями (рис. 25). В ячейке С3 используется формула {=КОРЕНЬ(СУММ((СМЕЩ(‘Рис. 13′!$H$2:$H$33;0;’Рис. 25’!C$1)-СМЕЩ(‘Рис. 13′!$H$2:$H$33;0;’Рис. 25’!$A3))^2))}. И это снова формула массива. Если вы не знакомы с функцией СМЕЩ, рекомендую Excel. Примеры использования функции СМЕЩ (OFFSET). Естественно, что расстояния по диагонали матрицы равны нулю.
Рис. 25. Матрица расстояний между покупателями
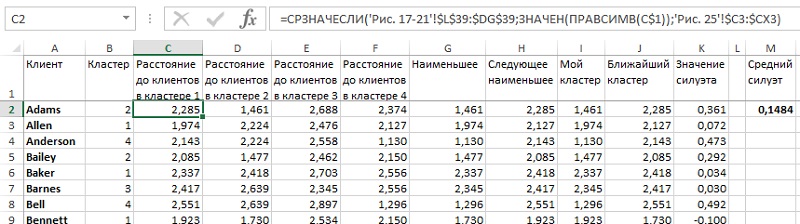
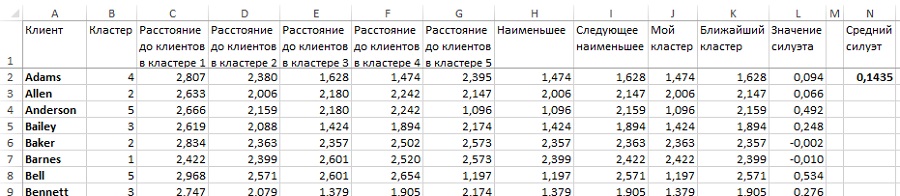
Логику определения силуэта для 4-кластерной модели можно проследить по формулам на листе «Рис. 26» Excel-файла. Итоговый силуэт (0,1484) ближе к нулю, чем к 1, что явно не очень хорошо. В принципе, ничего удивительно, ведь мы смогли удовлетворительно интерпретировать только два кластера. Что же дальше?
Рис. 26. Силуэт кластеризации по 4 средним
Попробуем поднять k до 5 и посмотрим, как изменится среднее значение силуэта (рис. 27). Промежуточные вычисления сделаны на листе «5 кластеров» Excel-файла. Значение среднего силуэта еще хуже, чем при k = 4. Может быть, наоборот следовало уменьшить k? На рис. 28 рассчитан силуэт для случая k = 3. Результат также несколько хуже, чем при k = 4. Что еще настораживает, только несколько кластеров при любом k могут быть интерпретированы. Откуда появляются другие непонятные кластеры, полные шума?
Рис. 27. Силуэт кластеризации по 5 средним
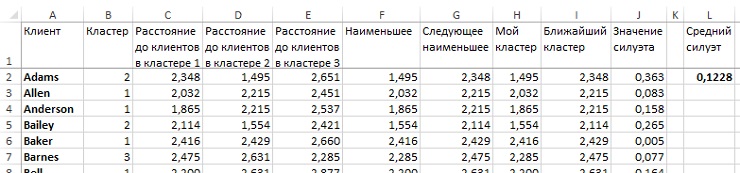
Рис. 28. Силуэт кластеризации по 3 средним
K-медианная кластеризация и асимметрическое измерение расстояний. Как правило, стандартной кластеризации по k-средним бывает вполне достаточно, но в нашем примере мы столкнулись с проблемами, которые часто встречаются при кластеризации данных, имеющих большой разброс (розничная ли это торговля, классификация ли текстов или биоинформатика).
Кластерные центры выражены десятыми долями от единицы, притом, что вектор сделок каждого покупателя — точный ноль или единица. Что на самом деле значит 0,113 для сделки? Хочется, чтобы кластерные центры выражали либо совершение сделки, либо ее отсутствие! Для этого используется кластеризация по k-медианам, а не по k-средним. Если вы не хотите изменять евклидовым расстояниям, то все, что вам нужно — это добавить бинарное условие в модель Поиске решения для всех кластерных центров.
Однако, переключившись с k-средних на k-медианы, обычно перестают пользоваться евклидовым расстоянием и начинают использовать нечто под названием манхэттенское расстояние, или метрика городского квартала. Несмотря на то, что расстояние от точки А до точки В измеряется по прямой, такси на Манхэттене приходится перемещаться по сети прямых улиц, где возможны движения лишь на север, юг, запад или восток. Поэтому, если на рис. 14 кратчайшее расстояние равняется 4,47, его манхэттенское расстояние будет равно 6 (4 + 2).
В терминах бинарных данных, таких как данные о продажах, манхэттенское расстояние между кластерным центром и покупательским вектором — это просто число несоответствий. Если у кластерного центра 0 и у меня 0, то в этом направлении расстояние будет 0, а если встречаются 0 и 1, то есть числа не совпадают, то в этом направлении расстояние равно 1. Складывая их, вы получаете общее расстояние, которое является просто числом несовпадений.
Что значит «покупатель не совершил сделку»? Значит ли это, что он не хотел этот товар настолько, насколько хотел тот, который купил? Одинаково ли сильны положительный и отрицательный сигналы? Может, он и любит шампанское, но уже держит запас в подвале. Может, он просто не видел вашу рассылку за этот месяц. Есть масса причин, почему кто-то чего-то не делает, но всего несколько — почему действия совершаются. Другими словами, стоит обращать внимание на заказы, а не на их отсутствие. Это и есть «асимметрия» данных. Единицы более ценны, чем нули. Если один покупатель совпадает с другим по трем единицам, то это более важное совпадение, чем с третьим покупателем по трем нулям.
Самый, наверное, широко используемый метод подсчета асимметричного расстояния для данных формата 0–1 называется расстоянием по косинусу. Рассмотрим пару двумерных бинарных векторов (1,1) и (1,0). В первом векторе были заказаны оба товара, в то время как во втором только первый. Вы можете представить эти векторы в пространстве и увидеть, что угол между ними — 45° (рис. 29). Можно сказать, что их близость равна косинусу 45°, что составляет 0,707. Оказывается, косинус угла между двумя бинарными заказами — это число совпадений заказов в двух векторах, разделенное на произведение квадратных корней количества заказов первого и второго векторов.
Рис. 29. Близость по косинусу на примере бинарных векторов
В нашем случае два вектора (1,1) и (1,0) имеют один совпадающий заказ, так что в числителе будет 1, а в знаменателе — квадратный корень из 2 (две заключенные сделки), умноженный на корень из 1 заключенной сделки. В результате имеем 0,707.
Что примечательного в этом расчете?
- счетчик в формуле считает только совпадения сделок, то есть он асимметричен и поэтому отлично подходит к данному случаю;
- квадратные корни из количества сделок по каждому вектору в знаменателе обращают наше внимание на тот факт, что вектор, в котором совершены все сделки – назовем его неразборчивым – гораздо дальше отстоит от другого вектора, чем тот, в котором совершены те же сделки и не совершены несколько других. Вам нужно совпадение векторов, «вкусы» которых совпадают, а не один вектор, содержащий «вкусы» другого.
- для бинарных данных эта близость находится в промежутке от 0 до 1, причем у двух векторов не получается 1, пока все их заказы не совпадут. Это означает, что 1 — близость по косинусу может использоваться как мера расстояния, называемая расстоянием по косинусу, которое также варьируется от 0 до 1.
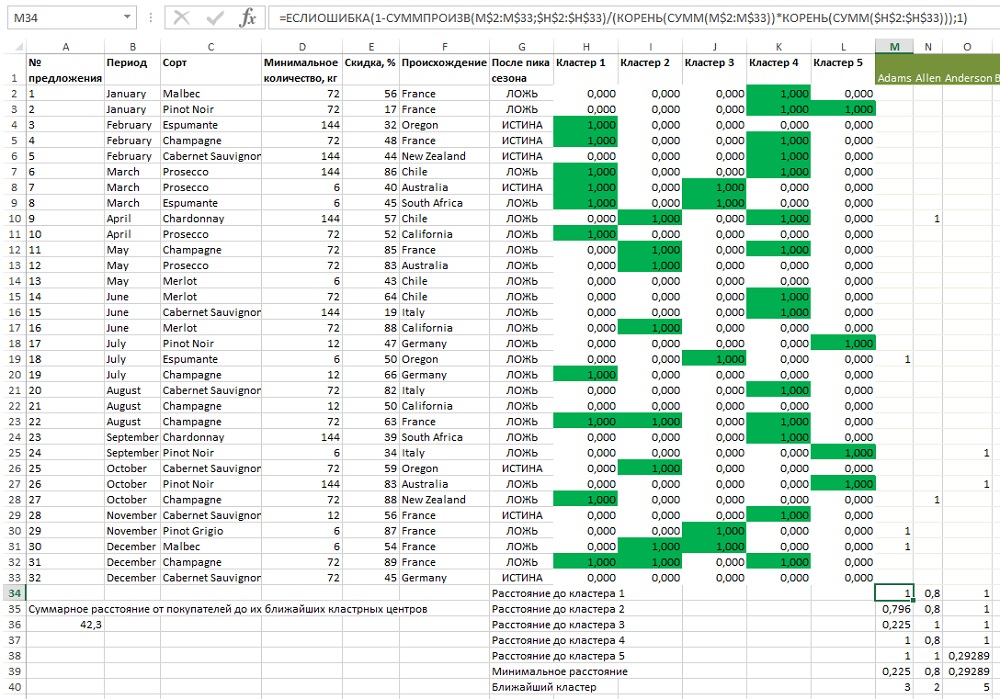
Кластеризация с помощью расстояния по косинусу также иногда называется сферической по k-средним. Теперь начнем со случая k = 5. Отличие от анализа по k-средним заключается в 1) добавлении бинарного условия в Поиск решения, 2) изменении формулы для расчета расстояния (строки 34–38). Например, в ячейки М34 (рис. 30), в которой находится расстояние между Адамсом и центром кластера 1 следует использовать формулу =ЕСЛИОШИБКА(1-СУММПРОИЗВ(M$2:M$33;$H$2: $H$33)/(КОРЕНЬ(СУММ(M$2:M$33))*КОРЕНЬ(СУММ($H$2:$H$33)));1). Обратите внимание, что функция СУММПРОИЗВ не требует формулы массива, так как уже сама по себе является функцией массива (подробнее см. Удивительная функция СУММПРОИЗВ). Откройте Поиск решения и измените условие «<= 1» для Н2:L33 на бинарное. Нажмите Выполнить.
После окончания расчетов вы сразу заметите, что все кластерные центры теперь — бинарные, так что у условного форматирования остаются два оттенка, что сильно повышает контраст. Мой Поиск решения выдал оптимальное значение 42,8, хотя ваше может отличаться.
Рис. 30. Медианы 5 кластеров
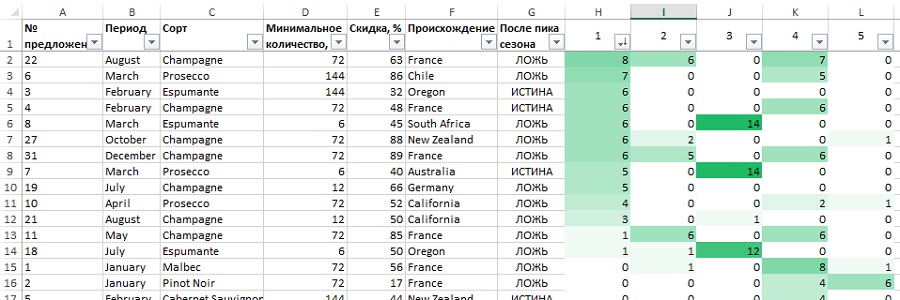
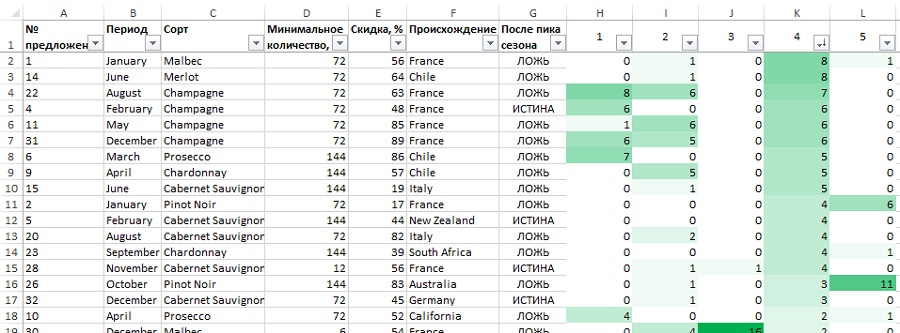
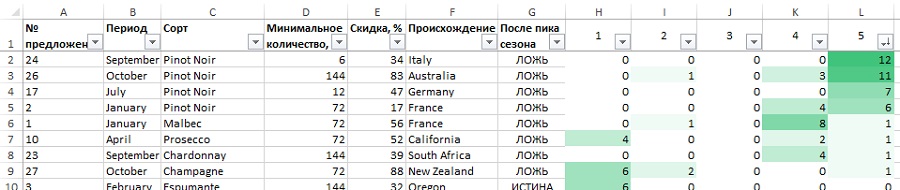
Используем метод подсчета сделок (как ранее на рис. 22–24). Ваши кластеры могут немного отличаться от моих и по порядку, и по составу из-за эволюционного алгоритма. Давайте пройдемся по кластерам и посмотрим, как алгоритм разделил покупателей. В кластер 1 попали покупатели, приобретающие только игристые вина, которые доминируют в первых 11 позициях (рис. 31). Кластер 2 — не так ярко выражен, но похож на франкофилов. Три самые крупные сделки — на французские вина (рис. 32). Сортировка кластера 3: похоже, это мелкооптовый кластер (рис. 33). Что касается кластера 4, то здесь только крупные сделки. И все самые популярные сделки — с большой скидкой и еще не прошли ценовой максимум (рис. 34). И, наконец, кластер 5 снова оказался кластером Pinot Noir (рис. 35).
Так получше, не правда ли? Это оттого, что метод k-медиан, используя асимметричные методы измерения расстояний вроде равенства косинусов, позволяет кластеризировать клиентов, основываясь больше на их предпочтениях, чем на антипатиях. Ведь нас интересует именно это!
Рис. 31. Сортировка кластера 1 — игристые вина
Рис. 32. Сортировка кластера 2 — франкофилы
Рис. 33. Сортировка кластера 3 — мелкооптовые покупатели
Рис. 34. Сортировка кластера 4 — большие объемы
Рис. 35. Сортировка кластера 5 — любители Pinot Noir
Теперь вы можете использовать эти значения для настройки вашей маркетинговой рассылки по кластерам. Это должно помочь вам лучше подбирать покупателей и управлять продажами.