Статья написана с целью ликвидации большого разрыва, сложившегося между англоязычной и русскоязычной литературой по проблеме контрольных карт Шухарта. Авторы считают, что правильное применение контрольных карт – одно из ключевых условий повышения качества российской науки, техники, образования, управления и т.д.
См. также Д. Уилер, Д. Чамберс. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта». – М: Альпина Бизнес Букс, 2009. – 409 с.
Ю.П. Адлер, О.В. Максимова, В.Л. Шпер. Контрольные карты Шухарта в России и за рубежом: краткий обзор современного состояния (статистические аспекты). – Журнал «Стандарты и качество», июль–август, 2011 (полная версия статьи доступна на сайте издательства).
Скачать конспект (краткое содержание) в формате Word или pdf
Основные идеи и принципы контрольных карт Шухарта
Изобретенный в 1924 году Уолтером Шухартом инструмент анализа изменчивости любых процессов, называемый чаще всего Контрольной Картой Шухарта (ККШ), приобретает всё большую популярность в самых различных организациях и сферах деятельности. Уолтер Шухарт понял, какую фундаментальную роль играет в нашем мире вариабельность (или изменчивость) [1], и открыл способ минимизировать влияние вариабельности на решения, которые мы принимаем. Однако, практическая реализация идей Шухарта идет крайне медленно, встречая жесткое сопротивление людей, привыкших с детства к детерминистским суждениям.
Суть идеи ККШ состоит в следующем. Практически все процессы и явления, с которыми сталкиваются люди в своей деятельности, подвержены вариабельности. Вариабельность оказывает влияние на всё, что окружает человека: на результаты наших действий, на принимаемые нами решения, на результаты измерений, на методы управления, на способы и методы обучения, лечения, воспитания, и т.д. Основное достоинство ККШ в том, что она позволяет по словам Шухарта «разумным образом разбить вариабельность на две компоненты, обусловленные разными причинами:
- собственно, системную («случайные причины» как называл их доктор Шухарт), ответственность менеджмента; и
- причины, которые можно чему-то приписать, Деминг назвал их «особыми (специальными)», они оказываются характерными для некоторого временного (мимолётного) события, причину которого обычно можно выявить к удовольствию специалиста, выполняющего данную работу, и устранить».
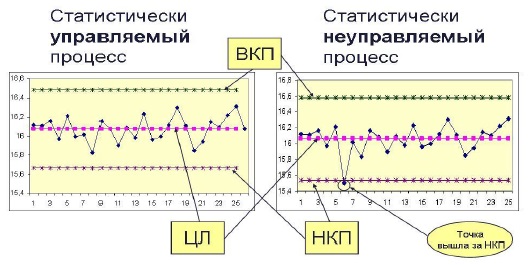
Контрольная карта Шухарта – это картинка, выполняющая работу по разделению вариабельности на ту, что вызвана общими (случайными) и специальными/особыми (временными) причинами. Она состоит из графика хода самого процесса и трех дополнительных линий: центральной линии, верхнего и нижнего контрольных пределов (рис.1). Предложенное Шухартом правило чтения этой картинки очень просто: если все точки находятся между верхним и нижним контрольным пределом, то специальные причины отсутствуют, и процесс по определению считают статистически управляемым (стабильным), что означает его предсказуемость (без чего никакое управление, а, следовательно, и совершенствование невозможны). Если есть точки, выходящие за верхний или нижний контрольные пределы, то специальные причины присутствуют, и процесс по определению предлагается считать неуправляемым (нестабильным), что означает его непредсказуемость со всеми вытекающими отсюда следствиями. Всё это чрезвычайно важно для любого бизнеса, поскольку из вышесказанного сразу следует алгоритм улучшения любых процессов, и ответ на вопрос: надо ли вмешиваться в процесс, и, если надо, то кому?
Рис. 1. Контрольная карта Шухарта
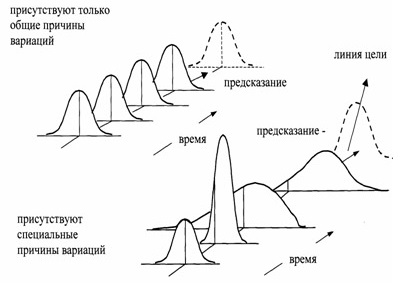
Рис. 2. Стабильный и нестабильный процессы. Когда процесс стабилен, мы можем предсказать поведение системы в будущем (верхняя часть рисунка). Когда процесс нестабилен, предсказания существенно менее надежны.
Пусть имеется определенная статистика, полученная по результатам измерения некоторой количественной (непрерывной) характеристики у. Пусть в качестве показателя настройки процесса выбрано среднее арифметическое ӯ, а в качестве показателя вариабельности – выборочное стандартное отклонение (СО) ![]() Тогда центральная линия (ЦЛ), верхний и нижний контрольный предел (ВКП и НКП) для данной карты будут равны:
Тогда центральная линия (ЦЛ), верхний и нижний контрольный предел (ВКП и НКП) для данной карты будут равны:
где k1 и k2 – расстояния от ЦЛ до соответствующих контрольных пределов, выраженные в единицах СО (подробнее о построении ККШ, см. Пример построения контрольной карты Шухарта в Excel).
Расчет границ ККШ
Для коэффициентов k1 и k2 Шухарт после тщательных экспериментов и долгих размышлений предложил выбрать значение 3. При этом он понимал, что решает принципиально иную задачу, нежели нахождение доверительных границ для среднего (на что формула (1) внешне очень похожа). В частности, Шухарт пишет: «Также очевидно, что проблема установления приемлемой зоны разброса фундаментально отлична от проблемы, разрешенной Стьюдентом. Его теория говорит о том, как сделать правомерное предсказание числа случаев, когда можно ожидать, что последовательность переменных интервалов с переменными центрами для оцениваемого параметра включит в себя теоретическое истинное его значение, в то время как для того, чтобы установить правомерную зону разброса, мы должны быть способны разумно предсказать, как много раз можно ожидать, что будущие наблюдения попадут между заданной парой фиксированных пределов». Это замечание Шухарта тесно связано с проблемой соотношения между теорией ККШ и статистической теорией проверки гипотез (о последней подробнее см. Проверка гипотезы о нормальном распределении и Проверка гипотез: одновыборочные критерии).
В рамках обычного статистического подхода мы имеем некую генеральную совокупность, из которой мы извлекаем выборку, оцениваем по выборке, например, математическое ожидание (МО) с помощью выборочного среднего, а затем по этому среднему и объему выборки находим концы случайного интервала с центром в этом среднем значении. которые определяются с заранее выбранной вероятностью Р. Доверительный P-процентный интервал Стьюдента говорит о том, что если мы много раз будем брать из этой генеральной совокупности независимые выборки одинакового объема, и по каждой построим такой интервал, то в Р процентах случаев истинное значение МО (т.е. точное среднее, рассчитанное по всем значениям генеральной совокупности) будет накрыто нашими случайными интервалами. В теории контрольных карт у нас нет никакой генеральной совокупности. У нас есть бесконечный развивающийся во времени процесс, у которого нет, и не может быть, никакого точного среднего значения. Вместо этого мы имеем набор некоторых прошлых данных, по которым мы хотим разумно оценить границы, внутри которых, как мы ожидаем. будет меняться наш процесс, если определяющая его система будет оставаться стабильной.
Деминг добавляет: «Контрольные пределы не устанавливают вероятностей. Правила для обнаружения особых причин… – это не критерии для проверки статистической гипотезы о том, что процесс находится в стабильном состоянии». Т.е., ККШ трактуется как операциональное определение стабильного или нестабильного процесса (подробнее см. Определение – ключ к овладению понятием).
В начале 80-х годов XX в. возникла новая трактовка термина «статистическое мышление», опирающаяся не на статистические методы, а на понимание вариабельности нашего мира. В соответствии с ней «статистическое мышление – это философия обучения и действий, основывающаяся на следующих фундаментальных принципах:
- Любая работа осуществляется в системе взаимосвязанных процессов.
- Во всех процессах присутствуют вариации.
- Понимание и уменьшение вариаций – ключ к успеху».
Начиная с середины XX в. были предложены различные типы контрольных карт. Попытки применить ККШ для самых различных процессов привели не только к их большому разнообразию, но и к появлению так называемых дополнительных правил их чтения. Дело в том, что, когда ККШ стали широко применяться на практике, было обнаружено, что в ряде случаев, даже когда точки не выходят за верхний или нижний контрольный пределы, в процесс явно что-то вмешивается (например, когда виден явный тренд и т.п.). Процесс может считаться неуправляемым, если:
- Одна или более точек находится за пределами трехсигмовых контрольных границ.
- Две из трех последовательных точек находятся за пределами двухсигмовых предупредительных границ.
- Четыре из пяти последовательных точек находятся на расстоянии одна сигма или более от ЦЛ.
- Восемь последовательных точек находятся с одной стороны от ЦЛ.
(Мое исследование на эту тему, см. Контрольные карты Шухарта. Правила определения отсутствия управляемости. – Прим. Багузина.)
С чисто технической стороны применение ККШ не представляет никаких проблем. Но есть три подводных камня, препятствующих эффективному использованию этого инструмента в реальной жизни:
- Выбор типа ККШ в зависимости от процесса.
- Выбор длительности фазы 1 (об этом ниже).
- Выбор объема и правила формирования подгрупп.
Принципиальный момент состоит в следующем: все эти три проблемы не имеют формализованного решения. Их можно и нужно решать путем соединения глубокого понимания сути процесса с пониманием принципов и техники ККШ. (Поскольку я не теоретик, а практик, то вообще не понимаю, почему вокруг правил расчета границ столько шумихи. В конце концов, это лишь вопрос, как интерпретировать конкретную точку – как сигнал или шум. – Прим. Багузина.)
Уилер и Чамберс рекомендуют использовать для расчета границ средний скользящий размах, и не использовать обычную формулу для σn–1.
Ещё одна проблема, связанная с расчетом границ на ККШ, вызвана тем, что на практике мы обычно не знаем ни истинного среднего для интересующего нас процесса, ни соответствующего стандартного отклонения, и определяем их по некоторому количеству начальных подгрупп (фаза I). Если число этих исходных подгрупп невелико, найденные нами значения среднего средних и среднего размахов (если рассмотреть обычную карту среднего и размахов) будут сильно отличаться от истинных значений. Это означает, что вероятности выхода точки за границы контрольной карты, на которые ориентирует нас теория, будут существенно иными.
Стоит подчеркнуть, что у бесконечного во времени процесса нет никакого определенного «истинного» значения, поскольку не существует абсолютно стабильных процессов. Поэтому говорить об истинном значении в обычном смысле как о значении, полученном при стремлении числа наблюдений к бесконечности здесь бессмысленно. У реальных процессов такой предел в принципе не существует.
Для для оценки эффективности ККШ и сравнения различных типов карт используют понятие средней длины серии (СДС). Обозначим вероятность выхода точки за контрольные пределы при условии, что процесс стабилен, через α (вероятность ошибки первого рода), а вероятность невыхода точки за контрольные пределы при условии, что процесс не стабилен, через β (вероятность ошибки второго рода). Тогда:
ARL0 = 1/α
где ARL0 – средняя длина серии для стабильного процесса,
ARL1 = 1/(1–β)
где ARL1 – средняя длина серии для нестабильного процесса.
В 2000 году Вудал сформулировал следующие проблемы:
- Двухэтапный подход к работе с ККШ. Следует тщательно различать две фазы работы с ККШ. В фазе I мы анализируем исторические данные с целью ответа на вопрос, находится ли процесс в статистически стабильном (управляемом) состоянии. В фазе II мы регулярно извлекаем выборки из стабильного (управляемого) процесса с целью обнаружить сигналы о выходе процесса из стабильного состояния.
- Контрольные карты и проверка гипотез. Вудал считает, что контрольные карты в фазе I скорее служат инструментом исследовательского анализа, однако в фазе II контрольная карта сильно напоминает повторяющуюся проверку гипотез.
Эндрю Палм предложил рассматривать не два, а три этапа работы с КК:
- Стадия А – настройка ККШ, где устанавливается центральная линия и происходит расчет и нанесение контрольных границ после того, как собраны данные;
- Стадия В – улучшение процесса, которая включает совершенствование оборудования, окружающей среды, улучшение используемых материалов, измерительной системы, включая работу людей. После всего этого контрольные пределы и центральная линия пересчитываются;
- Стадия С – мониторинг процесса, где мы обнаруживаем новые специальные причины после стадии В.
ККШ и Энтропия
Нет сомнения в том, что для любой замкнутой системы выполняется второй закон термодинамики. Это значит, что если такую систему предоставить самой себе, то она обязательно, рано или поздно, скорее рано, придет в состояние хаоса. Поэтому наивно думать, что, построив ККШ для произвольной системы, мы обнаружим управляемый процесс. Скорее наоборот, что вполне подтверждается практикой, этот процесс будет не управляемым. Исходя из этого, Уилер и Чамберс построили классификацию возможных состояний процесса. А если процесс не стационарен, то нет основания говорить о среднем, относительно которого варьируют данные. Да и оценить это среднее по прошлым данным тогда не удается. Хотя у нас нет среднего, зато всегда есть целевое значение. (На это давно обратил внимание Тагути.)
Как же, все-таки, на практике удается поддерживать многие процессы в управляемом состоянии в течение длительного времени? Здесь термодинамика не оставляет нам выбора: только за счет введения в систему энергии извне. Тогда ККШ можно рассматривать как индикатор того, что система требует дополнительной энергии. А поскольку для этого нужны ресурсы и время, задача состоит в том, чтобы минимизировать расход дополнительной энергии и увеличить, насколько можно, интервалы времени между внешними воздействиями. Один из возможных способов организации таких воздействий – это автоматическое регулирование с обратной связью. Остается, конечно, и «ручной» способ, который рассматривали Шухарт и Деминг.
ККШ в работах на русском языке
В 1990 году выходит книга Хитоси Куме, посвященная семи простым методам контроля качества – Статистические методы повышения качества. Среди этих семи важнейшее место принадлежит простым ККШ. Их описание в книге Куме, на наш взгляд, представляет образец простоты и доходчивости изложения в соединении с тщательностью обсуждения. Рассмотрены семь типов ККШ: средних, размахов, индивидуальных значений и 4 типа качественных карт. Мы считаем, что для обучения практическому построению ККШ, книга Куме до сих пор остается одним из самых лучших русскоязычных пособий.
В 1995 году была переведена книга Миттаг Х.Й., Ринне Х. Статистические методы обеспечения качества. Это фундаментальный учебник для самостоятельных занятий, написанный с немецкой тщательностью, и переведенный и отредактированный с российской небрежностью. В книге подчеркнуто, что границы на ККШ не имеют отношения к допускам, и допуска нельзя изображать на ККШ. Это замечание очень существенно для России, где нанесение допусков на карту средних – одна из самых распространенных ошибок.
Адлер, Шпер предложили определение терминов:
- Статистическое мышление – это понимание вариабельности, присущей любым процессам, и диагностика их стабильности и воспроизводимости.
- Статистическое управление процессами — это основанная на статистическом мышлении и теории вариабельности методология постоянного совершенствования процессов, использующая простые и эффективные методы анализа и решения проблем.
Что же касается трехсигмовых границ, которые некоторые авторы называют жесткими и необоснованными, то следует иметь в виду, что:
- Шухарт не считал трехсигмовые границы обязательными;
- в своей книге 1931 года Шухарт подробно обосновал, чем вызвана даваемая им рекомендация;
- 80-летний мировой опыт применения ККШ доказал, что Шухарт гениально угадал правило, которое работает.
Отметим, что известный статистик Ллойд Нельсон в своей колонке в журнале Journal of Quality Technology так отвечает на вопрос «Когда границы на контрольной карте Шухарта должны быть иными, чем средняя линия ±3 сигмы?» «Всегда, когда у вас есть основательная причина».
В 2009 году происходит важное событие – выходит русский перевод книги Д. Уилер, Д. Чамберс Статистическое управление процессами. Это фактически первая книга на русском языке, в которой просто, понятно, с большим количеством практических примеров изложен операциональный подход к построению и анализу ККШ. В частности, Уилер и Чамберс на основе богатого практического опыта применения контрольных карт и проведенных ими специальных теоретических исследований развенчивают ряд мифов, касающихся практики применения ККШ:
- интерпретация ККШ как инструмента проверки статистических гипотез,
- требование нормальности распределения параметров,
- утверждение о том, что ККШ работают благодаря центральной предельной теореме теории вероятностей,
- требование независимости исходных данных.
Кроме указанных Уилером, Чамберсом ошибок понятийного характера, на российских предприятиях довольно часто встречаются и более грубые ошибки, например, нанесение допусков на карты средних или постоянный пересчет границ по всем имеющимся в каждый момент данным.
В 2004 г. выходит книга Левина и др. Статистика для менеджеров с использованием Microsoft Excel. В ней понятия об управляемом и неуправляемом процессах изложены с позиций Шухарта–Деминга. Очень кратко рассказано, как строить ККШ в стандартном и расширенном пакетах Excel. Также изложен эксперимент Деминга «Красные бусы», и обсуждаются выводы из этого эксперимента (см. раздел «Эксперимент с красными шарами: вариация процесса» заметки Статистические методы управления качеством и производительностью труда).
Избранная литература на русском языке
Адлер Ю. П., Шпер В. Л. (2003) Методы менеджмента качества, №№ 1, 3, 5, 7, 11.
Адлер Ю. П., Шпер В. Л. (2004) Методы менеджмента качества, №№ 2, 3, 6.
Адлер Ю. П., Жулинский С. Ф., Шпер В. Л. (2009). Проблемы применения методов статистического управления процессами на отечественных предприятиях. – Методы менеджмента качества, №8, с.36–40; №9, с.24–29.
Бендерский А. М., Богатырев А. А., Баумгартен Л. В. (1983) Стандартизация статистических методов управления качеством. – М.: Изд-во стандартов. – 152 с.
Деминг Э. (1950) Лекция перед японскими менеджерами.
Деминг Э. (2006) Новая экономика. – М.: ЭКСМО. – 208 с.
Деминг Э. (2007) Выход из кризиса. Новая парадигма управления людьми, системами и процессами. – М.: Альпина Бизнес Букс. – 370 с.
Ефимов В. В., Барт Т. В. (2006) Статистические методы в управлении качеством продукции. – М.: КНОРУС. – 240 с.
Жулинский С.Ф., Новиков Е. С., Поспелов В. Я. (2001) Статистические методы в современном менеджменте качества. – М.: Фонд «Новое тысячелетие», 2001. – 208 с.
Кане М. М., Иванов Б. В., Корешков В. Н., Схиртладзе А. Г. (2008) Системы, методы и инструменты менеджмента качества. Учебное пособие. – СПб.: Питер. – 580 с.
Клячкин В. Н. (2007) Статистические методы в управлении качеством: компьютерные технологии: учеб. пособие. – М.: Финансы и статистика. – 304 с.
Коуден Д. (1961) Статистические методы контроля качества. – М.: Физматлит. – 624 с.
Круглов М. Г., Шишков Г. М. (1999) Управление качеством. – М.: МГТУ «СТАНКИН», 1999. – 234 с.
Лагутин М. Б. (2007) Наглядная математическая статистика. – М.: БИНОМ Лаборатория знаний. – 472 с.
Левин Д. М., Стефан Д., Кребиль Т. С., Беренсон М. Л. (2004) Статистика для менеджеров с использованием Microsoft Excel. – М.: Вильямс. – 1312 с.
Мердок Дж. (1986) Контрольные карты. – М.: Финансы и статистика. – 152 с.
Миттаг Х.Й., Ринне Х. (1995) Статистические методы обеспечения качества. – М.: Машиностроение, 1995. – 616 с.
Нив Г. (2005) Пространство доктора Деминга: Принципы построения устойчивого бизнеса. – М.: Альпина Бизнес Букс. – 370 с.
Ноулер Л., Хауэлл Дж., Голд Б. и др. (1984). Статистические методы контроля качества продукции. – М.: Издательство стандартов, 1984. – 104 с.
Седдон Дж. (2009) Свобода от приказов и контроля. Путь к эффективному сервису. – М.: РИА «Стандарты и качество». – 232 с.
Сигел Э. Ф. (2002) Практическая бизнес-статистика. – М.: Вильямс. – 1056 с.
Куме Х. Статистические методы повышения качества. – М.: Финансы и статистика, 1990. – 304 с.
Уилер Д., Чамберс Д. (2009) Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. – М: Альпина Бизнес Букс. – 409 с.
Шпер В. Л. (2008) Кому и зачем нужны системное и статистическое мышление? – Менеджмент качества, № 1.
Шторм Р. (1970) Теория вероятностей. Математическая статистика. Статистический контроль качества. – М.: Мир. – 368 с.
Эфрон Б. (1988) Нетрадиционные методы многомерного статистического анализа. – М.: Финансы и статистика. – 263 с.
[1] Строго говоря, прямой перевод английского термина variability – это изменчивость. Термин вариабельность вошел в основном в специальную литературу по статистическим методам. Авторы обзора предлагают использовать термин изменчивость применительно к естественным системам (например, изменчивость климата), а термин вариабельность применительно к искусственным системам (например, вариабельность параметров или процессов).