Рациональная группировка данных при построении контрольной карты Шухарта

Это заметка показывает важность группировки данных при построении контрольной карты Шухарта. В зависимости от того, как данные сгруппированы, мы получим ответ на тот или иной вопрос. [1] Рассмотрим пример.

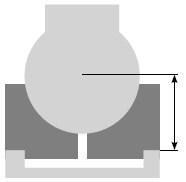
Шаровые муфты отливаются под давлением, по четыре штуки в одной изложнице (рис. 1). На момент сбора данных на производстве проходила смена материалов и технологии. Требовалась сертификация процесса перед тем, как запустить его в полномасштабное производство. Дейв, руководитель производства, решил использовать контрольные карты для оценки хода сертификации.

Рис. 1. Сечение шаровой муфты

Скачать заметку в формате Word или pdf, примеры в формате Excel

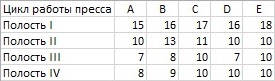
Поскольку была только одна изложница, процесс сертификации шел на одном прессе, с одним оператором. Собранные данные описывали рабочую толщину шаровой муфты в сотых долях миллиметра. Поскольку одна из сторон муфты была круглой, для измерения толщины использовали специально разработанный для этой цели шаблон. Он был сделан так, что измерялось превышение толщины муфты в 12,00 мм. Дейв подходил к прессу раз в час и отбирал для измерения все четыре муфты, выпущенные в течение пяти последовательных циклов работы пресса. Таким образом, он получал для измерения по 20 изделий каждый час. Будучи очень внимательным, Дейв отмечал, из каких полостей изложницы взяты муфты, после чего вписывал эти 20 измерений в следующую таблицу.

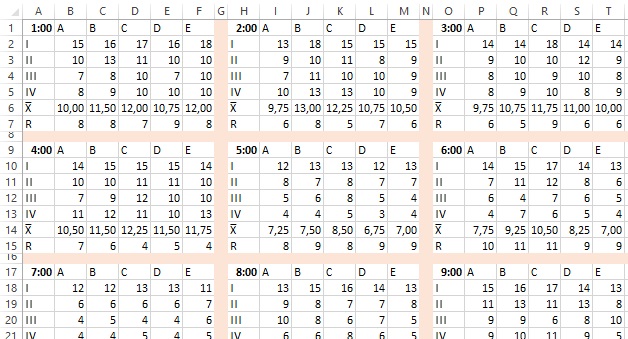
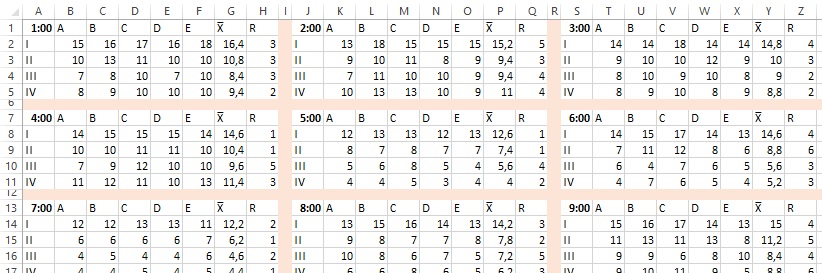
Рис. 2. Данные о толщине муфты

Существует три возможных источника вариации этих данных. Во-первых, это временная вариация, происходящая от часа к часу, которая отражается различными наборами по 20 измерений. Во-вторых, это вариация между циклами работы пресса, представленная в разных столбцах таблицы данных на рис. 2 (A, B, C, D, E). В-третьих, это вариация, порождаемая различными полостями пресс-формы (зафиксированная в различных строках таблицы данных, от Полость I до Полость IV). Дейв должен был решить, каким образом разбить эти данные по подгруппам и как организовать подгруппы на контрольных картах. Для иллюстрации сделаем это тремя разными способами.

Первый из способов группировки показан на рис. 3. Здесь для образования подгрупп используются столбцы с рис. 2. Т.е., внутригрупповая вариация отражает различия между полостями пресса, а межгрупповая – между циклами работы пресса, и от часа к часу.

Рис. 3. Первый способ организации данных о толщине муфт; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

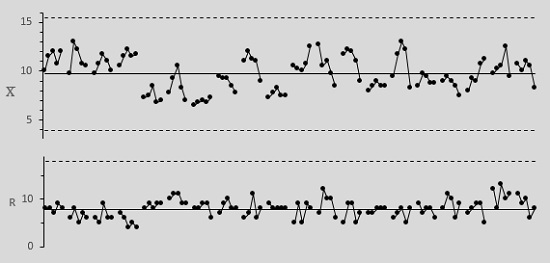
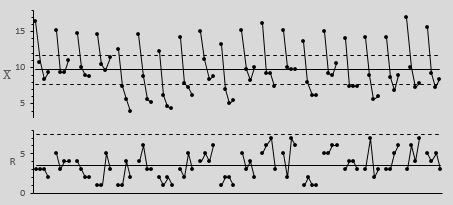
Например, данные для первого и второго часов оказываются в разных подгруппах, поэтому временную вариацию можно заметить только при переходе от подгруппы к подгруппе. Точно так же данные цикла А попадают в иную подгруппу, чем данные цикла В, и т.д., поэтому различия между циклами будут проявляться между подгруппами. В отличие от этих двух видов вариации, вариация, обусловленная различными полостями изложницы, проявляется внутри каждой подгруппы. Межгрупповые вариации будут отражаться на карте средних. Внутригрупповая вариация – на карте размахов (рис. 4).

Рис. 4. Контрольные карты, первый способ группирования данных

UCL_X̅ = X̿ + A₂R̅ = 9,7375 + 0,729 · 7,90 = 15,50 – верхняя граница карты средних;
CL_X̅ = X̿ = 9,7375 – центральная линия карты средних;
LCL_X̅ = X̿ – A₂R̅ = 9,7375 – 0,729 · 7,90 = 3,98 – нижняя граница карты средних;
UCL_R = D₄R̅ = 2,282 · 7,90 = 18,03 – верхняя граница карты размахов;
CL_R = R̅ = 7,90 – центральная линия карты размахов;
LCL_R = D₃ R̅ = (не существует для n = 4) – нижняя граница карты размахов.

Подробнее о том, как рассчитать контрольные границы см. Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами, глава 3; для случая, когда размер группы n = 4.

Второй способ организации данных о толщине муфт (рис. 5). В качестве признака группировки использованы строки с рис. 2. В этом случае временная вариация и вариация, вызванная различиями в полостях, обнаруживаются при переходе от подгруппы к подгруппе, а вариация между циклами работы пресса — внутри подгруппы.

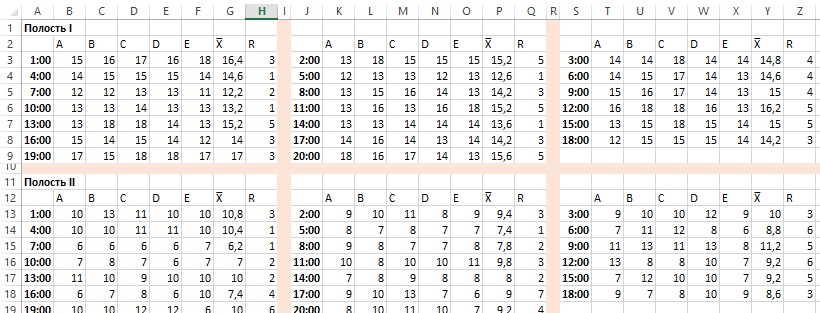
Рис. 5. Второй способ организации данных о толщине муфт

Этот способ обобщения данных позволяет получить 80 подгрупп по пять элементов. Генеральное среднее не изменилось — 9,74, а средний размах стал меньше – 3,51. Контрольные пределы для карты средних — 7,71 и 11,76. Верхний контрольный предел карты размахов — 7,43 (рис. 6; формулы см. в приложенном Excel-файле).

Рис. 6. Контрольные карты, второй способ группирования данных

Контрольные карты на рис. 4 и 6 значительно отличаются, хотя и отражают одни и те же данные, и это различие объясняется исключительно способом образования подгрупп. Карта средних на рис. 6 обладает одним очевидным свойством: каждое четвертое значение превышает верхний контрольный предел. Эти значения соответствуют изделиям, отлитым в первой полости, следовательно, в ней получаются муфты, которые заметно толще муфт из трех других полостей.

Почему это не было видно на рис. 4? Да потому, что не был задан правильный вопрос! Мы спросили:

• заметны ли различия от часа к часу;
• заметны ли различия от цикла к циклу;
• стабильны ли различия между полостями?

Во втором случае исходная информация была иной. Т.е., мы задали иные вопросы:

• заметны ли различия от часа к часу;
• стабильны ли различия от цикла к циклу;
• заметны ли различия от полости к полости?

Поскольку различия между отдельными циклами намного меньше, чем различия между полостями, расстояние между контрольными пределами на рис. 6 значительно уже, чем на рис. 4. Следовательно, кроме того, что эти две карты отвечают на разные вопросы, контрольная карта на рис. 6 еще и более чувствительна.

Третий способ обобщения данных основан на перераспределение подгрупп из рис. 5: подгруппы, соответствующие каждой из полостей, собраны вместе. Это позволяет построить свою контрольную карту для каждой полости (рис. 7).

Рис. 7. Третий способ организации данных о толщине муфт

Теперь мы можем детально рассмотреть различия в толщинах муфт, отливаемых в разных полостях (рис. 8).

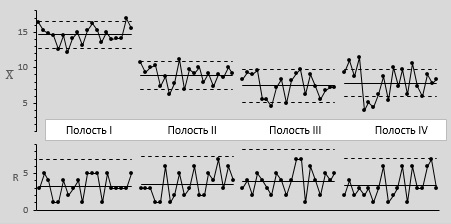
Рис. 8. Контрольные карты, третий способ группирования данных

Полость 1: среднее средних — 14,65; средний размах — 3,30; нижний контрольный предел для карты средних — 12,75; верхний контрольный предел для карты средних — 16,55; верхний контрольный предел для карты размахов — 6,98.

Полость 2: среднее средних — 8,97; средний размах — 3,45; нижний контрольный предел для карты средних — 6,98; верхний контрольный предел для карты средних — 10,96; верхний контрольный предел для карты размахов — 7,29.

Полость 3: среднее средних — 7,47; средний размах — 3,95; нижний контрольный предел для карты средних — 5,19; верхний контрольный предел для карты средних — 9,75; верхний контрольный предел для карты размахов — 8,35.

Полость 4: среднее средних — 7,86; средний размах — 3,35; нижний контрольный предел для карты средних — 5,93; верхний контрольный предел для карты средних — 9,79; верхний контрольный предел для карты размахов — 7,08.

При построении всех четырех карт средних в одном и том же масштабе различия между полостями становятся совершенно очевидными. Кроме того, по-прежнему ощущается нехватка статистической управляемости. Этот способ группирования позволяет также непосредственно сравнить долговременную вариацию (от часа к часу) с кратковременной (от цикла к циклу). Карта очень четко демонстрирует чрезмерность долговременной вариации. Следовательно, существуют какие-то особые причины, из-за которых детали получаются то толще, то тоньше. Идентификация и ликвидация особых причин помогут добиться значительно большей однородности изделий практически без дополнительных затрат.

Итак, третий способ группирования данных оказался наиболее чувствительным из рассмотренных, поскольку он позволяет непосредственно сравнить вариацию от полости к полости. Кроме того, он показал отсутствие статистической управляемости от часа к часу.

Изменения в процессе

Дейв использовал третий способ представления данных, показанный на рис. 8. Он заметил, что толщина муфт, отливаемых в полости 1, значительно завышена, т.е. процесс неуправляем. По этому поводу он высказался так: «Я не знал, как вернуть процесс в управляемое состояние. Раньше я никогда этого не делал! Но я точно знал, что делать с полостью 1!»

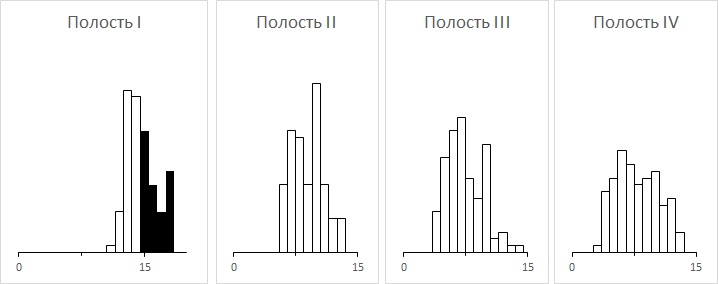
И тогда он решил отыскать причину различий между полостями. Гистограммы для всех четырех полостей (рис. 9) построены при допуске от 0 до 15. Значения, соответствующие полости 1, расположились вокруг верхней границы допуска, причем 28 из 100 значений оказались за его пределами. Значения для полости 2 располагались в верхних двух третях поля допуска. И только полости 3 и 4 оказались хорошо центрированными относительно этих допусков. Основываясь на этих данных, Дейв вынул изложницу из-под пресса и отослал ее в инструментальную мастерскую.

Рис. 9. Гистограмма по четырем полостям

Он хотел сместить столбики гистограммы полости 1 в сторону уменьшения на 0,075 мм, поэтому попросил подложить под нее специальную прокладку толщиной 0,003 дюйма. Гистограмму полости 2 требовалось сместить на 0,025 мм, поэтому под эту полость нужно было подложить прокладку толщиной 0,001 дюйма. Через пару дней он получил эту изложницу назад, установил ее под тот же самый пресс и приступил к сбору данных, после чего построил контрольную карту (как на рис. 8), пересчитал контрольные пределы и посмотрел, к чему привела установка прокладок.

Оказалось, что толщина деталей, отливаемых во всех четырех полостях, стала меньше: в первом углублении — на 0,005 дюйма, во втором — на 0,003 дюйма, в третьем — на 0,001 дюйма, в четвертом — на 0,002 дюйма.

—     Что вы сделали с пресс-формой? — спросил Дейв у мастера-инструментальщика.

—     Только то, о чем вы просили! — ответил тот.

—     Тогда почему второе и третье углубления стали мельче, чем прежде?

—     Не знаю, я только подложил прокладку толщиной 0,003 мм под первую полость и толщиной 0,001 мм — под вторую!

—     А вы делали с этой пресс-формой что-нибудь еще?

—     Практически нет!

—     Что значит «практически»?

—     В ней было много воска… Я просто вычистил ее как следует!

И тогда в голове Дейва будто бы зажглась лампочка. Конечно же, в изложнице постоянно накапливается воск, который оператор должен периодически вычищать. Но он не делал этого достаточно часто, что и послужило причиной неустойчивости процесса от часа к часу! Как только пресс-форму стали прочищать регулярно, этот источник неуправляемой вариации исчез. Убедившись, что процесс стал устойчивым и стабильным, Дейв пришел к выводу о возможности начала серийного производства.

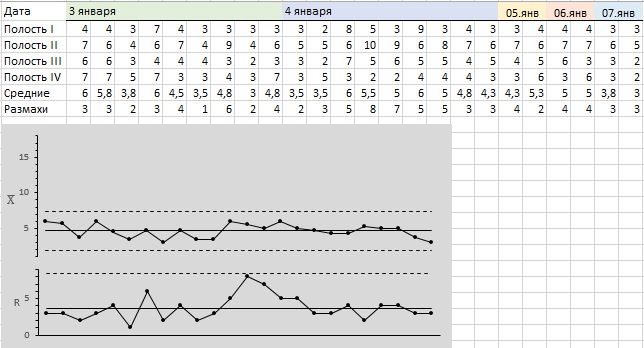
Когда был начат выпуск серийной продукции, у оператора под рукой всегда была контрольная карта. Для удобства все четыре полости образовывали одну подгруппу (рис. 10). Как видим, процесс показывает вполне допустимую степень статистической управляемости. Представленная карта описывает четырехдневный временной интервал, имевший место через четыре месяца после начала серийного производства. Первые девять точек получены на следующий день после окончания двухнедельных рождественских каникул, вторые девять — днем позже; затем подгруппы стали отбираться по две в день.

Рис. 10. Контрольная карта для толщины муфт после изменений

Между картами, изображенными на рис. 4 и 10, есть принципиальная разница. При построении карт на рис. 4 не было известно, одинаковы ли полости или нет; было сделано допущение, что они работают одинаково. Это было неверно, поэтому карты на рис. 4 были нечувствительными. Предположение, что параллельные операции абсолютно идентичны, всегда опасно. Для проверки этого допущения нужно использовать специально предназначенные для этой цели контрольные карты (как на рис. 8).

При построении графиков на рис. 10 полости были отрегулированы, и было известно, что они одинаковы, поэтому их группирование не вызвало зашумления информации. Идентичность свойств полостей можно увидеть так. Средний размах, равный 3,71 на рис. 10, соответствует различиям «от полости к полости», что дает значение σ(Х), равное 1,80. Средний размах, равный 3,51 на рис. 6, соответствует различиям «от цикла к циклу». Это дает значение сигма от Х, равное 1,51. Таким образом, вариация «от полости к полости» практически не отличается от вариации «от цикла к циклу» для одной полости. Во всех четырех полостях производятся детали примерно одинаковой толщины. При таких условиях объединение измерений деталей, отлитых в этих четырех полостях, в одну общую подгруппу сколь-нибудь значительно чувствительность контрольной карты не ухудшает, что существенно облегчает для оператора работу с ней.

Если данные отражают параллельные операции, то всегда лучше собирать их в отдельные подгруппы. Если каждая из параллельных операций будет представлена на отдельной карте, то она будет более чувствительной и легко интерпретируемой. Однако при наличии серьезных свидетельств того, что параллельные операции идентичны, их можно, конечно же, объединить в одну подгруппу.

Другой вывод из рис. 10 — возможность переменного объема подгрупп. В первые два дня после двухнедельной остановки данные собирались гораздо чаще, чем в последующие дни. Это дало больше данных для вычисления пределов и позволило вести мониторинг процесса более тщательно с самого начала. Как только выяснилось, что процесс ведет себя предсказуемо, число образцов уменьшили.

Итак, способ разбиения данных на подгруппы и порядок их отображения на контрольных картах определяются вопросами, которые мы хотим выяснить. Источники вариации, которые представлены внутригрупповыми различиями, должны представлять меньший интерес, в то время как межгрупповые источники вариации должны быть самыми интересными. Различия, которые фиксированы (как, например, различия между полостями) можно учесть при помощи разных контрольных карт.

Наконец, всегда нужно суметь выразить словами, какие источники вариации существуют между подгруппами и внутри их. Пока это не сделано, от контрольных карт большой пользы не будет.

[1] По материалам книги: Д. Уилер, Д. Чамберс. Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта. М.: Альпина Паблишер, 2016. – С. 133–143.