Я уже несколько раз сталкивался с тем, что существуют две статистики, обе называемые стандартное отклонение, для описания меры рассеивания случайной величины. Недавно это произошло при чтении книги Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами. Чтобы эти статистики различать, в книге они названы по-разному. Корень из среднего квадрата отклонения sn, определен для ряда, состоящего из n элементов формулой:
Стандартное отклонение рассчитывается по формуле:
Скачать заметку в формате Word или pdf, примеры в формате Excel
При этом авторы вскользь упоминают: «Несмотря на то что некоторые учебники говорят о применении s для генеральных совокупностей, а sn — для выборок, и то, и то — статистики, они обе — просто арифметические функции данных». На мой взгляд, то ли авторы, то ли переводчики напутали, потому что, как раз наоборот. «Некоторые учебники» трактуют sn, как меру рассеивания генеральной совокупности, а s, как меру рассеивания выборки.
Не добавляют понимания и определения в Википедии, где говорится, что sn – среднеквадратичное отклонение, а s – стандартное отклонение, или оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии. В статье Несмещенная дисперсия можно прочитать, что sn – выборочная дисперсия, а s – исправленная выборочная дисперсия. Причем sn является смещённой, а s – несмещённой оценками параметра σ2.
Excel не отстает от теории и содержит две функции для определения стандартного отклонения: СТАНДОТКЛОН.В – оценивает стандартное отклонение по выборке, и использует в формуле знаменатель (n – 1); СТАНДОТКЛОН.Г – вычисляет стандартное отклонение по генеральной совокупности, и в знаменателе – n.
Ситуация с двумя формулами прояснилась для меня при чтении книги Фишер. Статистический вывод. Фишер рассматривал генеральные совокупности, которые описываются параметрами, традиционно обозначаемыми греческими буквами. Параметры нам не известны. Мы пытаемся оценить их, извлекая отдельные выборки, и измеряя их статистики (статистика – число, характеризующее выборку; статистики традиционно обозначаются латинскими буквами). Фишер сформулировал несколько критериев хорошей оценки. И среди них – смещение. Оценка статистики Т считается правильной и несмещенной для параметра Θ, если среднее значение Т (по множеству выборок) стремится к истинному значению Θ. Иначе оценка считается смещенной.
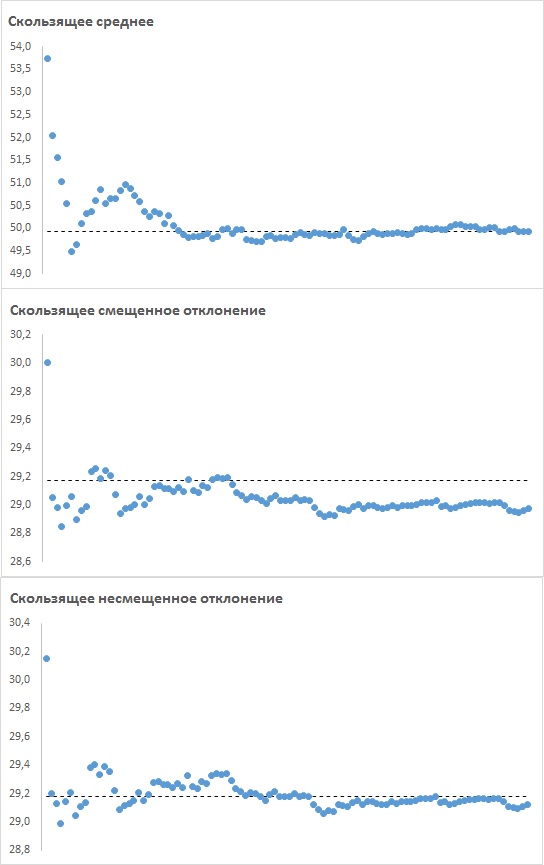
Для иллюстрации я создал модель в Excel, и случайным образом задал 10 000 чисел в диапазоне от 0 до 100. А затем создал 100 выборок по 100 последовательных значений: от 1 до 100, от 101 до 200 и т.д. Далее построил три графика: для среднего значения, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В. На каждый график в виде пунктирной линии нанес среднее значение, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В для всех 10 000 случайных чисел, а также в виде точек – скользящее среднее этих статистик для последовательности выборок. Например, первая точка – значение статистики для первой выборки: 1…100, вторая точка – среднее статистик двух выборок: 1…100 и 101…200 и т.д. Видно, что среднее выборок стремится к своему истинному значению – среднему по всей совокупности, так же ведет себя и СТАНДОТКЛОН.В. А вот скользящее среднее СТАНДОТКЛОН.Г стремится к числу меньшему, чем значение СТАНДОТКЛОН.Г для всех 10 000 чисел. Это и означает, что статистика СТАНДОТКЛОН.В дает несмещенную оценку параметра дисперсии σ2, а СТАНДОТКЛОН.Г – смещенную.
Рис. 1. Три статистики – среднее значение, СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В – дают оценку параметров генеральной совокупности; среднее значение и СТАНДОТКЛОН.В – несмещенную оценку, а СТАНДОТКЛОН.Г – смещенную; откройте Excel-файл и нажмите F9; случайные числа пересчитаются, и графики изменятся; неизменным будет только стремление среднего значения и СТАНДОТКЛОН.В по выборкам к своим истинным значениям (по всей совокупности), и постоянно заниженная оценка статистики СТАНДОТКЛОН.Г; Excel-файл тяжелый, поэтому пересчет происходит медленно
Если тема вас заинтересовала, но не полностью отложилась в голове, рекомендую также заметку Выборочная несмещенная дисперсия.
Дополнение от 15.12.2022. Еще один подход к описанию различий формул (1) и (2) я встретил в книге Александра Орлова «Математика случая». Рекомендую))
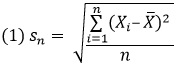
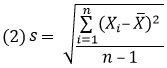
Доброе утро. Существует ли возможность в эксель вычислить стандартное отклонение по условию Например для каждого года. Что то типа формулы массива {=Стандотклон(если(
"Диапазон дат"=дата в строке;"диапазон расчета стандартного отклонения";;))}Фильтровать по дате не всегда дают. хотелось бы универсального решения. Если будет нужен файл в качестве примера — направлю.
Руслан, в лоб такой возможности нет. Можно, например, сделать сводную таблицу, вывести в заголовок столбца год, и уже по отфильтрованному году использовать функцию СТАНДОТКЛОН. Второй вариант использовать модель данных в Power Pivot и формулы DAX, которые позволяют применить фильтр по годам прежде чем искать стандартное отклонение. См., например, DAX-функция CALCULATE().
Большое спасибо за ответ Сергей Викторович. Я тоже пришел к такому выводу. К сожалению формулы массива не всесильны. Необходимо изучать и искать решения в PP и DAX.
Подскажите, как в excel рассчитать стандартную неопределенность тип А, те же формулы только в знаменателе n(n-1).
Вадим, мне такая функция не знакома. Допустим данные находятся в диапазоне А1:А20, тогда можно воспользоваться формулой =КОРЕНЬ(ДИСП.В(A1:A20)/СЧЁТЗ(A1:A20)).
Сергей Викторович благодарю за ответ. Воспользовался вашей формулой, потому что возникли сомнения в правильности используемой =СТАНДОТКЛОН В(А1:А10)/КОРЕНЬ(n) где n=СЧЕТ(А1:А10), результат идентичен! Мне не совсем понятно какая тогда формула в excel, почему так странно преобразовано выражение.
формула в знаменателе которой n(n-1) используется в методиках измерительной лаборатории, взята например из ГОСТ 6581-75 привожу ссылку https://ibb.co/mTbtfrv
Добрый день , я рассчитала по вашей статье доверительный интервал и его границы с уровнем значимости 5%, не могу понять как рассчитать генеральное среднее и генеральное стандартное?
Вложение