Рональд Фишер — ученый, снабдивший статистику инструментами, благодаря которым она обрела то огромное значение, которое имеет сегодня. Его основной вклад — статистический вывод, инновационный подход, связанный с понятием вероятности, который дал статистике, состоявшей прежде на службе других дисциплин, необходимый импульс для того, чтобы она стала полноправной наукой. Этому британскому математику и биологу мы обязаны статистическим методом, который применяется в планировании научных экспериментов. Он был ярым сторонником евгеники, зародившейся в первой половине XX века, и в этом контексте его исследования касались также генетики и современной эволюционной теории.
По теме см. также Левин. Статистика для менеджеров с использованием Microsoft Excel
Наука. Величайшие теории: выпуск 47: Возможно да, возможно нет. Фишер. Статистический вывод. — М.: Де Агостини, 2015. — 176 с.
Скачать конспект (краткое содержание) в формате Word или pdf, примеры в формате Excel
Глава 1. Статистика до Фишера
Принято считать, что статистика состоит из двух взаимосвязанных, но самостоятельных разделов: описательной статистики, которая занимается эксплоративным (пробным, разведочным) анализом данных, и статистического вывода, отвечающего за предсказания в условиях неопределенности.
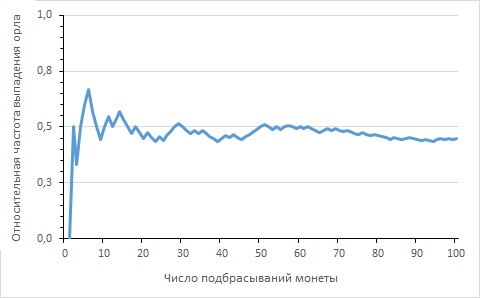
Золотая теорема Бернулли, известная сегодня как просто теорема Бернулли, гласит, что относительная частота события стремится к фиксированному числу (вероятности события) по мере того, как увеличивается количество повторений эксперимента (рис. 1).
Рис. 1. Относительная частота выпадения орла после 100 подбрасываний монеты; откройте файл Excel и поэкспериментируйте, нажимая F9; поскольку график основан на формуле, использующей случайные числа, его вид будет постоянно меняться, но стремление к среднему значению будет неизменным
На рубеже XVIII и XIX веков Пьер-Симон де Лаплас (1749–1827) утверждал, что ситуации, связанные со случайностью, бывают двух типов. В ситуациях первого типа случай проявляется в результатах. Известно, что в урне находятся белые и черные шары; вопрос: какой шар мы вытащим? На основе причин (количество белых и черных шаров в урне) вычислим вероятность результата: вытащим ли мы белый или черный шар? В ситуациях второго типа случай проявляется не в результатах, а в причинах. Мы знаем результат опыта (например, мы вытащили черный шар) и хотим вычислить состав содержимого урны, который нам неизвестен (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей).
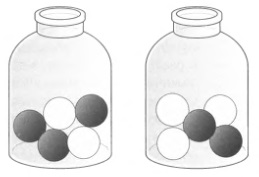
Представим себе урну, в которой могут быть два разных набора шаров: 2 белых и 3 черных или 3 белых и 2 черных (рис. 2). Вытаскиваем случайный шар, он оказывается черным; какой набор шаров в урне более вероятен? Теорема Байеса обеспечивает численную оценку этой вероятности (подробнее см. Идеи Байеса для менеджеров). Если предположить a priori, что два состава равновероятны (вероятность каждого равна 0,5), после применения формулы Байеса вероятность первого состава увеличивается до 0,6 из-за извлечения черного шара, тогда как вероятность второго состава уменьшается до 0,4. Вероятности a priori (0,5 и 0,5) корректируются a posteriori (0,6 и 0,4). Для Лапласа, как и для Байеса, эта важная теорема означала возможность обучения через опыт.
Рис. 2. Теорема Байеса в действии. Если мы вытащили черный шар, то согласно теореме Байеса, вероятность a posteriori состава на рисунке слева выше, чем вероятность состава на рисунке справа
В 1835 году ученик Лапласа, Симеон Дени Пуассон исследовал вопросы электоральной математики и юриспруденции и сформулировал «закон больших чисел», который обеспечивал лучшую основу применению исчисления вероятностей к социальным проблемам, объясняя статистическую стабильность в социальных изменениях. Большое количество индивидуумов, действуя в рамках системы, определяют регулярность, которая не зависит от их взаимной координации.
Неполнота генетических теорий Чарльза Дарвина (1809–1882) подтолкнула его кузена Фрэнсиса Гальтона (1822–1911) к попытке разрешить проблемы наследования признаков при помощи математического анализа биологических данных. В книге «Наследственность таланта, ее законы и последствия» (1869) он утверждает: «Точно так же, как методами тщательной и умелой селекции в рамках естественных ограничений удается получить стабильную породу собак или лошадей, обладающих особенными способностями к бегу или к чему-либо еще, представляется вполне возможным произвести высокоталантливую расу людей путем рассчитанных браков в течение нескольких последовательных поколений».
Гальтон считал, что союз двух умных людей приведет к рождению еще более умных детей, точно так же как у двух высоких людей рождаются еще более высокие дети. Однако эксперименты с наследованием, которые он проводил в течение всей жизни, привели к открытию другой статистической закономерности, отличной от ожидаемой. В своей книге «Естественное наследование» (1889) он назвал ее «возвращением к посредственности», а позднее — «регрессией к среднему». Сегодня мы знаем, что это не столько биологическая, сколько исключительно статистическая закономерность: более вероятно, что значения нормальной случайной величины будут ближе к ее среднему, ожидаемому значению (подробнее см. Даниэль Канеман. Думай медленно… решай быстро).
Гальтон обнаружил следующее линейное соотношение:
рост ребенка, см = 85 см + 0,5 * рост родителя, см
Это и была одна из прямых регрессии.
Глава 2. Карл Пирсон и биометрическая школа
Карл Пирсон (1857–1936) родился в Лондоне. Его семья принадлежала к среднему классу, что позволило юноше изучать математику в Кембридже, а после окончания в 1879 году продолжить обучение в университетах Гейдельберга и Берлина.
Одним из первых введенных им понятий было «стандартное отклонение». Далее он придумал коэффициент вариации, определив его как связь между стандартным отклонением и средним в абсолютном значении. Пирсон разработал еще два описательных показателя, коэффициент асимметрии и эксцесс. Пирсон сделал использование абстрактной математики в статистике обязательным и анализировал большие наборы данных (более 1000 объектов). Пирсон первым предупреждал об опасности выявления «ложных корреляций»: две переменные могут коррелировать между собой в отсутствие причинно-следственной связи или общей причины. В 1900 году Пирсон вывел критерий хи-квадрат (χ2) для определения качества подгонки наблюдаемого и теоретического, или ожидаемого, распределения.
В 1901 году Уэлдон и Пирсон, при участии Фрэнсиса Гальтона, основали журнал «Биометрика». В 1914 году Пирсон получил для публикации в «Биометрике» статью, подписанную 24-летним студентом по имени Р.А. Фишер. Статья была посвящена выборочным распределениям. Этот вопрос превращался в важную тему для дальнейшего развития статистического вывода, так как позволял количественно оценить надежность предположений, сделанных на основании репрезентативной выборки, имеющей своей целью узнать характеристики генеральной совокупности, набора объектов, который считался слишком большим, чтобы исследовать его полностью.
Характеристики генеральной совокупности, которые нужно было оценить, стали называть параметрами: генеральное среднее μ, стандартное отклонение генеральной совокупности σ или коэффициент корреляции генеральной совокупности ρ. Значения, вычисленные на основе данных выборки для оценки этих параметров, окрестили статистиками: выборочное среднее, стандартное отклонение выборки S.
Уильям Сили Госсет (1876–1937) по образованию был химиком, а познакомился со статистикой после работы в биометрической лаборатории Пирсона. В 1908 году он издал свою знаменитую статью «Возможная ошибка среднего» под псевдонимом Стьюдент. Причиной такой таинственности послужило то, что дублинская пивоварня Гиннесс, где он работал, не разрешала сотрудникам публиковать результаты исследований, проведенных на производстве. Стремясь контролировать качество производимого пива, Стьюдент собирал небольшие выборки (из соображений экономии). Он обнаружил, что один из типов кривых Пирсона соответствовал распределению, удобному для проведения этих экспериментов в малом масштабе. Так, если Стьюдент хотел оценить среднюю кислотность пива, произведенного на заводе за определенный период, он вычислял среднее из уровней кислотности, измеренных в дюжине бочек, которые составляли выборку. Проблема заключалась в том, что Стьюдент не знал возможную ошибку, возникающую при оценке среднего генеральной совокупности по выборочному среднему, то есть число, необходимое для определения точности статистического вывода и допустимого предела кислотности. Чтобы определить это, Стьюденту нужно было знать распределение выборочного среднего. Было замечено, что если выборка достаточно большая — 30 или более объектов, — распределение выборочного среднего приближается к нормальному (благодаря центральной предельной теореме), но если выборка маленькая, то дело обстоит иначе.
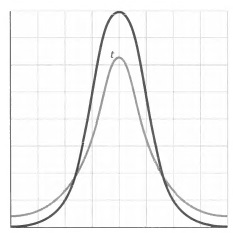
Стьюдент вычислил верное распределение, известное сегодня — после того как в 1925 году его отметил Фишер — как распределение t Стьюдента. На самом деле это целое семейство распределений, зависящих от количества степеней свободы; в общем случае оно более плоское, чем нормальное распределение, с более длинными хвостами, что отражает большую неуверенность в выводах. Эта вероятностная модель оказалась неотъемлемой частью статистических методов наших дней ввиду своей надежности, поэтому она используется не только для выводов на основании малых выборок из нормальной генеральной совокупности (для которой среднее и стандартное отклонение неизвестны), но также и для ненормально распределенных данных. Распределение t оказалось практически нечувствительным к гипотезе нормальности (рис. 3).
Рис. 3. Распределение t Стьюдента (серый цвет) обладает более широкими хвостами по отношению к нормальному (черный цвет)
Глава 3. Математические основы статистического вывода
В 1920-е годы Фишер принял эстафету у поколения статистиков, сформировавшегося вокруг Пирсона. Его статья «О математических основах теоретической статистики» и последовавшие за ней книги «Статистические методы для исследователей» и «Планирование экспериментов» ознаменовали становление статистического вывода как математической дисциплины. В них Фишер изложил критерий значимости, дисперсионный анализ и рандомизацию в качестве основных принципов любой работы ученого-натуралиста с фактами.
Статистический вывод — это набор методов, которые позволяют формулировать суждения об общем (генеральная совокупность) на основании частного (выборка), предоставляя меру уверенности в предсказании, вероятность ошибки.
До Фишера статистика, в которой доминировал титан Карл Пирсон, находилась в следующей ситуации. В описательной статистике, хотя и не существовало явного различия между выборкой и генеральной совокупностью, были известны простые графические представления (столбчатая диаграмма, гистограмма, диаграмма рассеяния) и вычислялись основные показатели центральной тенденции (среднее, медиана, мода), дисперсии (стандартное отклонение, хотя оно было и не единственной мерой), позиции (квартили и перцентили) и формы (асимметрия и эксцесс). Переход от разведывательного анализа данных к математической теории вероятностей проходил через подгонку теоретических распределений — нормальной кривой или кривых Пирсона — к наблюдаемым распределениям частот методом наименьших квадратов или методом моментов. Качество подгонки оценивалось с помощью критерия хи-квадрат. Наконец, статистический вывод мог похвастаться только двумя быстрыми методами: предсказаниями, основанными на анализе регрессии и корреляции, и в особенности обратными вероятностными методами, базирующимися на теореме Байеса (байесовский, или субъективный вывод).
Фишер заполнил пробел в этом важнейшем секторе, заложив основы методов оценки и вывода. Если Пирсон учил, как извлекать интересующую информацию из путаницы данных, Фишер показал, как познать целое (генеральную совокупность), наблюдая часть (выборку). Можно сказать, что Фишер довел до абсолюта создание методологического корпуса статистики: выбор теоретической модели на основании эмпирических данных, математическая дедукция свойств этой модели, оценка неизвестных параметров и заключительная проверка модели с помощью эксперимента. Подход, состоящий в сборе информации в ходе эксперимента и подготовке выводов на ее основе, составляет суть статистического вывода, и в отличие от вычисления вероятностей это не индуктивный, а дедуктивный процесс, сопровождающийся определенными ошибками, которые можно оценить количественно.
Сосредоточившись на проблемах теории оценки, Фишер утверждал, что речь шла о выборе наиболее подходящего значения из параметров генеральной совокупности традиционно обозначаемых греческими буквами, например, Θ на основании данных выборки, или, точнее, на базе статистик — обозначаемых латинскими буквами (например, Т), — которые вычисляются по наблюдаемым данным. Теория статистической оценки, разработанная Фишером, определяет, каким критериям должна удовлетворять хорошая оценка.
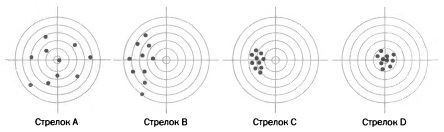
Сегодня три критерия, приведенные Фишером, претерпели небольшие изменения, хотя их смысл сохранился. Смещение. Оценка Т считается правильной и несмещенной для параметра Θ, если для любого размера выборки среднее значение ее распределения равно Θ, то есть если ожидаемое значение статистики Т является истинным значением Θ. Иначе оценка считается смещенной (рис. 4; подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?). Эффективность. Эффективность, или точность, оценки определяется как величина, обратная дисперсии ее выборочного распределения: чем больше дисперсия оценки, тем менее точна эта оценка, и наоборот. Это понятие имеет особенное значение для сравнения несмещенных оценок, так как среди них предпочтение должно отдаваться более эффективным, то есть обладающим наименьшей дисперсией.
Рис. 4. Пример смещения и эффективности оценки. Если мы сравним статистические оценки с выстрелами нескольких стрелков, то сможем лучше понять, какими качествами должна обладать хорошая оценка. Выстрелы стрелка А не отклоняются в каком-то одном направлении, но видно, что они очень разбросаны (это соответствует несмещенной, но неэффективной оценке). Выстрелы стрелка В смещены влево и разбросаны (оценка смещенная и неэффективная). Выстрелы стрелка С кучные, но отклоняются (смещенная и эффективная оценка).
Чтобы понять функцию правдоподобия, заново введенную Фишером и одну из самых важных для вывода, следует четко различать два довольно близких понятия. Пусть Θ — неизвестный параметр генеральной совокупности, а X — случайная выборка из этой совокупности. С одной стороны, существует вероятность получения выборки X при условии некоторого значения Θ (предполагается, что оно известно), обозначаемая р(Х|Θ) (X — переменная, Θ фиксирован) и определяющая вероятность появления всякой выборки. В проблеме оценки случай противоположный: наблюдается выборка X, но значение Θ неизвестно. Тем не менее описанная функция остается полезной, так как, заменив X на наблюдаемые значения, из Р(Х|Θ) для каждого Θ у нас будет вероятность получить выборочное значение X.
Изменяя Θ при фиксированном X, можно получить функцию, называемую функцией правдоподобия, L(Θ|Х), где X фиксирован, а Θ — переменная. Следует отметить, что после перемены ролей X и Θ в соответствии со сменой точки зрения, возникающей при выводе, функция правдоподобия не является распределением вероятности, следовательно, не подчиняется правилам исчисления вероятностей (когда подставляются конкретные значения из выборки). Эта функция отражает наши знания о параметре генеральной совокупности. И вместо предположения известного Θ и вычисления вероятности наблюдать различные выборки X допустим, что наблюдается конкретная выборка X, и оценим правдоподобие различных значений Θ.
Во время Второй мировой войны статистики, работавшие на стороне союзников, столкнулись с трудно разрешимой проблемой: как оценить общее количество немецких танков по серийным номерам захваченных у противника машин? Допустим, у захваченных танков следующие серийные номера: 2, 3, 7, 16. Сколько всего выпущено танков? Наилучшей возможной оценкой будет эффективная оценка (несмещенная и с минимальной дисперсией), формула которой для N следующая: m + (m –n)/n, где m — наибольший наблюдаемый серийный номер и n — размер выборки. Эту формулу можно интерпретировать как сумму выборочного максимума и «пустого среднего» выборки. К максимальному значению прибавляется среднее из промежутков между имеющимися наблюдениями, исходя из предположения, что за максимумом находится еще столько же элементов, сколько пропущено между имеющимися значениями. В нашем примере лучшей оценкой для N будет: 16 + (16-4)/4 = 19 танков всего (см. также Малые выборки в конкурентной разведке).
Фишер в качестве оценки Θ предлагал выбирать то значение, которое соответствует максимальной вероятности появления наблюдаемых значений выборки. Другими словами, выбрать такое значение параметра, которое, оказавшись реальным, максимизирует вероятность иметь данные, наблюдаемые в реальности.
Пусть имеется монета, вероятность выпадения сторон которой, р, неизвестна. Монету подбрасывают четыре раза и получают следующую серию: 0Р00 (орел-решка-орел-орел). Из исчисления вероятностей мы знаем, что Р(ОРОО|р) = р3(1 – р). Следовательно, функция правдоподобия: L(p|ОРОО) = р3(1 – р). Функция правдоподобия достигает максимума для значения 0,75. Таким образом, наша оценка, основанная на имеющейся выборке, будет р = 0,75. В сущности, это и есть основа метода оценки параметров с помощью максимального правдоподобия.
В период с 1923 по 1924 год Фишер писал книгу «Статистические методы для исследователей», которая увидела свет в 1925 году и на сегодняшний день выдержала 14 переизданий. Это самый влиятельный и известный труд Фишера. Он больше похож на учебник, чем на научную работу, благодаря убедительному стилю и характерному отсутствию математических доказательств. Возможно, этим и обусловлен его успех.
Фишер пишет, что статистика — не что иное, как математика, примененная к результатам наблюдений. При исследовании доступных выборок статистик делает выводы о полной совокупности, но они должны быть выражены не языком вероятности (как считали сторонники теоремы Байеса, или обратных вероятностных методов), а скорее языком правдоподобия.
Краеугольный камень всего произведения — «критерий значимости». В чем он состоит? В первую очередь в нулевой гипотезе Н0, которая устанавливает, например, что истинное значение неизвестного параметра таково, что Θ = Θ0. Затем выбирается статистика Т и вычисляется ее значение по данным имеющейся выборки X, которое обозначается как Т(Х). Так как распределение статистики Т в выборке известно, определяется вероятность того, что статистика Т примет значение, равное или большее наблюдаемому значению Т(Х), при условии, что нулевая гипотеза верна.
Математически это выглядит так: Р(Т ≥ Т(Х)|Н0). Это число было названо p-значением. Отсюда, если значение р достаточно мало — обычно меньше 0,05,— считается, что критерий оказался значимым и поэтому позволил опровергнуть нулевую гипотезу Н0. В противоположном случае тест оказывается незначимым для заранее заданного уровня значимости α = 0,05, отклонить нулевую гипотезу Н0 оказывается невозможным, ее временно принимают.
Нулевая гипотеза отвергалась только в том случае, когда вероятность наблюдать выборку вроде имеющейся была очень низка. Статистическое рассуждение основывалось на следующей логической дизъюнкции: «Или произошло исключительное событие (очень маловероятное), или нулевая гипотеза неверна». Очень малое р-значение указывало на то, что наблюдаемая выборка сильнее отличается от ожидаемой, чем это можно объяснить чистой случайностью, и поэтому исследователь имеет дело с неправдоподобной нулевой гипотезой, которую следует отвергнуть.
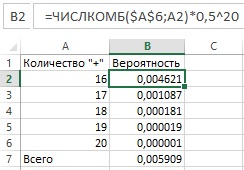
Закрепим эти понятия с помощью простой иллюстрации. Предположим, мы использовали новое удобрение на 20 растениях и наблюдали их рост в течение определенного периода времени, чтобы измерить влияние нового удобрения: увеличение (+) или уменьшение (–) скорости роста по отношению к росту без удобрения. Нашей нулевой гипотезой будет отсутствие всякого положительного эффекта от удобрения, то есть распределение ускорений (+) и замедлений (–) будет полностью случайным, как выпадение «орла» и «решки» при подбрасывании совершенно симметричной монеты. Поэтому, согласно нулевой гипотезе Н0, вероятность «+» будет равна вероятности «–», а именно Θ = 0,5. Представим, что после эксперимента мы видим 16 «+» и только 4 «–». Если мы выберем в качестве статистики Т количество наблюдаемых «+», то выяснится, что вероятность получить 16 или более «+» исходя из предположения, что вероятность положительного эффекта равна 0,5, составляет, как легко вычислить (см. рис. 5), только 0,006. То есть: Р(Т ≥ Т(Х)|Н0) = 0,006. Так как значение р ниже порогового α = 0,05, тест оказался значимым, и мы можем отвергнуть исходную нулевую гипотезу: есть эмпирические данные, противоречащие гипотезе, что удобрение не оказывает эффекта. Наоборот, все указывает на то, что оно стимулирует рост растений.
Рис. 5. Таблица расчета вероятности получить 16 и более «+» согласно формуле биномиальной вероятности:
Фишер предупреждал, что уровень значимости α не должен быть фиксированным, жестким. Впрочем, его предупреждение забыли и уровень 0,05 широко приняли, вплоть до того, что значение р = 0,051 стали считать незначимым, а 0,049 — значимым. Выбор этого граничного значения — вопрос не математический, универсальный, а зависит от прагматического контекста: если проверяется новое лекарство, то уровень значимости 0,05 несет 5%-ный риск того, что неэффективное лекарство будет признано эффективным (в этом случае, как и в некоторых других, уровень 0,01 или 0,001 может оказаться более подходящим).
Фишер описывал критерий значимости как способ отвергнуть нулевую гипотезу, которая никаким образом не может быть доказана и установлена окончательно. Этот подход, связанный с опровержением, соответствовал направлению «фальсификации», инициированному философом Карлом Поппером (1902–1994). Для статистика и философа наука характеризуется постановкой экспериментальных доказательств, которые могут опровергнуть или фальсифицировать теории, описываемые учеными (подробнее см. Карл Поппер. Логика научного исследования).
Методологически подход Фишера был разновидностью фальсификации в приложении к статистике: он состоял в опровержении гипотез, для которых наблюдения были относительно неправдоподобными. Нулевая гипотеза никогда не подтверждалась, но ее можно было опровергнуть. Если критерий оказывался значимым, гипотеза оказывалась неприемлемой в свете имеющихся данных; если нет, это говорило лишь о том, что гипотеза была совместима с данными.
Кроме критерия значимости, книга Фишера описывала дисперсионный анализ — другую инновационную статистическую методику, известную во всем мире по английской аббревиатуре ANOVA (англ. ANalysis Of VAriance; подробнее см. Однофакторный дисперсионный анализ).
В 1935 году Фишер издает книгу «Планирование экспериментов». Биологические исследования требуют проведения контролируемых экспериментов. Пассивного наблюдения недостаточно. Выборочная техника состоит в исследовании репрезентативной выборки из генеральной совокупности и измерении изучаемых показателей. Планирование экспериментов, наоборот, заключается в фиксации одних параметров и наблюдении за другими, с измерением возникающих изменений.
Объекты, получающие «обработку», являются экспериментальными единицами. Каждая обработка должна встречаться как минимум два раза, а лучше — несколько раз. Если мы хотим сравнить обработку А и В, в идеале следует применить их одновременно на множестве участков. Может случиться, что наблюдаемая разница между обработками А и В связана просто с разной плодородностью почвы на разных участках, а не с тем, например, что А эффективнее, чем В. Принцип повторения, сформулированный Фишером, помогал ограничить ошибку эксперимента, то есть случайную вариацию, не контролируемую экспериментатором (как, например, разная плодородность участков, на которых применяются обработки А и В).

Ух ты! Спасибо за наводку. Надо брать. ))