В основу этой книги легли знаменитые лекции Ричарда Фейнмана, прочитанные им в 1964 году в Корнуолльском университете. В них прославленный физик рассказывает о фундаментальных законах природы и величайших достижениях мировой физики, не утративших своей актуальности и по сей день, – рассказывает простым доступным языком, понятным даже самому обычному читателю. Чего только стоит его знаменитая аналогия с мокрым человеком, который пытается вытереться мокрым полотенцем, на примере которой он объясняет закон сохранения энергии!..
См. также Леонард Млодинов. Радуга Фейнмана. Поиск красоты в физике и в жизни.
Ричард Фейнман. Характер физических законов. – М.: АСТ, 2016. – 256 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon или Лабиринте
Лекция 1. Пример физического закона – закон тяготения
Любуясь закатами, волнами в океане, хороводом звезд на небе,.. мы испытываем эстетическое наслаждение. Вместе с тем в явлениях природы есть формы и ритмы, недоступные глазу созерцателя, но открытые глазу аналитика. Эти формы и ритмы мы называем физическими законами. В первой лекции я расскажу об одном физическом законе – законе всемирного тяготения. Мы будем говорить не о том, как мы умны, что открыли этот закон, но о том, как мудра природа, которая соблюдает его.
Закон тяготения заключается в том, что два тела действуют друг на друга с силой, которая обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их масс:
Вкратце история его такова. Еще древние, наблюдая за движением планет на небе, догадались, что все они, вместе с Землей, «ходят» вокруг Солнца. Позднее, когда люди забыли то, о чем знали прежде, это открытие заново сделал Коперник. И тогда возник новый вопрос: как именно планеты ходят вокруг Солнца, каково их движение?
После Коперника снова настали смутные времена и разгорелись великие споры о том, ходят ли планеты вместе с Землей вокруг Солнца или Земля находится в центре Вселенной. Тогда человек по имени Тихо Браге придумал, как можно ответить на этот вопрос. Он решил, что нужно очень внимательно следить за тем, где появляются на небе планеты, точно это записывать и тогда уже выбирать между двумя враждебными теориями. Это и было началом современной науки, ключом к правильному пониманию природы наблюдать за предметом, записывать все подробности и надеяться, что полученные таким способом сведения послужат основой для того или иного теоретического истолкования.
Помощник Браге – немецкий астроном Иоганн Кеплер – открыл, что орбита планеты представляет собой эллипс; за равные промежутки времени радиус вектор планеты описывает равные площади и время (период) обращения планеты вокруг Солнца пропорционально величине орбиты в степени три вторых, т.е. квадратному корню из куба величины орбиты.
Затем наступила очередь Ньютона, которому удалось вычислить, какую форму должна иметь орбита, если закон обратной пропорциональности квадрату расстояния справедлив; он нашел, что орбита должна быть эллипсом.
С развитием науки измерения производились все точнее и подтверждения ньютоновских законов становились все более убедительными. Первые точные измерения касались спутников Юпитера. Выяснилось, что спутники Юпитера появлялись в расчетных точках то на 8 мин раньше, то на 8 мин позже, чем полагалось бы согласно законам Ньютона. Обнаружилось, что они опережают график, когда Юпитер сближается с Землей, и отстают, когда Юпитер и Земля расходятся, очень странное явление.
И вот что еще интересно. Обратно пропорциональная зависимость от квадрата расстояния встречается и в других законах, например, в законах электричества. Электрические силы также обратно пропорциональны квадрату расстояния, но уже между зарядами, и невольно возникает мысль, что в этой закономерности таится глубокий смысл. Если мы возьмем две элементарные частицы, два электрона, то за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Вопрос: каково отношение силы тяготения к электрической силе? Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Это вызывает глубочайшее недоумение. Откуда могло взяться такое огромное число? Если бы у нас когда-нибудь появилась общая теория для двух этих явлений, то как она давала бы такую диспропорцию для двух электронов:
Каким должно быть общее уравнение, если, решая его для двух видов сил гравитационного притяжения и электрического отталкивания, мы приходим к такому фантастическому отношению?
Эйнштейну пришлось изменить законы Ньютона. Эти изменения, уточнения очень малы, Одно из них состоит вот в чем: поскольку свет имеет энергию, энергия эквивалентна массе, а все массы притягиваются, свет тоже притягивается и, значит, проходя мимо Солнца, должен отклоняться. Так оно и происходит на самом деле. Сила тяготения тоже слегка изменена в теории Эйнштейна. Но этого очень незначительного изменения в законе тяготения как раз достаточно, чтобы объяснить некоторые кажущиеся неправильности в движении Меркурия.
Лекция 2. Связь математики с физикой
Математика приносит огромную пользу физике там, где речь идет о деталях сложных явлений, если установлены основные правила игры. Я привел уравнение закона тяготения, чтобы поразить вас тем, насколько быстро математические символы могут передавать информацию. Но, почему такой закон может быть основным законом. Что делает планета? Неужели она смотрит на Солнце, видит, насколько оно удалено, и вычисляет на своем арифмометре обратный квадрат расстояния, чтобы узнать, как нужно двигаться? Еще Ньютона спрашивали о его теории: «Но ведь она ничего не говорит, она ничего не объясняет?» Ньютон отвечал: «Она говорит, как движутся тела. Этого должно быть достаточно. Я сказал вам, как они движутся, а не почему».
Если бы существовал только один закон такого характера, то это было бы интересным, хотя и досадным исключением. Но, оказывается, чем больше мы исследуем, чем больше законов мы открываем, чем глубже проникаем в природу, тем более хронической становится болезнь. Каждый новый ваш закон чисто математическое утверждение, притом довольно сложное и малопонятное. Почему? Не имею ни малейшего понятия. Моя цель в том и состоит, чтобы лишь сообщить об этом факте. В нем и заключается смысл всей лекции: нельзя честно объяснить все красоты законов природы так, чтобы люди восприняли их одними чувствами, без глубокого понимания математики. Как ни прискорбно, но, по-видимому, это факт.
Возможны два взгляда на математику. Для удобства один из них я назову вавилонской традицией, а другой – греческой традицией. Вавилонский подход заключается в том, что вы знаете самые разные теоремы, многие связи между ними, но не осознаете до конца, что все они могут быть выведены из набора аксиом. Самая же современная математика делает упор на аксиому и доказательства, исходя из очень четких соглашений о том, что можно и что нельзя считать аксиомами.
Если в системе знаний таится какая-то погрешность, но построена система на удачных аксиомах, то впоследствии вы обнаружите, что неверна лишь одна из них, а остальные справедливы; в этом случае потребуются лишь незначительные переделки. Но если вы строили систему на других аксиомах, то она может вся развалиться из-за того, что целиком опирается на одну единственную слабую деталь.
Мы не можем сказать заранее, не прибегая к интуиции, как лучше всего строить систему, чтобы прийти к новому закону. Мы постоянно должны иметь в виду все возможные способы описания; поэтому физики занимаются вавилонской математикой и уделяют мало внимания аксиоматическому построению своей науки. Мне это всегда представлялось загадкой. Я не понимаю, почему правильные законы физики допускают такое огромное количество разных формулировок.
Говорят, что один царь, которого Евклид пытался обучить геометрии, стал жаловаться на трудности. Евклид ответил: «Нет царского пути к геометрии». И его действительно нет. Физику нельзя перевести ни на какой другой язык. И если вы хотите узнать Природу, оценить ее красоту, то нужно понимать язык, на котором она разговаривает. Она дает информацию лишь в одной форме, и мы не вправе требовать от нее, чтобы она изменила свой язык, стараясь привлечь наше внимание.
Лекция 3. Великие законы сохранения
Изучая физику, вы обнаруживаете, что существует огромное количество сложных и очень точных законов законы гравитации, электричества и магнетизма, законы ядерных взаимодействий и т.д. Но все это многообразие отдельных законов пронизано некими общими принципами, которые так или иначе содержатся в каждом законе. Примерами таких принципов могут служить законы сохранения, некоторые свойства симметрии, общая форма квантовомеханических принципов и тот приятный для одних и досадный для других факт, что все законы являются математическими.
Проще всего понять закон сохранения электрического заряда; с него я и начну. Существует число, полный электрический заряд мира, которое остается постоянным, что бы ни произошло. Если вы теряете заряд в одном месте, то находите его в другом. Сохранение относится только к полному электрическому заряду. Это опытным путем установил Фарадей.
Согласно принципу относительности Эйнштейна, закон сохранения заряда локален, и то же самое можно сказать обо всех остальных законах сохранения. Как выяснилось, этот принцип распространяется на все сохраняющиеся величины.
Если мы хотим, чтобы от науки была какая-то польза, мы должны строить догадки. Чтобы наука не превратилась в простые протоколы проделанных экспериментов, мы должны выдвигать законы, простирающиеся на еще не изведанные области. Ничего дурного тут нет, только наука оказывается из-за этого недостоверной. А если вы думали, что наука достоверна, вы ошибались.
Лекция 4. Симметрия физических законов
Нам нравится смотреть на проявление симметрии в природе. Однако сейчас мне хотелось бы поговорить не о симметрии предметов, а о симметрии самих законов физики. Известный математик Герман Вейль (1885–1955) предложил прекрасное определение симметрии, согласно которому симметричным называется такой предмет, который можно как-то изменять, получая в результате то же, с чего вы начали. Именно в этом смысле говорят о симметрии законов физики. При этом мы имеем в виду, что физические законы или способы их представления можно изменять так, что это не отражается на их следствиях.
Простейшим примером симметрии такого рода может служить симметрия относительно пространственного переноса. Возьмем в качестве иллюстрации закон всемирного тяготения. Уже то, что в законе всемирного тяготения используется «расстояние между двумя телами», а не какое-то расстояние до центра Вселенной, показывает, что этот закон допускает переносы в пространстве.
Другое свойство симметрии связано с тем, что для физических законов не существенны и сдвиги во времени. Закон всемирного тяготения говорит о скорости и нигде не пользуется понятием абсолютного времени, в определенный момент которого необходимо начать измерения. (Известно, что в одном отношении это на самом деле не так. Факты свидетельствуют, по-видимому, о том, что Вселенная имеет определенное начало во времени и что сейчас эта Вселенная постоянно расширяется.)
Еще один закон симметрии связан с фиксированными пространственными поворотами. Если проводить какой-либо опыт с установкой, построенной в каком-нибудь определенном месте, а затем взять другую точно такую же установку и повернуть ее так, чтобы все ее оси имели другую ориентацию, то установка будет работать точно таким же образом, как и раньше.
Еще один очень интересный пример закона симметрии. Он связан с равномерным движением по прямой. Считается, что законы физики не меняются при равномерном движении по прямой. Это утверждение получило наименование принципа относительности, и впервые было высказано Ньютоном. Изучая Солнечную систему и траектории движения планет вокруг Солнца, мы не можем решить, неподвижно ли Солнце относительно нашей Вселенной или оно движется. В соответствии с законом Ньютона такое движение Солнца никак не отражается на движении планет вокруг Солнца. Поэтому Ньютон добавлял: «Движение тел в пространстве относительно друг друга одно и то же, независимо от того, неподвижно ли это пространство относительно звезд или движется по прямой с постоянной скоростью».
Теперь вам может показаться, что все законы физики симметричны относительно любых изменений. Чтобы вы так не думали, я приведу несколько примеров. Первый из них – изменение масштаба. Тот факт, что законы физики не остаются неизменными при изменении масштаба, впервые был обнаружен Галилеем. Рассуждая о прочности костей и балок, он приводит такие соображения. Если вам требуются кости для более крупного животного, которое, скажем, в два раза выше, толще и длиннее нормального, то вес этого животного увеличится в восемь раз, и, следовательно, вам нужны кости, которые выдерживали бы восьмикратную нагрузку. Но прочность кости зависит от размеров ее поперечного сечения, а поэтому если вы увеличите все кости по сравнению с прежним в два раза, то их поперечное сечение увеличится лишь в четыре раза, и, следовательно, они смогут выдерживать лишь четырехкратную нагрузку.
Симметричны ли законы физики относительно изменения правого на левое и наоборот? Ли Тзундао и Янг Чженьнин высказали предположения, что, может быть, принцип симметрии относительно правого и левого, согласно которому природа не реагирует на зеркальное отображение, неверен, и тогда это позволит разрешить целый ряд загадок. Оказалось, что отличить правое от левого можно, а значит, закон о симметрии мира относительно правого и левого рухнул.
Лекция 5. Различие прошлого и будущего
Каждому ясно, что события, происходящие в нашем мире, явно необратимы. Другими словами, все происходит так, а не наоборот. Роняешь чашку, она разбивается, и сколько ни жди, черепки не соберутся снова, и чашка не прыгнет обратно тебе в руки. Однако, во всех законах физики, обнаруженных до сих пор, не наблюдается никакого различия между прошлым и настоящим. Например, для закона всемирного тяготения безразлично направление времени; если вам показывают задом наперед любой фильм о событиях, связанных лишь с законами тяготения, то все, что вы увидите на экране, будет выглядеть совершенно естественным.
Это свойство заложено в самой формулировке закона всемирного тяготения, утверждающего, что под действием силы изменяется скорость. Если изменить направление времени, то силы не изменятся и, следовательно, на соответствующих промежутках времени не изменятся и приращения скорости. Поэтому каждая скорость претерпит точно такие же изменения, как и раньше, только в обратной последовательности. Так что доказать обратимость во времени закона всемирного тяготения совсем не трудно.
Законы электричества и магнетизма тоже обратимы во времени. Так что нам придется поискать какое-нибудь другое объяснение этой необратимости. Пусть у нас есть вода, подсиненная чернилами, и обычная вода, без чернил, и пусть они налиты в банку из двух половин, разделенных очень тонкой перегородкой. Осторожно вытащим перегородку. В самом начале вода разделена: синяя справа, чистая слева. Но погодите. Мало-помалу синяя вода начинает перемешиваться с обычной, и через некоторое время вся вода оказывается голубой, причем интенсивность синего цвета уменьшится наполовину. Это значит, что чернила равномерно распределились по всему объему. Теперь, сколько бы мы ни ждали, наблюдая воду, мы не дождемся, чтобы она разделилась на синюю и обычную.
В этом и заключается ответ на наш вопрос. События нашего мира необратимы в том смысле, что их развитие в одну сторону весьма вероятно, а в другую – хотя и возможно, хотя и не противоречит законам физики, но случается один раз в миллион лет. Один из законов природы состоит в том, что все меняется от порядка к беспорядочности.
Некоторые полагают, что наш мир стал упорядоченным следующим образом. В нашем мире, где беспорядочное движение все шло и шло своим чередом, произошла флуктуация. А теперь мы наблюдаем, как все потихоньку возвращается к хаосу. Лично мне такая теория кажется неверной. Мне кажется, что в прошлом Вселенная была более упорядоченной (в физическом смысле этого слова), чем сегодня. Я думаю, именно этого дополнительного утверждения нам не хватает для того, чтобы поставить все на свои места, чтобы до конца разобраться в явлениях необратимости.
Движение от порядка к беспорядку еще называют законом возрастания энтропии. Смысл его в том, что свободная пригодная для использования энергия может только уменьшаться. И это характерное свойство нашего мира в том смысле, что оно вытекает из хаотичности движения молекул.
Лекция 6. Вероятность и неопределенность – квантовомеханический взгляд на природу
В нашей повседневной жизни мы имеем дело с огромными скоплениями частиц, очень медленными процессами и другими очень специфичными условиями, так что наш опыт дает нам лишь очень ограниченное представление о природе. Из непосредственного опыта можно почерпнуть сведения лишь об очень малой доле естественных явлений. И только при помощи очень тонких измерений и тщательно подготовленных опытов можно добиться более широкого взгляда на вещи.
Начнем с истории изучения света. Сначала предполагалось, что свет очень похож на дождь из частиц, или корпускул, летящих как пули, выпущенные из ружья. Однако последующие исследования показали, что такое представление неверно и на самом деле свет ведет себя как волны, например, как морские волны. Затем уже в XX веке, после дополнительных исследований, вновь стало казаться, что в очень многих случаях свет ведет себя как поток частиц. Наблюдая фотоэлектрический эффект, можно подсчитать число этих корпускул, теперь их называют фотонами.
Все нараставшая путаница была разрешена в 1925–1926 гг. открытием точных уравнений квантовой механики. Теперь мы знаем, как ведет себя свет. Но как я могу назвать такой характер поведения? Сказать, что они ведут себя как частицы, значило бы создавать у вас неправильное представление. То же самое получится, если я скажу, что они ведут себя как волны. Они ведут себя таким образом, что это ни в коей степени не напоминает чего-нибудь, с чем вы сталкивались раньше. Ваш опыт, основанный на том, с чем вы сталкивались раньше, неполон. Просто-напросто все то, что происходит в очень маленьком масштабе, происходит совсем по-другому.
Я собираюсь рассказать вам об опыте с двумя отверстиями. Именно в нем заключена основная загадка. Начнем с пуль (рис. 1). Пусть у нас имеется источник пуль, и перед ним установлен экран с отверстием, пропускающим пули. На большом расстоянии от первого щита поставим другой щит с двумя отверстиями. На большом расстоянии от второго щита поставим еще и третий, позволяющий устанавливать в разных местах детектор, в котором пули застрянут, после чего их можно будет сосчитать.
Рис. 1. Поведение пуль
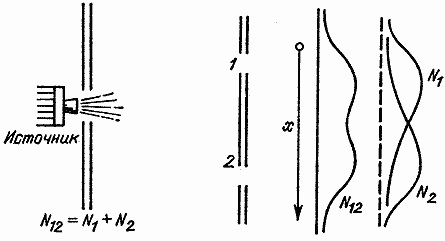
Первое, что мы заметим в нашем опыте с пулями, это то, что все здесь происходит дискретными порциями. Например, энергия, поглощенная мишенью. Она может увеличиться только скачком на величину энергии одной пули. Попасть одновременно в два ящика невозможно, потому что каждая пуля – это одна нерасчленяемая и опознаваемая порция. Полученные кривые мы обозначим через N1, N2 и N12 (где индексы указывают на то, какие отверстия открыты). Так, кривая N12 дает число пуль, зарегистрированных нашим детектором за час в случае, когда открыты оба отверстия.
Рассматривая кривую N12, мы можем заметить, что ее легко интерпретировать как сумму двух других кривых: одной, которую я обозначу через N1 и которая описывает число попаданий, если отверстие 2 закрыто броневой заслонкой, и другой, N2, описывающей число попаданий при открытом отверстии 2 и закрытом отверстии 1.
N12 = N1 + N2 (отсутствие интерференции)
Покончив с пулями, начнем все с самого начала, на этот раз с морскими волнами (рис. 2).
Рис. 2. Поведение волн
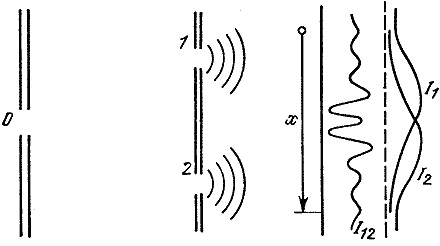
Математика образования I12 на самом деле довольно интересна. Дело в том, что высота воды, которую мы будем обозначать через h, в случае, когда открыты оба отверстия, равна сумме высот, создаваемых волнением в случае одного открытого отверстия 1 и в случае одного открытого отверстия 2. Поэтому, если из отверстия 2 приходит впадина волны, соответствующая высота h отрицательна, и она компенсирует положительную высоту h для волны, пришедшей из отверстия 1. Волнение воды можно характеризовать ее высотой, но оказывается, что интенсивность волнения в любом случае, например тогда, когда открыты оба отверстия, не совпадает с высотой воды в данной точке, а пропорциональна квадрату этой высоты. И именно потому, что мы имеем дело с квадратами, получаем наши очень интересные кривые:
h12= h1+ h2
I12 = I1 + I2 (интерференция)
I12 = (h12)2
I1 = (h1)2
I2 = (h2)2
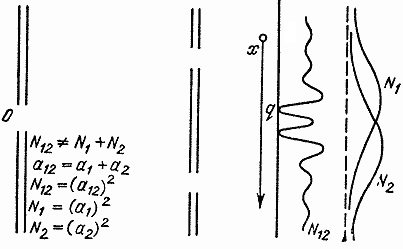
Теперь об электронах (рис. 3). Прежде всего мы заметим, что наш электрический детектор, на выходе которого мы поставим достаточно мощный усилитель, все время щелкает: электроны попадают в него дискретно, строго по порциям. Каждый щелчок это заряд определенной величины, и эта величина все время постоянна. Если вы уменьшите накал источника, щелчки будут все реже, но все равно заряд каждого щелчка тот же, что и раньше. Если же усилить накал, щелчки посыплются, как из мешка, и в усилителе возникнет затор. А это значит, что возникающие события происходят дискретно, порциями, причем у каждой порции вполне определенная, постоянная для всех величин, и что в данный момент времени такая порция может находиться лишь в одном месте. Итак, электроны или фотоны попадают в детектор по одному, дискретно, порциями. Поэтому мы можем поступить так же, как и в случае с пулями: мы можем измерить вероятность появления.
Рис. 3. Поведение электронов
Теперь мне нужно проверить еще один факт: выяснить, есть ли здесь интерференция или нет. Например, если детектор установить в положении q и открыть оба отверстия, в него практически ничего не попадет, но в то же время стоит мне закрыть одно из них, детектор начнет работать независимо от того, какое из отверстий было закрыто. Опять откроем оба отверстия, и вновь ничего. Мы позволили электронам пролетать в детектор через оба отверстия, а они сразу перестали прилетать совсем.
Итак, электроны попадают в детектор дискретными порциями, как если бы это были частицы, но вероятности попадания этих частиц определяются по тем же законам, по каким определяется интенсивность волнения воды. Именно в этом смысле можно говорить, что с одной точки зрения электрон ведет себя, как частица, а с другой как волна. Он ухитряется одновременно быть двумя совершенно разными понятиями (рис. 4).
Рис. 4. Сравнительная таблица поведения пуль, волн и электронов
Когда Гейзенберг открывал законы квантовой механики, он заметил, что эти новые законы природы оказываются непротиворечивыми только в том случае, если можно принять, что наши экспериментальные возможности принципиально ограничены некоторым образом, хотя мы и не замечали этого ранее. В связи с этим Гейзенберг предложил свой принцип неопределенности: «Нельзя сконструировать какой-либо прибор, при помощи которого можно было бы определить, через какое из отверстий пролетит электрон, не изменив при этом его движения настолько, что это разрушит интерференционную картину».
Вовсе не незнанием внутреннего механизма, внутренней сложности источника электронов объясняется появление вероятностных законов природы. По-видимому, это в какой-то степени неотъемлемое свойство природы. Кто-то выразился об этом так: «Даже сама природа не знает, по какому пути полетит электрон».
Лекция 7. В поисках новых законов
Я собираюсь поговорить о том, как открывают новые законы. Вообще говоря, поиск нового закона ведется следующим образом. Прежде всего о нем догадываются. Затем вычисляют следствия этой догадки и выясняют, что повлечет за собой этот закон, если окажется, что он справедлив. Затем результаты расчетов сравнивают с тем, что наблюдается в природе, с результатами специальных экспериментов или с нашим опытом, и по результатам таких наблюдений выясняют, так это или не так. Если расчеты расходятся с экспериментальными данными, то закон неправилен. В этом простом утверждении самое зерно науки. Неважно, насколько ты умен, кто автор догадки, известен он или нет если теория расходится с экспериментом, значит теория неверна. Вот и все.
У нас всегда есть возможность опровергнуть теорию, но, обратите внимание, мы никогда не можем доказать, что она правильна. Предположим, что вы выдвинули удачную гипотезу, рассчитали, к чему это ведет, и выяснили, что все ее следствия подтверждаются экспериментально. Значит ли это, что ваша теория правильна? Нет, просто-напросто это значит, что вам не удалось ее опровергнуть (подробнее о принципе фальсификации см. Карл Поппер. Логика научного исследования).
Вот почему у законов типа законов движения планет Ньютона такая долгая жизнь. Ньютон угадал закон всемирного тяготения, вывел из него самые различные следствия для Солнечной системы, сравнил их с результатами наблюдений и потребовалось несколько столетий, прежде чем было замечено незначительное отклонение движения планеты Меркурий от предсказанного. На протяжении всех этих лет теория Ньютона не была опровергнута, и временно ее можно было считать верной. Но ее правильность никогда нельзя было доказать, потому что уже завтра эксперимент, может быть, покажет вам неправильность того, что вам казалось верным еще сегодня. Можно только удивляться тому, что нам удается придумывать теории, которые выдерживают натиск эксперимента столь длительное время.
Наука приносит пользу только тогда, когда говорит вам о еще непоставленных экспериментах. Она никому не нужна, если позволяет судить лишь о том, что известно из опыта, что только что произошло. Поэтому всегда необходимо распространять идеи за рамки того, на чем они уже опробованы.