Серьезные идеи (а может быть, и все!? :)) нельзя глубоко постичь с первого «прочтения». Со мной так случается часто. Вот и контрольные карты Шухарта – тема, с которой я впервые познакомился в конце 90-х. Тогда мне попалась на глаза брошюра по курсу менеджмента качества. В памяти практически ничего не отложилось и никаких идей о практическом применении не возникло. И только с 2005-го года я начал использовать сбор данных и построение графиков для контроля над различными параметрами логистических процессов. Тогда я еще не отдавал себе отчета, что строю контрольные карты. И у меня не было важного их компонента – 3-сигмовых контрольных границ, благодаря которым менеджер и понимает, какого рода решения следует принять!
В 2009-м я прочитал книгу Д. Уилера, Д. Чамберса «Статистическое управление процессами. Оптимизация бизнеса с использованием контрольных карт Шухарта» и после этого построение контрольных карт стало значительно более осмысленным. Но… раздел, посвященный критериям определения отсутствия управляемости, на меня не произвел особого впечатления, и на практике я использовал только один признак потери статистической управляемости процесса – выход за 3-сигмовые границы.
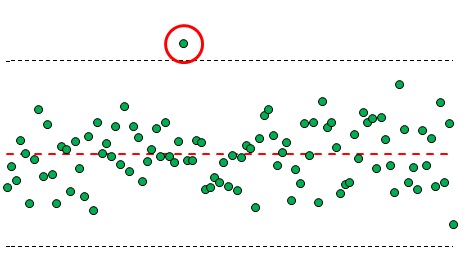
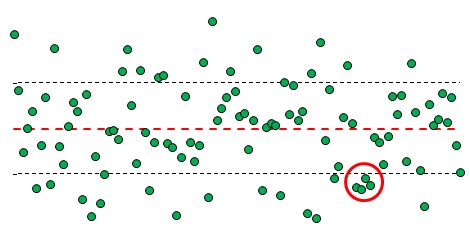
Рис. 1. Пример выхода точки за 3-сигмовые границы
Скачать заметку в формате Word или pdf, примеры в zip-файле
В настоящей заметке я обсуждаю тонкие моменты, связанные с контрольными картами Шухарта. Для тех, кто не в теме, предлагаю начать с:
Контрольные карты Шухарта
Пример построения контрольной карты Шухарта в Excel
Семь основных инструментов контроля качества
Использование методов менеджмента качества в работе оптовой торговой компании
Вкратце. Контрольная карта Шухарта используется для графического отображения информации о исследуемом параметре процесса. На контрольной карте наносят экспериментально измеренные значения, а также линию среднего (m), верхнюю (m+3s) и нижнюю (m–3s) границы. Если процесс статистически управляем, то есть отклонение точек от среднего связано лишь с естественной вариабельностью присущей процессу, то все точки лежат между границами. В этом случае для уменьшения вариабельности (ширины коридора между границами) и/или среднего значения необходимы усилия, направленные на совершенствование процесса. Если процесс характеризуется отсутствием управляемости, то есть некоторые точки выходят за контрольные границы, усилия должны быть направлены на выявление особых причин вариабельности и их устранение. Примеры особых причин вариабельности: плохо обученные исполнители, бракованная партия комплектующих, износ обрабатывающего станка, поломка автомобиля и др. Еще раз подчеркну, контрольная карта показывает, какого рода решение должен принять менеджер: совершенствовать процесс или найти и исключить особые причины.
Таким образом, одна из задач контрольной карты Шухарта – выявление ситуаций, свидетельствующих об отсутствии статистической управляемости процессом.
В упомянутой выше книге, авторы предлагают четыре правила определения отсутствия управляемости:
- выход одной точки за 3-сигмовые пределы
- выход хотя бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за 2-сигмовые пределы
- выход, по меньшей мере, 4 из 5 последовательных точек, лежащих по одну сторону от центральной линии, за 1-сигмовые пределы
- расположение, по меньшей мере, 8 последовательных точек по одну сторону от центральной линии
И вот недавно меня осенило! Так ведь все эти критерии, похоже, соответствуют одной и той же вероятности указанных событий! Давайте проверим.
Критерий 1. Выход одной точки за 3-сигмовые пределы указывает на отсутствие управляемости
О чем идет речь? На рис. 1 изображено 100 значений случайно величины, одно из которых вышло за пределы 3-сигмовой границы. На рисунок также нанесены линия среднего и 3-сигмовые границы.
С помощью функции =НОРМСТРАСП (см. также одноименный лист Excel-файла) построим табличку зависимости вероятности выхода случайной величины за n-сигмовую окрестность от среднего (рис. 2) и представим интегральную вероятность распределения случайной величины графически (рис. 3).
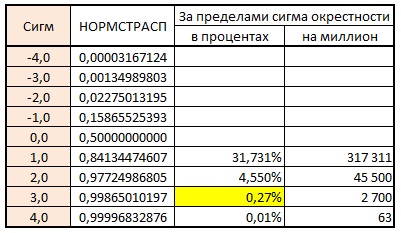
Рис. 2. Вероятность выхода за 3-сигмовую окрестность
Рис. 3. Интегральная вероятность распределения случайной величины
Релевантность первого критерия составляет 99,73%. То есть только с вероятностью 0,27% выход за пределы 3-сигмовой границы не будет связан со специальными причинами, а будет обусловлен «выбросом» случайной (статистически управляемой) величины – ложна тревога.
Для моделирования поведения случайной нормально распределенной величины воспользуемся функцией Excel =НОРМСТОБР(СЛЧИС()) (см. лист «Исходный). Функция СЛЧИС() является волатильной, т.е., возвращает новое значение после любого изменения на листе. В связи с этим графики в файле, как увидите их вы, будут отличаться от представленных ниже. Контрольная карта процесса моделирования изображена на рис. 4.
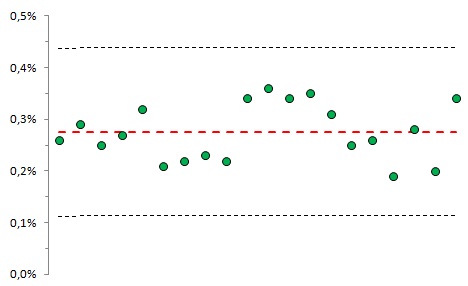
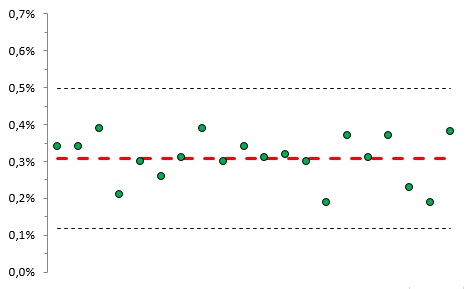
Рис. 4. Вероятность выхода за 3-сигмовые границы
Каждая точка графика соответствует вероятности выхода за 3-сигмовые границы в серии из 10 000 испытаний (всего 20 серий). Для данной контрольной карты среднее = 0,28%, что вполне соответствует теоретическим 0,27%. Если открыть лист «Критерий1» приложенного Excel-файла и понажимать на клавиатуре кнопку F9, то карта на глазах будем немного меняться.
Критерий 2. Выход хотя бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за 2-сигмовые пределы указывает на отсутствие управляемости
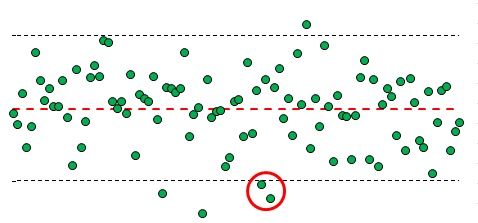
Рис. 5. Пример выхода хотя бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за 2-сигмовые пределы
Обратимся еще раз к таблице на рис. 2. Вероятность выхода случайной величины за пределы 2-сигмовой окрестности составляет 4,55%. Вероятность выхода только по одну из сторон от среднего (выше или ниже) составляет 4,55 / 2 = 2,275%. Вероятность выхода за пределы 2-сигмовой окрестности по одну сторону от среднего двух точек[1] = (4,55 * 2,275%) = 0,104%. Если взять любые три соседние точки, то за пределы 2-сигмовой окрестности могут выйти первая и вторая точки, первая и третья, вторая и третья. Таким образом, вероятность того, что, хотя бы две из трех последовательных точек, лежащих по одну сторону от центральной линии, выйдут за 2-сигмовые пределы, составляет = 0,104 * 3 = 0,312%.
Результаты моделирования приведены на рис. 6.
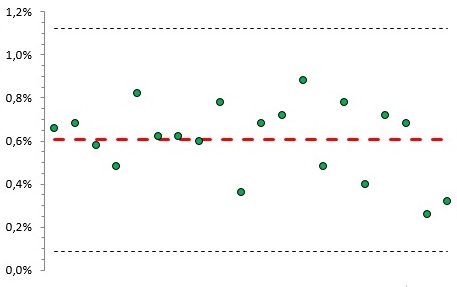
Рис. 6. Вероятность серии из двух точек из трех последовательных за пределами 2-сигмовых границ
Каждая точка графика соответствует вероятности выхода хотя бы двух из трех последовательных точек, лежащих по одну сторону от центральной линии, за 2-сигмовые пределы. Для данной контрольной карты среднее = 0,308%, что вполне соответствует теоретическим 0,312%.
Релевантность второго критерия, указывающего на отсутствие управляемости, чуть ниже, чем для первого критерия, и составляет 99,69%. То есть, с вероятностью 0,312% выход за пределы 2-сигмовой границы хотя бы двух из трех последовательных точек не будет связан со специальными причинами, а будет обусловлен «выбросом» случайной (статистически управляемой) величины.
Критерий 3. Выход, по меньшей мере, 4 из 5 последовательных точек, лежащих по одну сторону от центральной линии, за 1-сигмовые пределы указывает на отсутствие управляемости
Рис. 7. Серия четырех точек из пяти последовательных за пределами 1-сигмовой границы
Теоретическая вероятность выхода случайной величины за пределы 1-сигмовой границы = 31,73% (см. таблицу на рис. 2). Вероятность выхода за пределы 1-сигмовой окрестности по одну сторону от среднего четырех точек = 31,731*(15,866%)3 = 0,127%. Пятая точка в серии может быть любой, а располагаться она может на 1-м, 2-м, …, 5-м месте. Итого, вероятность, что 4 точки из 5 выйдут за пределы 1-сигмовой окрестности составляет 0,127%*5 = 0,634%.
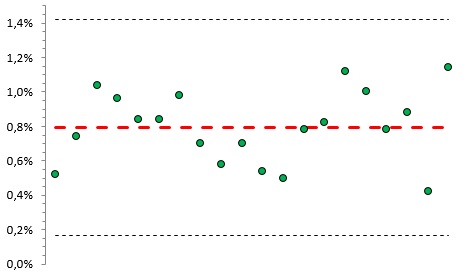
Рис. 8. Вероятность появления серии, в которой, по крайней мере, четыре точки из пяти последовательных, выходят за пределы 1-сигмовых границ
Каждая точка графика соответствует вероятности выхода хотя бы четырех из пяти последовательных точек, лежащих по одну сторону от центральной линии, за 1-сигмовые пределы. Для данной контрольной карты среднее = 0,606%, что вполне соответствует теоретическим 0,634%.
Критерий 4. Расположение, по меньшей мере, 8 последовательных точек по одну сторону от центральной линии указывает на отсутствие управляемости
Рис. 9. Серия из восьми последовательных точек по одну сторону от центральной линии
Вероятность того, что случайная величина восемь раз подряд примет значение по одну сторону от среднего, составляет (1/2)8 = 0,391%. Поскольку 8 точек могут расположиться, как выше, так и ниже среднего, эту вероятность следует умножить на 2. Итого 0,782%. Моделирование неплохо это подтверждает (рис. 10)
Рис. 10. Вероятность появления серии из восьми последовательных точек по одну сторону от центральной линии
Каждая точка графика соответствует вероятности появления, по меньшей мере, восьми последовательных точек по одну сторону от центральной линии. Для данной контрольной карты среднее = 0,794%.
Сведем полученные данные в единую таблицу
Рис. 11. Критерии отсутствия управляемости
Релевантность означает, что критерий действительно сигнализирует о специальной причине вариабельности; хотя вероятность «холостого выстрела» не равна нулю, и в зависимости от критерия колеблется от 0,27 до 0,78%.
Если использовать все критерии совместно, то вероятность ложных тревог составит около 1%.
P.S. Благодарю читателя блога Дмитрия, обратившего мое внимание на неточности в расчетах. Я внес исправления.
[1] Первая точка может выйти за пределы 2-сигмовой границы как выше, так и ниже среднего, но вторая точка должна выйти по ту же сторону, что и первая; вероятность чего в два раза меньше…



Сергей Викторович, добрый день.
Попробовал тоже изучить вероятности ошибки 1 рода критериев («холостых выстрелов»).
Но сделал несколько иначе: генерировал столбец 100 000 случайных чисел через функцию НОРМ.СТ.ОБР(СЛЧИС())
Для критерия «8 точек по одну сторону от середины» использовал формулу
ЕСЛИ(ИЛИ(И(B25>1σ;B24>1σ;B23>1σ;B22>1σ;B21>1σ; B20>1σ;B19>1σ;B18>1σ);И(B25<-1σ;B24<-1σ; B23<-1σ;B22<-1σ;B21<-1σ;B20<-1σ;B19<-1σ; B18<-1σ));
«Да";"Нет"))) и протянул ее до конца массива (в ячейке B25 находится восьмой член массива).А далее 100*кол-во
"Да"/(100000-7) и получилось 0,08%, т.е. больше, чем у Вас.Где я мог ошибиться?
По аналогии за пределами 3 сигм у меня получилась ошибка 1 рода — 0,3%, 2 из 3 — 0,3%, 4 из 5 — 0,6%.
Дмитрий, не понял приведенное вами описание. Пришлите Excel-файл на s_bag@mail.ru
Дмитрий, благодаря вашим вопросам я выполнил повторный анализ, и нашел две неточности. Поправил. Спасибо. Также немного отредактировал ваш комментарий, устранив и вашу неточность))