Олигополия – это тип рынка несовершенной конкуренции, характеризующийся присутствием на рынке товара нескольких производителей. [1]
Важной чертой олигополии, отличающей ее от других типов несовершенной конкуренции, является взаимозависимость фирм в отрасли. Олигополисты – не только конкуренты, но и одновременно негласные партнеры. При небольшом количестве производителей в отрасли фирме-олигополисту необходимо планировать свою стратегию с учетом поведения остальных участников рынка. Ведь размер ее прибыли зависит от объемов выпуска и цен, установленных другими олигополистами. Например, если фирма-олигополист произведет слишком мало продукции, то цены на нее будут выше, чем у других участников олигополистического рынка. Если, наоборот, фирма увеличит выпуск настолько, что ее цены будут ниже уровня цен в отрасли, то это может вызвать агрессивную реакцию других олигополистов. В обоих случаях фирма сталкивается с угрозой падения прибыли. Таким образом, ценовое поведение олигополистов сковано взаимозависимостью.
Олигополисты как бы находятся в «одной лодке», они слишком крупны и несогласованные телодвижения опасны. Однако у них нет возможности договориться между собой, так как сговор воспрещается антимонопольным законодательством. Вступление же в тайное соглашение довольно рискованно, поскольку нет уверенности в прочности союза с конкурентом. Поэтому для олигополиста очень важно уметь предвидеть, или предугадывать, поведение своих конкурентов.
Скачать заметку в формате Word или pdf
Аналогичные ситуации исследуются в теории игр. Поведение участников команды, которые должны принять наилучшее для всех решение, но не имеют возможности договориться, называется некооперативным. Наиболее простая и распространенная матричная модель (платежная матрица), с помощью которой исследуется некооперативное поведение, называется дилеммой заключенного. [2] Рассмотрим ее классический сценарий.
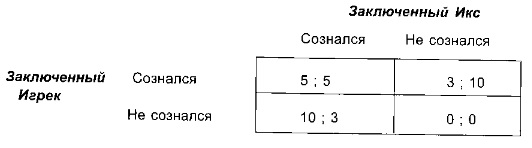
Два заключенных, например, мистер Икс и мистер Игрек, обвиняются в совместном преступлении, которое карается десятью годами лишения свободы. Однако, если один из них признается в содеянном и свалит инициативу преступления на другого, то ему «скостят» срок заключения до трех лег, а другой получит сполна (10 лет). Если в преступлении сознаются оба, то им дадут по пять лет. Возможно, что оба заключенных будут отрицать свою причастность к преступлению, и тогда их отпустят на свободу за недоказанностью вины. Однако, для этого им нужно сговориться. Но заключенные содержатся в разных камерах и не могут согласовать свое поведение на допросе. Какое решение примет каждый из них? Все возможные варианты выбора занесены в следующую матрицу:
Рис. 1. Дилемма заключенного
Конечно же, каждый хочет, чтобы его отпустили на свободу, но для этого оба заключенных не должны сознаваться. В то же время, несознавшийся рискует остаться в тюрьме на десять лет, если сознается его напарник. Признаться, или не признаться – вот в чем вопрос. Очевидно, что в условиях некооперативного поведения каждый выберет наименее рискованный для себя вариант. Рациональным в данном случае будет предположение о худшем (подельник сознается). При такой стратегии оба преступника сознаются и получат по пять лет.
В данной ситуации существует два равновесных решения. Одно (когда оба заключенных не сознаются и их отпускают) – Парето-эффективное решение [3], максимизирующее полезность обеих сторон. В результате другого решения (обоюдное признание) – достигается равновесие по Нэшу, при котором ни один из игроков (заключенных) не может увеличить свой выигрыш, в одностороннем порядке меняя свое решение. Равновесие по Нэшу – это ситуация, когда стратегия каждого из игроков является наилучшей реакцией на действия другого игрока.
Подобная ситуация характерна и для олигополистов, так как они тоже осуществляют некооперативный выбор, находясь в условиях взаимозависимости. Допустим, рынок разделен между двумя олигополистами: фирмой «Аполлон» и фирмой «Венера». Если бы обе фирмы могли сотрудничать (т.е. сговориться), то, сократив выпуск и назначив монопольно высокие иены, они получили бы и высокую прибыль по 100 млн. руб. Однако эти фирмы, прежде всего, конкуренты. У каждой есть искушение нарушить негласный договор: вопреки ожиданиям соперника понизить цены и захватить часть его рынка, сорвав еще большую прибыль в 130 млн. рублей. Тогда прибыль соперника резко сократится и составит, например, только 10 млн. рублей. Пытаясь обойти соперника, каждый игрок выберет низкие цены, и обе фирмы получат прибыль по 70 млн. руб. вместо вожделенных 130. Варианты прибылей в зависимости от выбора цен изображены в платежной матрице (рис. 2). Рассмотрев матрицу, мы увидим, почему фирмы не действуют сообща и не используют возможности получить более высокие прибыли за счет своего конкурента.
Рис. 2. Стратегия ценообразования олигополии
Итак, фирма «Аполлон» и фирма «Венера» не могут действовать сообща и делают выбор на основе логики ценового поведения конкурента. Обе фирмы не решаются выбрать самые высокие цены и получают одинаковую прибыль по 70 млн. руб. В результате риски минимизированы, и олигополистический рынок оказывается в условиях равновесия по Нэшу. Это частичное равновесие, так как фирмы не максимизируют свою полезность. Устойчивость равновесия сохранится до тех пор, пока у олигополистов не появится стимулов к изменению объемов выпуска.
[1] Цитируется по учебнику для вузов Курс экономической теории под общей редакцией проф. Чепурина М.Н., проф. Киселевой Е. А., Киров. – «АСА», 2006. – стр. 167–169
[2] Описание дилеммы заключенного неоднократно встречалась мне в литературе; см., например, Микаэль Крогерус. Книга решений. 50 моделей стратегического мышления
[3] Итальянский экономист Вильфредо Парето не только вывел свое знаменитое правило 20/80, но также изучал критерии эффективного распределения ресурсов. Ресурсы можно считать эффективно, а значит, оптимально распределенными при заданном уровне возможностей, когда ни один участник рынка не сможет улучшить своего положения, не ухудшив тем самым положений других. Такое распределение называется эффективным по Парето, или Парето-оптимальным распределением. Если же существует возможность хотя бы для одного участника рынка улучшить свое положение, не нанеся ущерба другим, то такое распределение экономических благ не оптимально.