Люди в осуществлении своей экономической деятельности неизбежно идут на риск. [1] Под риском понимается ситуация, когда, зная вероятность каждого возможного исхода, все же нельзя точно предсказать конечный результат. Рассмотрим некоторые основные понятия, связанные с поведением человека в условиях неопределенности. Участие в лотерее – типичный пример рисковой деятельности.
Ожидаемое значение случайной величины (например, выигрыш или проигрыш в лотерее) подсчитывается по формуле математического ожидания:
Е(х) = р1х1 + р2х2 + … + pnxn
где р1, р2, … pn – вероятности каждого исхода, х1, х2, … xn – значения каждого исхода.
Скачать заметку в формате Word или pdf
При этом важно учитывать, что вероятности могут иметь различную природу, то есть быть как объективными, так и субъективными. Те ученые, которые придерживаются концепции объективной природы вероятностей, полагают, что значения вероятностей потенциально определимы на математической основе. Так, французский астроном, математик и физик Пьер Лаплас определял вероятность исследуемого события как отношение количества благоприятных исходов данного события к количеству всех возможных исходов (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей). Сторонники субъективного подхода (например, американский экономист и статистик Леонард Сэвидж) полагали, что вероятности – это степени убежденности в наступлении тех или иных событий. В любом случае, какую бы трактовку природы вероятностей мы ни приняли, нам важно различать математическое ожидание (предполагаемое значение исхода) и ожидаемую полезность.
Истоки математического обоснования теории ожидаемой полезности можно встретить в работах швейцарских математиков Габриэля Крамера и Даниила Бернулли, последний из которых предложил свое решение знаменитого Санкт-Петербургского парадокса (см. также Даниил Бернулли. Опыт новой теории измерения жребия).
Формулировка парадокса. Рассматривается следующая задача. Вступая в игру, игрок платит некоторую сумму, а затем подбрасывает монету (вероятность каждого исхода — 50 %), пока не выпадет орёл. При выпадении орла игра заканчивается, а игрок получает выигрыш, рассчитанный по следующим правилам. Если орёл выпал при первом броске, игрок получает 20, при втором броске — 21 и так далее: при n-ном броске — 2n-1. Другими словами, выигрыш возрастает от броска к броску вдвое, пробегая по степеням двойки — 1, 2, 4, 8, 16, 32 и так далее.
Математическое ожидание денежного выигрыша при первом броске составляет р1 * х1 = 0,5*20 = 0,5 * 1 = 0,5 доллара. При втором броске оно составит р2 * х2 = (0,5*0,5)*21 = 0,25*2 = 0,5 долл. Общее ожидаемое значение представляет собой сумму ожиданий на каждой стадии игры и = 0,5 долл. + 0,5 долл. + 0.5 долл. + … Сумма этого бесконечного ряда представляет бесконечно большую величину.
Нужно определить, какой размер вступительного взноса делает такую игру справедливой, то есть найти математическое ожидание выигрыша игрока. Парадокс заключается в том, что вычисленное значение этого справедливого взноса равно бесконечности, то есть выше любого возможного выигрыша. Иными словами суть парадокса: индивиды готовы заплатить относительно небольшую сумму денег за участие в игре, в которой математическое ожидание выигрыша бесконечно велико.
Итак, ожидаемый денежный выигрыш в игре бесконечен, однако большинство людей уклонится от участия в ней. Почему же так происходит? Чтобы объяснить Санкт-Петербургский парадокс, Д. Бернулли предположил, что в данном случае индивиды стремятся к максимизации не ожидаемого денежного выигрыша, а морального ожидания, впоследствии названного ожидаемой полезностью выигрыша. А это не одно и то же. Рассмотрим эту проблему подробнее в связи с отношением людей к риску.
Идеи Д. Бернулли получили развитие в работах американских экономистов Джона фон Неймана и Оскара Моргенштерна, которых часто называют основоположниками теории ожидаемой полезности. Они показали, что в условиях неполной информации рациональным выбором индивида будет выбор с максимальной ожидаемой полезностью. Ожидаемая полезность каждого варианта подсчитывается следующим образом:
U – ожидаемая полезность (от англ. utility), где рi – вероятность исхода, xi – полезность исхода. Затем индивид сравнивает ожидаемые полезности вариантов и осуществляет выбор, стремясь максимизировать ожидаемую полезность. Каково же будет его отношение к риску?
Людям свойственно различное отношение к риску. В экономической теории принято выделять:
- нейтральных к риску;
- любителей риска;
- испытывающих антипатию к риску, или противников риска.
В некоторых случаях математическое ожидание при осуществлении рисковой деятельности может быть равно в денежном выражении нерисковому варианту, и все же люди поведут себя по-разному. Например, ваш должник вместо того, чтобы вернуть вам 10 долл., предлагает бросить монету. Если вы выиграете, то получите не 10, а 20 долл. (т. е. ваш чистый выигрыш составит 10 долл.), но если проиграете – не получите ничего (т. е. потеряете свои 10 долл.). Математическое ожидание Е(х) в этом случае составит: (0,5 * 10) + (0,5 * (–10+) = 0. Оно равно нулю, и получается, что вам, вроде бы, безразлично, играть в орлянку с должником или потребовать просто свои деньги назад.
Но кто-то пожелает пойти на риск в надежде получить больше, а кто-то предпочтет не предпринимать никаких действий, связанных с риском. Для того, чтобы объяснить выбор экономических агентов, необходимо включить в наш анализ концепцию ожидаемой полезности.
Практика показывает, что в основной своей массе люди не склонны к рисковой деятельности. Такое поведение обычно объясняется, помимо особенностей человеческой психики, чисто экономической причиной, а именно: действием закона убывающей предельной полезности.
Предположим, что у вас есть 100 долл. Вы можете сыграть в рулетку и поставить «на красное» 50 долл. В случае выигрыша у вас будет 150 долл.: 50 долл., которые вы не ставили, плюс 50 долл. * 2 – ваш выигрыш. Таким образом, вы увеличите свое первоначальное богатство, равное 100 долл., на 50 долл. В случае проигрыша у вас останется всего 50 долл., т. е. вы уменьшите свое первоначальное богатство на 50 долл. Математическое ожидание выигрыша в денежном выражении составит: (0,5 * 50) + (0,5 * (–50)) = 0.
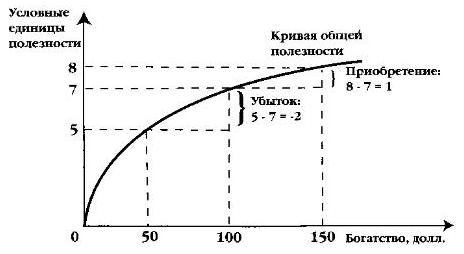
Но предельная полезность, как видно из графика общей полезности, убывает, поэтому в условных единицах полезности ожидаемая полезность будет иметь отрицательное значение: (0,5 * (–2)) + (0,5 * 1) = –0,5.
Рис. 1. Кривая общей полезности для индивида, испытывающего антипатию к риску
Иначе говоря, в случае проигрыша ваши убытки будут в условных единицах полезности больше, чем ваше приобретение в случае выигрыша. Таким образом, в категориях полезности ситуация выглядит иначе, чем в денежном исчислении, и вы не будете склонны рисковать. Вот почему мы говорили ранее о необходимости различать математическое ожидание денежной суммы выигрыша и ее ожидаемую полезность. Выражаясь более простым языком, можно сказать, что, конечно, вам доставит радость получить больше того, что вы имеете, но для вас гораздо ощутимее будет потеря того, к чему вы уже привыкли. В экономической теории данный феномен получил название эффекта владения. Эффект владения заключается в том, что люди гораздо выше оценивают то, чем они владеют чем то, что пока им не принадлежит.
Возвращаясь к Санкт-Петербургскому парадоксу, мы можем теперь сказать, что индивиды, отказываясь от игры в подбрасывание монеты, несмотря на бесконечно большое значение математического ожидания, руководствуются, согласно гипотезе Бернулли, прежде всего ожидаемой полезностью выигрыша. А предельная полезность дохода с каждым его приростом снижается. При уменьшающейся предельной полезности денежного выигрыша люди будут требовать все возрастающих выплат, для того, чтобы компенсировать свой риск в случае проигрыша.
[1] Цитируется по учебнику для вузов Курс экономической теории под общей редакцией проф. Чепурина М.Н., проф. Киселевой Е. А., Киров. – «АСА», 2006. – стр. 191–195
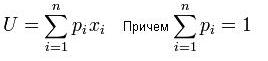
Gospodin Serghei ya znagu shto segodnea u vas deni rojdenya xoxhyu pozdraviti i pojelati mnogo mnogo let i seastia vam,i uda4u i spasibo vam za etu rabotu kotoruyu vi dlea mas delaete,s uvajeniem Igari iz Moldavii
Игорь, спасибо))
Zdrastvuite u menea k vam esti vopros…skajite pojalusta s kakix knig lu4e na4iati shtobi osvoiti mir finansov..klyu4evie pokazateli eto kniga u menea uje esti,ili bilo b xorosho poiti na kursi bugaltera?mne vajno znati vashe mnenie zaranee ogromnoe spasibo
Игорь, на мой взгляд, «Ключевые показатели» Уолша очень хороши для многих целей. Если Ваша цель, освоить бухгалтерию, то курсы — неплохой выбор. Если Вас интересует управленческий учет, финансовый анализ, то курсы бухучета не помогут. Рекомендую изучить замечательный ресурс http://www.cfin.ru. Там по каждому направлению выложены учебники.
Ogromnoe spasibo!:-) budete v Moldove obezatelino daite znati..:-)
Все очень понятно и доходчиво:) Огромное Вам спасибо!
Horosho istolkovano!
Неправильная формула (0,5 * (–2)) + (0,5 * 1) = –1.
Правая часть равна -0,5 , а не -1.
Спасибо! Поправил.