В современной экономической теории, различают позитивный и нормативный аспекты. [1] Основная проблема, решаемая [нормативной] теорией общественного благосостояния, состоит в выработке критерия оценки желательности или нежелательности того или иного состояния экономики, или ее организации. При этом речь идет о благосостоянии не отдельного субъекта, а всего общества, всех его членов, т.е. об общественном благосостоянии.
Главное отличие теории общественного благосостояния от позитивной экономики заключается в том, что последняя является наукой или по крайней мере претендует на то, чтобы быть ею. Используемые позитивной экономикой предположения и получаемые выводы могут быть так или иначе проверены, подтверждены или опровергнуты. Иначе говоря, позитивная экономическая теория отвечает критерию фальсифицируемости (подробнее см. Томас Кун. Структура научных революций). Другое дело теория благосостояния, имеющая нормативный характер. Ее основные предпосылки являются скорее ценностными суждениями, которые любой экономист, да и любой субъект вообще, волен принять или отвергнуть, и нет способа подтвердить или опровергнуть их. Теория благосостояния научна лишь в той мере, в какой ее выводы опираются на положения позитивной экономической теории.
Скачать заметку в формате Word или pdf
Современная теория общественного благосостояния возникла из двух источников, что и по сей день сказывается на ее бицентристском характере. Одним из них является нормативный анализ персонального благосостояния, или полезности, извлекаемой индивидом из окружающей его среды. Он восходит к концепции утилитаризма, основоположником которой был Иеремия Бентам (1748–1832), оставивший экономистам в наследие и сам термин «полезность». Другим ее источником была математическая теория выборов и коллективных решений, восходящая к работам французских математиков Жана-Шарля Борда (1733–1799) и Мари-Жана-Антуана Кондорсе (1743-1794). В русле этой теории лежали работы специалиста по математической логике Чарлза Доджсона (1832–1898), более известного как Льюис Кэролл, автора сказочных повестей об Алисе, и Дункана Блэка, чья книга о теории выборов (вместе со знаменитой работой американского экономиста К. Эрроу) стала ядром формирования обособляющейся от теории благосостояния теории общественного выбора.
Теория общественного благосостояния изучает оптимальное распределение благ между людьми и производственных ресурсов между отраслями, производящими эти блага. Поэтому она тесно связана с теорией общего равновесия. Оптимальность распределения какого-либо ресурса или потребительского блага не может быть определена исходя лишь из частичного равновесия на рынке данного ресурса или блага. Она в решающей степени зависит от ситуации на смежных рынках, от их взаимосвязи и взаимозависимости.
Действие «невидимой руки» А. Смита (идея разработана в 1776 году), описывают силу, направляющую рынок к общему равновесию. Эта движущая сила – стремление к прибыли и конкуренция, которые заставляют каждого отдельного предпринимателя максимизировать свою прибыль, минимизируя издержки. Оптимизируя частное производство, предприниматели действуют в интересах всего общества. Однако, это возможно только при эффективном использовании ресурсов. Под эффективным использованием ресурсов понимается достижение наибольшей отдачи в сфере оптимального использования данных ресурсов, или, другими словами, отсутствие потерь в виде упущенной полезности.
Условием же эффективного производства является эффективное распределение. Следовательно, именно конкуренция является естественным стимулом и организатором эффективного распределения.
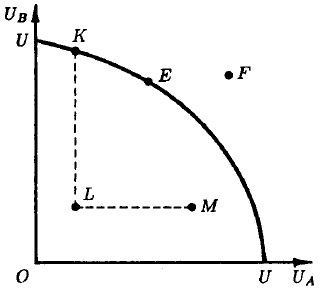
Дальнейший шаг в разработке идей А. Смита сделал итальянский экономист Вильфредо Парето. Он определил критерий эффективного распределения ресурсов. Но, прежде чем определить Парето-эффективность, целесообразно ввести связанные с ним понятия Парето-предпочтительности и Парето-несравнимости. На рис. 1 представлено благосостояние субъект А (UA) и субъекта В (UВ). Область, ограниченная кривой UU, представляет все множество возможных благосостоянии двух субъектов, а сама кривая UU называется границей возможных благосостояний. Ее конфигурация определяется конечными ресурсами этой двухсубъектной экономики, знаниями и применяемой технологией. Понятно, что, как и при рассмотрении границы производственных возможностей, увеличение производственных ресурсов и применяемой технологии сдвигает границу возможных благосостояний вправо вверх. Каждая точка на плоскости UВOUА представляет определенную комбинацию благосостояний двух субъектов. Очевидно, что комбинация F является недостижимой, так как лежит вне области возможных благосостояний.
Рис. 1. Парето-предпочтительность, Парето-несравнимость, Парето-эффектнвность
Состояние экономики называется Парето-предпочтительным по отношению к другому ее состоянию, если в первом случае благосостояние хотя бы одного субъекта выше, а всех остальных не ниже, чем во втором. Так, точки К, Е, М Парето-предпочтительны в отношении точки L. Действительно, в точке К благосостояние субъекта В выше, а субъекта А не ниже, чем в точке L. Напротив, в точке М благосостояние А выше, а В не ниже, чем в точке L. Наконец, в точке Е благосостояние обоих субъектов выше, чем в точке L. С другой стороны, точка К не является Парето-предпочтительной в отношении точки М, поскольку в точке К благосостояние В выше, а благосостояние А ниже, чем в точке М. Соответственно и точка М не является Парето-предпочтительной в отношении точки К, поскольку в ней благосостояние А выше, а В ниже, чем в точке К. Такие состояния экономики называют Парето-несравнимыми. Следовательно, не ко всякой паре точек, характеризующих разные состояния экономики, применимо понятие Парето-предпочтительности. Оно применимо лишь в том случае, если определенную пару точек в пространстве благосостояний можно соединить отрезком прямой, имеющим неотрицательный наклон (например, KL или LM).
Теперь мы можем дать определение Парето-оптимальному, или Парето-аффективному, состоянию экономики. Парето-оптимальным называется такое состояние экономики, при котором невозможно изменить производство и распределение таким образом, чтобы благосостояние одного или нескольких субъектов увеличилось без уменьшения благосостояния других. Парето-оптимальные состояния в нашей двухсубъектной модели представлены точками К, Е и всеми другими точками, лежащими на границе благосостояний (кривой UU). Переход из одной такой точки в другую обязательно сопряжен с повышением благосостояния одного субъекта и снижением благосостояния другого.
Понятия Парето-оптимальности и Парето-предпочтительности связаны друг с другом. Парето-оптимальное состояние экономики можно определить как такое, по отношению к которому не существует ни одного Парето-предпочтительного. В то же время любая точка, лежащая на границе возможных благосостояний, например точка К или Е, является Парето-несравнимой в отношении любой другой точки на этой границе. Поэтому можно сказать, что множество Парето-оптимальных состояний есть набор всех Парето-несравнимых состояний, остающийся после исключения из рассмотрения всех нежелательных состояний экономики на основе критерия Парето-предпочтительности. Действительно, после исключения из рассмотрения всех точек, лежащих внутри области возможных благосостоянии, у нас останется лишь сама эта граница, UU, все точки которой окажутся Парето-оптимальными относительно точек, лежащих внутри области возможных благосостоянии, но Парето-несравнимыми друг с другом.
Плодотворность использования в экономическом анализе рассмотренных понятий определяется прежде всего тем, что они в явной форме учитывают несовпадение интересов различных субъектов экономики. То, что представляется желательным (хорошим) для одного, может оказаться нежелательным (плохим) для другого. Очевидно, что субъект А сочтет состояние, характеризуемое точкой М, более предпочтительным для себя, чем Парето-оптимальные состояния, представленные точками К или Е. В то же время эти понятия позволяют хотя бы частично упорядочить по предпочтительности все достижимые состояния экономики. И если одна хозяйственная система приводит экономику в состояние, представленное точкой Е, а другая — в состояние, характеризуемое точкой L, то бесспорно, что первая система функционирует более эффективно. Поэтому естественным является требование к такой организации экономики, которая приводила бы ее в Парето-оптимальное или, во всяком случае, близкое к нему состояние.
Итак, критерием рыночной эффективности является Парето-оптимальность, и возможность ее достижения – серьезное преимущество рыночной системы по сравнению с командно-административной. Очень важно, что эффективность распределения по Парето предполагает максимизацию общественной полезности, хотя и является социально нейтральным критерием. Поэтому равноправное, но отнюдь не равное распределение при достижении наибольшей суммарной полезности в рыночной системе корректируется через перераспределительную систему, т.е. с помощью государства.
Но как максимизируется общественное благосостояние? Это один из главных вопросов неоклассической теории экономики благосостояния, предметом которой является создание модели экономического оптимума и решение проблемы соотношения между эффективностью экономической системы и справедливостью распределения. Отправным пунктом в исследовании возможности максимизировать благосостояние является модель, называемая «ящик Эджворта». Данная модель представляет собой диаграмму полезностей двух контрагентов и помогает выявить условия достижения оптимального распределения экономических благ, при обмене которыми достигается максимальная полезность участников обмена.
Впервые модель описана британским экономистом и философом Фрэнсисом Эджвортом в 1881 году, далее развита в работах Вильфредо Парето и Артура Боули. Ящик Эджворта является одним из инструментов в теории общего равновесия и иногда называется «ящиком обмена благ». Он удобен для анализа распределения двух благ между двумя экономическими субъектами в экономике обмена в теории потребителя или для анализа распределения двух производственных ресурсов в теории производства.
Ящик Эджворта состоит из двух диаграмм с кривыми безразличия – по одной кривой для каждого индивида. Кривая безразличия для одного индивида и двух товаров приведена на рис. 2. [2]
Рис. 2. Кривая безразличия
Ящик создается пересечением четырех осей координат, каждая пара которых соответствует одному индивиду (рис. 3). Расположенные друг напротив друга точки начала отсчета систем координат изображают состояния, в которых один из индивидов располагает всеми единицами обоих благ, а другой не располагает ни одной. Например, в точке В индивид А обладает максимальным количеством, и товара А, и товара В, а индивид В не обладает товарами А и В вовсе. Пространство, ограниченное четырьмя осями двух систем координат графически представляет все теоретически возможные распределения обоих благ. Длина каждой из осей измеряет количество изображаемого блага.
Рис. 3. Ящик Эджворта с двумя кривыми безразличия и начальной аллокацией [3] Е1
Кривые безразличия, выражающие комбинации благ, имеющие для экономического субъекта равную ценность, представляют предпочтения обоих экономических субъектов. Чем дальше находится кривая безразличия от индивидуальной точки начала отсчета (А или В), тем больший уровень полезности достигается экономическим субъектом при владении той или иной комбинацией обоих благ.
При любом начальном распределении благ между экономическими субъектами существуют две кривые безразличия, проходящие через точку (Е1) в ящике Эджуорта, соответствующую данному распределению, и отражающие конкретный уровень полезности, на котором находится каждый из субъектов. Если эти кривые не касаются друг друга в данной точке, оба экономических субъекта могут улучшить своё положение с помощью обмена. В этом случае кривые безразличия образуют «линзу» в пространстве ящика Эджуорта (рис. 3), любая точка внутри которой выводит каждого из участников на более высокий уровень полезности. Такая новая ситуация является Парето-улучшением по отношению к начальному распределению благ.
Если кривые безразличия касаются друг друга в данной точке, то любое другое распределение ресурсов будет хуже хотя бы для одного из участников, то есть в этом случае не существует взаимовыгодного обмена. Эти точки называются эффективными по Парето, а множество всех таких точек представляет собой договорную кривую.
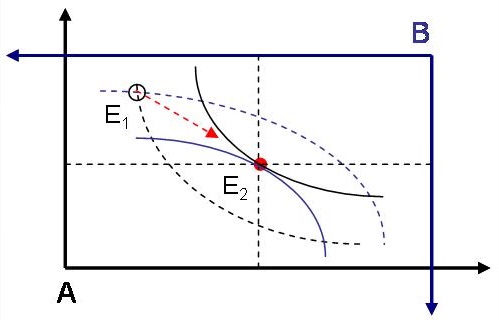
Если начальное распределение ресурсов неэффективно (то есть соответствующая точка не лежит на кривой контракта), то при рациональности обоих экономических субъектов добровольный обмен благами будет проводиться до тех пор, пока полученное распределение не станет Парето-эффективным (рис. 4). Эта точка, от которой невыгодно отклоняться ни одному из субъектов, называется равновесием в экономике обмена. Множество равновесий образует ядро экономики и является подмножеством договорной кривой.
Рис. 4. Улучшение ситуации обоих субъектов с помощью обмена до аллокации Е2
Рассмотрим модель обмена двумя товарами между двумя потребителями, например, Аней и Васей, которые олицетворяют две общественные группы. На рис. 5 изображены две системы координат. Правый верхний угол прямоугольника – начало координат 0А в системе которых расположена карта кривых безразличия Ани (поэтому и символ А). Левый нижний угол – начало координат OВ, в системе которых расположена карта кривых безразличия Васи. По горизонтальной оси отмечено количество хлеба, по вертикальной – шоколада, в количестве 10 и 6 единиц соответственно.
Рис. 5. Пример ящика Эджворта
Пусть изначально блага распределены в точке 1, т.е. 7 единиц хлеба и 1 единица шоколада у Васи (поэтому он ценит шоколад больше, чем хлеб). В той же точке 1 мы видим, что у Ани 3 единицы хлеба и 5 единиц шоколада [4] (она, имея больше шоколада, оценивает хлеб выше, чем Вася). В этой точке предельные нормы замещения (MRS) участников сделки не совпадают: [5] MRSА=3, MRSB=1/2, что позволяет заключать взаимовыгодные сделки. Кривые безразличия UA1 и UB1, оответствующие набору предпочтений Ани и Васи, пересекаются в точке 1, образуя область взаимовыгодных сделок (заштрихованная часть рисунка). Однако не при каждой взаимовыгодной сделке распределение эффективно. Например, в точке 2 сделка взаимовыгодна (Вася приобретет дополнительную плитку шоколада, а Аня – еще одну буханку хлеба, т.е. то, что они больше ценят). Но так как кривые безразличия в этой точке пересекаются, предельные нормы замещения (MRS) у контрагентов не равны. Условием же эффективного распределения является равенство MRS участников обмена, в результате которого благосостояние контрагентов нельзя улучшить, не ухудшив положения одного из них, т.е. условие Парето-эффективного распределения. Оно соответствует точкам 3, 4 и 5, в которых кривые безразличия касаются друг друга и имеют в этих точках одинаковый наклон. Следовательно, MRSA = MRSВ. Данное правило распространяется и на множество контрагентов, обменивающихся множеством товаров: распределение эффективно только в том случае, если MRS любой пары товаров одинаковы для всех участников обмена. Таким образом, одновременное равновесие участников обмена устанавливается при заключении эффективной сделки:
MRSАшок., хл. = (Ршок./Рхл.) = MRSВшок., хл.,
где Р – цена.
Данная формула отражает условие достижения равновесия на конкурентных рынках. Конкурентным равновесием экономисты называют равновесие по Вальрасу. В основе достижения конкурентного равновесия лежит установление такого набора цен, при котором спрос равен предложению на всех имеющихся рынках в условиях конкуренции.
Вернемся к рис. 5. Кривая, проходящая из точки 0А в точку ОВ соединяет все точки касания кривых безразличия контрагентов Ани и Васи, в которых их предельные нормы замещения равны. Такая кривая, отражающая все эффективные сделки, т.е. все случаи эффективного распределения, называется кривой контрактов. Именно кривая контрактов и служит графическим изображением Парето-эффективного распределения между двумя агентами.
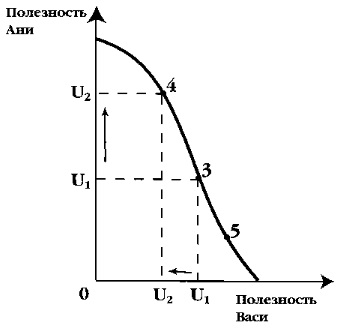
На рисунке 6 изображена кривая контрактов, вогнутая по отношению к началу системы координат. Она представляет собой только что изученную кривую из «ящика Эджворта» (рис. 5), полученную при проведении линии через все точки касания кривых безразличия (точки 4, 3, 5). Любая точка этой кривой представляет собой эффективное распределение по Парето, максимизирующее суммарную полезность распределения благ в обществе. Иначе говоря, это кривая достижимой полезности для общества. Допустим, что все общество состоит из двух лиц, Ани и Васи, олицетворяющих две общественные группы. При продвижении из точки 3 в точку 4 полезность благ для одной группы общества, которую представляет Вася, уменьшается. Напротив, полезность для другой группы, которую олицетворяет Аня, возрастает. Но в какой точке на кривой достижимой полезности максимизируется общественное благосостояние? Ведь эффективное по Парето распределение не дает ответа на вопрос о распределении благосостояния между людьми с точки зрения его желательности для общества. Даже самые крайние точки на кривой достижимой полезности, когда всё достается какому-либо одному из субъектов (или одной общественной группе), Парето-оптимальны. (Мы еще раз убедились в социальной нейтральности критерия Парето-эффективности.)
Рис. 6. Кривая достижимой (возможной) полезности
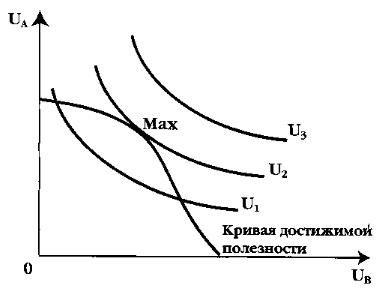
Кривая достижимой полезности (рис. 7) показывает все варианты полезности, достижимой при Парето-эффективном распределении данного количества благ между двумя членами общества. Выпуклыми по отношению к началу системы координат изображены новые для нас графики – общественные кривые безразличия, или кривые равного благосостояния. Общественная кривая безразличия, по аналогии с индивидуальной кривой безразличия, показывает все комбинации полезностей различных социальных групп, соответствующих одному и тому же уровню общественного благосостояния, а поэтому одинаково приемлемых (одинаково безразличных) для общества. Существует множество общественных кривых безразличия (карта общественных кривых безразличия), которые обозначают разные уровни благосостояния общества. Чем выше уровень благосостояния, тем дальше соответствующая ему общественная кривая безразличия расположена от начала координат. Однако самый высокий уровень благосостояния, которого общество может реально достичь при заданных возможностях, отражает та общественная кривая безразличия, которая имеет только одну общую точку (или общую касательную) с кривой достижимой полезности. Таким образом, распределение, максимизирующее общественное благосостояние, будет достигнуто в точке касания общественной кривой безразличия и кривой достижимой полезности.
Рис. 7. Максимизация общественного благосостояния
В связи с проблемой максимизации общественного благосостояния рассмотрим две теоремы экономики благосостояния. Первая теорема экономики благосостояния заключается в том, что распределение в условиях конкурентного равновесия эффективно по Парето. Значит, если всем участникам сделки удается максимизировать свою полезность, то в результате достигается общественно эффективное распределение, максимизирующее общественное благосостояние. Данная теорема указывает на инструмент достижения эффективности по Парето: это – механизм конкурентного рынка. С его помощью можно достичь Парето-эффективного распределения благ среди сотни тысяч участников, не прибегая к созданию специальных структур по сбору информации и принятию централизованных решений. Необходимо и достаточно, чтобы каждый участник распределения обладал информацией о конкурентной рыночной цене того или иного товара.
Вторая теорема экономики благосостояния гласит, что в определенных условиях[6] при Парето-эффективном размещении благ может быть достигнуто конкурентное равновесие. Иными словами, каждая точка кривой контрактов – это случай конкурентного равновесия. Данная теорема проводит разграничение между аллокативной и дистрибутивной ролью ценового сигнала. С одной стороны, рыночная цена определяет относительную редкость того или иного блага, с другой, – показывает, какой объем различных товаров каждый рыночный агент в состоянии приобрести.
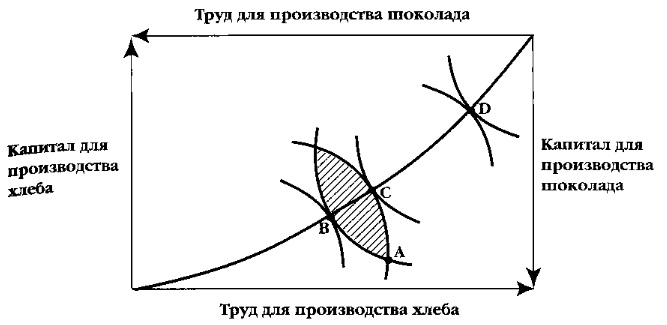
Однако для достижения общей эффективности экономики недостаточно эффективного распределения благ среди потребителей. Необходимо, чтобы и производители распоряжались экономическими благами эффективно. Для рассмотрения условий эффективного использования факторов производства можно вновь использовать «ящик Эджворта» (рис. 8). На повернутых друг к другу осях координат расположены факторы производства хлеба и шоколада. Каждая точка диаграммы показывает затраты труда и капитала для производства этих двух товаров.
Набор изоквант показывает уровни выпусков хлеба и шоколада при различных комбинациях затрат труда и капитала. Распределение факторов производства эффективно, если выпуск одного товара не может быть увеличен без хотя бы минимального сокращения производства другого товара. В точке А, например, выпуск не эффективен, так как варианты выпуска в заштрихованной области дают лучшие результаты. Точки В, С и D – пример эффективного распределения затрат, а значит, и производства. В этих точках изокванты производителей хлеба и шоколада имеют одинаковый наклон и, следовательно, одинаковую предельную норму технологического замещения капитала трудом.
Рис. 8. «Ящик Эджворта» для рассмотрения эффективности производства
В равновесных точках производители данных продуктов минимизируют свои издержки, комбинируя труд и капитал таким образом, что соотношение предельных продуктов этих факторов равно соотношению их цен:
MPL / МPK = PL / PK,
где MPL – предельный продукт, производимый трудом, МPK – предельный продукт, производимый капиталом, PL – цена труда, PK – цена капитала
Значит факторы производства могут эффективно использоваться при условии равенства:
MRTSKL = PL / PK,
где MRTSKL – предельная норма технологического замещения капитала трудом и наоборот.
Кривая, на которой расположены все точки эффективного распределения и использования факторов производства (рис. 8), называется кривой производственных контрактов. Она показывает все комбинации максимального (эффективного) выпуска хлеба и шоколада при имеющемся количестве труда и капитала. Эта кривая и есть граница производственных возможностей.
Однако для эффективного выпуска необходимо, чтобы товары производились в таких количествах, которые соответствуют желанию потребителей заплатить за них. Поэтому необходимым условием эффективного выпуска является равенство предельной нормы замещения – предельной норме технологического замещения факторов производства:
MRS = MRTS
Это и есть состояние оптимальности в экономике. Выполнение данного равенства для всех потребителей и производителей, т.е.
ΣMRS = ΣMRTS
называется первым наилучшим распределением, идеально оптимизирующим благосостояние всего общества. Однако оно труднодостижимо: современный рынок находится в условиях несовершенной конкуренции и претерпевает множество искажений.
Монополизм, асимметричность информации, нерациональность налогообложения и другие проблемы несовершенной конкуренции мешают оптимальному распределению ресурсов. Поэтому экономисты рассматривают принцип «второго наилучшего», т.е. предлагаются варианты такого распределения, которое было бы наилучшим среди неоптимальных. Такого рода распределение называется квазиоптимумом, или «вторым наилучшим распределением». Рассмотрим на примере выпуска двух товаров, хлеба и шоколада, возможность достижения квазиоптимума посредством налогообложения. Допустим, хлеб производится в чисто конкурентных условиях, а шоколад – в монопольных. Цены на шоколад завышены, по сравнению с конкурентными, за счет его недопроизводства. В условиях общего равновесия ресурсы шоколадной отрасли, не нашедшие применения, поглощаются конкурентным рынком хлебных изделий. В результате конкурентное равновесие на этом рынке наступает, когда хлеб производится в большем объеме и при более низкой цене, по сравнению с теми, которые могли бы установиться, если бы шоколад также производился в условиях совершенной конкуренции.
Как можно воспрепятствовать переливу ресурсов, нарушающему эффективный объем производства товаров? Допустим, государство вводит налог на хлеб, нарушая конкурентное равновесие на рынке хлебных изделий. Это вызовет сокращение производства хлеба и повышение его цены для потребителей. Стремление рынка к восстановлению общего равновесия с учетом налога будет стимулировать перелив части ресурсов производства хлеба в шоколадную отрасль. Несмотря на монополизм, производство шоколада сможет расшириться и несколько снизится его цена. В результате на обоих рынках установится новое равновесное распределение, квазиоптимум, компенсирующий монопольное недопроизводство шоколада искажением конкурентного равновесия на рынке хлеба. Однако такое равновесие будет лучше, чем другие менее эффективные варианты. Главная идея теории квазиоптимума состоит в том, что за счет отказа от конкурентного равновесия на одном рынке, устраняются искажения в распределении и производстве на других рынках, т.е. балансируется рыночная система в целом.
[1] При написании заметки использованы материалы: Курс экономической теории под редакцией проф. Чепурина М.Н., проф. Киселевой Е. А., Киров. – «АСА», 2006. – С. 325–333; Гальперин В. М., Игнатьев С. М., Моргунов В. И. Микроэкономика. – СПб, Институт «Экономическая школа», 2004. – С. 437–448; Википедия.
[2] Подробнее см., например, Курс экономической теории глава 5, параграф «Спрос и полезность. Теория потребительского выбора»
[3] В экономической теории аллокация – система распределения недостаточных ресурсов, в зависимости от стоящих целей.
[4] Примем за единицу измерения хлеба 1 буханку, а для шоколада – 1 плитку.
[5] В этом легко убедиться: проведите через точку 1 касательные к соответствующей кривым безразличия Ани и Васи. Вы увидите, что у них разный наклон. Касательная к кривой безразличия UA имеет наклон –3, а наклон касательной к кривой безразличия UВ равен –1/2.
[6] Условие, при котором выполняется вторая теорема благосостояния, заключается в том, что предпочтения участников распределения должны выражаться кривыми безразличия, имеющими такую же форму, как в модели «ящик Эджворта», т.е. выпуклыми. Тогда между парой кривых безразличия пройдет единственная общая касательная, которую можно представить в виде общего бюджетного ограничения для двух участников распределения что говорит о достижении равновесия каждого из них. Если же кривые безразличия участников распределения будут иметь другую форму (например, волнистую), не позволяющую провести между ними общую касательную, то равновесия при Парето-эффективном распределении достигнуто не будет.