Описывая доверительные интервалы, мы сосредоточили внимание на математическом ожидании и доле признака в генеральной совокупности. Эти средства статистического анализа нашли весьма широкое применение в аудиторском деле. [1] Аудит — это сбор и оценка информации, позволяющей оценить состояние экономического объекта, например, компании, акционерного общества, корпорации или правительственного агентства. Цель аудита — оценить, насколько деятельность проверяемого объекта соответствует установленным критериям.
Основных преимуществ выборочного исследования, применяемого при аудите.
- Результаты выборочного исследования объективны и обоснованы. Поскольку определение объема выборки основано на точно сформулированных статистических принципах, результаты аудиторской проверки можно защищать в суде.
- Метод выборочного исследования позволяет заранее определить объем выборки.
- Метод позволяет оценить ошибку выборочного исследования.
- Этот подход можно применять для более точной оценки параметров, поскольку исследование большой генеральной совокупности может занять много времени и даже сопровождаться значительными ошибками нестатистического характера.
- Метод выборочного исследования могут применять сразу несколько аудиторов. Поскольку этот метод является научно обоснованным, можно считать, что в параллельной проверке принимает участие один аудитор.
- Метод выборочного исследования позволяет объективно оценить результаты проверки, поскольку его точность известна заранее.
Скачать заметку в формате Word или pdf
Оценка суммы элементов генеральной совокупности
В аудиторском деле часто приходится оценивать сумму элементов генеральной совокупности. Она определяется по следующей формуле:
где N – объем генеральной совокупности, ![]() – выборочное среднее.
– выборочное среднее.
Границы доверительного интервала, содержащего сумму элементов генеральной совокупности:
где tn – 1 – степени свободы, S – стандартное отклонение выборки, n – объем выборки
Чтобы продемонстрировать применение этой формулы, вернемся к задаче об аудиторской проверке в компании. Предположим, что для вычисления общей суммы накладных из информационной системы извлечены 100 записей, сделанных за последний месяц. Вся генеральная совокупность состоит из 5000 накладных. Итак, N = 5000, n = 100, ![]() = 110,27, S = 28,95, доверительный уровень равен 95%, a t99 = 1,9842.
= 110,27, S = 28,95, доверительный уровень равен 95%, a t99 = 1,9842.
Сумма = 5000 х 110,27 = 551 350
Границы доверительного интервала:
522 914 ≤ Сумма элементов генеральной совокупности ≤ 579 786.
Следовательно, вероятность того, что сумма элементов генеральной совокупности не меньше 522 914 и не больше 579 786, равна 95%.
Оценка разности
Оценка разности применяется тогда, когда аудитор считает, что в анализируемой генеральной совокупности содержатся ошибки, которые необходимо оценить на основе выборочных данных. Для этого выполняются следующие процедуры.
1. Определяется необходимый объем выборки.
2. Вычисляются разности между величинами, обнаруженными в ходе аудита, и номинальными величинами. Обратите внимание на то, что разность Di равна нулю, если обнаруженная величина правильна; является положительной величиной, если обнаруженная величина больше номинальной; и отрицательной — если обнаруженная величина меньше номинальной.
3. Вычисляется средняя выборочная разность ![]() , которая является результатом деления суммы разностей на объем выборки.
, которая является результатом деления суммы разностей на объем выборки.
где Di = обнаруженная величина – (минус) номинальная величина.
4. Вычисляется стандартное отклонение разностей SD. Элементам выборки, не являющимся ошибками, соответствуют нулевые разности.
5. Вычисляются границы доверительного интервала, содержащего сумму разностей элементов генеральной совокупности:
Продемонстрируем применение этой формулы на примере аудиторской проверки в компании. Предположим, что компания желает построить 95%-ный доверительный интервал, содержащий полную разность между фактическими суммами, указанными в накладных, и суммами, занесенными в информационную систему. В выборку, состоящую из 100 записей, входят 12 накладных, не соответствующих действительности. Перечислим эти разности, выраженные в долларах: 9,3; 7,47; 17,32; 8,30; 5,21; 10,80; 6,22; 5,63; 4,97; 7,43; 2,99; 4,63. В остальных 88 накладных ошибок нет, следовательно, их разности равны нулю. Итак,
Таким образом, границы доверительного интервала, содержащего полную разность генеральной совокупности, состоящей из 5000 накладных, вычисляются по формуле:
Следовательно, вероятность того, что полная разность генеральной совокупности накладных не меньше 1 797 и не больше 7 203, равна 95%.
Односторонняя оценка доли нарушений установленных правил
Организации часто используют механизмы внутреннего контроля, чтобы убедиться в том, что сотрудники следуют правилам, принятым в компании. Например, администрация компании настаивает, чтобы товары не отгружались со склада без заверенной складской расписки. В ходе ежемесячной проверки ревизоры попытались определить долю продукции, отправленной со склада без соответствующих документов. Такое явление мы будем называть нарушением правил. Чтобы оценить их количество, ревизоры извлекают из генеральной совокупности накладных выборку и подсчитывают количество нарушений. Затем аудиторы сравнивают результаты с предельно допустимым уровнем нарушений, принятым в компании. Этот уровень представляет собой максимальную долю нарушений, которую компания считает приемлемой. При оценке количества нарушений обычно применяют односторонний доверительный интервал. Иначе говоря, ревизоры вычисляют только верхнюю границу доверительного интервала, содержащего долю нарушений:
где pS — выборочная доля признака, равная Х/n, т.е. количеству успехов, деленному на объем выборки, Z — критическое значение стандартизованного нормального распределения, соответствующее интегральной вероятности, равной 1 – α, N – объем генеральной совокупности, n — объем выборки.
Если предельно допустимый уровень нарушений выше верхней границы этого интервала, ревизоры считают, что деятельность компании не выходит за пределы установленных норм. В противном случае аудиторы фиксируют систематическое нарушение установленных правил. Аудиторы могут потребовать увеличить объем выборок. Предположим, что ежемесячная проверка коснулась 400 накладных, извлеченных из генеральной совокупности, состоящей из 10 000 накладных. Среди проверенных накладных оказалось 20 неправильных. Предельно допустимый уровень нарушений, принятый в компании, равен 6%. Постройте односторонний 95%-ный доверительный интервал.
рS = 20/400 = 0,05, Z = 1,645
Верхняя граница доверительного интервала равна 6,75%. Поскольку предельно допустимый уровень нарушений равен 6%, следует зафиксировать нарушение правил компании и потребовать для проверки более крупную выборку.
Предыдущая заметка Определение объема выборки
Следующая заметка Проверка гипотез: одновыборочные критерии
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 480–488
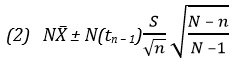

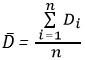
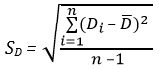
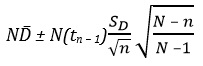

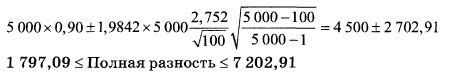
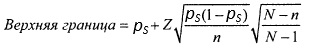
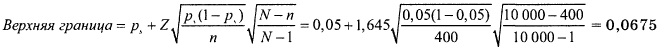
Сергей, добрый день.
Подскажите, пожалуйста, почему в последнем примере величина Z = 1,645 при построении 95% доверительного интервала?
Максим, в заметке указано, что Z — есть критическое значение стандартизованного нормального распределения, соответствующее интегральной вероятности, равной 1 – α. Если α = 0,05, то значение Z в Excel можно определить по формуле =НОРМ.СТ.ОБР(0,95) = 1,645.
Сергей, спасибо за столь быстрый ответ.
Честно говоря, я немного запутался с этим магическим Z (который всего лишь расстояние от мат. ожидания в среднеквадр. отклонениях) в связке с заметкой «определение объема выборки». Мы здесь разве не должны делить α на 2 части и рассчитывать для 0.975? Почему здесь вся α отдается на откуп интересующей нас «плюсовой поправке»?
Максим, я сам «плаваю», когда брать всю α, а когда половину))
Всю альфу берем для оценки симметричного двустороннего интервала, а для оценки положительно или отрицательного отдельно берем a/2, так как Z — в данном случае ни что иное как функция Лапласа от альфа, которая в свою очередь — интеграл от функции нормального распределения(или распределения Стьюдента), показывающая площать.
Например, если в ноль-гипотезе у нас b=100 (условно), а в альтернативной b не равно 100 или b отлична на 10(не ясно больше или меньше), то мы можем и должны взять альфа целиком, а если спрашивается конкретный случай, когда b> или < , то берем половику, т.е. один из двух "хвостов" распределения.