Рассматривая простую регрессию, мы сосредоточили внимание на модели, в которой для предсказания значения зависимой переменной, или отклика Y, использовалась лишь одна независимая, или объясняющая, переменная X. Однако во многих случаях можно разработать более точную модель, если учесть не одну, а несколько объясняющих переменных. По этой причине мы рассмотрим в этой заметке модели множественной регрессии, в которых для предсказания значения зависимой переменной используется несколько независимых переменных. [1]
Материал будет проиллюстрирован сквозным примером: прогнозирование объемов продаж компании OmniPower. Представьте себе, что вы — менеджер по маркетингу в крупной национальной сети бакалейных магазинов. В последние годы на рынке появились питательные батончики, содержащие большое количество жиров, углеводов и калорий. Они позволяют быстро восстановить запасы энергии, потраченной бегунами, альпинистами и другими спортсменами на изнурительных тренировках и соревнованиях. За последние годы объем продаж питательных батончиков резко вырос, и руководство компании OmniPower пришло к выводу, что этот сегмент рынка весьма перспективен. Прежде чем предлагать новый вид батончика на общенациональном рынке, компания хотела бы оценить влияние его стоимости и рекламных затрат на объем продаж. Для маркетингового исследования были отобраны 34 магазина. Вам необходимо создать регрессионную модель, позволяющую проанализировать данные, полученные в ходе исследования. Можно ли применить для этого модель простой линейной регрессии, рассмотренную в предыдущей заметке? Как ее следует изменить?
Модель множественной регрессии
Для маркетингового исследования в компании OmniPower была создана выборка, состоящая из 34 магазинов с приблизительно одинаковыми объемами продаж. Рассмотрим две независимые переменные — цена батончика OmniPower в центах (Х1) и месячный бюджет рекламной кампании, проводимой в магазине, выраженный в долларах (Х2). В этот бюджет входят расходы на оформление вывесок и витрин, а также на раздачу купонов и бесплатных образцов. Зависимая переменная Y представляет собой количество батончиков OmniPower, проданных за месяц (рис. 1).
Рис. 1. Месячный объем продажа батончиков OmniPower, их цена и расходы на рекламу
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Интерпретация регрессионных коэффициентов. Если в задаче исследуются несколько объясняющих переменных, модель простой линейной регрессии можно расширить, предполагая, что между откликом и каждой из независимых переменных существует линейная зависимость. Например, при наличии k объясняющих переменных модель множественной линейной регрессии принимает вид:
(1) Yi = β0 + β1X1i + β2X2i + … + βkXki + εi
где β0 — сдвиг, β1 — наклон прямой Y, зависящей от переменной Х1, если переменные Х2, Х3, … , Хk являются константами, β2 — наклон прямой Y, зависящей от переменной Х2, если переменные Х1, Х3, … , Хk являются константами, βk — наклон прямой Y, зависящей от переменной Хk, если переменные Х1, Х2, … , Хk-1 являются константами, εi — случайная ошибка переменной Y в i-м наблюдении.
В частности, модель множественной регрессии с двумя объясняющими переменными:
(2) Yi = β0 + β1X1i + β2X2i + εi
где β0 — сдвиг, β1 — наклон прямой Y, зависящей от переменной Х1, если переменная Х2 является константой, β2 — наклон прямой Y, зависящей от переменной Х2, если переменная Х1 является константой, εi — случайная ошибка переменной Y в i-м наблюдении.
Сравним эту модель множественной линейной регрессии и модель простой линейной регрессии: Yi = β0 + β1Xi + εi. В модели простой линейной регрессии наклон β1 представляет собой изменение среднего значения переменной Y при изменении значения переменной X на единицу и не учитывает влияние других факторов. В модели множественной регрессии с двумя независимыми переменными (2) наклон β1 представляет собой изменение среднего значения переменной Y при изменении значения переменной X1 на единицу с учетом влияния переменной Х2. Эта величина называется коэффициентом чистой регрессии (или частной регрессии).
Как и в модели простой линейной регрессии, выборочные регрессионные коэффициенты b0, b1, и b2 представляют собой оценки параметров соответствующей генеральной совокупности β0, β1 и β2.
Уравнение множественной регрессии с двумя независимыми переменными:
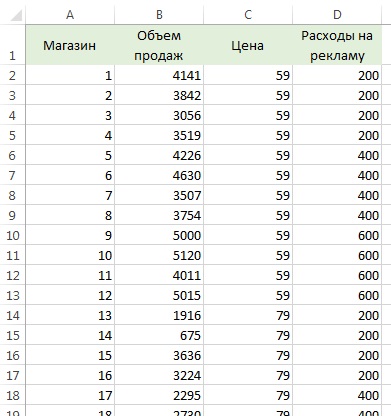
Для вычисления коэффициентов регрессии используется метод наименьших квадратов. В Excel можно воспользоваться Пакетом анализа, опцией Регрессия. В отличие от построения линейной регрессии, просто задайте в качестве Входного интервала Х область, включающую все независимые переменные (рис. 2). В нашем примере это $C$1:$D$35.
Рис. 2. Окно Регрессия Пакета анализа Excel
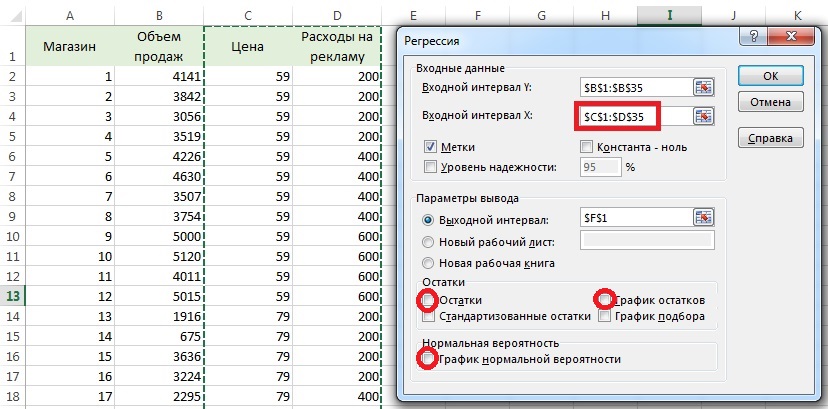
Результаты работы Пакета анализа представлены на рис. 3. Как видим, b0 = 5 837,52, b1 = –53,217 и b2 = 3,163. Следовательно, ![]() = 5 837,52 –53,217X1i + 3,163X2i , где Ŷi — предсказанный объем продаж питательных батончиков OmniPower в i-м магазине (штук), Х1i — цена батончика (в центах) в i-м магазине, Х2i — ежемесячные затраты на рекламу в i-м магазине (в долларах).
= 5 837,52 –53,217X1i + 3,163X2i , где Ŷi — предсказанный объем продаж питательных батончиков OmniPower в i-м магазине (штук), Х1i — цена батончика (в центах) в i-м магазине, Х2i — ежемесячные затраты на рекламу в i-м магазине (в долларах).
Рис. 3. Множественная регрессия исследования объем продажа батончиков OmniPower
Выборочный наклон b0 равен 5 837,52 и является оценкой среднего количества батончиков OmniPower, проданных за месяц при нулевой цене и отсутствии затрат на рекламу. Поскольку эти условия лишены смысла, в данной ситуации величина наклона b0 не имеет разумной интерпретации.
Выборочный наклон b1 равен –53,217. Это значит, что при заданном ежемесячном объеме затрат на рекламу увеличение цены батончика на один цент приведет к снижению ожидаемого объема продаж на 53,217 штук. Аналогично выборочный наклон b2, равный 3,613, означает, что при фиксированной цене увеличение ежемесячных рекламных затрат на один доллар сопровождается увеличением ожидаемого объема продаж батончиков на 3,613 шт. Эти оценки позволяют лучше понять влияние цены и рекламы на объем продаж. Например, при фиксированном объеме затрат на рекламу уменьшение цены батончика на 10 центов увеличит объем продаж на 532,173 шт., а при фиксированной цене батончика увеличение рекламных затрат на 100 долл. увеличит объем продаж на 361,31 шт.
Интерпретация наклонов в модели множественной регрессии. Коэффициенты в модели множественной регрессии называются коэффициентами чистой регрессии. Они оценивают среднее изменение отклика Y при изменении величины X на единицу, если все остальные объясняющие переменные «заморожены». Например, в задаче о батончиках OmniPower магазин с фиксированным объемом рекламных затрат за месяц продаст на 53,217 батончика меньше, если увеличит их стоимость на один цент. Возможна еще одна интерпретация этих коэффициентов. Представьте себе одинаковые магазины с одинаковым объемом затрат на рекламу. При уменьшении цены батончика на один цент объем продаж в этих магазинах увеличится на 53,217 батончика. Рассмотрим теперь два магазина, в которых батончики стоят одинаково, но затраты на рекламу отличаются. При увеличении этих затрат на один доллар объем продаж в этих магазинах увеличится на 3,613 штук. Как видим, разумная интерпретация наклонов возможна лишь при определенных ограничениях, наложенных на объясняющие переменные.
Предсказание значений зависимой переменной Y. Выяснив, что накопленные данные позволяют использовать модель множественной регрессии, мы можем прогнозировать ежемесячный объем продаж батончиков OmniPower и построить доверительные интервалы для среднего и предсказанного объемов продаж. Для того чтобы предсказать средний ежемесячный объем продаж батончиков OmniPower по цене 79 центов в магазине, расходующем на рекламу 400 долл. в месяц, следует применить уравнение множественной регрессии: Y = 5 837,53 – 53,2173*79 + 3,6131*400 = 3 079. Следовательно, ожидаемый объем продаж в магазинах, торгующих батончиками OmniPower по цене 79 центов и расходующих на рекламу 400 долл. в месяц, равен 3 079 шт.
Вычислив величину Y и оценив остатки, можно построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика. Ранее мы рассмотрели эту процедуру в рамках модели простой линейной регрессии. Однако построение аналогичных оценок для модели множественной регрессии сопряжено с большими вычислительными трудностями и здесь не приводится.
Коэффициент множественной смешанной корреляции. Напомним, что модель регрессии позволяет вычислить коэффициент смешанной корреляции r2. Поскольку в модели множественной регрессии существуют по крайней мере две объясняющие переменные, коэффициент множественной смешанной корреляции представляет собой долю вариации переменной Y, объясняемой заданным набором объясняющих переменных:
где SSR – сумма квадратов регрессии, SST – полная сумма квадратов.
Например, в задаче о продажах батончика OmniPower SSR = 39 472 731, SST = 52 093 677 и k = 2. Таким образом,
Это означает, что 75,8% вариации объемов продаж объясняется изменениями цен и колебаниями объемов затрат на рекламу.
Анализ остатков для модели множественной регрессии
Анализ остатков позволяет определить, можно ли применять модель множественной регрессии с двумя (или более) объясняющими переменными. Как правило, проводят следующие виды анализа остатков:
- Распределение остатков по
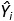 (рис. 4).
(рис. 4). - Распределение остатков по Х1i (рис. 5).
- Распределение остатков по Х2i (рис. 5).
- Распределение остатков по времени.
Первый график (рис. 4а) позволяет проанализировать распределение остатков в зависимости от предсказанных значений ![]() . Если величина остатков не зависит от предсказанных значений
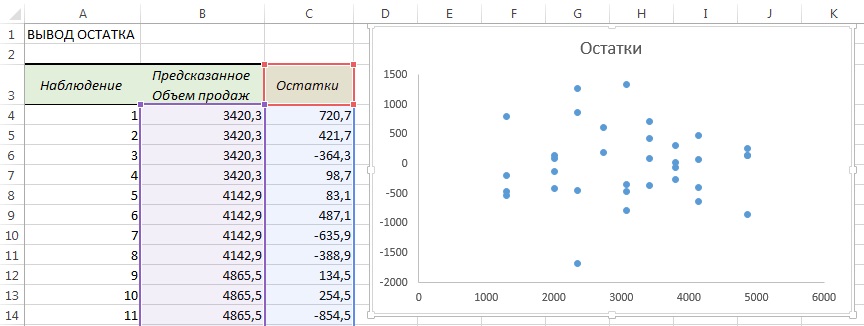
. Если величина остатков не зависит от предсказанных значений ![]() и принимает как положительные так и отрицательные значения (как в нашем пример), условие линейной зависимости переменной Y от обеих объясняющих переменных выполняется. К сожалению, в Пакете анализа этот график почему-то не создается. Можно в окне Регрессия (см. рис. 2) включить Остатки. Это позволит вывести таблицу с остатками, а уже по ней построить точечный график (рис. 4).
и принимает как положительные так и отрицательные значения (как в нашем пример), условие линейной зависимости переменной Y от обеих объясняющих переменных выполняется. К сожалению, в Пакете анализа этот график почему-то не создается. Можно в окне Регрессия (см. рис. 2) включить Остатки. Это позволит вывести таблицу с остатками, а уже по ней построить точечный график (рис. 4).
Рис. 4. Зависимость остатков от предсказанного значения ![]()
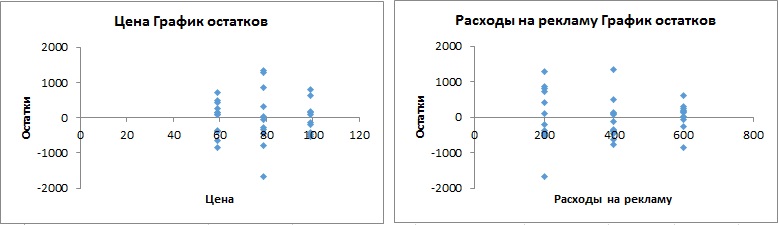
Второй и третий график демонстрируют зависимость остатков от объясняющих переменных. Эти графики могут выявить квадратичный эффект. В этой ситуации необходимо добавить в модель множественной регрессии квадрат объясняющей переменной. Эти графики выводятся Пакетом анализа (см. рис. 2), если включить опцию График остатков (рис. 5).
Рис. 5. Зависимость остатков от цены и затрат на рекламу
Четвертый график применяется для проверки независимости данных, собранных в течение определенного времени. Для этого надо наблюдения расположить по времени, и построить зависимость предсказанного значения ![]() от времени. Поскольку в примере с OmniPower все измерения делались одновременно, такой график не применим. Для выявления положительной автокорреляции между остатками можно вычислить статистику Дурбина-Уотсона (подробнее см. соответствующий раздел заметки Простая линейная регрессия).
от времени. Поскольку в примере с OmniPower все измерения делались одновременно, такой график не применим. Для выявления положительной автокорреляции между остатками можно вычислить статистику Дурбина-Уотсона (подробнее см. соответствующий раздел заметки Простая линейная регрессия).
Проверка значимости модели множественной регрессии.
Убедившись с помощью анализа остатков, что модель линейной множественной регрессии является адекватной, можно определить, существует ли статистически значимая взаимосвязь между зависимой переменной и набором объясняющих переменных. Поскольку в модель входит несколько объясняющих переменных, нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = β2 = … = βk = 0 (между откликом и объясняющими переменными нет линейной зависимости), Н1: существует по крайней мере одно значение βj ≠ 0 (мжду откликом и хотя бы одной объясняющей переменной существует линейная зависимость).
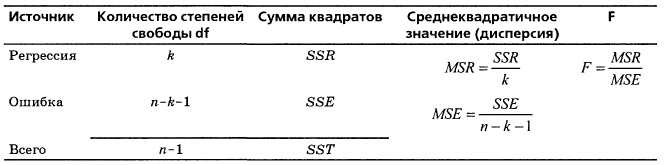
Для проверки нулевой гипотезы применяется F-критерий – тестовая F-статистика равна среднему квадрату, обусловленному регрессией (MSR), деленному на дисперсию ошибок (MSE):
где F – тестовая статистика, имеющая F-распределение с k и n – k – 1 степенями свободы, k – количество независимых переменных в регрессионной модели.
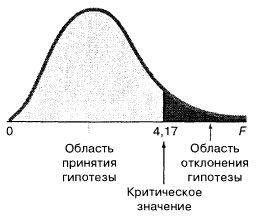
Решающее правило выглядит следующим образом: при уровне значимости α нулевая гипотеза Н0 отклоняется, если F > FU(k,n – k – 1), в противном случае гипотеза Н0 не отклоняется (рис. 6).
Рис. 6. Сводная таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициентов множественной регрессии
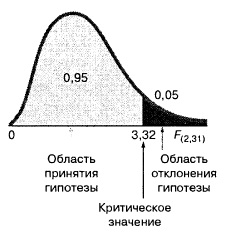
Сводная таблица дисперсионного анализа, заполненная с использованием Пакета анализа Excel при решении задачи о продажах батончиков OmniPower, показана на рис. 3 (см. область А10:F14). Если уровень значимости равен 0,05, критическое значение F-распределения с двумя и 31 степенями свободы FU(2,31) = F.ОБР(1-0,05;2;31) = равно 3,305 (рис. 7).
Рис. 7. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости α = 0,05, с 2 и 31 степенями свободы
Как показано на рис. 3, F-статистика равна 48,477 > FU(2,31) = 3,305, а p-значение близко к 0,000 < 0,05. Следовательно, нулевая гипотеза Н0 отклоняется, и объем продаж линейно связан хотя бы с одной из объясняющих переменных (ценой и/или затратами на рекламу).
Статистические выводы о генеральной совокупности коэффициентов регрессии
Чтобы выявить статистически значимую зависимость между переменными X и Y в модели простой линейной регрессии, была выполнена проверка гипотезы о наклоне. Кроме того, для оценки наклона генеральной совокупности был построен доверительный интервал (см. Простая линейная регрессия).
Проверка гипотез. Для проверки гипотезы, утверждающей, что наклон генеральной совокупности β1, в модели простой линейной регрессии равен нулю, используется формула t = (b1 – β1)/Sb1. Ее можно распространить на модель множественной регрессии:
где t – тестовая статистика, имеющая t-распределение с n – k – 1 степенями свободы, bj — наклон переменной хj по отношению к переменной Y, если все остальные объясняющие переменные являются константами, Sbj – среднеквадратичная ошибка регрессионного коэффициента bj, k — количество объясняющих переменных в уравнении регрессии, βj — гипотетический наклон генеральной совокупности откликов j-й относительно переменной, когда все остальные переменные фиксированы.
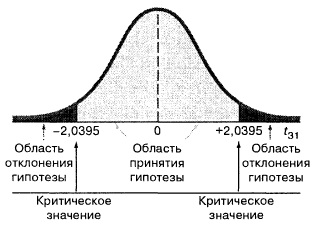
На рис. 3 (нижняя таблица) показаны результаты применения t-критерия (полученные с помощью Пакета анализа) для каждой из независимых переменных, включенных в регрессионную модель. Таким образом, если необходимо определить, оказывает ли переменная Х2 (затраты на рекламу) существенное влияние на объем продаж при фиксированной цене батончика OmniPower, формулируются нулевая и альтернативная гипотезы: Н0: β2 = 0, Н1: β2 ≠ 0. В соответствии с формулой (6) получаем:
Если уровень значимости равен 0,05, критическими значениями t-распределения с 31 степенями свободы являются tL = СТЬЮДЕНТ.ОБР(0,025;31) = –2,0395 и tU = СТЬЮДЕНТ.ОБР(0,975;31) = 2,0395 (рис. 8). р-значение =1-СТЬЮДЕНТ.РАСП(5,27;31;ИСТИНА) и близко к 0,0000. На основании одного из неравенств t = 5,27 > 2,0395 или р = 0,0000 < 0,05 нулевая гипотеза Н0 отклоняется. Следовательно, при фиксированной цене батончика между переменной Х2 (затраты на рекламу) и объемом продаж существует статистически значимая зависимость. Таким образом, существует чрезвычайно малая вероятность отвергнуть нулевую гипотезу, если между затратами на рекламу и объемами продаж нет линейной зависимости.
Рис. 8. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости α = 0,05, с 31 степенью свободы
Проверка значимости конкретных коэффициентов регрессии фактически представляет собой проверку гипотезы о значимости конкретной переменной, включенной в регрессионную модель наряду с другими. Следовательно, t-критерий для проверки гипотезы о значимости регрессионного коэффициента эквивалентен проверке гипотезы о влиянии каждой из объясняющих переменных.
Доверительные интервалы. Вместо проверки гипотезы о наклоне генеральной совокупности можно оценить значение этого наклона. В модели множественной регрессии для построения доверительного интервала используется формула:
(7) bj ± tn–k–1Sbj
Воспользуемся этой формулой для того, чтобы построить 95%-ный доверительный интервал, содержащий наклон генеральной совокупности β1 (влияние цены X1 на объем продаж Y при фиксированном объеме затрат на рекламу Х2). По формуле (7) получаем: b1 ± tn–k–1Sb1. Поскольку b1 = –53,2173 (см. рис. 3), Sb1 = 6,8522, критическое значение t-статистики при 95%-ном доверительном уровне и 31 степени свободы tn–k–1 =СТЬЮДЕНТ.ОБР(0,975;31) = 2,0395, получаем:
–53,2173 ± 2,0395*6,8522
–53,2173 ± 13,9752
–67,1925 ≤ β1 ≤ –39,2421
Таким образом, учитывая эффект затрат на рекламу, можно утверждать, что при увеличении цены батончика на один цент объем продаж уменьшается на величину, которая колеблется от 39,2 до 67,2 шт. Существует 95%-ная вероятность, что этот интервал правильно оценивает зависимость между двумя переменными. Поскольку данный доверительный интервал не содержит нуля, можно утверждать, что регрессионный коэффициент β1 имеет статистически значимое влияние на объем продаж.
Оценка значимости поясняющих переменных в модели множественной регрессии
В модель множественной регрессии следует включать только те объясняющие переменные, которые позволяют точно предсказать значение зависимой переменной. Если какая-либо из объясняющих переменных не соответствует этому требованию, ее нужно удалить из модели. В качестве альтернативного метода, позволяющего оценить вклад объясняющей переменной, как правило, применяется частный F-критерий. Он заключается в оценке изменения суммы квадратов регрессии после включения в модель очередной переменной. Новая переменная включается в модель лишь тогда, когда это приводит к значительному увеличению точности предсказания.
Для того чтобы применить частный F-критерий для решения задачи о продажах батончика OmniPower, необходимо оценить вклад переменной Х2 (затраты на рекламу) после включения в модель переменной X1 (цена батончика). Если в модель входят несколько поясняющих переменных, вклад объясняющей переменной хj можно определить, исключив ее из модели и оценив сумму квадратов регрессии (SSR), вычисленную по оставшимся переменным. Если в модель входят две переменные, вклад каждой из них определяется по формулам:
Оценка вклада переменной Х1 при условии, что в модель включена переменная Х2:
(8а) SSR(X1|Х2) = SSR(X1 и Х2) – SSR(X2)
Оценка вклада переменной Х2 при условии, что в модель включена переменная Х1:
(8б) SSR(X2|Х1) = SSR(X1 и Х2) – SSR(X1)
Величины SSR(X2) и SSR(X1) соответственно представляют собой суммы квадратов регрессии, вычисленных только по одной из объясняемых переменных (рис. 9).
Рис. 9. Коэффициенты модели простой линейной регрессии, учитывающей: (а) объем продаж и цену батончика – SSR(X1); (б) объем продаж и затраты на рекламу – SSR(X2) (получены с помощью Пакета анализа Excel)
Нулевая и альтернативная гипотезы о вкладе переменной Х1 формулируются следующим образом: Н0 — включение переменной Х1 не приводит к значительному увеличению точности модели, в которой учитывается переменная Х2; Н1 — включение переменной Х1 приводит к значительному увеличению точности модели, в которой учтена переменная Х2. Статистика, положенная в основу частного F-критерия для двух переменных, вычисляется по формуле:
где MSE – дисперсия ошибки (остатка) для двух факторов одновременно. По определению F-статистика имеет F-распределение с одной и n–k–1 степенями свободы.
Итак, SSR(X2) = 14 915 814 (рис. 9), SSR(X1 и Х2) = 39 472 731 (рис. 3, ячейка С12). Следовательно, по формуле (8а) получаем: SSR(X1|Х2) = SSR(X1 и Х2) – SSR(X2) = 39 472 731 – 14 915 814 = 24 556 917. Итак, для SSR(X1|Х2) = 24 556 917 и MSE (X1 и Х2) = 407 127 (рис. 3, ячейка D13), используя формулу (9), получаем: F = 24 556 917 / 407 127 = 60,32. Если уровень значимости равен 0,05, то критическое значение F-распределения с одной и 31 степенями свободы =F.ОБР(0,95;1;31) = 4,16 (рис. 10).
Рис. 10. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости, равном 0,05, с одной и 31 степенями свободы
Поскольку вычисленное значение F-статистики больше критического (60,32 > 4,17), гипотеза Н0 отклоняется, следовательно, учет переменной Х1 (цены) значительно улучшает модель регрессии, в которую уже включена переменная Х2 (затраты на рекламу).
Аналогично можно оценить влияние переменной Х2 (затраты на рекламу) на модель, в которую уже включена переменная Х1 (цена). Проведите вычисления самостоятельно. Решающее условие приводит к тому, что 27,8 > 4,17, и следовательно, включение переменной Х2 также приводит к значительному увеличению точности модели, в которой учитывается переменная Х1. Итак, включение каждой из переменных повышает точность модели. Следовательно, в модель множественной регрессии необходимо включить обе переменные: и цену, и затраты на рекламу.
Любопытно, что значение t-статистики, вычисленное по формуле (6), и значение частной F-статистики, заданной формулой (9), однозначно взаимосвязаны:
где а — количество степеней свободы.
Регрессионные модели с фиктивной переменной и эффекты взаимодействия
Обсуждая модели множественной регрессии, мы предполагали, что каждая независимая переменная является числовой. Однако во многих ситуациях в модель необходимо включать категорийные переменные. Например, в задаче о продажах батончиков OmniPower для предсказания среднемесячного объема продаж использовались цена и затраты на рекламу. Кроме этих числовых переменных, можно попытаться учесть в модели расположение товара внутри магазина (например, на витрине или нет). Для того чтобы учесть в регрессионной модели категорийные переменные, следует включить в нее фиктивные переменные. Например, если некая категорийная объясняющая переменная имеет две категории, для их представления достаточно одной фиктивной переменной Xd: Xd = 0, если наблюдение принадлежит первой категории, Xd = 1, если наблюдение принадлежит второй категории.
Для иллюстрации фиктивных переменных рассмотрим модель для предсказания средней оценочной стоимости недвижимости на основе выборки, состоящей из 15 домов. В качестве объясняющих переменных выберем жилую площадь дома (тыс. кв. футов) и наличие камина (рис. 11). Фиктивная переменная Х2 (наличие камина) определена следующим образом: Х2 = 0, если камина в доме нет, Х2 = 1, если в доме есть камин.
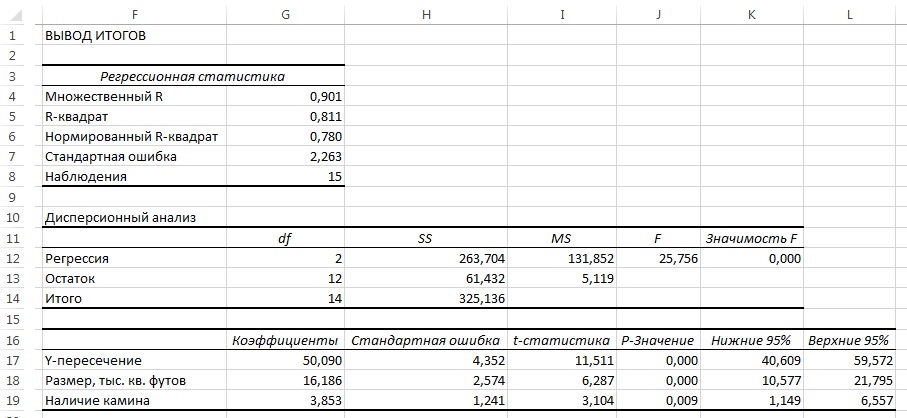
Рис. 11. Оценочная стоимость, предсказанная по жилой площади и наличию камина
Предположим, что наклон оценочной стоимости, зависящей от жилой площади, одинаков у домов, имеющих камин и не имеющих его. Тогда модель множественной регрессии выглядит следующим образом:
Yi = β0 + β1X1i + β2X2i + εi
где Yi — оценочная стоимость i-гo дома, измеренная в тысячах долларов, β0 — сдвиг отклика, X1i,— жилая площадь i-гo дома, измеренная в тыс. кв. футов, β1 — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной, X1i,— фиктивная переменная, означающая наличие или отсутствие камина, β1 — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной β2 — эффект увеличения оценочной стоимости дома в зависимости от наличия камина при постоянной величине жилой площади, εi – случайная ошибка оценочной стоимости i-гo дома. Результаты вычисления регрессионой модели представлены на рис. 12.
Рис. 12. Результаты вычисления регрессионой модели для оценочной стоимости домов; получены с помощью Пакета анализа в Excel; для расчета использована таблица, аналогичная рис. 11, с единственным изменением: «Да» заменены единицами, а «Нет» – нулями
В этой модели коэффициенты регрессии интерпретируются следующим образом:
- Если фиктивная переменная имеет постоянное значение, увеличение жилой площади на 1000 кв. футов приводит к увеличению предсказанной средней оценочной стоимости на 16,2 тыс. долл.
- Если жилая площадь постоянна, наличие камина увеличивает среднюю оценочную стоимость дома на 3,9 тыс. долл.
Обратите внимание (рис. 12), t-статистика, соответствующая жилой площади, равна 6,29, а р-значение почти равно нулю. В то же время t-статистика, соответствующая фиктивной переменной, равна 3,1, а p-значение – 0,009. Таким образом, каждая из этих двух переменных вносит существенный вклад в модель, если уровень значимости равен 0,01. Кроме того, коэффициент множественной смешанной корреляции означает, что 81,1% вариации оценочной стоимости объясняется изменчивостью жилой площади дома и наличием камина.
Эффект взаимодействия. Во всех регрессионных моделях, рассмотренных выше, считалось, что влияние отклика на объясняющую переменную является статистически независимым от влияния отклика на другие объясняющие переменные. Если это условие не выполняется, возникает взаимодействие между зависимыми переменными. Например, вполне вероятно, что реклама оказывает большое влияние на объем продаж товаров, имеющих низкую цену. Однако, если цена товара слишком высока, увеличение расходов на рекламу не может существенно повысить объем продаж. В этом случае наблюдается взаимодействие между ценой товара и затратами на его рекламу. Иначе говоря, нельзя делать общих утверждений о зависимости объема продаж от затрат на рекламу. Влияние рекламных расходов на объем продаж зависит от цены. Это влияние учитывается в модели множественной регрессии с помощью эффекта взаимодействия. Для иллюстрации этого понятия вернемся к задаче о стоимости домов.
В разработанной нами регрессионной модели предполагалось, что влияние размера дома на его стоимость не зависит от того, есть ли в доме камин. Иначе говоря, считалось, что наклон оценочной стоимости, зависящей от жилой площади дома, одинаков у домов, имеющих камин и не имеющих его. Если эти наклоны отличаются друг от друга, между размером дома и наличием камина существует взаимодействие.
Проверка гипотезы о равенстве наклонов сводится к оценке вклада, который вносит в модель регрессии произведение объясняющей переменной X1 и фиктивной переменной Х2. Если этот вклад является статистически значимым, исходную модель регрессии применять нельзя. Результаты регрессионного анализа, включающего переменные Х1, Х2 и Х3 = Х1*Х2 приведены на рис. 13.
Рис. 13. Результаты, полученные с помощью Пакета анализа Excel для регрессионной модели, учитывающей жилую площадь, наличие камина и их взаимодействие
Для того чтобы проверить нулевую гипотезу Н0: β3 = 0 и альтернативную гипотезу Н1: β3 ≠ 0, используя результаты, приведенные на рис. 13, обратим внимание на то, что t-статистика, соответствующая эффекту взаимодействия переменных, равна 1,48. Поскольку р-значение равно 0,166 > 0,05, нулевая гипотеза не отклоняется. Следовательно, взаимодействие переменных не имеет существенного влияния на модель регрессии, учитывающую жилую площадь и наличие камина.
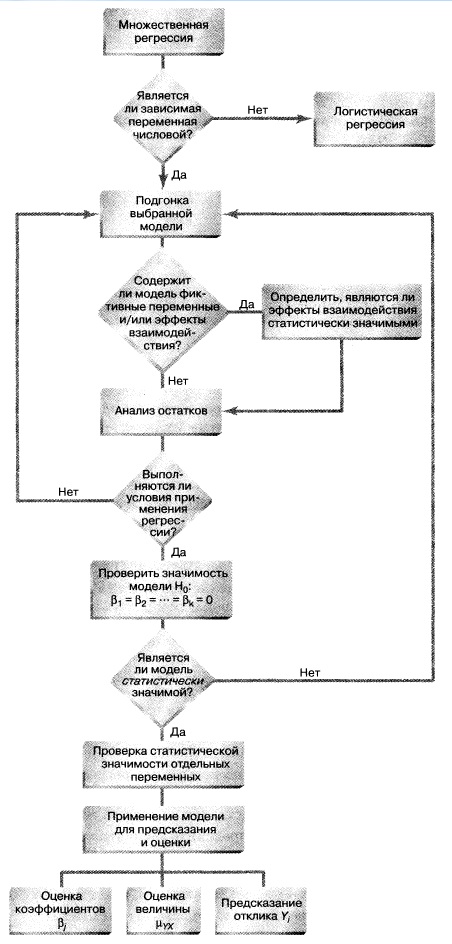
Резюме. В заметке показано, как менеджер по маркетингу может применять множественный линейный анализ для предсказания объема продаж, зависящего от цены и затрат на рекламу. Рассмотрены различные модели множественной регрессии, включая квадратичные модели, модели с фиктивными переменными и модели с эффектами взаимодействия (рис. 14).
Рис. 14. Структурная схема заметки
Предыдущая заметка Простая линейная регрессия
Следующая заметка Построение моделей множественной регрессии
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 873–936
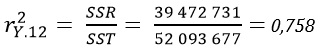
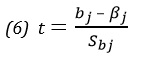

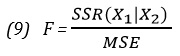



Подскажите, как называется тип регрессии, где определяются не только прямое, но и взаимное влияние факторов.
Например, имеем статистику по смертям — курил ли человек, занимался ли он спортом и сколько лет он прожил.
На основе данных регрессионная модель находит базовый возраст, добавляет 5 лет за спорт, и забирает 5 лет за курение. Но если человек и курит и занимается спортом? Мы можем таких индивидов выделить и определить, что они живут на 20 лет короче, но ведь обычная регрессия такого не умеет. Существует ли такая регрессия, которая умеет или надо сразу на нейронную сеть переходить?
Добрый день!
У меня есть вопрос: корреляционная таблица была создана по 11 переменным и показала высокий уровень корреляции первых 5-х. Но, когда получила таблицы по регрессионной статистике, р-значение первых двух переменных равно «#ЧИСЛО!». Не могу понять, где у меня ошибка. Можете проконсультировать?
Заранее большое спасибо!
Добрый день!
Меня мучит один вопрос. Дело касается прогнозирования при множественной регрессии. А вопрос такой: насколько можно увеличивать независимые факторы (Хi), что бы получить приемлемое прогнозное значение (У)? Если Хi это количество различных профилактических мероприятий, которые влияют на снижение преступности (У). Получается, что, например, увеличивая количество бесед с населением можно снизить преступность до 0, но мы понимаем, что это не так. Где остановится при увеличении Х, при 10%, 20%, при 100%? Подскажите кто может! С уважением и благодарность Николай (nlp009@mail.ru