Недавно прочитал любопытную книгу Стивен Строгац. Удовольствие от х. Автор рассказывает около 30 занимательных (и поучительных) историй из области математики. В одной из историй говорится о принципах работы PageRank – алгоритма ссылочного ранжирования, впервые использованного в Google. Тема актуальна и довольна проста для понимания. Так что слово Стивену Строгацу…
В те далекие времена, когда Google еще не существовало, поиск в сети был безнадежным занятием. Сайты, предлагаемые старыми поисковыми машинами, часто не соответствовали запросу, а те, которые содержали нужную информацию, были либо глубоко запрятаны в списке результатов, либо вообще отсутствовали. Алгоритмы на основе анализа ссылок решили проблему, проникнув в суть парадокса, подобного коанам дзен: в результате поиска в интернете должны были отображаться лучшие страницы. А что же, делает страницу лучшей? Когда на нее ссылаются другие не менее хорошие страницы.
Скачать заметку в формате Word или pdf
Звучит подобно рассуждениям про замкнутый круг. Так и есть. Именно поэтому все настолько сложно. Ухватившись за эту идею и превратив ее в преимущество, алгоритм анализа ссылок дает решение поиска в сети в стиле джиу-джитсу. Этот подход построен на идеях, взятых из линейной алгебры, изучения векторов и матриц. Если вы хотите выявить закономерности в огромном скоплении данных или выполнить гигантские вычисления с миллионами переменных, линейная алгебра предоставит для этого все необходимые инструменты. С ее помощью был построен фундамент для алгоритма PageRank [1], положенного в основу Google. Она также помогает ученым классифицировать человеческие лица, провести анализ голосования в Верховном суде, а также выиграть приз Netflix (вручаемый команде, сумевшей улучшить более чем на 10% систему Netflix, на основе которой составляются рекомендации для просмотра лучших фильмов).
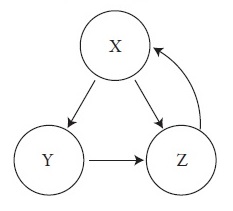
Чтобы изучить линейную алгебру в действии, рассмотрим, как работает алгоритм PageRank. А чтобы выявить его сущность без лишней суеты, представим игрушечную паутину, состоящую всего из трех страниц, связанных между собой следующим образом:
Рис. 1. Небольшая сеть из трех сайтов
Стрелки указывают, что страница X содержит ссылку на страницу Y, однако Y не отвечает ей взаимностью. Наоборот, Y ссылается на Z. Тем временем X и Z ссылаются друг на друга.
Какие страницы самые важные в этой маленькой паутине? Вы можете подумать, что это невозможно определить из-за недостатка информации об их содержимом. Но такой способ мышления устарел. Беспокойство по поводу контента вылилось в неудобный способ ранжирования страниц. Компьютеры мало понимают в смысловом наполнении, а люди не справляются с тысячами новых страниц, которые каждый день появляются в сети.
Подход, придуманный Ларри Пейджем и Сергеем Брином, аспирантами университета и основателями Google, состоял в том, чтобы позволить страницам самим ранжироваться в определенном порядке, голосуя ссылками. В приведенном выше примере страницы X и Y ссылаются на Z, благодаря чему Z становится единственной страницей с двумя входящими ссылками. Следовательно, она и будет самой популярной страницей в данной среде. Однако если ссылки поступают со страниц сомнительного качества, они станут работать против себя. Популярность сама по себе ничего не значит. Главное — иметь ссылки с хороших страниц.
И здесь мы снова оказывается в замкнутом круге. Страница считается хорошей, если на нее ссылаются хорошие страницы, но кто изначально решает, какие из них хорошие? Это решает сеть. Вот как все происходит. [2]
Алгоритм Google назначает для каждой страницы дробное число от 0 до 1. Это численное значение называется PageRank и измеряет «важность» страницы по отношению к другим, высчитывая относительное количество времени, которое гипотетический пользователь потратит на ее посещение. Хотя пользователь может выбирать более чем из одной исходящей ссылки, он выбирает ее случайно с равной вероятностью. При таком подходе страницы считаются более авторитетными, если они чаще посещаются.
А поскольку индексы PageRank определяются как пропорции, их сумма по всей сети должна составлять 1. Этот закон сохранения предполагает другой, возможно, более осязаемый способ визуализации PageRank. Представьте его как жидкое вещество, текущее по сети, количество которого уменьшается на плохих страницах и увеличивается на хороших. С помощью алгоритма мы пытаемся определить, как эта жидкость распределяется по Интернету на протяжении длительного времени.
Ответ получим в результате многократно повторяющегося следующего процесса. Алгоритм начинается с некоего предположения, затем обновляет все значения PageRank, распределяя жидкость в равных частях по исходящим ссылкам, после этого она проходит несколько кругов, пока не установится определенное состояние, при котором страницы получат причитающуюся им долю.
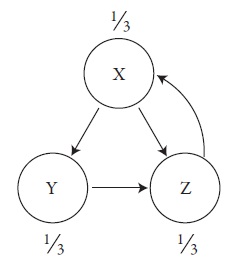
Изначально алгоритм задает равные доли, что позволяет каждой странице получить одинаковое количество PageRank. В нашем примере три страницы, и каждая из них начинает движение по алгоритму со счетом 1/3.
Рис. 2. Начальные значения PageRank
Затем счет обновляется, отображая реальное значение каждой страницы. Правило состоит в том, что каждая страница берет свой PageRank с последнего круга и равномерно распределяет его по всем страницам, на которые ссылается. Следовательно, обновленное значение страницы X после прохождения первого круга по-прежнему равно 1/3, поскольку именно столько PageRank она получает от Z, единственной страницы, которая на нее ссылается. При этом счет страницы Y уменьшается до 1/6, так как она получает только половину PageRank от X после предыдущего круга. Вторая половина переходит к странице Z, что делает ее победителем на данном этапе, поскольку она добавляет себе еще 1/6 от страницы X, а также 1/3 от Y, и всего получается 1/2. Таким образом, после первого круга мы имеем следующие значения PageRank:
Рис. 3. Значения PageRank после одного обновления
В последующих кругах правило обновления остается прежним. Если обозначить через х, у, z текущий счет страниц X, Y и Z, то в результате обновления получим такой счет:
х’ = z
у’ = ½ x
z’ = ½ х + у,
где штрихи говорят о том, что произошло обновление. Подобные многократно повторяющиеся вычисления удобно выполнять в электронной таблице (или вручную, если сеть маленькая, как в нашем случае).
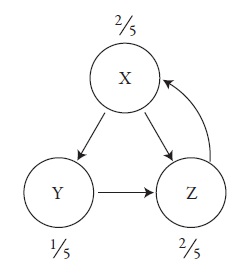
После десяти повторений обнаружим, что от обновления к обновлению цифры практически не меняются. К этому моменту доля X составит 40,6% от всего PageRank, доля Y — 19,8%, а Z — 39,6%. Эти значения подозрительно близки к числам 40, 20 и 40%, что говорит о том, что алгоритм должен к ним сходиться. Так и есть. Эти предельные значения алгоритм Google и определяет для сети как PageRank.
Рис. 4. Предельные значения PageRank
Вывод для данной маленькой сети такой: страницы X и Z одинаково важны, несмотря на то что у Z в два раза больше входящих ссылок. Это и понятно: страница X равна Z по значимости, поскольку она получает от нее полное одобрение, однако взамен дает ей лишь половину своего одобрения. Вторая половина отправляется Y. Это также объясняет, почему Y достается только половина от долей X и Z.
Интересно, что эти значения можно получить, не прибегая к многократным итерациям. Надо просто подумать над условиями, определяющими стационарное состояние. Если после очередного обновления ничего не меняется, то x’ = x, y’ = y и z’ = z. Поэтому, заменив переменные со штрихом в уравнениях обновлений на их эквиваленты без штрихов, получим систему уравнений
х = z
y = ½ x
z = ½ x + y,
при решении которой x = 2y = z. Поскольку сумма значений x, y и z должна равняться 1, отсюда следует, что x = 2/5, y = 1/5 и z = 2/5, что соответствует ранее найденным значениям.
Сложности начинаются там, где в уравнениях присутствует огромное количество переменных, как это происходит в реальной сети. Поэтому одной из центральных задач линейной алгебры является разработка более быстрых алгоритмов для решения больших систем уравнений. Даже незначительные усовершенствования этих алгоритмов ощущаются практически во всех сферах жизни — от расписания авиарейсов до сжатия изображения.
Однако самой существенной победой линейной алгебры, с точки зрения ее роли в повседневной жизни, безусловно, стало решение парадокса дзен-буддизма для ранжирования страниц. «Страница хороша в той мере, в какой хорошие страницы ссылаются на нее». Переведенный в математические символы, этот критерий становится алгоритмом PageRank.
Поисковик Google стал тем, чем он есть сегодня, после решения уравнения, которое и мы с вами только что решили, но с миллиардами переменных — и, соответственно, с миллиардными прибылями.
[1] Согласно Google термин PageRang происходит от имени одного из основателей Google Ларри Пейджа, а не от английского слова page (страница).
[2] Для простоты я представлю только базовую версию алгоритма PageRank. Для обработки сетей с некоторыми другими структурными свойствами его необходимо изменить. Предположим, в сети есть страницы, которые ссылаются на другие, но те, в свою очередь, на них не ссылаются. В процессе обновления эти страницы потеряют свой PageRank. Они отдают его другим, и он больше не восполняется. Таким образом, в конце концов они получат значения PageRank, равные нулю, и с этой точки зрения становятся неразличимыми.
С другой стороны, существуют сети, где некоторые страницы или группы страниц открыты для накапливания PageRank, но при этом не делают ссылок на другие страницы. Подобные страницы действуют как накопители PageRank.
Чтобы избежать подобных результатов, Брин и Пейдж изменили свой алгоритм следующим образом. После каждого этапа в процессе обновления данных все текущие значения PageRank уменьшаются на постоянный коэффициент, так что их сумма будет меньше 1. Затем остатки PageRank равномерно распределяются между всеми узлами в сети, как будто «сыплются с неба». Таким образом, алгоритм завершается действием уравнивания, распределяющим значения PageRank между самыми «бедными» узлами.
Более тщательно математика PageRank и интерактивные исследования рассматриваются в работе E. Aghapour, T. P. Chartier, A. N. Langville, and K. E. Pedings, Google PageRank: The mathematics of Google (http://www.whydomath.org/node/google/index.html).