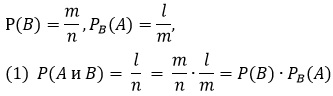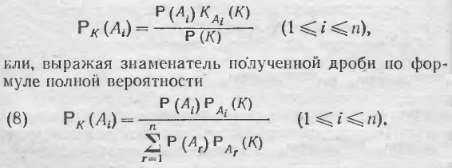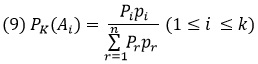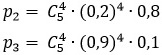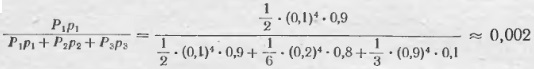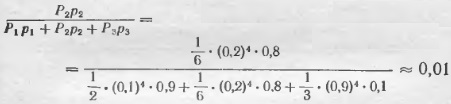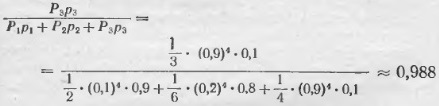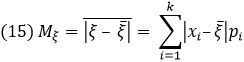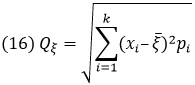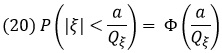Элементарное введение в теорию вероятностей было написана в 1945 году двумя выдающимися математиками, классиками теории вероятностей Б.В.Гнеденко и А.Я.Хинчиным. Она выдержала несколько изданий в СССР общим тиражом более полумиллиона экземпляров, издавалась в тринадцати зарубежных странах, была переведена на пятнадцать языков. Целый ряд примеров связаны с артиллерийской стрельбой, а книга была адресована поколению, переходящему от войны к миру. Сегодня мне трудно нарисовать портрет читателя этой книги. Хотя я получил удовольствие от чтения, а ряд разделов весьма познавательны.
Борис Гнеденко, Александр Хинчин. Элементарное введение в теорию вероятностей. – М.: ЛЕНАНД, 2016. – 208 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon
Глава 1. Вероятности событий
Если массовая операция такова, что событие А (например, попадание в цель) наблюдается в среднем а раз среди b единичных операций (выстрелов), то вероятность события А в данных условиях составляет a/b. Вероятностью «удачного» исхода единичной операции мы называем отношение в среднем наблюдающегося числа таких «удачных» исходов к числу всех единичных операций, составляющих данную массовую операцию.
Условимся обозначать через Р(А) вероятность события А. Каково бы ни было это событие, 0 ≤ Р(А) ≤ 1. Если Р(А) = 0, то событие А никогда не наступает, его можно считать невозможным. Если Р(А) = 1, то событие А наступает всегда, его можно считать достоверным.
Глава 2. Правило сложения вероятностей
Вероятность наступления в некоторой операции какого-либо одного (безразлично какого именно) из результатов А1, А2, …, Аn равна сумме вероятностей этих результатов, если каждые два из них несовместимы между собой:
P(A1, либо А2, либо А3, …) = P(A1) + P(A2) + P(A3) + …
Сумма вероятностей двух противоположных событий равна единице: P(A1) + P(A2) = 1. Пусть имеется n (любое число) событий А1, А2, …, Аn, таких, что в каждой единичной операции обязательно должно наступить одно и только одно из этих событий; условимся такую группу событий называть полной системой. Сумма вероятностей событий, образующих полную систему, равна единице:
P(A1) + P(A2) + … + P(An) = 1
Глава 3. Условные вероятности и правила умножения
Если мы обозначим через А некое событие и через В некое другое событие, то обычно обозначают через Р(А) безусловную вероятность события А и через РВ(А) вероятность того же события при условии, что состоялось событие В. Пример 1. Производившиеся в некотором районе многолетние наблюдения показали, что из 100 000 детей, достигших десятилетнего возраста, до 40 лет доживает в среднем 82 277, а до 70 лет — 37 977. Найти вероятность того, что если человек достигнет сорокалетнего возраста, то он доживет и до 70 лет.
Так как из 82 277 сорокалетних до 70 лет доживает в среднем 37 977, то вероятность сорокалетнему дожить до семидесяти лет равна 37 977/82 277 ≈ 0,46. Если через А и В обозначить события, состоящие: первое — в доживании десятилетнего ребенка до 70 лет, а второе – в достижении им 40-летнего возраста, то имеем Р(А) = 0,37 977 ≈ 0,38; РВ(А) ≈ 0,46.
Пусть в каждой серии из n операций результат В наступает в среднем m раз, а в каждой серии из m таких операции, где результат В наблюдался, l раз наступает результат А. Тогда в каждой серии из n операций совместное наступление событий В и А будет наблюдаться в среднем l раз. Таким образом,
Правило умножения. Вероятность совместного наступления двух событий равна произведению вероятности первого события на условную вероятность второго, вычисленную в предположении, что первое событие состоялось.
Разумеется, мы можем называть первым любое из двух данных событий, так что на равных основаниях с формулой (1) можем писать и
(1’) P(A и B) = P(A)PA(B)
откуда получаем важное соотношение
(2) P(B)PB(A) = P(A)PA(B)
Если события А и В независимы, то PB(A) = P(A) и P(A и B) = Р(А)Р(В). В общем случае, вероятность совместного наступления любого числа взаимно независимых событий равна произведению вероятностей этих событий.
Пример 2. Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,9, для второго 0,8 и для третьего 0,85. Найти вероятность того, что по крайней мере один из трех станков не потребует внимания рабочего в течение часа.
Пойдем от обратного. Вероятность того, что станок потребует внимания рабочего, равна 0,1 для первого станка, 0,2 для второго и 0,15 для третьего. Так как эти три события взаимно независимы, то вероятность того, что осуществятся все эти три события, равна 0,1∙0,2∙0,15 = 0,0003. Но события «все три станка потребуют к себе внимания» и «по крайней мере один из трех проработает спокойно», очевидно, представляют собой пару противоположных событий. Поэтому сумма их вероятностей равна единице, и, следовательно, искомая вероятность равна 1 – 0,0003 = 0,9997 или 99,97%.
Рассмотрим в общем случае вероятность P(A1, или А2, …, или Аn) наступления по меньшей мере одного из нескольких взаимно независимых событий А1, А2, …, Аn. Если мы обозначим через ![]() , событие, состоящее в том, что Ak не наступает, то события
, событие, состоящее в том, что Ak не наступает, то события ![]() и Ak взаимно противоположны, так что P(Ak) + P(
и Ak взаимно противоположны, так что P(Ak) + P(![]() ) = 1. С другой стороны, события
) = 1. С другой стороны, события ![]() ,
, ![]() , …,
, …, ![]() , очевидно, взаимно независимы, так что
, очевидно, взаимно независимы, так что
Р(![]() и
и ![]() , …, и
, …, и ![]() ) = Р(
) = Р(![]() )Р(
)Р(![]() ) … Р(
) … Р(![]() ) = [1–Р(А1)][1–Р(А2)] … [1–Р(Аn)].
) = [1–Р(А1)][1–Р(А2)] … [1–Р(Аn)].
Наконец, события (А1 или А2, …, или Аn) и (![]() и
и ![]() , …, и
, …, и ![]() ), очевидно, противоположны друг другу (одно из двух: либо наступает по меньшей мере одно из событий Аk, либо наступают все события
), очевидно, противоположны друг другу (одно из двух: либо наступает по меньшей мере одно из событий Аk, либо наступают все события ![]() ). Поэтому
). Поэтому
(3) P(A1, или А2, …, или Аn) = 1 – Р(![]() и
и ![]() , …, и
, …, и ![]() ) = 1 – [1–Р(А1)][1–Р(А2)] … [1–Р(Аn)].
) = 1 – [1–Р(А1)][1–Р(А2)] … [1–Р(Аn)].
В частном случае, когда все события Аk имеют одну и ту же вероятность р
(4) P(A1, или А2, …, или Аn) = 1 – (1 – p)n
Пример 3. Вытачивается деталь прибора в виде прямоугольного параллелепипеда. Деталь считается удачной, если длина каждого из ее ребер отклоняется от заданных размеров не более чем на 0,01 мм. Вероятность отклонений, превышающих 0,01 мм, составляет: по длине p1 = 0,08, по ширине р2 = 0,12, по высоте p3 = 0,1. Найти вероятность Р непригодности детали.
Для того чтобы деталь оказалась неудачной, нужно по крайней мере в одном направлении иметь уклонение от заданного размера, превышающее 0,01 мм; обычно эти три события могут считаться взаимно независимыми (ибо они в основном вызываются различными причинами), поэтому для решения задачи можно применить формулу (4); это дает вероятность равную: 1 – (1 – р1)(1 – р2)(1 – р3) ≈ 0,27. Следовательно, удачными из каждых 100 деталей окажутся в среднем 73.
Глава 4. Следствия правил сложения и умножения
Вероятность наступления одного из двух событий
(5) Р(А или В) = Р(А) + Р(В) – Р(А и В)
где Р(А и В) – вероятность наступления двух событий одновременно. Поскольку Р(А и В) ≥ 0, то
(6) Р (А или В) ≤ Р(А) + Р(В)
То есть, вероятность наступления по менышей мере одного из нескольких событий никогда не превышает суммы вероятностей этих событий.
Пусть операция допускает результаты А1, А2, …, Аn, образующие полную систему событий (т.е., любые два из этих событий друг с другом несовместимы и что какое-нибудь из них обязательно должно наступить). Тогда для любого возможного результата К этой операции имеет место соотношение
Это правило обычно называют формулой полной вероятности.
Формула Байеса. Пусть снова события А1, А2, …, Аn представляют собой полную систему результатов некоторой операции. Если К означает произвольный результат этой операции, то по правилу умножения
Это — формула Байеса, имеющая много приложений в практике вычисления вероятностей. Чаще всего приходится применять ее в положениях, которые иллюстрируются следующим примером. Пусть стрельба ведется по цели, расположенной на прямолинейном участке MN (рис. 1), который мы мысленно разбили на пять небольших участков. Допустим, что точное местоположение цели нам неизвестно мы знаем только вероятности того, что цель лежит на том или другом из наших пяти участков; пусть эти вероятности равны Р(а) = 0,48; Р(b’) = Р(b’’) = 0,21; Р(с’) = Р(с’’) = 0,05, где через а, b’, b’’, с’, с’’ обозначены следующие события: цель находится в отрезке а, b’, b’’, с’, с’’ (сумма этих чисел равна единице).
Рис. 1. Участок MN, разбитый на пять небольших участков
Наибольшая вероятность соответствует отрезку а, куда мы поэтому, естественно, и направляем наш выстрел. Однако из-за неизбежных ошибок стрельбы цель может оказаться пораженной и тогда, когда она находится не в а, а в каком-либо из других отрезков. Пусть вероятность поражения цели (вероятность события К) составляет:
Ра(К) = 0,56, если цель лежит в отрезке а,
Рb’(К) = 0,18, если цель лежит в отрезке b’,
Рb’’(К) = 0,16, если цель лежит в отрезке b’’,
Рc’(К) = 0,06, если цель лежит в отрезке c’,
Рc’’(К) = 0,02, если цель лежит в отрезке c’’,
Допустим, что выстрел произведен и цель оказалась пораженной (состоялось событие К). В результате этого вероятности различных положений цели, которые мы имели раньше (т.е. числа Р(а), Р(b’), …) подвергаются переоценке; качественная сторона этой переоценки ясна без всяких вычислений; мы стреляли по отрезку а и попали в цель — ясно, что вероятность Р(а) при этом должна увеличиться; но мы хотим точно количественно учесть произведенную нашим выстрелом переоценку, т.е. мы хотим найти точное выражение вероятностей РК(a), РK(b’), … различных возможных положений цели при условии, что произведенным выстрелом цель была поражена. Формула Байеса (8) сразу дает нам ответ на этот вопрос: РК(a) ≈ 0,8. Мы видим, что РК(a) действительно больше, чем Р(а).
Подобным же образом легко находим и вероятности РK(b’), … других положений цели. Для вычисления полезно заметить, что выражения, даваемые для этих вероятностей формулой Байеса, отличаются друг от друга только своими числителями; знаменатель же у них один и тот же; он равен Р(К) ≈ 0,34.
Общая схема подобного рода положений может быть описана так. Условия операции содержат некоторый неизвестный элемент, относительно которого может быть сделано n различных гипотез: А1, А2, …, Аn, образующих полную систему событий; по тем или другим причинам нам известны вероятности Р(Ai) этих гипотез до испытания; известно также, что также, что при гипотезе Ai некоторое событие К (например, попаданию в цель) имеет вероятность РАi(К) (1 ≤ i ≤ n) (РАi(К) есть вероятность события К, вычисленная при условии, что справедлива гипотеза Аi). Если в результате опыта событие К наступило, то это вызывает переоценку вероятностей гипотез Аi, и задача состоит в том, чтобы найти новые вероятности РK(Ai) этих гипотез; ответ дается формулой Байеса.
Для сокращения записи положим в рассмотренной нами общей схеме
Р(Ai) = Рi, PAi(K) = pi, (1 ≤ i ≤ n)
так что формула Байеса получает простой вид
Допустим, что произведено s испытаний, причем результат К наступил m раз и не наступил s – m раз. Обозначим через K* полученный результат серии из s испытаний. Тогда
где Сsm – число сочетаний из s элементов по m.
Формула Байеса примет вид:
Пример 4. При исследовании больного имеется подозрение на одно из трех заболеваний: А1, А2, А3. Их вероятности в данных условиях равны соответственно: Р1 = ½, Р2 = 1/6, Р3 = 1/3. Для уточнения диагноза назначен некоторый анализ, дающий положительный результат с вероятностью 0,1 в случае заболевания А1 с вероятностью 0,2 в случае заболевания А2 и с вероятностью 0,9 в случае заболевания А3. Анализ был произведен пять раз и дал четыре раза положительный результат и один раз отрицательный. Требуется найти вероятность каждого заболевания после анализа.
В случае заболевания А1 вероятность указанных исходов анализов равна, по правилу умножения,
Для второй и третьей гипотез эти вероятности равны
По формуле Байеса находим, что после анализов вероятность заболевания А1 оказывается равной:
вероятность заболевания А2 –
и вероятность заболевания А3 –
Так как эти три события А1, А2, А3 и после опыта образуют, очевидно, полную систему событий, то для контроля произведенного расчета можно сложить три полученных числа и убедиться, что сумма их по-прежнему равна единице.
Глава 5. Схема Бернулли
Одна из главных схем теории вероятностен состоит в том, что рассматривается последовательность взаимно независимых испытаний, т.е. таких испытаний, что вероятность того или иного результата в каждом из них не зависит от того, какие результаты наступили или наступят в остальных. В каждом из этих испытаний может наступить (или не наступить) некоторое событие А с вероятностью р, не зависящей от номера испытания. Описанная схема получила название схемы Бернулли: ее изучение ведет свое начало от известного швейцарского ученого Якоба Бернулли, жившего в конце XVII века.
Пусть при некоторых условиях вероятность появления события А в каждом испытании равна р; найти вероятность того, что серия из n независимых испытаний даст k появлений и n – k непоявлений события А.
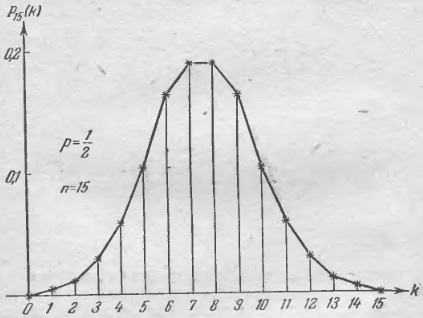
Формулу (12) обычно называют формулой Бернулли. Более яркую картину дают диаграммы изменения величины Рn(k) с ростом k, когда число n становится большим; так, при n = 15 и р = 1/2 диаграмма имеет вид, изображенный на рис. 2. Для практики иногда требуется знать, какое число наступлений события является наивероятнейшим, т.е. при каком числе k вероятность Рn(k) наибольшая. Покуда k, возрастая, не достигнет величины nр – (1 – р), мы будем все время иметь Рn(k+1) > Рn(k), т.е. с ростом числа k вероятность Рn(k) будет все время возрастать. Так, например, в схеме, которой соответствует диаграмма на рис. 2, р = 1/2, n = 15, nр – (1 – р) = 7; значит покуда k < 7, т. е. для всех k, от 0 до 6 включительно, мы имеем Рn(k+1) > Рn(k). Это и подтверждает диаграмма.
Рис. 2. Распределение вероятности Рn(k)
Глава 6. Теорема Бернулли
Если мы производим серию из большого числа n испытаний, то с вероятностью, близкой к единице, мы можем ожидать, что число k появлений события А будет очень близко к своему наивероятнейшему значению, отличаясь от него лишь на незначительную долю общего числа, n произведенных испытаний.
Это предложение, известное под именем теоремы Бернулли и открытое в начале восемнадцатого столетия, представляет собой один из важнейших законов теории вероятностей.
Глава 7. Случайная величина и закон распределения
Для полной характеристики случайной величины необходимо знать:
- перечень всех возможных значений этой случайной величины и
- вероятность каждого из этих значений.
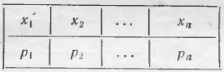
В общем случае случайная величина, возможные значения которой суть х1, х2, …, хn, а соответствующие вероятности – р1, р2, …, рn, определяется таблицей
Рис. 3. Распределение случайной величины
Задать такую таблицу, т.е. задать все возможные значения случайной величины вместе с их вероятностями, означает, как говорят, задать закон распределения случайной величины.
Глава 8. Среднее значение
Допустим, что некоторая случайная величина задана таблицей как на рис. 3. Среднее значение ξ̅ случайной величины, соответствующее отдельной операции будет равно ξ̅ = х1р1 + х2p2 + … + хkpk. Для получения среднего значения случайной величины надо каждое из ее возможных значений помножить на соответствующую ему вероятность и сложить между собой все полученные произведения. Среднее значение квадрата любой случайной величины всегда больше, чем квадрат ее среднего значения.
Глава 9. Средние значения суммы и произведения
Среднее значение суммы всегда равно сумме средних значений слагаемых. Если ξ и η — две совершенно произвольные случайные величины, то
Эта формула верна, как для независимых ξ и η, так и для зависимых друг от друга ξ и η.
Среднее значение произведения ![]() величины ξη в общем случае определить нельзя (т.е. при одних и тех же и возможны различные значения величины ). Однако, для взаимно независимых случайных величин среднее значение произведения равно произведению средних значений сомножителей:
величины ξη в общем случае определить нельзя (т.е. при одних и тех же и возможны различные значения величины ). Однако, для взаимно независимых случайных величин среднее значение произведения равно произведению средних значений сомножителей:
Глава 10. Рассеяние и среднее уклонение
Часто бывает, что наиболее важные для практических целей черты случайной величины ни в какой мере не определяются только ее средним значением, а требуют более детального знакомства с Се законом распределения. Наша задача — найти число, которое разумным образом могло бы давать нам меру рассеяния случайной величины, которое хотя бы ориентировочно указывало нам, сколь больших отклонений этой величины от ее среднего значения нам следует ожидать.
Для решения этого вопроса существует много различных способов, из которых наиболее употребительны на практике следующие три.
Среднее уклонение. За ориентировочное значение случайной величины |ξ – ξ̅ | естественнее всего принять ее среднее значение ![]() . Это среднее значение абсолютной величины уклонения называют средним уклонением величины ξ (сейчас чаще употребляют термин средний размах):
. Это среднее значение абсолютной величины уклонения называют средним уклонением величины ξ (сейчас чаще употребляют термин средний размах):
Среднее квадратическое уклонение (сейчас чаще говорят отклонение).
Величина Qξ называется средним квадратическим уклонением случайной величины ξ, а квадрат ее, т.е. величина Qξ2 – ее дисперсией. Измерять ориентировочную величину уклонения с помощью среднего уклонения — очень естественно, но вместе с тем и очень неудобно практически, так как вычисления и оценки с абсолютными величинами часто бывают сложны. Использование средних квадратичных уклонений Qξ значительно упрощает вычисления. При этом, среднее квадратическое уклонение всегда больше среднего уклонения.
Срединное (вероятное) уклонение – такое число, что уклонение ξ – ξ̅ с одинаковой вероятностью может оказаться по абсолютному значению как больше, так и меньше этого числа. Срединное уклонение величины ξ мы будем обозначать через Еξ. В артиллерии принято для оценки всех уклонений пользоваться именно величиной Еξ.
Теоремы о среднем квадратическом уклонении. Пусть мы имеем случайные величины ξ1, ξ2, …, ξn со средними квадратическими уклонениями q1, q2, …, qn. Дисперсия суммы взаимно независимых случайных величин равна сумме их дисперсий:
Для средних квадратических уклонений мы отсюда получаем:
Возможность просто выразить среднее квадратическое уклонение суммы через средние квадратические уклонения ее слагаемых в случае их взаимной независимости и представляет собой одно из важнейших преимуществ средних квадратических уклонений сравнительно со средними, срединными и другими уклонениями.
При сложении случайных величин относительная ошибка уменьшается. Т.е., среднее арифметическое большого число взаимно независимых величин обладает во много раз меньшим рассеянием, чем каждая из этих величин в отдельности.
Глава 11. Закон больших чисел
Если случайные величины ξ1, ξ2, …, ξn независимы и если все они имеют одно и то же среднее значение а и одно и то же среднее квадратическое уклонение, то величина η = (ξ1 + ξ2 +… + ξn)/n при достаточно большом n будет с вероятностью, как угодно близкой к единице, как угодно мало отличаться от а. Т.е., при большом числе испытаний среднее значение по выборке будет практически равно среднему значению по выборке.
Глава 12. Нормальные законы
Среди случайных величин, встречающихся нам в практике, очень многие носят характер «случайных погрешностей», или «случайных ошибок». Такие случайные величины приблизительно распределены по нормальным законам. На рис. 4 изображено несколько кривых распределения по нормальному закону. У них ясно выраженные общие им всем черты:
- Все кривые имеют одну наивысшую точку, при удалении от которой вправо или влево они непрестанно понижаются.
- Все кривые симметричны относительно вертикальной прямой, проведенной через наивысшую точку.
- Все кривые имеют колоколообразную форму.
Рис. 4. Семейство нормальных кривых
Уравнение кривой, изображающей нормальный закон, имеет вид:
где а и σ2 представляют собой среднее значение и дисперсию случайной величины.
Если мы имеем основание заранее предполагать, что случайная величина распределена по одному из нормальных законов, то заданием ее среднего значения и дисперсии закон распределения однозначно определяется. Отношение срединного (вероятного) уклонения к среднему квадратическому уклонению одно и то же для всех нормальных законов. Обозначим его λ; вычислено, что λ = 0,674. Значит, для любого нормального закона ε = λq.
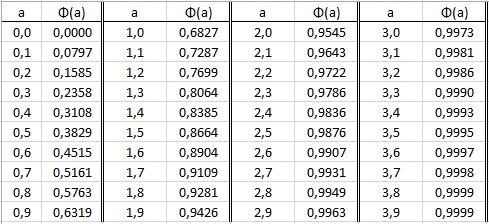
Условимся называть основным нормальным законом закон, для которого среднее значение равно нулю, а дисперсия — единице. Если ξ есть случайная величина, подчиненная основному нормальному закону, то условимся для краткости писать Р(|ξ|<A) = Ф(а) для любого положительного числа а. Таким образом, Ф(а) есть вероятность того, что величина ξ, подчиненная основному нормальному закону, по абсолютному значению не превзойдет числа а. Для величины Ф(а) составлена очень точная таблица, дающая ее значения для различных значений числа а. На рис. 5 приведен ее фрагмент. (В Excel для вычисления Ф(а) можно воспользоваться формулой =НОРМ.СТ.РАСП(а;ИСТИНА)-НОРМ.СТ.РАСП(-а;ИСТИНА). – Прим. Багузина)
Рис. 5. Таблица значений функций Φ(а) (см. также Excel-файл)
В общем случае, если случайная величина ξ распределена по нормальному закону со средним значением ξ̅ и средним квадратическим уклонением Qξ, то вероятность того, что уклонение ξ – ξ̅ по абсолютному значению не превзойдет числа а:
Пример 5. На станке изготовляется некоторая деталь. Оказывается, что ее длина ξ представляет собой случайную величину, распределенную по нормальному закону, и имеет среднее значение 20 см и дисперсию, равную 0,2 см. Найти вероятность того, что длина детали будет заключена между 19,7 см и 20,3 см, т.е. что уклонение в ту или другую сторону не превзойдет 0,3 см.
В силу формулы (20) и таблицы (рис. 5):
Глава 13. Введение в теорию случайных процессов
Предположим, что процесс ξ(t) обладает следующим свойством. Для любых моментов времени t0 и t, t0 < t, вероятность перейти из состояния х0 в момент времени t0 в состояние х в момент t зависит только от t0, х0, t и х, и дополнительное знание состояний, в которых был процесс в предшествующие t0 моменты времени, ее не изменяет. Для таких процессов вся история их развития как бы концентрируется в достигнутом в момент t0 состоянии х0 и только через х0 влияет на последующее его развитие. Именно такие процессы и называются марковскими.
Во многих практически важных или же интересных в познавательном отношении ситуациях приходится выяснять закономерности появления определенного типа событий: прибытие судов в морской порт, отказы в работе сложного устройства, замена перегоревших электрических лампочек и т.д. Расчет многих предприятий бытового обслуживания — парикмахерских, касс магазинов, количества общественного транспорта, необходимого числа коек в больницах, пропускной способности шлюзов, переездов, мостов и т.д. тесно связан с изучением такого рода потоков.
В результате наблюдений оказалось, что во всех указанных случаях с достаточно хорошим приближением появление этих событий хорошо описывается следующей закономерностью. Обозначим через t промежуток времени, который нас интересует, и положим, что Pk(t) есть вероятность появления k событий потока за этот промежуток времени. Тогда при k = 0, 1, 2, … с большой точностью выполняется равенство
где λ — положительная постоянная, характеризующая собой «интенсивность» поступления событий потока. В частности, вероятность того, что за промежуток времени t не поступит пи одного события потока, равна