Как пишет сам автор: «Эта книга – большой трактат, основная цель которого — раскрыть тайну Я». В поисках этого Я автор обращается к знаменитым парадоксам пространства и времени, находит параллели между картинами Эшера, музыкой Баха и революционными открытиями математика Курта Гёделя. Автор – поклонник русского языка, перевел на английский и издал в США «Евгения Онегина».
Книга переведена на 17 языков, и является в некотором смысле культовой. Тираж давно раскуплен, а у букинистов цены запредельные. Однако, у меня сложилось впечатление, что автор уж слишком любуется собой. А его многочисленные (на мой взгляд, чересчур) отступления не проясняют, а лишь запутывают изложение. Книгу прочитал в два захода. В какой-то момент перестал понимать содержание и отложил. И лишь изучив теорему Гёделя по другим книгам, смог вернуться к Хофштадтеру.
Даглас Хофштадтер. Гедель, Эшер, Бах. Эта бесконечная гирлянда. – Самара: Издательский дом «Бахрах-М», 2001. – 752 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Попытаться купить бумажную книгу в Ozon (букинистическая редкость)
ЧАСТЬ I. ГЭБ
Интродукция. Музыко-логическое приношение
Один из канонов «Музыкального приношения» Баха особенно необычен. Это трехголосный канон под названием «Тональный канон» (канон – полифоническое произведение, в котором основная мелодия сопровождается подобными ей, вступающими через некоторый промежуток времени после её начала). Отличительным свойством этого канона является то, что в конце – или, вернее, когда нам кажется, что канон заканчивается – его тональность меняется с до минора на ре минор. Бах каким-то образом ухитряется смодулировать (поменять тональность) прямо под носом слушателей! Канон сконструирован таким образом, что его кажущийся финал неожиданно плавно переходит в начало; этот процесс можно повторить.
Однако, чудесным образом, после шести модуляций мы возвращаемся все к тому же до минору. Бах, упивался возможностью продолжать этот процесс бесконечно. Может быть, поэтому он и написал на полях «Пусть Королевская слава возрастает подобно этой модуляции». Чтобы подчеркнуть заложенную в описанном каноне возможность естественного бесконечного движения, я буду называть его Естественно Растущий Канон. В этом каноне Баха мы впервые сталкиваемся с примером Странных Петель. Странная Петля получается каждый раз, когда, двигаясь вверх или вниз по уровням иерархической системы, мы неожиданно оказываемся в исходном пункте (в нашем примере это система музыкальных тональностей).
Как мне кажется, самые яркие и впечатляющие зрительные реализации идеи Странных Петель представлены в работах голландского графика Маурица Корнелиса Эшера, жившего с 1898 по 1971 год. Эшер был создателем одних из самых интеллектуально стимулирующих рисунков всех времен. Многие из них берут свое начало в парадоксе, иллюзии или двояком значении. Литография «Подъем и спуск» (рис. 1), на которой монахи плетутся по лестнице, навсегда уловленные Петлей, является самой свободной версией, так как Петля здесь содержит множество ступеней. Более «тугая» Петля представлена в «Водопаде» (рис. 2), который содержит всего шесть ступеней (я насчитал только 5).
Рис. 1. Эшер. Подъем и спуск [1]
Рис. 2. Эшер. Водопад
Если затянуть Петлю еще туже, мы получим замечательную картину «Рисующие руки» (рис. 3), на которой каждая из рук рисует другую – двухступенчатая Странная Петля. Наконец, самая тугая Петля представлена в «Картинной галерее» (рис. 4): это картина картины, содержащей саму себя. Или это картина галереи, содержащей саму себя? Или города, содержащего самого себя? Или молодого человека, содержащего самого себя?
Рис. 3. Эшер. Рисующие руки
Рис. 4. Эшер. Картинная галерея
В концепции Странных Петель скрыта идея бесконечности, ибо что такое Петля, как не способ представить бесконечный процесс в конечной форме? Бесконечность играет важную роль во многих картинах Эшера. Копии какой-либо темы часто вставлены друг в друга, создавая зрительные аналогии с канонами Баха. Несколько таких структур можно увидеть на знаменитой эшеровской гравюре «Метаморфозы» (рис. 5).
Рис. 5. Эшер. Метаморфозы
Во всех примерах Странных Петель, которые мы видели у Баха и Эшера, присутствует конфликт между конечным и бесконечным, конфликт, рождающий ощущение парадокса. Подобно Петлям Баха и Эшера, основанным на простых и привычных образах (музыкальная гамма, лестница), открытие Странных Петель в математических системах, принадлежащее Курту Гёделю, берет свое начало в простых и интуитивных идеях. В самой упрощенной форме открытие Гёделя сводится к переводу на язык математики одного из старинных философских парадоксов, так называемого парадокса Эпименида (или парадокса лжеца). Критский философ Эпименид был автором бессмертного суждения: «Все критяне – лжецы». В более прямой форме парадокс звучит так: «Это высказывание – ложь». Это суждение грубо нарушает обычное представление о том, что все суждения делятся на истинные и ложные.
Гёдель попытался использовать математические рассуждения для анализа самих же математических рассуждений. Идея заставить математику заняться «самоанализом» оказалась необычайно продуктивной; теорема Гёделя о неполноте, пожалуй, самое важное её следствие. Саму теорему можно сравнить с жемчужиной, а метод доказательства – с устрицей, её скрывающей. Мы восхищаемся сияющей простотой жемчужины; устрица же является сложным живым организмом, в чьем нутре зарождается эта таинственно простая драгоценность.
В переводе с математического языка на обычный теорема звучит так: Все непротиворечивые аксиоматические формулировки теории чисел содержат неразрешимые суждения.
Это наша жемчужина. В ней трудно увидеть Странную Петлю, потому что эта Петля спрятана в «устрице» – в доказательстве. Доказательство теоремы Гёделя о неполноте вращается вокруг автореферентного (описывающего самого себя) математического суждения.
Теорема Гёделя произвела электризующий эффект на логиков, математиков и философов, заинтересованных в основах математики, поскольку она показала, что ни одна установленная система, какой бы сложной она не была, не может отразить всей сложности целых чисел: 0, 1, 2, 3…
Фактически, теорема Гёделя имеет параллель в теории вычислений: Алан Тьюринг открыл существование неизбежных «дыр» в возможностях даже самого могучего компьютера (подробнее см. Эндрю Ходжес. Игра в имитацию). В начале 1950-х годов казалось, что до механического разума – рукой подать; однако за каждой преодоленной вершиной вставала новая, препятствуя созданию по-настоящему думающей машины. Никто не знает, где пролегает граница между разумным и неразумным поведением; в самом деле, возможно, что само предположение о существовании четкой границы звучит глупо. Компьютеры, по определению, являются самыми негибкими, безвольными и послушными приказам существами. Несмотря на свою быстроту, они, тем не менее, сама бессознательность. Как же, в таком случае, можно запрограммировать разумное поведение? Не является ли уже само это предположение кричащим противоречием? Одна из основных идей этой книги – показать, что это вовсе не противоречие.
Это и составляет предмет исследований науки об искусственном интеллекте (ИИ). Работа специалистов по ИИ кажется странной и удивительной именно потому, что они разрабатывают строго формальные правила, говорящие негибким машинам, как стать гибкими. Что же это за правила, могущие описать всю сложность поведения разумных существ? Безусловно, это должны быть правила самых разных уровней – «простые» правила, «метаправила» для модификации «простых», «метаметаправила» для модификации метаправил, и так далее. Гибкость нашего разума зависит именно от огромного количества правил и сложности их иерархии. Без сомнения, Странные Петли, правила, изменяющие сами себя, находятся в самом сердце разума.
Глава 1. Головоломка MU
Формальные системы. Одним из центральных понятий этой книги является понятие формальной системы. Наша первая формальная система — назовем ее системой MIU — использует лишь три буквы: М, U, I. Дана исходная строка MI. Можете ли вы из нее получить MU? Вам доступны следующие правила преобразования строк:
- Если у вас есть строчка, кончающаяся на I, вы можете прибавить U в конце.
- Если у вас имеется Мх, вы можете прибавить к вашей коллекции строк Мхх.
- Если в какой-либо строчке встречается последовательность UU, вы можете ее опустить.
- Если в какой-либо строчке встречается III, вы можете получить новую строчку, где вместо III будет U.
Попробуйте поэкспериментировать! Вам понравится…
Строчки, выведенные путем применения правил, называются теоремами. Термин теорема широко используется в математике и имеет там совсем другое значение: какое-либо утверждение на естественном языке, доказанное с помощью строгих рассуждений (например, Теорема Эвклида о бесконечном количестве простых чисел). Однако в формальных системах теоремы — не утверждения, а лишь строчки символов. Такие теоремы не доказываются, а просто производятся автоматически при помощи неких типографских правил.
В первой формальной системе я «подарил» вам теорему MI. Такая «дареная» теорема называется аксиомой. Каждая формальная система обладает набором правил обращения с символами, таких, как четыре правила системы MIU. Подобные правила называются порождающими правилами или правилами вывода. Выводом теоремы называется последовательное, шаг за шагом, объяснение того, как можно получить данную теорему согласно правилам формальной системы.
Компьютер возможно запрограммировать таким образом, что тот никогда не заметит даже самых очевидных закономерностей в том, что он делает; человеку, однако, свойственно подмечать определенные закономерности. Человеческому интеллекту свойственно умение, выпрыгивая за пределы системы, смотреть на то, что он делает, со стороны; при этом он ищет — и часто находит — какую-либо схему, закономерность.
Изучая формальные системы, очень важно отличать работу внутри системы от наших наблюдений над системой. Наверное, подобно большинству читателей, вы начали работу над головоломкой MU внутри системы; однако в какой-то момент ваше терпение лопнуло, и вы вышли из системы, пытаясь проанализировать результаты вашей работы и понять, почему вам до сих пор не удалось получить MU. Возможно, вы смогли ответить на этот вопрос; это — пример размышления о системе. В человеческих делах часто почти невозможно точно отделить работу внутри системы от ее анализа. Два способа работы с формальными системами мы будем называть механический режим (способ М) и интеллектуальный режим (способ I). Каждой букве системы MIU соответствует один из режимов. В дальнейшем я опишу последний режим — ультра-режим (режим U), свойственный дзен-буддистскому подходу к вещам.
Глава 2. Содержание и форма в математике
Рассмотрим вторую формальную систему pr. В этой системе три символа: p r – (две английские буквы и тире). Система pr имеет бесконечное множество аксиом. Определение: хр–rх– является аксиомой, когда х состоит только из тире. Система pr имеет только одно правило вывода: пусть х, у и z — строчки, состоящие только из тире. Пусть xpyrz является теоремой. Тогда xpy–rz– также будет теоремой. Пусть, например, х – –, у – – –, z –. Правило говорит нам: если – – p – – – r – является теоремой, то и – – p – – – – r – – тоже теорема.
Вернемся к алгоритму разрешения. Для того, чтобы строчка считалась теоремой, первые две группы тире в сумме должны давать третью группу. Возможно, у вас уже мелькнула мысль, что теоремы pr напоминают сложение. Строчка – – p – – – r – – – – – является теоремой, потому что 2 плюс 3 равняется 5. Может быть, вы даже подумали, что теорема – – p – – – r – – – – – не что иное как записанное необычной нотацией утверждение, означающее, что 2 плюс 3 равняется 5. На самом деле я нарочно выбрал буквы р и r, чтобы напомнить вам о словах «плюс» и «равняется». Так что же, строчка – – p – – – r – – – – – на самом деле означает «2 плюс 3 равняется 5»? Что заставляет нас думать подобным образом? Мне кажете, что в этом виноват замеченный нами изоморфизм между системой pr и сложением (изоморфизм – трансформация, сохраняющая информацию).
Специалисты пытаются создать такую формальную систему, теоремы которой изоморфно отражали бы какие-либо фрагменты действительности. В этом случае выбор символов так же важен, как выбор типографских правил вывода. Задумав систему pr, я очутился как раз в таком положении. Читателю, вероятно, уже понятно, почему я выбрал именно такие символы. Теоремы системы pr не случайно изоморфны сложению; это получилось потому, что я искал способ представить сложение типографским путем (можете попытаться выбрать интерпретации, отличные от моей).
Нам придется различать два типа интерпретаций формальных систем. Во-первых, мы можем говорить о незначащей интерпретации, которая не устанавливает никакой изоморфной связи между теоремами системы и реальностью. Другой тип интерпретации может быть назван значащим. В такой интерпретации, теоремы и истины совпадают — то есть, между теоремами и фрагментами реального мира существует изоморфизм. Поначалу абстрактные символы неизбежно приобретают некое значение, по крайней мере, если мы находим какой-либо изоморфизм
А теперь я хочу рассеять ваши иллюзии по поводу того, что мы нашли единственно правильное значение для символов системы pr. Рассмотрим следующее соотношение [формы и смысла]:
- р <==> равняется
- r <==> отнятое от
- – <==> один
- – – <==> два и т. д.
Теперь – – p – – – r – – – – – приобретает новое значение: «2 равняется 3 отнятым от 5». Ясно, что глупо спрашивать, какое из двух значений является истинным на самом деле. Любая интерпретация истинна, если только она аккуратно отражает определенный изоморфизм с действительностью. Когда какие-либо аспекты действительности (в данном случае, сложение и вычитание) изоморфны между собой, одна и та же система может быть изоморфна обоим этим аспектам и в результате иметь два пассивных значения.
Возможно ли заключить всю теорию чисел в рамки одной формальной системы? Действительно ли числа так чисты, ясны и регулярны, что их природа может быть полностью описана правилами какой-либо формальной системы? Картина «Освобождение», одно из самых прекрасных произведений Эшера, иллюстрирует этот удивительный контраст между формальным и неформальным и поразительную зону перехода между ними (рис. 6).
Рис. 6. Эшер. Освобождение
Глава 3. Рисунок и фон
Умножение (немного более сложное понятие, чем сложение) также можно уловить в сети типографских правил. Назовем такую систему ur (u = «умноженное на»). Предположим, что X, Y, Z — это количество тире в строчках х, у, z. Мы хотим, чтобы строчка xuyrz была теоремой только в том случае, когда X, умноженное на Y, равняется Z. Например, – – u – – – r – – – – – – должно быть теоремой, так как 2, умноженное на 3, равняется 6. Аксиома системы ur: хu–rх является аксиомой, когда х — строчка, состоящая из тире. Правило вывода: предположим, что х, у, z — строчки тире, и что хuуrz – старая теорема. Тогда xuy–rzx будет новой теоремой.
Попробуем составить формальную систему для простых и составных чисел. Используя систему ur, определим новое множество теорем вида Sx (S – составные числа), которые характеризуют составные числа. Правило: предположим, что х, у, z — строчки тире. Если x–uy–rz является теоремой, то Sz также будет теоремой. Это означает, что Z (число тире в z) является составным, если оно — произведение двух чисел, больших единицы (а именно, Х+1 – число тире в х– и Y+1 – число тире в у–).
Весьма соблазнительно от теорем типа S сразу перескочить к теоремам типа Р (Р – простые числа), путем введения следующего правила: предположим, что х — строчка тире. Если Sx не является теоремой, то Рх является теоремой. Роковая ошибка здесь заключается в том, что проверка «нетеоремности» Sx — не типографская операция. Чтобы узнать наверняка, что MU — не теорема MIU, нам пришлось бы выйти из системы.
Теоремы нашей системы Sх: S(4), S(6), S(8), S(9)… «Дырки» в этом списке как раз и являются не-теоремами. Есть ли у них какая-то общая «форма»? Можно ли предположить, что лишь постольку, поскольку они являются пробелами в некотором упорядоченном списке, они обладают какими-то общими чертами? И да, и нет. Нельзя отрицать, что у них есть общие типографские черты; вопрос в том, правомочно ли называть эти черты «формой». Дело в том, что дырки определены только негативно: они представляют из себя то, что осталось от позитивно определенного списка.
Это напоминает известное разграничение между рисунком и фоном в живописи. Когда предмет или «положительное пространство» рисуется внутри рамки, неизбежным следствием этого является появление на картине дополняющей формы, также называющейся «фоном», или «негативным пространством». В большинстве картин отношение между фоном и рисунком почти не играет роли; как правило, художник в основном занят рисунком. Однако иногда его внимание привлекает также и фон (рис. 7).
Рис. 7. Эшер. Деление пространства при помощи птиц
Давайте условимся различать два типа рисунков: курсивно рисуемые и рекурсивные (эти термины не являются общеупотребительными — их придумал я сам). В курсивно рисуемом рисунке фон является лишь побочным продуктом. В рекурсивном рисунке, наоборот, фон может рассматриваться как отдельный самостоятельный рисунок. Приставка «ре» здесь выражает тот факт, что как рисунок, так и фон могут быть нарисованы курсивно, то есть, такая картина «двукурсивна». Любой контур на рекурсивном рисунке — это обоюдоострый меч. М. К. Эшер был мастером подобных картин.
Перенесем понятие рисунка и фона обратно в область формальных систем. В нашем примере роль позитивного пространства играют теоремы типа S, а роль негативного пространства — строчки, в которых количество тире выражается простым числом. Пока что единственный способ, который нам удалось найти для выражения простых чисел типографским путем, это негативное пространство. Существует ли какой-нибудь способ выразить простые числа в виде позитивного пространства, то есть в виде множества теорем некой системы? Интуиция подсказывает разным людям разные ответы. Я отчетливо помню, как был озадачен и заинтригован, заметив разницу между негативной и позитивной характеристиками. Я был совершенно уверен в том, что не только простые числа, но и вообще любое негативно определяемое множество чисел может быть определено позитивно. Интуитивное обоснование моей уверенности заключалось в следующем вопросе: «Как это возможно, чтобы рисунок и фон не содержали совершенно одинаковой информации?» Мне казалось, что они представляют собой одну и ту же информацию, закодированную двумя разными способами (рис. 8).
Рис. 8. Эта диаграмма отношений между различными классами строчек в Типографской Теории Чисел (ТТЧ) весьма богата зрительным символизмом. Самый большой прямоугольник – множество всех строчек ТТЧ. Следующий прямоугольник — все правильно построенные строчки ТТЧ. Внутри него находится множество всех предложений ТТЧ. Именно на этом уровне начинают происходить интересные вещи. Множество теорем изображено в виде дерева, чей ствол — множество аксиом. Символ дерева был выбран из-за того, что оно растет «рекурсивно»; новые ветви (теоремы) вырастают из старых. Пальцеобразные ветви проникают во все уголки области, представляющей множество истинных высказываний, однако они не могут занять эту область целиком. Граница между областями истинных и ложных высказываний представляет собой изломанную «береговую линию», которая, как бы близко вы ее не рассматривали, всегда имеет еще более мелкие уровни структуры и таким образом, не поддается описанию каким-либо конечным методом (подробнее см., например, Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах). Отраженное дерево справа представляет отрицания теорем все они ложны, но вкупе они не в состоянии заполнить всю область ложных высказываний.
Оказывается, что существуют такие формальные системы, чье негативное пространство (множество не-теорем) не является позитивным пространством никакой другой формальной системы. Из этого вытекает следующий результат: существуют такие формальные системы, у которых нет типографского алгоритма разрешения. Из чего это следует? Предположим, что мы нашли множество R (R — рисунок) натуральных чисел, которое мы можем вывести каким-либо формальным путем — вроде множества составных чисел. Предположим, что его дополнением является множество F (F — фон) — простые числа. Вместе взятые, R и F дают все натуральные числа. Мы знаем правило, позволяющее вывести все числа множества R; для чисел множества F такого правила не существует.
Давайте вернемся к этому расплывчатому понятию «формы». Обратимся снова к нашим множествам R — рисунки и F — фон. Легко согласиться с тем, что все числа в множестве R имеют какую-то общую «форму» — но можно ли сказать то же самое о числах множества F? Странный вопрос. С самого начала имея дело с бесконечным множеством всех натуральных чисел, весьма сложно прямо и четко определить «дырки», остающиеся в списке после изъятия оттуда неких чисел. Таким образом, возможно, что на самом деле у этих дырок нет никаких общих характеристик «формы». Неясно, стоит ли вообще использовать здесь такое соблазнительное словечко как «форма». Может быть лучше не определять это понятие, оставив ему некую интуитивную гибкость.
Глава 4. Непротиворечивость, полнота и геометрия
Смысл явный и неявный (рис. 9).
Рис. 9. Наглядное объяснение принципа, лежащего в основе Теоремы Гёделя: два тесно связанных изоморфизма, дающие неожиданный эффект бумеранга. Первый — от звуковых дорожек к звуку, получаемый при помощи патефона. Другой — знакомый всем нам, но обычно оставляемый без внимания — от звука к вибрации патефона. Обратите внимание на то, что второй изоморфизм существует независимо от первого: не только музыка, играемая на патефоне, но и вообще все звуки вблизи от него вызывают в нем вибрацию. Перефразировка Теоремы Гёделя звучит так: для любого патефона существуют такие пластинки, которые нельзя на нем проигрывать, так как это косвенно способствует разрушению патефона.
Тот факт, что в любой достаточно сложной формальной системе истинных утверждений больше, чем теорем, называется «неполнотой» этой системы. Удивительно то, что методы рассуждения, используемые Гёделем в его доказательстве, по-видимому, невозможно заключить в рамки формальных систем. С первого взгляда кажется, что Гёделю впервые удалось выразить необычайно глубокую и важную разницу между человеческой логикой и логикой машины. Это загадочное несоответствие между мощью живых и неживых систем отражено в несоответствии между понятием «истинности» и понятием «теоремности»; таков возможный романтический взгляд на эту ситуацию.
Давайте создадим новую формальную систему, чуть-чуть изменив нашу старую знакомую, систему pr. Добавим к ней еще одну схему аксиом, сохранив при этом как старую схему, так и единственное правило вывода. Схема аксиом 2: Если х является строчкой тире, то хр–rх будет аксиомой. Ясно, что как – – р – r – –, так и – – р – r – – – будут теоремами новой системы. Однако они интерпретируются, соответственно, как «2 плюс 1 равняется 2» и «2 плюс 2 равняется 3». Легко увидеть, что такая система будет содержать массу ложных высказываний (если считать строчку высказыванием). Таким образом, наша новая система противоречива по отношению к окружающему миру. Как говорится, беда не приходит одна в новой системе есть также и внутренние проблемы. Она содержит высказывания, противоречащие друг другу, такие как – р – r – – (старая аксиома) и – р – r – (новая аксиома). Так что же, лучше совсем отказаться от новой системы? Ни в коем случае! Я нарочно описал эти «противоречия» в «лапшевешательном» стиле, изложив довольно туманные аргументы с уверенностью, призванной запутать читателя. Вполне возможно, что вы уже заметили ошибки в моих рассуждениях. Основная ошибка состоит в том, что я безоговорочно принял для новой системы ту же интерпретацию, что была верна для прежней системы.
Вспомните, что мы тогда остановились на словах «плюс» и «равняется» только потому, что в такой интерпретации символы действовали изоморфно понятиям, с которыми мы их сравнивали. Когда мы изменяем правила системы, этот изоморфизм неизбежно страдает. С этим ничего не поделаешь. Таким образом, проблемы, на которые я жаловался в предыдущих абзацах, могут рассеяться как дым, как только мы найдем подходящую интерпретацию для некоторых символов новой системы. Обратите внимание, что я сказал «некоторых» – совсем не обязательно в каждом случае менять интерпретацию всех символов. Некоторые из них могут сохранить прежнее значение, в то время как другие изменятся. Предположим, например, что мы интерпретируем по-новому лишь символ r, оставляя все остальные символы без изменения; в частности, символ r будет означать «больше или равно». Теперь наши «противоречивые» теоремы – р – r – и – р – r – – звучат совершенно безобидно: «1 плюс 1 больше или равно 1» и «1 плюс 1 больше или равно 2». Мы одновременно избавились от противоречий (1) с окружающим миром и (2) внутри системы. К тому же, наша новая интерпретация значима, в то время как прежняя не имела смысла.
Эвклид привел пять постулатов, легших в фундамент геометрии. Четыре первые постулата кратки и элегантны:
- Любые две точки могут быть соединены отрезком прямой;
- Любой отрезок прямой может быть продолжен бесконечно и превращен в прямую линию;
- На основе любого отрезка прямой можно нарисовать круг, принимая этот отрезок за радиус и один из его концов — за центр круга;
- Все прямые углы конгруэнтны.
Пятый постулат далеко не так грациозен: если две прямые пересекают третью так, что сумма внутренних углов с одной стороны меньше двух прямых углов, то это прямые неизбежно пересекутся на этой стороне.
Хотя Эвклид нигде не сказал об этом прямо, он считал свой пятый постулат в каком-то смысле хуже других, поскольку он нигде не использовал его в доказательстве первых двадцати восьми утверждений. Таким образом, мы можем сказать, что эти утверждения составляют так называемую «геометрию четырех постулатов» — ту часть геометрии, которая может быть выведена на основе первых четырех постулатов «Элементов», без помощи пятого (ее также часто называют абсолютной геометрией).
Открыватели неэвклидовой геометрии не отрицали пятого постулата прямо; вместо этого они отрицали эквивалентный, так называемый параллельный постулат: через точку, лежащую вне прямой, можно провести одну и только одну прямую, не пересекающуюся с первой прямой, сколько бы мы их не продолжали. В таком случае мы говорим, что вторая линия параллельна первой. Предполагая, что таких линий вообще не существует, вы входите в область эллиптической геометрии; утверждая же, что таких прямых существует по крайней мере две, вы оказываетесь в гиперболической геометрии. Говоря об этих вариантах, мы все еще используем термин «геометрия» поскольку в них присутствует основной элемент — абсолютная геометрия или геометрия четырех постулатов. Именно это «ядро» позволяет нам считать, что эти варианты — описания свойств некого геометрического пространства, хотя это пространство не так легко интуитивно представить, как обычное (см. также Леонард Млодинов. Евклидово окно).
Мы начали с введения формальной системы, которая, на первый взгляд, не только находилась в противоречии с внешним миром, но и имела внутренние противоречия. Однако через несколько минут нам пришлось взять эти «обвинения» обратно и признать свою ошибку; оказывается, дело было в том, что мы выбрали неудачную интерпретацию для символов системы. Изменив интерпретацию, мы вернули системе ее непротиворечивость! Становится ясно, что непротиворечивость — не свойство формальных систем как таковых, но зависит от интерпретации, предложенной для данной системы. Совершенно так же не является свойством формальных систем как таковых и противоречивость.
Разные виды непротиворечивости. Все это время мы говорили о «непротиворечивости» и «противоречивости», не давая определений этим понятиям. При этом мы опирались на старый добрый здравый смысл. Давайте теперь точно определим, что имеется в виду под непротиворечивостью формальной системы (вместе с ее интерпретацией). Это означает, что каждая теорема, будучи интерпретирована, становится истинным утверждением. С другой стороны, если среди интерпретированных теорем найдется хоть одно ложное утверждение, мы говорим о противоречивости данной системы.
Формальные системы часто строятся по последовательному или иерархическому типу. Например, можно придумать Формальную Систему I, с правилами и аксиомами, дающими некие пассивные значения ее символам. Эта Формальная Система I включается в более широкую систему с большим количеством символов — Формальную систему II. И т.д. Именно это и происходит в случае евклидовой геометрии в сравнении с неевклидовой.
Подобным иерархическим образом мы приобретаем новые знания, расширяем наш словарный запас или воспринимаем незнакомые предметы. Это особенно интересно, когда мы пытаемся понять картины Эшера, скажем, такие, как «Относительность» (рис. 10), где часто встречаются совершенно невозможные образы. Можно предположить, что в таком случае мы должны пытаться интерпретировать картину снова и снова, пока не найдем непротиворечивой интерпретации — однако мы поступаем совершенно иначе. Мы сидим перед картиной, заинтригованные лестницами, ведущими во всех воображаемых направлениях, и людьми, идущими по одной и той же лестнице в противоречащих друг другу направлениях. Лестницы являются тем «островком уверенности», на котором мы основываем нашу интерпретацию всей картины. Увидев в них знакомый предмет, мы пытаемся затем установить, как они связаны друг с другом. На этом этапе мы сталкиваемся с проблемой. Однако если бы мы попытались отказаться от своих взглядов и поставить под сомнение сами «островки уверенности», то столкнулись бы с трудностями иного рода. Мы никак не можем «перерешить» то, что лестницы — это лестницы. Не рыбы, кнуты или руки, а именно лестницы. (На самом деле, выход у нас все-таки есть: можно оставить все линии картины вообще без интерпретации, как «бессмысленные символы» формальной системы. Этот путь — пример «способа U», или отношения дзен-буддизма к символизму.)
Рис. 10. Эшер. Относительность
Таким образом, иерархическая природа нашего восприятия заставляет нас видеть либо сумасшедший мир, либо кучу бессмысленных линий. Когда зритель видит парадокс на высшем уровне, уже поздно возвращаться и пытаться поменять исходные интерпретации объектов нижнего уровня. Могут ли существовать миры, в которых противоречия — нормальное и обыденное явление, миры, где противоречия не являются противоречиями? Если мы хотим хоть как-то общаться, то, по видимости, нам придется установить некую общую базу, включающую логику. (Существуют системы верований, отрицающие подобную точку зрения за то, что она слишком логична. В частности, дзен-буддизм с одинаковой готовностью принимает как противоречия, так и непротиворечия. Это может показаться непоследовательным, но непоследовательность — органическая часть дзен-буддизма; ну что тут можно сказать?)
Большинство современных математиков считают, что центральная теория чисел существует; вкупе с логикой она является необходимой частью всех возможных миров. Эта сердцевина теории чисел, соответствующая абсолютной геометрии, называется арифметика Пеано, ее определение будет дано в главе 8. Также уже точно установлено, что теория чисел действительно разветвляется на стандартную и нестандартные версии (это прямое следствие теоремы Гёделя). В отличие от ситуации с геометрией, однако, количество «сортов» теории чисел бесконечно, что делает положение с ней значительно более сложным.
Эйнштейн открыл общую теорию относительности, утверждающую, что геометрия вселенной определяется количеством материи, в ней содержащейся — таким образом, никакой тип геометрии не присущ пространству как таковому. Это значит, что на вопрос «какой тип геометрии является истинным?» природа дает двусмысленный ответ.
Если непротиворечивость — это минимальное условие, при котором символы приобретают пассивные значения, то ее дополнение, полнота — максимальное признание этих пассивных значений. Непротиворечивость означает, что «все, что производит система, истинно»; полнота же, наоборот, утверждает, что «все истинные утверждения производятся данной системой». Более точное определение полноты следующее: каждое истинное утверждение, которое может быть выражено в нотации данной системы, является теоремой.
- Непротиворечивость: когда каждая теорема, будучи интерпретирована, оказывается истинной (в каком-либо из возможных миров).
- Полнота: когда все утверждения, которые истинны (в каком-либо из возможных миров) и выразимы в виде правильно сформированных строчек системы, являются теоремами.
Теорема Гёделя о неполноте говорит, что любая «достаточно мощная» система уже в силу своей мощности является неполной, в том смысле, что имеются хорошо сформированные строчки, которые выражают истинные утверждения теории чисел, не являясь при этом теоремами (иными словами, в теории чисел имеются истинные утверждения, не доказуемые внутри самой системы). Если система непротиворечива, но не полна, то существует несоответствие между символами системы и их интерпретациями.
Глава 5. Рекурсивные структуры и процессы
Что такое рекурсия? Рекурсия — весьма общее понятие (рассказы внутри рассказов, фильмы внутри фильмов, картины внутри картин, матрешечки внутри матрешек (даже скобки внутри скобок!). [2]
Проталкивание, выталкивание и стек. Протолкнуть означает прервать работу над очередным делом, при этом не забывая, на чем вы остановились, и начать работать над следующим заданием. Обычно говорят, что новое дело находится на «низшем уровне» по сравнению с предыдущим занятием. Вытолкнуть означает обратное: прекратить работу на одном уровне и вновь приняться за работу на высшем уровне, начав с того, на чем вы остановились. Как же нам удается точно помнить, где мы были на каждом уровне? Для этого мы сохраняем нужную информацию в стеке. Таким образом, стек — это просто табличка, сообщающая нам 1) на чем было прервано каждое незаконченное занятие (на компьютерном жаргоне это называется «обратный адрес») и 2) какие факты нам надо знать о моменте, когда задание было прервано («переменная связка»). Когда вы выталкиваетесь наверх, чтобы возобновить работу над чем-либо, именно стек восстанавливает ваш контекст, чтобы вы не потерялись.
Знаменитый ряд чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Этот ряд был открыт в 1202 году Леонардом из Пизы, сыном Боначчи — отсюда Филиус Боначчи или, сокращенно, Фибоначчи. Это числа описываются рекурсивно, с помощью следующей пары формул:
FIBO(n) = FIBO(n – 1) + FIBO(n – 2) для n > 2
FIBO(2) = FIBO (1) = 1
Закон Хофштадтера. На любое дело требуется больше времени, чем казалось в начале, даже если вы учитывали при этом закон Хофштадтера.
Глава 6. Местонахождение значения
Ранее мы сформулировали вопрос: «Когда две вещи похожи друг на друга?» Сейчас мы рассмотрим оборотную сторону этого вопроса: «Когда одна и та же вещь не похожа сама на себя?» Мы попытаемся выяснить, присуще ли значение самому сообщению или же оно всегда порождается взаимодействием разума (или механизма) с этим сообщением. Я постараюсь показать универсальность по крайней мере некоторых сообщений, не утверждая этого для всех сообщений вообще. Идея «объективности значения» некоего сообщения интересным образом соотносится с тем, насколько легко может быть описан разум.
Рассмотрим пример генетической информации, содержащейся в двойной спирали дезоксирибонуклеиновой кислоты (ДНК). Молекула ДНК — генотип — превращается в физический организм — фенотип — путем весьма сложного процесса, включающего выработку белков, воспроизведение ДНК, воспроизведение клеток, постепенное различение типов клеток, и т.д. Процесс превращения генотипа в фенотип — эпигенез — представляет собой пример наиболее запутанной из запутанных рекурсий. Эпигенез зависит от множества сложнейших химических реакций и петель обратной связи. К тому времени, когда создание организма закончено, его физические характеристики не имеют ни малейшего сходства с его генотипом.
Структура ДНК содержит информацию о структуре фенотипа — иными словами, эти структуры изоморфны. Это пример экзотического изоморфизма; я имею в виду, что разделить фенотип и генотип на «части», которые могут быть отображены друг в друге — весьма нетривиальная задача. Напротив, прозаическим изоморфизмом являлся бы такой, в котором части двух структур отображались бы друг в друге без труда. Пример тому — изоморфизм между пластинкой и музыкальным произведением – мы знаем, что для каждого звука в произведении существует его точное «изображение» в структуре звуковых дорожек и что, если потребуется, его можно всегда аккуратно указать.
Изоморфизм между структурой ДНК и структурой фенотипа необыкновенно сложен. Например, было бы весьма трудно найти ту часть ДНК, которая в ответе за форму вашего носа или кончиков пальцев. У нас имеются два противоречивых взгляда на природу информации в генотипе. Один из них утверждает, что, поскольку большое количество информации содержится вне ДНК, мы должны рассматривать ДНК не более как очень сложный набор пусковых механизмов, что-то вроде кнопок на музыкальном автомате; другой взгляд — что вся информация содержится в ДНК, только в очень неявной форме. Выражая ту же мысль короче, первый взгляд утверждает, что для выяснения значения ДНК необходим химический контекст; другая точка зрения утверждает, что для раскрытия присущего ДНК значения необходим только разум.
Еще один блестящий пример расшифровка старинных текстов, написанных на неизвестных языках и алфавитах. После того, как письменность или язык текста оказываются расшифрованными, никто не сомневается, что значение лежит в самом тексте, а не в методах расшифровки — так же как музыка «живет» в записи, а не в проигрывателе. Именно так мы и определяем декодирующие механизмы они не добавляют никакого значения к знакам или предметам, которые служат им вводом, они лишь выявляют значение, присущее этим знакам или предметам. В итоге мы можем утверждать, что значение является частью самого предмета постольку, поскольку этот предмет воздействует на разум определенным предсказуемым способом.
Начинает казаться, что от теории «музыкального автомата» нам никуда не деться. Эта теория гласит, что никакое сообщение не имеет присущего ему значения, поскольку, чтобы понять какое-либо сообщение, его надо сначала ввести в «музыкальный автомат»; это значит, что информация, содержащаяся в этом автомате должна быть добавлена к сообщению — только тогда у него появится значение. Идея в том, что, прежде чем понять любое сообщение, нам необходимо сообщение, говорящее нам, как понять это сообщение; иными словами, что существует бесконечная иерархия уровней сообщений, которая не позволяет понять ни одного из них. Однако все мы знаем, что эти парадоксы недействительны, поскольку правила все-таки используются и сообщения понимаются. Как же это происходит?
Это происходит потому, что наш разум не бестелесен; он расположен в физических объектах — в наших мозгах. Их структура сформировалась в процессе долгой эволюции, и их действие подчиняется законам физики. Поскольку они являются физическими телами, наши мозги действуют, не нуждаясь в инструкциях к действию. По-видимому, в нашем мозгу уже есть встроенная «аппаратура», позволяющая нам распознавать сообщения в некоторых объектах — и затем эти сообщения декодировать. Эта минимальная врожденная способность извлекать внутренние сообщения делает возможным в высшей степени рекурсивный, подобный снежному кому, процесс усвоения языков.
Сказанное позволяет нам изменить наше описание того, где находится значение. Мы можем приписать все значения (рамку, внешнее и внутреннее) самому сообщению, поскольку сами декодирующие механизмы универсальны.
Земной шовинизм. Было бы прекрасно, если бы могли определить разум как-нибудь иначе, чем «то, что интерпретирует символы таким же образом, как и мы». Ведь если это — единственное определение, которое мы можем дать разуму, то наше доказательство неотъемлемости значения было бы круговым, а, следовательно, свободным от содержания. Мы должны попытаться определить множество характеристик, заслуживающих имя «разума», независимым способом.
Основная проблема, с которой мы сталкиваемся, и которая весьма напоминает проблему двух пластинок, формулируется следующим образом: «Какое количество контекста, необходимого для понимания данного сообщения, может быть восстановлено на основе самого этого сообщения?»
Глава 7. Исчисление Высказываний
В этой главе автор предлагает типографскую (формальную) систему для высказываний русского языка. Одна из полученных теорем имеет очень странную частичную интерпретацию: из Р и не Р вместе взятых следует Q. Поскольку Q можно интерпретировать любым предложением, мы можем считать, что эта теорема утверждает, что «из противоречия следует что угодно»! Поэтому системы, основанные на исчислении высказываний, не могут содержать противоречий — противоречия мгновенно заражают всю систему, подобно глобальному раку.
Это не похоже на человеческую мысль. Если вы обнаружите в своих рассуждениях противоречие; вряд ли это разрушит все здание вашего мышления. Вместо этого вы, скорее всего, попытаетесь найти те идеи или методы рассуждения, которые явились причиной противоречия. Иными словами, вы попытаетесь, насколько это возможно, выйти из ваших внутренних систем, приведших к противоречию, и попробуете их исправить. В действительности, противоречия — это важный источник прогресса во всех областях жизни, и математика не является исключением.
Глава 8. Типографская теория чисел
Построение Гёделя состоит из описания как формы, так и содержания строчек формальной системы, которая описана в этой главе — Типографской Теории Чисел. Неожиданный поворот состоит в том, что при помощи хитроумного отображения, открытого Гёделем, форма строчек может быть описана в самой формальной системе.
Глава 9. Мумон и Гёдель
С тех пор, как на первом курсе университета профессор английской литературы прочитал нам «МУ» Джошу, я начал бороться с дзен-буддистскими аспектами жизни и, наверное, никогда не перестану. Для меня дзен подобен зыбучим пескам — анархия, темнота, бессмыслица, хаос. Одна из главных идей дзен-буддизма в том, что его невозможно определить. Буддизм не приемлет слова. Буддистские коаны — центральная часть изучения дзена, хотя они и состоят из слов. Коаны призваны служить «триггерами» — сами по себе они не содержат достаточно информации, чтобы вызвать Просветление, но могут привести в действие внутренние механизмы, ведущие к Просветлению. Но в общем дзен утверждает, что слова и истина несовместимы — словами невозможно уловить истину.
Возможно, чтобы лучше выразить эту идею, монах Мумон (что в переводе означает «Нет выхода»), живший в тринадцатом веке, собрал сорок восемь коанов, снабдив каждый из них комментарием и небольшим «стихотворением». Этот труд называется «Безвыходный выход» или «Мумонкан». Те, кто попытаются найти смысл в коанах «Мумонкана», будут горько разочарованы, поскольку как сами коаны, так и комментарии к ним и стихотворения абсолютно туманны. Теория говорит нам, что только отходя от логики, человек может достичь Просветления. Но что же такого плохого в логике? Почему она не позволяет нам совершить скачок к Просветлению? Возможно, что самым коротким определением Просветления было бы следующее – выход за пределы дуализма.
Дуализм настолько же процесс восприятия мира, как и его понимания. Иными словами, человеческое восприятие по своей природе дуалистично — что делает борьбу за Просветление титанической, если не сказать большего. В сердце дуализма, согласно дзену, лежат слова — простые, обыкновенные слова. Использование слов всегда дуалистично — очевидно, что каждое слово представляет собой определенную умозрительную категорию. Отсюда следует, что большая часть дзена посвящена борьбе против доверия к словам. Одно из лучших оружий в этой борьбе — коан, поскольку со словами он обращается настолько неуважительно, что наш разум тут же забуксует, если мы попытаемся воспринимать коан серьезно. Может быть, неверно говорить, что врагом Просветления является логика; скорее, это дуалистичное, словесное мышление. Или даже еще проще, восприятие. Воспринимая предмет, вы тут же отграничиваете его от всего остального мира; вы делите мир на части и, таким образом, отходите от Пути.
Вот пример коана: Шузан протянул вперед свою короткую палку и сказал: «Если вы скажете, что это короткая палка, то согрешите против действительности. Если вы не скажете, что это короткая палка, то проигнорируете факт. Так что же вы скажете?»
Почему назвать это короткой палкой означало пойти против действительности? Может быть, потому, что подобная категоризация дает иллюзию углубления в действительность, в то время как на самом деле это утверждение даже не поцарапало ее поверхности. Можно сравнить его с утверждением «5 — простое число». Это утверждение оставляет без внимания огромное, бесконечное количество фактов. С другой стороны, не назвать ее короткой палкой — означает проигнорировать этот факт, как бы незначителен он не был. Следовательно, слова ведут к частичной истинности — и, возможно, к частичной ложности — но, безусловно, не к полной истине. Надеяться на слова, чтобы найти истину — все равно, что надеяться на неполную формальную систему, чтобы найти истину. Формальная система даст вам некоторые истины, но, как мы скоро увидим, формальная система, какой бы мощью она не обладала, не может привести ко всем истинным высказываниям. Дилемма математиков такова: на что еще можно опираться, кроме формальных систем? Дилемма последователей дзена такова: на что еще можно опираться, кроме слов? Мумон выражает эту дилемму с предельной ясностью: «Это нельзя выразить словами, и это нельзя выразить без слов».
Если слова — плохи, и мышление — плохо, то что же тогда хорошо? Сущность дзена в том, чтобы подавить восприятие, подавить логическое, словесное, дуалистичное мышление. Это и есть режим U — Ультра. Дзен — это холизм, доведенный до логической крайности. Если холизм (от английского whole — целое) утверждает, что вещи могут быть поняты только как целое, а не как сумма их частей, то дзен идет еще дальше, утверждая, что мир вообще не может быть разделен на части. Делить мир на части — это создавать иллюзии.
Дзен признает свои ограничения, точно так же, как математики научились признавать ограничения аксиоматического метода для нахождения истины. Дзен не знает ответа на то, что лежит за его пределами, так же, как у математиков нет ясного понимания форм рассуждений, лежащих за пределами формализации. В своих сомнениях относительно восприятия и своей любви к абсурдным загадкам без ответа дзен имеет единомышленника — М.К. Эшера. Взгляните на «День и ночь» (рис. 11) — шедевр «переплетения негативного и позитивного» (говоря словами Мумона).
Рис. 11. Эшер. День и ночь
Вспомним главу 1. Обладает ли MU природой теоремы? Согласно приведенным выше наблюдениям, MU — не более как головоломка о натуральных числах, одетая в типографский костюм. Если вы попробуйте подсчитать количество I в теоремах, то вскоре заметите, что оно никогда не равняется 0. Будем называть количество I в каждой строчке величиной I данной строчки. Заметьте, что величина I-аксиомы MI — 1. Правила I и IV совершенно не затрагивают величины I. Так что нам придется иметь дело только с правилами II и III. Правило III уменьшает величину I ровно на 3. Правило II удваивает величину I. Это – ключ к головоломке MU! Мы знаем следующее. Величина I начинается с 1 (1 не делится на 3). Два правила вообще не влияют на величину I. Два оставшихся правила влияют на величину I, но таким образом, что они не могут создать делимое на 3 число, если таковое не дано в начале. Отсюда следует типично «наследственное» заключение: величина I никогда не может стать делимой на 3. В частности, 0 — пример запрещенной величины I. Таким образом, MU не является теоремой системы MIU.
В теорию чисел возможно включить все проблемы о любой формальной системе. Это возможно сделать благодаря открытию Гёделем специального типа изоморфизма. Найдена такая строчка ТТЧ, которая является недвусмысленным высказыванием о некоторых арифметических свойствах натуральных чисел: более того, рассуждая вне системы, мы можем определить не только то, что это высказывание истинно, но и то, что эта строчка не является теоремой ТТЧ. Таким образом, если мы спросим у ТТЧ, истинно ли это высказывание, она не сможет ответить ни да, ни нет.
ЧАСТЬ II. ЭГБ
Глава 10. Уровни описания и компьютерные системы
Одна из основных областей исследования в сегодняшней науке об искусственном интеллекте называется автоматическим программированием. Автоматическое программирование работает над созданием языков наиболее высоких уровней, языков, которых смогут проделывать хотя бы некоторые из следующих удивительных вещей: обобщать на основе примеров, исправлять типографские или грамматические ошибки, пытаться понять двусмысленные описания, при помощи упрощенной модели пытаться угадывать, что на уме у пользователя, задавать вопросы, когда машине что-то непонятно, использовать человеческий язык и т.д. Может быть, со временем удастся найти компромисс между гибкостью и строгостью.
В чем именно состоит разница между программным обеспечением и аппаратурой? Это разница между программами и машинами — между длинными и сложными последовательностями команд и физическими аппаратами, которые эти команды выполняют. Я сказал бы, что программное обеспечение — это «то, что можно передать по телефону», а аппаратура — это «все остальное». Пианино — это аппаратура, а ноты — программное обеспечение. Телефонный аппарат — это аппаратура, а телефонный номер — программное обеспечение. В нас, человеческих существах, тоже есть аспекты «аппаратуры» и «программного обеспечения». Мы привыкли к негибкости нашей физиологии: мы не можем усилием воли вылечить себя от всех болезней или заставить расти у нас на голове волосы любого цвета. Однако мы можем «перепрограммировать» наш мозг, чтобы оперировать в рамках новых понятий.
Существуют аспекты нашего мышления, не поддающиеся контролю. Мы не можем, по желанию, стать сообразительнее; не можем выучить новый язык так быстро, как бы нам хотелось; не можем заставить себя думать о нескольких вещах сразу. Основная цель этой книги — предложить пути примирения между аппаратурой — мозгом и программным обеспечением — интеллектом.
Системы, построенные из многих частей, бывают двух типов. Первый их них характеризуется тем, что поведение одних частей аннулирует поведение других. В подобных системах не столь важно, что делается на низшем уровне, поскольку результатом любых происходящих там событий будет почти одинаковое поведение высшего уровня. Примером такой системы может служить баллон с газом, молекулы которого сталкиваются друг с другом в результате множества сложных микроскопических процессов; однако макроскопическое целое — это стабильная система в спокойном состоянии, в которой определены температура, давление и объем. В системах второго типа микроскопические изменения на низшем уровне могут возрасти до такой степени, что в результате заметно изменится макроскопический уровень. Примером такой системы является сборочный конвейер. Если один из сборщиков ошибется, с конвейера сойдет бракованная деталь.
Системы, состоящие только из «надежных» подсистем, — то есть таких подсистем, чье поведение может быть с уверенностью предсказано на основании описания их частей, — играют важнейшую роль в нашей повседневной жизни, поскольку они являются оплотом стабильности. Мы можем быть уверены, что стены не упадут нам на голову, что тротуар окажется сегодня там же, где вчера, что солнце не исчезнет с небосвода, что часы показывают правильное время и так далее. Блочные модели подобных систем практически полностью детерминистские. Разумеется, другой тип системы, играющей важную роль в нашей жизни, это система, чье поведение варьируется в зависимости от внутренних микроскопических параметров, — зачастую огромного множества таких параметров, — которые не поддаются прямому наблюдению. Наша блочная модель подобной системы будет выражаться в терминах некоего «пространства» ее действия и будет включать вероятностные оценки того, в каком месте этого пространства «приземлится» система в данный момент.
Глава 11. Мозг и мысль
С появлением компьютеров люди начали работать над созданием «думающих машин». Все странности нашего мышления, его слабые и сильные стороны, причуды и изменчивость вышли на поверхность, когда мы получили возможность экспериментировать с самодельными формами мышления. За это время выяснилось много нового о малом и о большом масштабах «аппаратуры» нашего мозга. Мысль должна зависеть от отражения действительности аппаратурой мозга. В предыдущих главах мы разработали формальные системы, отражающие области математической действительности с помощью символов. До какой степени подобные формальные системы могут служить моделями обращения мозга с идеями?
В мозгу есть активные элементы, которые могут хранить информацию, а также передавать ее и получать новую информацию от других активных элементов. Таким образом, у нас есть активные символы вместо пассивных типографских символов. В мозгу правила смешаны с самими символами, в то время как на бумаге символы — это статичные единицы, а правила находятся у нас в голове.
Мы можем изобретать несуществующих людей, придумывая их описания, совместить два описания, обнаружив, что они относятся к одному и тому же человеку, разделить одно описание на два, если обнаружим, что оно относится не к одному, а к двум предметам, и так далее. Это «исчисление описаний» находится в самом сердце мышления. Считается, что оно интенсионально, а не экстенсионально. Это означает, что описания могут свободно «плавать на поверхности», а не стоять на якоре, привязанные к определенным, известным предметам. Интенсиональность мышления связана с его гибкостью, она дает нам возможность изобретать воображаемые миры, соединять разные описания в одно, разделять одно описание на два, и так далее.
Выдумка и факт тесно переплетаются в нашем сознании, и это происходит потому, что мышление предполагает способность к изобретению сложных описаний и манипуляции ими, эти описания совсем не обязательно должны быть привязаны к реальным фактам или вещам. В основе мышления — гибкое, интенсиональное представление о мире. Как же физиологическая система, такая как мозг, позволяет производить подобное представление?
Самые важные клетки мозга — это нервные клетки или нейроны; их в мозгу около десяти миллиардов. У каждого нейрона есть несколько синапсов (на компьютерном жаргоне, «портов ввода»), расположенных на дендритах (и иногда — на теле клетки), и один аксон – «канал вывода» (рис. 12). Ввод и вывод представляют собой электрохимические потоки, то есть движущиеся ионы. Между портом ввода и выводным каналом находится тело клетки, где принимаются «решения». Эти решения, которые нейрону приходится принимать иногда до тысячи раз в секунду, следующего типа: нужно ли ему возбудиться — то есть, послать по аксону ионы. Эти ионы рано или поздно достигнут входных портов других нейронов, которым придется тогда принимать такое же решение. Решение принимается очень просто: если сумма всех входных импульсов превышает некий порог, то нейрон возбуждается; в противном случае этого не происходит. После того, как нейрон возбудится, ему необходимо некоторое время, чтобы «восстановить силы» – обычно это время измеряется миллисекундами, так что нейрон может возбуждаться до тысячи раз в секунду.
Рис. 12. Схема нейрона
Несмотря на сложность входных импульсов, каждый нейрон может ответить одним из двух способов — либо возбуждаясь, либо нет. Это дает весьма небольшое количество информации. Безусловно, чтобы передавать и обрабатывать большой объем информации, необходимо участие множества нейронов. Можно предположить, что существуют более крупные структуры, состоящие из многих нейронов, которые работают с понятиями высшего уровня. Мозг состоит из различных анатомических частей, таких как головной мозг, мозжечок и гипоталамус (рис. 13).
Рис. 13. Человеческий мозг (вид слева)
Головной мозг — это самая большая часть человеческого мозга; он разделен на правое и левое полушария. Снаружи каждое из них покрыто слоями «коры», достигающей толщины в несколько миллиметров; эта оболочка так и называется корой головного мозга. С анатомической точки зрения, именно размеры коры головного мозга — наиболее бросающееся в глаза отличие между мозгом человека и мозгом менее разумных биологических видов.
Известно, например, что языковыми способностями в основном управляет одно из полушарий — обычно левое. Мозжечок — это область, управляющая двигательной активностью. Но каким образом эти области выполняют свои функции, остается загадкой.
Как индивидуальные различия представлены в физиологии мозга? Если мы считаем, что мысленный опыт расположен в мозгу, можно ли найти те места или те физические подсистемы мозга, где расположены знания и другие аспекты интеллектуальной жизни? Открытия, сделанные до сих пор в области организации мозга, интересны тем, что пока не удалось найти соответствия между крупномасштабной «аппаратурой» и «программным обеспечением высшего уровня». Например, зрительная кора — это крупномасштабная часть аппаратуры, полностью посвященная обработке зрительной информации; однако все известные нам процессы, происходящие там, все еще протекают на низших уровнях. Ничего похожего на узнавание предметов пока в зрительной коре не обнаружено.
Давайте называть гипотетические нейронные комплексы, нейронные модули, нейронные группы, нейронные сети и мультинейронные единицы символами. Символы — отражения понятий в аппаратуре мозга. Активацию символов другими символами можно соотнести с событиями в реальном (или придуманном) мире.
Итак, в наших попытках понять процессы мышления мы столкнулись с двумя основными проблемами. Одна состоит в том, чтобы понять, каким образом активация нейронов на низшем уровне вызывает активацию символов на высшем уровне. Другая проблема — в том, чтобы объяснить активацию символов на высшем уровне, не прибегая при этом к терминологии низшего, нейронного уровня.
Если последнее возможно (как утверждает рабочая гипотеза, лежащая в основе большинства современных исследований по искусственному интеллекту), то интеллект может возникнуть и в других, отличных от мозга, типах аппаратуры. Таким образом, можно представить интеллект как характеристику, отделимую от аппаратуры, в которой она заключается — иными словами, интеллект был бы заключен не в аппаратуре, а в программе. Это означало бы, что явления сознания и интеллекта — это явления высшего порядка в том же смысле, как и многие другие сложные явления природы; они управляются своими законами высшего уровня, которые, разумеется, зависят от низшего уровня, но, тем не менее, могут быть от него отделены. С другой стороны, если бы схемы активации символов оказались совершенно неосуществимыми без нейронов аппаратуры (или их симуляции), это означало бы, что интеллект неотделим от мозга, и что его гораздо труднее объяснить, чем какую-либо другую систему, основанную на иерархии законов на нескольких различных уровнях.
Способность производить примеры на основе классов и классы на основе примеров лежит в основе нашего интеллекта. Это одно из основных различий между процессом мышления человека и процессом мышления других животных. Пчелы и другие насекомые по-видимому не умеют обобщать — то есть развивать новые символы классы на основе примеров, которые показались бы человеку почти идентичными.
В науке об искусственном интеллекте различаются два типа знания: процедурное и декларативное. Знание называется декларативным, если оно хранится в памяти явно, так что к нему имеют доступ не только программист, но и сама программа. Его можно «прочитать», словно энциклопедию. Обычно это значит, что такое знание локализовано, а не распространено по всей памяти. С другой стороны, процедурное знание закодировано не в форме фактов, а в форме программ. Программист может взглянуть на них, и сказать: «Я знаю, что благодаря этим процедурам, программа «умеет» писать русские предложения». Такое процедурное знание обычно разбросано по памяти в виде кусков, и на него невозможно указать пальцем. Это не отдельная деталь, но общее следствие работы программы. Иными словами, кусок процедурного знания — это эпифеномен. [3]
Одним из самых замечательных и трудноописуемых свойств сознания является его способность создавать зрительные образы. С помощью какого волшебства нам удается смешивать два или три образа в один, даже не думая о том, как мы это делаем? Знания о том, как это делается, — один из самых ярких примеров процедурных знаний, поскольку мы почти ничего не знаем о том, что такое зрительные образы. Возможно, что мысленные образы основаны на нашей способности подавлять моторную деятельность. Я имею в виду следующее: когда вы воображаете себе апельсин, в коре вашего мозга могут возникнуть команды взять его, понюхать, осмотреть, и так далее. Ясно, что эти команды не могут быть исполнены, поскольку апельсин находится только у вас в воображении. Но они могут быть направлены по обычным каналам в мозжечок или другие подсистемы мозга, пока в некий критический момент «мысленный кран» не закрывается, предотвращая действительное исполнение команд. В зависимости от того, насколько далеко расположен этот «кран», образы могут казаться более или менее жизненными и натуральными.
Глава 12. Разум и мысль
Теперь, когда мы выдвинули предположение о существовании в мозгу активных подсистем высшего уровня (символов), мы можем вернуться к вопросу о возможном изоморфизме, полном или частичном, между двумя мозгами. С самого начала ясно, что 100%-ного изоморфизма между любой парой человеческих существ не существует, так как это означало бы, что мысли одного из них полностью совпадают с мыслями другого. Чтобы это было так, их память также должна быть идентичной — то есть они должны вести абсолютно одинаковую жизнь. Даже однояйцевые близнецы весьма далеки от такой идеальной ситуации.
А как насчет одного-единственного индивида? Когда вы перечитываете то, что сами написали несколько лет назад, то зачастую думаете: «Какой ужас!» — и улыбаетесь, удивляясь тому, какими когда-то были. Хуже того, иногда вы реагируете таким образом на то, что сказали или написали пять минут тому назад. Когда это происходит, это значит, что вы не совсем понимаете того человека, каким были несколько мгновений назад. Между мозгами людей, которые мыслят схожим образом, существует некий частичный изоморфизм на уровне программ — в частности, изоморфизм между (1) репертуаром символов и (2) способами их активации.
Почему так важно, являются ли два мозга изоморфными, или почти изоморфными, или не изоморфными вообще? Ответ в том, что мы интуитивно чувствуем, что, хотя другие люди сильно отличаются от нас, они все же «такие же» как мы на некоем глубоком и важном уровне. Было бы очень заманчиво найти эту неизменную квинтэссенцию человеческого интеллекта и затем описать все возможные «украшения», которые делают каждого из нас единственным и неподражаемым воплощением этого загадочного качества под названием «разум».
Большая часть любой человеческой сети символов универсальна. Мы не замечаем в другом человеке тех стандартных общих качеств, которые принимаем за должное, признавая его «человечность»; игнорируя это основное сходство, мы обычно находим важные различия. Сравнивая нашу сеть символов с сетью француза или немца, мы надеемся найти у них некий похожий стандартный набор символов, несмотря на разницу в языках.
Хотя мы должны признать, что на мышление в большой степени влияет культура, мы не должны переоценивать роль языка в формировании мыслей. Например, то, что мы можем назвать двумя «столами», для англичанина может быть объектами двух разных классов table и desk (стол и письменный стол). Люди, чей родной язык английский, острее, чем мы, воспринимают эту разницу, с другой стороны, люди, выросшие в деревне, острее воспринимают разницу между мерином и жеребцом, в то время как горожанин может назвать их одним словом — «конь». Разница в восприятии возникает из-за разницы не столько в языке, сколько в культуре (или субкультуре). Это в большой степени определяется внешними обстоятельствами. В зависимости от обстоятельств один и тот же мозг может породить две полностью противоречивые мысли.
Правильное прочтение состояния мозга может дать нам лишь условное описание выбора маршрутов. Таким образом, блочное описание состояния мозга представляет собой список возможных мыслей и эмоций, которые могут возникнуть в зависимости от обстоятельств. Пытаться обобщить чьи-нибудь идеи и убеждения, не учитывая при этом контекста, так же наивно, как рассуждать о возможном потомстве одного человека, не упоминая о его партнере. Сознание — это прямое следствие сложной аппаратуры и программного обеспечения мозга. Парадоксы интеллекта возникают потому, что разумное существо может воспринимать самого себя, так же как другие вещи, но при этом оно не является делимым на части. Одним из основных свойств нашего разума является его способность размышлять о себе самом и критически воспринимать собственные действия — и для этого не требуется никакая дополнительная часть.
Главным вопросом спора о машинном интеллекте является не то, как возникает разум, а то, как он оперирует. Основным тезисом механистов является то, что модель интеллекта должна действовать согласно «механическим принципам»; это означает, что действие целого может быть понято, исходя из действия его частей, и что действие каждой отдельной части должно либо определяться ее начальным состоянием и конструкцией машины, либо быть случайным выбором между определенным числом определенных операций. Если машина становится такой сложной, что это определение перестает действовать, тогда мы уже не можем считать ее машиной, как бы она ни была построена. Тогда пришлось бы сказать, что мы создали разум. Мы должны подчеркнуть, что, хотя наши создания выглядели бы как машины они тем не менее таковыми бы не являлись поскольку они были бы большим, чем сумма их частей. Было бы невозможным предсказать их поведение на основе знания их конструкции и начального состояния их частей. Мы не знали бы границ того на что они способны поскольку они отвечали бы верно даже на заданные им вопросы Геделева типа. На самом деле нужно отметить что любая система, которую не сбить с толку Геделевым вопросом это не машина Тьюринга то есть не машина в обычном смысле слова.
Глава 13. Блуп, Флуп и Глуп
Блуп, Флуп и Глуп — это не имена гномов, не разговоры лягушек в пруду и не бульканье воды в засорившейся раковине. Это компьютерные языки, каждый из которых имеет особое предназначение. [4] Блуп – язык программирования, использующий только конечные циклы. С помощью диагонального метода Кантора можно показать, что на Блупе нельзя выразить все действительные числа (о диагональном методе см. Чарльз Петцольд. Читаем Тьюринга). Действительные числа не перечислимы.
Флуп – язык, отличающийся от Блупа тем, что содержит бесконечные циклы. Но и на Флупе нельзя выразить все действительные числа. Например, на Флупе невозможно придумать разрешающую процедуру для определения, будет ли та или иная программа останавливаться, или попадет в бесконечный цикл? Все современные языки программирования обладают мощностью Блупа. Попытки разработать еще более мощный язык – Глуп – пока не привели к успеху. По-видимому, Глуп – это химера.
Выражение «вычислимый на Блупе» эквивалентно выражению «примитивно-рекурсивный». С другой стороны, функции, вычислимые на Флупе, можно подразделить на две категории. Функции, вычислимые с помощью кончающихся программ Флупа, называются общерекурсивными; функции, вычислимые только с помощью не кончающихся программ Флупа, называются частично рекурсивными. То же самое применимо и к утверждениям (предикатам.)
Глава 14. О формально неразрешимых суждениях ТТЧ и родственных систем
Название этой главы – адаптация заглавия знаменитой статьи Гёделя, опубликованной в 1931 году; [5] я заменил «Principia mathematica» на ТТЧ. Гёдель написал эту статью строго техническим языком, стараясь дать безупречное доказательство своей теоремы; в этой главе я постараюсь изложить его идеи более интуитивно. Сосредоточусь на двух идеях, лежащих в основе Гёделева доказательства. Первая идея — это открытие того факта, что некоторые строчки ТТЧ могут быть интерпретированы как суждения о других строчках ТТЧ; иными словами, ТТЧ оказалась языком, способным к самоанализу. Этот факт вытекает из Гёделевой нумерации. Вторая идея — это то, что данное свойство может быть сконцентрировано полностью в одной строке: в фокусе такой строки — она сама. Этот прием восходит, в принципе, к диагональному методу Кантора.
Является ли G теоремой ТТЧ? Если это так, то она должна утверждать истинный факт. Но что именно утверждает G? Свою собственную нетеоремность. Следовательно, из ее теоремности вытекала бы ее нетеоремность. Противоречие! С другой стороны, что, если G не теорема? Это можно принять, так как противоречия здесь не возникает. Но G утверждает именно собственную нетеоремность — следовательно, G утверждает истинный факт. Значит, поскольку G не теорема, мы можем заключить, что существует по меньшей мере один истинный факт, не являющийся теоремой ТТЧ.
Поскольку интерпретация G истинна, интерпретация ее отрицания ~G — ложна. Мы знаем, что в ТТЧ невозможно вывести ложные утверждения. Следовательно, ни G, ни ее отрицание ~G не могут быть теоремами ТТЧ. Мы нашли в нашей системе «дыру» — неразрешимое суждение. Пока ТТЧ остается непротиворечивой, ее клятва в собственной непротиворечивости – не теорема. Таким образом, ТТЧ весьма сильна в выражении идей, но слабовата в их доказательстве. Это очень интересный результат, если метафорически приложить его к проблеме человеческого самосознания.
ТТЧ страдает ω-неполнотой. Это означает, что существует некая бесконечная пирамидальная семья строчек, каждая из которых является теоремой — но при этом соответствующая «итоговая» строчка теоремой не является.
Поскольку интерпретация G истинна, интерпретация ее отрицания ~G ложна. Из нашего предположения о непротиворечивости ТТЧ следует, что в ней не могут быть выведены ложные утверждения. Таким образом, ни G, ни ее отрицание ~G не являются теоремами ТТЧ. Мы нашли в нашей системе дыру — неразрешимое суждение. Это означает, что ТТЧ можно дополнить, как можно дополнить абсолютную геометрию. В действительности, ТТЧ, как и абсолютную геометрию, можно расширить в двух направлениях. Она может быть расширена в стандартном направлении, что соответствует расширению абсолютной геометрии в Эвклидовом смысле; или же, она может быть расширена в нестандартном направлении, что, разумеется, соответствует расширению абсолютной геометрии в неэвклидовом смысле (подробнее см. Леонард Млодинов. Евклидово окно). Стандартным дополнением будет
добавление G в качестве новой аксиомы.
Это кажется довольно безвредным и даже желательным, поскольку G всего-навсего утверждает некую истину о системе натуральных чисел. А как насчет нестандартного расширения? Если следовать аналогии с ситуацией аксиомы параллельности, оно должно означать
добавление отрицания G в качестве новой аксиомы.
Что означала бы добавка ~G в качестве аксиомы ТТЧ? Подумайте только, на что была бы похожа современная математика, если бы люди не решили в свое время добавить к ней аксиом типа:
∃a:(a+a)=S0
∃a:Sa=0
∃a:(a·a)=SS0
∃a:S(a·a)=0
Каждое из этих утверждений означает значительное и замечательное расширения понятия целых чисел: рациональные числа, отрицательные числа, иррациональные числа, мнимые числа. ~G пытается открыть нам глаза на такую возможность. В прошлом каждое новое расширение системы натуральных чисел встречалось в штыки. Это можно заметить по именам, данным непрошенным пришельцам: иррациональные, мнимые. Оставаясь верными традиции, давайте назовем числа, которые порождает ~G, супернатуральными, поскольку они противоречат всем понятиям разума и здравого смысла.
Нестандартная теория чисел не угрожает старому доброму факту, что дважды два — четыре Она отличается от привычной нам теории чисел только тем, как она обращается с понятием бесконечности. В конце концов, любая теорема ТТЧ остается теоремой в любой расширенной версии ТТЧ. Так что банкирам не надо волноваться о том, что с приходом нестандартной теории чисел в финансовом мире воцарится хаос.
Глава 15. Прыжок из системы
В чем же была причина недостатков ТТЧ? Ее уязвимость объяснялась тем, что она была способна говорить о себе самой. В частности, источником неприятностей было высказывание: «Я не могу быть доказано в формальной системе ТТЧ». В случае с формальными системами, неполнота возникает, когда мы определяем предполагаемый рецепт выражения теоретико-численной истины. Именно в этом заключалась проблема ТТЧ. Как только вы вводите все хорошо определенные G в ТТЧ, там тут же появляется некое новое G, непредусмотренное вашей схемой аксиом. Так что же делать? Конца этому не предвидится. Кажется, что ТТЧ, даже если расширять ее до бесконечности, всегда будет оставаться неполной. Поэтому говорят, что ТТЧ непополнима, поскольку неполнота является неотъемлемой характеристикой ТТЧ: это одно из ее основных свойств и избавиться от него невозможно.
Удивительная повторяемость Геделева аргумента использовалась многими — в частности Дж. Р. Лукасом — как оружие для защиты идеи, что человеческий разум отличается неким специфическим качеством, которое невозможно имитировать при помощи «механических автоматов» — то бишь, компьютеров.
Могут ли люди, выйти за пределы самих себя — и могут ли это сделать компьютерные программы? Разумеется, программа может модифицировать себя — но возможность всякой модификации должна быть заложена в программе с самого начала, так что это не может служить примером «выхода из системы». Как бы программа не вертелась и не извивалась, чтобы вырваться за свои пределы, она все же следует заложенным в ней правилам. Она так же не может выйти за пределы самой себя, как человек не может по желанию перестать следовать законам физики. Физика — это система, выхода из которой не существует. Однако возможно осуществить нечто подобное в меньшем масштабе — а именно, выйти из подсистемы собственного мозга в более широкую подсистему. Иногда удается сойти с наезженной колеи. Это все еще объясняется взаимодействием различных подсистем мозга, но на вид это весьма похоже на полный выход из себя. Подобно этому, можно представить, что нам удастся создать программу, умеющую частично «вылезать из своей шкуры».
Однако важно не упускать из вида разницы между восприятием самого себя и выходом из самого себя. Воспринимать себя вы можете различными способами: в зеркале, на фотографиях, в фильмах, на пленке, по описаниям других, по результатам психоанализа и так далее. Но вы не можете выйти из собственной кожи и встать снаружи себя самого. ТТЧ может говорить о себе, но она не может выйти из себя. Компьютерная программа может модифицировать себя, но она не может нарушить своих собственных инструкций — большее, на что она способна, это изменить себя частично, следуя тем же инструкциям.
Глава 16. Авто-реф и авто-реп
В этой главе мы рассмотрим несколько механизмов, порождающих автореференцию в различных контекстах, и сравним их с механизмами, позволяющими некоторым системам самовоспроизводиться (или «авторепродуцироваться»). Вот высказывания, которые на первый взгляд кажутся простейшими примерами автореферентности:
- Это высказывание содержит пять слов
- Это высказывание бессмысленно, так как оно автореферентно
- Это высказывание без глагола
- Это высказывание ложно
Я буду называть самовоспроизводящиеся объекты авто-реп (сокращение от «авторепродукция»), а самоупоминающие объекты — авто-реф (сокращение от «автореференция»).
Самовоспроизводящаяся песня. Представьте себе музыкальный автомат в местном баре; вы нажимаете на кнопку 1-Я, и раздается песня на мотив «Славного моря» с такими словами:
Все, что мне нужно — монетка твоя,
Славная скрасит нам песенка ночку.
Денежку сунь и нажми «1-Я» —
Петь я не буду в рассрочку.
Мы можем нарисовать маленькую диаграмму того, что при этом получается:
Рис. 14. Самовоспроизводящаяся песня
Хотя в результате песня воспроизводится, было бы странно называть ее настоящим авто-репом, поскольку, когда она проходит через стадию 1-Я, в ней находится не вся информация. Информация может быть восстановлена только благодаря тому, что она полностью записана в музыкальном автомате — то есть в стрелках нашей диаграммы, а не в ее овалах. Неясно, содержит ли эта песня полные инструкции, необходимые для ее воспроизводства, поскольку символ 1-Я — не копия, а всего лишь пусковой механизм.
Автореференция ТТЧ очень созвучна с авторепродукцией ДНК (рис. 15).
Рис. 15. Автореференция ТТЧ и авторепродукция ДНК
Глава 17. Чёрч, Тьюринг, Тарский и другие
Один из основных тезисов этой книги – любой аспект мышления можно рассматривать как описание на высшем уровне некой системы, которая на низшем уровне управляется простыми и даже формальными правилами. Под «системой» здесь, разумеется, имеется в виду мозг — если не упоминать мыслительные процессы, протекающие в другой среде, такой, скажем, как электрические цепи компьютера. Это создает образ формальной системы, лежащей в основе «неформальной системы» — такой, которая сочиняет каламбуры, находит численные закономерности, забывает имена, «зевает» фигуры в шахматной партии и так далее. То, что мы видим снаружи, — это ее неформальный, явный уровень, уровень программ. С другой стороны, в системе есть также формальный, скрытый уровень (или «субстрат’), уровень аппаратуры — удивительно сложный механизм, переходящий от одного состояния к другому по определенным, физически встроенным в него правилам, согласно поступающим извне сигналам (входным данным).
Из этого взгляда, как кажется, следует то, что в своей основе мозг является неким «математическим» объектом. На самом деле, это, в лучшем случае, довольно неуклюжая модель мозга. Дело в том, что даже если в техническом и абстрактном смысле мозг и представляет собой некий тип формальной системы, математики работают с системами простыми и элегантными, в которых все четко определено. Мозгу же, с его десятью миллиардами частично независимых нейронов, соединенных почти случайным образом, далеко до такой ясности, так что он никогда не станет объектом изучения математиков. Если определить «математику» как нечто, чем математикам нравится заниматься, то приходится признать, что свойства мозга — не математические.
Цель искусственного интеллекта (ИИ) — понять, что происходит, когда в мозгу из мириад возможностей делается бесшумный и невидимый выбор той единственной, которая кажется наиболее подходящей в данной сложной ситуации. Во многих жизненных ситуациях дедуктивные рассуждения не годятся — не потому, что они привели бы к неправильным ответам, но потому, что существует огромное множество истинных, но неважных для данной ситуации суждений; приходится принимать в расчет слишком много факторов, и потому логические рассуждения оказываются неэффективными.
Здесь необходимо понимание того, что важно и что неважно; с этим связано чувство простоты и красоты. Откуда берутся эти интуитивные понятия? Каким образом они могут родиться из формальной системы мозга?
ТЕОРЕМА ЧЁРЧА: Не существует универсального метода, позволяющего отличать теоремы ТТЧ от не-теорем.
Это утверждение было доказано в 1936 году американским логиком Алонзо Чёрчем, оно находится в тесной связи с тем, что я называю
ТЕОРЕМОЙ ТАРСКОГО-ЧЁРЧА-ТЬЮРИНГА: Не существует универсального метода, позволяющего отличать истинные суждения теории чисел от ложных.
Или…
ТЕЗИС ЧЁРЧА-ТЬЮРИНГА, ВЕРСИЯ ИЗОМОРФИЗМА: Предположим, что существует метод, при помощи которого разумное существо может разделять числа на два класса. Предположим также, что этот метод всегда приводит к ответу за конечный отрезок времени и что этот ответ — всегда один и тот же для одного и того же числа. Тогда существует некая конечная программа на Флупе (то есть, некая общерекурсивная функция), которая будет давать точно такие же ответы, как и разумное существо. Более того, мыслительный процесс и эта программа Флупа будут изоморфны в том смысле что на каком-то уровне будет существовать соответствие между операциями, выполняемыми компьютером и мозгом.
Изоморфизм существует на уровне арифметических действий, а не на уровне нейронов мозга и электрических цепей компьютера.
Одним из способов представлять отношения между высшими и низшими уровнями мозга является следующий. Возможно построить такую нейронную сеть, которая на местном уровне (то есть на уровне отдельных нейронов) работала бы точно так же, как нейронная сеть мозга, но в которой не возникало бы никакого значения на высшем уровне. То, что низший уровень состоит из взаимодействующих нейронов, еще не гарантирует появления значения на высшем уровне, подобно тому, как наличие макаронных буковок в алфавитном супе не гарантирует того, что в тарелке будут плавать слова и предложения. Значение высшего уровня — это факультативная черта нейронных сетей, которая может возникнуть в процессе эволюции, как результат воздействия окружающей среды.
ТЕЗИС ЧЁРЧА-ТЬЮРИНГА, РЕДУКЦИОНИСТСКАЯ ВЕРСИЯ Все процессы, происходящие в мозгу, опираются на субстрат, поддающийся вычислению.
Эта версия Тезиса утверждает, что процесс мышления, хотя он и имеет больше уровней организации, не более загадочен, чем, скажем, процесс пищеварения. В наше время никто не осмелился бы выдвинуть предположение, что люди переваривают пищу не благодаря обыкновенным химическим процессам, а благодаря некой магической и мистической «ассимиляции». Эта версия Тезиса Ч-Т просто применяет те же рассуждения к мышлению Короче, в ней высказывается предположение, что мозговые процессы, в принципе, возможно понять. Поэтому я и назвал это мнение символом редукционистской веры. Это утверждение является, пожалуй, сильнейшей теоретической поддержкой для возможности создания Искусственного Интеллекта.
Рассмотрим еще одну версию Тезиса Т-Ч — версию, с которой молчаливо соглашаются многие люди и которая была по-разному изложена разными авторами К числу самых знаменитых сторонников этой версии принадлежат философы Губерт Дрейфус, С. Жаки, Мортимер Таубе, и Ж. Р. Лукас, биолог и философ Майкл Полани (убежденный холист; подробнее см. Майкл Полани. Личностное знание) и знаменитый австралийский нейрофизиолог Джон Экклз.
ТЕЗИС ЧЁРЧА-ТЬЮРИНГА, ВЕРСИЯ ДУШИ. Некоторые происходящие в мозгу процессы могут быть приблизительно воспроизведены на компьютере — но не большинство этих процессов и, безусловно, не самые интересные из них. Но даже если бы удалось симулировать все процессы мозга, то все равно осталось бы объяснить душу, на что не способен никакой компьютер.
Мысль о «несовместимости иррационального с самим духом компьютеров» основана на серьёзном смешении уровней. Это ошибочное мнение опирается на идею, что поскольку компьютеры — безошибочно функционирующие машины, они, таким образом, должны быть «логичными» на всех уровнях. Однако совершенно очевидно, что компьютер может быть запрограммирован таким образом, чтобы напечатать серию нелогичных высказываний — или, для разнообразия, несколько высказываний со случайными значениями истинности. И все же, следуя подобным инструкциям, компьютер не совершит никакой ошибки! Наоборот, ошибкой было бы, если бы компьютер выдал что-либо отличное от высказываний, которые ему было приказано напечатать. Это показывает, как безошибочная работа на одном уровне может лежать в основе манипуляций символами на высшем уровне — и цель высшего уровня может быть совершенно отлична от провозглашения истины.
Мы можем подвести итоги нашему обсуждению различия между уровнями и дать последнюю, наиболее сильную версию Тезиса Черча-Тьюринга.
ТЕЗИС ЧЁРЧА-ТЬЮРИНГА. ВЕРСИЯ ИИ. Любые мыслительные процессы могут быть симулированы при помощи компьютерной программы, написанной на языке, равномощном Флупу (то есть языке, на котором возможно запрограммировать все частично-рекурсивные функции).
Глава 18. Искусственный интеллект: взгляд в прошлое
В 1950 г. Алан Тьюринг написал дерзкую и пророческую статью об искусственном интеллекте. Она называлась Вычислительные машины и интеллект и была опубликована в журнале Mind. Статья Тьюринга начинается с фразы: «Рассмотрим вопрос: Может ли машина думать?» Поскольку, как он указывает, эти термины слишком многозначны, очевидно, что мы должны искать практическое решение проблемы. Для этого Тьюринг предлагает игру, которую он называет игрой в имитацию; сегодня она известна под названием тест Тьюринга.
Со времен Паскаля и Лейбница люди мечтали о машинах, способных выполнять интеллектуальные задания. В девятнадцатом веке Буль и Де Морган разработали «законы мысли», по существу являвшиеся Исчислением Высказываний и, таким образом, сделали первый шаг по пути создания программ ИИ, тогда же Чарльз Бэббидж сконструировал первую «вычисляющую машину» — предшественницу компьютерной аппаратуры и, следовательно, ИИ. Можно сказать, что ИИ зарождается в тот момент, когда машины начинают выполнять задания ранее доступные только человеческому уму.
Глава 19. Искусственный Интеллект: виды на будущее
Один из моих друзей сказал мне: «Мой дядя был почти президентом США!» «Правда?! — спросил я. «Конечно», — ответил он, — «он был капитаном торпедного катера ПТ108». (Джон Ф. Кеннеди был капитаном ПТ109.) У нас в голове каждый день рождаются мысленные варианты ситуаций, с которыми нам приходится сталкиваться, идей, которые у нас возникают или событий, происходящих вокруг. При этом некоторые детали остаются без изменений, в то время как другие «сдвигаются». Какие детали мы сдвигаем? Какие нам даже в голову не приходит изменить? Какие события воспринимаются нами на некоем глубинном интуитивном уровне как близкие родственники событий, случившихся на самом деле? Что мы считаем «почти» случившимся, чем-то, что «могло» случиться, хотя совершенно точно знаем, что в действительности этого не произошло? Какие альтернативные версии событий сами собой возникают у нас в мозгу, когда мы слышим какой-нибудь рассказ? Совершенно ясно, что чего не было, того не было. У «неслучаемости» нет никаких степеней. То же самое верно и в отношении «почти» случившихся ситуаций. Мы часто жалуемся, что какое-то событие «чуть не случилось»; не менее часто мы произносим те же слова с облегчением. Но это «чуть не» находится в нашем мозгу, а не во внешних фактах. Мне кажется, что гипотетические «почти» ситуации и бессознательно вырабатываемые возможные миры представляют из себя один из богатейших источников информации о том, каким образом люди организуют и классифицируют свои впечатления о мире.
Создание «гипотетических миров» происходит настолько случайно и естественно, что мы почти не отдаем себе отчета в том, что делаем. Мы выбираем из всех воображаемых миров тот, который в каком-то внутреннем, интеллектуальном смысле ближе всего к реальности.
Термин фрейм (кадр, группа данных) сейчас в моде среди специалистов по искусственному интеллекту; его можно определить, как численное представление данного контекста.
Любопытные задачи предложил в своей книге Проблема узнавания русский ученый Михаил Моисеевич Бонгард. Сформулируйте правила для следующих двух задач (рис. 16): чем отличаются шесть левых фреймов от шести правых?
Рис. 16. Задача Бонгарда: требуется найти правила, отличающие шесть левых фреймов от шести правых
Теория философа Куна о том, что странные события, которые он называет сдвигами парадигмы, отмечают границу между «нормальной» наукой и «концептуальными революциями», не кажется подходящей, поскольку в данной системе сдвиги парадигмы происходят все время и на всех уровнях. Это объясняется гибкостью описаний (подробнее см. Томас Кун. Структура научных революций). Настоящая наука не делится на «нормальные» периоды и периоды «концептуальных революций», сдвиги парадигм происходят в ней постоянно, большие и маленькие, на различных уровнях.
Некоторые проблемы узнавания структур, которые полностью вросли в наше подсознание, довольно удивительны. Они включают:
- узнавание лиц (неизменность лиц при возрастных изменениях, различных выражениях, разном освещении, разном расстоянии, под другим углом зрения и так далее);
- узнавание тропинок в лесах и в горах — почему-то это всегда казалось мне одним из наиболее удивительных случаев узнавания схем. Однако это умеют делать и животные…
- прочтение текста, написанного сотней, если не тысячей различных шрифтов.
Машины (пока) на такое не способны. Перед ИИ лежит долгий путь. Иногда кажется, что, поскольку человеческое поведение настолько сложно, оно не управляется никакими правилами. Но это только иллюзия — все равно, что считать, что кристаллы и металлы появляются на свет, следуя жестким правилам, а жидкости и цветы — нет.
Глава 20. Странные Петли или Запутанные Иерархии
В самом начале я написал, что центральной темой этой книги будет обсуждение вопроса «подчиняются ли слова и мысли формальным правилам»? Одной из моих основных задач было показать многоуровневость интеллекта и мозга и объяснить, почему конечным ответом на этот вопрос является «да, если спуститься на низший уровень — уровень аппаратуры — и найти там правила». Думая, мы, безусловно, меняем наши мысленные правила. Но это правила «программ». При этом фундаментальные правила, правила «аппаратуры», остаются неизменными. Нейроны всегда действуют одинаково. Мы не можем уговорить нейроны повести себя «ненейронным» образом; все, что нам удается сделать, это поменять тему или стиль наших мыслей. Правила программ могут варьироваться на разных уровнях — правила аппаратуры всегда остаются одними и теми же. Именно этим фактом и объясняется гибкость программ! Это вовсе не парадокс, а фундаментальный, простой факт, касающийся механизмов разума.
Я хочу показать, что в каждой системе есть некий «защищенный» уровень, на который не действуют правила других уровней, какими бы запутанными не были их взаимодействия между собой. Вернемся к картине Эшера «Рисующие руки» (см. рис. 3). Здесь левая рука (ЛР) рисует правую руку (ПР), в то время как ПР рисует ЛР. Снова уровни, обычно понимаемые как иерархические — рисующее и рисуемое — замыкаются друг на друга, создавая Запутанную Иерархию. Этот пример, разумеется, подтверждает идею данной главы, поскольку за ним стоит ненарисованная, но рисующая рука самого Эшера — создателя как ЛР, так и ПР. Эшер стоит вне пространства этих рук, и это хорошо видно на рис. 17. Мы могли бы еще раз «Эшеризировать» картину Эшера, сфотографировав рисующую ее руку… и так далее.
Рис. 17. Абстрактная диаграмма, представляющая картину Эшера «Рисующие руки». Внизу приведено ее решение
Теперь мы можем соотнести эту картину с мозгом. Когда мы думаем, символы в нашем мозгу активируют другие символы, и все они взаимодействуют. Более того, символы могут заставить друг друга измениться внутренне и стать чем-то вроде программ, действующих на другие программы. Благодаря Запутанной Иерархии символов, у нас создается иллюзия, что неизменяемого уровня в мозгу не существует. Однако такой уровень есть. Это – мириады нейронов — «неизменного субстрата», лежащего в основе переплетения символов.
Запутанная Иерархия получается тогда, когда строго иерархичные на первый взгляд уровни внезапно начинают действовать друг на друга в нарушение всех правил иерархии. Элемент неожиданности здесь очень важен; именно поэтому я называю Странные Петли «странными». Простое переплетение, такое, как обратная связь, не нарушает установленных различий между уровнями. Например, когда вы стоите под душем и моете правую руку левой рукой и наоборот, это в порядке вещей. Эшер не случайно решил нарисовать руки, рисующие руки!
В языке получаются странные петли тогда, когда он прямо или косвенно говорит сам о себе. Возможно, что нас смущает некое неопределенное чувство топологической неправильности: стирание различия между внутренним и внешним, как в знаменитой бутыли Клейна. Мы чувствуем, что мы самопрограммирующие. Более того, мы и не можем чувствовать иначе, поскольку мы защищены от низшего уровня, уровня нейронных сплетений. Нам кажется, что наши мысли живут в своем собственном пространстве, создавая новые мысли и изменяя старые; мы не замечаем помогающих этому нейронов! Но так и должно быть. Мы просто не можем их заметить.
Аналогия с Теоремой Гёделя, которая кажется мне интересной, намекает на то, что мы не можем полностью понять собственного разума/мозга. Мы не можем увидеть своими глазами собственное лицо; не разумно ли ожидать, что мы также окажемся не в состоянии полностью отразить собственную психическую структуру в тех символах, которые ее составляют? Теорема остановки Тьюринга, Теорема Тарского об истине — все они чем-то напоминают старинные сказки, предупреждающие читателя о том, что «поиск самопознания — это путешествие, которое… обречено быть неполным, не может быть изображено ни на каких картах, никогда не остановится и не сможет быть описано».
Мир слишком сложен, чтобы позволить человеку роскошь примирить между собой все его убеждения. Мигель де Унамуно однажды сказал. «Если кто- то никогда не противоречит сам себе, скорее всего, это потому, что он вообще никогда ничего не говорит.» Я сказал бы, что мы все находимся в том же положении, как тот мастер дзена, который, высказав подряд несколько противоречивых суждений, сказал сбитому с толку Доко: «Я сам себя не понимаю».
Известно, что между двумя языками, субъективным и объективным, большая разница. Например, «субъективное» чувство красного и «объективная» длина волны, соответствующая красному цвету. Многим людям эти языки кажутся в принципе несовместимыми. Я так не считаю. Мне кажется, они не более несовместимы, чем два восприятия Эшеровских рисующих рук. «изнутри системы», где руки рисуют одна другую, и извне, где Эшер рисует обе руки Субъективное ощущение красного появляется благодаря самосознанию в мозгу; объективная длина волны соответствует взгляду извне системы. Хотя никому не удастся выйти из системы настолько, чтобы увидеть «всю картину разом», мы не должны забывать, что такая картина существует. Необходимо помнить, что все это вызвано к жизни физическими законами, глубоко-глубоко в нейронных закоулках и трещинках, куда не достигают наши «зонды», запущенные с высшего уровня наблюдения.
[1] Рисунки Эшера взяты с сайта http://www.mcescher.ru
[2] Рекурсия великолепно воплощена режиссером Кристофером Ноланом в фильме Начало (в главной роли Леонардо Ди Каприо).
[3] Эпифеномен (др.-греч. επι — «при, после, возле» и φαινωμενον — «являющееся») — придаток к феномену, побочное явление, сопутствующее другим явлениям, но не оказывающее на них никакого влияния; термин, применяемый для истолкования сознания как совершенно пассивного, а потому не играющего никакой существенной роли, отражения материального (или идеального) содержания мира. Употребляется представителями естественнонаучного материализма (Т. Гексли, Ф. Ле-Дантек) и некоторыми философами-идеалистами (Э. Гартман, Ницше, Сантаяна), а также сторонниками бихевиоризма.
[4] Я начал читать Хофштадтера в феврале 2014 г., и дошел до 13-й главы. В тот момент я испытал две трудности: читать в электронном виде было неудобно, и, начиная с 13-й главы я стал терять нить повествования. Я решил поискать книгу в бумажном виде. Поиски успехом не увенчались, зато за прошедший год я почитал и про Гёделя, и про Тьюринга (см. Чарльз Петцольд. Читаем Тьюринга). Надо заметить, что у Петцольда многие идеи Хофштадтера изложены более понятно (по крайней мере, на мой взгляд), так что я решил закончить работу над ГЭБ.
[5] Издание этой статьи на русском языке мне найти не удалось.


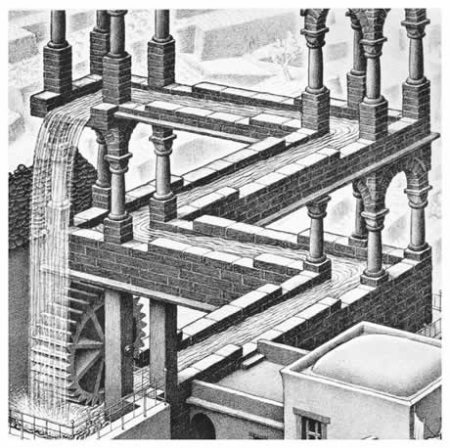
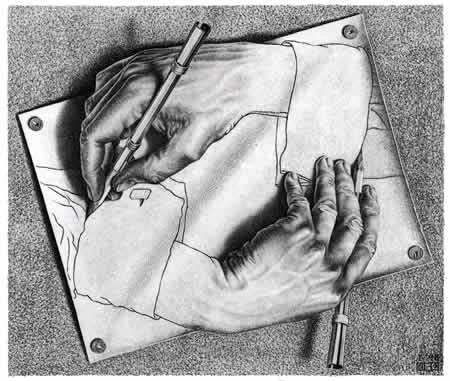




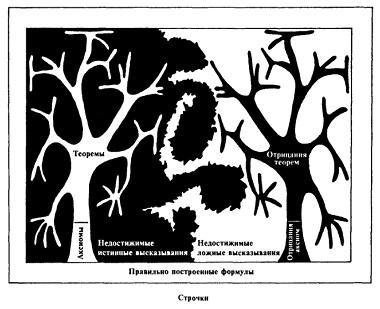
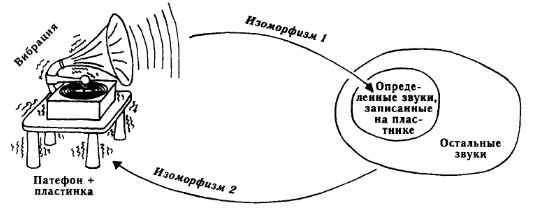


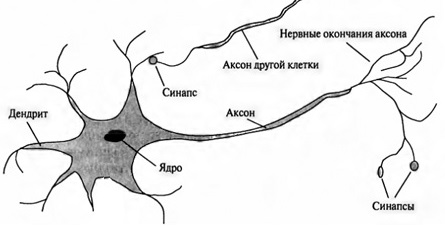
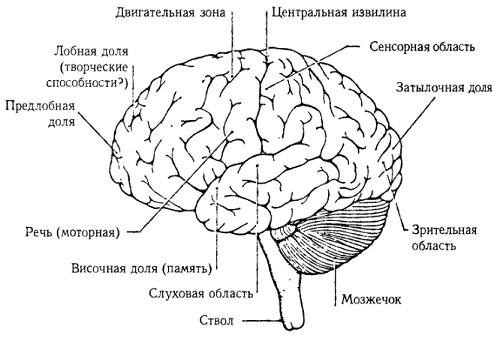
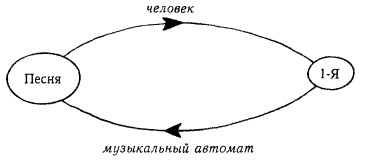
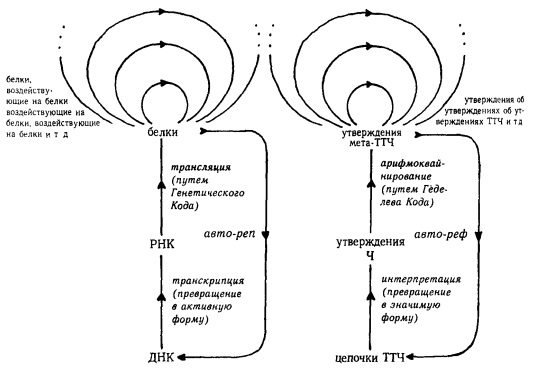
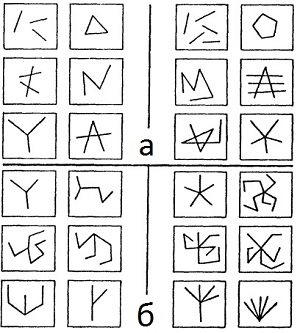
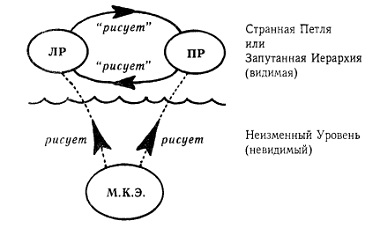
Спасибо за конспект и примечания. Совпал с вами по ощущению от книги. Нашел эту запись после того, как и вы, потерял запал на 13-14 главе. Дочитал оставшиеся главы по вашему конспекту. Начинал чтение, потому что книгу хвалили за ясность изложения, но на деле всё оказалось наоборот. Возможно русский перевод так сильно искажает оригинал, но скорее и сама структура изложения у Хофштадтера оставляет желать лучшего. Книга не стоила для меня потраченного времени и усилий.