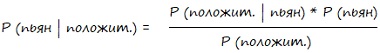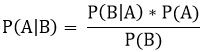Недавно я перевел книгу Скотта Хартшорна почти с тем же названием. Однако, недостаток литературы по теореме Байеса на русском языке столь значителен, что и представляемая книга показалась мне полезной. Хартшорн делает ставку на Excel с его формулами и диаграммами, в то время, как Моррис больше рассуждает, а в визуальном ряде опирается на диаграмму Венна и деревья решений – самые простые способы представить идеи без формул и Excel’я. Если вы впервые знакомитесь с предметом, эта книга то, что вам нужно.
Дэн Моррис. Теорема Байеса: визуальное введение для начинающих. – Blue Windmill Media, 2016.
Скачать заметку в формате Word или pdf
Байес повсюду
Если вы недавно искали что-то в Google, теорема Байеса использовалась для отображения результатов поиска. Теорема работает в алгоритмах Netflix, хедж-фондов и беспилотных автомобилей.[1]
По своей сути, теорема Байеса является простой математической формулой, которая произвела революцию в том, как мы понимаем неопределенность и обрабатываем ее. Если жизнь воспринимается как черное и белое, теорема Байеса помогает нам заглянуть в серые области. Когда появляются новые доказательства, они обновляют наши убеждения и могут изменить мнение.
Для начала вам нужно понять, что теорема Байеса – один из законов теории вероятности. Она помогает нам пересматривать и понимать вероятности, когда возникают новые свидетельства. Иными словами, теорема дает количественную оценку того, насколько должны измениться наши убеждения в связи со вновь обнаруженными доказательствами.
Вот несколько примеров:
- У вас только что был тест на рак, и он оказался положительным. Какова вероятность того, что у вас действительно рак, если тест положительный?
- Ваш друг утверждает, что цены на акции будут снижаться, если процентные ставки вырастут. Какова вероятность того, что цены на акции снизятся, если процентные ставки увеличатся?
- Вас только что остановила полиция и проверила на алкотестере. Результат оказался положительным. Какова вероятность того, что вы действительно пьяны, учитывая, что тест положительный?
Три способа объяснить теорему Байеса
- Теорема Байеса помогает нам обновить ранее имевшееся мнение, основываясь на новых доказательствах.
- Теорема Байеса помогает нам пересмотреть вероятности нескольких первоначально имевшихся альтернатив при возникновении новых фактов.
- Теорема Байеса помогает нам обновить гипотезу, основанную на новых доказательствах.
Есть, правда, проблема, но зато, какая! Применение теоремы не интуитивно, по крайней мере, для большинства людей. Визуализация использования теоремы, надеюсь, поможет разобраться.
Визуальные помощники
При работе с небольшими объемами данных можно использовать:
- диаграмму Венна;
- дерево решений;
- буквы (например, О, Р, Р, Р для бросков монеты – орел/решка);
- физические объекты (например, реальные монеты).
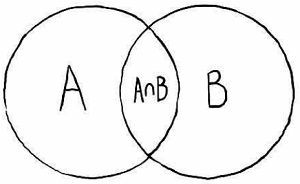
Рис. 1. Диаграмма Венна
Рис. 2. Дерево решений
Визуальное вступление. Часть 1
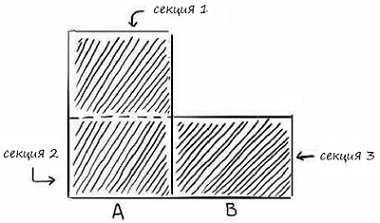
Если у вас есть несколько возможностей, которые одинаково вероятны, их удобно представить в виде прямоугольника, разделенного на равные части (рис. 3).
Рис. 3. Несколько возможностей и их вероятности: а) две возможности, б) три возможности
В следующем примере имеется два равно вероятных исхода: А и В.
Рис. 4. Два равно вероятных исхода
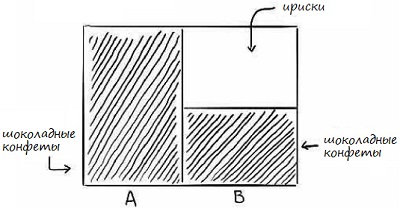
Теперь представьте, что каждая возможность – это коробка с 10 конфетами. В коробке А 10 шоколадных конфет. Чтобы продемонстрировать это, мы заштрихуем ее. В коробке В – 5 шоколадных конфет и 5 ирисок. Мы разделим коробку пополам, и заштрихуем только часть с шоколадными конфетами.
Рис. 5. Две коробки с конфетами
Если взглянуть на прямоугольник целиком, вы увидите шоколадные конфеты в форме буквы L. Эти области представляют все наши шоколадные конфеты в обеих коробках, в то время как белая область – ириски.
Представьте, что вы закрыли глаза, перемешали коробки, и наугад достали одну конфету. Она оказалась шоколадной. Если бы вам нужно было угадать, из какой коробки вы вытащили конфету, какую бы вы выбрали? Многие выбирают коробку А. И вот, почему. Обе коробки содержат шоколадные конфеты, но в коробке А их в два раза больше! Ваш мозг оценил это и подсказал ответ. И это пример очень простого, естественного использования теоремы Байеса.
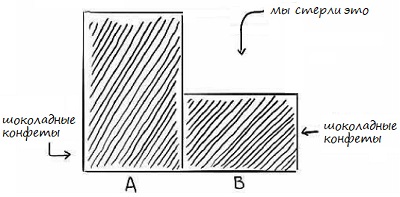
Обратите внимание, когда вы вытащили шоколадную конфету, кое-что исчезло: исчезла вероятность выбрать ириску. Чтобы визуализировать это, давайте сотрем часть коробки, которая относилась к ирискам.
Рис. 6. Остались только части коробок с шоколадными конфетами
В коробке А вдвое больше конфет, чем в коробке B. Если бы мы разбили коробки на равные секции, у нас было бы 3 области: 2 секции в коробке A и 1 секция в коробке В.
Рис. 7. Три секции в двух коробках
Коробка В имеет может быть выбрана с вероятностью 1/3, или 33%. Коробка А может быть выбрана с вероятностью 2/3, или 66%. Эта разница в вероятности – то, что ваш мозг примерно рассчитал раньше. Именно это – причина, по которой вы выбрали коробку A.
Только что мы продемонстрировали концепцию теоремы Байеса и решили проблему без использования формулы. Теперь, прежде чем мы решим эту же проблему с помощью формулы, введем определение теоремы Байеса.
Формула Байеса: обзор
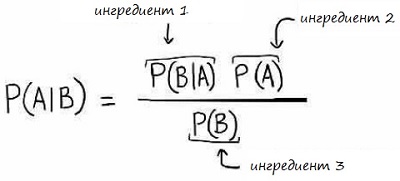
Формула содержит три компонента. На мой взгляд, полезно называть их ингредиентами, а решая задачи, думать о том, как комбинировать эти ингредиенты.
Рис. 8. Формула Байеса
Здесь:
- вертикальная черта | используется для обозначения условных вероятностей,
- P – вероятность,
- А и В – события,
- P(A) и P(B) – вероятности событий A и B. Каждое событие независимо от другого и не влияет на другое.
- P(A|B) – условная вероятность того, что событие А истинно, если событие В истинно.
- P(B|A) – условная вероятность того, что событие В истинно, если событие А истинно.
Используя эти определения, формулу можно прочитать следующим образом:
Рис. 9. Формула Байеса с пояснениями
Каждый раз, когда вы используете формулу, всё, что вам нужно – это вспомнить про три ингредиента, найти их, а затем включить в формулу. Вы получите обновленную вероятность на основе новой информации. У вас будет P(A|B), которая называется апостериорной вероятностью и является нормализованным взвешенным значением.
Визуальное вступление. Часть 2
В части 1 вступления мы решили задачу с конфетами без использования формулы. Сейчас мы увидим, как получить те же числа, используя формулу (см. рис. 5, описание до и после него). Используем четыре шага, чтобы найти ответ с помощью формулы Байеса.
Шаг 1. Для начала мы должны определить, что мы хотим найти. Мы хотим знать вероятность того, что выбрали коробку А с учетом того, что мы выбрали шоколадную конфету.
Шаг 2. Запишите, что вы хотите найти в виде формулы:
Рис. 10. Формула Байеса для коробки с конфетами
Шаг 3. Найдите каждый ингредиент.
P (коробка А) = 0,5. Чтобы ответить на этот вопрос, мы спрашиваем: какова вероятность выбрать из коробки А? Помните, что эта вероятность не зависит от других событий. Поскольку существует только две коробки – А и В (рис. 4), и вероятности их выбора равны, ответ 0,5.
P (шок. конфета) = 0,75. Для ответа на этот вопрос мы спрашиваем: какова вероятность того, что мы выберем шоколадную конфету? Помните, что эта вероятность не зависит от других событий. Всего в обеих коробках 20 конфет, из них 15 шоколадных (рис. 5). Итак, 15/20 = 0,75.
P (шок. конфета | коробка А) = 1. Чтобы ответить на этот вопрос, мы спрашиваем: какова вероятность выбора шоколадной конфеты, учитывая, что мы выбрали из коробки A? Поскольку в коробке А есть только шоколадные конфеты, вероятность равна 1.
Подставим все ингредиенты в формулу:
Рис. 11. Решение задачи про конфеты
Итак, существует вероятность 66%, что мы выбрали из коробки А, если выбранная конфета была шоколадной.
Раздел 1. Нахождение одной условной вероятности, когда три ингредиента известны
Далее мы рассмотрим несколько задач, для решения которых используем диаграмму Венна. Всегда начинайте с определения того, что вы хотите найти. Не путайте P(A|B) с P(B|A). Это довольно распространенная ошибка инверсии.[2]
Пример 1. Грипп
Допустим, вы почувствовали себя неважно, и оказались в постели. Вы припоминаете, что недавно ваш коллега болел гриппом. Что, если он вас заразил? У вас болят голова и горло, и вы знаете, что люди больные гриппом имеют аналогичные симптомы примерно в 90% случаев. Неужели у вас грипп?
Желая получить больше информации, вы лезете в телефон. Google выдает авторитетную статью, в которой говорится, что только 5% населения болели гриппом в этом году. Ладно, вероятность наличия гриппа, в целом, составляет всего 5%. Затем вы обнаружите еще одну статистику, которая говорит, что 20% населения в принципе страдает головной болью и болью в горле. Так что у вас грипп? Что нужно делать?
Вспомним, что делает теорема Байеса: она помогает нам обновить гипотезу при появлении новых доказательств. Ваша гипотеза заключается в том, что у вас грипп, а ваша головная боль и боль в горле являются вашими доказательствами. Увидев, что у 90% людей с гриппом есть ваши симптомы, многие на вашем месте остановятся и придут к выводу, что у вас грипп. (Обратите внимание, эта статистика говорит, что, если вы больны гриппом, то с вероятностью 90% у вас есть указанные симптомы; но нигде не сказано, что если у вас есть симптомы, то вы с вероятностью 90% больны гриппом. Это и есть ошибка инверсии – Прим. Багузина.)
Эта реакция типична и называется ошибкой базовой ставки или пренебрежением базовой вероятностью (а здесь всё верно, именно ошибка базовой ставки. – Прим. Багузина). У ЦРУ есть отличная книга об этом, и она объясняет, почему люди тяготеют к самой простой информации, доступной при принятии решений.
Вот где теорема Байеса приходит нам на помощь, чтобы дать более адекватную картину происходящего. В примере есть еще две порции информации, которые помогут нам прийти к более точной вероятности того, что у нас грипп, учитывая наши симптомы.
Давайте рассмотрим всю информацию, которую мы имеем, прежде чем двигаться дальше.
- Мы знаем, что у людей с гриппом болит голова и горло примерно в 90% случаев.
- Мы знаем, что вероятность наличия гриппа, в целом, составляет всего 5%.
- Мы знаем, что 20% населения страдают головной болью и болью в горле.
Итак, что мы хотим найти? Мы хотим знать, какова вероятность заболевания гриппом, учитывая наши текущие симптомы. Сначала мы рассмотрим визуальное решение с помощью диаграммы Венна, а затем математическое решение с помощью формулы Байеса.
Чтобы визуализировать проблему, мы нарисуем два круга в виде диаграммы Венна (рис. 12). Область внутри круга 1 представляет все возможные исходы, т.е. всех людей, которые в данном случае могут заболеть гриппом. Круг А – это 5% больных гриппом. Эта вероятность представлена в нашей формуле как P(A).
Рис. 12. Диаграмма Венна больных гриппом
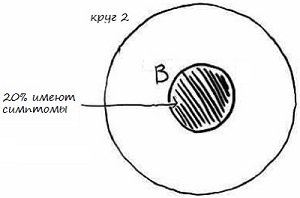
Область внутри круга 2 также представляет все возможные исходы (рис. 13). В данном случае – это все люди, которые могут иметь ваши симптомы (головную боль и боль в горле). Круг B – 20% населения, у которого есть симптомы. Эта вероятность представлена в нашей формуле как P(B).
Рис. 13. Диаграмма Венна имеющих симптомы
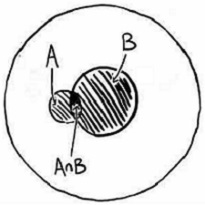
В круге 3 мы объединили оба события A и B (рис. 14). Белая область внутри этого круга представляет людей, у которых нет, ни гриппа, ни симптомов. Круг А охватывает людей, у которых только грипп. Круг В показывает людей, у которых только симптомы. На пересечении кругов А и В образовалась область людей, которые больны гриппом, и у которых есть симптомы. Мы хотим знать P(A|B) – вероятность наличия гриппа, учитывая наши симптомы. Диаграмма Венна не дает ответ, она лишь наглядно представляет ситуацию.
Рис. 14. Диаграмма Венна больных гриппом, одновременно имеющих симптомы
Теперь решим проблему с помощью формулы Байеса.
Шаг 1. Определите, что вы хотите найти. Мы хотим знать, какова вероятность заболевания гриппом, учитывая наши текущие симптомы.
Шаг 2. Запишите это в левой части:
Продолжите формулу в стиле описаний, представленных на рис. 9:
Шаг 3. Найдите значения ингредиентов.
P(A) в нашем примере – это ингредиент под названием P(грипп), и отвечает на вопрос: какова вероятность того, что у вас грипп? 0,05.
P(B|A) в нашем примере носит имя P(симптомы | грипп), и отвечает на вопрос: какова вероятность симптомов при наличии гриппа? 0,9.
P(B) в нашем примере – P (симптомы), и отвечает на вопрос: какова вероятность того, что у вас есть симптомы? 0,2.
Получаем:
Таким образом, если у вас болит горло и голова, вероятность заболевания гриппом составляет 22,5%. Изначально мы думали, что эта вероятность достигает 90%! Это мнение было основано на вероятности Р(В|А). Но это ошибка инверсии. Наш правильный ответ – это расчет P(A|B), который приводит к результату 22,5%.
Этот пример является фантастической иллюстрацией силы, которую дает теорема Байеса при столкновении с неопределенностью. В следующий раз, когда будете думать, что заболели, вспомните Байеса!
Пример 2. Алкотестер
Вы полицейский в Балтиморе, и в канун Нового года проверяете водителей на наличие алкоголя. Около 2 часов ночи тест выдает положительный результат. Вы предполагаете, что тест является точным и даже думать не хотите, что водитель может быть трезв. После окончания смены вы разговариваете со своим напарником, который сообщает вам любопытную статистику:
- Если водитель истинно пьян, алкотестер в 100% случаев даст положительный результат. Под истинно пьяным мы подразумеваем, что анализ крови подтвердит, что человек превысил лимит алкоголя в крови.
- По статистике лишь 1 из 1000 водителей ездит пьяным, поэтому вероятность того, что любой водитель будет пьян, составляет 0,1%.
- Также известно, что алкотестер даст положительный результат 8% времени независимо от того, пьян ли водитель.
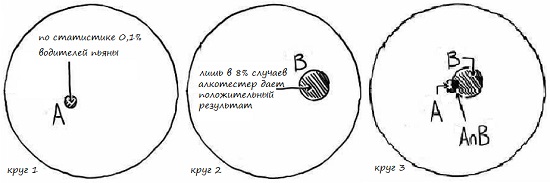
Что мы хотим определить? Мы хотим знать вероятность того, что кто-то действительно пьян, при условии, что тест положительный. Мы визуализируем проблему с помощью диаграммы Венна, а затем решим задачу количественно, применив формулу Байеса.
Круг 1 представляет все возможные исходы (рис. 15а). В этом примере – это все водители, которые могут быть пьяны или трезвы. Круг A представляет собой 0,1% водителей (1 на 1000), которые на самом деле пьяны. А – это событие, и его вероятность 0,1%. Эта вероятность представлена в нашей формуле как P(A).
Круг 2 представляет все возможные результаты теста. Круг B – это 8% тестов, которые являются положительными. B является событием, и его вероятность составляет 8%. Эта вероятность представлена в нашей формуле как P(B).
В Круге 3 мы объединили оба события А и В. Белая область внутри этого круга представляет людей, которые не пьяны, и тесты которых являются отрицательными. Круг А – область, охватывающая пьяных водителей. Круг В – область, в которой алкотестер дает положительный результат. Взгляните на темную область, где два круга А и В перекрываются. Это то, что нас действительно интересует! Это вопрос, на который мы хотим получить ответ. Мы хотим знать P(A|B) – вероятность того, что водитель пьян, учитывая, что тест положительный. Видно, что эта область очень мала.
Рис. 15. Диаграмма Венна для теста на алкоголь: круг 1 – водители; круг – 2 результаты теста; в) пересечение кругов
Формула на рис. 9 в нашем случае приобретает следующий вид:
P(A) = P(пьян) и отвечает на вопрос: какова вероятность того, что водитель пьян? 0,001.
P(B|A) = P(положит. | пьян) и отвечает на вопрос: какова вероятность того, что тест будет положительным, если водитель пьян? 1.
P(B) = P(положит.) и отвечает на вопрос: какова вероятность того, что тест будет положительным? 0,08.
Т.е., если результат теста положительный, вероятность того, что водитель пьян составляет всего 1,25%. Другими словами, на каждые 1000 тестируемых водителей:
- У нас есть 1 действительно пьяный водитель, который дал положительный результат на алкотестере.
- У нас есть 79 других водителей, для которых алкотестер также дал положительный результат, но они не пьяны.
- В итоге мы имеем 80 водителей с положительным результатом теста, из которых только один действительно пьян; это соответствует вероятности 1/80 = 1,25%.
Это сенсационно! Помните, что делает теорема Байеса? Она помогает нам количественно оценить вероятности после наступления события. Первоначально мы думали, что вероятность того, что водитель будет пьян, довольно высока, но теперь мы видим, что она составляет лишь 1,25%. Поняв это, полицейский будет совершенно по-другому относиться к тестам.
Раздел 2. Нахождение одной условной вероятности, когда Р(В) не известна
В этом разделе мы используем деревья решений для визуализации и расчетов. Мы используем те же примеры, что и в разделе 1, но изменим некоторые исходные данные.
Пример 1. Грипп
Вы почувствовали себя неважно, и первое, что проходит вам в голову – пищевое отравление. Затем вы припоминаете, что недавно ваш коллега болел гриппом. Что, если он вас заразил? Желая получить больше информации, вы лезете в телефон. Google сообщает, что около 5% населения болеют гриппом в этом году. Проходит несколько минут, и вы вспоминаете, что недавно загрузили новое приложение, которое предсказывает болезнь. Вы открываете его и вводите свои симптомы. Приложение предсказывает, что вы больны, а также отражает следующее:
- Приложение выдает корректные предсказания гриппа 75% времени.
- 20% времени приложение предсказывает, что люди больны гриппом, хотя это и не так.
Мы хотим знать вероятность наличия у вас гриппа, учитывая, что приложение предсказало, что у вас грипп.
Для начала мы решим эту проблему с помощью дерева решений.
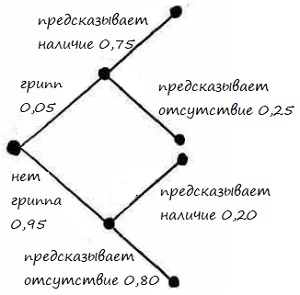
Шаг 1. Начните с двух линий, исходящих из одной точки (рис. 16). Эти линии представляют собой возможности того, что у вас грипп или нет гриппа. Мы обозначим вероятность гриппа, известную по условиям задачи (0,05), и вычислим вероятность отсутствия гриппа = 1 – 0,05 = 0,95. Естественно, в сумме обе ветви дают 1.
Рис. 16. Дерево решений для гриппа: первый этап
Шаг 2. Добавим еще по две ветви к каждой начальной ветви (рис. 17). Каждая новая пара ветвей представляет собой вероятность приложения дать верный или ложный прогноз. Обратите внимание, что каждая пара ветвей также в сумме дает 1.
Рис. 17. Дерево решений для гриппа: второй этап
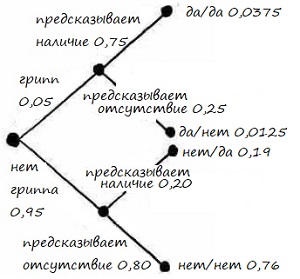
Шаг 3. Вычислим значения в каждой конечной точке маршрута (рис. 18). Всего их четыре:
- Грипп есть, и он предсказан = 0,05 * 0,75 = 0,0375
- Грипп есть, но он не предсказан = 0,05 * 0,25 = 0,0175
- Гриппа нет, но он предсказан = 0,95 * 0,2 = 0,19
- Гриппа нет, и он не предсказан = 0,95 * 0,8 = 0,76
Рис. 18. Дерево решений для гриппа: третий этап
Шаг 4. Суммируем вероятности по пути 1 и 3: 0,0375 + 0,19 = 0,2275. Мы нашли Р(В). Другими словами, мы нашли вероятность того, что приложение предсказывает грипп (неважно, есть он или нет).
Шаг 5. Разделим результат по пути 1 на сумму, найденную на шаге 4: 0,0375/0,2275 = 0,1648 = 16,5%. Мы нашли условную вероятность P(A|B), т.е. вероятность того, что грипп есть, если он предсказан. Обратите внимание, что результат по пути 1 был получен перемножением ингредиентов, соответствующих P(A) и P(B|A).
Итак, вероятность того, что у вас грипп, учитывая, что приложение предсказало его составляет только 16,5%.
Решим этот пример с помощью формулы Байеса. Мы хотим знать вероятность наличия гриппа, при условии, что приложение его предсказало. Формула с рис. 9 приобретет следующий вид:
P (A) = P (грипп) и отвечает на вопрос: какова вероятность того, что у вас грипп? 0,05.
P (B|A) = Р (предсказан грипп | грипп) и отвечает на вопрос: какова вероятность предсказания гриппа, если он таки есть? 0,75.
Ингредиента P(B) не хватает. Он скрыт за несколькими фразами в условии задачи:
- Приложение выдает корректные предсказания гриппа 75% времени.
- 20% времени приложение предсказывает, что люди больны гриппом, хотя это и не так.
В обозначениях формулы Байеса первая фраза говорит, что при наличии гриппа, предсказывается грипп в 75% случаев – Р (предск. да | грипп) = 0,75. Вторая фраза говорит, что при отсутствии гриппа, он всё равно предсказывается в 20% случаев – Р (предск. да | нет гриппа) = 0,20. Чтобы найти вероятность Р (В) = Р (предск. да), нужно найти сумму:
Р (предск. да | грипп) * Р (грипп) + Р (предск. да | нет гриппа) * Р (нет гриппа)
Или:
0,75 * 0,05 + 0,20 * 0,95 = 0,2275 = 22,75%
Мы получили третий ингредиент: P (B) = Р (предсказан грипп); он отвечает на вопрос: какова вероятность предсказания гриппа, неважно есть он или нет? 0,2275.
Р (грипп | предск. да) = 0,75 * 0,05 / 0,2275 = 0,1648 = 16,5%
Что это значит для вас? Ну, 16,5% – не очень большое значение. Можно считать, что вероятность гриппа, довольно низкая. Вы решили остаться на работе и не брать пол дня за свой счет…
Пример 2. Алкотестер
Вы полицейский в Балтиморе, и несмотря на то, что Новый год прошел, вы проверяете водителей на наличие алкоголя. Вы на дежурстве с тем же напарником, что и предыдущей ночью, и у вас не идет из головы разговор с ним. Теперь вы гораздо более скептически относитесь к точности тестов. На самом деле, вы почти полностью им не доверяете. Напарник говорит, что нашел еще несколько интересных фактов:
- Примерно 3 из каждых 1000 водителей управляют в нетрезвом состоянии.
- Алкотестер не всегда обнаруживает пьяного. Теперь это не 100%, как считалось ранее, а только 98%.
- В 4% случаев тест дает положительный результат, хотя водитель трезв. Это называется ложным срабатыванием.
Мы хотим знать вероятность того, что кто-то действительно пьян, учитывая, что тест положительный.
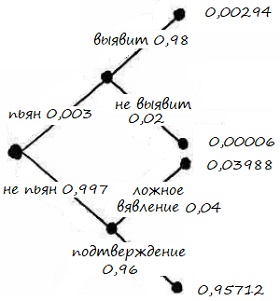
Для начала воспользуемся деревом решений (рис. 19). Ветви первого уровня: пьян (0,3%) или трезв (99,7%). Если пьян, что тест в 98% случае выявит это, а в 2% – не выявит. Если трезв, то тест в 4% случаев даст ложный положительный результат, а в 96% – подтвердит трезвость.
Рис. 19. Дерево решений для алкотестера
Всего положительный результат теста будет с вероятностью 0,00294 + 0,03988 = 0,04282. А вероятность того, что водитель пьян, если тест положителен = 0,00294/0,04282 = 0,06866 = 6,9%. Это число мало, но с другой стороны, оно в 23 раз больше, чем априорная вероятность в 0,3%.
Формула Байеса
P(A) = P(пьян) и отвечает на вопрос: какова вероятность того, что водитель пьян? 0,003.
P(B|A) = Р(положит. | пьян), и отвечает на вопрос: какова вероятность положительного теста, если водитель пьян? 0,98.
Р(В) = Р(положит.) и отвечает на вопрос: какова вероятность, что результат теста будет положительным? Это число не дано в явном виде в условиях задачи. Его можно вычислить на основании следующих двух фраз:
- Алкотестер обнаруживает пьяного в 98% случаев.
- Даже если водитель трезв, в 4% случаев тест даст положительный результат.
Р (положит. | пьян) * Р (пьян) + Р (положит. | трезв) * Р (трезв) = 0,98*0,003 + 0,04*0,997 = 0,04282
Это и есть P(B). Теперь у нас есть все ингредиенты для вычисления искомой условной вероятности:
Р (пьян | положит.) = 0,98 * 0,003 / 0,04282 = 0,06866 = 6,9%
Раздел 3. Решение для двух возможных исходов, когда все ингредиенты известны
Иногда у нас есть две возможности, и мы хотим знать, какая более вероятна. Например, вы чихаете и кашляете. Это аллергия или простуда? Учитывая имеющуюся у вас информацию (симптомы), какая версия вероятнее?
Пример 1. Грипп или пищевое отравление
После обеда вы почувствовали себя неважно. В чем причина? Ваш друг на работе недавно болел гриппом, так что, возможно, и у вас грипп. Вы также только что съели рыбу в новом ресторане. У вас может быть пищевое отравление. Вы берете смартфон и находите следующую информацию:
- У вас небольшая головная боль и боль в горле, и вы видите, что у людей с гриппом те же симптомы, что и у вас в 90% случаев. Люди с пищевыми отравлениями имеют те же симптомы 75% времени.
- В целом вероятность заболеть гриппом 5%, а получить пищевое отравление – 16%.
- Затем вы обнаружите, что 20% населения будут иметь головную боль и боль в горле в любой момент времени.
Для решения задачи необходимо применить теорему Байеса к обеим возможностям, и сравнить результаты. Начнем с гриппа.
Р (грипп | симптомы) = 0,9 * 0,05 / 0,20 = 0,225 = 22,5%
Теперь давайте оценим пищевое отравление.
Р (отравление | симптомы) = Р (симптомы | отравление) * Р (отравление) /
Р (симптомы) = 0,75 * 0,16 / 0,20 = 0,6 = 60%
Вероятность того, что у вас пищевое отравление почти в 3 раза выше, чем вероятность того, что у вас грипп. Исходя из этого, вы, вероятно, захотите отправиться в клинику, чтобы вас осмотрел врач. Если бы это был грипп, вы бы, скорее всего, отправились домой. Но если у вас пищевое отравление, вам могут понадобиться антибиотики.
История и истории
Теорема Байеса имеет впечатляющую 200-летнюю историю, и есть ряд отличных книг, которые описывают ее довольно глубоко. Есть также много интересных историй о том, как теорема Байеса используется в реальной жизни.
Томас Байес родился в Лондоне в 1702 году. Он изучал логику и теологию в Эдинбургском университете и служил в Пресвитерианской церкви в Танбридже, Уэллс (35 миль от Лондона). Он ушел в отставку в 1752 году и скончался в 1762 году.
Помимо своей веры, Байес любил математику. Он увлекся вероятностью, в частности обратной вероятностью. Байес был поглощен выяснением… приблизительной вероятности будущего события, о котором он ничего не знал, кроме его прошлого, то есть количества раз, когда событие произошло или не произошло.
Когда-то в 1740-х годах Байес придумал решение, которое можно суммировать следующим образом: первоначальное мнение + новое доказательство = новое суждение. Но, по неизвестным причинам, он никогда ничего не публиковал до своей смерти в 1762 году. После того, как он скончался, его друг Ричард Прайс обнаружил теорему, увидел ее важность и в течение двух лет работал над ней. Затем Прайс представил труд Королевскому обществу, и через год статья была опубликована.
В 1774 году французский математик Пьер-Симон Лаплас повторил решение Байеса. В то время он ничего не знал об открытии Байеса и пришел к нему независимо. Почти 40 лет он работал над теоремой, и где-то между 1810 и 1814 он доработал его, и в конце концов опубликовал. Лаплас сделал большую часть работы, но к теореме приклеилось имя Байеса.
Теорема Байеса не была принята математиками до середины ХХ в. Она подвергалась критике как субъективная. Во время Второй Мировой войны формула была использована Аланом Тьюрингом (блестящим математиком, которого сыграл Бенедикт Камбербэтч в Игре в имитацию), чтобы взломать немецкий код Энигма, но эта информация была засекречена в течение длительного времени. Только в 1980-х годах с появлением персональных компьютеров теорема Байеса получила широкое признание. Сейчас она широко используется во многих отраслях и касается нашей повседневной жизни.
Поиск и спасение
Что, если вы потерялись в море? Как поисково-спасательные службы могут вас найти? В 2014 году с помощью теоремы Байеса был обнаружен пропавший рыбак. Это увлекательная история, о которой писала New York Times. Джон Олдридж рыбачил почти два десятилетия. В 2006 году он и его партнер Энтони Сосинский приобрели лодку и до 2014 году успешно ловили крабов и омаров. 24 июля 2014 года партнеры находились в 40 милях от побережья Лонг-Айленда, ловя лобстеров. Ночью пока Сосинский спал, Олдридж работал и упал за борт. Используя свои резиновые сапоги в качестве понтонов, ему удалось удержаться на плаву в воде при температуре 22°С, пока он не был найден почти 12 часов спустя береговой охраной.
Для поиска Олдриджа береговая охрана использовала программу SAROPS (Search and Rescue Optimal Planning System). SAROPS создает карту вероятности, которая отображает потенциальные области, где могут находиться выжившие на основе исходной информации. Эта карта затем постоянно обновляется, чтобы отразить изменения, дополнительные подсказки и районы, где не было найдено выживших. В случае Олдриджа у береговой охраны была следующая первоначальная информация: приблизительное местоположение и время падения за борт. После того, как эта информация была загружены в SAROPS, она постоянно обновлялась на основе данных об океанических течениях, подсказок от Сосинского и скорости ветра.
Теорема Байеса была использована во многих поисково-спасательных операциях, включая поиск подводной лодки USS Scorpion в 1968 г. и самолета Air France Flight 447 в 2009 году.
Спам фильтры
Если вы ненавидите спам, вы любите теорему Байеса. Это правда, даже если вы не имеете понятия о том, что такое теорема Байеса. Фильтрация спама значительно улучшилась за последнее десятилетие до такой степени, что большинство из нас больше не думают о спаме. В 1998 году Microsoft подала заявку на патент на спам-фильтр, который использовал Байесовский подход. Конкуренты вскоре присоединились к MS, и теорема Байеса быстро стала основой фильтрации спама.
Байесовские фильтры определяют, является ли письмо спамом или нет на основе содержимого сообщения. Для каждого слова определяется вероятность того, что оно является спамом или законным (иногда говорят спам или ветчина; второе значение английского слова spam – консервированный колбасный фарш). Что отличает Байесовские фильтры от других фильтров электронной почты? Первые учатся и адаптируются к каждому отдельному пользователю. Вот почему они настолько эффективны.
Спам-фильтры, построенные на Байесовской сети, как правило, предварительно заполняются списком потенциальных слов и характеристик, которые содержит спам. Вспомните, какие слова всплывают у вас в памяти, когда вы думаете о спаме? Обычно, все, что связано с сексом, сделками, секретами, выигрышами… Этот список можно продолжить. Фильтр анализирует слова в теле сообщения, в заголовке, в метаданных. Этот список постоянно обновляется по мере получения каждого письма, и фильтр узнает все больше и больше о том, что искать. Фильтр учится двумя разными способами:
- на основе собственных решений;
- на основе решений пользователя (вы проверяете электронную почту, и отправляете часть писем в спам).
Например, если слово спорт часто появляется в вашей электронной почте, фильтр может заключить, что оно имеет очень низкую вероятность быть спамом (по шкале от 0 до 1, может быть. 0,1). Однако, если вы не интересуетесь спортом, фильтр может заключить, что письма с этим словом имеют высокую вероятность быть спамом (например, 0,65). Вот как теорема Байеса может быть использована при обнаружении спама:
Р (спам | определенное слово) = Р (опр. слово | спам) * Р (спам) / Р (опр. слово)
Беспилотные автомобили
Сторонники беспилотных транспортных средств считают, что такие автомобили станут более безопасными. Тесла, Google и Ford разрабатывают и тестируют автомобили без водителя. А Uber в августе 2016 г. запустил свой первый беспилотный флот в Питтсбурге. Google был первым, кто начал тестировать беспилотные автомобили в 2009 году на базе Toyota Prius. Автомобили Google к сентябрю 2016 проехали более 1,5 миллионов миль по всем США.
Согласно статье на веб-сайте университета Стэнфорда, беспилотные автомобили Google используют формулу Байесовского моделирования, чтобы помочь автомобилю узнать его местоположение. Для получения более подробной информации, рекомендую статью в Time Magazine.
Думать в байесовском стиле
Большинство людей в восторге от теоремы Байеса, но в глубине души многие сомневаются, что это полезно в реальной жизни. Теорема Байеса может показаться интересной в учебнике, но что дальше? Дело в том, что при обучении теореме используют примеры с костями, азартными играми и скринингом рака. Полезна ли Теорема Байеса в повседневной жизни? Можете ли вы знания, полученные в этой книге, использовать на практике? И даже если можете, выиграете ли от этого?
Ответ – громкое да, и вот почему:
- Во-первых, байесовский подход можно применить практически к любой сфере жизни.
- Во-вторых, думая, как Байес, вы сможете принимать лучшие решения и чувствовать себя более уверенно в тех решениях, которые вы приняли.
Идеи, которые мы представим в этом разделе, основаны на видео Джулии Галеф.
Когда мы говорим, о пользе теоремы Байеса, мы не собираемся писать формулу по любому поводу на клочке бумаги. Это не практично. Всё что мы хотим – это быстро прикинуть в уме шансы события, а не вероятность не пойми чего.
Если вы хотите рассчитать вероятность, вам нужно использовать формулу и достать ручку и бумагу. Но если вы оцениваете шансы, вы способны сделать это в уме. Любопытно, что большинство людей интуитивно понимают шансы лучше, чем процент. Вы можете прочитать об этом подробнее в статье из библиотеки ЦРУ.
Пример 1. Знакомства
Ты на первом свидании. Только что закончился ужин в ресторане. Ты много разговаривал, даже подавился макаронами. Она поддерживала разговор, иногда смеялась и, казалось, флиртовала с тобой. Так ты ей понравился?
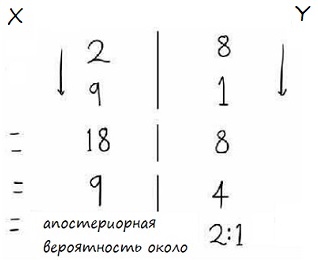
Мы собираемся в уме быстро определить четыре числа и вычислить шансы. Помните, что все числа – лишь твое мнение. Во-первых, какова вероятность того, что ты ей понравился, независимо ни от чего другого? Основываясь на прошлых успехах, ты бы сказал, что по крайней мере двум из 10 девушкам ты нравился. Для простоты все наши числа будут целыми в диапазоне от 1 до 10.
Во-вторых, какова вероятность, что ты не понравился, независимо от чего-либо еще? Просто дополняем до 10 предыдущие шансы, и получаем, что в 8 случаях из 10, это не твой день. В-третьих, какова вероятность того, что девушка смеется и флиртует, если ты ей понравился? Допустим, что шансы 9 из 10. И, наконец, какова вероятность того, что девушка смеется и флиртует, если ты ей не понравился? Ты думаете, что это маловероятно, поэтому даешь лишь один шанс из 10.
Запиши числа в виде пропорции:
Умножь левую и правую части раздельно и сократи:
Основываясь на быстром расчете, шансы, что ты ей понравился 9 к 4, что немного больше, чем 2 к 1. И это хорошо, правда!?
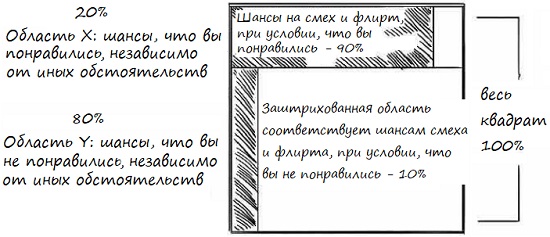
Перед тобой та же проблема, но теперь решим ее визуальными средствами. Нарисуй квадрат. Представь, что весь квадрат – это 100%. Раздели квадрат на две области: одна – ты понравился независимо от иных обстоятельств, вторая – не понравился (рис. 20). Для простоты все наши числа будут целыми между 1 и 10. Площадь зоны Х = 2, Y = 8.
Рис. 20. Шансы понравиться без дополнительных условий
Теперь, если ты нравишься девушке, насколько вероятно, что она будет флиртовать и смеяться? Заштрихованная часть области X – наш ответ – 90% (рис. 21). А если ты не нравишься девушке? Насколько вероятно, что она будет флиртовать и смеяться? Узкая полоска слева – 10%.
Рис. 21. Шансы понравится при условии флирта
Теперь у нас есть четыре числа. Давайте запишем из в виде пропорции, перемножим и упростим. Зона – слева, Y – справа.
Пример 2. Можете ли вы доверять своему механику?
Вы недавно переехали в новый город. Однажды утром вы застряли в пробке, и автомобиль начинает издавать странные звуки. Пока вы добрались до работы шумы усилились, и вы начинаете беспокоиться. Во время обеда вы спрашиваете коллег, знают ли они надежного механика, и они рекомендуют гараж Джо. Вы гуглите этот гараж и видите, что отзывов нет. Но так как ваш друг рекомендовал этот гараж, а вы в затруднительном положении, то после работы оставляете машину у Джо.
Дома вы исследуете гараж Джо более тщательно и обнаруживаете несколько отзывов, которые пропустили раньше. Есть хорошие отзывы, есть и плохие,.. очень плохие. И вы начинаете нервничать. Вы сделали хороший выбор?
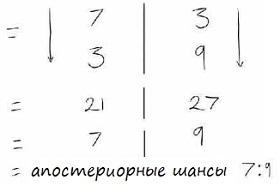
Как и в примере выше, во-первых, определим вероятность того, что механик честен, независимо от чего-либо еще. Основываясь на вашем опыте, вы думаете, что 7 из 10 механиков честны. Соответственно, 3 из 10 таковыми не являются. Какова вероятность того, что ваш механик имеет плохие отзывы, если он честен. Люди всегда будут жаловаться, даже если обслуживание фантастическое, но не так часто. Таким образом, вы предполагаете, что есть три шанса из 10, что ряд отзывов будут плохими, даже если механик хорош. И наконец, вероятность того, что ваш механик имеет плохие отзывы, если он нечестен, вы оцениваете, как 9 шансов из 10.
Мы видим, что шансы быть нечестным, чуть выше чем быть честным. Зная это, вы захотите быть осторожными и осмотреть всё, когда будете забирать автомобиль из ремонта. Вы также можете привести с собой коллегу, который рекомендовал вам этого механика.
Определения
Вероятность – это шанс, что что-то произойдет. Вероятность выражается числом между 0 и 1.
Вероятность = 0 означает, что вероятность возникновения события равна 0%. Вероятность = 1 означает, что существует 100% вероятности наступления события.
Допустим, у вас есть честная монета. Если ее подбросить 3 раза, какова вероятность 3 орлов? Есть 8 возможностей выпадения монеты: ООО, ООР, ОРО, РОО, ОРР, РОР, РРО, РРР. Все исходы равновероятны, поэтому вероятность выпадения 3 орлов = 1/8 или 0,125 или 12,5%.
Условная вероятность – это вероятность того, что событие А истинно, при условии, что событие В истинно. Условная вероятность отвечает на вопрос: как изменится вероятность события, если у нас есть новые доказательства (новая информация)? Условные вероятности всегда включают два независимых события: А и В.
В приведенном выше примере мы пришли к выводу, что вероятность подбрасывания 3 орлов подряд равна 1/8, или 12,5%. Что, если бы нам дали новую информацию, что первая брошенная монета упала орлом? Как это повлияет на нашу вероятность?
Теперь мы имеем дело с условной вероятностью, потому что мы принимаем во внимание, что первое падение монеты было орлом вверх. У нас всего 4 комбинации для второго и третьего бросков: ОО, ОР, РО, РР. Все исходы одинаково возможны, поэтому вероятность подбрасывания 3 орлов подряд равна 1/4, или 25%. Итак, вероятность того, что монета упадет тремя орлами подряд, при условии, что первый раз она упала орлом, равна 1/4 или25%.
В формуле Байеса есть две условные вероятности: P(A|B) и P(B|A). P(A|B) – это апостериорная вероятность. Это то, что мы ищем. Пусть A = три орла подряд. Пусть В = первый бросок – орел. Мы хотим знать вероятность бросания трех орлов подряд, учитывая, что первый бросок был орлом. В этом примере, В является новым доказательством, которое изменяет вероятность A.
P(B|A) называют правдоподобием; его часто путают с P(A|B). В реальной жизни P(B|A) – число, на котором мы фокусируемся и на основании которого делаем выводы. К сожалению, это ошибочный подход. Скажем, у вас грипп, и вы исследуете свои симптомы. Пусть вероятность гриппа P(A), а вероятность симптомом P(B). В Интернете вы узнаете, что 90% людей больных гриппом имеют ваши симптомы. Это P(B|A) – вероятность симптомов при наличии гриппа. Большинство людей останавливаются здесь и считают, что у них грипп, но теорема Байеса требует сделать еще один шаг, чтобы найти P(A|B) – вероятность гриппа, при наличии симптомов.
Апостериорная вероятность – наше измененное суждение после использования теоремы Байеса. Это то, что мы пытаемся найти. Технически – это вероятность того, что событие А истинно, учитывая, что событие В истинно, что записывается P(A|B). Также – это условная вероятность и нормализованное взвешенное значение.
Априорная вероятность или априорные шансы – наше мнение до опыта. В теореме Байеса и Р(А), и Р(В) являются априорными вероятностями. P(B) появляется в знаменателе формулы для нормализации ответа. Нормализацию можно трактовать по-разному. Ее можно определить, как операцию, приводящую сумму всех возможных ответов к единице.
Событие означает один (или несколько) результатов. Например, бросание монеты и выпадение орла, сдача онкологического теста и получение положительного результата. Существует три типа событий:
- Независимые: на эти события не влияют другие события.
- Зависимые: на эти события могут влиять предыдущие события.
- Взаимоисключающие: события не могут происходить одновременно. Например, при подбрасывании монеты у вас может быть орел или решка, но не оба одновременно.
Обозначения
При использовании теоремы Байеса вы увидели следующие записи:
P(A) = вероятность того, что произойдет событие A.
P(B) = вероятность того, что произойдет событие В.
P(A|B) = условная вероятность того, что событие А истинно, при условии, что В истинно.
Кроме того, полезно знать следующее:
P (A’) = вероятность дополнения события A.
Дополнение события – A’ соответствует тому, что событие А не происходит. Например, если событие А заключается в том, что выпало три орла подряд, дополнение к этому событию A’ соответствует выпадению любой комбинации, кроме трех орлов подряд.
P(AꓵВ) = вероятность пересечения событий A и B. Другими словами, вероятность одновременного возникновения событий A и В. Пересечение – это набор элементов, принадлежащих двум множествам. Например, если установить А как множество элементов {10,15,25} и установить В как множество {5,10,15}, на пересечении окажутся {10,15}. В этом примере 10 и 15 являются двумя элементами, которые являются общими для набора A и набора B. Визуально пересечения лучше всего демонстрируются с помощью диаграммы Венна. В диаграмме Венна пересечение – это место, где оба множества перекрываются.
Доказательство
Существует множество способов доказательства теоремы Байеса. Мы приведем самый простой способ. Если вам интересны другие доказательства, рекомендуем объяснение Эдинбургского Университета и Университета Пенсильвании.
Итак, у нас есть события А и В. Запишем вероятность пересечения этих событий:
Р(АꓵВ) = Р(В|А)*Р(А)
Мы предположили, что событие А истинно, тогда для нахождения пересечения событий А и В, нужно умножить вероятность события А, на вероятность события В, при условии, что А истинно.
Но, с другой стороны:
Р(ВꓵА) = Р(А|В)*Р(В)
Мы предположили, что событие В истинно, тогда для нахождения пересечения событий А и В, нужно умножить вероятность события В, на вероятность события А, при условии, что В истинно.
Понятно, что
Р(АꓵВ) = Р(ВꓵА)
или
Р(В|А)*Р(А) = Р(А|В)*Р(В)
Перепишем это равенство относительно Р(А|В):
Это и есть формула Байеса!
[1] На днях в Евроньюс передали информацию о ДТП с участием беспилотного автомобиля. В марте 2018 г. он сбил на шоссе женщину на велосипеде. Как сообщили в компании Google, разработчике алгоритма, был установлен слишком высокий порог определения незначительности помехи. Одной из проблем были листья и полиэтиленовые пакеты, несущиеся навстречу авто, которое каждый раз останавливалось. Чтобы избежать этого, порог повысили, и велосипедистка не была идентифицирована, как критическое препятствие… – Прим. Багузина.
[2] У автора используется термин Base rate fallacy – ошибка базовой ставки; я думаю, что это опечатка, и верно читать – ошибка инверсии.