Путеводитель по лжи – книга о том, как распознавать проблемы с помощью тех фактов, которые вам встречаются, проблемы, которые могут привести вас к неправильным выводам. Иногда те, кто предлагает вам какие-то факты, так и ждут, что вы сделаете неверное заключение. Как определить, не содержатся ли в новостях псевдофакты, искажения данных или откровенная ложь? Эта книга поможет вам распознавать ложь и критически обрабатывать любую информацию.
По теме см. также: Дарелл Хафф. Как лгать при помощи статистики, Как с помощью диаграммы приукрасить действительность? или о факторе лжи Эдварда Тафти.
Дэниел Левитин. Путеводитель по лжи. Критическое мышление в эпоху постправды. – М.: Манн, Иванов и Фербер, 2017. – 272 с.
Скачать конспект (краткое содержание) в формате Word или pdf (конспект составляет около 7% от объема книги)
Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon или Лабиринте
Введение. Критическое мышление
В 2016 году словом года в Оксфордском словаре стало понятие «постправда», которое определяют, как «нечто, относящееся к обстоятельствам или обозначающее обстоятельства, в которых объективные факты влияют на формирование общественного мнения меньше, чем обращение к эмоциям и личным убеждениям». Уверен, нам нужно снова вернуться к старому доброму слову «правда». Лучшая защита против хитрых и изворотливых людей — умение критически мыслить. Наш мозг — такой механизм, который прекрасно придумывает и рассказывает истории: если нам дать оригинальную идею, мы можем легко придумать заковыристое объяснение, почему она хороша. Но в этом и заключается различие между образным и критическим мышлением, между ложью и истиной: истина подкрепляется фактами, объективными доказательствами.
Самый важный компонент критического мышления, которого так не хватает в нашем обществе, — смирение. Это простая, но очень глубокая мысль: если мы поймем, что знаем далеко не всё, то сможем узнать больше. Если мы будем думать, что знаем всё, научиться чему-нибудь будет невозможно.
ЧАСТЬ 1. ОЦЕНКА ЦИФР
Правдоподобие
Статистика — это не факты, это интерпретация. И ваша интерпретация может быть такой же хорошей (равно как и такой же плохой), как и та, что вам предлагает другой человек. Для начала проще всего быстренько проверить числа на правдоподобие. Далее у вас могут возникнуть вопросы трех типов: как данные были собраны, как они были интерпретированы и как представлены графически. Ответы на них помогут вам сформулировать правильные выводы.
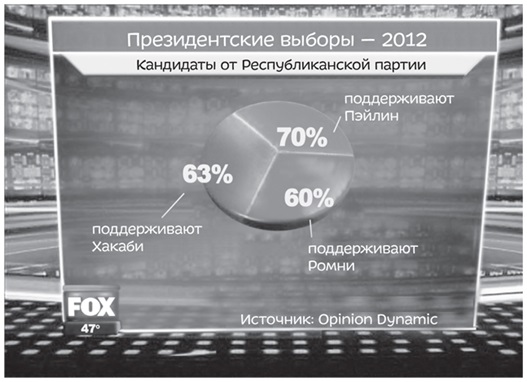
Давайте взглянем на простой инструмент, который часто используют неверно. С помощью круговой диаграммы легко представить себе процентные соотношения — то, каким образом распределены разные части единого целого. Главное правило круговых диаграмм — сумма процентов во всех секторах должна быть равна 100. Fox News, однако, это не смутило, и они опубликовали вот такую диаграмму:
Рис. 1. Главное правило круговых диаграмм: сумма процентов во всех секторах должна быть равна 100
Можно легко объяснить, как такое могло произойти. У избирателей есть возможность отдать свой голос более чем за одного кандидата. Однако в таком случае нельзя представлять результаты в виде круговой диаграммы.
Чехарда со средним
Среднее значение может быть весьма полезно, да и разобраться с ним проще, чем с круговой диаграммой. Оно позволяет нам охарактеризовать огромное количество информации одним-единственным числом. Однако средние могут быть обманчиво сложными. Есть три вида средних, и они могут выражаться разными числами (подробнее см. Определение среднего значения, вариации и формы распределения. Описательные статистики). Поэтому те, кто всерьез занимается статистикой, избегают слова «среднее», отдавая предпочтение другим, более точным терминам, как то: среднее арифметическое, медиана или мода. И только так. Иногда все эти величины совпадают, но чаще они различаются. Если вам встретилось слово «среднее», оно, как правило, означает «среднее арифметическое», но нельзя быть в этом абсолютно уверенным.
Чаще других из этих трех встречается среднее арифметическое; оно равно сумме всех данных, поделенной на их количество. Проблема со средним арифметическим в том, что оно слишком чувствительно к выбросам.
В уголовном судопроизводстве то, как представлена информация, т. е. фрейминг, оказывает сильное воздействие на мнение присяжных относительно виновности подсудимого. Хотя математически эти два утверждения эквивалентны, фраза: «Вероятность того, что обнаруженная на месте преступления кровь совпадет с кровью подозреваемого, если только это действительно не его кровь, составляет всего 0,1%» (один к тысяче) гораздо убедительнее, чем заявление: «Кровь одного человека из каждой тысячи жителей Хьюстона тоже соответствует найденной».
Будьте осторожны со средними, а также с тем, как их интерпретируют. Один из способов ввести в заблуждение, используя средние, — усреднять данные по выборкам из несопоставимых совокупностей. Этот способ может привести к абсурдным выводам, как то: «В среднем у каждого человека одно яичко».
Кроме этого, нужно быть внимательным и помнить, что среднее ничего не говорит о размахе значений. Средняя годовая температура в Долине Смерти в Калифорнии равна 25°С, что считается комфортным. Но размах может быть просто убийственным, с колебанием температуры от –9 до 57°C, — факт, зафиксированный приборами.
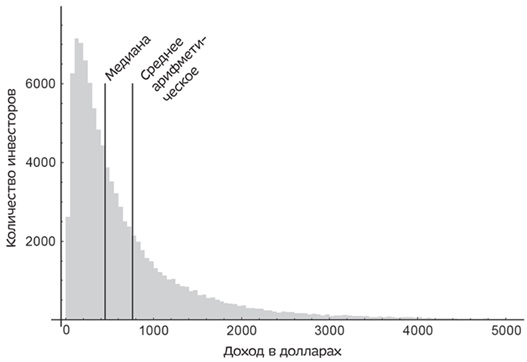
В одном исследовании средний доход от инвестиции 100 долларов на срок 30 лет составил 760 долларов, или 7% в год. Но 9% инвесторов потеряли деньги, а огромному числу инвесторов, 69%, не удалось достигнуть показателя среднего дохода. Так случилось потому, что среднее арифметическое было смещено из-за нескольких человек, заработавших больше среднего. На графике, предложенном ниже, среднее арифметическое смещено вправо благодаря тем счастливчикам, которым удалось заработать состояние.
Рис. 2. Доходность инвестиции в 100 долларов через 30 лет
Обратите внимание: большинство людей получили доход меньше среднего арифметического, а немногие счастливчики — в пять раз больше среднего.
Махинации с осями координат
Наши глаза автоматически ищут шаблоны и схемы в данных, представленных визуально, поэтому мы полагаемся на схемы и графики. Последние бывают двух видов: они либо показывают каждую точку данных (как в графике рассеяния), либо каким-то образом преобразуют данные, обобщают их, фокусируясь при этом, например, только на средних или медианах.
Есть много способов использовать графики для манипуляции и искажения данных. Основной способ манипуляции с помощью статистических графиков — не обозначать оси координат. Если оси никак не названы, вы можете выдумать что угодно. Если вы отражаете в графике любое количественное множество, которое может принимать нулевое значение, — тогда ноль должен быть минимальной точкой отсчета. Но если ваша цель — посеять панику или ужас, начните свой график поближе к нижней границе значений, это подчеркнет разницу, которую вы пытаетесь выделить, потому что наш глаз привлекает разница, показанная на графике, а настоящий ее размер остается незамеченным.
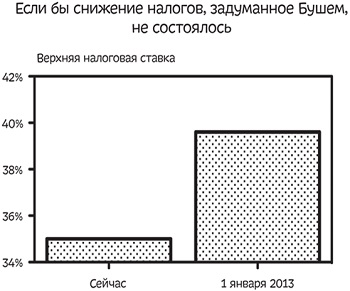
В 2012 году Fox News показали приведенный ниже график, чтобы показать, что могло бы случиться, если бы снижение налогов, задуманное Бушем, не состоялось. Этот график создает визуальное впечатление, что размер налогов возрос бы, и намного: столбик справа в шесть раз выше столбика слева.
Рис. 3. Ось Y начинается не с нуля
Если бы ось Y начиналась с нуля, мы бы заметили лишь небольшой рост:
Рис. 4. Ось Y начинается с нуля
Возможные уловки при сообщении данных
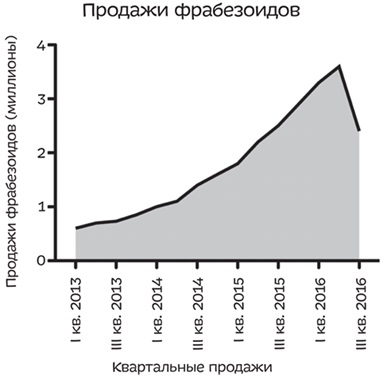
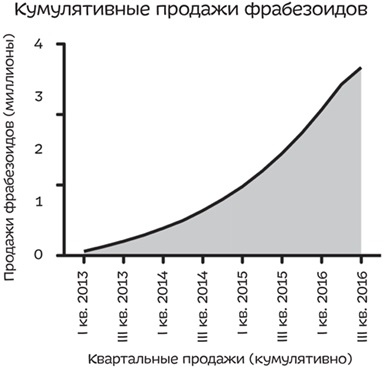
Предположим, вы работаете в отделе по связям с общественностью в компании, производящей какого-то рода устройства — назовем их фрабезоиды. На протяжении последних нескольких лет эту продукцию охотно покупали, и продажи сильно выросли. Однако в последнем квартале количество проданных фрабезоидов упало на 12% по сравнению с предыдущим кварталом. Если вы честно отобразите данные по продажам за последние четыре года, ваш график будет выглядеть следующим образом:
Рис. 5. Квартальные продажи фрабезоидов
Кривая, идущая вниз, — это проблема. Если бы только был способ сделать так, чтобы она снова пошла вверх! И такой способ есть — график кумулятивных продаж:
Рис. 6. Кумулятивные квартальные продажи фрабезоидов
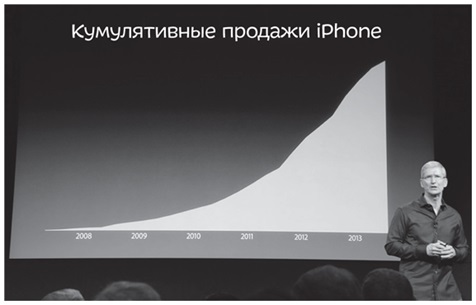
Так же поступил и Тим Кук, CEO компании Apple, во время своей презентации по продажам iPhone:
Рис. 7. Кумулятивные квартальные продажи iPhone (см. здесь)
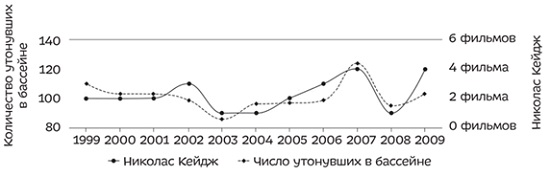
Известно, что корреляция не подразумевает причинность, однако об этом правиле часто забывают в рассуждениях. Для ошибок такого рода в формальной логике есть две формулировки: Post hoc, ergo propter hoc (после этого, следовательно, по причине этого), Cum hoc, ergo propter hoc (вместе с этим, следовательно, по причине этого). Тайлер Виджен, студент юридического факультета Гарвардского университета, написал книгу и создал сайт, где собрал примеры странных совпадений — корреляций, например, таких:
Рис. 8. Число людей, утонувших в бассейне, коррелирует с числом фильмов, в которых сыграл Николас Кейдж
Инфографика в большом почете у разных ловкачей и пройдох, которым нужно сформировать мнение аудитории, и полагаются они на то, что большинство людей не станут вникать в то, что выглядит убедительно. Вот, например, посмотрите на этот рисунок. Возможно, с его помощью кто-то хотел напугать вас и заставить думать, что быстро растущая инфляция съедает все ваши с таким трудом зарабатываемые деньги:
Рис. 9. Инфографика, преувеличивающая влияние инфляции на стоимость жизни
Выглядит страшновато, правда? Но присмотритесь. Ножницы отрезают не 4,2% от банкноты, а около 42%. Когда ваша визуальная система сталкивается с логической, первая всегда выходит победителем, если только вы не приложите усилий, чтобы переломить это предубеждение. Точная инфографика выглядела бы похоже, но производила бы менее сильный эмоциональный эффект:
Рис. 10. Инфографика без преувеличения
Манипуляция фреймами предоставляет бесконечное количество способов заставить кого-нибудь верить в то, чего на самом деле нет. 2014 год принес наибольшее количество смертей в результате авиакатастроф: 22 падения самолета и 992 человеческие жертвы. Но сегодня путешествия на самолете стали безопаснее, чем когда-либо. А так как и летают теперь намного чаще, это число, 992 погибших, говорит о значительном уменьшении числа смертей на миллион пассажиров (или миллион миль). На рейсе крупной авиакомпании вероятность погибнуть составляет один на пять миллионов. Гораздо выше риск погибнуть при других обстоятельствах: переходя дорогу или жуя бутерброд (смерть от того, что человек поперхнулся или отравился, вероятнее в тысячу раз).
К статистике часто прибегают, когда хотят понять, есть ли разница между двумя вещами: двумя разными удобрениями, лекарствами, манерами преподавания. Статистический уровень значимости представляет в количественной форме, насколько легко результаты объясняются чистой случайностью. При большом количестве наблюдений даже самые незначительные отклонения бывает сложно объяснить в рамках используемой статистической модели. Не критерии определяют, что заслуживает внимания, а что нет, — тут нужны человек и его оценка (о критериях оценки см. Проверка гипотез: одновыборочные критерии, Применение χ2-критерия для проверки гипотезы о равенстве двух или нескольких долей, Фишер. Статистический вывод).
Отличный способ жульничать с помощью статистики — сравнивать отличающиеся друг от друга вещи (данные, совокупности, типы продуктов) и при этом делать вид, что разницы между ними нет. Но, как гласит известное выражение, «мухи отдельно, котлеты отдельно».
Остерегайтесь меняющихся выборок, когда делаете выводы! Допустим, вы захотели поговорить о безработице как об общей проблеме, но тут возникает риск объединения в одной выборке людей с самым разным жизненным опытом. Некоторые безработные физически недееспособны; другие были уволены по объективной причине, например, потому что были пойманы с поличным во время кражи или потому что пришли на работу в нетрезвом виде. Кто-то хотел бы работать, но ему не хватает квалификации; кто-то отбывает срок; кто-то больше не хочет работать, потому что снова начал учиться, ушел в монастырь или находится на иждивении. Когда статистику используют, чтобы повлиять на государственную политику, собрать деньги на какое-то дело или чтобы выпустить газету с заголовком поярче, нюансы часто опускают. А ведь именно они порой кардинально меняют дело.
Как собирают данные
Специалисты используют выборки и на их основании строят оценки. Если выборки сделаны правильно, то оценка может быть в высшей степени точной. Выборка должна быть репрезентативной. А это бывает в случае, когда каждый человек или предмет в изучаемой группе имеет равные шансы быть выбранным. Если это не так, то ваша выборка окажется нерепрезентативной (перекошенной).
В задачу статистика входит составление списка того, что имеет значение для получения репрезентативной выборки. Некоторые наиболее творческие прорывы в науке оказались возможны потому, что были предложены способы измерить важные показатели, которые раньше измерять не умели.
Из-за формирования выборок сбор данных может превратиться в бесконечную битву за отсутствие предвзятости. И исследователи побеждают не всегда. Всякий раз, читая в газете, что 71% британцев отдают чему-то предпочтение, мы должны спрашивать себя: «Да, но 71% каких именно британцев?»
Выборка дает нам оценки чего-либо, и почти всегда они отличаются от истинного значения, сильно или не очень. Это называется погрешностью. Погрешность показывает, насколько близки полученные результаты к истинным значениям, а доверительный интервал — это степень уверенности в том, что оценка не выходит за пределы этой погрешности. Например, в стандартном опросе, предполагающем выбор из двух возможностей, случайная выборка из 1067 взрослых американцев даст погрешность в 3% в любую сторону (напишем ±3%).
Насколько мы уверены в том, что погрешность равна 3%? Мы находим доверительный интервал. В приведенном мной примере рассматривался интервал с уровнем доверия 95%. Это означает, что, если бы мы проводили голосование сто раз при использовании тех же самых выборочных методов, в 95 случаях из этих 100 полученный интервал содержал бы истинное значение. В 5 случаях из 100 истинное значение выходило бы за полученные рамки.
Допустим, вы работаете в Гарвардском университете и хотите показать, что выпускники вашего учебного заведения, как правило, получают большие зарплаты уже через два года после окончания вуза. Вы рассылаете анкету выпускникам. И уже на этой стадии возникают сложности: те, кто переехал куда-то, не известив об этом университет, те, кто сейчас в тюрьме, или те, кто стал бездомным, попросту не получат ваши вопросы. А среди тех, кто на них ответит, большую часть, скорее всего, составят успешные люди, благодарные университету за то, что он для них сделал, а не те, кто в итоге потерял работу и теперь обижен на жизнь. Те, чьего мнения вы не учитываете, вносят свою лепту в ошибку пропущенных данных. Иногда данные при этом искажаются систематически. В результате возникает особый тип смещения выборки, который называется ошибкой пропущенных данных.
Если ваша цель — показать, что образование, полученное в стенах Гарварда, напрямую обуславливает последующую высокую зарплату, то такое исследование поможет вам убедить большинство. Но критическое мышление, присущее отдельным людям, подскажет им, что тех, кто учится в Гарварде, ни в коем случае нельзя назвать средними представителями: это, как правило, выходцы из семей с высоким доходом, а данный показатель коррелирует с зарплатой выпускника. Студенты Гарварда отличаются предприимчивостью и энергией. Они могли бы заработать столько же и в том случае, если бы посещали колледж с репутацией похуже или вовсе бы не получили образования (Марк Цукерберг, Мэтт Деймон и Билл Гейтс — финансово успешные люди, которые когда-то вылетели из Гарварда).
Тест на IQ — из тех, что чаще всего получает неверную трактовку. Его используют, чтобы оценить умственные способности человека, как будто это какое-то одно качество. На самом деле, конечно, это не так — способности проявляются в самых разных формах: ориентировании в пространстве, знании искусства, математики и т. д. Как известно, в тестах на IQ есть некий перекос в сторону белых людей среднего класса. По результатам такого теста мы хотим понять, насколько человек подходит для усвоения определенной школьной программы или выполнения работы. Тесты на IQ могут предсказывать успешность испытуемых в таких ситуациях, но, вероятно, не потому, что человек с высоким IQ гораздо умнее, а потому, что у него много других преимуществ (экономических, социальных), которые и выявил тест.
Вероятности
В основе одного из видов вероятности — классической — лежит идея симметрии и равной вероятности: у игрового кубика шесть граней, у монеты — две стороны, у колеса рулетки — 37 слотов. Все исходы равновозможны. Классическая вероятность ограничена подобного рода структурами, в которых уже все четко определено и задано.
Второй вид вероятности возникает потому, что в повседневной жизни мы часто хотим знать вероятности событий, которые не включены в такую симметричную схему. Нам интересно, какова вероятность того, что лекарство поможет пациенту или что клиенты, предпочтут один сорт пива другому. В этом случае нам нужно сначала оценить параметры системы, потому что изначально они не заданы. Чтобы определить, что же собой представляет второй тип вероятности, мы делаем наблюдения или проводим эксперименты, а также считаем, сколько раз получился желаемый результат. Это так называемая частотная, или статистическая, вероятность.
И классическая, и частотная вероятность имеют дело с повторяющимися, воспроизводимыми событиями, а также с долей случаев, которые приводят к определенному исходу в практически неизменных условиях. Третий вид вероятности отличается от описанных выше тем, что ее не получают экспериментально и определяют не для повторяющихся событий, — скорее она выражает мнение или степень уверенности в том, что какое-то событие произойдет. Она называется субъективной вероятностью (один из ее видов — байесовская вероятность).
Когда ведущая прогноза погоды сообщает, что вероятность дождя завтра 30%, мы знаем, что она не проводила экспериментов в течение нескольких идентичных в плане погодных условий дней (даже если бы такое было возможно). Цифра в 30% выражает степень ее уверенности (по шкале от одного до 100) в том, что будет дождь.
В Гидрометцентре России имеют в виду совсем иное, когда дают вероятностный прогноз. В разделе «Борьба с неопределенностью» сообщают: Строго говоря, неопределенность присуща не только прогнозам погоды, но и даже степени оценки текущего состояния атмосферы. Если бы можно было выразить присущую неопределенность количественным образом, то ценность прогнозов для лиц, принимающих решения, значительно бы возросла. Решение этой проблемы состоит в использовании группы прогнозов (ансамбля) по ряду отличающихся начальных условий для одной модели или группы моделей численного прогноза с различными, но равновозможными приближениями. Ансамбль прогнозов охватывает ряд возможных результатов, обеспечивая диапазон данных, где могут возрастать неопределенности. В результате по ансамблю прогнозов можно автоматически получить информацию о вероятностях, применительно к требованиям потребителей.
Субъективные вероятности окружают нас, при том что мы в большинстве своем их не замечаем. Это все разовые, невоспроизводимые события. И репутация экспертов и предсказателей зависит от того, насколько правильны их прогнозы.
Комбинации вероятностей
Одно из самых важных правил теории вероятностей — правило умножения. Если два события независимы друг от друга — то есть одно из них никак не влияет на исход другого, — вы получите вероятность того, что они оба произойдут, перемножив вероятности каждого. Если вы подкидываете монету и вытягиваете карту, то вероятность того, что у вас получатся и орел, и черви, высчитывается с помощью умножения двух отдельных вероятностей: 1/2*1/4 = 1/8.
Не все события независимы. Например, вероятность того, что официант принесет вам кетчуп, при условии, что вы только что заказали гамбургер, выглядит так:
P (кетчуп | гамбургер),
где вертикальная прямая | читается как «при условии». Благодаря подобной записи исчезает необходимость в большом количестве слов, и математическая формула получается короткой.
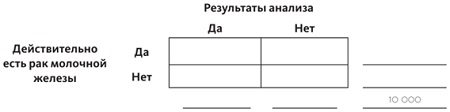
Вы можете подсчитать вероятности, используя формулу Байеса, но гораздо проще и нагляднее это сделать с помощью таблички, состоящей из четырех частей и описывающей все возможные сценарии (см. также метод деревьев или естественной частоты).
Рассмотрим пример. Вероятность того, что у женщины есть рак молочной железы, равна 0,8%. Если рак молочной железы есть, то вероятность того, что маммография его покажет, равна только 90%, так как сам аппарат неидеален и, бывает, идентифицирует не все случаи заболевания. Если же у женщины нет рака молочной железы, вероятность положительного результата равна 7%. А теперь предположим, что у женщины, выбранной для опроса случайно, тест показал положительный результат, — какова вероятность того, что у нее и правда рак молочной железы?
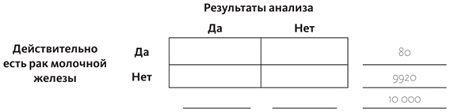
Для начала нарисуем нашу табличку. Чтобы нам было легче считать, давайте возьмем круглое число: предположим, речь идет о 10 тысячах женщин:
Вероятность того, что у женщины рак, равна 0,8%, иными словами, он у 80 женщин из 10 тысяч. Так как, общая сумма равна 10 тысячам, получается, что во второй строке нужно вписать 10 000 – 80 = 9920:
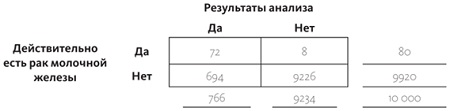
Что касается 80 женщин, у которых действительно есть рак молочной железы, у 90% из них результаты будут положительными (90% от 80 равно 72), а у 10% результат будет отрицательным (10% от 80 равно 8):
У 7% женщин, у которых нет рака молочной железы, анализы все равно покажут положительный результат. 7% от 9920 составляет 694. А это значит, что в нижнюю правую ячейку таблицы нужно занести число 9920 – 694 = 9226:
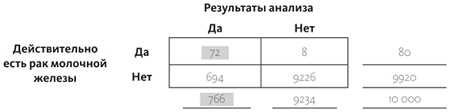
Условная вероятность того, что у женщины рак молочной железы, при условии, что результаты анализов были положительны, подсчитывается так: делим показатель левой верхней ячейки на итог под левым столбцом, это 72/766. Т.е., даже с положительной маммографией вероятность того, что у вас на самом деле есть рак молочной железы, равна всего 9,4%. Все объясняется тем, что заболевание достаточно редкое (оно встречается менее чем в одном случае из тысячи), а аппараты, с помощью которых проводят диагностирование, неидеальны:
Условные вероятности не работают в обратном направлении. Множество судебных дел стали результатом неправильного использования условных вероятностей, которое внесло путаницу в ранее установленные факты. Судебный эксперт может правильно подсчитать, что вероятность случайного совпадения крови с места преступления с кровью подсудимого составляет 1%. И это совсем не то же самое, что сказать, что вероятность невиновности подсудимого равна 1%. Судебный эксперт говорит о вероятности совпадения группы крови при условии, что подсудимый невиновен.
P (совпадение крови | невиновность).
Говоря простым языком, о «вероятности того, что мы бы нашли совпадение, если бы подсудимый был на самом деле невиновен». Но это не та же самая цифра, которую вы хотите узнать, — какова вероятность того, что подсудимый невиновен при условии, что кровь совпала:
P (совпадение крови | невиновность) ≠ P (невиновность | совпадение крови).
ЧАСТЬ 2. ОЦЕНКА СЛОВ
Откуда мы знаем?
Человек — существо социальное, мы любим рассказывать истории, и мнение другого человека легко может сбить нас с толку. Столкнувшись с новыми или противоречивыми утверждениями, мы тщательно изучаем их, и принимаем решение, будучи и судьей, и присяжными в одном лице. Важная часть этого процесса — поиск экспертного мнения.
Поиск экспертов
Даже самые авторитетные эксперты могут ошибаться. В начале 2000-х правительство США сильно заблуждалось насчет наличия у Ирака оружия массового поражения. Если приводить примеры из других, менее политизированных сфер, то можно вспомнить о том, что ученые годами считали, что у человека 24 пары хромосом, а оказалось 23.
Не то чтобы эксперты никогда не ошибаются, просто чисто статистически у них больше шансов оказаться правыми. При этом, интеллект и компетенция обычно проявляются в какой-то определенной области, в противовес распространенному убеждению, что сведущий человек сведущ во всем.
Иерархия источников. Научные статьи, рецензируемые специалистами в данной области, обычно более надежны, нежели книги, а книги, выпущенные крупными издательствами, как правило, имеют лучшую репутацию, чем самиздат (подробнее см. Ася Казанцева. В интернете кто-то неправ! Научные исследования спорных вопросов). Некоторые источники, находящиеся на хорошем счету, предпочитают проверять факты, прежде чем их публиковать. Однако в последнее время в сети появилось много источников, которые не придерживаются единых стандартов, а в некоторых случаях и сообщают горячие непроверенные новости. Как и в случае с графиками и статистическими данными, нельзя слепо верить всему, что мы читаем в достоверном источнике, точно так же, как и нельзя автоматически отвергать все, что мы узнаем из сомнительного источника.
Оценивая слова эксперта, нужно помнить, что он может выражать предвзятое мнение, сам того не осознавая. В случае с опухолью хирург-онколог может назначить операцию, радиационный онколог — облучение, а онколог-терапевт — химиотерапию. Психиатр может порекомендовать лекарство от депрессии, в то время как психолог ограничится психотерапией. Как гласит одна старая поговорка, «когда у вас есть молоток, все вокруг похоже на гвозди».
Специальный сервис Google позволяет вам посмотреть, кто еще ссылается на ту же страничку, на которой находитесь вы. Вбейте слово «link:» («ссылка»), а затем URL сайта, и Google найдет все сайты, которые на него ссылаются (например, на запрос link:breastcancer.org выдаст две сотни сайтов, которые ссылаются на соответствующий сайт).
Alexa.com рассказывает о демографических данных посетителей сайта: из какой они страны, какое у них образование, какие сайты они посетили непосредственно до того, как зайти на этот. Подобная информация позволит вам лучше понять тех, кто пользуется вашим сайтом, а также их мотивацию.
Сайт Scholar.Google.com содержит больше ограничений, чем Google или другая поисковая система, он ограничивает результаты поиска научными статьями, хотя и не проверяет журналы, и тут тоже попадаются псевдонаучные публикации. Но он отлично отсеивает то, что даже не похоже на научную статью.
Пропущенные, недооцененные альтернативные объяснения
Оценивая заявление или какой-то довод, спросите себя, нет ли иной причины — помимо той, о которой вам известно, — которая могла бы вызвать рассматриваемую ситуацию. Всегда найдутся какие-то альтернативные объяснения, и наша задача — их взвешивание и сравнение с теми, что предлагаются.
Менталисты, предсказатели судьбы, экстрасенсы зарабатывают неплохие деньги, демонстрируя, казалось бы, невиданное мастерство чтения мыслей. Их умения можно было бы объяснить тем, что им известен некий секрет, доступна некая скрытая сила, идущая вразрез со всем, что мы знаем о причинах и следствиях, а также о самой природе пространства-времени. Есть альтернативное объяснение: они только иллюзионисты, они показывают фокусы и попросту лгут о том, как им удается все то, что они делают.
Те, кто пытается предсказать будущее, не обладая никакими талантами экстрасенса, — военные лидеры, экономисты, бизнес-стратеги, — часто заблуждаются в своих выводах, потому что не учитывают альтернативное объяснение. Это привело к возникновению в мире бизнеса такого термина, как сценарное планирование, — когда приходится рассматривать все возможные варианты развития событий, даже те, что кажутся маловероятными. Порой это бывает очень сложно, и ошибаются даже эксперты (см. Матс Линдгрен, Ханс Бандхольд. Сценарное планирование: связь между будущим и стратегией).
Предположим, у вас есть гипотеза. Вы даже можете найти доказательства, подтверждающие вашу точку зрения. Но если вы всецело настроены на поиски только доводов в поддержку своей идеи, ваше исследование нельзя назвать качественным, потому что вы игнорируете доказательства обратного — их может быть мало, а может и много, но вы о них не узнаете, потому что не обратили на них внимания. Ученые это называют «избирательный подход» — вы выбираете только те данные, которые доказывают вашу гипотезу. Качественное же исследование требует сохранения объективности в любом вопросе.
Если попросить сто человек в одной комнате подбросить монетку пять раз, то шанс, что у одного из них пять раз подряд выпадет решка, равен 97%. Почему это так парадоксально? Эволюция не подготовила нас к интуитивному пониманию случайности. Также помните, что маленькие выборки обычно не очень репрезентативны. В целом аномалии вероятнее в маленьких выборках. Большие выборки отражают то, что происходит в мире, гораздо точнее. Статистики называют это законом больших чисел.
Давайте представим себе уличную игру: в шляпе или корзине лежат три карты, у каждой из которых две стороны, — одна карта красного цвета с обеих сторон, одна белая с обеих сторон, а третья белого цвета с одной стороны и красного с другой. Мошенник на удачу вытягивает карту и не глядя на нее, кладет на стол. Все видят красную сторону карты. Он ставит пять долларов, что оборотная сторона тоже будет красной. Он хочет, чтобы вы думали, будто вероятность тут 50 на 50, — вы соглашаетесь, делаете ставку, думая, что оборотная сторона будет белой. Ход ваших мыслей может быть таким: Одна сторона красная. То есть он вытянул либо красно-красную карту, либо красно-белую. Следовательно, оборотная сторона будет либо красная, либо белая — вероятность одинакова в обоих случаях. Могу себе позволить принять эту ставку.
Попробуем представить себе происходящее визуально. Вот эти три карты:
Рис. 12. Три карты
Если на столе красная сторона карты, то это может быть один из трех возможных вариантов. В двух из них другая сторона красная и только в одном случае белая. Поэтому ваш шанс один из трех, а не один из двух. Многие из нас забывают, что в случае с красно-красной карты она может лечь любой из сторон. Если бы на стол легла белая сторона карты, мошенник сделал бы ставку на то, что вторая сторона также белая.
Контрзнание
«Контрзнание» — термин, который придумал британский журналист Дэмиен Томпсон. Это дезинформация, поданная как факт, в который уже начала верить некая критическая масса людей. Контрзнанию помогает развиваться интрига: а что, если все это правда? Люди — существа социальные, любящие слушать и рассказывать истории. Да, мы ценим удачную выдумку. Контрзнание изначально привлекает нас налетом знания, со всеми этими цифрами или статистическими данными, но дальнейшее изучение показывает, что под всем этим нет никакой базы — распространители контрзнания надеются, что цифры так вас впечатлят (или запугают), что вы просто слепо их примете. А еще они часто цитируют «факты», которые таковыми не являются.
Томпсон вспоминает случай, когда один его друг, говоря о теракте 9/11, завладел вниманием слушателей благодаря одному весьма правдоподобно звучащему наблюдению. «Обратите внимание», — сказал он. — Башни осели вертикально, а не обрушились. Температура горения авиационного топлива недостаточна для плавления стали. Это под силу только управляемому взрыву».
Ученые и другие сторонники рационального мышления различают вещи, которые являются истиной (например, фотосинтез или то, что Земля вращается вокруг Солнца), и те, что, вероятно, истинны, например, что атака 9/11 была осуществлена с помощью двух угнанных самолетов, а не силами правительства США. По этим версиям существует разное количество доказательств, и они в разной степени убедительны. И небольшое количество алогичностей не ставит под сомнение и уж тем более не подрывает теорию, которая зиждется на тысячах доказательств. Хотя все эти алогичности лежат в основе теорий заговора. Разница между ложной теорией и истиной — вероятностная.
Когнитивный психолог Пол Словик показал, что люди сильно переоценивают относительные риски, если ситуации, их вызывающие, получают повышенное внимание со стороны прессы (см. Канеман, Словик, Тверски. Принятие решений в неопределенности: Правила и предубеждения). Отчасти освещение события в прессе зависит от того, получится ли из него хорошая история. Смерть в результате утопления более драматична, неожиданна, и, возможно, ее легче предотвратить, чем смерть от рака желудка, — налицо все элементы, необходимые для хорошей, хотя и печальной истории. Поэтому о случаях утопления сообщают чаще — а нам кажется, что они происходят чаще.
ЧАСТЬ 3. ОЦЕНКА МИРА
Существует два укоренившихся мифа о том, как работает наука. Согласно первому, наука развивается без сучка и задоринки, а ученые всегда и во всем согласны друг с другом. Согласно второму, один-единственный проведенный эксперимент дает нам ответы на все вопросы об изучаемом явлении, а после публикации результатов эксперимента наука делает скачок вперед. Настоящая наука полна противоречий, сомнений и споров о том, что уже известно.
Особенность процесса познания такова, что стоит сформировать убеждение или принять какое-то утверждение, как нам становится очень сложно выбросить его из головы, даже несмотря на огромное количество контраргументов.
Чтобы подготовить хороший эксперимент — или оценить тот, что уже был кем-то проведен, — нужно уметь находить альтернативные объяснения. Получая в результате эксперимента неожиданные данные, мы радуемся, потому что узнали то, чего не знали раньше.
Насколько мы знаем, есть известное известное, то есть вещи, о которых мы знаем, что мы их знаем. Мы также знаем, что существует известное неизвестное: иными словами, есть вещи, которых мы не знаем. Но ведь существует и неизвестное неизвестное — вещи, о которых мы не знаем, что мы их не знаем.
Министр обороны США Дональд Рамсфелд
Мы можем наглядно представить варианты, предложенные министром Рамсфелдом, в такой четырехчастной табличке:
Байесовский метод в науке и в суде
Пользуясь байесовским методом, мы назначаем гипотезе субъективную вероятность (априорную), а затем уточняем ее в свете собранных данных (апостериорная вероятность, потому что именно эти данные мы получаем, проведя эксперимент). Согласно байесовской теории, маловероятные утверждения требуют большей доказательной базы, чем те, что заслуживают большего доверия. Ученым следует быть гораздо требовательней к тем доводам, которые идут вразрез со стандартными теориями или моделями, нежели к тем, что согласуются с ними.
Применение правила Байеса, возможно, лучше всего можно проиллюстрировать на примере из судебной практики. Один из краеугольных принципов судебного дела был сформулирован французским врачом и юристом Эдмоном Локаром: любой контакт оставляет след. По его мнению, правонарушитель либо оставляет следы на месте преступления, либо забирает их с собой — на себе, на одежде, — и тогда можно легко понять, где он был и что делал.
Предположим, злоумышленник пробрался в конюшню, чтобы дать допинг лошади накануне большой гонки. Нам может быть известно, что не было следов взлома, следовательно, подозреваемый должен быть одним из 50 человек, имевших доступ к конюшне.
Наша априорная гипотеза состоит в том, что подозреваемый виновен с вероятностью 0,02 (один из 50 человек, имевших доступ). А теперь представим, что нашему злоумышленнику пришлось попотеть, чтобы справиться с лошадью, и на месте преступления остались следы крови. Как уверяют судебные эксперты, вероятность того, что образец крови подозреваемого совпадет с образцом, взятым на месте преступления, равна 0,85. Мы чертим четырехчастную табличку:
Теперь мы можем вычислить данные, которые должны будут оценить судья и присяжные.
P (Виновен | Совпадение) = 0,85 / 8,2 = 0,10
P (Невиновен | Совпадение) = 7,35 / 8,2 = 0,90
С учетом улик вероятность невиновности подозреваемого в девять раз выше, чем виновности. Начинали мы с 2%-ной вероятности, что он виновен, новая информация увеличила эту вероятность в пять раз, но все же вероятность того, что он невиновен, больше. Дополнительные улики могут еще больше сместить вероятности в сторону виновности.
Критическое мышление — это не то, что можно попробовать один раз и потом бросить. Это активный и постоянный процесс, требующий от нас байесовского мышления, обновления своих знаний по мере поступления новой информации.
Литература на русском языке
Гладуэлл М. Давид и Голиаф. Как аутсайдеры побеждают фаворитов. М.: Альпина Паблишер, 2014.
Хафф Д. Как лгать при помощи статистики. М.: Альпина Паблишер, 2015.
Хокинг С. Краткая история времени. СПб.: Амфора, 2010.
Уилан Ч. Голая статистика. Самая интересная книга о самой скучной науке. М.: Манн, Иванов и Фербер, 2016.