Ранее был рассмотрен полностью рандомизированный эксперимент и связанный с ним однофакторный дисперсионный анализ. В настоящей заметке будет изучен двухфакторный дисперсионный анализ, в ходе которого одновременно оцениваются два фактора. Мы рассмотрим лишь ситуации, в которых выборки имеют одинаковый объем n‘. [1]
Применение статистики в этой заметке будет показано на сквозном примере. Предположим, что вы — руководитель производства в компании Perfect Parachute («Идеальный парашют»). Парашюты изготавливаются из синтетических волокон, поставляемых четырьмя разными поставщиками. Совершенно очевидно, что одной из основных характеристик парашюта является его прочность. Вам необходимо убедиться, что все поставляемые волокна обладают одинаковой прочностью. Более того, на фабрике используется два вида ткацких станков: Jetta и Turk. Можно ли утверждать, что парашюты, изготовленные на станке фирмы Jetta, так же прочны, как и парашюты, произведенные на станках компании Turk? Существует ли разница между прочностью парашютов, сотканных из синтетических волокон разных поставщиков на разных станках? Чтобы ответить на этот вопрос, следует разработать схему эксперимента, в ходе которого измеряется прочность парашютов, сотканных из синтетических волокон разных поставщиков на разных станках. Информация, полученная в ходе этого эксперимента, позволит определить, какой поставщик и какой тип станка обеспечивают наибольшую прочность парашютов.
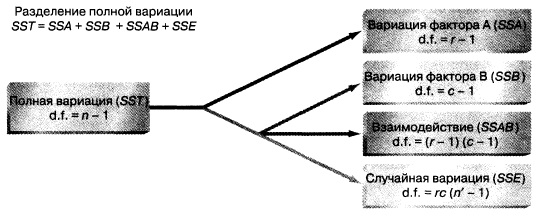
Вследствие сложности вычислений, особенно при большом количестве уровней каждого фактора и реплик, для двухфакторного анализа следует применять либо Excel, либо специализированное программное обеспечение. В двухфакторном эксперименте факторы А и В считаются взаимодействующими, если эффект фактора А зависит от уровня фактора В. Напомним, что в полностью рандомизированном плане полная сумма квадратов (SST) подразделяется на межгрупповую сумму квадратов (SSA) и внутригрупповую сумму квадратов (SSW). В двухфакторном эксперименте с одинаковым количеством реплик в каждой ячейке полная вариация (SST) подразделяется на сумму квадратов, соответствующую фактору A (SSA), сумму квадратов, соответствующую фактору В (SSB), сумму квадратов, учитывающую взаимодействие факторов А и В (SSAB), и сумму квадратов, возникающую вследствие случайной ошибки (SSE) (рис. 1).
Рис. 1. Разделение полной вариации в двухфакторном эксперименте
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
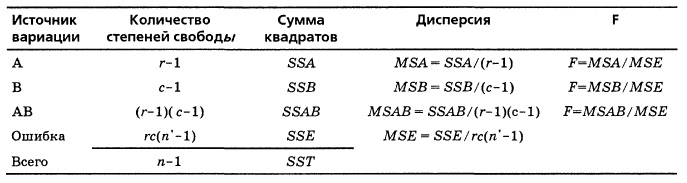
В двухфакторном дисперсионном анализе применяются три разных критерия:
- Для проверки гипотезы об отсутствии эффекта фактора А
- Для проверки гипотезы об отсутствии эффекта фактора В
- Для проверки гипотезы об отсутствии эффекта взаимодействия факторов А и В (рис. 2).
Каждая из трех нулевых гипотез отклоняется, если при заданном уровне значимости α соответствующая F-статистика (см. последнюю колонку рис. 2) больше верхнего критического значения F-распределения FU.
Рис. 2. Дисперсионный анализ в двухфакторном эксперименте
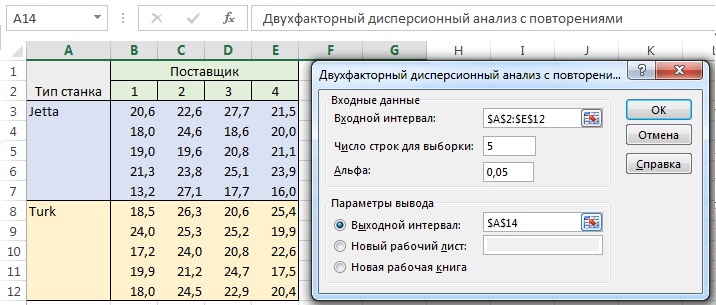
Для иллюстрации двухфакторного дисперсионного анализа вернемся к нашему сценарию. Допустим, что, будучи руководителем производства, вы решили сравнить поставщиков синтетических волокон, и оценить, на каком из станков выпускаются более прочные парашюты: Jetta или Turk. Кроме того, необходимо определить, зависит ли разница между четырьмя поставщиками от типа станков, на которых производятся парашюты. Итак, необходимо разработать план эксперимента, в котором каждому поставщику и типу станка соответствует пять парашютов (рис. 3). Для проведения анализа пройдите по меню Данные → Анализ данных и выберите строку Двухфакторный дисперсионный анализ с повторениями.
Рис. 3. Двухфакторный дисперсионный анализ с повторениями в Пакете анализа Excel
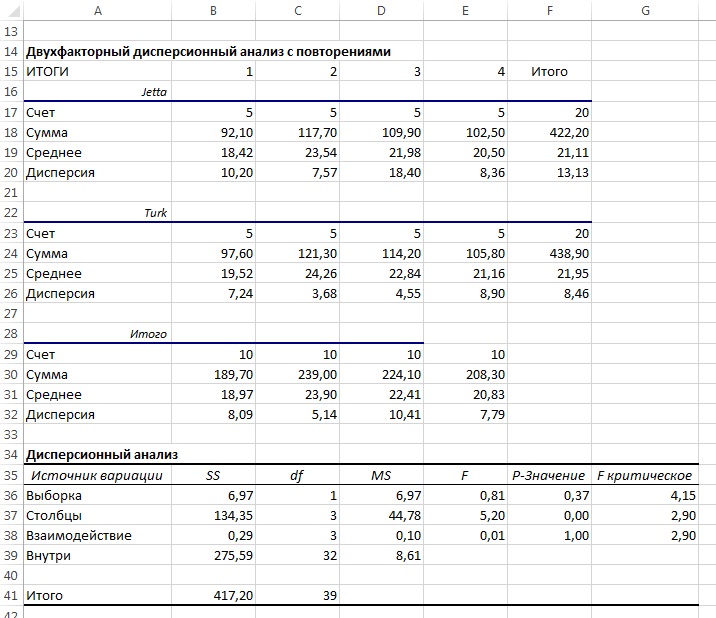
На рис. 4 показаны результаты двухфакторного дисперсионного анализа данных: объем выборки, сумма, арифметическое среднее и дисперсия каждой комбинации типа станка и поставщика. В первых двух таблицах приведены результаты дисперсионного анализа для всех типов станка, а в третьей — для каждого поставщика. В сводной таблице дисперсионного анализа идентификатор df обозначает количество степеней свободы, SS — сумму квадратов, MS — среднее квадратичное отклонение, F — вычисленную F-статистику.
Рис. 4. Результат двухфакторного дисперсионного анализа прочности парашютов
Чтобы проанализировать эти результаты, сначала следует проверить, существует ли взаимодействие между факторами А (типами станка) и В (поставщиками). Если эффект взаимодействия является значительным, дальнейший анализ ограничивается лишь оценкой этого эффекта. С другой стороны, если эффект взаимодействия незначителен, необходимо сосредоточиться на главных эффектах — потенциальных различиях между типами станков (фактор А) и поставщиками (фактор В).
Чтобы определить наличие эффекта взаимодействия при уровне значимости, равном 0,05, применяется следующее решающее правило: нулевая гипотеза об отсутствии эффекта взаимодействия отклоняется, если вычисленное значение F-статистики (см. таблицу Дисперсионный анализ, строку Взаимодействие столбец F на рис. 4), больше верхнего критического значения F-распределения (там же, столбец F-критическое). Поскольку F = 0,01 < FU = 2,90, а р-значение равно 0,998, гипотеза Н0 не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что факторы станка и поставщика взаимодействуют друг с другом. Следовательно, необходимо проанализировать главные эффекты.
При заданном уровне значимости, равном 0,05, в основе проверки разности между двумя станками (фактор А) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение F-статистики больше верхнего критического значения F-распределения (см. таблицу Дисперсионный анализ, строку Выборка на рис. 4). Поскольку F = 0,81 < FU = 4,15, а р-значение равно 0,37 и больше уровня значимости α = 0,05, гипотеза Н0 не отклоняется. Следовательно, у нас недостаточно оснований утверждать, что между прочностью парашютов, произведенных на разных станках, существует значимая разница.
При заданном уровне значимости, равном 0,05, в основе проверки разности между поставщиками (фактор В) лежит следующее решающее правило: нулевая гипотеза отклоняется, если вычисленное значение F-статистики больше верхнего критического значения F-распределения (см. таблицу Дисперсионный анализ, строку Столбцы на рис. 4). Поскольку F = 5,20 > FU = 2,92, а р-значение равно 0,005 и меньше уровня значимости, гипотеза Н0 отклоняется. Следовательно, можно утверждать, что между прочностью парашютов, произведенных из волокна, приобретенного у разных поставщиков, существует значимая разница. [2]
Интерпретация эффектов взаимодействия
Чтобы лучше разобраться во взаимодействии факторов, следует построить график средних значений в ячейках (т.е. средних значений, соответствующих конкретным уровням факторов), как показано на рис. 5 (в качестве данных для построения графика использованы области В19:Е19 и В25:Е25 рис. 4). Из графика средней прочности для каждой комбинации станок–поставщик следует, что две линии, соответствующие разным станкам, проходят почти параллельно друг другу. Это означает, что разности между средними величинами прочности парашютов, произведенных на разных станках, практически одинаковы для всех четырех поставщиков. Иначе говоря, между этими двумя факторами нет связи, что полностью подтверждается F-критерием.
Рис. 5. График средних значений прочности парашютов в зависимости от станков и поставщиков
В чем проявляется эффект взаимодействия? В некоторых ситуациях определенные уровни фактора А могут оказаться связанными с конкретными уровнями фактора В. Например, предположим, что некоторые парашюты оказываются более прочными, если они сотканы из определенных волокон на станках Jetta, а другие — если они сотканы из волокон других поставщиков на станках Turk. Если бы это было правдой, линии на рис. 5 не были бы параллельными и взаимодействие между факторами было бы статистически значимым. Следовательно, в этих ситуациях разница между станками не будет одинаковой при разных поставщиках. Это усложняет интерпретацию главных эффектов, поскольку разности, соответствующие одному фактору (например, типу станка), не согласуются с другим фактором (например, поставщиком). Проиллюстрируем эту ситуацию следующим примером.
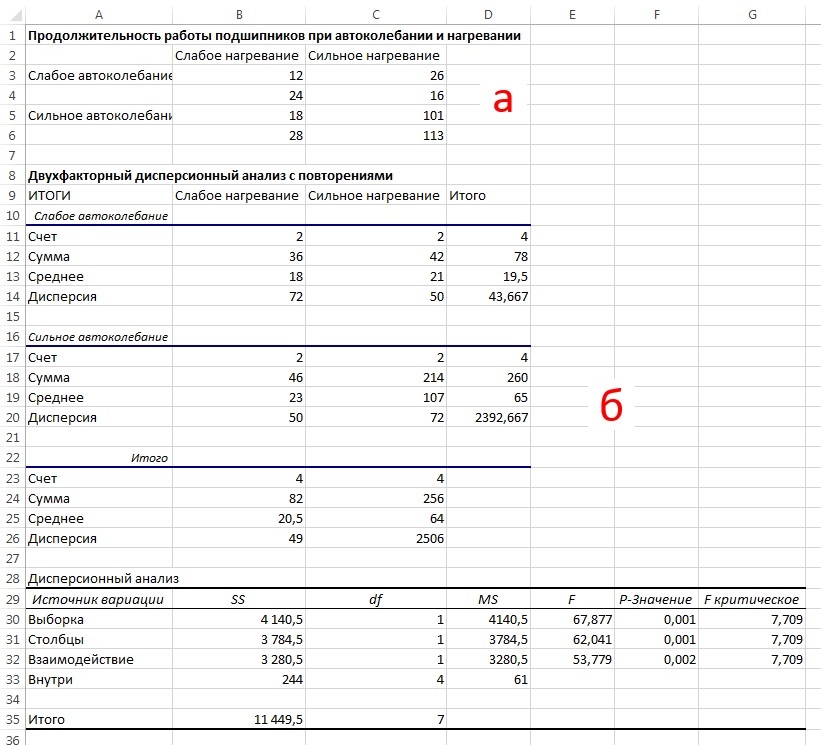
Пример.1. Интерпретация статистически значимых эффектов взаимодействия. Данные, приведенные на рис. 6а, характеризуют продолжительность работы подшипников под воздействием двух факторов: автоколебания и нагревания. Как влияют автоколебания и нагревание на продолжительность работы подшипников? Результаты двухфакторного дисперсионного анализа продолжительности работы подшипников, полученные с помощью Пакета анализа в Excel приведены на рис. 6б. Обратите внимание на то, что, кроме сводной таблицы дисперсионного анализа, Excel вычисляет среднее значение для каждой комбинации двух факторов: степени автоколебаний и нагревания, а также среднее значение для каждого уровня факторов. Для того чтобы проанализировать эти результаты, сначала необходимо определить, наблюдается ли статистически значимый эффект взаимодействия факторов автоколебания (фактор А) и нагревания (фактор В). При уровне значимости α = 0,05 нулевую гипотезу об отсутствии эффекта взаимодействия следует отклонить, поскольку p-значение равно 0,0018, т.е. меньше 0,05. Кроме того, F-статистика равна 53,78 и превышает величину 7,71 — верхнее критическое значение F-распределения с одной степенью свободы в числителе и четырьмя степенями свободы в знаменателе.
Рис. 6. (а) Продолжительность работы подшипников при автоколебании и нагревании; (б) Результаты двухфакторного дисперсионного анализа продолжительности работы подшипников
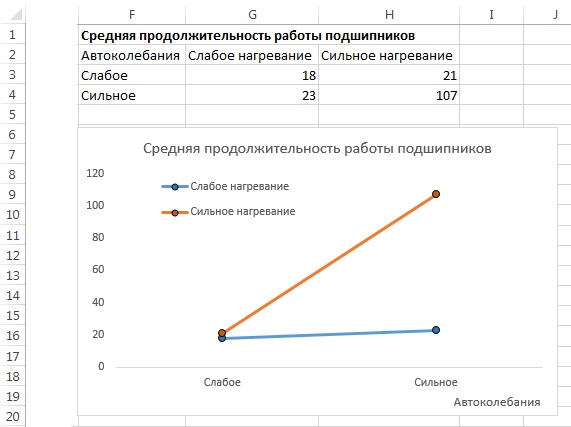
Значимый эффект взаимодействия между автоколебанием и нагреванием можно проследить на рис. 7. Поскольку графики средних значений продолжительности работы подшипников при слабом и сильном нагревании, соответствующие двум степеням автоколебаний, не параллельны, разности между средними значениями продолжительности работы при двух типах автоколебаний и двух степенях нагревания неодинаковы. Наличие эффекта взаимодействия факторов усложняет анализ основных эффектов. Теперь невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабых и сильных автоколебаниях, поскольку при разных степенях нагревания эта разность неодинакова. Аналогично невозможно определить, существует ли статистически значимая разница между средними продолжительностями работы подшипников при слабом и сильном нагревании, поскольку при разных степенях автоколебаний эта разность неодинакова.
Рис. 7. График средних значений продолжительности работы подшипников по ячейкам
Множественные сравнения
Если эффект взаимодействия факторов не важен, для множественного сравнения нескольких факторов можно применять процедуру Тьюки-Крамера.
Критический размах процедуры Тьюки-Крамера для фактора А
где QU — верхнее критическое значение распределения стьюдентизированного размаха, имеющего r степеней свободы в числителе и rc(n’ – 1) степеней свободы в знаменателе.
Критический размах процедуры Тьюки-Крамера для фактора B
где QU — верхнее критическое значение распределения стьюдентизированного размаха, имеющего с степеней свободы в числителе и rc(n’ – 1) степеней свободы в знаменателе.
Применим процедуру Тьюки-Крамера к задаче о прочности парашютов (см. рис. 3). Анализ сводной таблицы дисперсионного анализа, представленной на рис. 4, показывает, что статистически значимым является лишь один главный эффект. При уровне значимости, равном 0,05, нет оснований утверждать, что между двумя типами станков (Jetta и Turk) существует значимая разница (фактор А), однако между четырьмя поставщиками (фактор В) эта разница существует. Таким образом, дальнейший анализ должен концентрироваться на разностях между поставщиками.
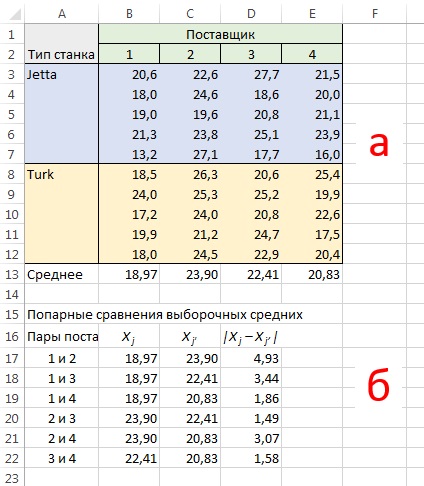
Поскольку компания, производящая парашюты, имеет четыре фирмы-поставщика, следует проверить 4(4 – 1)/2 = 6 пар поставщиков (рис. 8а). Вычислим модули разности между соответствующими средними значениями по выборкам отдельных поставщиков (рис. 8б).
Рис. 8. (а) Исходные данные о прочности парашютов; (б) попарные сравнения средних значений по выборкам отдельных поставщиков
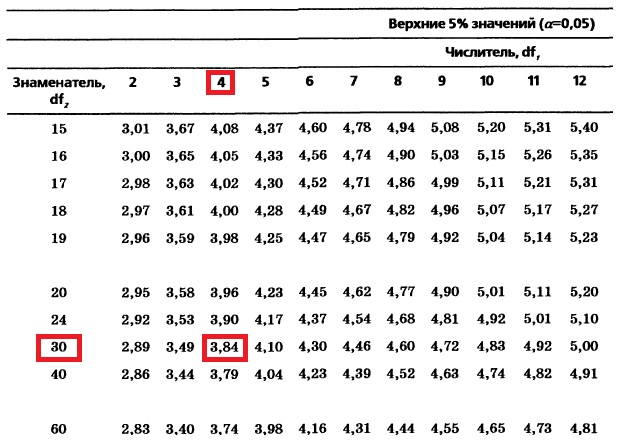
Чтобы вычислить критический размах, обратимся к данным на рис. 4: MSE = 8,61, r = 2, с = 4, n’ = 5, rc(n’ – 1) = 32. При α = 0,05, с = 4 и rc(n’ – 1) = 32 по таблицам размаха (рис. 9) определим, что QU — верхнее критическое значение F-статистики с двумя степенями свободы в числителе и 32 степенями свободы в знаменателе — приближенно равно 3,84. Используя формулу (2), получаем:
Рис. 9. Критическое значение стьюдентизированного размаха QU; к сожалению, в Excel нет функции, рассчитывающей такой размах
Только одно значение разности между средними значениями (рис. 8б) больше 3,56. Статистически значимая разница существует лишь между первым и вторым поставщиком. Как и при однофакторном дисперсионном анализе, приходим к выводу, что средняя прочность парашютов, сотканных из волокон, приобретенных у первого поставщика, значительно ниже, чем у второго.
Предыдущая заметка Однофакторный дисперсионный анализ
Следующая заметка Блочный рандомизированный эксперимент
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 664–676
[2] К аналогичному выводу мы пришли и при проведении однофакторного дисперсионного анализа по поставщикам.


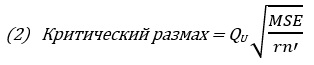
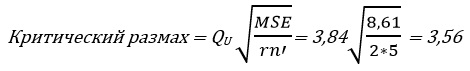
Можно выводить значения из Таблицы значений критерия Стьюдента (t-критерия) в Excel по функции: =СТЬЮДРАСПОБР(0,05;30)
мои благодарности автору. Считаю это самым доступным объяснением двухфакторного анализа с повторением.