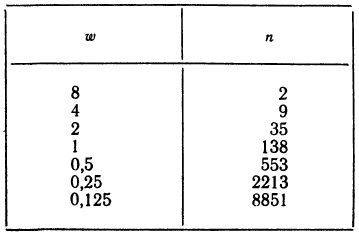
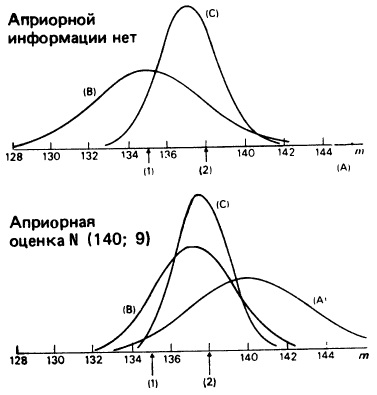
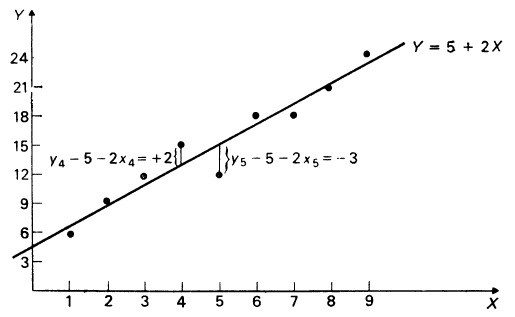
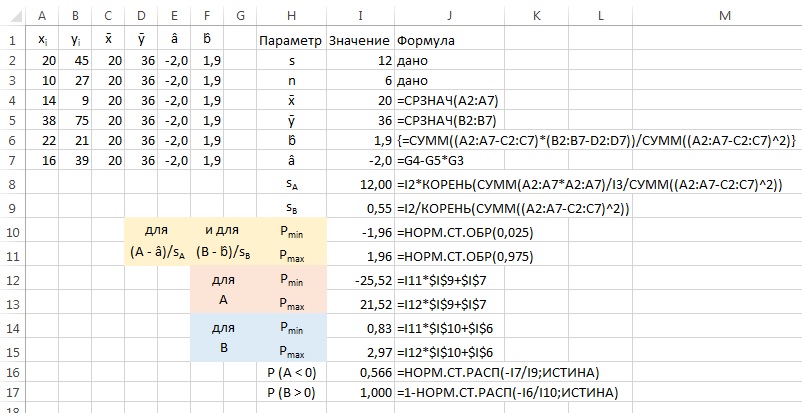
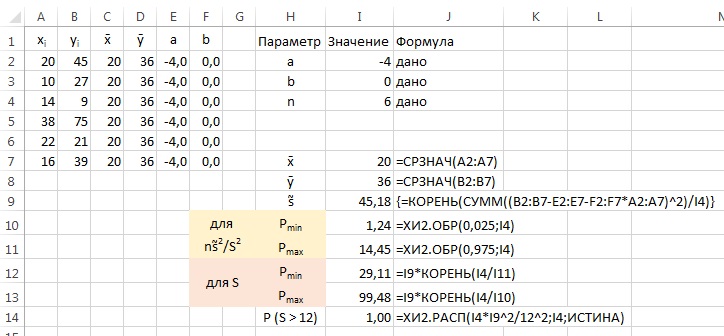
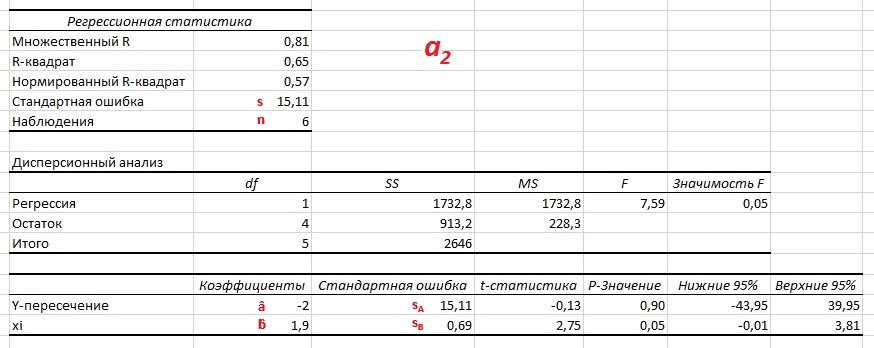
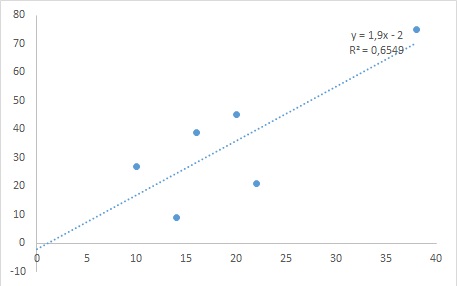
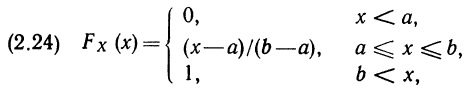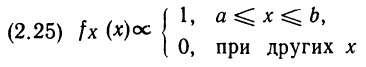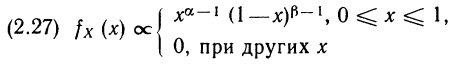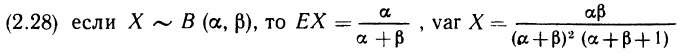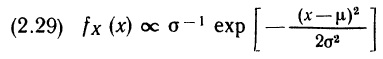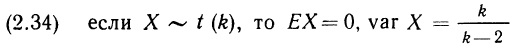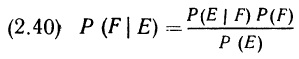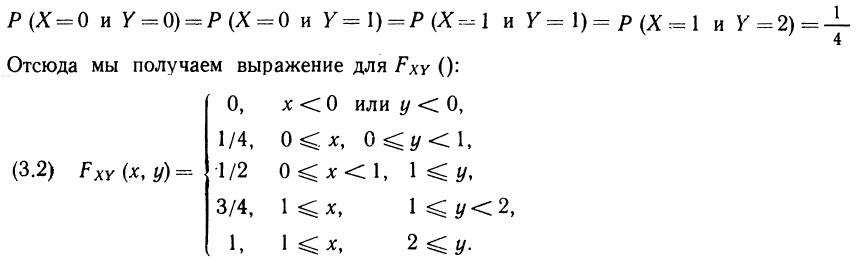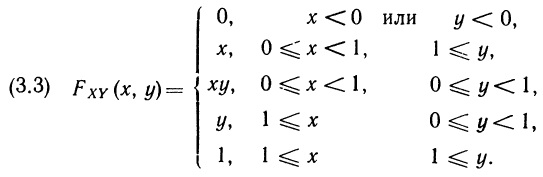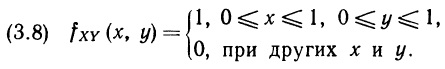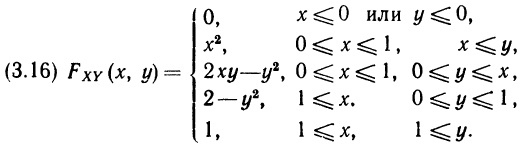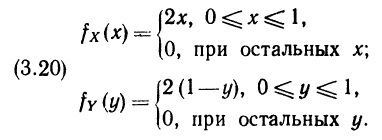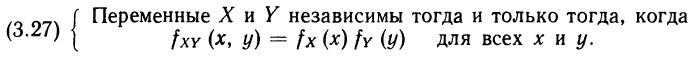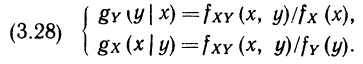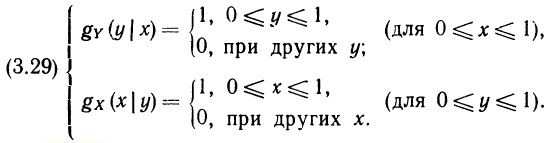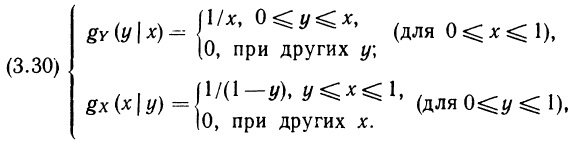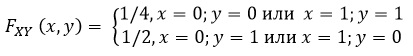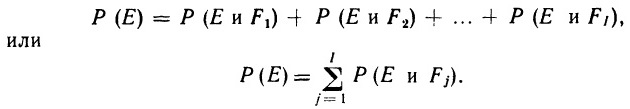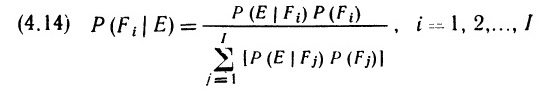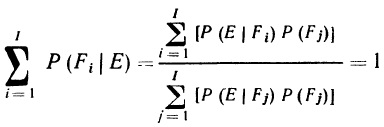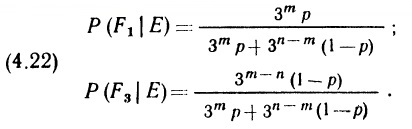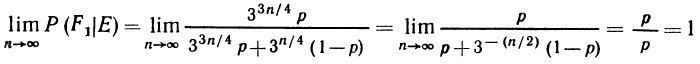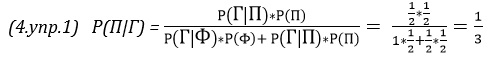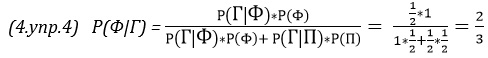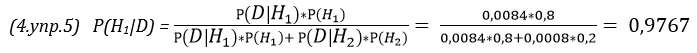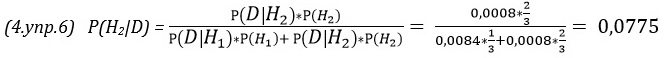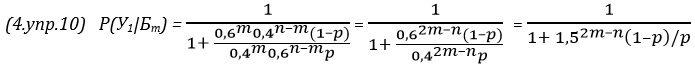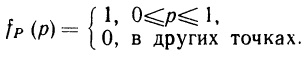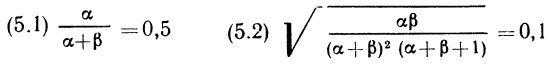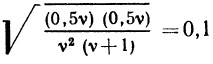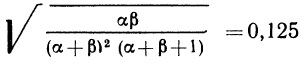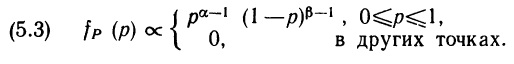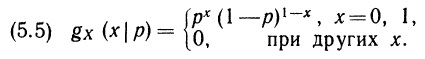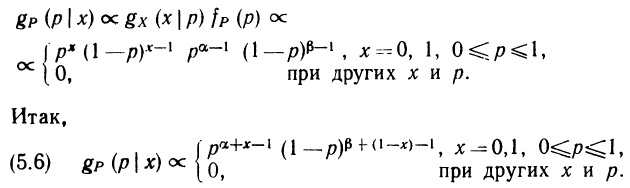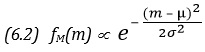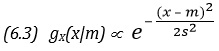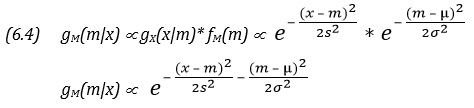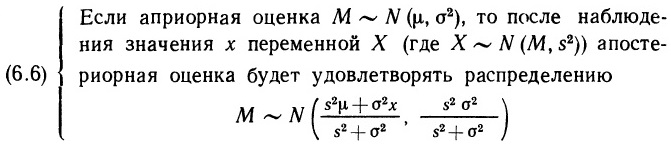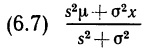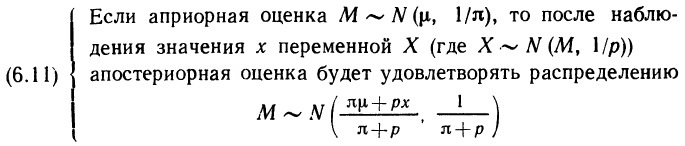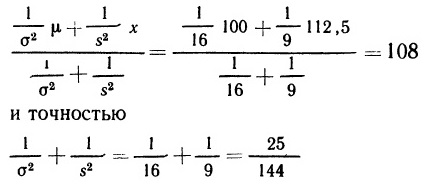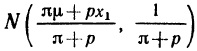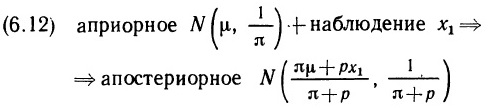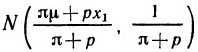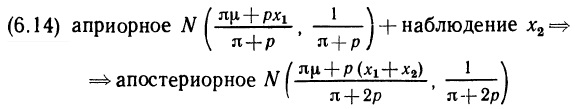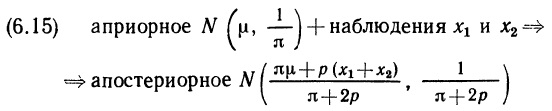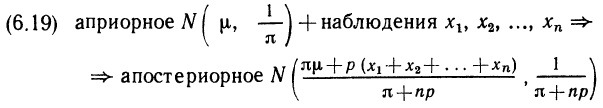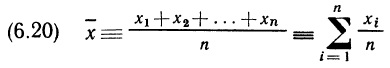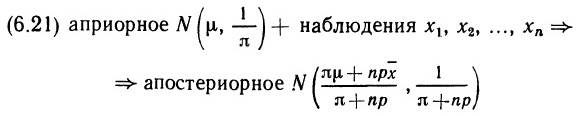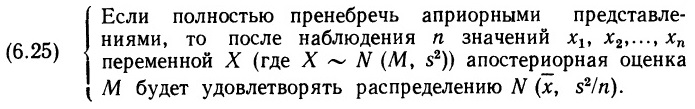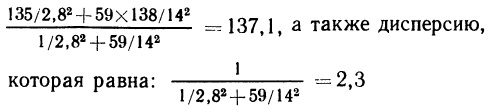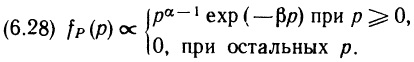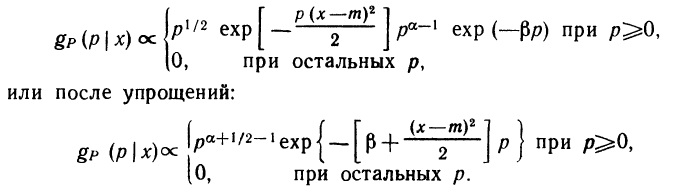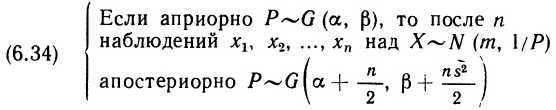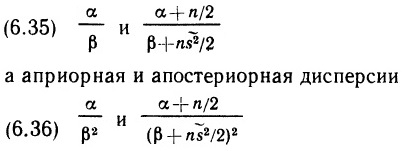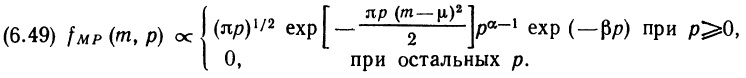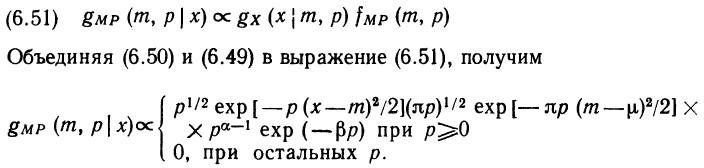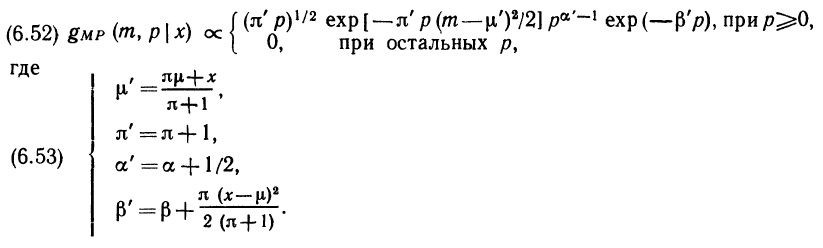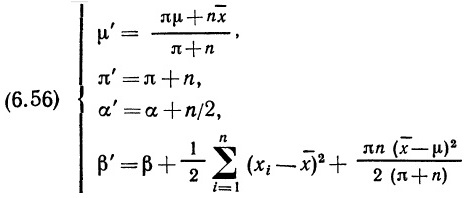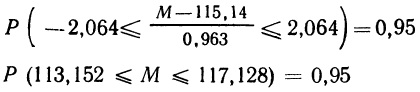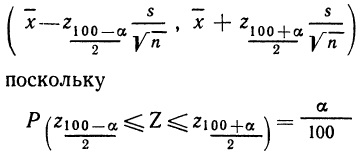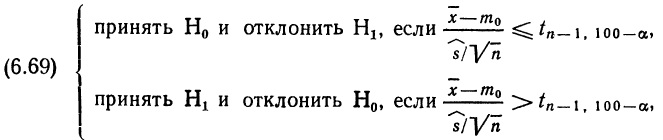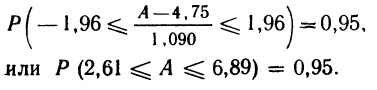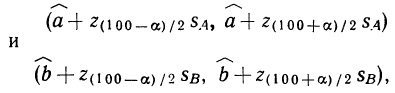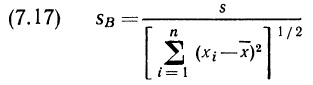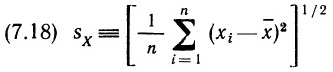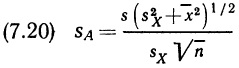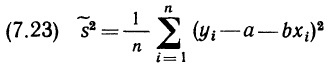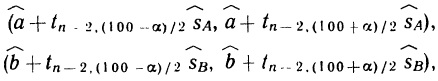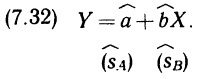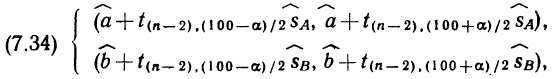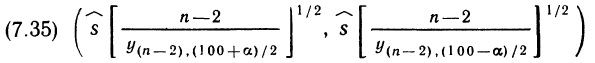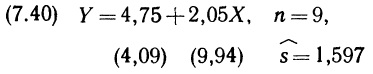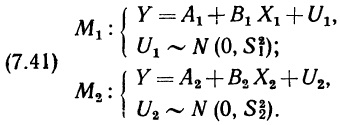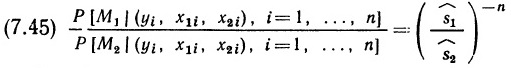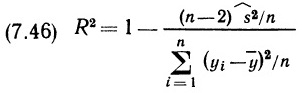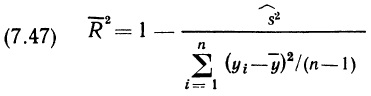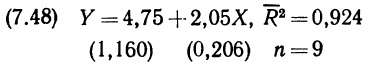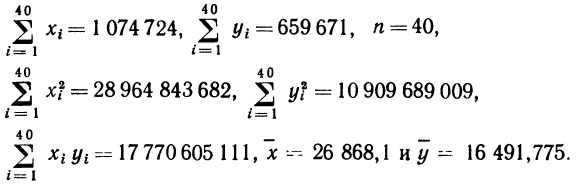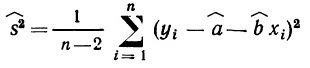Почему меня интересует байесовская статистика, я недавно описал в заметке Идеи Байеса для менеджеров. В какой парадигме действуют большинство менеджеров: если я наблюдаю нечто, какие выводы могу из этого сделать? Чему учит Байес: что должно быть на самом деле, чтобы мне довелось наблюдать это нечто? На мой взгляд, новая (Байесианская) парадигма позитивно влияет на качество принимаемых управленческих решений. На русском языке довольно много беллетристики на тему Байеса (см., например, список литературы, приведенный в конце упомянутой выше заметки). А вот серьезное изложение я нашел только в представляемой сегодня книге.
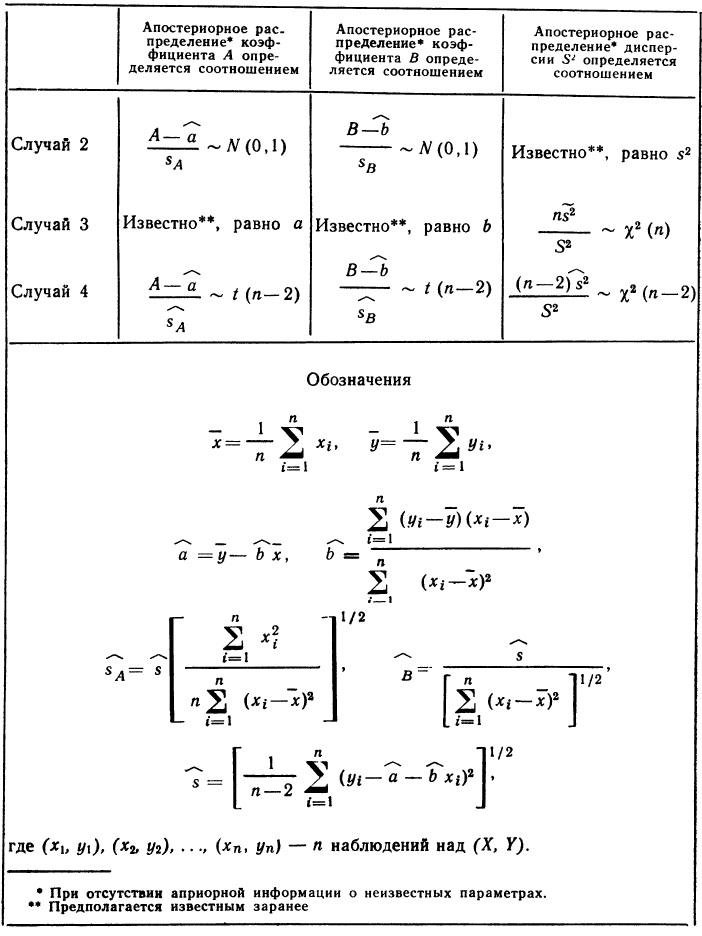
Перед вами учебное пособие по теории статистического вывода, обладающее тремя отличительными особенностями. Во-первых, оно рассчитано на тех, для кого статистика является инструментом в работе (в первую очередь, на экономистов). Во-вторых, оно написано просто, поскольку адресовано читателю, имеющему минимальную предварительную подготовку. В-третьих, методологической основой предлагаемого курса является байесовский подход, уже давно развиваемый в математической статистике в качестве альтернативы классическому.
Хей Дж. Введение в методы байесовского статистического вывода. — М.: Финансы и статистика, 1987. — 336 с.
Скачать подробный конспект в формате Word или pdf, примеры в формате Excel2013
(в тексте много математических символов, поэтому рекомендую файлы Word и pdf, которые содержат меньше неточностей в обозначениях)
Глава 1. Введение
Глава 2. Основные понятия теории вероятностей
Глава 3. Вероятностные распределения нескольких переменных
Глава 5. Доли элементов совокупности
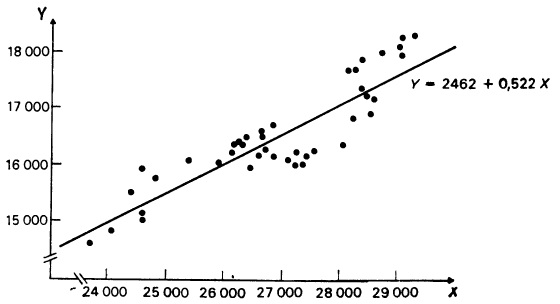
Глава 7. Элементарный регрессионный анализ
Глава 8. Развитие регрессионного анализа (главы 8 и 9 не законспектированы)
Глава 9. Уравнения с одновременными уравнениями
Глава 1. Введение
Статистика разрабатывает инструментарий, помогающий принимать решения в условиях неопределенности. Эта книга посвящена статистике и адресована в первую очередь экономистам. Ее цель — показать, как статистика может помочь экономисту принимать решения в условиях неопределенности. Процесс накопления экономических знаний содержит две ключевые составляющие: описание представлений о некоторой конкретной теории или конкретном явлении, накопленных к определенному моменту времени, и ревизия этих представлений в свете новой информации о данной теории или данном явлении. По существу, наша книга и посвящена обсуждению этих двух составляющих.
Глава 2. Основные понятия теории вероятностей
Понятие вероятности играет ключевую роль в статистике. Статистические утверждения об экономических параметрах и экономических гипотезах формулируются в вероятностных терминах. Например, анализ данных о доходе и потреблении проливает свет на значение предельной склонности к потреблению и позволяет сделать вывод в следующей форме: «имеющиеся наблюдения свидетельствуют, что с вероятностью 0,95 значение предельной склонности к потреблению лежит между 0,59 и 0,63».
Центральной для данной книги является идея субъективной вероятности, состоящая в том, что вероятностные утверждения трактуют как субъективные ожидания. Так, например, я могу выразить свою точку зрения на исход предстоящих парламентских выборов, сказав: «Я полагаю, что имеется 50 шансов «за» и 50 шансов «против» того, что консервативная партия сформирует очередное правительство». Аналогично вы можете выразить свой взгляд на возможный исход следующего мирового чемпионата по футболу, сказав: «Я думаю, английская команда имеет 1 шанс из 10 стать победительницей». То обстоятельство, что эти вероятности субъективны, конечно, не должно препятствовать согласию между отдельными индивидами по поводу какого-либо конкретного обстоятельства или явления. Например, мы оба можем согласиться с тем, что «при подбрасывании монеты имеется 50 шансов из ста появления герба». Вообще можно ожидать, что формируемые людьми вероятностные оценки зависят как от количества имеющейся в их распоряжении информации, так и от способа (или процесса) ее использования. Таким образом, можно ожидать большего согласия между людьми, обладающими большей долей общей для них информации. Пусть теперь ряд индивидов, каждый из которых является «рациональным человеком» (этот термин мы разъясним позже), сталкивается с одним и тем же большим количеством информации. Тогда их оценки после получения этой информации будут обнаруживать тенденцию к сближению независимо от того, какими были субъективные априорные ожидания каждого из них.
Индивидуальные вероятностные оценки некоторой неопределенной переменной или события зависят от аккумулированной индивидом информации об этой переменной или об этом событии. Правомерно ожидать изменения таких оценок по мере получения новой информации. Укажем на важное различие между понятиями «переменные» и «события». Занятия economics, как правило, предопределяют интерес к переменным, которые предполагаются квантифицированными; в частности, это могут быть доходы, цены, инвестиции. Однако в ряде случаев, в особенности, когда того требует более ясное описание ситуации, приходится обращаться к событиям. Например, «монета выпала гербом», «англичане победили на чемпионате мира», «консервативная партия формирует очередное правительство». (На практике различие становится менее явным, если удается квантифицировать множество событий или описать переменную в терминах событий.)
2.2. Распределение, функция распределения вероятностей и функция плотности распределения вероятностей
Предположим, что перед нами стоит задача описания и обобщения некоторой вероятностной оценки, соответствующей одной случайной переменной. Обозначим эту переменную X. Договоримся теперь о важных для дальнейшего изложения обозначениях и будем пользоваться прописными буквами для обозначения самой переменной величины, а соответствующими строчными буквами для обозначения принимаемых ею значений. Например, если нас интересует предельная склонность к сбережению, то эту переменную величину можно обозначить через Х, а х будет одно из ее конкретных значений, скажем 0,59 или 0,63. Если же речь идет о личном недельном доходе (в фунтах стерлингов), то через X можно обозначить этот доход, а х будет использоваться для обозначения конкретного значения дохода, допустим 120 или 150.
Вероятностное утверждение будет сокращенно записываться в виде Р(), где в скобках должно заключаться некоторое утверждение относительно переменной величины. Так, например,
Р (0,59 ≤ X ≤ 0,63) = 0,9 есть сокращенная запись того, что «с вероятностью 0,9 значения переменной X лежат на отрезке с концами 0,59 и 0,63» (здесь это утверждение рассматривается, конечно, как субъективная оценка того, кто его сформулировал). Аналогично запись Р(120 ≤ X) = 0,5 можно расшифровать следующим образом: «имеется 50 шансов из 100, что значения переменной X не меньше 120». В более общем случае выражение Р(х1 ≤ X ≤ х2) = а означает, что «с вероятностью а значения переменной X лежат между х1 и х2». Конечно, параметр а, в силу его смысла, заключен между 0 и 1, т. е. 0 ≤ а ≤ 1.
Введем теперь понятие функции распределения вероятностей, с помощью которого можно реализовать один из способов описания индивидуальных вероятностных оценок относительно некоторой переменной X. Функция распределения вероятностей переменной X (или просто функция распределения переменной X) обозначается FХ () и определяется тождеством
(2.1) FХ(х) ≡ Р(X ≤ х)
Таким образом, FХ() выражает вероятность того, что значение переменной X не превосходит х. Обычно, когда не возникает неясности, индекс X опускают и вместо FХ() пользуются упрощенной записью F(). Функция FХ() определена для всех значений х между –∞ и +∞; она принимает значения от 0 до 1 включительно. Более того, следующие свойства функции FХ() имеют место независимо от того, о какой переменной X идет речь:
Все эти свойства вытекают из того, что FХ(х) служит мерой вероятности, «накопленной» на всем интервале от –∞ до х включительно, т.е. кумулятивной вероятности.
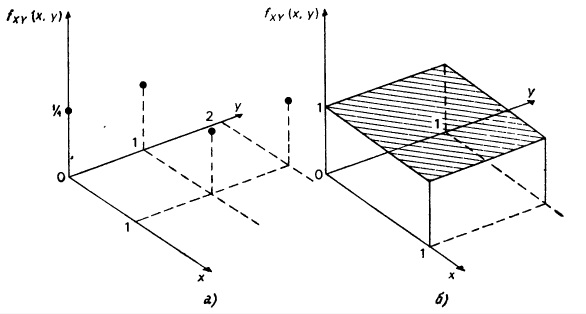
Приведем три простых примера, иллюстрирующих понятие функции распределения вероятностей. В первом примере переменная X — число, изображенное на выпавшей грани игральной кости. Возможные значения х — числа 1, 2, 3, 4, 5 и 6. Вообще говоря, вероятностные оценки относительно каждого из этих значений переменной X могут варьироваться от индивида к индивиду. Предположим, однако, что мы имеем дело со случаем, когда некто долгое время наблюдал бросание этой кости и пришел к выводу, что все ее шесть граней совершенно одинаковы. Эту индивидуальную оценку можно выразить так:
Определим теперь FХ(х) для всех возможных значений х. Очевидно, что FХ(х) = 0 для всех х < 1, поскольку переменная X не может принять значение, меньшее 1. FХ(1) = 1/6, ибо вероятность того, что переменная X примет значение, не превосходящее 1, в точности совпадает с вероятностью того, что эта переменная будет равна 1; FХ(х) = 1/6 для х в диапазоне от 1 до 2 (исключая края), так как между значения 1 и 2 нет ни одного значения, которое может принять переменная X. Далее, FХ(2) = 2/6. Вероятность для переменной X оказаться меньшей или равной 2 в точности равна вероятности для этой переменной принять одно из двух значений: 1 или 2, т.е. равна 2/6. И т.д. Изображенный на рис 2.1 график проясняет ситуацию.
Рис. 2.1. Функция распределения для чисел, выпадающих при бросании кости
Рассмотрим теперь второй пример, в котором переменная величина X имеет совершенно иную природу. Представим себе горизонтально расположенный диск, в центре его укреплена короткая вертикальная ось и на ней свободно вращается стрелка. Предположим, что диск по окружности равномерно и непрерывно калиброван от 0 до 1 (рис. 2.2, а). Определим теперь переменную X как принимающую значения, на которые указывает стрелка в момент ее останова после вращения. Как и прежде, вероятностные оценки по поводу ожидаемого значения переменной X могут изменяться от индивида к индивиду (в зависимости от аккумулированной каждым из них информации об эксперименте), но мы вновь будем рассматривать оценки индивида, считающего стрелку несмещенной и потому с одинаковым успехом ожидающего ее останова в любом возможном положении. В этом случае легко вывести вид функции распределения вероятностей. Так, FХ(0,5) = 0,5, поскольку имеется 1 шанс из 2, что стрелка остановится в правом полукруге; аналогично FХ(0,25) = 0,25, ибо есть лишь 1 шанс из 4.
Рис. 2.2. Эксперимент со стрелкой: а) окружность, непрерывно калиброванная от 0 до 1, б) функция распределения вероятностей переменной Х
Здесь обнаруживается закономерность, которую можно описать следующим образом: FХ(х) = х при 0 ≤ х ≤ 1. X не принимает значений, меньших 0, т.е. FХ(х) = 0 при х ≤ 0, и X не может стать больше 1, т.е. FХ(х) = 1 для х ≥ 1.
Сравнивая функции распределения из двух рассмотренных примеров, мы обнаружим одно их существенное сходство: графики обеих функций имеют горизонтальные линии. Эти линии указывают на значения х, которые переменная X не принимает (в первом случае это все числа, кроме целых от 1 до 6, во втором — все числа вне отрезка [0;1]). Мы можем также отметить и существенное различие между этими двумя функциями: горизонтальные линии графика первой функции соединяются вертикальными отрезками, т.е. функция совершает в каждой из шести точек скачок, а горизонтальные части графика второй функции соединяются отрезком наклонной прямой, что свидетельствует о непрерывном возрастании функции распределения. Отмеченное различие отражает неодинаковую природу исходных переменных величин: в первом примере переменная X дискретная, а во втором – непрерывная. (Во втором примере переменная X принимает все значения от 0 до 1, как бы пробегая их непрерывно, в то время как в первом примере значениями X являются только некоторые дискретные точки.) Как мы видели, трактовка основных понятий в дискретном и непрерывном случаях различна.
Заметим, что в каждом из двух рассмотренных примеров существует некоторое множество возможных значений переменной X и имеет место неопределенность относительно того, какое конкретное значение переменной можно будет наблюдать в данном частном случае (в результате бросания кости или вращения стрелки). В нашей книге речь идет главным образом о проблемах, постановка которых непременно связана с существованием неопределенности. Когда неопределенность отсутствует, то язык теории вероятностей не нужен. Вместе с тем определенность, или детерминированность, есть специальный случай неопределенности, и потому соответствующие методы могут быть применены и в этом вырожденном случае.
Рассмотрим переменную X, определенную как мой возраст на 26 сентября 1984 г. При отсутствии какой-либо информации обо мне ваша оценка X окажется неопределенной. (Как будет выглядеть ваша функция распределения?) Если же я скажу вам, что родился во время второй мировой войны, то это значительно сузит рамки неопределенности. (Какой станет ваша функция распределения теперь?) Если же я сообщу вам, что родился 26 сентября 1944 г., то всякая неопределенность исчезнет: мы окажемся перед фактом, что X = 40. Ваша функция распределения (в данном случае у каждого она окажется одной и той же) будет иметь вид, как на рис. 2.3а, с единственным скачком от 0 до 1 в точке х = 40.
Когда я прошу кого-то из своих студентов оценить мой возраст (значение переменной X в данном примере), типичный ответ до того, как я поделюсь с ними какой-либо информацией, таков: «Думаю, вы старше 36 лет, но вам не больше 42; в этом промежутке все значения кажутся мне одинаково возможными». Этой оценке соответствует функция распределения, изображенная на рис. 2.3б.
Рис. 2.3. Две функции распределения возраста автора: а) вырожденная (неопределенность отсутствует); б) невырожденная (неопределенность имеет место)
Функция распределения дает нам один из возможных способов представления вероятностных оценок значений некоторой переменной. Эта функция удобна тем, что ею можно пользоваться как в случае дискретных, так и в случае непрерывных переменных. Существует, однако, иное представление вероятностных оценок, интуитивно более оправданное и геометрически лучше интерпретируемое. Некоторое неудобство, правда, связано с тем, что формы этого представления различны для дискретного и непрерывного случаев. Начнем с первой, дискретной, формы.
Как уже отмечалось, отличительным свойством функции распределения дискретной переменной является наличие последовательности горизонтальных линий на ее графике, соединенных между собой вертикальными отрезками (скачками, ступенями) Эти скачки соответствуют тем дискретным значениям, которые переменная принимает, а величина скачка в каждой точке равна вероятности, с какой переменная принимает соответствующее значение. Чтобы описать скачок формально, предположим, что он происходит в точке X = х; в основании ступени значение функции распределения равно Р(X < х), а на вершине ступени оно равно Р(X ≤ х); разность между этими значениями есть Р(X ≤ х) — Р(X < х), т.е. Р(Х = х). Теперь мы можем определить новую функцию, обозначаемую fХ(), следующим образом: [1]
Следовательно,
(2.7) fX(х) = Р(X = х) для всех х,
что объясняет, почему fX() называют функцией вероятностей переменной X. Для первого из наших примеров график функции вероятностей переменной X изображен на рис. 2.4а.
Рис. 2.4. Функции вероятностей: а) X – число на выпавшей грани игральной кости; б) X — число выпадений герба при двукратном бросании монеты; в) функция распределения для варианта (б)
Еще один пример доставляет нам функция вероятностей переменной X, определенная как число благоприятных исходов при двух бросаниях «правильной» монеты (рис. 2.4б). На рис. 2.4в изображена соответствующая функция распределения. Следует отметить, что функция вероятностей равна нулю всюду, за исключением тех дискретных значений, которые может принимать переменная (целые числа от 1 до 6 — в первом примере, числа 0, 1, 2 — во втором).
Если мы попытаемся распространить данное только что определение на случай непрерывной переменной, то столкнемся с серьезными трудностями. Начнем хотя бы с отсутствия скачков у функции распределения непрерывной переменной (см. рис. 2.2б и 2.3б), в силу чего определение (2.6) применить непросто. Следует ли стремиться к сохранению свойства (2.7)? Обратимся к нашему второму примеру (см. рис. 2.2). Что такое, например, Р (X = 0,1)? Нуль! (В самом деле, Р (0,1 ≤ Х ≤ 0,9) = 0,8; Р (0,1 ≤ X ≤ 0,5) = 0,4; вообще, Р (0,1 ≤ X ≤ 0,1 + а) = а. Таким образом, положив а = 0, мы получим Р (0,1 ≤ X ≤ 0,1) = 0, т. е. Р (X = 0,1) = 0). Более того Р (X = х) = 0 для всех х! (Это вытекает из общего результата, в силу которого Р (х ≤ X ≤ х + а) = а.) Итак, если мы определим функцию вероятностей по аналогии с (2.7), то придется согласиться с тем, что она равна нулю при всех х (т.е. у функции распределения нет скачков). Подобная функция вероятностей вряд ли окажется полезной и ничего не сообщит нам о вероятностных оценках во втором примере.
Проблема в том, что во втором примере переменная X является непрерывной. Когда х пробегает значения от 0 до 1, вероятности накапливаются непрерывно; таких крупных «вкладов» в общую сумму, как могла внести точка в случае дискретной переменной, здесь не будет. В непрерывном случае нельзя, указав точку х, спросить, какова вероятность того, что именно она окажется интересующим нас частным значением. Оправданным будет вопрос о скорости аккумуляции вероятностей для каждого значения х. (Здесь может быть полезна аналогия: в какой бы точке ни находился движущийся автомобиль, неправомерно спрашивать, как далеко он уехал в данный момент; правильнее задать вопрос о скорости, с которой автомобиль в данный момент движется.) Скорость, с которой аккумулируется вероятность, задает тангенс угла наклона графика функции распределения к оси абсцисс: чем круче его наклон, тем быстрее идет накопление вероятностей в функции распределения. Теперь мы можем определить новую функцию, которую будем обозначать
(2.8) fХ(х) = F’Х(х) = dFХ(x)/dx
(≡ тангенсу угла наклона касательной FХ(х) к оси х). Введем следующее определение:
которое является следствием (2.8) и (2.1). Числитель выражения в квадратных скобках есть вероятность того, что X лежит в интервале [х, x + Δx], а знаменатель — длина этого интервала — есть плотность распределения вероятностей на интервале [х, x + Δx]. Таким образом, fX(x) — мера плотности вероятностей в точке х. Функцию fX() называют функцией плотности вероятностей переменной X или просто функцией плотности вероятностей. (Мы будем пользоваться одной и той же буквой для обозначения функции вероятностей в дискретном случае и функции плотности вероятностей в непрерывном случае, не опасаясь недоразумений, поскольку из контекста всегда ясно, о чем идет речь.)
Чтобы получить функцию плотности вероятностей непрерывной переменной из функции распределения вероятностей, нужно последнюю просто продифференцировать, см. (2.8). Так, функция плотности вероятностей для второго из рассмотренных выше примеров (эксперимент со стрелкой, см. рис. 2.2) задается (в силу (2.5)) соотношением:
(рис. 2.5, а). Как мы видим, функция плотности вероятностей принимает одно и то же значение в каждой точке отрезка [0, 1]; так как одинаково правдоподобен останов стрелки в любой точке данного интервала. Поскольку действия дифференцирования и интегрирования взаимно обратны, а fX() является производной от FX(), то функция FX() в свою очередь должна получаться из fX() интегрированием. Можно записать:
Рис. 2.5. Функция плотности вероятностей для эксперимента со стрелкой. Площадь заштрихованная на рис. 2.5, б равна 0,25 = Р (0,5 ≤ Х ≤ 0,75)
Геометрически такая запись попросту означает, что FХ(x) — площадь под той частью кривой fХ(). которая расположена левее х. Из (2.11) вытекает, что
Левая часть (2.12) есть не что иное, как разность Р (Х ≤ х2) – Р (X ≤ х1), т.е. Р (х1 < X ≤ х2); таким образом, (2.12) можно записать в виде
Геометрический смысл этого выражения весьма прост: вероятность того, что переменная X лежит между х1 и х2, задается площадью трапеции, которая образуется под частью кривой функции плотности вероятностей, ограниченной значениями х1 и х2. Итак (и это очень важное свойство), площади под кривой функции плотности вероятностей сами являются вероятностями. Отсюда сразу же следует, что общая площадь между графиком функции плотности вероятностей и осью ОХ равна единице, поскольку во всех случаях общая вероятность равна единице.
Чтобы проиллюстрировать этот важный результат, вновь обратимся к рис. 2.5, где изображена функция плотности вероятностей переменной X из эксперимента со стрелкой. Очевидно, что общая площадь под кривой fХ() равна 1. Более того, площади сами являются вероятностями, что видно на примере рис. 2.5, б: заштрихованная площадь равна 0,25 (прямоугольник высотой 1 и шириной 0,25) и этому же равна вероятность того, что переменная X лежит между 0,5 и 0,75 (другими словами, что стрелка остановится в юго-западном секторе круга).
Возвращаясь к общему случаю, заметим, что для непрерывной переменной различие, скажем, между Р (X ≤ х) и Р (X < х) несущественно, поскольку Р (X = х) равна нулю. Если же такого объяснения вам недостаточно, то обдумайте следующий эвристический аргумент: «Поскольку между 0 и 1 имеется бесконечно много равновероятных значений переменной X, то вероятность того, что эта переменная в точности равна одному из них, будет 1/∞, т.е. нуль».
Рассмотрим связь между функцией плотности вероятностей fX() и функцией распределения FX(). Первая из них характеризует тангенс угла наклона (к оси абсцисс) касательной, проведенной к графику второй в точке х, а вторая — площадь части плоскости между графиком первой и осью абсцисс до вертикальной прямой, соответствующей значению х. Пояснить эту взаимосвязь можно с помощью аналогии между предельными и совокупными затратами или предельным и совокупным доходом. Можно представлять себе FХ(х) как суммарную (общую) вероятность появления значений вплоть до х a fХ(х) — как предельную (маржинальную, дополнительную) вероятность значения х.
Обратимся вновь к эксперименту со стрелкой (см. рис. 2.2, а), но предположим теперь, что выбрана новая система измерений; северо-восточному сектору окружности соответствуют значения от 0 до 2, изменяющиеся непрерывно и равномерно, южной полуокружности — значения от 2 до 3, тоже непрерывно и равномерно меняющиеся, и, наконец, северо-западному сектору — значения от 3 до 5 (рис. 2. 6, а). Пусть переменная X определена как прежде, и мы предположим, что стрелка является «правильной», т. е. одинаково правдоподобно, что она остановится в любом из возможных положений. Прежде всего, построим функцию распределения; это можно осуществить, вычисляя ее значения для специфических значений переменной, включая точки на границах и внутри соответствующих промежутков, либо на основе некоторых более общих соображений. (Можно найти значение функции распределения для специфических значений аргумента: FX (1) = 0,125; FX (2) = 0,25; FX (2,25) = 0,375; FX (2,5) = 0,5; FX (2,75) = 0,625; FX (3) = 0,75; FX (4) = 0,875; FX (5) = 1)
Рис. 2.6. Модифицированный эксперимент со стрелкой: а) описание эксперимента; б) функция распределения; в) функция плотности вероятностей
Зная функцию распределения, нетрудно получить функцию плотности вероятностей путем дифференцирования. График первой из этих функций, изображенный на рис. 2.6, б, позволяет установить, что FX() имеет тангенс угла наклона к оси абсцисс, равный 1/8 на промежутке от 0 до 2; равный 1/2 на промежутке от 2 до 3; равный 1/8 на промежутке от 3 до 5 и равный 0 во всех остальных точках. Таким образом, fX () принимает значение 1/8 на промежутке от 0 до 2; значение 1/2 на промежутке от 2 до 3; значение 1/8 на промежутке от 3 до 5 и значение 0 в остальных точках (рис. 2.6, в). Из рис. 2.6, в видно, что общая площадь между графиком функции fX () и осью абсцисс равна 1, что непременно должно иметь место, если функция fX () построена правильно. (Это полезный и достаточно надежный способ проверки, которым следует пользоваться для самоконтроля.) Можно проверить, что площади трапеций под графиком функции fX () совпадают с соответствующими величинами вероятностей. Например, площадь между графиком функции fX () и осью абсцисс, ограниченная значениями переменной 1 и 2, равна 1/8, т. е. вероятности, что стрелка остановится в одной из точек этой дуги.
В данном разделе были введены три важные функции, с помощью которых можно описать вероятностные утверждения в случае одной переменной. Первая — функция распределения, применимая как для дискретных, так и для непрерывных переменных и позволяющая измерить кумулятивную вероятность. Вторая — функция вероятностей, она предназначена только для описания случая дискретной переменной и измеряет вероятность появления каждого из ее значений. Третья — функция плотности распределения вероятностей, она определена лишь для непрерывной переменной и служит мерой маргинальной (предельной) вероятности.
2.3. Обобщающие характеристики
Из определения функции распределения вероятностей (равным образом это относится и к функции вероятностей, и к функции плотности вероятностей) следует, что она содержит всю информацию об индивидуальной вероятностной оценке в случае одной переменной, т.е. является полной характеристикой. Эта полнота может в одних ситуациях оказаться удобной, а в других, когда возникают трудности с сопоставлением различных элементов, она становится препятствием для применения таких обобщающих функций. Наконец, не всегда подобная полнота необходима, поскольку лишь некоторые свойства оценок, построенных с помощью рассматриваемых функций, могут оказаться полезными при решении конкретной проблемы. Нас будет в дальнейшем интересовать случай, когда обобщение ключевых свойств вероятностной оценки оправдано, и целесообразно использование полученных функций в качестве полных характеристик. Обобщающие характеристики можно разбить на две основные группы: вероятностные интервалы (наименьшей длины) и более распространенные измерители центральной тенденции и разброса. Начнем с первой из этих двух групп.
Часто бывает полезным знать промежуток фиксированной длины, в который (в соответствии с индивидуальной точкой зрения) переменная попадает с наибольшей вероятностью, или же минимальный промежуток, в который эта же переменная попадает с фиксированной вероятностью. В частности, нас будет интересовать информация, содержащаяся в индивидуальных оценках типа: «переменная X почти наверняка (это значит, что с вероятностью 0,95) лежит между 120 и 132». Для достижения указанных целей введем понятие α-процентного вероятностного интервала: в общем случае это некоторый промежуток [х1; х2], для которого Р (х1 ≤ X ≤ х2) = α/100, т. е. имеется α процентов шансов, что переменная X лежит в этом промежутке. Рассмотрим эксперимент со стрелкой (см. рис. 2.2, а), а вероятностную оценку, содержащуюся в функции распределения, возьмем из рис. 2.2, б. Легко заключить, например, что 80-процентным вероятностным интервалом будет промежуток [0,1; 0,9]; 90-процентным—промежуток [0,05; 0,95], а 100-процентным вероятностным интервалом окажется промежуток [0; 1]. Однако не случайно речь шла о некотором вероятностном интервале, а не о конкретном, ибо существует много вероятностных интервалов, соответствующих одному процентному уровню. Чтобы ограничить число возможных вариантов, можно рассматривать симметричные вероятностные интервалы, как это было сделано в приведенных только что примерах. В более общем случае (в нашем примере это уже не приведет к уменьшению числа возможных интервалов) можно рассматривать α-процентный вероятностный интервал наименьшей длины, который формально определяется так:
Проиллюстрируем это определение на примере функции плотности вероятностей, график которой изображен на рис. 2.7.
Рис. 2.7. Треугольная функция плотности вероятностей
Для данного случая 95-процентный вероятностный интервал наименьшей длины будет задан промежутком с концами –0,7764 и + 0,7764 (точнее, от –1 + ![]() до 1 –
до 1 – ![]() . Вы можете проверить этот результат, равно как и то, что еще один 95-процентный вероятностный интервал будет задан конечными точками — 1 и +0,6838 (точнее, от —1 до 1 —
. Вы можете проверить этот результат, равно как и то, что еще один 95-процентный вероятностный интервал будет задан конечными точками — 1 и +0,6838 (точнее, от —1 до 1 — ![]() ). Заметим, что этот второй промежуток имеет большую длину (она равна 1,6838) в сравнении с первым, длина которого равна 1,5528, и является наименьшей. Обратим внимание и на то, что в нашем конкретном примере интервал наименьшей длины симметричен относительно нуля. Это отражает то обстоятельство, что функция плотности вероятностей также симметрична относительно нуля. Полученный результат может быть сформулирован и доказан в более общем виде: любой вероятностный интервал наименьшей длины для симметричной функции плотности вероятностей, имеющей единственную «вершину», имеет ту же ось симметрии. Это утверждение формулируется для непрерывной переменной следующим образом. Пусть Р (х1 ≤ X ≤ х2) = α/100. Промежуток [х1; х2] будет α-процентным вероятностным интервалом наименьшей длины для переменной X тогда и только тогда, когда fХ (х1) = fХ (х2). В дальнейшем будут рассматриваться только вероятностные интервалы наименьшей длины и поэтому соответствующее уточнение будет опускаться.
). Заметим, что этот второй промежуток имеет большую длину (она равна 1,6838) в сравнении с первым, длина которого равна 1,5528, и является наименьшей. Обратим внимание и на то, что в нашем конкретном примере интервал наименьшей длины симметричен относительно нуля. Это отражает то обстоятельство, что функция плотности вероятностей также симметрична относительно нуля. Полученный результат может быть сформулирован и доказан в более общем виде: любой вероятностный интервал наименьшей длины для симметричной функции плотности вероятностей, имеющей единственную «вершину», имеет ту же ось симметрии. Это утверждение формулируется для непрерывной переменной следующим образом. Пусть Р (х1 ≤ X ≤ х2) = α/100. Промежуток [х1; х2] будет α-процентным вероятностным интервалом наименьшей длины для переменной X тогда и только тогда, когда fХ (х1) = fХ (х2). В дальнейшем будут рассматриваться только вероятностные интервалы наименьшей длины и поэтому соответствующее уточнение будет опускаться.
Для непрерывной переменной всегда существует интересующий нас α-процентный вероятностный интервал. Однако для дискретных переменных его не всегда можно указать, поскольку неизбежно скопление значительных «масс» вероятности в дискретных точках. Рассмотрим в качестве иллюстрации пример с бросанием игральной кости, для которого функция распределения вероятностей изображена на рис. 2.1, а функция вероятностей— на рис. 2.4, а. Мы видим, что промежуток [3; 4] является 33,3-процентным вероятностным интервалом, промежуток [2; 5] — 66,7-процентным вероятностным интервалом, а [1; 6] — 100-процентным вероятностным интервалом. Однако невозможно обнаружить, например, 90-процентный или 80-процентный вероятностные интервалы. Проблема возникает, конечно, из-за того, что вероятности сосредоточены в шести точках, по 1/6 в каждой. Вместе с тем из-за этого вряд ли возникнут серьезные трудности при решении практических задач.
Обратимся теперь ко второй группе обобщающих характеристик, куда входят более употребительные измерители центральной тенденции и измерители разброса. Начнем с первых. Идея измерения центральной тенденции непосредственно отражается в таких понятиях, как «типичное», «среднее» или «представительное» значение переменной. Существуют различные способы для выражения этих понятий и все зависит от того, как их интерпретировать и какой смысл в них вкладывать.
Рассмотрим несколько наиболее распространенных способов измерения. Одной из естественных характеристик служит значение переменной X, которое является наиболее правдоподобным (в соответствии с индивидуальными вероятностными оценками). Это значение X, если оно единственно, называют модальным значением переменной X, или просто модой X. Формально понятие моды можно определить, как для дискретного, так и для непрерывного случаев следующим образом:
Итак, для дискретной переменной мода — такое значение переменной, которому соответствует наибольшая вероятность, а для непрерывной переменной это значение переменной, которому соответствует наибольшее значение плотности вероятностей. В двух из рассмотренных в этой главе примеров мода единственна: на графике, изображенном на рис. 2.4, б (функция вероятностей числа выпавших гербов при двукратном бросании монеты), мода равна 1; на графике, изображенном на рис. 2.7, мода равна 0. В остальных примерах модальное значение не было единственным: из рис. 2.4, а следует, что все значения переменной одинаково правдоподобны и потому каждое из них является модальным; то же самое можно сказать по поводу ситуации, соответствующей рис. 2.5; на графике, изображенном на рис. 2.6, в, можно указать отрезок модальных значений [2; 3].
Другой «представительной» характеристикой распределения служит значение переменной X, находящееся как бы в середине в том смысле, что большие его значения столь же правдоподобны для X, как и меньшие. Это значение X, если оно существует и единственно, называется медианным значением переменной X, или медианой X. Для непрерывной переменной медиану можно просто определить следующим образом:
Итак, Р (X ≤ mX) = Р (X ≥ mX) = 0,5. Другими словами, имеется 50 на 50 шансов, что значение X окажется больше или меньше медианы. На графике, изображенном на рис. 2.5, а, медиана равна 0,5; на графике рис. 2.6, в она равна 2,5; на графике рис. 2.7 она равна 0. Для дискретных переменных определение (2.16) не обязательно ведет к получению единственного значения mX: например, как видно из рис. 2.1, уравнению FX (x) = 0,5 удовлетворяют все значения х такие, что 3 ≤ х ≤ 4. В этом случае можно либо договориться, что все значения между 3 и 4 являются медианными, либо считать медианой значение 3,5. В других случаях определение (2.16) удается применить непосредственно. Например, в ситуации, соответствующей рис. 2.4, медиана, очевидно, равна 1.
Третьей характеристикой и последней из тех, которые мы рассматриваем в качестве «претендентов» на «представительное» отражение всех значений переменной X, является обычная арифметическая средняя величина. Для дискретных переменных это просто взвешенная средняя всех возможных значений переменной X, где весами служат соответствующие вероятности. Формально это определение записывают так:
Здесь суммирование осуществляется по всем значениям х (можно также сказать, что по всем значениям от –∞ до +∞ или по всем возможным значениям, поскольку fX(х) обращается в нуль, когда переменная не принимает соответствующих значений х).
Объясним теперь выбор обозначения ЕХ для арифметической средней. Воспользуемся двумя иллюстративными примерами. Первый — бросание игральной кости (см. рис. 2.4, а). Здесь X принимает значения 1, 2, 3, 4, 5 и б, причем каждому соответствует вероятность 1/6. Пользуясь определением (2.17), вычислим значение ЕХ:
Второй пример — два бросания монеты (см. рис. 2.4, б). Здесь X — число выпадений герба в двух бросаниях — может принимать значения 0, 1 и 2, которым соответствуют вероятности 1/4, 1/2 и 1/4. С помощью определения (2.17) получим:
Этот последний результат можно интерпретировать так: в среднем число выпадений герба при двух бросаниях монеты равно 1. Такая интерпретация естественна. Однако на полученное в итоге значение 1 можно взглянуть с иной точки зрения — как на ожидаемое число выпадений герба в двух бросаниях монеты. Именно в силу этого рассматриваемая нами средняя величина записывается как EX: Е — начальная буква английского слова expected, и ЕХ означает ожидаемое значение X.
Возвращаясь теперь к примеру с бросанием кости, отметим некоторую «экстравагантность» выражения: «ожидаемое число, изображенное на выпавшей грани, равно 3,5» — ведь грани с таким числом не существует! Предположим, однако, что вы принимаете участие в игре в которой каждый поочередно бросает кость и за каждую единицу выпавшего числа платит 1 фунт. Тогда вы можете ожидать, что один круг этой игры обойдется вам (в среднем) в 3,5 фунта.
Выражение (2.17) определяет ожидаемое значение для дискретной переменной; для непрерывной переменной соответствующее определение имеет вид:
Интегрирование здесь ведется по всем значениям х (безразлично, будем ли мы говорить, что оно ведется по всем значениям от –∞ до +∞ или утверждать, что рассматриваются все возможные значения х, так как итог будет один и тот же, ибо fХ (х) обращается в нуль при всех значениях х, которые не относятся к возможным). Выражение (2.18) означает, что ЕХ является взвешенной средней (всех!) различных значений Х, причем роль весов выполняют плотности вероятности для соответствующих значений х. Например, в эксперименте со стрелкой, соответствующая функция плотности вероятностей приведена в (2.10), а ее график — на рис. 2.5, а. С помощью (2.18) мы обнаружим, что
Таким образом, ожидаемое значение X в эксперименте со стрелкой равно 1/2, что вполне согласуется с интуитивными представлениями.
Если распределение симметрично, то ожидаемое значение переменной определяет ось симметрии. Более того, если у симметричного распределения существуют единственная мода и единственная медиана, то они также совпадают с точкой, через которую проходит ось симметрии. Таким образом, для симметричного унимодального (т.е. с единственной модой) распределения все три характеристики — мода, медиана и средняя совпадают. Этот результат интуитивно совершенно ясен. Для несимметричных распределений подобное утверждение не имеет места.
Помимо сведений о «среднем» или «типичном» значении вероятностной оценки, полезно знать что-то о «разбросе», или «рассеянии», около этой величины. Как и для «средней» можно указать различные числовые меры разброса. Здесь мы рассмотрим лишь некоторые из них. В качестве одной из наиболее очевидных мер рассеяния можно указать длину некоторого α-процентного вероятностного интервала. Так, если 95-процентный вероятностный интервал переменной X имеет длину 10 единиц, а 95-процентный вероятностный интервал переменной Y равен 5 единицам, то естественно заключить, что у переменной X разброс больше, чем у переменной Y. Конечно, при этом каждому значению а будет соответствовать своя мера разброса, и понятие дисперсии не получит тем самым однозначного числового отражения.
Альтернативный подход к измерению разброса основан на измерении рассеяния по отклонению значений переменной от ее средней: если одной переменной соответствуют большие отклонения от ее средней величины, чем другой переменной, то естественно считать первую более «дисперсной» по сравнению со второй. Однако нельзя взять в качестве подобной меры просто взвешенную среднюю всех отклонений, поскольку эта величина окажется тождественно равной нулю. Преодолеть возникшее препятствие можно, заменив среднюю самих отклонений на среднюю их абсолютных величин или среднюю квадратов отклонений. Последний вариант лучше, ибо полученное в итоге выражение удобнее для математических преобразований. Найденная таким образом мера разброса известна как дисперсия переменной X. Для случая дискретной переменной формальное определение выглядит так:
Здесь суммирование вновь ведется по всем х. К сожалению, использование квадратов отклонений приводит к тому, что размерность дисперсии оказывается вдвое большей по сравнению с размерностью Х; так, если переменная X измеряется в дюймах, то ее вариация — в дюймах в квадрате. Чтобы мера дисперсии обладала такой же размерностью, как исходная переменная, приходится извлечь из вариации квадратный корень; полученную в итоге величину называют стандартным отклонением переменной X:
Для иллюстрации вновь обратимся к примеру с бросанием игральной кости, функция вероятностей для которого изображена на рис. 2.4. Переменная X принимает значения 1, 2, 3, 4, 5 и 6, причем каждое с вероятностью 1/6. Это приводит к тому, что ожидаемое значение X равно 3,5. Поэтому отклонения от средней соответственно составят: –2,5; –1,5; –0,5; 0,5; 1,5 и 2,5. (Заметим, что взвешенная средняя этих величин равна нулю, — на это указывалось выше.) Соответствующие значения квадратов отклонений: 6,25; 2,25; 0,25; 0,25; 2,25 и 6,25. Применяя (2.20), определим дисперсию переменной X:
Оба результата интуитивно не очевидны.
Формула (2.20) позволила получить дисперсию для дискретной переменной. Для случая непрерывной переменной воспользуемся таким определением:
Здесь интегрирование, как и в случае других определений, ведется по всем х. Заметим, что соотношения (2.20) и (2.22) связаны одно с другим так же, как в (2.17) и (2.18): в случае дискретной переменной используется знак ∑, а в случае непрерывной переменной — знак ∫; когда в выражение для дискретной переменной входит fХ (х), в соответствующем выражении для непрерывной переменной участвует fХ (х) dx. Стандартное отклонение для непрерывной переменной будет равно корню квадратному из значения дисперсии, как в формуле (2.21).
Для иллюстрации вновь обратимся к примеру со стрелкой, функция плотности вероятности для которого имеет вид (2.10), а ее график изображен на рис. 2.5, а. Мы уже вычислили ожидаемое значение X; оно оказалось равным 0,5. Воспользуемся определением (2.22) и рассчитаем для данного примера дисперсию:
Вновь оба полученные результата нельзя назвать интуитивно ясными.
Существует несколько способов измерения разброса, отличных от только что рассмотренных, но мы не будем на них останавливаться поскольку это не потребуется для дальнейшего изложения. Можно характеризовать с помощью числовых выражений не только центральную тенденцию и дисперсию, но и другие свойства вероятностной оценки, скажем ее асимметрию (они также здесь не приводятся). Все обобщающие характеристики, которыми мы будем дальше пользоваться, были выше рассмотрены. Это — вероятностные интервалы, средние, дисперсии и стандартные отклонения.
2.4. Некоторые важные распределения (случай одной непрерывной переменной)
Есть ряд стандартных вероятностных распределений, с которыми приходится часто сталкиваться на практике, в частности в экономической статистике. Чтобы упорядочить описание случайной переменной, таким стандартным распределениям дают названия и обозначения, выводят их свойства и наиболее часто встречающиеся числовые характеристики. В этом разделе мы рассмотрим пять стандартных распределений, наиболее часто встречающихся в последующих главах: равномерное (прямоугольное) распределение, бета-распределение, нормальное распределение, гамма-распределение и t-распределение. Их практическое применение описано далее, а в этом разделе рассматриваются их свойства и общие характеристики.
Все пять стандартных распределений определяют для непрерывных переменных и поэтому пользуются функциями плотности вероятности, которые применяют и для графического изображения соответствующих распределений. Прежде чем двигаться дальше, напомним основные свойства этих функций: неотрицательность во всех точках; площадь прямоугольной трапеции между графиком или частью графика функции и осью абсцисс интерпретируется как вероятность; вся площадь между графиком функции и осью абсцисс равна 1.
Начнем с равномерного (прямоугольного) распределения. С ним мы уже сталкивались, рассматривая эксперимент со стрелкой (см. рис. 2.2); соответствующая ему функция плотности вероятностей изображена на рис. 2.5. Заметим, что эта функция постоянна на всем отрезке [0; 1]. Поэтому о переменной X из этого примера можно сказать, что она удовлетворяет равномерному распределению на отрезке [0; 1]. Тем самым учтены свойство несмещенности стрелки и то, что шкала от 0 до 1, охватывающая всю окружность, является равно мерной и непрерывной. Если шкала с такими же свойствами и на этой же окружности имеет начальное значение а, а конечное значение b, то переменная X будет удовлетворять равномерному (прямоугольному) распределению на отрезке [а; b]. Соответствующая функция плотности вероятностей имеет вид:
График этой постоянной на отрезке [а; b] функции изображен на рис. 2.8, а. Параллельный оси абсцисс отрезок графика отстоит от нее на расстоянии 1/(b – а), что вытекает из того общего для функций плотности вероятностей факта, что площадь между графиком такой функции и осью абсцисс равна 1 (в данном конкретном случае равна 1 площадь прямоугольника, опирающегося на отрезок [а; b]).
Рис. 2.8. Равномерное распределение на отрезке [а; b]: а) функция плотности вероятностей; б) функция распределения
Соответствующая функция распределения выглядит следующим образом:
а ее график изображен на рис. 2.8, б. Видно, что fХ () и FХ () связаны одна с другой: значение первой равно тангенсу угла наклона касательной к графику второй в данной точке, в то время как значение второй равно площади, заключенной между графиком первой и частью оси абсцисс (от –∞ до вертикальной границы, проходящей через данную точку).
Как мы уже отмечали, общая площадь под графиком любой функции плотности вероятностей должна быть равна 1. Начиная с данного момента, мы будем пользоваться этим важным свойством, чтобы упростить большую часть интересующих нас алгебраических выражений. В частности, с помощью этого свойства мы упростим запись функции плотности вероятностей для равномерного распределения (2.23):
Символ ∝ означает «пропорционально». Например, если у = 2х, или у = 5,3х, или в более общем случае у = kx, то у пропорционален х, т. е. у ∝ х. Множитель пропорциональности в формуле (2.25) определяется из условия, что общая площадь под кривой fХ () должна быть равна единице. Благодаря этому свойству мы можем не записывать множитель пропорциональности каждый раз, когда нас интересует форма распределения.
Анализируя рис. 2.8, б, можно заключить, что распределение симметрично относительно середины отрезка [а, b], т.е. относительно точки (а + b)/2 — средней для этого распределения. Воспользовавшись формулами (2.22) и (2.23), можно найти его дисперсию; она равна (b – а)2/12.
Введем теперь для утверждения «переменная X равномерно распределена на отрезке [a; b] сокращенную запись «X ~ U [а; b] и объединим полученные результаты:
Перейдем теперь к бета-распределению, хотя пока его практическая ценность не очевидна. Начнем с определения. Переменная X удовлетворяет бета-распределению с параметрами α и β (обозначают: X ~ В (α, β)), если ее функция плотности вероятностей имеет вид:
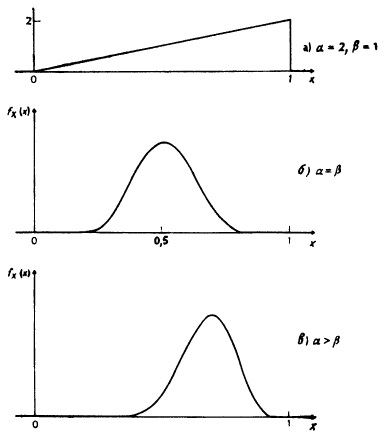
Здесь α ≥ 1, β ≥ 1, а множитель пропорциональности определяется так, чтобы площадь под кривой fX() равнялась 1. Заметим, что переменная X принимает значения только из отрезка [0; 1]; за его пределами функция плотности вероятностей обращается в нуль. Форма графика функции на отрезке [0; 1], очевидно, зависит от значений параметров α и β. Для некоторых значений параметров график функции можно легко построить. Во-первых, при α = β = 1 выражение (2.27) принимает вид (2.10), т.е. если X ~ В (1,1), то одновременно X ~ U [0,1]. Таким образом, равномерное распределение на отрезке [0, 1] представляет собой частный случай бета-распределения. Во-вторых, если α = 2 и β = 1, то функция плотности вероятностей выглядит как «правотреугольная» (рис.2.9, а). В-третьих, при α = 1, β = 2 функция плотности вероятностей становится «левотреугольной». Можно рассмотреть и другие примеры. Следует обратить внимание на одно важное свойство: если α больше β, то вершина распределения будет смещена вправо (как на рис. 2.9, в), если же α меньше β, то вершина будет смещена влево. Когда α и β равны, распределение симметрично (рис. 2.9, б).
Рис. 2.9. Примеры функции плотности вероятностей для бета-распределения
Среднее значение и дисперсия:
Можно доказать, что с увеличением α + β величина дисперсии уменьшается: если отношение α к β определяет положение средней, то сумма α + β характеризует величину дисперсии (другими словами, в первом случае важны относительные значения α и β, а во втором — абсолютные).
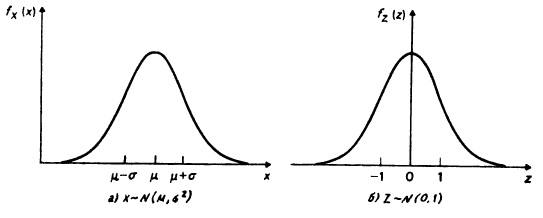
Перейдем теперь к наиболее часто применяемому распределению, которое называют нормальным, и тоже начнем с его определения. Переменная X удовлетворяет нормальному распределению со средней μ и дисперсией σ2 (сокращенно записывают X ~ N (μ, σ2)), если функция плотности вероятностей имеет вид:
Здесь коэффициент пропорциональности снова выбирается так, чтобы площадь под кривой fХ () равнялась 1. График функции плотности вероятностей нормального распределения изображен на рис. 2.10, а. С помощью (2.29) и рис. 2.10, а можно вывести ряд свойств нормального распределения. Во-первых, переменная X может принимать любые значения от —∞ до +∞, причем плотность вероятностей стремится к 0, когда х стремится к —∞ или к +∞. Во-вторых, распределение симметрично относительно своей средней. В-третьих, оно «колоколообразно», т. е. имеет форму опрокинутого вниз колокола. В-четвертых, у функции плотности вероятностей две точки перегиба: при х = μ – σ и х = μ + σ. (В точках перегиба вторая производная f”Х (.) обращается в нуль, и в этих точках тангенс угла наклона касательной к функции fX() достигает своего наибольшего (в точке μ – σ) или наименьшего в (в точке μ + σ) значения.) Дисперсия, как это можно установить, подставив (2.29) в (2.22), равна σ2, а величина стандартного отклонения равна σ. Таким образом, расстояние по оси абсцисс от точек перегиба до средней равно стандартному отклонению. Об этом свойстве полезно помнить, так как оно поможет правильно построить график функции плотности вероятностей нормального распределения (2.29).
Рис. 2.10. Два нормальных распределения
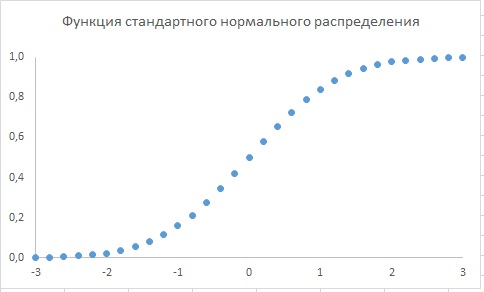
Важен частный случай нормального распределения при μ = 0 и σ = 1. В этом случае говорят, что переменная удовлетворяет единичному (или стандартному) нормальному распределению (ее обозначают буквой Z). Мы можем записать: Z ~ N (0, 1). Функция плотности вероятностей для Z является частным случаем (2.29), а графически она изображена на рис. 2.10, б. Заметим, что график этой функции симметричен относительно оси ординат, а ее точки перегиба соответствуют значениям ±1.
Обратим внимание и на то, что масштабы графиков, изображенных на рис. 2.10, различны как по горизонтали, так и по вертикали. Вместе с тем площади под каждым из этих графиков одинаковы и равны 1, как и должно быть для функции плотности вероятностей. Более того, поскольку обе функции имеют одинаковый вид, это означает, что площади соответственно равны: площадь между μ – σ и μ для fX () должна быть равна площади между –1 и 0 для fZ (); аналогично площадь под кривой fX () вправо от μ + σ должна быть равна площади под кривой fZ () вправо от 1. Так как площади под кривой плотности являются вероятностями, то можно записать, например, что
Функцию нормального распределения не удается вывести аналитически (поскольку невозможно проинтегрировать функцию плотности вероятностей (2.29)). Поэтому приходится прибегать к численным, а не аналитическим методам нахождения площадей под функцией плотности, которые необходимы при формировании вероятностных утверждений о нормально распределенных переменных. Именно в силу этого результат (2.30) приобретает большое значение: он позволяет вероятностное утверждение, относящееся к произвольной нормально распределенной переменной, преобразовать в вероятностное утверждение относительно переменной, удовлетворяющей единичному (стандартному) нормальному распределению. Тем самым для вычисления любых площадей любых трапеций под кривой плотности любого нормального распределения достаточно располагать одним множеством численных результатов, содержащим значения площадей, соответствующих функции плотности единичного (стандартного) нормального распределения.
Чтобы определить величину площади под кривой стандартного нормального распределения между любыми двумя z1 и z2 (z2 > z1) удобно воспользоваться формулой Excel =НОРМ.СТ.РАСП(z2;ИСТИНА) – НОРМ.СТ.РАСП(z1;ИСТИНА). Найденное значение площади и есть вероятность обнаружить Z между z1 и z2. Можно упростить формулу, используя, во-первых, симметрию функции плотности относительно 0 и, во-вторых, равенство общей площади под кривой 1.
Чтобы определить площади, а затем сформировать вероятностные утверждения для произвольных нормальных распределений, пользуются преобразованием (2.30). Не забывайте, что книга вышла из печати в 1987 г. Сегодня для тех же целей используют функцию Excel =НОРМ.РАСП(х;среднее; стандартное_откл;интегральная), где х – точка на оси абсцисс, среднее – μ, стандартное_откл – σ, интегральная принимает значение ИСТИНА или ЛОЖЬ (нас интересует ИСТИНА, так как мы хотим, чтобы функция =НОРМ.РАСП() вернула площадь под кривой от –∞ до х)
Пусть, например, X ~ N (4, 9), т.е. переменная X удовлетворяет нормальному распределению со средней 4 и дисперсией 9 (μ = 4, σ2 = 9). Тогда стандартное отклонение этого распределения σ = 3. Теперь, чтобы найти, например, Р (X ≤ 7), мы применим формулу =НОРМ.РАСП(7;4;3;ИСТИНА) = 0,8413.
Мы уже отмечали, что преобразование (х – μ)/σ позволяет установить, сколько раз величина стандартного отклонения укладывается на отрезке между х и средним значением μ, а результат (2.30) вытекает из того, что значению z, измеренному в стандартных отклонениях от средней, соответствует определенное значение площади под кривой плотности независимо от вида нормального распределения, т. е. от μ и σ2.
Как мы увидим, нормальное распределение широко применяется в экономической статистике; многие вероятностные оценки, непрерывных переменных получены с помощью либо нормального, либо близкого к нему распределения. Например, если X — рост случайно выбранного студента, то наиболее подходящие оценки для X можно получить, считая распределение приблизительно нормальным. Аналогично можно поступить, если X — индекс IQ, характеризующий уровень интеллектуального развития студентов и, возможно, когда X — доход. Более того, нормальное распределение часто выступает в роли приближенной характеристики более сложных распределений. Например, если α и β «достаточно велики», то переменная величина, удовлетворяющая бета-распределению с параметрами α и β, может быть аппроксимирована нормальным распределением (в том смысле, что функция плотности бета-распределения и функция плотности нормального распределения с одинаковыми средней и дисперсией почти совпадают). Эти свойства будут более подробно изучены в следующих разделах.
Рассмотрим теперь гамма-распределение и t-распределение. Как и в случае бета-распределения, о практической ценности этих распределений можно будет судить лишь в дальнейшем. В настоящей главе мы ограничимся определениями и перечислением некоторых основных свойств. Переменная X удовлетворяет гамма-распределению с параметрами α и β (сокращенно записывают X ~ G (α, β)), если функция плотности вероятностей задана в виде
Коэффициент пропорциональности и здесь выбирается так, чтобы площадь под кривой fX () равнялась 1. Заметим, что X принимает только неотрицательные значения; для отрицательных х плотность вероятностей равна нулю. Средняя и дисперсия для гамма-распределения вычисляются по общим формулам.
Обратим внимание на частный случай гамма-распределения при α = k/2 и β = 1/2, где k — натуральное число. В этом случае говорят, что переменная X удовлетворяет распределению хи-квадрат (χ2) с k степенями свободы (точный смысл этой фразы станет ясным позднее, когда будет введено понятие степеней свободы). Сокращенно записывают: X ~ χ2 (k).
Переменная X удовлетворяет t-распределению с k степенями свободы (сокращенно записывают X ~ t (k)), если функция плотности вероятностей задана в виде
Коэффициент пропорциональности снова выбирается так, чтобы обеспечивалось равенство единице площади под кривой плотности. Заметим, что X может принимать любые значения между –∞ и + ∞, а плотность вероятностей стремится к нулю, когда х стремится к –∞ или к + ∞. Значения средней и дисперсии:
Из (2.33) вытекает, что функция плотности вероятностей симметрична относительно нуля и ее график имеет колоколообразную форму. Во многом t-распределение схоже со стандартным нормальным распределением, за исключением того, что оно обладает большим разбросом (дисперсия t-распределения больше дисперсии стандартного нормального распределения, равной 1). Однако при возрастании числа степеней свободы k функция плотности вероятностей t-распределения все теснее приближается к функции плотности стандартного нормального распределения; при этом второе становится предельным случаем первого при неограниченном возрастании k.
2.5. Основные вероятностные законы
До сих пор мы говорили о вероятности, ограничиваясь понятием переменной. В этом разделе мы продолжим обсуждение, пользуясь понятием события, которое позволяет существенно упростить изложение. Сначала формально сформулируем два вероятностных закона; мы неявно ими уже неоднократно пользовались. Затем введем особенно важное для нас понятие условной вероятности. После этого сформулируем третий закон, устанавливающий связь между условной и безусловной вероятностями, и применим его к выводу теоремы Байеса — фундаментального положения всего последующего анализа.
Сформулируем теперь законы и определения в терминах событий, для обозначения которых воспользуемся буквами Е и F. Под событиями мы будем понимать то, что произошло, происходит или может произойти: «Англия выиграла чемпионат мира по футболу», «консервативная партия формирует очередное правительство», «при бросании игральной кости выпадет 6».
(2.35) Первый закон. Если Е – любое событие, то 0 ≤ Р (Е) ≤ 1. Если Е несомненно должно случиться, то Р (Е) = 1.
Мы по-прежнему воспринимаем все эти утверждения как субъективные оценки; поэтому, например, слова «несомненно должно случиться» означают, что индивид, чью оценку мы описываем, считает такое событие неизбежным. Конечно, он может при этом ошибаться в своих оценках, но поскольку он рассматривает событие Е как несомненное или определенное, то приписывает событию Е вероятность 1.
(2.36) Второй закон. Если Е и F — взаимно исключающие события, то Р (Е или F) = Р (Е) + Р (F), где «Е или F» обозначает событие, состоящее в том, что произошло хотя бы одно из событий: либо Е, либо F.
Очевидный смысл этого закона можно пояснить на простом примере. Обратимся к предстоящему чемпионату мира по футболу и пусть Е — событие «Англия станет победительницей», a F — событие «Шотландия станет победительницей». Ясно, что обе команды победить не могут, поэтому события Е и F взаимно исключают друг друга. Пусть теперь ваша оценка состоит в следующем: Р (Е) = 0,1 и Р (F) = 0,2 (шотландцам последнее время больше сопутствовала удача!); тогда второй закон означает, что Р (Е или F) = 0,1 + 0,2 = 0,3. Другими словами, вы оцениваете общие шансы Англии и Шотландии на выигрыш как 3 из 10.
В качестве другого примера рассмотрим извлечение одной карты из хорошо перетасованной колоды; пусть Е обозначает событие «извлечена карта пиковой масти», a F — событие «извлечена карта трефовой масти». Ясно, что события Е и F — взаимно исключают друг друга, поскольку одна карта не может быть и пиковой и трефовой масти. Допустим, мы считаем механизм перемешивания карт и механизм извлечения карты из колоды «честными», т.е. Р (Е) = Р (F) = 1/4. Тогда на основе второго закона получим: Р (Е или F) = 1/4 + 1/4 = 1/2. Другими словами, по вашей оценке имеется 1 шанс из 2, что будет извлечена карта черной масти. Этот результат вполне соответствует ожиданиям.
До сих пор мы имели дело только с безусловными вероятностями. Введем теперь очень важное для дальнейшего изложения понятие условной вероятности. Это понятие позволяет установить, как новая информация может быть использована при формировании вероятностных оценок. Начнем с нового обозначения. Запись «Р (F | Е)» будет означать «вероятность события F при условии, что событие Е имеет место». Это условное вероятностное утверждение. Символ | (вертикальная черта) читается «при условии» или «при данном»; следовательно, «|Е» означает «при данном Е» или «при условии Е» — это условие, при котором формулируется вероятностное утверждение относительно F. Что означает Р (F|E)? Можно ответить так: вероятность F в свете «информации» Е. Поясним это на примере. Предположим, что игральную кость (мы считаем ее «правильной») бросают дважды. Пусть Е — событие, состоящее в том, что при первом бросании выпало число очков, большее, чем 4, и пусть F — событие, при котором сумма очков, выпавших при двух бросаниях игральной кости, не превосходит 10. Тогда Р (F | Е) — вероятность получить в результате двух бросаний либо 10 очков, либо меньше 10 очков при условии, что первый раз выпало более 4 очков. Для вычисления этой условной вероятности можно поступить следующим образом. Дано, что при первом бросании выпало более 4 очков, т. е. после двух бросаний возможны только следующие пары исходов:
(5; 1) (5; 2) (5; 3) (5; 4) (5; 5) (5; 6) (6; 1) (6; 2) (6; 3) (6; 4) (6; 5) (6; 6)
Здесь число, стоящее в скобках первым, соответствует исходу первого бросания, а число, стоящее вторым, — исходу второго бросания игральной кости. Для девяти пар из двенадцати число очков не превосходит 10:
(5; 1) (5; 2) (5; 3) (5; 4) (5; 5) (6; 1) (6; 2) (6; 3) (6; 4)
Если, как мы уже отмечали, игральная кость «правильная», то все двенадцать пар равновероятны и потому вероятность появления одной из девяти пар, для которых сумма очков не превосходит 10, равна 9/12. Таким образом, в нашем примере Р (F | Е) = 9/12. С помощью аналогичных рассуждений можно установить, что Р (Е | F) = 9/33. Р (Е | F) означает: какова вероятность, что при первом бросании кости выпало больше 4 очков, если в результате двух бросаний выпало менее 10.
Подведем итог: Р (F | Е) указывает вероятность F при наличии «информации» Е; утверждение, выступающее в роли условия (т. е. | Е), доставляет информацию, которая может изменить вероятность свершения события F.
В рассмотренном выше примере с игральной костью условная вероятность Р (F | Е) отличается от безусловной вероятности Р (F): первая равна 9/12, а вторая равна 33/36. Поэтому в данном примере «информация» Е изменила оценку вероятности свершения события F. Аналогично условная вероятность Р (Е | F) отличается от безусловной вероятности Р (Е); первая равна 9/33, а вторая равна 12/36. Здесь вновь «информация» F изменила оценку вероятности свершения события Е. Однако так происходит не всегда. Обратимся к примеру, в котором одна карта извлекается из хорошо перетасованной колоды. Пусть Е в этом примере будет событием извлечения червы, a F — событием извлечения туза. Если мы уверены в том, что колода хорошо перетасована, а карты извлекаются случайным образом, то вероятность появления каждой из содержащихся в колоде карт равна, что позволяет рассчитать остальные вероятности: P(F|E) = 1/13, P(F) = 4/52, P(E|F) = 1/4, P(E) = 13/52.
В этом примере условная вероятность Р (F|Е) и безусловная вероятность Р (F) равны. Таким образом, «информация» Е не повлияла на вероятностную оценку события F. Точно так же оказались равными условная вероятность Р (Е|F) и безусловная вероятность Р (E), т. е. «информация» F тоже не влияет на вероятностную оценку Е. Естественно теперь задаться вопросом, почему это происходит. Объяснение может быть следующим. При случайном механизме выбора карт знание масти извлеченной из колоды карты не помогает нам установить ее достоинство, равно как знание достоинства карты не дает дополнительных сведений о ее масти. В этом случае «информация» оказалась неинформативной.
Тем не менее в примере с игральной костью «информация» была информативной: если при первом бросании выпало достаточно большое число очков, то шансы для общего количества очков быть малым уменьшились; аналогично если общее количество очков невелико, то уменьшаются шансы того, что при первом бросании выпало большое число очков.
Введем теперь специальные термины, чтобы различать эти два случая (когда «информация» информативна и когда она неинформативна). Два события Е и F независимы тогда и только тогда, когда
(2.37) Р (F|Е) = Р (F) и Р (Е|F) = Р (E)
Одно из этих условий лишнее, поскольку каждое из них является следствием другого. Это подкрепляется и интуитивным соображением, в силу которого независимость — симметричное свойство; в самом деле, невозможно представить себе ситуацию, в которой Е зависит от F, в то время как F от Е не зависит. Если условие, сформулированное в (2.37), не имеет места, то Е и F называют зависимыми событиями.
В примере с игральной костью события Е и F зависимы; в примере с картами Е и F независимы. Пользуясь этой терминологией, мы можем заключить, что «информация» Е неинформативна по отношению к F, если Е и F независимы, и информативна, если Е и F зависимы. Это согласуется с интуитивным представлением о том, что «информация» только тогда значима, когда она касается интересующих нас вещей. Итак
(2.38) Третий закон. Р (Е и F) = Р (F|Е)*Р (Е) = Р (Е|F)*Р (F), где запись «Е и F» обозначает событие, при котором оба события и Е, и F имеют место.
Этот закон содержит два равенства, хотя оба они, вообще говоря, свидетельствуют об одном. Равенство первых двух членов в (2.38) означает, что вероятность совместного осуществления событий Е и F равна произведению вероятности свершения события Е и условной вероятности свершения события F при данном Е. Поясним это на примере. Пусть Р(Е) = 1/2, т.е. имеется 50 шансов из 100, что событие Е произойдет. Предположим также, что Р (F|Е) = 1/4, т.е. если событие Е произойдет, то имеется 1 шанс из 4, что произойдет и событие F. Тогда исходя из (2.38) можно сделать вывод о существовании 1 шанса из 8, что оба события, Е и F, произойдут вместе. Свяжем эти числовые характеристики с конкретной ситуацией. Допустим, что нужно случайным образом выбрать одного студента среди учащихся университета, где обучается 50% мужчин, а из них 25% — экономистов. В таком случае, если процесс выбора организован «справедливо», то окажется 1 шанс из 8, что выбранный студент будет одновременно и мужчиной, и экономистом. (Здесь событие Е состоит в выборе мужчины, а событие F — в выборе экономиста.)
Равенство первого и последнего членов в (2.38) свидетельствует о том же, но позволяет объяснить связь между событиями по-другому: вероятность того, что произойдут сразу оба события, Е и F равна произведению вероятности события F на условную вероятность события Е при данном F. Итак, в общем случае из (2.38) следует: для того, чтобы произошли два события, должно произойти одно из них и, если это уже случилось, должно произойти второе.
Третий закон можно теперь преобразовать так, чтобы получить общий результат относительно условной вероятности. Из (2.38) следует:
(2.39) Р (F|Е) = Р (Е и F) / Р (Е)
Убедимся в том, что условная вероятность, найденная в двух рассмотренных выше примерах «интуитивно», вычисляется с помощью формулы (2.39). Так, для примера с картами Р (Е) = 13/52, а Р (Е и F) = 1/52 (вероятность того, что из колоды будет извлечен туз червей, равна 1/52). Из (2.39) находим Р (F | Е) = (1/52)/(13/52) = 1/13, что совпадает с полученным ранее значением.
Заметим, что последнее равенство в соотношениях третьего вероятностного закона (2.38) можно переписать так:
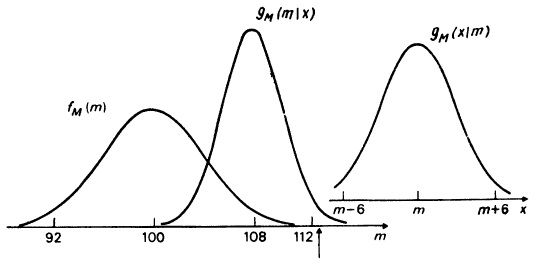
По сути, формула (2.40) и есть теорема Байеса. Этот важный результат будет нам весьма полезен в дальнейшем.
Резюме. В этой главе было раскрыто содержание понятия вероятность. Вначале речь шла о вероятностных оценках для переменных величин и, в частности, о том, как такие оценки могут быть описаны, как они взаимодействуют друг с другом и каким образом их удается обобщить. В разделе 2.2 были введены три наиболее важные функции, применяемые для описания вероятностных оценок в случае одной переменной: функция распределения (ею пользуются как для дискретной, так и для непрерывной переменной), она измеряет кумулятивную вероятность; функция вероятностей, предназначенная только для дискретной переменной и измеряющая сами вероятности; функция плотности вероятностей (ею пользуются только для непрерывной переменной) — она измеряет предельную (маргинальную) вероятность. Затем в разделе 2.3 было показано, как обобщают вероятностные оценки; при этом было введено очень важное понятие вероятностного интервала (наименьшей длины) и были проанализированы различные способы измерения центральной тенденции и рассеяния, среди которых особую роль играют средняя величина и дисперсия. Раздел 2.4 представляет собой «каталог» стандартных распределений, таких, как равномерное, бета-распределение, нормальное, гамма-распределение и t-распределение. В разделе 2.5 мы снова обратились к вероятностным оценкам, но уже событий, и сформулировали три основных вероятностных закона, с помощью последнего из которых определили понятие условной вероятности. Были также введены понятия зависимости и независимости и установлена их связь с информативностью «информации». Здесь впервые упомянута и сформулирована теорема Байеса.
В данной главе неоднократно указывалось, что мы придерживаемся субъективной трактовки понятия вероятности. При этом вероятностные утверждения выглядят как выражение субъективных представлений и ожиданий. Такова методологическая основа байесовского подхода к статистике.
Упражнения
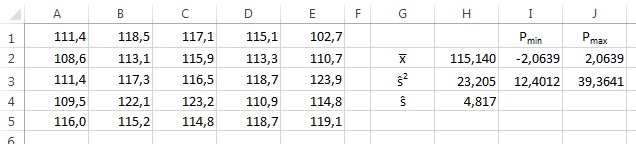
2.4. Пусть X — дискретная переменная, которая принимает значения, равные общему количеству очков, выпадающих при одновременном бросании двух (конечно, «правильных») игральных костей. Заметьте, что X принимает целые значения от 2 до 12. Изобразите функцию распределения X и функцию вероятностей X. Установите связь между этими двумя функциями.
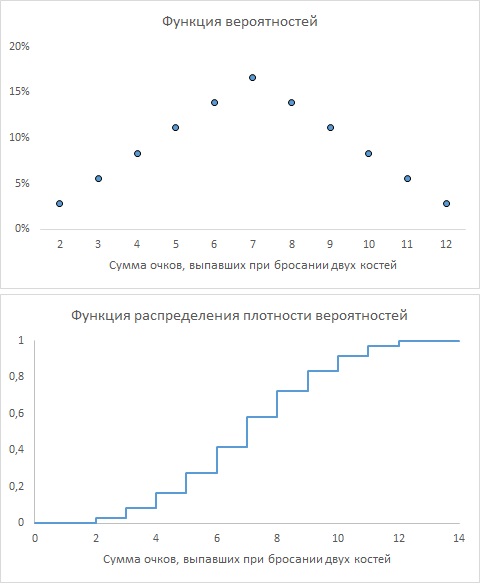
2.6. Дискретная переменная X определена как число выпадений герба при трех бросаниях монеты (в предположении, что монета «правильная»). Изобразите функцию распределения и функцию вероятностей для переменной X. Покажите, как эти две функции соотносятся одна с другой.
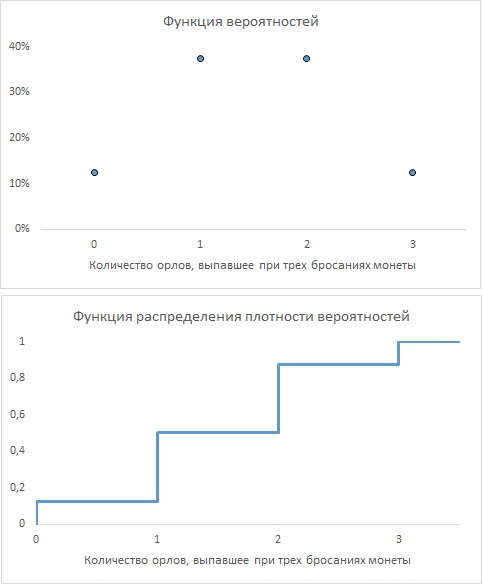
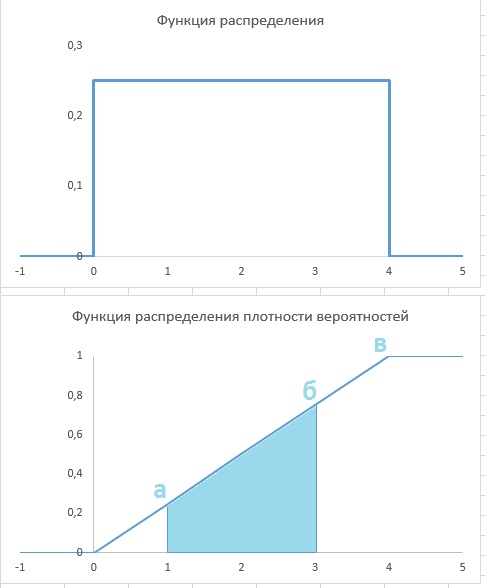
2.7. Стрелка (предполагаемая «правильной») вращается над кругом, на всей окружности которого задана равномерная и непрерывная шкала с начальной точкой 0, а концевой точкой 4. Пусть X — непрерывная переменная, и ее значения соответствуют положению стрелки в момент останова после вращения. Постройте функцию распределения для переменной X. Выведите с ее помощью функцию плотности вероятностей для X. Покажите, что площадь под графиком последней функции между значениями 1 и 3 равна 1/2; между значениями 2 и 3 равна 1/4 Проинтерпретируйте эти величины площадей в терминах вероятностей.
2.11. Постройте функцию стандартного нормального распределения.
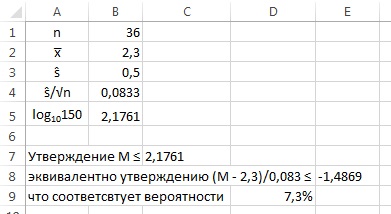
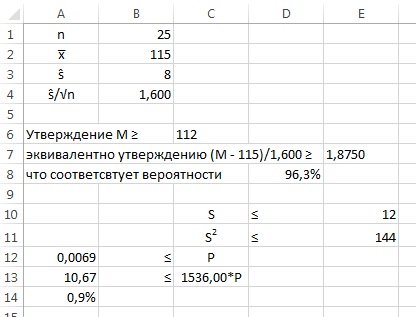
2.15. Определите 90-процентный вероятностный интервал (наименьшей длины) для распределений из упражнений 2.7 и 2.11.
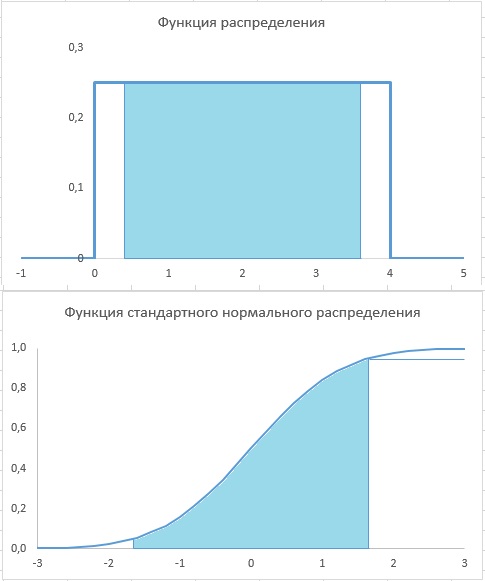
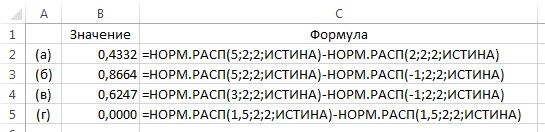
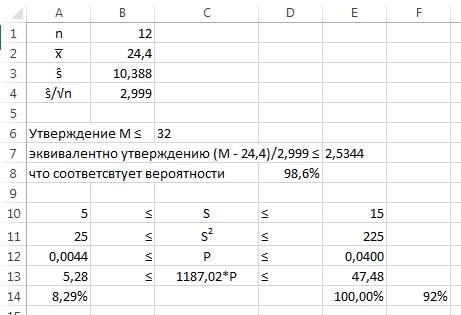
2.21. Для X ~ N (2,4) найдите вероятность того, что X (а) лежит между 2 и 5; (б) лежит между –1 и 5; (в) лежит между –1 и 3; (г) равно 1,5.
2.22. Две урны наполнены шарами, причем в 1-й содержится 25% белых и 75% черных шаров, а во 2-й – 75% белых и 25% черных шаров. Если одна из этих урн выбрана случайно и случайным образом из нее извлечен один шар, то как вы оцените вероятность того, что этот шар белый?
2.23. Исследователь в связи с проведением эксперимента подсчитал, что если справедлива теория А, то можно наблюдать X с вероятностью около 0,9; если же справедлива теория В, то эта вероятность примерно равна 0,3. Он полагает, что теория А примерно вдвое более правдоподобна, чем теория В. Кроме теорий А и В других способов рационального объяснения наблюдаемых явлений нет. С какой вероятностью исследователь может ожидать появления X в ходе данного эксперимента?
2.24. Предположим, что новый прибор, «анализирующий» выдыхаемый воздух, позволяет с вероятностью 0,95 выявить превышение допустимого уровня содержания алкоголя в организме индивида и с вероятностью 0,95 установить, что этот уровень не превышен. Если в некоторый момент у 5% обследуемых уровень алкоголя в организме выше допустимого, то какова вероятность, что при осмотре случайно выбранного из этой совокупности индивида прибор зарегистрирует превышение уровня, и это будет соответствовать действительности.
Решения
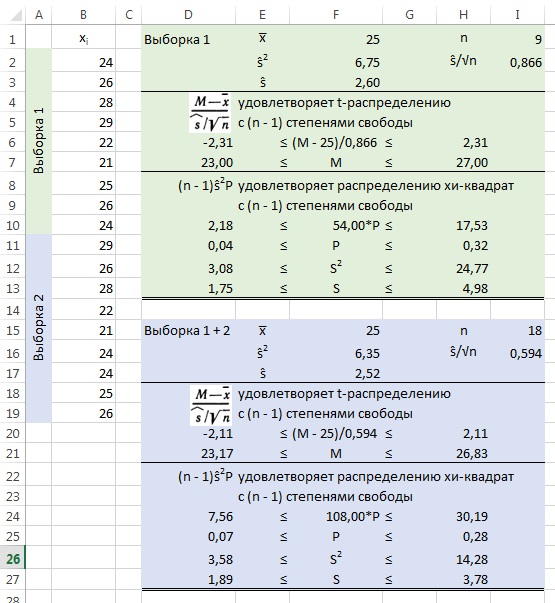
2.4. Сначала комбинируем все возможные пары исходов бросания двух костей (см. лист Упр.2.4 Excel-файла). Затем с помощью сводной таблицы подсчитываем число исходов, соответствующее всем возможным суммам двух костей (от 2 до 12). Затем определяем долю исходов (в%), а затем строим функцию распределения (вероятности накопительным итогом)
2.6. Аналогично 2.4, расчеты см. лист Упр.2.5 Excel-файла
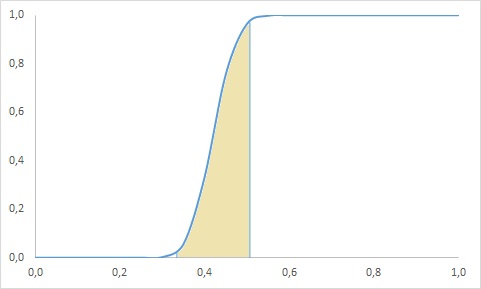
2.7. Площадь под графиком функции распределения плотности вероятностей между значениями 1 и 3 равна площади трапеции 1аб3. Т.е. по определению трапеции равна произведению полусуммы оснований на высоту: ([1, а] + [3, б])*[1,3]/2 = (0,25 + 0,75)*2/2 = 1. Полная площадь под графиком функции распределения плотности вероятностей между значениями 0 и 4 равна площади треугольника 0в4: [0, 4] * [4, в] / 2 = 4*1/2 = 2. Т.е. площадь трапеции составляет 1/2 площади треугольника. Это можно интерпретировать следующим образом: вероятность останова стрелки между делениями 1 и 3 составляет 50%.
2.11. Функция стандартного нормального распределения:
2.15. Для функции распределения из упр. 2.7 не существует единственного 90-процентного вероятностного интервала наименьшей длины; таких интервалом множество; начало интервала должно приходиться на отрезок [0; 0,4], а длина интервала по оси Х составляет 3,6 (см. рис. ниже). Для функции стандартного нормального распределения из упр. 2.11 90-процентный вероятностный интервал (наименьшей длины) лежит симметрично относительно среднего значения μ = 0. Нижняя граница 90% интервала лежит на 45% ниже середины и значение Z вычисляется по формуле: =НОРМ.СТ.ОБР(5%) = –1,6449. Соответственно, верхняя граница 90% интервала лежит на 45% выше среднего и значение Z вычисляется по формуле: =НОРМ.СТ.ОБР(95%) = 1,6449.
2.21. Напомним, что нормальное распределение сокращенно записывают в виде: X ~ N (μ, σ2). Таким образом:
В случае (г) нет ничего странного, так как для любого непрерывного распределения не имеет смысла говорить о вероятности наблюдать какое-либо конкретное значение.
2.22. Вероятность вытащить белый шар при условии выбора 1-й урны Р(Б|1) = 25%, вероятность вытащить белый шар при условии выбора 2-й урны Р(Б|2) = 75%. Вероятность вытащить белый шар Р(Б) = Р(Б|1)*Р(1) + Р(Б|2)*Р(2) = 50%, где Р(1) = Р(2) = 50% – вероятность выбора 1-й (2-й) урны.
2.23. Вероятность наблюдать Х в ходе эксперимента Р(Х) = Р(Х|A)*P(A) + P(X|B)*P(B), где Р(Х|A) – вероятность наблюдать Х, если верна теория А, Р(А) – вероятность, что теория А верна, Р(Х|A) – вероятность наблюдать Х, если верна теория В, Р(В) – вероятность, что теория В верна. По условиям задачи Р(А) относится к Р(В), как 2 к 1, следовательно Р(А) = 2/3, Р(В) = 1/3. Итого Р(Х) = 0,9*2/3 + 0,3*1/3 = 0,7. Исследователь может ожидать появления X в ходе данного эксперимента с вероятностью 70%.
2.24. Априорная вероятность того, что уровень алкоголя (УА) в крови испытуемого выше допустимого Р(УА) = 0,05 (5%). В случае, если у испытуемого уровень алкоголя выше допустимого, тест даст положительный результат (ПР) в 95% случаев: Р(ПР|УА) = 0,95. Р(ПР|УА) читается так: вероятность положительного результата теста в случае, если у испытуемого уровень алкоголя выше допустимого. Но в условии задачи сказано тест только с вероятностью 0,95 позволяет установить, что уровень алкоголя не превышен, то есть, существует 5%-ная вероятность, что тест испытуемого с нормальным уровнем алкоголя также даст положительный результат: Р(ПР|~УА) = 0,05. Р(ПР|~УА) читается так: вероятность положительного результата теста в случае, если у испытуемого уровень алкоголя в пределах нормы (не УА). По теореме Байеса: Р(УА|ПР) = Р(ПР|УА)* Р(УА)/Р(ПР). Р(УА|ПР) читается так: вероятность того, что у испытуемого уровень алкоголя выше допустимого, при условии положительного результата теста. Р(ПР) = Р(ПР|УА)* Р(УА) + Р(ПР|~УА)*Р(~УА). Выражение читается так: вероятность положительного результата теста равна произведению вероятности положительного результата теста, при условии, что уровень алкоголя в крови превышен на вероятность того, что уровень алкоголя превышен, плюс произведение вероятности положительного результата теста, при условии, что уровень алкоголя в крови в норме на вероятность того, что уровень алкоголя в норме. Р(УА|ПР) = 0,95*0,05/(0,95*0,05 + 0,05*0,95) = 0,5. Неожиданный результат, не так ли? Вероятность того, что уровень алкоголя в крови превышен при условии, что тест дал положительный результат, только 50%!
К оглавлению
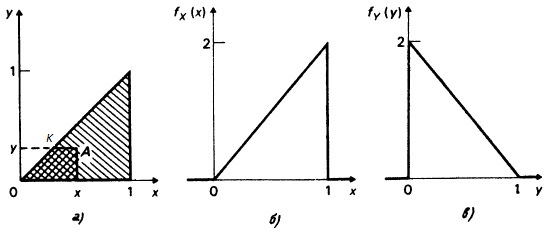
Глава 3. Вероятностные распределения нескольких переменных
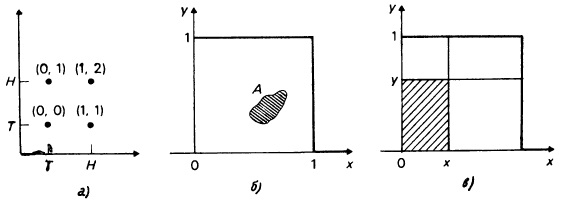
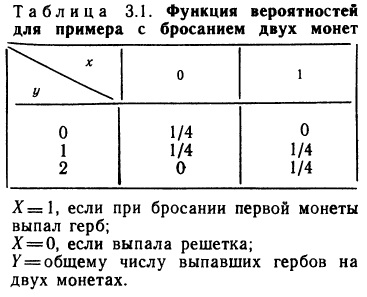
В гл. 2 вы познакомились с основными идеями и понятиями теории вероятностей. При этом речь шла только о вероятностных оценках событий и о вероятностных оценках одной переменной. В этой главе мы обобщим материал гл. 2 и рассмотрим случай нескольких переменных. Основное внимание будет уделено вероятностным оценкам двух переменных, поскольку изложение тем самым существенно упрощается, а дальнейшие обобщения, как правило, не требуют введения новых понятий.
В разделе 3.2 определяется вероятностное распределение двух переменных. Как мы увидим, сформулировать вероятностное утверждение относительно двух переменных можно, лишь рассмотрев их совместное распределение и предполагая обе переменные равноправными. Вместе с тем часто необходимо располагать сведениями о каждой из них в отдельности, поэтому мы введем в разделе 3.3 понятие маргинального (предельного) распределения вероятностей. В разделе 3.4 речь идет об условном вероятностном распределении — о распределении одной переменной при наличии некоторой информации относительно другой переменной. Мы приходим к этому понятию путем естественного расширения понятия условной вероятности, с которым мы познакомились в разделе 2.5. Все рассмотренные в 3.2–3.4 понятия (совместного, маргинального и условного распределения) для случая многих переменных формулируются в разделе 3.5. В разделе 3.6 даны обобщающие характеристики (подобные тем, с которыми мы встречались в 2.3) для вероятностного распределения нескольких переменных. Раздел 3.7 содержит резюме третьей главы, а раздел 3.8 — упражнения к ней.
3.2. Двумерное распределение вероятностей
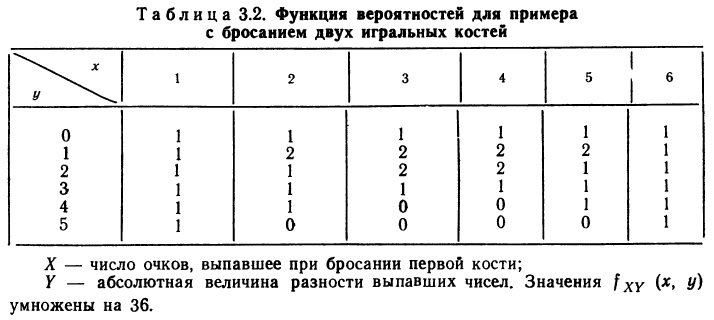
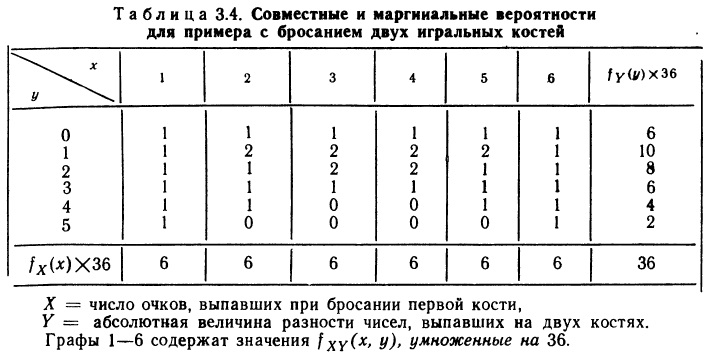
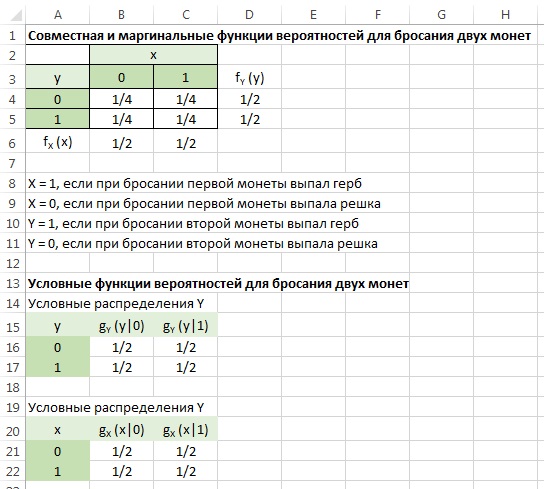
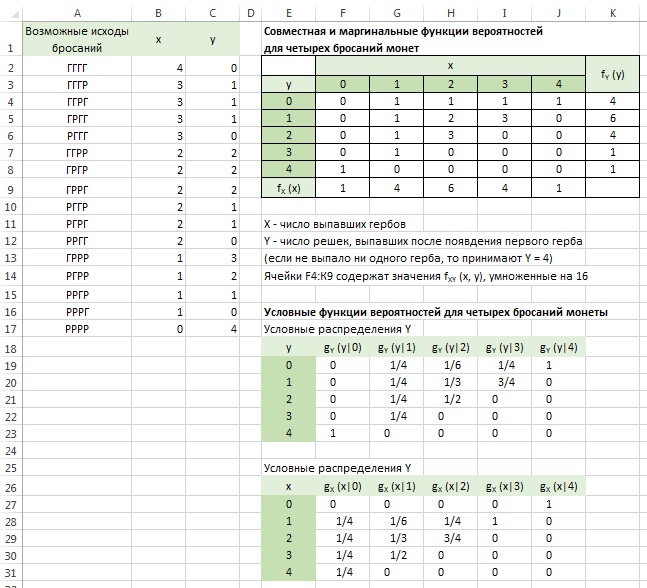
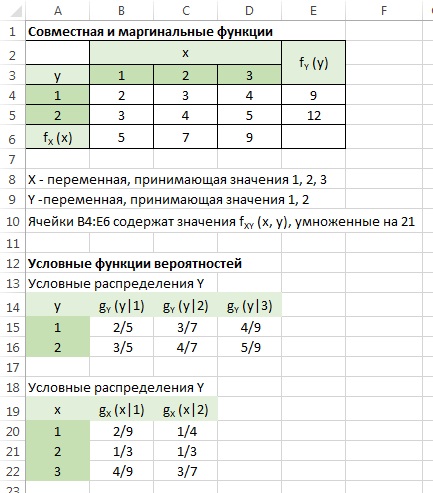
Нас будут интересовать одновременно две переменные. Мы обозначим эти переменные прописными буквами X и Y, а строчными буквами х и у — соответственно конкретные значения этих переменных. Предположим, что мы рассматриваем объект или процесс, который описывается двумя представляющими для нас интерес переменными X и Y, каждая из которых может принимать некоторые упорядоченные (по величине) значения. Как и в случае одной переменной, мы можем представить индивидуальные вероятностные оценки X и Y, воспользовавшись либо функцией распределения, либо функцией вероятностей, либо функцией плотности вероятностей, в зависимости от того, какая-из этих функций окажется подходящей. Определим три указанные функции для двумерного вероятностного распределения по аналогии с тем, как это было сделано в гл. 2 для случая одной переменной.
Начнем с функции распределения, которая существует и для дискретных, и для непрерывных переменных. Определение (2.1) для одной переменной, сводилось к тому, что функция распределения измеряет кумулятивную вероятность. Распространение этого определения на двумерный случай не вызывает затруднений. Мы обозначим двумерную (совместную) функцию распределения переменных X и Y через FXY () и определим ее с помощью равенства:
(3.1) FXY (х, у) = Р(Х ≤ х и Y ≤ у)
Как и в случае одной переменной, мы будем опускать подстрочные индексы X и Y, если это не приведет к недоразумениям. Как можно заключить из (3.1), FXY (х, y) измеряет кумулятивную вероятность для всех значений переменных X и Y, таких, что X не превосходит х, a Y не превосходит у. Таким образом, мы имеем дело с вероятностным утверждением относительно обеих переменных X и Y; вот почему мы говорим о двумерной (совместной) функции распределения. В гл. 2 мы часто пользовались графиками функций. Функция одной переменной допускает непосредственное изображение на диаграмме; при этом значения исходной переменной откладывают по горизонтальной оси, а значения функции — по вертикальной оси. Для изображения функции двух переменных хорошо бы иметь трехмерное пространство: по одной оси для каждой переменной и одну ось для значений функций. Поскольку не так легко изображать трехмерные диаграммы, мы постараемся в этой главе не прибегать к графикам, а чаще обращаться к таблицам и алгебраическим представлениям и только в некоторых случаях к двумерному изображению трехмерных объектов.
Приведем два примера, иллюстрирующие (3.1). В первом примере рассмотрим одновременное бросание двух (конечно, «правильных») монет и предположим, что переменные X и Y определены следующим образом: X принимает значение 1, если при бросании первой монеты выпал герб, и значение 0 — в противном случае; Y принимает значение, равное общему числу гербов, выпавших при бросании двух монет. На рис. 3.1, а схематически изображены возможные исходы этого эксперимента и для каждого из исходов в скобках указаны соответствующие ему значения X и Y. Если монеты «правильные», каждому из четырех возможных исходов отвечает одинаковый уровень правдоподобия. Поэтому
Рис. 3.1. Два примера, иллюстрирующие случай двумерного распределения: а) по оси абсцисс — исход бросания первой монеты, по оси ординат — исход бросания второй монеты; Т — решетка, Н — герб. В скобках около точек указаны соответствующие им значения (х, у)
График (3.2) в трехмерном пространстве выглядит как последовательность ступенек. Как и в случае одной переменной, дискретная двумерная функция распределения является ступенчатой функцией.
Второй пример схематически изображен на рис. 3.1, б. Мы рассмотрим квадрат со стороной 1 и предположим, что действует некий механизм, обеспечивающий равновероятный выбор любой точки, лежащей внутри квадрата или на его границе. Поэтому вероятность выбора точки из некоторой области (взятой вместе с ее границей), например А, заштрихованной на рис. 3.1, б, определяется только площадью этой области и не зависит от ее расположения в квадрате. Пусть переменным X и Y соответствуют координаты х и у выбранной точки. Тогда двумерная функция распределения FXY () имеет вид:
Значения функции в первой и последней строках не требуют комментария. Значение в средней строке объясняется тем, что если точка (х, у) лежит внутри квадрата, то FXY (х, у) = Р (X ≤ х и Y ≤ у) = заштрихованной площади (см. рис. 3.1, в) S = ху, поскольку площадь прямоугольника равна произведению его ширины х на высоту у. Значения функции во второй и четвертой строках вычисляются непосредственно. Если вы представите (3.3) графически в трехмерном пространстве, то обнаружите, что у графика имеются две горизонтальные плоские части (это, во-первых, все области, где одна из переменных отрицательна, во-вторых, область, где обе переменные больше единицы), соединенные наклонной плоскостью. Как и в одномерном случае, двумерная функция распределения непрерывной переменной не имеет скачков.
Из двух приведенных примеров ясно, что пользоваться функцией распределения для характеристики двумерного распределения не всегда удобно. Поэтому мы рассмотрим другие способы задания двумерного распределения — функцию вероятностей для дискретного случая и функцию плотности вероятностей для непрерывного. Функция вероятностей для одномерной дискретной переменной была определена равенством (2.7) (или эквивалентным ему равенством (2.6)). Распространим это понятие на случай двух переменных. Будем обозначать (двумерную) функцию вероятностей дискретных переменных X и Y через fXY (), (подстрочные индексы можно опустить, если это не вызовет недоразумений) и определим ее равенством:
Эта функция изображена на рис. 3.2, а. Можно также представить эту же функцию в табличной форме (табл. 3.1). «Входами» таблицы являются значения переменных X и Y, а на пересечении столбца и строки стоит соответствующее точке (х; у) значение вероятности.
Рис. 3.2. Функция вероятностей и функция плотности вероятностей: а) функция вероятностей в примере с двумя монетами; функция равна нулю, за исключением 4 отмеченных на рисунке точек; б) функция плотности вероятностей в примере, которому соответствует рис. 3.1, б; значения функции равны нулю во всех точках
Приведем еще один пример с дискретными переменными, прежде чем перейти к непрерывному случаю. Пусть бросают две («правильные») игральные кости. Определим переменную X как число очков, выпавших на первой кости, а переменную Y как абсолютную величину разности между числами, выпавшими на двух костях. Рассмотрев все 36 возможных исходов, вы легко рассчитаете вероятность для каждого из возможных значений (х, у). Эти вероятности, образующие fXY (х, у) (они умножены на 36), приведены в табл. 3.2. Если мы хотим найти вероятность, соответствующую х = 3 и у = 2, то заметим, что эти значения неизвестных могут появиться лишь при двух из 36 возможных исходах, а именно (3; 1) и (3; 5). Следовательно, fXY (3; 2) = 2/36, что и указано в табл. 3.2.
Перейдем к непрерывному случаю и введем двумерную функцию плотности вероятностей, которую для переменных X и Y будем также обозначать fXY (), опуская подстрочные индексы, когда это не мешает пониманию. Как и в одномерном случае, fXY () оправдывает свое название и служит мерой плотности вероятностей, в частности она измеряет плотность вероятностей в точке (х, у). Чтобы прийти к этому, мы сначала вычислим плотность вероятностей в прямоугольной области, примыкающей к точке (х, у), а затем установим, чему равна плотность, когда эта область «стягивается» к точке (x, у). Итак, рассмотрим прямоугольник, ограниченный сторонами х и х + Δх (перпендикулярными к оси x), а также сторонами у и у + Δу (перпендикулярными к оси у). Площадь этого прямоугольника равна Δx*Δу (его ширина Δx, а высота Δу). Вероятность того, что значения (X, У) лежат в данном прямоугольнике, есть Р (х ≤ X ≤ х + Δх и y ≤ Y ≤ y + Δу), а плотность вероятности в прямоугольнике равна ![]() . Определим теперь плотность вероятностей в точке (x, у) как предел этого выражения при Δx и Δу стремящихся к нулю, т. е.
. Определим теперь плотность вероятностей в точке (x, у) как предел этого выражения при Δx и Δу стремящихся к нулю, т. е.
Двумерная функция распределения для этого примера была определена соотношениями (3.3). Соответствующая (3.3) двумерная функция плотности вероятностей имеет вид:
Эта функция изображена на рис. 3.2, б. Из рисунка, так же, как и из аналитической формы функции, видно, что перед нами равномерное на квадрате 0 ≤ х ≤ 1, 0 ≤ у ≤ 1 распределение. Это соответствует исходному предположению, в силу которого выбор любой точки данного квадрата (вместе с его границей) равновероятен, поскольку механизм выбора является «справедливым».
Ряд положений раздела заслуживает особого внимания, и их нужно твердо усвоить. Во-первых, для работы с дискретными переменными нужна информация о функции вероятностей, при этом fXY (x, у) указывает вероятность того, что переменная X принимает значение х, а переменная Y — значение у. Во-вторых, в непрерывном случае нам требуется информация о функции плотности вероятностей fXY (х, у), которая характеризует совместную плотность вероятностей в точке, где переменная X равна х, и переменная Y равна у.
3.3. Маргинальные распределения
Часто встречается ситуация, в которой мы, хотя и имеем дело с двумерным случаем, должны сосредоточить внимание на одной из двух переменных, а другую временно не принимать во внимание. Таким образом, получают вероятностные утверждения относительно X, если не учитывается переменная Y, или относительно Y, если не учитывается переменная X. Но тогда мы придем к одномерному случаю и сможем описать полученные вероятностные утверждения с помощью аппарата гл. 2, т. е. нам потребуются одномерные функции для описания вероятностных оценок X, когда игнорируется Y, и оценок Y, когда игнорируется X.
Рассмотрим простой (дискретный) пример (см. рис. 3.1, а из предыдущего раздела) с бросанием двух («правильных») монет. Переменная X принимает значение 1, если при бросании первой монеты выпадает герб, и 0 — в противном случае; переменная Y определена как число гербов, выпавших при бросании двух монет. Хотя речь идет о двух переменных, мы легко найдем распределение вероятностей для каждой из них в отдельности. Начнем с переменной X, принимающей значения 1 и 0. Поскольку предполагается, что монеты «правильные», оценка вероятности X может быть выражена в терминах функции вероятностей X:
(3.9) fX (0) = fX (1) = 1/2
Аналогично оценка вероятности переменной Y, принимающей значения 0, 1 и 2, может быть выражена в терминах функции вероятностей этой переменной:
(3.10) fY (0) = fY (2) = 1/4, fY (1) = 1/2
(Напомним, что Y = 0 соответствует наблюдению на двух монетах решеток; Y = 1 — наблюдению решетки на первой монете и герба на второй, а также герба на первой и решетки на второй; Y = 2 –наблюдению герба и на первой, и на второй монетах.)
Все сказанное свидетельствует о том, что каждая из функций fX () и fY () как функция одной переменной может быть получена отдельно. Но в каком отношении находятся эти две функции с совместной функцией вероятностей, приведенной в табл. 3.1? Сначала обратим внимание на столбцы этой таблицы: в первом указаны вероятности всех возможных исходов, если X принимает значение 0, во втором — всех возможных исходов, если X принимает значение 1. К этому следует добавить, что общая вероятность всех исходов, записанная в первом столбце, равна вероятности того, что X принимает значение 0; аналогично общая вероятность всех исходов, занесенная во второй столбец, равна вероятности того, что X принимает значение 1. Общее правило можно сформулировать так:
Суммирование ведется по всем значениям у (или по всем возможным значениям Y — различие несущественно, поскольку fXY (х, у) обращается в нуль для значений у, которые переменная Y принять не может). Точно так же устанавливается, что путем суммирования всех элементов в каждой строке таблицы можно получить функцию вероятностей Y. Таким образом, в общем случае:
где суммирование ведется по всем значениям х. Иллюстрирует это табл. 3.3. В ней значения функции вероятностей X образуют нижнюю строку, а значения функции вероятностей Y образуют ее правый столбец. Именно в силу такого «крайнего», «предельного» положения распределение переменной X и распределение переменной Y называют предельными, или маргинальными, распределениями X и Y соответственно. Итак, обозначение fXY () используется для двумерной (совместной) функции вероятностей, a fX () и fY () – для обозначения маргинальных функций вероятностей переменных X и Y соответственно.
Теперь становится ясным соотношение между маргинальной и совместной функциями вероятностей: чтобы получить маргинальную функцию вероятностей Х, суммируют значения совместной функции вероятностей для каждого значения х по всем значениям у (равенство (3.12)). Суммирование по всем у (или по всем х) в конечном счете означает, что нас не интересуют значения, которые принимает переменная Y (или переменная X).
Для того чтобы пояснить сказанное, вернемся ко второму из приведенных в начале этой главы дискретных примеров. В нем речь шла о бросании двух («правильных») игральных костей. При этом переменная X была определена как число очков, выпавших при бросании первой кости, а переменная У как абсолютная величина разности между числами, выпавшими при бросании двух костей. Значения совместной функции вероятностей содержатся в табл. 3.2. Чтобы получить значения маргинальных функций вероятностей для переменных X и Y, воспользуемся равенствами (3.11) и (3.12) соответственно. В первом случае значения табл. 3.2 суммируются по столбцам, а во втором — по строкам, что позволяет получить предельные функции вероятностей. Результаты этих процедур приведены в табл. 3.4 (Как и в табл. 3.2, мы умножили все табличные значения на 36, благодаря чему избежали громоздких выражений. Поэтому каждое из содержащихся в таблице чисел, прежде чем им воспользоваться, следует умножить на 1/36. Мы думаем, что это не внесет путаницы в результаты.)
Из табл. 3.4 мы видим, что маргинальная функция вероятностей X принимает одинаковые значения при всех значениях переменной: fХ (1) = fХ (2) = fХ (3) = fХ (4) = fХ (5) = fХ (6) = 6/36= 1/6. Это действительно так, поскольку, как мы уже отмечали, вероятность появления каждой из шести граней при бросании игральной кости, если она «правильная», равна 1/6. Значения маргинальной функции вероятностей для переменной Y содержатся в правом «крайнем» столбце таблицы: fY (0) = 6/36, fY (1) = 10/36, fY (2) = 8/36, fY (3)= 6/36, fY (4) = 4/36, fY (5) = 2/36. Вы можете проверить это самостоятельно. Рассмотрим, например, Y = 0. Это значение Y достигается, когда при бросании обеих игральных костей выпадают одинаковые количества очков, что имеет место для 6 из 36 (общего числа) возможных исходов, т. е. интересующая нас вероятность равна 6/36. В свою очередь значение Y = 5 может появиться только в двух случаях: если при бросании первой кости выпала 1, а при бросании второй 6, или наоборот. Вероятность появления данного значения Y равна 2/36.
Рассмотрим теперь второй пример, изображенный схематически на рис. 3.3, а. В нем с помощью уже хорошо известного механизма случайного выбора выбирается точка из заштрихованного треугольника. Переменные X и Y определены как координаты х и у полученной таким образом точки. Мы хотим найти совместное распределение и его функцию плотности вероятностей, а также маргинальные функции плотности.
Рис. 3.3. Второй пример непрерывного двумерного распределения: а) условия примера; б) маргинальная функция плотности переменной X; в) маргинальная функция плотности переменной Y
Рассмотрим произвольную точку этого треугольника, скажем А. Чтобы рассчитать значение FXY (х, у) в точке (x, у), мы вычислим долю площади дважды заштрихованной части треугольника (эта часть получается, если провести через точку А вертикальную и горизонтальную линии и взять принадлежащую треугольнику область) от всей площади треугольника. Тем самым мы найдем вероятность того, что выбранная точка попадет в часть треугольника, отсеченную вертикальной и горизонтальной линиями, проходящими через А, т. е. Р (X ≤ х и Y ≤ у). Площадь треугольника равна 1/2, а площадь отсеченной его части равна х*у — у2/2 (это будет площадь прямоугольника ОхАу за вычетом площади треугольника Оky). Таким образом, FXY (х, у) = 2ху – у2, если точка (х, у) лежит в данном треугольнике. Аналогично если точка (х, у) лежит над треугольником (это означает, что одновременно 0 ≤ х ≤ 1 и х ≤ у), то FXY (х, у) = х2. Продолжая анализ, получим:
Конечно, практического значения такие функции не имеют, но они полезны для иллюстрации основных положений теории.
Найдем теперь маргинальные функции плотности вероятностей. Для этого имеются два пути: прямой — можно воспользоваться условиями примера и косвенный — с помощью функции плотности вероятностей. Воспользуйтесь прямым путем самостоятельно и проверьте следующие результаты, полученные косвенным методом:
Графики этих двух функций приведены на рис. 3.3, б и 3.3, в. Как мы видим, распределение переменной X «правотреугольное», а распределение переменной Y «левотреугольное». Далее, воспользовавшись обозначениями из раздела 2.4, запишем: X ~ В (2,1) и Y ~ В (1,2). Площадь под графиком каждой из функций плотности равна единице, что свидетельствует о корректности их вывода.
3.4. Условные распределения
В двумерном случае маргинальное распределение — это распределение одной из двух переменных, если другая переменная игнорируется. В отличие от маргинального распределения условное распределение, которому посвящен данный раздел, представляет собой распределение одной переменной при наличии некоторой информации о другой переменной. Условные распределения, изучаемые в данном разделе, есть распределения одной переменной при заданных частных значениях другой переменной. Так, кто-то может утверждать, что значение Y равно 3; мы узнаем в этом разделе, как такая информация повлияет (если влияние будет иметь место) на вероятностную оценку переменной X.
Как мы уже убедились, понятие условного распределения является обобщением понятия условной вероятности, введенного в разделе 2.5 для событий. Вспомним общий результат (2.39), полученный для условной вероятности события F при наличии информации о том, что произошло событие Е:
(3.21) Р (F|Е) = Р (Е и F)/P (Е)
Рассмотрим числитель и знаменатель правой части (3.21): в терминологии данной главы числитель является совместным вероятностным утверждением, а знаменатель — маргинальным вероятностным утверждением. Тем самым мы готовы обобщить формулу (3.21), выведенную для событий, на случай переменных, воспользовавшись понятиями и обозначениями данной главы.
Обратимся вначале к дискретному случаю и предположим, что Е — «событие», при котором X принимает значение х, a F — «событие», при котором Y принимает значение у. Тогда согласно (3.21):
(3.22) Р (Y = у|X = х) = Р (X = x и Y = у)/Р (X = х)
В правой части (3.22) стоят хорошо известные нам выражения: в числителе — совместная вероятность fXY (х, у), а в знаменателе — предельная вероятность fX (х). В левой части (3.22) находится вероятностное утверждение относительно Y при данном конкретном значении X, т.е. условное вероятностное утверждение. Введем для него обозначение gY (у|х), т. е.
(3.23) gY (у|х) = Р (Y = у | X = х)
Обратите внимание на три важных момента, связанных с обозначением «gY ( .|x)»: во-первых, индекс «Y» указывает, что это утверждение относится к переменной Y; во-вторых, запись «|x» свидетельствует об условном характере утверждения, причем условием является равенство переменной X ее значению х; в-третьих, использование строчной (а не прописной) буквы «g» говорит о том, что мы имеем дело с функцией вероятностей (а не с функцией распределения). С помощью нового обозначения соотношение (3.22) можно записать так:
(3.24) gY (у|х) = fXY (x, y)/fX (х)
Этот общий и очень важный результат показывает, как может быть выведено условное вероятностное утверждение. В точности такие же соображения позволяют получить следующий результат, раскрывающий смысл условного вероятностного утверждения относительно X:
(3.25) gX (х|у) = fXY (х, y)/fY (y)
Здесь, конечно, gX (.|у) обозначает функцию вероятностей переменной X, когда известно, что Y принимает значение у, т. е. условную функцию вероятностей.
Чтобы проиллюстрировать понятие условной вероятностной оценки, рассмотрим два двумерных примера с дискретными переменными, уже обсуждавшиеся в этой главе. Первый пример — бросание двух монет; причем X принимает значение 1 (или 0), когда при бросании первой монеты выпадает герб (решетка), а значение Y равно числу гербов, выпавших при бросании двух монет. В табл. 3.3 были приведены значения совместной и маргинальных (для X и Y) функций вероятностей. Рассмотрим теперь различные условные распределения вероятностей для переменной Y. Поскольку переменная X принимает лишь два значения (0 и 1), существуют два условных распределения Y: одно — при условии X = 0 и другое — при условии X = 1. Чтобы найти соответствующие условные функции вероятностей мы воспользуемся соотношением (3.24), из которого следует, что получить, например, gY (.|0) можно, разделив значения fXY (0, у) на fX (0). Мы просто разделим значения из столбца х = 0 табл. 3.3 на суммарную для этого столбца вероятность fX (0). Аналогично мы найдем gY (.|1), разделив табличные значения столбца х= 1 на суммарную для этого столбца вероятность fX (1). Результаты этих вычислений сведены в табл. 3.5, а.
Убедимся в том, что значения из табл. 3.5, а согласуются с нашими интуитивными представлениями. Начнем с распределения при условии X = 0. Как следует из таблицы, когда X = 0, переменная Y может с одинаковой вероятностью принимать значения 0 и 1 (но не может принять значение 2). Это означает, что когда при бросании первой монеты выпала решетка (т.е. X = 0), общее число выпавших при бросании двух монет гербов может с одинаковой вероятностью стать равным либо 0, либо 1 (но не может равняться 2). Это не вызывает сомнения. Из этой же таблицы видно, что когда X = 1, переменная Y с одинаковой вероятностью принимает значение 1 или 2 (но не может принять значение 0). Таким образом, если бросают две монеты и при бросании первой выпал герб (т.е. X = 1), то общее число гербов при бросании двух монет может с одинаковой вероятностью равняться 1 или 2 (но не может быть равным 0). Это также соответствует здравому смыслу.
Чтобы найти условные распределения для X, мы поступим аналогичным образом со значениями из табл. 3.3. Как записано в (3.25), нужно разделить каждую строку табл. 3.3 на соответствующую этой строке сумму вероятностей. Результат этого преобразования приведен в табл. 3.5, б. Вновь проверим, что эти результаты согласуются с нашими интуитивными представлениями. Как следует из таблицы, при Y= 0 переменная X непременно принимает значение 0. Это соответствует тому, что если при бросании двух монет не выпало ни одного герба, то при бросании первой монеты обязательно выпала решетка. Аналогично, когда Y = 2, переменная X должна быть равна 1. Наконец, когда Y = 1, переменная X может с одинаковой вероятностью принимать значения 0 или 1.
Перейдем теперь ко второму из двух наших примеров с дискретными переменными, а именно к примеру с бросанием двух игральных костей. В нем X – число очков на первой игральной кости, a Y – абсолютная величина разности между очками, выпавшими при бросании двух костей. В табл. 3.4 приведены значения совместной функции распределения и маргинальных функций распределения для переменных X и Y. Чтобы найти условные распределения Y (или X), мы поступим точно так же, как в предыдущем примере: разделим значения каждого столбца (или строки) из табл. 3.4 на соответствующую этому столбцу (или строке) суммарную вероятность. В табл. 3.6 содержатся результаты такой процедуры для переменной Y; читатель имеет возможность самостоятельно провести вычисления для переменной X. Из табл. 3.6 видно, например, что когда переменная X принимает значение 1, то переменная Y может с одинаковой вероятностью принять любое из шести значений: 0, 1, 2, 3, 4 и 5. Это вполне соответствует здравому смыслу. Вторая игральная кость при бросании может с одинаковой вероятностью упасть одной из шести своих граней: 1, 2, 3, 4,5 или 6. После сопоставления с числом 1 на первой кости мы получим возможные и равновероятные значения разностей: 0, 1, 2, 3, 4 и 5 соответственно. Согласно этой же таблице при условии X = 3 переменная Y может принять одно из значений 0, 1, 2 и 3 соответственно с вероятностями 1/6, 2/6, 2/6 и 1/6. И вновь табличные данные подтвердятся результатами содержательного анализа самого примера. В самом деле, при бросании второй кости может выпасть любое количество очков: 1, 2, 3, 4, 5 и 6. Однако мы знаем, что при бросании первой кости выпало 3 очка. Следовательно, абсолютные величины разностей в «показаниях» двух костей будут 2, 1, 0, 1, 2 и 3 соответственно, т.е. значениям 0 и 3 для Y соответствуют вероятности 1/6, значениям 1 и 2 — 2 вероятности 2/6, а остальным двум значениям — нулевые вероятности.
Вы, наверное, обратили внимание на то, что в рассмотренных нами примерах иногда условное распределение вероятностей и соответствующее безусловное распределение совпадают, а иногда они различны. Так, в примере с бросанием двух монет маргинальное распределение для X (см. табл. 3.3) имело значения fX (0) = 1/2, fX (1) = 1/2, в то время как три условных распределения (см. табл. 3.5) имели значения gX(0|0) = 1; gX(1|0) = 0; gX (0|1) = 1/2; gX (1|1) = 1/2; gX (0|2) = 0; gX (1|2) = 1.
Таким образом, fX () совпадает с gX (.|1), но отличается и от gX (.|0) и от gX (.|2). Аналогичная ситуация уже рассматривалась в разделе 2.5, где отмечалось, что когда условная вероятность P(F| Е) и безусловная вероятность Р (F) различны, то событие Е «информативно» для события F в той мере, в какой последнее с ним связано. Вернемся к примеру с двумя монетами. Если вам сказали, что Y равняется нулю, то «информативно» ли это в отношении X? Конечно, да. Если же вы получили сведения, что Y = 1, то «информативно» ли это для X? Ясно, что, нет. (Знание того, что при бросании одной из двух монет выпал герб, не помогает нам установить результат бросания другой монеты, которая может лечь и гербом, и решеткой; однако сведения о том, что гербом не упала ни одна из двух монет, позволяют немедленно сделать вывод о том, что герб не выпал при бросании первой монеты.) Как видно из приведенных примеров, fX () и gX (.|y) совпадают, когда знание о том, что Y принимает значение у, неинформативно в отношении Х, и, наоборот, fX () и gX (.|y) различны, когда информация о равенстве переменной Y своему значению у информативна в отношении X.
В разделе 2.5 два события E и F были названы независимыми, если Р (Е|F) = Р (Е) и Р (F|Е) = Р (F), что означает равенство условных и соответствующих безусловных вероятностей. В точности так же мы назовем две переменные X и Y независимыми, если условные и соответствующие им безусловные функции вероятностей будут равны при всех значениях X и Y. Формально это определение записывается так:
Ясно, что если X и Y независимы, то сведения относительно значения, принимаемого переменной Y (переменной Х), всегда неинформативны в отношении значений, принимаемых переменной X (соответственно переменной Y). Если две переменные не являются независимыми (т.е. условия (3.26) не удовлетворяются), то их называют зависимыми. В таких случаях сведения о значении переменной Y (переменной X) могут оказаться информативными для вывода о том, какие значения принимает переменная X (переменная Y). В каждом из рассмотренных двух примеров с двумя дискретными переменными X и Y зависимы, и лишь отдельные значения X или Y оказались неинформативными. Если объединить условие независимости (3.26) с общими результатами для условных вероятностей (3.24) и (3.25), то получим следующий очень важный результат:
Итак, две переменные независимы тогда и только тогда, когда их совместная функция вероятностей равна произведению маргинальных функций вероятностей. Для функций, представленных в табличной форме (см. табл. 3.3 и 3.4), это равносильно равенству каждого табличного значения совместной функции вероятностей произведению суммарных (маргинальных) вероятностей, соответствующих столбцу и строке, на пересечении которых это значение находится. Ясно, что это справедливо не для всех значений из табл. 3.3 и 3.4 и отражает наличие зависимости между X и Y в наших примерах.
Можно считать, что все необходимое для определения условных вероятностных распределений в случае дискретных переменных мы сказали. Основные результаты содержатся в равенствах (3.24) и (3.25), выражающих условные функции вероятностей через совместные и маргинальные функции вероятностей. Перейдем теперь к непрерывному случаю. Как это было уже не раз, нужно только дать функциям, входящим в (3.24) и (3.25), новую интерпретацию, чтобы эти соотношения стали основными результатами и для непрерывного случая. Если соответствующие переменные непрерывны, то fXY (.,.), fX (.) и fY (.) являются функциями плотности вероятностей. Остается дать такую же интерпретацию функциям gY (.|x) и gX (.|y). Чтобы быть точными, скажем, что gY (.|x) есть условная функция плотности вероятностей переменной Y при данном значении переменной X, которое равно х, a gX (.|у) — условная функция плотности вероятностей переменной X при данном значении переменной Y, которое равно у. Как мы уже отмечали, эти функции определяются, как и в дискретном случае, с помощью соотношений (3.24) и (3.25). Приведем снова эти два соотношения:
Чтобы получить условную функцию плотности вероятностей для переменной Y (для переменной X) при данном значении x (значении у) другой переменной, нужно разделить совместную функцию плотности вероятностей на маргинальную функцию плотности вероятностей для переменной X (для переменной Y).
Проиллюстрируем сказанное двумя уже рассмотренными в данной главе примерами непрерывного двумерного распределения. В первом примере (см. рис. 3.1, б) точка случайным образом выбирается из единичного квадрата, а переменные X и Y определены как значения х и у, принимаемые координатами выбранной точки. Чтобы получить различные условные распределения, нам нужно, в силу (3.28), знать совместное и маргинальные распределения. Совместная функция плотности вероятностей приведена в (3.8), при этом очевидно, что совместная плотность вероятностей (или, что то же самое, плотность совместной вероятности) равномерна на единичном квадрате. Получаем для различных условных функций плотности вероятностей:
(Заметим, что условное распределение Y (X) при данном х (у) за пределами отрезка [0; 1] не определено и лишено смысла. С этого момента мы примем соглашение, в силу которого значения х или y, выступающие в роли условия, могут выбираться только среди допустимых или возможных значений.) Итак, любое условное распределение переменной Y безотносительно данного значения х однородно на отрезке [0; 1]. Аналогично любое условное распределение переменной X однородно на отрезке [0; 1] независимо о того, какое значение у дано в качестве условия. Соответствует ли этот результат вашим интуитивным представлениям?
Второй пример непрерывного двумерного распределения был схематично изображен на рис. 3.3, б. В нем случайным образом выбиралась точка из заштрихованного треугольника, а переменные X и Y определялись, как значения координат х и у этой выбранной точки. Маргинальные функции плотности для переменных X и Y указаны в (3.20); при этом распределение X оказалось «правотреугольным» на отрезке [0; 1], а распределение Y — «левотреугольным» на отрезке [0; 1]. Условные распределения для X и Y:
Проинтерпретируем полученные результаты. Условная плотность для переменной Y (при данном х) не зависит от у. В самом деле, она является константой и равна значению 1/х на всем отрезке [0; х]. Таким образом, условное распределение переменной Y при данном значении X = х однородно на отрезке [0; х]. Если мы вернемся к рис. 3.3, а, то увидим, в чем смысл подобной зависимости: как только в нашем распоряжении оказалась информация X = х, то при наличии информации о применении случайного механизма выбора мы можем сделать вывод о том, что переменная Y с одинаковой вероятностью принимает любые значения между 0 (ось абсцисс) и х (значение переменной Y на пересечении диагонали первого координатного угла и вертикальной прямой X = х). Аналогично (3.30) означает, что условное распределение переменной X при данном Y = у равномерно на отрезке [у; 1]. Вновь обращаясь к рис. 3.3, а, мы обнаружим в этом простой геометрический смысл: благодаря информации Y = у и действию случайного механизма выбора мы можем заключить, что X с одинаковой вероятностью принимает любое значение из отрезка между у (значение переменной X на пересечении диагонали первого квадранта с горизонтальной прямой Y = у) и 1 (правая граница треугольника).
Важно различие двух рассмотренных примеров. В первом условное распределение переменной Y при данном X = х не зависит от х; более того, каждое условное распределение в точности совпадает с маргинальным распределением, т.е. gY (у|х) = fY (у) для всех у и х. Аналогично в этом же примере условное распределение переменной X при данном Y = у не только не зависит от у, но и все условные распределения в точности совпадают с маргинальным распределением, т.е. gX (х|у) = fX (х) для всех х и у. Таким образом, ясно, что в первом примере переменные X и Y независимы (ср. (3.26)). Другими словами, знание значения переменной X неинформативно в отношении переменной Y, а знание значения переменной Y неинформативно в отношении переменной X.
Во втором примере ситуация противоположная — переменные X и Y зависимы. Как следует из (3.30), условное распределение переменной Y зависит от х, равно как и условное распределение переменной X зависит от у. Более того, условные распределения и соответствующие им безусловные (т.е. маргинальные) распределения различны. Ясно, что в этом втором примере знание значения X информативно по отношению к Y, а знание значения Y информативно по отношению к X. Так, если имеется информация х = 0,5, то мы оценим Y как Y ~ U (0; 0,5), если же х = 0,1, то Y ~ U (0; 0,1).
Из предшествующего обсуждения следует, что условия независимости и зависимости для непрерывного и дискретного случаев имеют одинаковый вид. Так, (3.26) служит определением независимости для каждого из этих двух случаев, а (3.27) — необходимое и достаточное условие независимости, применимое также в обоих случаях.
Вот, пожалуй, и все, что мы хотели сказать об условном распределении. Отметим еще раз основные моменты: даны определение условной функции вероятностей (для дискретного случая) и определение условной функции плотности вероятностей (для непрерывного случая). Алгебраически эти два определения эквивалентны (см. (3.24), (3.25), а также (3.28)) и позволяют представить условные распределения с помощью совместного распределения и маргинальных распределений. В этом разделе мы обобщили также ключевое понятие независимости (введенное в разделе 2.5 для событий), которое применимо теперь и к переменным. Как было показано, независимость между двумя переменными — синоним их взаимной неинформативности. [2]
Для выявления связи между двумя переменными X и Y используется характеристика, называемая ковариацией. Ее обозначают cov (X, Y) и определяют для дискретного случая с помощью равенства:
которому соответствует очевидный непрерывный эквивалент:
С этой характеристикой связана другая, называемая коэффициентом корреляции между X и Y. Коэффициент корреляции обозначают через rXY и определяют следующим образом:
где sd – стандартное отклонение.
Коэффициент корреляции rXY всегда лежит на отрезке между –1 и +1; он измеряет тесноту линейной связи между переменными. В частности, rXY равен 0, когда линейная зависимость между X и Y отсутствует; он равен –1, когда между X и Y существует точная отрицательная линейная зависимость, и равен +1, если между переменными имеется точная положительная линейная связь.
Резюме. Данная глава посвящена обобщению базовых характеристик распределения вероятностей, введенных в гл. 2, на случай двух и многих переменных. Мы начали со случая двух переменных и ввели сначала понятие совместного распределения вероятностей, а затем показали, как маргинальные распределения (их определяют для каждой переменной в отдельности) связаны с совместным распределением. Затем было введено исключительно важное понятие условного распределения вероятностей, которое представляет собой распределение одной переменной при наличии конкретной информации о другой переменной. Было показано, как условные, совместные и маргинальные распределения связаны между собой. Мы также сформулировали важное условие независимости переменных. Одним из самых важных понятий, сформулированных в этой главе, является понятие условного распределения. Как будет показано в следующей главе, это понятие необходимо при моделировании процесса объединения новой информации и уже имеющихся вероятностных оценок.
Упражнения
3.1. Рассмотрим эксперимент с двукратным бросанием «правильной» монеты. Пусть X принимает значение 1 (0), если при первом бросании выпадает герб (решетка), a Y принимает значение 1 (0), если герб (решетка) появляется при втором бросании. Постройте совместную, маргинальные и условные функции вероятностей (в табличной форме). (Должны получиться одно совместное, два маргинальных и четыре условных распределения.) Являются ли X и Y независимыми?
3.2. Рассмотрим эксперимент в ходе которого «правильная» монета подбрасывается четыре раза. Пусть X — число выпавших гербов, а Y — число решеток, выпавших после появления первого герба (если не выпало ни одного герба, то принимают Y = 4). Постройте в табличной форме совместную, маргинальные и условные функции вероятностей. (Должны получиться одно совместное, два маргинальных и десять условных распределений.) Будут ли X и Y независимыми?
3.5. Предположим, что совместная функция вероятностей дискретных переменных X и Y задана в виде fXY (х, y) = (x + y)/21, x = 1, 2, 3; y = 1, 2. Найдите маргинальные и условные распределения. Будут ли X и Y независимыми?
Решения
3.1. См. рис. ниже. Ячейки В4:С5 содержат совместную функцию вероятности fXY (x, y), в ячейках В6, С6, D4 и D5 маргинальные функции вероятностей. Видно, что переменные Х и Y являются независимыми, так как gX (x|y) = fX (x) = 1/2 а gY (y|x) = fY (y) = 1/2. Совместная функция вероятностей имеет вид:
3.2. См. рис. ниже. Переменные Х и Y являются зависимыми, так как в общем случае gX (x|y) ≠ fX (x).
3.5. См. рис. ниже. Переменные Х и Y являются зависимыми, так как в общем случае gX (x|y) ≠ fX (x).
До сих пор мы занимались описанием и обобщением «статических» вероятностных оценок, т.е. в соответствии с некоторым фиксированным объемом информации. Теперь мы выясним, как изменяются вероятностные оценки при появлении новой информации. Таким образом, данная глава посвящена изучению того, как новая информация может быть объединена с уже существующими вероятностными оценками.
Нас интересует, каким образом новая информация воздействует на вероятностные оценки. Чтобы отличить оценки, сделанные до поступления информации, от оценок после ее получения и инкорпорирования, будем называть первые априорными ожиданиями (априорными оценками), а вторые — апостериорными ожиданиями (апостериорными оценками). Применение термина «ожидание» позволяет подчеркнуть, что мы продолжаем трактовать вероятностные оценки как субъективные оценки некоего индивида. (К сожалению, прилагательные «априорный» и «апостериорный» используются лишь статистиками байесовского направления; многие специалисты, в частности экономисты, по глубоко укоренившейся традиции применяют вместо этих прилагательных латинские выражения «ех ante» и «ех post».)
Ясно, что на апостериорные ожидания влияют как априорные ожидания, так и новая информация. Более того, относительные веса, приписываемые априорным ожиданиям и новой информации при определении апостериорных ожиданий, зависят от сравнительной степени доверия к априорным ожиданиям и к новой информации. Цель данной главы — установить формальные и точные связи между апостериорными ожиданиями, с одной стороны, априорными ожиданиями и новой информацией — с другой. Как мы увидим, подобная формализация достигается при помощи теоремы Байеса, с которой мы впервые встретились в разделе 2.5.
Теореме Байеса посвящен раздел 4.3. До этого в разделе 4.2 мы познакомимся с несколькими простыми примерами инкорпорирования новой информации. Возникшие в связи с этим идеи будут формализованы в 4.3 путем применения теоремы Байеса. В разделах 4.4 и 4.5 описаны примеры более существенных приложений этой теоремы, причем в 4.4 эти приложения относятся к случаю, когда рассматриваются события, а в 4.5 — переменные. К этому моменту мы уже выясним, каким образом новая информация воздействует на априорные ожидания. Поэтому в разделе 4.6 остановимся на обсуждении того, как относиться к отсутствию априорной информации и можно ли ею полностью пренебречь. Материал этого раздела окажется полезным в ситуации, когда у нас не будет оснований для формирования какого-либо априорного суждения и для получения апостериорных выводов придется полностью опираться на новую информацию.
4.2. Учет новой информации. Простые примеры
Наверное, проще всего проиллюстрировать учет новой информации на примере ситуации, когда эта новая информация полностью исключает всякую неопределенность. Вернемся к примеру из гл. 2 и предположим, что нас интересует переменная X, определенная как возраст автора этой книги на 26 сентября 1984 г. Если вам не известно истинное значение X, то в вашей оценке X будет содержаться некоторая степень неопределенности. В зависимости от того, что вы обо мне знаете, или от вашей склонности к риску, вашей оценкой переменной X может стать либо U (36, 42), либо U (30, 50), либо U (20, 80), либо N (40, 9), либо что-то еще. [3] Но предположим, что я сообщил вам дату своего рождения – 26 сентября 1944 г. Допустим, вы мне доверяете (т.е. считаете информацию точной). Тогда любая неопределенность в отношении X исчезнет: вам известно, что X равняется 40.
Итак, каковы бы ни были ваши априорные ожидания по поводу X, ваши апостериорные ожидания есть U (40, 40) (или, что тоже самое, N (40, 0) — и в том, и в другом случае распределение вырождается в единственное значение 40). Ясно, что в данном случае, если считать информацию точной, то «рациональным» будет принять ее в качестве апостериорного ожидания: любые апостериорные ожидания, кроме X = 40, не оправданы. Эти представления о «рациональности» могут быть обобщены, что и сделано далее. (Мы оставим пока в стороне весьма интересный вопрос о формировании апостериорного распределения в случае, когда поступившая информация не воспринимается адресатом как точная, и он относится к ней с некоторым подозрением. Подумайте, что бы вы предприняли в такой ситуации.)
Рассмотрим еще один пример, когда часть информации полностью исключает неопределенность. Предположим, что весьма подозрительного вида человек обратился к вам в поезде с предложением «сыграть на пятерку» в «орлянку» и при этом извлек из своего кармана монету, которую не разрешил вам осмотреть. По его словам, это совершенно обычная, «правильная» монета. Однако вы, естественно, насторожились и предположили, что монета может оказаться двусторонней, т.е. с обеих сторон иметь герб. Будучи все-таки человеком непредубежденным, вы готовы согласиться на 50 шансов из 100, что ваш попутчик говорит правду. Он в свою очередь высказал готовность вначале трижды опробовать монету, чтобы уменьшить ваши опасения. Предположим, что во время этих трех пробных бросаний появилась решетка. Тогда (по отношению к вашим априорным ожиданиям) всякая неопределенность исчезнет. Монета, очевидно, не имеет гербов с двух сторон и вам остается сделать вывод, что она «правильная». (Обратите внимание на специфический характер этого примера, отражающего ту крайнюю ситуацию, в которой в соответствии с априорными ожиданиями имеются только две возможности — либо монета «правильная», либо у нее два герба. На деле вам следовало бы рассмотреть и другие возможности, например, монета может быть неровной, т.е. иметь смещение, вследствие чего герб выпадает чаще.) Итак, когда поступила новая информация о том, что выпала решетка, неопределенность исчезла. Однако, если бы новая информация состояла в том, что трижды выпал герб, неопределенность осталась бы, но предпочтительнее стала бы гипотеза о наличии у монеты двух гербов.
В двух приведенных сейчас примерах часть имеющейся информации полностью исключила всякую неопределенность относительно имевших место подозрений. Это весьма необычная ситуация. Гораздо чаще поступившая информация уменьшает неопределенность, но не исключает ее полностью. Вернемся вновь к переменной X, характеризующей возраст автора на 26 сентября 1984 г. Вообразите, что вам неизвестна дата рождения автора и ваша оценка состоит в том, что X ~ U (36, 42), Предположим, я сообщил вам, что родился не ранее 26 сентября 1943 г., т.е. к дате, для которой определяется переменная X, мне исполнилось не более 41 года. Какой станет ваша апостериорная оценка X в свете полученной информации (в предположении, что вы считаете сообщенные мною сведения истинными)? По-видимому, U (36, 41). (До получения информации вы считали одинаково возможными все значения X от 36 до 42; информация состояла в том, что X не превосходит 41; поэтому будет правильным сделать вывод, в силу которого X с одинаковой вероятностью может принимать любые значения от 36 до 41.) Пусть, далее, я сообщил вам, что родился не позднее 26 сентября 1946 г., т. е. к дате, для которой определяется X, прошло не более 38 лет. Какова ваша апостериорная оценка X, учитывающая и эту дополнительную информацию? Наверное, U (38, 41).
Вы можете обобщить последний пример. Пусть чьи-либо априорные ожидания по поводу X выражаются распределением U (a, b), где а меньше b. С появлением информации (предполагаемой истинной), что X не превосходит d, где а < d < b, апостериорные ожидания будут соответствовать распределению U (a, d). После того как поступит дополнительная (тоже предполагаемая истинной) информация о том, что X не меньше с, где а < с < d, новые апостериорные ожидания будут отвечать распределению U (с, d).
Этот пример удобен также для иллюстрации явления, описанного в гл. 2 и 3 и названного нами неинформативностью информации. Предположим, чья-то априорная информация о переменной X характеризовалась распределением U (а, b). Пусть теперь в распоряжении этого индивида оказалась информация о том, что X больше с, где с меньше а. Такая информация, очевидно, не может повлиять на оценку X, поскольку в силу априорных ожиданий уже предполагалось, что X больше с. Таким образом, апостериорные ожидания будут характеризоваться тем же распределением U (а, b). В этом случае и говорят о неинформативности информации. (Это вовсе не означает, что та же самая информация не окажется информативной для кого-либо другого, например, для того, чьим априорным распределением было U (е, f), где е < с < f.)
Возвращаясь к обсуждению проблем независимости в разделах 2.5 и 3.4, мы можем добавить, что информация по поводу некоторой переменной (или события) неинформативна, если эта информация и рассматриваемая переменная (или событие) независимы. Например, значение некоторой переменной Y называют неинформативным в отношении переменной X, если переменные X и Y независимы. Формально это выражается условием независимости между переменными (см. (3.26)), а именно
(4.1) gX (x|у) = fX (х) для всех х и у
В терминах данной главы gX (.|у) аккумулирует апостериорные ожидания о переменной X в свете информации о том, что Y равняется у, в то время как fX (.) обобщает априорные ожидания по поводу X. Уравнение (4.1) отражает формально тот очевидный факт, что при независимости X и Y апостериорные ожидания (после получения «информации» у) в точности совпадают с априорными ожиданиями. Таким образом, поступившая «информация» не изменила имевшейся оценки. Мы вновь встречаемся с проявлением «рациональной» реакции. Впрочем, вы вряд ли измените точку зрения на возраст автора, узнав, что один из торговых индексов в пятницу, 30 июля 1982 г., находился на отметке 556,5.
В данном разделе мы рассмотрели два крайних случая. В первом некоторая часть информации полностью исключала всякую неопределенность. Во втором полученная информация не оказала никакого воздействия на априорные вероятностные оценки. Мы кратко описали и промежуточный случай, когда поступившая информация изменяет априорную оценку, ведет к уменьшению неопределенности, но и не устраняет ее полностью. В следующем разделе мы рассмотрим этот случай более детально.
4.3. Учет новой информации. Теорема Байеса
Начнем с одного из простейших применений теоремы Байеса. Пре-положим, что нас интересует, произойдет или нет некоторое событие F. Для иллюстрации возьмем конкретный пример: предположим, F — событие, состоящее в том, что завтра будет дождь. Обозначим через ~F событие, являющееся отрицанием события F, т. е. в нашем примере ~F означает, что дождя завтра не будет. Ясно, что может произойти одно и только одно из событий F и ~F. В статистике такие события называют взаимно исключающими (только одно имеет место) и взаимно дополняющими (одно непременно имеет место). Теперь, опираясь на ваш опыт и знания, а также выглянув в окно, вы можете сформировать суждение об относительном правдоподобии F и ~F. Другими словами, вы можете указать некоторые оценки для Р (F) и Р (~F). (Это могут быть и не очень «хорошие» оценки, если рассматривать их с «объективных» позиций. Нас интересуют ваши оценки и то, как они изменятся в свете полученной вами новой информации.) Ваши оценки окажутся «рациональными» лишь при условии, что сумма вероятностей будет равна 1, т. е.
(4.2) P(F) + P(~F) = 1
Предположим вначале, что обе вероятности отличны от нуля: Р (F) > 0 и Р (~F) > 0. Позднее мы выясним, что произойдет, если одна из двух вероятностей равна нулю. (Таким образом, если вы живете, например, в Сахаре или в Манчестере, где одно из двух событий F или ~F выглядит вполне определенным, вам придется позаботиться о другом иллюстративном примере.) Предположим теперь, что вы решили послушать прогноз погоды на завтра. Этот прогноз представляет собой информацию по интересующему вас вопросу. Обычные прогнозы, конечно, многоаспектны, а информация, которую можно из них извлечь, многомерна. Однако мы рассмотрим частный и предельно простой вариант прогноза, когда, либо говорится, что завтра будет дождь, либо что дождя завтра не будет. Первый из этих прогнозов обозначим через Е, а второй — через ~Е. Итак, событие Е (оно служит для нас информацией) состоит в предсказании того, что завтра будет дождь, а событие ~Е (оно также служит информацией) — в предсказании того, что дождя завтра не будет.
Предположим, что на завтра предсказан дождь. (В наших обозначениях: произошло событие Е.) Какова после этого ваша оценка F? По-видимому, она зависит от степени вашего доверия прогнозам погоды и от уверенности в ваших собственных априорных ожиданиях. Это утверждение можно формализовать. Нас интересует величина Р (F|Е) — вероятность события F при наличии информации о событии Е, т. е. вероятность того, что завтра будет дождь, при условии, что бюро погоды предсказало дождь. Воспользуемся третьим законом вероятностей, сформулированным в (2.38), и запишем: Р (F|Е) = Р (Е и F)/P (Е). Числитель этого выражения можно раскрыть, если воспользоваться третьим законом еще раз. Тогда
Это соотношение является простейшей формой теоремы Байеса. Его можно интерпретировать по-разному, но нас будет интересовать наименее сложная интерпретация: в силу (4.3) апостериорная вероятность F (в свете информации Е) равна произведению априорной вероятности F на коэффициент Р (Е|F)/P (Е). В этом коэффициенте числитель представляет собой вероятность оправданного предсказания дождя, т.е. вероятность того, что бюро погоды предсказало дождь, и дождь на самом деле был; в знаменателе стоит просто вероятность предсказания дождя. Таким образом, частное от деления этих двух вероятностей можно рассматривать как отношение правдоподобия для правильно предсказанного дождя. В более общем случае это частное является отношением правдоподобия поступления «информации» Е, когда затем происходит событие F. Или, проще, это частное есть отношение правдоподобия Е при данном F.
Предположим, что вы пренебрежительно относитесь к прогнозам погоды, поскольку уверены в их бесполезности, хотя и не считаете, что с помощью прогнозов вас преднамеренно вводят в заблуждение. Ваше пренебрежительное отношение можно выразить формально
(4.4) P(E|F) = P(E|~F)
или, эквивалентно,
(4.5) P(~E|F) = P(~E|~F)
Уравнение (4.4) свидетельствует о том, что вероятность предсказания дождя будет такой же, независимо от того, пойдет дождь на самом деле или нет, и в то же время в силу уравнения (4.5) вероятность предсказания сухой погоды будет одной и той же как в случае, когда дождь пойдет, так и в случае, когда его не будет. Заметим, что (4.4) и (4.5) являются следствиями одно другого, поскольку сумма Р (Е|F) + Р(~Е|F) равняется единице, как и сумма Р (Е|~F) + Р (~Е|~F). Очень важно вытекающее из (4.4) следствие, в силу которого каждая из двух вероятностей, Р (Е|F) и Р (Е|~F), равна Р (Е). Другими словами, условные вероятности для Е совпадают с безусловной вероятностью наступления этого события. В этом можно убедиться следующим образом. Рассмотрим событие Е. Поскольку оно может произойти при наступлении одного и только одного из событий F и ~F, с помощью обозначений из раздела 2.5 можно записать
(4.6) Е ≡ (Е и F) или (Е и ~F)
Это тождество означает, что при наступлении события Е могут произойти либо оба события Е и F, либо оба события Е и ~F. Далее, поскольку событие (Е и F) и событие (Е и ~F) не могут произойти вместе, применим второй закон вероятностей (2.36) к тождеству (4.6) и получим
Р (Е) = Р (Е и F) + Р (Е и ~F)
Воспользуемся теперь третьим законом вероятностей (2.38) и раскроем два члена, стоящие в правой части полученного выражения:
(4.7) P(E) = P(E|F)*P(F) + Р(Е|~F)*Р(~F)
Уравнение (4.7) описывает вполне очевидный факт, что событие Е происходит, когда, либо F должно произойти и затем при данном F должно произойти E, либо F не должно произойти и уже при этом условии должно произойти Е. Пусть равенство (4.4) имеет место. Воспользуемся им для преобразования (4.7) и вспомним, что Р(F) + Р(~F) = 1:
Р(Е) = Р(Е|F)*[P(F) + Р(~F)] = Р(E|F)
Таким образом, если равны условные вероятности Р (Е|F) и Р (Е|~F), то они равны также и безусловной вероятности Р(E), т.е. равенство всех трех субъективных вероятностей является следствием вашей уверенности в бесполезности прогнозов погоды, которая и нашла отражение в соотношении (4.4). Точно так же можно вывести из соотношения (4.5), эквивалентного (4.4), равенство условных вероятностей Р(~Е|F) и Р(~Е|~F) безусловной вероятности Р(~Е). Если мы обратимся теперь к теореме Байеса (4.3), то увидим, что из (4.4) следует Р (F|Е) = Р(F), поскольку отношение взаимного правдоподобия Р (Е|F)/P(Е) обращается в 1. Тем самым мы показали, что из уверенности в бесполезности прогнозов погоды, чему соответствует соотношение (4.4), вытекает равенство между апостериорной вероятностью F и априорной вероятностью этого события: «информация» Е не изменяет нашей оценки.
После всех приведенных здесь рассуждений придется сообщить читателю, что они, в общем-то, излишни. Единственное, что следовало сделать, это обратить внимание на связь с понятием независимости. Ваша уверенность в бесполезности прогнозов, воплощенная в соотношении (4.4), не что иное, как независимость. Поэтому надо было лишь показать, что если «информация» не зависит от интересующего нас события (или переменной), то эта «информация» неинформативна. Действительно, мы можем установить указанное свойство в самом общем виде: если «информация» не зависит от интересующего нас объекта, то отношение правдоподобия (4.3) равно единице, т.е. апостериорная оценка совпадает с априорной оценкой.
Рассмотрим теперь другой крайний случай. Предположим, что прогноз погоды всегда соответствует действительности или, по крайней мере, что вы в это верите. Формально этому соответствуют равенства:
(4.8) P(E|F) = 1, P(~E|F) = 0, P(E|~F) = 0, P(~E|~F) = 1
Первые два из них (каждое из которых выводится из другого) означают, что дождь идет только тогда, когда он был предсказан. Два последующих (они также являются следствиями одно другого) свидетельствуют о том, что если дождя нет, то это было непременно предсказано. Заметим, что из двух первых не вытекают два оставшихся равенства, поскольку может случиться, что каждый дождливый день был действительно предсказан, однако в некоторых случаях дождь был обещан, но его не было. Если подставить равенства (4.8) в (4.7), то мы увидим, что Р (Е) = Р (F), а воспользовавшись последним равенством и формулами (4.8), подставив их в выражение для теоремы Байеса, получим Р (F|E) = 1.
Итак, гипотеза о совершенном (точном) прогнозе означает, что апостериорная оценка вероятности дождливой погоды, если такая погода была предсказана, равна 1, независимо от того, какой была априорная оценка.
Заслуживает внимания один крайний случай. Предположим, вы считаете, что посредством прогнозов вас умышленно вводят в заблуждение и что они совершенно не соответствуют действительности; формально это воплощается в уравнения:
(4.9) P(E|F) = 0, Р (~E|F) = 1, P(E|~F) = 1, P(~E|~F) = 0
Объединяя (4.9) с (4.7) и (4.3) получим Р (F|Е) = 0. Таким образом, для совершенно неверных прогнозов апостериорная оценка вероятности дождливой погоды при условии, что она была предсказана, равна нулю, независимо от того, какой была априорная оценка.
Теперь мы можем перейти к промежуточному случаю. Между отрицанием пользы прогнозов (этой гипотезе соответствуют соотношения (4.4) и (4.5)) и уверенностью в их совершенстве (эта гипотеза соответствует соотношениям (4.8)) находится «промежуточная позиция» относительно прогнозов, согласно которой они «лучше, чем ничего, хотя и несовершенны». Эта гипотеза формализуется с помощью цепочки неравенств
(4.10) P(E|F) > P(E) > P(E|~F)
или с помощью эквивалентной цепочки неравенств
(4.11) P(~E|F) < P(E) < P(~E|~F)
Прежде чем двигаться дальше, отметим ряд связей между (4.10) и (4.11). Во-первых, (4.10) и (4.11) следуют друг из друга. Во-вторых, из любых двух неравенств (4.10) и (4.11) вытекают все остальные неравенства этих соотношений. В-третьих, аналогичное предыдущему свойство имеет место для (4.11): из любых двух неравенств (4.11) вытекает третье.) Если неравенства (4.10) и (4.11) удовлетворяются, то отношение правдоподобия Р (Е|F)/P(Е) превосходит 1. Следовательно, по теореме Байеса (4.3) P(F|E) > P (F). Можно установить также, что в этом случае (см. упражнение 4.4) P(~F|E) < P(~F).
Итак, когда мы имеем дело с прогнозами, которые «лучше, чем ничего, хотя и несовершенны», предсказание дождя увеличивает вероятностную оценку того, что пойдет дождь, и уменьшает вероятностную оценку того, что дождя не будет. Ясно, что подобные аргументы можно привести и по поводу отношения к прогнозам как к «вводящим в заблуждение, хотя и не абсолютно».
Обобщим теперь результаты обсуждения: при совершенно надежных прогнозах апостериорная оценка Р (F|Е) равна 1 независимо от значения Р (F); при достаточно хороших прогнозах апостериорная вероятность больше априорной; при бесполезных прогнозах апостериорная вероятность совпадает с априорной; при частично ошибочных прогнозах апостериорная вероятность меньше априорной; при совершенно ошибочных прогнозах апостериорная вероятность равна 0 независимо от значения априорной вероятности. Таким образом, вероятностная оценка пересматривается либо в сторону повышения, либо в сторону понижения в свете поступившей (одинаковой по содержанию) информации, причем направление и характер этого пересмотра зависят от качества прогнозов (в смысле их связи с реальным исходом). Эти выводы из теоремы Байеса (4.3) имеют глубокий смысл.
Отметим еще одно следствие теоремы Байеса. Из (4.7) видно, что Р (Е) — взвешенная средняя величина двух условных вероятностей Р(Е|F) и Р(Е|~F), причем весами являются Р(F) и Р(~F), сумма которых равна 1. Поэтому для любой данной пары Р (Е|F) и Р(Е|~F), такой, что Р(Е|F) больше Р(Е|~F) (случай отношения к прогнозам, определенного нами как «лучше, чем ничего»), чем больше вероятность Р(F), тем больше вероятность Р(E). (Для рассматриваемого нами отношения к прогнозам — чем больше вероятность дождя, тем более вероятно, что будет предсказан дождь.) Теперь с помощью теоремы Байеса (4.3) мы можем убедиться в том, что с увеличением Р(F) уменьшается разность Р(F|Е) – Р(F).
Это соответствует принципу, которому все следуют интуитивно: априорные ожидания становятся тем более надежными, чем менее они нуждаются в пересмотре в связи с поступлением новой информации.
Проведенный анализ опирался на предположение о том, что и для F, и для ~F априорная вероятность отлична от нуля, т.е. Р(F) > 0 и Р(~F) > 0. Для полноты картины рассмотрим теперь случай, когда одна из этих вероятностей равна нулю. (Очевидно, что обе они в нуль не обращаются, поскольку их сумма равна 1.) Пусть, например, Р(F) = 0, и тогда Р(~F) = 1. Если взглянуть теперь на теорему Байеса (4.3), то можно увидеть, что в нашем случае Р(F|Е) = Р(Е|F)/P(Е). Однако из (4.7) (с учетом тех же условий) получим: Р(Е) = Р(Е|F). Итак, если Р(F) = 1, то Р (F|E) = 1. Поступившая информация не изменила нашей оценки. Не изменит она ее и в случае, когда P(F) = 0: при этом Р(F|Е) обращается в нуль, в силу теоремы Байеса.
На этом анализ основных следствий, вытекающих из теоремы Байеса, завершен. Нашей целью было показать в этом разделе применение теоремы Байеса в ее простейшей форме. В частности, мы убедились в том, что модель учета новой информации наряду с существующими вероятностными оценками интуитивно приемлема и что соотношение, связывающее апостериорные и априорные оценки и новую информацию, также соответствует интуитивным представлениям. Конечно, подобные ссылки на интуицию вовсе не обязательны для подтверждения логической корректности теоремы Байеса (поскольку эта теорема выводится логически из трех простых вероятностных законов, сформулированных в гл. 2), они свидетельствуют лишь о том, что логика и интуиция в рассматриваемых вопросах согласованы.
4.4. Применение теоремы Байеса к описанию событий
Хотя с формальной точки зрения формулировка теоремы Байеса для вероятностного описания событий, соответствующая равенству (4.3), является общей, и ей можно воспользоваться при решении различных вероятностных задач, она не приспособлена непосредственно для ответов на конкретные вопросы, возникающие на практике. В начале данного раздела мы приведем более удобную для этих целей формулировку, а затем рассмотрим ее применение.
В предыдущем разделе мы сосредоточили внимание на ситуации, когда имеется лишь одно, интересующее нас событие F и событие ~F, состоящее в том, что F не происходит. В данном разделе мы будем предполагать, что в поле нашего зрения находится I событий F1, F2, …, FI. Пусть эти I событий взаимно исключающие и образуют полное множество событий; другими словами, только одно из этих событий может произойти, но одно происходит обязательно. Формально это означает, что событие (Fi и Fj) невозможно при i ≠ j, а событие (F1 или F2 или … или FI), в записи которого учтены все возможные варианты, обязательно происходит.
Обозначим через Р(Fi), i = 1, 2, …, I, где = 1, — априорные оценки вероятностей I рассматриваемых событий. Как и прежде, будем обозначать через Е поступившую новую информацию, а апостериорные оценки вероятностей этих событий — через Р(Fi|Е), i = 1, 2, …, I. Поскольку простейшая форма записи (4.3) теоремы Байеса является наиболее общей, ею можно воспользоваться для определения Р(Fi|Е):
Знаменатель можно преобразовать, как мы это делали в разделе 4.3: Е ≡ (Е и F1) или (Е и F2) или … или (Е и FI), а поскольку любое событие (Е и Fi) и любое событие (Е и Fj) взаимно исключают друг друга при i ≠ j, то
Наконец, воспользуемся (2.38), чтобы записать Р (E и Fj) как Р (E|Fj)*Р (Fj). Получим
Возьмем теперь (4.13), чтобы преобразовать выражение для апостериорной оценки события Fj:
Мы получили обобщенную форму теоремы Байеса для событий.
Проведем обычную проверку правильности расчета вероятностей (4.14) и подсчитаем их сумму по всем i = 1, 2, …, I. Если ошибок в преобразованиях нет, то эта сумма должна равняться 1. (При проверке воспользуемся тем, что события F1, F2, …, FI взаимно исключают друг друга и образуют полное множество событий.) Суммируя (4.14) по i = 1, 2, …, I, получим
что позволяет надеяться на отсутствие ошибок. Заметим, что в процессе суммирования мы вынесли знаменатель за скобки, поскольку он не зависит от индекса, по которому ведется суммирование. Но более важное обстоятельство, на которое мы можем обратить внимание благодаря проведенной проверке, то, что знаменатель в (4.14) является просто масштабным множителем, обеспечивающим равенство суммы всех апостериорных вероятностей 1. Мы можем кратко (см. 2.4) записать выражение (4.14) в виде
(4.15) Р (Fi|Е) µ Р (Е|Fi)*Р(Fi), i = 1, 2, …, I,
где множитель пропорциональности выбирается так, чтобы обеспечивалось равенство суммы апостериорных вероятностей единице. Эта запись теоремы Байеса будет часто использоваться в дальнейшем.
Соотношение (4.15) допускает простую интерпретацию. Вспомним, что Р(Fi) обозначает априорную вероятность события Fi, Р(Fi|Е) — апостериорную вероятность, а Р(Е|Fi) — вероятность поступления информации при условии, что Fi имеет место. Чаще всего Р(Е|Fi) рассматривают как правдоподобие Е при данном Fi, т.е. меру того, насколько вероятно получить информацию E, если событие Fi считать свершившимся. Пользуясь этим термином, можно сформулировать теорему Байеса, записанную в виде (4.15), следующим образом:
(4.16) апостериорная оценка пропорциональна произведению априорной оценки на правдоподобие полученной информации.
Эта теорема формализует интуитивное представление, в силу которого апостериорная оценка представляет собой сочетание («смесь») новой информации с априорной оценкой.
Рассмотрим пример, более привлекательный своей простотой, нежели реалистичностью. Предположим, у вас есть три монеты: одну из них вы считаете «правильной»; вторую — смещенной так, что вероятность выпадения герба втрое больше, чем решетки, и третью — смещенной так, что вероятность выпадения решетки втрое больше, чем герба. Пусть некто случайным образом выбрал одну из трех монет, но не сообщил вам, какую. Затем он дважды ее подбросил, и оба раза выпал герб. Какова ваша апостериорная оценка того, какая монета выбрана, в свете полученной информации о появлении двух гербов при двух ее бросаниях?
Введем обозначения и сделаем два ключевых предположения. Пусть F1 обозначает событие, когда выбранная монета чаще выпадает гербом, F2 — выбрана «правильная» монета, F3 — выбранная монета чаще выпадает решеткой. Через Е обозначим информацию о том, что при двух бросаниях дважды появился герб. Чтобы приступить к расчетам, нам придется сделать предположения относительно процедуры выбора и механизма бросания. В силу отсутствия альтернативных соображений мы будем считать их «правильными», вкладывая в это следующий смысл. Во-первых, для процедуры выбора будем считать, что
(4.17) Р(F1) = Р(F2) = Р(F3) = 1/3
т.е. имелись одинаковые шансы выбрать любую из трех монет. Во-вторых, относительно механизма бросания предположим, что
(4.18) Р(Н|F1) = 3/4, Р(Н|F2) = 1/2, Р(Н|F3) = 1/4,
где через Н обозначено событие, состоящее в появлении герба при одном бросании монеты. В равенствах (4.18) отражены и уверенность в «правильности» самого механизма бросания, и ваши представления о свойствах каждой из трех монет.
Теперь мы имеем возможность рассчитать апостериорные вероятности. Для наглядности мы сначала применим теорему Байеса в ее развернутой записи (4.14), после чего повторим выкладки для случая сокращенной записи (4.15). Поскольку Е есть информация о том, что при двух бросаниях выбранной монеты дважды появился герб, с помощью (4.18) мы можем найти
Конечно, нам пришлось предположить, что исходы двух бросаний независимы. Аналогично Р(Е|F2) = 4/16 и Р(Е|F3) = 1/16. Теперь (с учетом (4.17)) мы располагаем всем необходимым для того, чтобы вычислить знаменатель выражения, стоящего в правой части (4.14): 9/16*1/3 + 4/16*1/3 + 1/16*1/3 = 14/48. Применяя (4.14) последовательно для каждого из событий F1, F2 и F3, получим:
Итак, апостериорные вероятности F1, F2 и F3 в свете информации о появлении двух гербов при двух бросаниях выбранной монеты равны 9/14, 4/14 и 1/14 соответственно. Из сравнения с априорными вероятностями 1/3, 1/3, и 1/3 становится ясно, что благодаря наблюдениям чаша весов существенно склонилась в пользу события F1 означающего выбор монеты, чаще выпадающей гербом.
Сокращенная запись теоремы Байеса (4.15) позволяет упростить арифметические выкладки. Соответствующие расчеты сведены в табл. 4.1. Столбец (2) содержит значение априорной вероятности для каждого i, столбец (3) — характеристики правдоподобия «информации» Е, столбец (4) получается перемножением значений двух предшествующих столбцов (ср. (4.16)). Чтобы найти множитель пропорциональности, определяем сумму значений столбца (4) и затем делим на эту величину каждое из содержащихся в столбце значений; тем самым получаем числа столбца (5). Для каждого i число, стоящее в столбце (5), пропорционально произведению априорной вероятности на правдоподобие информации, но, кроме того, сумма всех чисел этого столбца равна 1. Следовательно, в столбце (5) содержатся значения апостериорных вероятностей.
Конечно, вычисления можно еще упростить, если избавиться от дробей в столбцах (2), (3) и (4). Тогда в столбце (2) будут стоять числа 1, 1 и 1; в столбце (3) — числа 9, 4 и 1; в столбце (4) — числа 9, 4 и 1. Сумма элементов столбца (4) равна 14 и апостериорные вероятности равны соответственно 9/14, 4/14 и 1/14, как в табл. 4.1.
Безусловно, апостериорные вероятности зависят от полученной информации. Проведенные выше выкладки опираются на информацию о том, что при двух бросаниях выбранной монеты дважды появился герб. Но мы не обратили внимание читателя на то, что при получении различной информации мы придем к различным апостериорным вероятностям. Вы можете самостоятельно проверить правильность вычисления апостериорных вероятностей, приведенных в табл. 4.2, в левой части которой (табл. 4.2 (а)) использована информация о появлении при двух бросаниях одного герба и одной решетки, а в правой части (табл. 4.2 (б)) — двух решеток.
Мы еще вернемся к этому примеру, а теперь найдем те же значения другим способом. Упростим этот пример: выбранная монета подбрасывается только один раз. Зададимся тем же вопросом, что и прежде: каковы апостериорные оценки того, какая монета выбрана, если при одном ее бросании выпал герб? При тех же предположениях относительно процедуры выбора и механизма подбрасывания, что и раньше, правдоподобие информации Е (появление одного герба при одном подбрасывании монеты) для F1, F2 и F3 будет иметь значения:
(4.19) Р(E|F1) = 3/4, Р(E|F2) = 1/2, Р(E|F3) = 1/4,
Следовательно, если для априорных вероятностей сохраняются оценки (4.17), то апостериорные вероятности F1, F2 и F3 пропорциональны 3/12, 2/12 и 1/12 соответственно. После деления на масштабный множитель получим следующие значения апостериорных вероятностей:
(4.20) Р (F1|Е) = 3/6, Р(F2|Е) = 2/6, Р(F3|Е) = 1/6
Пусть теперь монету подбросили второй раз, и исходом снова было появление герба. Каковы по вашим предположениям апостериорные вероятности в свете этой информации? Ясно, что можно прибегнуть к той же процедуре, что и ранее. Соответствующие правдоподобия останутся теми же, что и в (4.19), поскольку в нашем конкретном примере мы предположили возможные исходы при втором бросании такими же, как при первом. Априорными вероятностями, соответствующими новой ситуации, будут значения (4.20), поскольку именно такими оценками вы располагали к моменту поступления новой порции информации — стал известен исход второго подбрасывания монеты. Итак, произведения соответствующих значений, характеризующих правдоподобие информации и априорные вероятности событий F1, F2 и F3, будут равны 9/24, 4/24 и 1/24 соответственно. Разделим их на масштабный множитель и получим апостериорные вероятности для ситуации, когда при двух последовательных бросаниях выбранной монеты дважды появлялся герб:
Р (F1|Е) = 9/14 Р(F2|Е) = 4/14, Р(F3|Е) = 1/14
Эти выражения в точности совпадают с теми, которые были получены в первоначальном примере, когда исходы двух подбрасываний рассматривались как одна порция информации. Таким образом, мы показали, что независимо от того, рассматриваем ли мы исходы двух бросаний монеты как одну порцию информации или же считаем их двумя порциями информации (пересматривая наши оценки после получения очередной порции), мы приходим в итоге к тем же самым апостериорным оценкам. Это весьма обнадеживающий результат. (В самом деле, благодаря тому, что он имеет место, у нас гораздо меньше трудностей, чем в противном случае.) Возможно, у вас появилось желание убедиться в том, что этот результат справедлив в гораздо более общем случае?
Сделаем несколько общих замечаний, прежде чем завершить этот раздел. Во-первых, еще раз укажем на факт, в пользу которого мы успели уже привести множество аргументов: «информация» становится неинформативной, если она и интересующее нас явление независимы. В терминах этого раздела независимость характеризуется условием Р (Е|Fi) = Р(Е) для всех i = 1, 2, …, I. Очевидно, что при подстановке этого равенства в (4.14) — запись одной из форм теоремы Байеса, мы получим Р(Fi|Е) = Р(Fi) для всех i = 1, 2, …, I. Поступление такой «информации» не вызывает изменения вероятностных оценок. Мы можем также обобщить проведенный ранее анализ на случай, когда априорная вероятность какого-либо из событий равна нулю. Из (4.14) тогда вытекает, что если Р(Fj) = 0, то Р(Fj|E) также обращается в нуль. Итак, если мы рассматриваем событие, которое изначально считаем невозможным, то никакое число наблюдений не убедит нас в обратном.
Укажем не совсем очевидное следствие последнего результата: апостериорная вероятность события зависит также и от множества других событий, которые мы считаем возможными. По сути, это утверждение неявно подразумевается в данном разделе, но было бы полезно убедиться в его справедливости непосредственно. Рассмотрим в чисто иллюстративных целях первоначальный пример с монетами. Пусть вновь в результате двух бросаний выбранной монеты дважды появился герб. Предположим теперь, что имеются только две возможности, которые могут реализоваться в отношении выбранной монеты, допустим F1 и F3. (Следовательно, априорная вероятность F2 равна нулю.) Вы можете убедиться в том, что если каждая из рассматриваемых возможностей равновероятна, то апостериорные вероятности после появления двух гербов при двух бросаниях будут
(4.21) Р(F1|Е) = 9/10 и Р(F2|E) = 1/10
Конечно, этот результат отличается от полученного в случае, когда все три возможности предполагались равновероятными; вместе с тем следует отметить, что отношение апостериорных вероятностей осталось тем же. Заметим также, что если информация Е и какое-либо событие Fj взаимно исключают друг друга (т.е. они не могут произойти одновременно), то появление Е автоматически ведет к невозможности появления Fj. Другими словами, Р(Fj|Е) = 0. Это вытекает из (4.14), так как Р(Е|Fj) должно обращаться в нуль, если Е и F — взаимно исключающие друг друга события.
Выше мы рассмотрели случай, когда Е и одно событие Fj взаимно исключают друг друга. Ситуация существенно усложняется, если появляется информация Е, которая оказывается взаимно исключающей с каждым событием Fi. При этом мы можем встретиться с неожиданностями. К сожалению, теорема Байеса не подсказывает выхода из создавшегося положения. (И числитель, и знаменатель в правой части соотношения (4.14) обращаются в нуль, поэтому апостериорную вероятность не удается определить.) Суть происходящего ясна: нужно убедиться в правильности всех построений, начиная с того, что множество F1, F2 и F3 содержит все возможные исходы даже в том случае, когда многим из них соответствуют очень малые априорные вероятности.
Нам осталось проиллюстрировать сделанное в начале гл. 2 замечание о том, что апостериорные оценки в свете большого количества поступающей информации сближаются независимо от исходных априорных оценок. Рассмотрим модификацию нашего примера с монетами, в которой все внимание сосредоточено на возможностях F1 и F3, а по поводу оставшейся третьей возможности принято предположение Р(F2) = 0. Пусть величина Р(F1) обозначена через р. Тогда Р(F3) = 1 — р. Предположим далее, что выбранная монета подбрасывается n раз, причем в m случаях из них появляется герб. Апостериорные оценки вероятностей в свете этой информации будут выглядеть следующим образом (см. упражнение 4.11):
Допустим, выбранная монета такова, что герб выпадает в три раза чаще решетки. Тогда при очень длинной серии подбрасываний m будет стремиться к Зn/4. Следовательно, в выражениях для Р(F1|Е) и Р (F3|Е) мы можем перейти к пределу при неограниченном возрастании n. Для первой из этих вероятностей получим
Аналогично убеждаемся, что P(F3|E) при неограниченном возрастании n стремится к нулю. Итак, если выбранная монета чаще выпадает гербом, то в пределе вы убедитесь в этом независимо от того, каким будет исходное значение р. Точно так же исследуется случай, когда выбранная монета чаще выпадает решеткой (в силу симметрии ситуации изменится только ее наименование). Этот результат, весьма обнадеживает и допускает обобщение.
4.5. Некоторые приложения теоремы Байеса для переменных
Теорема Байеса для переменных выводится так же, как-это было сделано в разделах 4.3 и 4.4 для событий. Поэтому мы опустим формальный вывод и просто дадим для переменных аналог сокращенной формы (4.15) записи этой теоремы:
(4.23) gY(у|х) µ gX(x|у)*fY(у) для всех х и у
Чтобы проинтерпретировать это соотношение, будем считать Y некоторой интересующей нас переменной, а X — наблюдением (в форме, присущей переменным), которое потенциально содержит «информацию» о Y. Левая часть соотношения (4.23) представляет собой апостериорные ожидания относительно Y в свете «информации» х. Первый сомножитель в правой части есть правдоподобие получения информации х при данном y, а второй сомножитель — априорные ожидания относительно Y. Вновь теорема Байеса, оказывается формализованным отражением интуитивного представления, в силу которого апостериорная оценка связана с новой информацией и априорной оценкой.
Следует сопоставить две записи теоремы Байеса (для переменных и для событий), т.е. соотношения (4.23) и (4.15). Наблюденному значению х в первом соответствует Е во втором, а значениям, принимаемым переменной Y в первом, — события F1, F2, FI во втором. Соответствуют друг другу так же обозначения апостериорных вероятностей gY(у|х) и Р(Fi|E), правдоподобий gX(х|у) и Р(Е|Fi) и, наконец, априорных вероятностей fY(у) и Р(Fi).
Сделаем несколько замечаний по поводу (4.23). Во-первых, это соотношение имеет место как для дискретных, так и для непрерывных переменных. Если X — дискретная переменная, то gX(.|у) — функция условных вероятностей; если же X — непрерывная переменная, то gX(.|у) — функция плотности условных вероятностей. Точно так же, если Y — дискретная переменная, то gY(.|х) и fY() — условная и безусловная функции вероятностей; если же Y — непрерывная переменная, то gY(.|х) и fY() — условная и безусловная функции плотности вероятностей. Однако множитель масштаба или множитель пропорциональности будет зависеть от того, дискретна или непрерывна переменная Y. Так, если Y — дискретная переменная, то множитель масштаба (т.е. множитель, который превращает (4.23) из соотношения пропорциональности в равенство) равен gX(х|у)*fY(у). Если переменная Y непрерывна, то соответствующий масштабный множитель равен gX(х|у)*fY(у)dy. И в том и в другом случае суммирование или интегрирование соответственно ведется по всем х. [4]
4.6. Предварительные замечания о случае, когда отсутствует априорная информация
Возможно, само понятие априорной оценки наводит вас на мысль о том, что рассматриваемые здесь методы связаны с существованием некоторого начального или исходного значения, которое изменяется под воздействием новой информации. Вы вправе в таком случае спросить, что предпринять, если на деле мы лишены априорных представлений об интересующем нас объекте (т.е. абсолютно ничего не знаем об Y, кроме только что полученной информации)? Как можно изменить то, чего нет?
В данный момент мы не ответим на поставленные вопросы — это будет сделано позже. Однако можем предложить пример, который несколько рассеет наши сомнения. Ранее (это было в опущенной мною части раздела 4.5) мы рассмотрели пример, в котором предполагалось, что априорная оценка Y удовлетворяет распределению N(µ, σ2). При этом чем больше σ2, тем больше разброс априорной оценки, и потому меньше к ней доверия. Предположим, что мы нашли способ, позволяющий выразить отсутствие априорной информации — «устремили» σ2 к бесконечности. Это равносильно тому, что мы действительно ничего не знаем об Y. Посмотрим теперь, что произойдет с (4.23), если «устремить» σ2 к бесконечности. Мы обнаружим, что апостериорное распределение в пределе превратится в N(х, s2). Иными словами, апостериорное распределение зависит исключительно от появившегося при наблюдении значения переменной X и от дисперсии этой переменной, что для нас весьма важно.
Резюме. В данной главе речь шла о новой информации и о том, как ею можно воспользоваться для уточнения уже существовавших к моменту ее поступления вероятностных оценок. Рассмотрев несколько простых примеров, мы вывели теорему Байеса, позволившую формально описать процесс учета новой информации при уточнении вероятностных оценок. Интуитивное представление о том, что апостериорные ожидания представляют собой смесь априорных ожиданий и новой информации, получило формальное отражение в теореме Байеса. По сути дела, эта теорема устанавливает пропорциональность апостериорной (функции плотности) вероятностей, с одной стороны, и произведения правдоподобия (поступления именно этой информации) и априорной (функции плотности) вероятностей — с другой. После обсуждения указанных вопросов мы рассмотрели ряд примеров: вначале примеры, относящиеся к событиям, а затем — к переменным.
Упражнения
4.2. Предположим, что ваши априорные представления об агрегированной предельной склонности к потреблению в некоторой национальной экономике (до вычета налогов) отражаются распределением U (0; 1). Пусть затем вам сообщили, что все жители страны вносят не менее 5% своего дохода (до вычета налогов) в фонд социального страхования. Каким будет распределение вашей апостериорной оценки предельной склонности к потреблению в этой экономике?
4.5. Некто носит в кармане одну «правильную» монету (с гербом и решеткой) и одну фальшивую (с двумя гербами). Он выбрал одну из этих монет случайным образом и когда подбросил ее, она упала вверх гербом. Какова вероятность того, что эта монета была «правильной»? (б) Предположим, что эта монета была подброшена еще раз и вновь выпал герб. Какова теперь вероятность того, что эта монета «правильная»? (в) Пусть монета подброшена в третий раз и упала решеткой вверх. Чему стала равна вероятность того, что монета правильная?
4.6. В коробке лежат три монеты. Одна — с двумя гербами, другая — с двумя решетками, а третья — «правильная». Случайным образом из коробки выбирается монета и после подбрасывания падает вверх гербом. Какова вероятность, что была выбрана монета с двумя гербами?
4.7. Два ученых, Джон и Смит, поставили эксперимент для проверки двух гипотез, Н1 и Н2. Априорную вероятность для гипотезы Н1 Джон оценил, как 0,8, а Смит думал, что Н2 вдвое «вероятнее», чем Н2. Данные (D) были получены, и на их основе рассчитаны правдоподобия: Р(D|Н1) = 0,0084, Р(D|Н2) = 0,0008. Покажите, что апостериорные ожидания двух ученых сблизились по сравнению с их априорными ожиданиями.
4.8. Вы знаете, что в одном частном университете 60% студентов одного пола и 40% другого, но вы забыли, кого больше, мужчин или женщин. Если первые два студента, которых вы встретили, женщины, то какова вероятность того что справедлива гипотеза, в силу которой женщины составляют большинство? Что вы скажите, если следующие повстречавшиеся вам студенты — мужчины? Не означает ли это, что информация оказалась бесполезной?
4.13. Пусть в каждой из двух урн содержится большое число белых и черных шаров: в первой – 40% белых, а во второй – 60% белых. Одна из двух урн выбрана с помощью механизма, обеспечивающего выбор первой урны с вероятностью р (если бы механизм был «правильным», то р = 1/2). Пусть n шаров извлечены из выбранной урны, причем m из них оказались белыми (а n – m соответственно черными). Определите апостериорную вероятность того, что была выбрана первая урна. Покажите, что если бы эта урна действительно оказалась первой, то найденная апостериорная вероятность при неограниченном возрастании n стремилась бы к 1, а если бы это была вторая урна, то апостериорная вероятность стремилась бы к нулю.
Решения
4.2. Новая информация говорит о том, что следует скорректировать первоначально имевшуюся нижнюю оценку: U’ [0,05; 1]
4.5. (а) Априорные вероятности выбрать «правильную» (П) и фальшивую (Ф) монеты составляли 1/2. Если выбрана правильная монета, вероятность выпадения герба P(Г|П) = 1/2; если выбрана фальшивая монета, вероятность выпадения герба P(Г|Ф) = 1. Таким образом, по теореме Байеса:
Апостериорная вероятность того, что была выбрана правильная монета составляет 1 шанс из 3, т.е. сократилась по сравнению с априорной вероятностью, которая составляла 1 шанс из 2.
(б) Можно воспользоваться ранее полученной апостериорной информацией Р(П|Г) и на ее основе повторить вычисления:
где Р(П|2Г) – вероятность обнаружить правильную монету, если выпало два герба, Р(П1) = 1/3 – вероятность правильной монеты после первого выпадения герба, Р(Ф1) = 2/3 – вероятность фальшивой монеты после первого выпадения герба.
(в) Сделаем еще один последовательный шаг:
Вероятность обнаружить правильную монету, если выпало три герба подряд составляют 1 шанс из 9.
4.6. Первоначальные (априорные) вероятности выбрать одну из трех монет были равны и составляли 1/3. Событие – выпадение герба – показало, что это точно не монета с двумя решетками, поэтому, можно смело воспользоваться формулой, аналогичной (4.упр.1):
Вероятность того, что была выбрана монета с двумя гербами составляет 2 шанса из 3, т.е. сократилась по сравнению с априорной вероятностью, которая составляла 1 шанс из 2
4.7. Априорные вероятности Джона: Р(Н1) = 0,8; Р(Н2) = 0,2. Его апостериорная вероятность:
До получения данных D Джон оценивал вероятность гипотезы Н1 в 80%; после получения данных D его уверенность в гипотезе Н1 возросла до 97,7%.
Априорные вероятности Смита: Р(Н1) = 2/3; Р(Н2) = 1/3. Его апостериорная вероятность:
До получения данных D Смит оценивал вероятность гипотезы Н2 в 66,7%; после получения данных D его вера в гипотезу Н2 была подвергнута серьезному испытанию и сократилась 7,8%.
До получения данных D априорные вероятности ученых сильно расходились. Например, в гипотезу Н2 Джон верил на 20%, а Смит – на 67,7%. После же получения данных D апостериорные вероятности сблизились: на долю Н2 Джон отводил 2,3%, а Смит – 7,8%.
4.8. Априорные вероятности выбрать сообщество, где женщин большинство или меньшинство, считаем равными (хотя в большинстве стран это не так – женщин больше): Р(П1) = Р(П2) = 50%, где событие П1 – сообщество с 60% женщин, П2 – сообщество с 40% женщин. Произошло событие – 2Ж – наблюдение двух женщин. Если женщин большинство, то вероятность наблюдения двух женщин Р(2Ж|П1) = 0,6*0,6 = 0,36. Если женщин меньшинство, то вероятность наблюдения двух женщин Р(2Ж|П2) = 0,4*0,4 = 0,16. Апостериорная вероятность того, что женщин большинство:
Если мы встретили двух женщин, вероятность того что это сообщество с преобладанием женщин составляет 69,2%.
Допустим после встречи двух женщин нам повстречались двое мужчин. Если в сообществе большинство женщин, то вероятность наблюдения этого события Р(2Ж+2М|П1) = 0,6*0,6*0,4*0,4 = 0,0576. Если же в сообществе большинство мужчин, то вероятность наблюдения этого события Р(2Ж+2М|П2) = 0,4*0,4*0,6*0,6 = 0,0576. То есть, вероятность Р(2Ж+2М|П1) = Р(2Ж+2М|П2). А раз сила свидетельств одинакова, то и влияния эта информация на априорные вероятности не оказала.
4.13. Априорная вероятность выбрать первую урну Р(У1) = р, априорная вероятность выбрать вторую урну Р(У2) = 1 – р. Вероятность вытащить m белых шаров, если выбрана первая урна Р(Бm|У1) = 0,4m0,6n–m , где ![]() – число сочетаний из n по m. Вероятность вытащить m белых шаров, если выбрана вторая урна Р(Бm|У2) =
– число сочетаний из n по m. Вероятность вытащить m белых шаров, если выбрана вторая урна Р(Бm|У2) = ![]() 0,6m0,4n–m. Апостериорная вероятность того, что выбрана первая урна, если мы наблюдаем m белых шаров:
0,6m0,4n–m. Апостериорная вероятность того, что выбрана первая урна, если мы наблюдаем m белых шаров:
Покажем, что, если выбранная урна действительно оказалась первой, то есть, если m < n/2, то найденная в (4.упр.9) апостериорная вероятность при неограниченном возрастании n стремится к единице. Разделим числитель и знаменатель на ![]() :
:
Видно, что если m < n/2, то второе слагаемое в знаменателе при возрастании n стремится к нулю, а вся дробь – к единице. Если же m > n/2, то есть, если реально выбрана вторая урна, то второе слагаемое в знаменателе стремиться к бесконечности, а вся дробь – к нулю. Что и требовалось доказать.
К оглавлению
Глава 5. Доли элементов совокупности
В этой главе рассматривается проблема вероятностного вывода относительно доли элементов совокупности, обладающих определенным свойством. Хотя сама по себе эта проблема не имеет большого значения, она привлекательна, во-первых, простотой постановки, а во-вторых, тем, что ее решение хорошо иллюстрирует общие положения, связанные с получением вероятностного вывода, к которым мы не раз будем обращаться при решении задач в последующих главах книги. Таким образом, данная глава готовит читателя к восприятию общих концептуальных идей теории байесовского вывода на материале, не перегруженном алгебраическими и техническими деталями. В дальнейшем вы столкнетесь с задачами, более интересными с прикладной точки зрения и требующими более сложного алгебраического аппарата. Однако новых положений самой теории байесовского вероятностного ввода вы уже не встретите.
В общем виде задачи, рассматриваемые в этой и следующих главах, могут быть сформулированы следующим образом: есть некоторый интересующий нас объект (таких объектов может быть несколько); мы не располагаем о нем точной информацией, иначе не было бы предмета для исследования, но можем иметь об этом объекте некоторые предварительные представления или связанные с ним априорные ожидания; может быть получена (или к нам может поступить) некоторая информация об интересующем нас объекте; эта информация побуждает нас (или позволяет нам) изменить (пересмотреть, уточнить) наши представления о нем. Таким образом, в данной задаче можно выделить две составляющие ее «подзадачи»: описать ожидания, связанные с объектом в каждый конкретный момент времени; указать способ изменения ожиданий в свете поступившей новой информации. По существу, необходимым для решения подобных задач аппаратом мы уже располагаем: в гл. 2 и 3 речь шла об описании ожиданий, а в гл. 4 — об учете новой информации. Теперь нужно приобрести опыт применения полученных знаний.
Экономисты всегда стремятся установить, насколько реалистичны конкурирующие между собой экономические теории. Например, можно ли утверждать, что монетаристская трактовка инфляции лучше, чем ее объяснение с помощью кривой Филлипса. При этом необходимо уметь отвечать на вопрос, чему равны в рамках данной конкретной экономической теории числовые значения важнейших экономических параметров (таких, как предельная склонность к потреблению, эластичность спроса на деньги в зависимости от ставки процента). Другими словами, речь идет о влиянии изменений одной экономической переменной на другую. Мы обсудим подобные проблемы позже. В данной главе и гл. 6 мы изучим конкретные экономические параметры: в данной главе — доли, а в гл. 6 — средние и дисперсии.
Нас интересует некоторая доля, например: доля рослых людей, читающих газету «Таймс»; доля появлений «черного» при вращении конкретной рулетки; доля коренных жителей стран Азии среди студентов Кембриджа и т.д. Контекст позволяет определить, во-первых, конкретное интересующее нас свойство (рослый, черный цвет, поля в рулетке, коренной житель азиатской страны), во-вторых, конкретное рассматриваемое нами множество (все читатели газеты «Таймс», все поля данной рулетки, все студенты Кембриджа). Таким образом, речь идет о доле элементов совокупности, обладающих определенным свойством.
В гл. 4, когда мы впервые столкнулись с подобной задачей, доля элементов совокупности обозначалась через Y, что соответствовало принятым в этой главе обозначениям. Здесь мы будем пользоваться более употребительным обозначением доли — Р. Заметим, что, как и прежде, прописные буквы будут обозначать переменные, а соответствующие строчные буквы — конкретные значения переменных. Конечно, в рассматриваемой здесь задаче точное значение Р для всей совокупности неизвестно, хотя предполагается, что точное истинное значение Р, которое мы обозначим р, существует. Стоящая перед нами цель — использовать информацию, полученную в результате более подробного изучения совокупности, для уточнения р; сформировавшиеся на некоторой стадии этого процесса индивидуальные оценки значения р задаются в виде (субъективного) распределения переменной Р. (Мы различаем переменные и параметры, точные значения которых не известны, и переменные и параметры, точные значения которых известны. Первые обозначим прописными буквами, а вторые — строчными. Например, если доля совокупности точно не известна, то для ее обозначения мы воспользуемся буквой Р, а если эта доля известна точно, то буквой р.)
В следующем разделе речь идет о способах представления оценок переменной Р, в частности, рассматривается конкретное семейство распределений — бета-распределения, наиболее удобных для формирования оценок долей. В разделе 5.3 говорится о том, как информация о Р может быть получена, а в разделе 5.4 показано, как эта информация инкорпорируется, как при этом изменяется априорная оценка Р и вычисляется апостериорная оценка распределения этой переменной. В разделе 5.5 более подробно изучается ситуация из раздела 4.6, когда приходится моделировать отсутствие априорной информации. В разделе 5.6 проводится параллель между байесовским и классическим подходами к статистическому выводу, в частности показано, как в рамках байесовского подхода интерпретируются понятия «доверительного интервала» и «критерия значимости».
5.2. Ожидания, связанные с долями
Значение Р — обязательно одно из чисел отрезка от 0 до 1. Если это значение Р не известно вам точно (или вы думаете, что не знаете его точно), то естественно выразить ваши ожидания по поводу Р в форме вероятностного распределения, заданного на отрезке [0; 1]. Если эти ожидания связаны с представлением о Р как о переменной, принимающей дискретные значения из [0; 1], то и распределение окажется дискретным; в ином случае нужно будет рассматривать непрерывное распределение. Например, вы считаете, что переменная Р может принимать значения 1/4 и 3/4, причем каждое с одинаковой вероятностью, это можно записать с помощью соответствующей функции вероятностей:
Если же вы считаете, что р с одинаковой вероятностью может принять (только) одно из n + 1 значений 0, 1/n, 2/n, …, (n — 1)/n, 1, то соответствующая этим вашим представлениям функция вероятностей будет иметь вид:
Когда вы исходите из того, что р может быть равным только одному из чисел 1/4, 1/2 и 3/4, причем второму с вероятностью, вдвое большей, чем любому из оставшихся, соответствующая функция вероятностей будет задана так:
В альтернативной (непрерывной) ситуации, когда вы полагаете, что Р с одинаковой вероятностью принимает любое из бесконечно большого числа возможных значений отрезка [0; 1], этой гипотезе соответствует функция плотности вероятностей:
Это, конечно, функция плотности вероятностей переменной, удовлетворяющей распределению U (0; 1), т.е. однородному распределению на отрезке от 0 до 1. Это также функция плотности бета-распределения с параметрами α = 1 и β = 1 (ср. с (2.27)).
Методы, которые мы рассмотрим и будем применять в этой главе, можно охарактеризовать как поиск подходящей формы вероятностной оценки. Однако мы ограничимся случаем, когда вероятностные оценки удовлетворяют бета-распределению. В частности, поскольку бета-распределения применимы только для непрерывных переменных, мы не будем останавливаться на случае дискретных оценок. Другие случаи (включая дискретный) довольно легко поддаются анализу на основе общих подходов (см., например, упражнения 4.5, 4.6, 4.8, 4.9, 4.11 и 4.13 из гл. 4), и вам следует попытаться разобрать их самостоятельно.
Может показаться, что, рассматривая только случаи, когда априорные оценки представимы в виде бета-распределения, мы вводим ограничения, чрезмерные даже для непрерывного случая. Однако это не так. Семейство бета-распределений является весьма гибкими и путем подбора параметров позволяет представить довольно широкий спектр разнообразных априорных оценок. Мы уже отмечали несколько частных случаев бета-распределения: при α = β = 1 оно превращается в равномерное распределение на отрезке [0; 1]; при α = 2, β = 1 — в правотреугольное распределение; при α = 1, β = 2 — в левотреугольное распределение. Более общее свойство: когда оба параметра α и β превосходят 1, то распределение унимодально и симметрично, если значения α и β совпадают; если же при этом α больше (меньше) β, то вершина распределения смещена вправо (влево). Для многих оценок унимодальные распределения оказываются вполне приемлемыми, например для оценки доли женщин среди студентов Йоркского университета или доли голосов поданных за социал-демократов в вашем избирательном округе.
Из раздела 2.4 известно, что бета-распределению с параметрами α и β соответствуют α/(α + β) — средняя и αβ/[(α + β)2 (α + β + 1)] — дисперсия. Более того, можно показать, что с увеличением суммы параметров α + β форма бета-распределения приближается к форме нормального распределения, т.е. при достаточно большом значении α + β (скажем, большем 30) бета-распределение можно приближенно представить в виде нормального распределения с той же средней и той же дисперсией, причем аппроксимация улучшается с увеличением α + β. Это весьма полезный результат, поскольку он позволяет установить некоторые статистические свойства бета-распределения, пользуясь в качестве его приближения нормальным распределением.
Конечно, если в повседневной жизни «человек с улицы» станет рассуждать о чем-либо в терминах бета-распределений, имеющих те или иные значения параметров, то это покажется неестественным. Наоборот, следует предположить, что в общем случае ожидания будут формулироваться так: «Я полагаю, что наиболее вероятным значением Р является ½ и почти наверняка это значение лежит между 0,3 и 0,7». При последующих уточнениях можно получить информацию о том, что распределение воспринимается как симметричное относительно значения ½ и как колоколообразное. Каким образом перевести подобного рода оценки на язык семейства бета-распределений, выбирая подходящего для конкретного случая представителя этого семейства? Другими словами, как подобрать подходящие значения параметров α и β?
Мы воспользуемся описанными выше свойствами бета-распределения (в частности, значениями средней и дисперсии, а также аппроксимирующим распределением) и свойством нормального распределения, для которого основная площадь под кривой функции плотности заключена между значениями, отстоящими от средней на величину в 2 стандартных отклонения. Таким образом, опираясь на приведенные выше числовые значения, мы находим среднюю (она равна 0,5) и стандартное отклонение, равное 0,1 (отрезок от 0,3 до 0,7 относительно его середины можно представить, как 0,5±0,2, откуда следует, что 2 стандартных отклонения равны 0,2). Тогда для определения параметров распределения α и β получаем два уравнения:
Систему уравнений (5.1), (5.2) можно решить, например, с помощью подстановки α + β = ν, что даст нам (из (5.1)) α = 0,5ν, а потому β = 0,5ν. Воспользовавшись этими выражениями, перепишем (5.2) в виде:
что дает нам 0,25/(ν + 1) = 0,01; ν = 24. Таким образом, решением системы уравнений (5.1) и (5.2) будет α = β = 12.
Мы показали, что бета-распределение с параметрами α = β = 12 служит возможной формой представления ожиданий, в соответствии с которыми распределение унимодально, симметрично относительно р = 1/2, колоколообразно и в основном расположено над отрезком от 0,3 до 0,7.
В данном примере средняя величина оценки переменной Р равнялась 0,5, а стандартное отклонение было равно 0,1. Предположим, что другая оценка имеет ту же среднюю, но большее стандартное отклонение, скажем 0,125. Каковы будут значения α и β для этой новой оценки? Очевидно, что уравнение (5.1) останется неизменным, т.е. если вновь обозначить α + β = ν, то и на этот раз придем к α = β = 0,5ν. Однако уравнение (5.2) станет несколько иным:
поскольку стандартное отклонение равно теперь 0,125. После подстановки α = β = 0,5ν придем к уравнению 0,25/(ν + 1) = (0,125)2, решив которое, найдем ν = 15. Следовательно, α = β = 7,5. Итак, бета-распределение с параметрами α = 7,5 и β = 7,5 имеет среднюю 0,5 и стандартное отклонение 0,125, что мы и должны были обеспечить.
В обоих примерах средняя распределения равна 0,5, т.е. это значение было «центральным» для нашей оценки, а оценка предполагалась симметричной относительно 0,5. Рассмотрим другую пару оценок со средней 0,6. Тогда для этих оценок параметры α и β должны удовлетворять уравнению α/(α + β) = 0,6.
Если мы вновь обозначим α + β = ν, то получим α = 0,6ν, β = 0,4ν. Обратимся опять к стандартному распределению. Предположим, что первая из этой пары оценок имеет стандартное отклонение 0,1. Тогда α и β должны удовлетворять уравнению
Если подставить в него α = 0,6ν и β = 0,4ν, то получим уравнение относительно ν и найдем ν = 23. Следовательно, α = 13,8 и β = 9,2. Итак, бета-распределение с параметрами α = 13,8 и β = 9,2 имеет среднюю 0,6 и стандартное отклонение 0,1. Пусть теперь вторая оценка этой же пары имеет стандартное отклонение 0,05. Таким же образом, как и выше, можно показать, что параметры этого распределения α = 57 и β = 38.
Приведенные примеры подтверждают общие свойства бета-распределения: средняя этого распределения меньше, равна или больше 0,5 соответственно, если параметр α меньше, равен или больше, чем β; по мере увеличения суммы α + β стандартное отклонение уменьшается.
Мы показали в этом разделе, как подобрать значения параметров α и β и тем самым выбрать из семейства бета-распределений такое, которое отражает оценку переменной Р, будучи унимодальным и примерно колоколообразной формы с заданными значениями средней и стандартного отклонения. Мы получили также возможность убедиться на конкретных примерах в воздействии изменений параметров на положение вершины, разброс и форму бета-распределений.
Далее в этой главе мы будем предполагать, что априорная оценка Р берется в форме бета-распределения с подходящим образом выбранными значениями параметров. Поэтому априорная функция плотности вероятностей для Р задается соотношением (см. (2.27)):
5.3. Природа (выборочной) информации
Нас интересует доля Р элементов некоторой совокупности (или популяции), обладающих определенным свойством. Причем естественным источником информации относительно Р будет сама изучаемая нами совокупность. Точнее, мы имеем возможность обследовать элементы этой совокупности. Размеры совокупности могут меняться от одной прикладной задачи к другой: совокупность может состоять, вообще говоря, из бесконечного числа элементов («все бросания монеты», «все вращения колеса рулетки»), а в других случаях она явно конечна («все читатели газеты «Таймс»», «все жители Глазго»). Изменяется от задачи к задаче и природа элементов совокупности: это могут быть люди, физические объекты или исходы физических экспериментов («бросание монеты»).
Информацию получают в результате обследования элементов совокупности с целью проверки, обладает ли каждый из выбранных для проверки элементов интересующим нас свойством или нет. Ясно, что число обследуемых элементов также подлежит выбору: в крайнем случае мы можем ограничиться обследованием одного элемента; противоположная крайность — обследовать все элементы; между этими двумя крайностями — возможность обследовать, скажем, n элементов. Мы начнем наш анализ с рассмотрения простейшего случая, когда для обследования выбирается только один элемент, а затем покажем, как полученные результаты могут быть обобщены на случай выбора n элементов.
Положим, выбирается и обследуется один элемент совокупности. Мы должны выяснить, как изменится наша априорная оценка, после того как будет получена информация о результатах обследования одного случайно выбранного из совокупности элемента. Рассмотрим возможные исходы обследования. Здесь возможны только два интересующих нас исхода: либо выбранный элемент совокупности обладает данным свойством, либо не обладает. Представим эти две возможности с помощью переменной X: будем писать X = 1, когда выбранный элемент обладает рассматриваемым свойством, и X = 0, когда он этим свойством не обладает. Наша задача — получить информацию о значении р (истинном, однако остающемся неизвестным значении переменной Р). Очевидно, что значение X не зависит от р, однако распределение X может зависеть от р, если мы выбрали элемент «подходящим» способом. Ясно, что «подходящим» механизмом выбора будет тот, который мы в предыдущих главах назвали «правильным»; это механизм, при котором вероятность появления X = 1 равна р, а вероятность появления X = 0 равна 1 – р. Формально это означает, что
(5.4) gX(1|p) = p, gX(0|p) = 1 –p
т. е. если доля элементов совокупности, обладающих данным свойством, равна р, то механизм выбора должен быть таким, чтобы вероятность выбора элемента, имеющего это свойство, равнялась р, а элемента, его не имеющего, равнялась 1 – р. Следовательно, если 50% элементов совокупности обладают данным свойством, то механизм выбора должен обеспечить равные шансы появления элемента, обладающего и не обладающего этим свойством; если же данное свойство присуще только 25% элементов совокупности, то механизм должен обеспечить ровно 1 шанс из 4 выбрать элемент с этим свойством. Если совокупность состоит из материальных объектов, то все сказанное означает, что каждый из ее элементов имеет равные шансы быть выбранным; в этом случае говорят о случайной (или рандомизированной) выборке, а слово случайная (рандомизированная) означает, что соответствующий механизм выбора был «правильный». Если же совокупность состоит из физических действий («бросание монеты»), то каждое конкретное рассматриваемое действие («выбор элемента») должно быть совершено «правильно» («правильное бросание монеты»).
Начиная с этого момента, будем предполагать, что выборка получена («элементы выбраны») с помощью некоторого случайного процесса, удовлетворяющего соотношениям (5.4). Заметим, что распределение переменной X зависит от р, поэтому полученное в результате наблюдения значение X информативно по отношению к р. Мы можем конкретизировать (5.4) с учетом формы бета-распределения:
Теперь мы имеем возможность перейти к изучению воздействия информации, полученной в результате обследования элементов совокупности, на априорную оценку. Этому посвящен следующий раздел.
5.4. Инкорпорирование выборочной информации
Мы исходим из предположения, что априорная оценка распределения переменной Р имеет форму бета-распределения с параметрами α и β и это распределение определяется функцией плотности (5.3). Мы также предполагаем существование механизма, обеспечивающего такое извлечение выборки из совокупности, что правдоподобие наблюдать х при данном р определено соотношением (5.5). Мы имеем теперь возможность с помощью (5.3) и (5.5) найти апостериорную оценку Р, зная значение х, полученное в результате наблюдения. Подставим (5.3) и (5.5) в (4.23):
Если сравнить соотношения (5.6) и (2.27), то обнаружим, что апостериорное распределение переменной Р есть бета-распределение с параметрами α + х и β + 1 – х. Вспомнив, что х = 1 означает наличие у выбранного элемента интересующего нас свойства, а х = 0 соответствует его отсутствию, мы можем выразить ту же мысль несколько более пространно.
(5.7) Если априорное распределение Р есть В(α, β) и выбранный случайно элемент обладает интересующим нас свойством, то апостериорное распределение Р есть В(α + 1, β).
Если априорное распределение Р есть В(α, β) и выбранный случайно элемент не обладает этим свойством, то апостериорное распределение Р есть В(α, β + 1).
Это важный результат. Во первых, формы априорного и апостериорного распределений совпадают и в том, и в другом случае это бета-распределение. Таким образом, поступление и учет новой информации не выводят оценки за рамки семейства бета-распределений. Во-вторых, переход в (5.7) от априорного распределения к апостериорному очень прост: 1 прибавляется к первому параметру, если выбранный элемент обладает рассматриваемым свойством, в противном случае 1 прибавляется ко второму параметру.
Ясно, что эти два обстоятельства обеспечивают возможность непосредственного обобщения полученных результатов на случай, когда выбираются и обследуются n элементов совокупности. Поскольку механизм выбора в свою очередь удовлетворяет соотношению (5.5), сходному по форме с (5.3) (это позволило вывести (5.7)), то отсюда и следует, что оценка всегда остается в рамках семейства бета-распределений, причем для каждого выбранного элемента, обладающего свойством, 1 прибавляется к первому параметру, а для каждого выбранного элемента, не обладающего этим свойством, прибавляется ко второму параметру. Формально мы можем записать следующее.
(5.8) Если априорное распределение Р есть В(α, β) и если случайным образом выбраны n элементов, из которых а элементов обладают интересующим нас свойством, а b – не обладают (а + b = n), то апостериорное распределение Р есть В(α + a, β + b).
Соотношение (5.8) — ключевой результат при изучении долей. Далее в настоящем разделе мы обсудим следствия этого соотношения. Мы уже обращали внимание на то, что, в силу (5.8), оценка Р всегда остается в рамках семейства бета-распределений независимо от размера выборки. Мы отметим и то, что инкорпорирование содержащейся в выборке информации (ее называют также выборочной информацией) ведет к увеличению первого параметра на число положительных исходов (число элементов выборки, обладающих рассматриваемым свойством) и к увеличению второго параметра на число отрицательных исходов (число элементов выборки, не обладающих этим свойством). Это означает, что сумма параметров тем самым увеличилась на n — величину, характеризующую объем выборки.
Посмотрим, как влияет полученная на основе выборки информация на значения средней и дисперсии. Начнем со средней. Вспомним, что средняя бета-распределения с параметрами α и β равна α/(α + β). Как следует из (5.8), средняя априорного распределения равна α/(α + β), а средняя апостериорного распределения равна: (α + a)/(α + a + β + b) = (α + a)/(α + β + n). Заметим, что апостериорное значение средней можно записать следующим образом:
Соотношение (5.11) устанавливает тот факт, что апостериорное значение средней является средневзвешенным априорного значения средней и отношения a/n с весами w и 1 – w соответственно. Отношение a/n — доля элементов выборки, обладающих рассматриваемым свойством; ее называют выборочной долей. Итак, из (5.11) можно заключить, что апостериорная средняя доли совокупности является средневзвешенной величиной априорной средней и выборочной доли. Интуитивно этот результат вполне осмыслен.
Рассмотрим теперь веса, стоящие при двух членах равенства (5.11): первый член, равный значению априорной средней, берется с весом ![]() , а второй, равный выборочной доле, — с весом
, а второй, равный выборочной доле, — с весом ![]() .
.
Таким образом, относительные веса зависят от отношения α + β к n и поэтому величина α + β очень важна. Чтобы раскрыть роль этой величины, вновь обратимся к (5.8). Поскольку информация, заключенная в выборке объема n, содержащей а положительных и b отрицательных исходов (а элементов обладают рассматриваемым свойством, а b элементов им не обладают), изменяет оценку, увеличивая первый параметр бета-распределения на а единиц, а второй его параметр — на b единиц, то мы можем рассматривать априорное распределение В (α, β) как «эквивалентное» наблюдению выборки объема α + β, в которой α элементов обладают данным свойством, a β элементов им не обладают. Таким образом, сумма α + β представляет собой «эквивалентный» априорному распределению объем выборки. Обозначим сумму α + β через ν; теперь ν измеряет объем выборки, «эквивалентной» распределению априорной оценки. Воспользовавшись этим обозначением, можно показать, что в (5.11) вес w при априорном среднем равен: w = ν/(ν + n), а вес при выборочной доле равен: 1 – w = n/(n + ν). Итак, относительные веса зависят от отношения ν к n, другими словами, чем больше (при прочих равных условиях) объем выборки, «эквивалентной» распределению априорной оценки, тем больший вес соответствует априорному среднему, и, наоборот, с увеличением объема выборки (при прочих равных условиях) увеличивается вес при выборочной доле. Этот вывод тоже интуитивно осмыслен.
Перейдем теперь к дисперсии. Поскольку дисперсия бета-распределения с параметрами α и β равна ![]() , то из (5.8) следует, что именно такой будет дисперсия априорного распределения, в то время как апостериорная дисперсия равна
, то из (5.8) следует, что именно такой будет дисперсия априорного распределения, в то время как апостериорная дисперсия равна ![]() .
.
Чтобы упростить это выражение, обозначим среднюю α/(α + β) через m, а апостериорную среднюю через m’. Тогда априорную и апостериорную дисперсии можно записать в виде
соответственно. Отсюда видно, что с увеличением ν уменьшаются как априорная, так и апостериорная дисперсии, а с увеличением n уменьшается апостериорная дисперсия. Таким образом, дисперсия апостериорной оценки уменьшается с увеличением объема эквивалентной априорному распределению выборки и с увеличением объема самой выборки. Вновь получен интуитивно осмысленный результат.
Обобщим сказанное. Апостериорная средняя является средневзвешенной априорной средней и выборочной доли, причем веса зависят от отношения объема выборки, эквивалентной априорному распределению (или от степени доверия, с которым мы принимаем априорную оценку), к объему реализованной выборки; апостериорная дисперсия уменьшается с уменьшением априорной дисперсии и с увеличением объема реализованной выборки.
Чтобы показать порядок и взаимодействие величин, участвующих в расчете, мы приводим в табл. 5.1 ряд числовых примеров применения ключевого результата (5.8). К одной и той же апостериорной оценке можно прийти различными путями. Например, априорное распределение В (11, 11) и последующие наблюдения а = 15, b = 5 приводят к тому же апостериорному распределению, что и априорное В (16, 6) в сочетании с исходом наблюдений а = 10, b = 10. Примеры еще раз подчеркивают оправданность интерпретации априорного распределения В (α, β) как «эквивалента» информации, полученной в результате наблюдения выборки, содержащей α элементов, обладающих рассматриваемым свойством, и β элементов, не обладающих этим свойством.
По существу, наш анализ завершен. Содержащееся в (5.8) утверждение отвечает на все поставленные нами вопросы: если априорной оценке соответствует бета-распределение, то и апостериорная оценка тоже характеризуется бета-распределением независимо от объема выборки; более того, первый параметр полученного апостериорного распределения равен сумме первого параметра априорного распределения и числа элементов выборки, обладающих рассматриваемым свойством; второй параметр апостериорного распределения равен сумме второго параметра априорного распределения и числа элементов выборки, не обладающих этим свойством. Если на любой стадии испытаний нам будет задан вопрос о нашей точке зрения относительно переменной Р, то мы просто укажем на наше апостериорное распределение, сложившееся к этому моменту. По форме ответ будет таким: «наша оценка переменной Р к данному моменту есть В (.,.)», где вместо точек должны стоять соответствующие числа. И это все, что требуется. Статистический вывод оказывается столь же простым, как этот ответ.
Конечно, может возникнуть желание сопроводить утверждение «наша оценка Р есть В (.,.)» указанием некоторых, а возможно, и всех обобщающих характеристик, рассмотренных в разделе 2.3. Например, мы предпочтем вести обсуждение в терминах средних и дисперсий наших оценок, как это было в предыдущем разделе. Или же нам может потребоваться охарактеризовать нашу оценку в терминах вероятностных интервалов. Принципиальных трудностей при этом не возникает, нужно лишь воспроизвести процедуры, о которых шла речь в разделе 2.3. Использование бета-распределения сопряжено на практике с определенными трудностями, поскольку значения его функции распределения могут быть найдены лишь путем обращения к численным методам интегрирования. [5] Однако возможность аппроксимировать бета-распределение с помощью нормального распределения (имеющего ту же среднюю и ту же дисперсию) облегчает достижение интересующей нас цели.
Итак, если наша оценка Р на определенной стадии наблюдений есть В (α, β) и если сумма α + β достаточно велика (скажем, больше 30), то мы можем приближенно представить нашу оценку с помощью нормального распределения, имеющего ту же среднюю и ту же дисперсию. Другими словами, мы можем записать, что наша оценка Р приближенно описывается распределением
после чего появляется возможность строить (приближенно) вероятностные интервалы для Р с помощью формул нормального распределения (в Excel). Например, предположим, что наша оценка переменной Р на некоторой стадии наблюдений имеет вид В (25, 25). Ее средняя равна: 25/(25 + 25) = 0,5, а дисперсия: 25*25/[(25+25)2*(25+25+1)] = 0,072. Поэтому мы можем считать нашу оценку переменной Р приближенно удовлетворяющей распределению N [0,5, 0,072]. Если теперь мы захотим определить 95-процентный вероятностный интервал для Р, то воспользуемся формулами: Хmin =НОРМ.ОБР(0,025;0,5;0,07) = 0,3628, Хmax =НОРМ.ОБР(0,975;0,5;0,07) = 0,6372. Поэтому наш приближенный 95-процентный вероятностный интервал для переменной Р определен так (0,3628; 0,6372). Если же рассчитаем 95-процентный вероятностный интервал для В (25, 25) в лоб с помощью Excel, то увидим, что Хmin =БЕТА.ОБР(0,025;25;25) = 0,3634, Хmax =БЕТА.ОБР(0,975;25;25) = 0,6366. Видно, что аппроксимация бета-распределения нормальным распределением весьма точная.
Подробный числовой пример, иллюстрирующий применение (5.8), будет приведен в следующем разделе, а данный раздел мы завершим обсуждением некоторого обстоятельства, связанного с (5.8), и подчеркнем ту роль, которую играет при этом одно из предположений, использованных при выводе (5.8). Рассмотрим сначала поведение апостериорной оценки, когда объем выборки n возрастает. Конкретнее, мы ограничимся случаем бесконечного объема исходной совокупности и выясним предельное поведение нашей апостериорной оценки при n стремящемся к бесконечности. Интуитивно ясно (и это можно доказать формально), что когда n стремится к бесконечности, выборочная доля а/n стремится к р (истинной или реальной) доле Р совокупности. Следовательно, из (5.11) следует, что апостериорная средняя нашей оценки Р стремится к р. Это верно независимо от нашей априорной оценки, ибо вес w, стоящий при ней в (5.11), стремится к 0 при n стремящемся к бесконечности. Более того, из (5.12) вытекает, что апостериорная дисперсия стремится при этом к нулю. Итак, когда n стремится к бесконечности, наша апостериорная оценка Р стремится к вырожденному распределению в точке, совпадающей с реальным значением р, независимо от нашей априорной оценки. Это наиболее обнадеживающий результат.
Вернемся теперь к соотношению (5.5); как вы помните, оно содержало гипотезу относительно механизма формирования выборки. Ключевой результат (5.8) опирался на (5.5). Соотношение (5.5) означает, что для каждого элемента выборки вероятность обладать интересующим нас свойством равняется р. Однако если выбор производится из конечной совокупности, то нужно не просто производить его случайным образом, но должен иметь место выбор с возвращением. Вот простой числовой пример, демонстрирующий, что произойдет, если мы не будем соблюдать это правило. Пусть рассматриваемая совокупность состоит из 100 человек, 50 из которых мужчины. Предположим, что шансы каждого элемента совокупности быть выбранным равны, но выбранный элемент не возвращается в совокупность, из которой производится выбор следующего элемента. Тогда при выборе первого элемента шанс выбрать мужчину равен 1/2. При выборе второго элемента шанс выбрать мужчину равен 49/99, если первым выбран мужчина, и равен 50/99, если первый раз была выбрана женщина. Ни в том, ни в другом случае мы не получили 1/2, т. е. (5.5) перестает быть верным. Таким образом, чтобы (5.5) было по-прежнему справедливо для конечной совокупности, надо производить выбор элементов с возвращением и тогда (5.8) также останется верным. (Существует, конечно, результат, аналогичный (5.8), и для выбора без возвращения, но поскольку его доказательство требует сложных алгебраических выкладок, мы не будем останавливаться на этом случае. На практике, если рассматриваемая совокупность, хотя и конечна, значительно больше объема выборки, то результат (5.8) остается приблизительно верным даже для выбора без возвращения.)
5.5. Случай отсутствия априорной информации
Может случиться, что тот, от кого требуется формирование априорной оценки переменной Р, чувствует себя совершенно неподготовленным к решению этой задачи. В данном разделе мы остановимся на том, как совместить рассматриваемые методы с подобной ситуацией. Вернемся к нашей интерпретации априорного распределения В (α, β) как «эквивалента» наблюдению выборки объема α + β, содержащей α элементов, обладающих рассматриваемым свойством, и β элементов, этим свойством не обладающих. После того как такая интерпретация известна, естественно при полном отсутствии априорной информации положить значения α и β равными нулю, поскольку априорное распределение В (0,0) должно быть «эквивалентно» рассмотрению выборки объема 0 (в которой 0 элементов обладают требуемым свойством и 0 элементов им не обладают). Посмотрим, к чему приведет одновременное обращение в нуль параметров α и β нашего априорного распределения.
Из (5.8) мы видим, что при α = β = 0 апостериорной оценке, опирающейся на выборку объема a + b (a положительных исходов и b —отрицательных), соответствует распределение В (a, b). Следовательно, такая апостериорная оценка зависит только от новой информации. При этом апостериорная средняя равна: а/(а + b) = а/n, т.е. равна выборочной доле. В свою очередь апостериорная дисперсия равна
где через ![]() обозначена выборочная доля а/n, т. е. выборочная дисперсия также оказывается зависящей только от выборочной информации, точнее, от выборочной доли и от объема выборки.
обозначена выборочная доля а/n, т. е. выборочная дисперсия также оказывается зависящей только от выборочной информации, точнее, от выборочной доли и от объема выборки.
Способ, с помощью которого мы формализовали случай полного отсутствия априорной информации или полного пренебрежения ею, положив оба параметра α и β равными нулю, нас вполне бы устроил. Единственное затруднение в том, что при определении бета-распределения (2.27) и α, и β предполагались положительными. Тем самым если α и β в выражении (2.27) приравнять нулю, то получится функция, площадь между графиком которой и осью абсцисс окажется бесконечной, независимо от выбора множителя масштаба, т.е. она не может быть функцией плотности вероятностей (площадь под графиком которой должна быть равна 1, что обеспечивается выбором множителя масштаба). Полученная функция, очевидно, не будет собственной функцией плотности. Поэтому функцию с параметрами α и β, одновременно обращающимися в нуль, называют несобственной функцией плотности. Несмотря на это, она «работает» в том смысле, что апостериорное распределение оказывается собственным, даже если априорное несобственное. Более того, она «работает хорошо», т.е. свойства апостериорного распределения находятся в полном согласии с интуитивными представлениями. Тем самым мы имеем возможность пользоваться подобной функцией в случае полного пренебрежения априорной информацией; поступая подобным образом, мы следуем практике применения байесовского подхода.
Как мы уже отмечали выше, если объем выборки равен а + b, причем она содержит а позитивных исходов и b негативных, и если мы начали с полного пренебрежения априорными ожиданиями (α = β =0), то апостериорное распределение имеет форму В (a, b). Его средняя ![]() и дисперсия
и дисперсия ![]() (1 –
(1 – ![]() )/(n + 1), где
)/(n + 1), где ![]() (≡ а/n) есть выборочная доля.
(≡ а/n) есть выборочная доля.
Когда сумма а + b достаточно велика, можно воспользоваться в качестве приближения нормальным распределением, что позволяет получить следующий важный результат:
Тем самым получена полная характеристика нашей апостериорной оценки. Обобщающие характеристики можно построить аналогично тому, как это было сделано прежде. Например, для построения 95-процентного вероятностного интервала переменной Р мы воспользуемся фактом, в силу которого в 95% случаев нормально распределенная переменная отстоит от среднего значения не более чем на 1,96 величины стандартного отклонения. Следовательно, (5.13) позволяет указать (приближенно) 95-процентный вероятностный интервал переменной Р
Например, начав с полного пренебрежения априорной оценкой и получив в качестве информации выборку объема 50 с 20 позитивными исходами, найдем ![]() = 0,4, и апостериорная оценка будет иметь приближенно распределение N [0,4, 0,06862], что соответствует (5.13). [6] С помощью (5.14) найдем 95-процентный вероятностный интервал, который равен 0,4±1,96*0,0686, т.е. (0,266; 0,534). Итак, на основе выборочной информации можно заключить, что с вероятностью 0,95 истинное значение переменной Р лежит на отрезке от 0,266 до 0,534.
= 0,4, и апостериорная оценка будет иметь приближенно распределение N [0,4, 0,06862], что соответствует (5.13). [6] С помощью (5.14) найдем 95-процентный вероятностный интервал, который равен 0,4±1,96*0,0686, т.е. (0,266; 0,534). Итак, на основе выборочной информации можно заключить, что с вероятностью 0,95 истинное значение переменной Р лежит на отрезке от 0,266 до 0,534.
Из (5.14) можно также заключить, что длина 95-процентного вероятностного интервала равна
Эта функция убывает с ростом объема выборки n, хотя ее значение зависит также от выборочной доли ![]() Поэтому с помощью подходящего выбора n нельзя обеспечить получение заранее заданной длины вероятностного интервала, но вероятностный интервал наибольшей длины может быть определен. Рассмотрим выражение (5.14а) как функцию
Поэтому с помощью подходящего выбора n нельзя обеспечить получение заранее заданной длины вероятностного интервала, но вероятностный интервал наибольшей длины может быть определен. Рассмотрим выражение (5.14а) как функцию ![]() оно принимает значение 0, когда
оно принимает значение 0, когда ![]() равняется 0, или 1 и положительно, если
равняется 0, или 1 и положительно, если ![]() располагается между этими крайними значениями; более того, функция достигает максимума при
располагается между этими крайними значениями; более того, функция достигает максимума при ![]() = 0,5. Поэтому наибольшая длина 95-процентного вероятностного интервала равна:
= 0,5. Поэтому наибольшая длина 95-процентного вероятностного интервала равна:
Поэтому выбор подходящего значения n может гарантировать, что наибольшая длина вероятностного интервала не превысит наперед заданного положительного числа. (Например, если потребовать, чтобы наибольшая ширина вероятностного интервала не превышала 0,4; 0,2; 0,1; 0,05; 0,02 и 0,01, то нужно выбрать значения n соответственно равными 23, 95, 384, 1536, 9603 и 38415. Как видно из приведенных примеров и как следует из общего результата, наибольшая длина вероятностного интервала уменьшается обратно пропорционально корню квадратному из объема выборки, т.е. чтобы эту длину уменьшить вдвое, потребуется вчетверо больший объем выборки.)
Рассмотрим теперь пример, где потребуется почти весь материал данной главы. Пусть вы предложили свои услуги секретарю местного отделения социал-демократической партии, которого интересуют шансы кандидата его партии на предстоящих выборах. Очевидно, ответ на этот вопрос зависит от р — доли избирателей, готовых отдать свои голоса социал-демократам, если их кандидат будет выдвинут; когда р достаточно велико, имеет, смысл участвовать в избирательной кампании, иначе это будет напрасной тратой партийных средств. Проблема, конечно, в том, что ни вы, ни местный секретарь не знаете значения р. Однако вы имеете возможность получить информацию относительно р, выясняя мнение части включенных в списки избирателей. Обратившись на местную почту, вы можете получить списки избирателей с последних выборов, отсюда следует сделать случайную выборку заранее определенного объема. (Один из возможных способов осуществить такую выборку: записать номер каждого избирателя на листке бумаги, опустить листки в шляпу, хорошо ее потрясти и извлечь из нее требуемое число листков, возвращая каждый снова в шляпу перед извлечением следующего. Менее трудоемкий путь состоит в случайном выборе одного избирателя среди первых m/n, значащихся в списках, а затем по одному из каждых следующих m/n избирателей, где m — объем совокупности, а n — объем выборки. Будет ли при этом удовлетворяться (5.5)?)
Предположим, вы решили проявить осторожность и вначале ограничились выборкой небольшого объема, состоящей, скажем, из 100 избирателей. (Кроме того, выборочное обследование требует затрат и оно может оказаться ненужным, если выборочная доля будет либо очень мала, либо очень велика.) Предположим, что наша «пилотная» выборка дала 25 избирателей, заявивших о своей готовности голосовать за социал-демократов, а 75 такого желания не выразили. Какова ваша оценка Р доли избирателей, готовых поддержать социал-демократическую партию, в свете полученной информации? Ответ на этот вопрос, очевидно, зависит от вашей априорной оценки.
Рассмотрим два случая: в первом будем исходить из предположения, что априорными ожиданиями вы полностью пренебрегаете; во втором сформируем свои ожидания на основе данных о голосах, полученных социал-демократами в другом районе страны. В первом случае вам нечего сказать относительно Р и поэтому ваша априорная оценка Р будет иметь вид В (0, 0). Из (5.8) следует, что ваша апостериорная оценка Р с учетом полученной при пилотном обследовании информации имеет вид В (25, 75). Этой оценке соответствует средняя 0,25, дисперсия (0,043)2, и оценку можно считать приближенно нормально распределенной. Итак, ваша апостериорная оценка имеет вид N [0,25, (0,043)2]. Если секретарь местного отделения социал-демократической партии не улавливает смысл подобного утверждения, то вы можете предложить ему то же утверждение в форме вероятностного интервала: 95-процентный вероятностный интервал будет равен 0,25±1,96*0,043, т.е. (0,166; 0,334). Теперь вы можете сообщить секретарю, что, по вашему мнению, имеется 95 шансов из 100 для кандидата его партии получить от 16,6 до 33,4 % голосов избирателей на предстоящих выборах.
Шансы таковы, что секретарь может быть ободрен полученным сообщением, особенно если в выборах участвуют три основные партии, но и озабочен широкими границами, в которых возможна ошибка (т.е. большой длиной вероятностного интервала). Он может поэтому побудить вас к продолжению исследований на основе выборки большего объема — соответствующие дополнительные расходы представляются ему оправданными. Предположим, что на этот раз вы остановились на выборке, содержащей 500 избирателей, фамилии которых вновь случайным образом извлекли из регистрационных списков. Пусть проведенное обследование на этот раз дало вам результат: 95 избирателей заявили о поддержке социал-демократов, а 405 избирателей сказали, что предпочитают другие две партии. Эта информация привела к пересмотру вашей оценки В (25,75) (полученной после «пилотного» обследования, но до новой выборки) и к формированию новой оценки В (120, 480) на основе соотношения (5.8). Ее средняя равна 0,2, дисперсия (0,0163)2, и эта оценка имеет приближенно нормальное распределение. Таким образом, ваша новая оценка имеет вид N [0,2, 0,01632], и соответствующий ей вероятностный интервал равен 0,2±1,96*0,0163, т.е. (0,168; 0,232). Теперь вы можете сообщить секретарю местного отделения социал-демократической партии, что, по вашему мнению, с вероятностью 95% шансы партии на выборах колеблются между 16,8 и 23,2% голосов избирателей. Эти шансы таковы, что секретарь вряд ли будет доволен результатами пересмотра предыдущей оценки!
Рассмотрим теперь второй случай: ваша априорная оценка переменной Р (она опиралась на результаты выборов в другом районе страны) до того, как вы произвели какую-либо выборку среди избирателей, существует и равна, например, В (3, 12). Ее средняя 0,2, стандартное отклонение 0,1, 95-процентный вероятностный интервал приблизительно равен (0,004; 0,396). На основе (5.8) после «пилотного» обследования, но до извлечения более объемной выборки вы можете свою оценку пересмотреть, и она примет вид В (28, 87), а после того, как получена информация о результатах основного обследования, пересмотреть ее еще раз и получить В (123, 492). Для промежуточной оценки 95-процентный вероятностный интервал равен (0,165; 0,322), а для последней оценки этот интервал будет равен (0,168; 0,232). Как вы могли убедиться на этих двух примерах, ваша априорная оценка очень быстро оказалась буквально «затопленной» выборочной информацией; произошло это потому, что ваша априорная оценка была недостаточно жесткой. Вы можете проанализировать ситуацию, когда эта оценка является более строгой, скажем В (30, 120) или В (120, 480).
Эти примеры фактически завершают данный раздел. Но одно заключительное замечание может оказаться полезным, особенно если вы ощущаете беспокойство в связи с применением несобственного априорного распределения В (0,0), когда нужно формализовать отсутствие априорной оценки или полное пренебрежение ею. Вы можете предпочесть в качестве подходящей альтернативы оценку В (1; 1), которая, как вы помните, совпадает с равномерным на отрезке [0; 1] распределением и соответствует предположению, что все значения Р от 0 до 1 считаются равновероятными. На практике, как это показал рассмотренный выше пример, различие между априорными оценками В (0; 0) и В (1; 1) несущественно, ибо для достаточно больших а и b оценки В (a, b) и В (а + 1, b + 1) почти неотличимы одна от другой.
5.6. Доверительные интервалы и проверка значимости
Суть байесовского подхода заключается в представлении ожиданий в форме вероятностных оценок и в пересмотре этих оценок с появлением новой информации. В ответ на вопрос о значении параметра или переменной (параметров или переменных) в какой-либо момент времени сторонник байесовского подхода просто сообщит вам свою оценку (оценки) на этот момент времени (это может быть полное описание распределения или указание соответствующих обстановке обобщающих характеристик). И это все, что данный подход предлагает в подобной ситуации. Статистик же классического направления поступает иным образом.
В данном разделе мы попытаемся, насколько это возможно, установить соответствие между утверждениями в рамках классического и байесовского подходов. Решающее отличие классического подхода от байесовского состоит в использовании понятия объективной вероятности и в отказе от концепции субъективных ожиданий. Отсюда следует, что вероятностные утверждения не могут относиться к фиксированным числам, таким, например, как реальная доля элементов совокупности, обладающих определенным свойством. Поэтому статистик классического направления будет считать утверждение «вероятность того, что переменная Р лежит между 0,168 и 0,232 равна 0,95» лишенным смысла, поскольку с его точки зрения Р либо лежит в этом интервале, либо находится вне его. Для классического подхода неприемлемо выражение «α-процентный вероятностный интервал переменной Р». Однако есть очень сходное по звучанию понятие классической статистики, а именно «α-процентный доверительный интервал для Р». Поэтому статистик «классик» может сказать, что «95-процентный доверительный интервал для Р, установленный на основе выборочной информации, равен (0,168; 0,232)». Как мы уже отмечали выше, это вовсе не означает, что данное утверждение можно трактовать как попадание Р с вероятностью 0,95 в интервал от 0,168 до 0,232. С точки зрения представителя классической школы, Р либо лежит между 0,168 и 0,232, либо нет. (Если говорить формально, то вероятность либо 1, либо 0.) Подходящая для него интерпретация понятия «95-процентный доверительный интервал для Р» выглядит так: «если рассмотреть все 95-процентные доверительные интервалы для (некоторого) Р, то 95 % этих интервалов будут содержать Р, хотя в оставшиеся 5% Р не попадет».
Итак, выражения «α-процентный вероятностный интервал для Р» и «α-процентный доверительный интервал для Р» имеют совершенно отличающиеся друг от друга интерпретации, что указывает на различия между субъективной трактовкой вероятности байесовской школой и объективной трактовкой этого понятия классической школой. (Что касается автора, то он придерживается точки зрения, в силу которой классическое понятие доверительного интервала в высшей степени искусственно, и большинство студентов, даже демонстрирующих свою приверженность классическому направлению, неявно пользуются интуитивно более ясной байесовской интерпретацией.)
Одно из следствий классического подхода к трактовке теории вероятностей состоит в автоматическом отрицании какой-либо роли априорных ожиданий. Поэтому окончательная оценка должна зависеть только и непосредственно от выборочной информации. Поэтому классическая статистика оказывается эффективной лишь в случае полного пренебрежения априорными представлениями. Это весьма незначительное подмножество реальных ситуаций с позиций байесовского подхода было рассмотрено в разделе 5.5. Ключевым в этом разделе был результат (5.13), характеризующий апостериорную оценку; из него следует оценка 95-процентного вероятностного интервала, приведенная в (5.14). Было установлено, что при полном пренебрежении априорными представлениями 95-процентный вероятностный интервал для Р, получаемый для выборки объема n с выборочной долей ![]() приближенно равен
приближенно равен
Представитель классической школы, столкнувшись с подобной ситуацией, сделает вывод о том, что 95-процентный доверительный интервал для Р приближенно равен
Если не считать интерпретации, единственным различием между (5.15) и (5.16) является присутствие делителя n + 1 в подкоренном выражении в первом случае и появление на его месте делителя n во второй формуле. Ясно, что при больших, n это различие между (5.15) и (5.16) становится неуловимым. Таким образом, доверительный интервал в классической статистике это, по сути, то же самое, что апостериорный вероятностный интервал, полученный в байесовской статистике при полном пренебрежении априорными представлениями. Итак, зная, что (0,168; 0,232) — 95-процентный доверительный интервал для Р, найденный в рамках классической статистики, мы можем воспользоваться им как апостериорным 95-процентным вероятностным интервалом в рамках байесовской статистики, если наши априорные ожидания относительно Р либо отсутствуют, либо мы ими полностью пренебрегаем.
Резюме. В этой главе рассмотрена одна из простейших задач статистического вывода, а именно вывод относительно неизвестной доли элементов некоторой совокупности, обладающих определенным свойством. При всей относительной простоте эта задача позволяет ввести основную процедуру байесовского вывода, состоящую в пересмотре априорных ожиданий в свете полученной новой информации. Для удобства изложения мы сосредоточили в этой главе внимание на случае, когда априорные ожидания относительно доли совокупности могут быть выражены в форме бета-распределения, хотя ясно, что рассмотренные здесь методы точно таким же образом можно применить к другим формам априорных оценок. Воздействие новой информации на априорную оценку зависит, конечно, и от формы, в которой эта новая информация поступает, в частности от способа, каким она была получена. В этой главе мы рассматривали «естественный» источник получения информации относительно доли элементов, обладающих интересующим нас свойством, –обследование случайно выбранных элементов совокупности.
Основным был результат, в силу которого при любом объеме случайной выборки апостериорная оценка удовлетворяет бета-распределению, если априорная оценка подчинялась распределению из этого же семейства. Другими словами, оценка (после учета новой информации) остается в рамках того же семейства (бета-распределений). Более того, параметры распределения изменяются при этом весьма простым образом: первый параметр увеличивается на число элементов выборки, обладающих рассматриваемым свойством, а второй параметр увеличивается на число элементов выборки, этим свойством не обладающих.
Мы показали, как естественно с точки зрения общих интуитивных представлений изменяются под воздействием новой информации значения средней и дисперсии нашей оценки. Мы обсудили вопрос о том, как можно формально выразить пренебрежение априорными представлениями, и убедились, что для этого нужно оба параметра априорного бета-распределения положить равными нулю. Наконец, мы сопоставили результаты этой главы с тем, что предлагает классическая статистика для решения тех же проблем, и продемонстрировали числовое совпадение классического доверительного интервала с байесовским вероятностным интервалом, рассчитанным в предположении о полном пренебрежении априорными ожиданиями (вместе с тем интерпретации этих понятий совершенно различны).
Упражнения
5.3. Пусть ваши априорные ожидания по поводу неизвестной доли Р выражены с помощью бета-распределения с параметрами α и β. Предположим, что средняя вашей априорной оценки есть 0,5. Найдите α и β, если заданы значения стандартных отклонений: (а) 0,125; (б) 0,1; (в) 0,05; (г) 0,025.
5.4. Пусть ваши априорные ожидания относительно неизвестной доли Р описаны с помощью бета-распределения с параметрами α и β, и средняя вашей априорной оценки равна 0,3. Найдите α и β, если стандартное отклонение принимает значения: (а) 0,1; (б) 0,05; (в) 0,025; (г) 0,02.
5.7. Рассмотрите случайную выборку объема 100, содержащую 40 элементов, обладающих некоторым свойством, и 60 элементов им не обладающих. Найдите апостериорное распределение Р и 95-процентный вероятностный интервал для Р, если априорное распределение соответствует: (а) упражнению 5.3 (б); (б) упражнению 5.4 (б). В каждом случае рассчитайте уменьшение длины 95-процентного вероятностного интервала (для апостериорного распределения в сравнении с априорным).
5.9. Пусть априорные ожидания Смита по поводу неизвестной доли Р описаны с помощью бета-распределения, имеющего среднюю 0,4 и стандартное отклонение 0,1. В то же время априорные ожидания Джона по поводу той же доли Р описаны бета-распределением со средней 0,6 и стандартным отклонением 0,1. Оба (и Джон, и Смит) наблюдают выборку объема 50, в которой число элементов, обладающих интересующим их свойством, равно числу элементов, не обладающих этим свойством. Найдите апостериорные распределения для Смита и Джона и укажите 95-процентные вероятностные интервалы.
5.14. Предположим, что ваши априорные представления относительно Р — доли потенциальных сторонников социал-демократической партии среди избирателей Северо-Восточного округа Бристоля — описаны в виде бета-распределения со средней 0,5 и стандартным отклонением 0,0625. Пусть опрос тридцати избирателей выявил 20 потенциальных сторонников социал-демократической партии. Найдите апостериорный 95-процентный вероятностный интервал для Р. Каким станет этот интервал после еще одного обследования тридцати избирателей, среди которых доля сторонников социал-демократической партии осталась такой же, как и в первой выборке?
5.15. (а) Если вы не располагаете никакими априорными представлениями относительно неизвестной доли Р элементов совокупности, обладающих определенным свойством, то какого объема выборка необходима, чтобы длина вашего апостериорного 95-процентного вероятностного интервала стала меньше, чем 0,2? (б) Пусть вы располагаете выборкой, объем которой определен в (а), и обнаружили, что 25% ее элементов обладают интересующим вас свойством. Какова длина апостериорного 95-процентного вероятностного интервала? Будет ли она равна 0,2? Почему?
5.16. (а) Если никаких априорных представлений относительно неизвестной доли Р элементов совокупности, обладающих определенным свойством, у вас нет, то какова наибольшая длина апостериорного 95-процентного вероятностного интервала, если объем выборки равен 25? (б) Что вы ответите на вопрос, поставленный в (а), если ваши априорные ожидания описываются бета-распределением со средней 0,5 и стандартным отклонением 0,0625? На основе этого оцените «ценность» такой априорной информации.
Решения
5.3. Воспользуемся формулой (2.28) и подстановкой α + β = ν, чтобы выразить α и β через среднее μ и стандартное отклонение sd. Получаем α = μν, β = (1 – μ)ν, ![]() . Соответствующие вычисления приведены в Excel-файле и на рисунке ниже:
. Соответствующие вычисления приведены в Excel-файле и на рисунке ниже:
5.4. Как и в упражнении 5.3 применим подстановку α + β = ν (формулы для расчета см. Excel-файл):
5.7. (а) Априорная вероятность Р равна В(12, 12), так как в упражнении 5.3 (б) α = β = 12. Длина 95-процентного вероятностного интервала для априорной вероятности: =БЕТА.ОБР(0,975;12;12) – БЕТА.ОБР(0,025;12;12) = 0,3882. Апостериорная вероятность Р равна В(12 + 40, 12 + 60); это бета-распределение представлено на рисунке ниже. Границы 95-процентного вероятностного интервала для апостериорной вероятности: Рmin =БЕТА.ОБР(0,025;52;72) = 0,3342; Рmax =БЕТА.ОБР(0,975;52;72) = 0,5069. Длина 95-процентного вероятностного интервала для апостериорной вероятности = 0,5069 – 0,3342 = 0,1727 уменьшилась более чем в два раза по сравнению с длиной такого же интервала для априорной вероятности.
(б) Априорная вероятность Р равна В(24,9, 58,1), так как в упражнении 5.4 (б) α = 24,9; β = 58,1. Длина 95-процентного вероятностного интервала для априорной вероятности: =БЕТА.ОБР(0,975;24,9;58,1) – БЕТА.ОБР(0,025;24,9;58,1) = 0,1953. Апостериорная вероятность Р описывается бета-распределением с параметрами6 В(24,9 + 40, 58,1 + 60). Границы 95-процентного вероятностного интервала для апостериорной вероятности: Рmin =БЕТА.ОБР(0,025;64,9;118,1) = 0,2871; Рmax =БЕТА.ОБР(0,975;64,9; 118,1) = 0,4252. Длина 95-процентного вероятностного интервала для апостериорной вероятности = 0,4252 – 0,2871 = 0,1381 уменьшилась по сравнению с длиной такого же интервала для априорной вероятности.
5.9. Параметры α и β для априорных распределений найдем на основе процедуры подробно описанной выше при решении упражнения 5.3. Апостериорные распределения построим на основе свойства Вапост.(α + а, β + b); в нашем случае a = b =25.
Отметим характерные особенности, описанные выше в тексте главы:
- апостериорные распределения компактнее по сравнению с априорными (за счет роста α и β);
- поскольку выборка показало равное число элементов, обладающих и не обладающих интересующим их свойством, апостериорные распределения Джона и Смита сместились в сторону значения 0,5 (Смита в сторону больших значений, Джона – в сторону меньших);
- различие между апостериорными ожиданиями Джона и Смита сблизились по сравнению с их априорными ожиданиями (разница между средними первоначально составляла 0,2; после наблюдения выборки эта разница уменьшилась до 0,063);
5.13. Пусть какие-либо априорные знания о неизвестной доле Р отсутствуют. Найдите апостериорное распределение, если вы располагаете выборкой объема 60, в которой ровно половина элементов обладает интересующим вас свойством. Пусть в вашем распоряжении оказались 80 дальнейших наблюдений и 30 из них указывают на наличие свойства, а 50 на его отсутствие. Каким станет ваше апостериорное распределение после получения этой информации? Определите 95-процентный вероятностный интервал для промежуточного и окончательного распределений.
5.13. См. рис. ниже. Обратим внимание, что, поскольку после первой выборки α = β, распределение имеет среднее 0,5. Поскольку выборка 2 показала больше наблюдений, указывающих на отсутствие свойства, среднее сместилось в сторону меньших значений. Длина 95%-ного доверительного интервала после наблюдения второй выборки сократилось с 0,25 до 0,1631 в силу роста α + β.
5.14. Поскольку и первая и вторая выборки дают больше сторонников социал-демократов, чем были наши априорные ожидания, среднее дважды сместилось в сторону больших значений 0,5 → 0,5538 → 0,6667. Благодаря росту объема опрошенных избирателей, длина 95%-ного доверительного интервала наоборот сократилась с 0,2005 до 0,1734:
5.15. Построим зависимость длины 95%-ного доверительного интервала от объема выборки n (см. верхний график). Видно, что при n = 95, длина апостериорного интервала становится меньше 0,2. Ни нижнем графике построена зависимость длины 95%-ного апостериорного доверительного интервала от соотношения элементов обладающих и не обладающих интересующим нас свойством. Видно, что наибольшая длина такого интервала достигается для a = b = n/2. Чем больше различие между а и b, тем меньше длина интервала.
5.16. (а) Как было показано в примере 5.15, наибольшая длина апостериорного 95-процентного вероятностного интервала соответствует бета-распределению с равными параметрами α = β. Таким образом длину интервала найдем по формуле =БЕТА.ОБР(0,975;12,5;12,5;0;1) – БЕТА.ОБР(0,025;12,5;12,5;0;1) = 0,3809. (б) Априорному бета-распределению со средней 0,5 и стандартным отклонением 0,0625 соответствуют параметры α = 31,5, β = 31,5. Опять же максимальная длина апостериорного 95-процентного вероятностного интервала будет достигнута при α + а = β + b, то есть для B(44, 44). Длину интервала найдем по формуле =БЕТА.ОБР(0,975;44;44;0;1) – БЕТА.ОБР(0,025;44;44;0;1) = 0,2072.
К оглавлению
В гл. 5 речь шла об оценке того, насколько распространенным является некоторое фиксированное свойство элементов интересующей нас совокупности. В том случае, когда для каждого элемента совокупности можно установить, обладает он рассматриваемым свойством или нет, степень распространенности этого свойства данной совокупности полностью характеризуется долей Р элементов, которые этим свойством обладают. Решение нашей задачи состояло в оценке неизвестного нам значения Р для всей совокупности.
Конечно, на практике наш интерес этим не ограничивается; хотелось бы узнать, среди элементов какого типа это свойство более распространено и почему. Однако такие вопросы выходят за рамки задач из гл. 5, и в поисках ответа мы должны перенести анализ в область экономических соотношений, которым посвящены гл. 7, 8 и 9. Конечно, нас интересует нечто большее, чем просто значение Р, и потому придется существенно расширить круг рассматриваемых проблем. Этому и будут посвящены следующие главы. Но сначала мы в данной главе обратимся к довольно простому способу обобщения материала гл. 5 и подготовим тем самым почву для исследования, которое будет проведено в гл. 7.
В гл. 5 мы столкнулись с дилеммой «все или ничего», поскольку каждый элемент интересующей нас совокупности либо обладал рассматриваемым свойством, либо не имел его вовсе. В более общем случае речь может идти о свойстве, присущем элементам совокупности в разной степени. Например, это могут быть доходы отдельных индивидов из определенной совокупности или их потребительские расходы, рост этих индивидов или их вес, расходы на покупку пива или характеристики их имущественного положения, или какой-либо иной показатель. Другими словами, это значения некоторой переменной, назовем ее X, соответствующие различным элементам совокупности. В общем случае эти значения меняются от элемента к элементу, т.е. существует распределение значений X на рассматриваемой совокупности. В зависимости от конкретной задачи нас может интересовать либо вся информация об этом распределении X, либо просто некоторые его обобщенные характеристики, скажем, средняя или дисперсия (или обе эти характеристики).
Как и в гл. 5, информация о распределении переменной X может быть получена путем обследования случайно выбранных элементов совокупности и определения соответствующих им значений X. Объединяя эту информацию с некоторой априорной оценкой распределения X, мы с помощью теоремы Байеса (подобно тому, как это было сделано в гл. 5) получим апостериорную оценку. Результат такой процедуры зависит, конечно, от точной формы априорной оценки и в особенности от свойств распределения переменной X.
Задача упрощается, если известна форма распределения переменной X в совокупности; например, если известно, что распределение является равномерным, бета-распределением, нормальным или каким-либо еще. В этих случаях распределение полностью описывается небольшим числом ключевых параметров: а и b для равномерного распределения (см. (2.23)); α и β в случае бета-распределения (см. (2.27); μ и σ2 для нормального распределения (см. (2.29)) и т.п. В каждом из этих случаев знание указанных ключевых параметров равносильно знанию распределения в целом.
Хотя методы, излагаемые в данной главе, применимы к любой форме распределения переменной X, мы ограничимся рассмотрением случая нормального распределения. Этот особенно важный случай очень часто встречается на практике. (Многие экономические переменные нормально распределены, а многие из оставшихся после соответствующих преобразований тоже удовлетворяют нормальному закону; так, при разбивке на группы по доходам недельные потребительские расходы приближенно удовлетворяют нормальному распределению, если недельный доход предварительно прологарифмировать.) Если переменная X распределена нормально, то это распределение полностью характеризуется значениями его средней и дисперсии (см. (2.29)). Поэтому знание средней и дисперсии означает знание всех деталей, связанных с конкретным нормальным распределением, т.е. узнать все о распределении — то же самое, что определить две его обобщающие характеристики — среднюю и дисперсию.
Ключевые параметры распределения — его среднюю и дисперсию— мы будем обозначать через М и S2 соответственно. Таким образом, через М обозначают среднюю (Mean), а через S — стандартное отклонение (Standard deviation) распределения переменной X в рассматриваемой совокупности.
Будем и здесь пользоваться прописной буквой для обозначения самого параметра, который может принимать различные значения, а соответствующей строчной буквой — для обозначения его конкретных значений. Поэтому реальное значение М в совокупности обозначают через m, а реальное значение S — через s (конечно, имеется в виду, что m и s — соответствующие значения переменных М и S). Возможны четыре случая, перечисленные в таблице.
Случай 1 тривиален и нет никаких проблем с его изучением, поскольку о распределении все известно. В трех остальных случаях задача нетривиальна, и информация потенциально полезна: для уменьшения неопределенности знания о средней в случае 2, для уменьшения неопределенности знания о дисперсии в случае 3, для уменьшения неопределенности знания о двух этих параметрах в случае 4.
Соответствующие обозначения в свою очередь меняются в зависимости от того, какой параметр известен, а какой неизвестен. Так, известное значение средней мы обозначаем через m, а если это значение неизвестно, то будем пользоваться буквой М; аналогично известному стандартному отклонению соответствует s, а неизвестному— S. Как быть, когда средняя и/или дисперсия неизвестны, было показано в гл. 5. Соответствующая процедура выглядит так: сначала формируется априорная оценка неизвестного параметра (параметров), затем осуществляется случайная выборка из совокупности и обследование ее элементов, наконец, выборочная информация используется для пересмотра априорной оценки и в результате получают апостериорную оценку. В данной главе поставлена цель — отыскать апостериорные оценки в случаях 2, 3 и 4 при некоторой данной априорной оценке. В разделе 6.2 рассмотрен случай 2, в разделе 6.3 — случай 3, а в разделе 6.4 — случай 4. В каждом из этих разделов рассматривается ситуация, когда априорные представления весьма расплывчаты. В разделе 6.5 показана связь результатов, полученных в разделах 6.2–6.4, с классическим анализом этих же задач.
6.2. Вывод при неизвестной средней и известной дисперсии
Мы рассмотрим в этом разделе случай 2 из помещенной выше таблицы. Мы имеем дело с некоторой интересующей нас переменной X, которая нормально распределена в рассматриваемой совокупности. Значение средней для переменной X неизвестно, и мы обозначаем его оценку М, а значение дисперсии мы знаем, оно равно s2. Покажем в этом разделе, как наблюдения над X могут быть использованы для пересмотра априорной оценки М неизвестного значения средней. Эти предположения можно выразить так:
(6.1) X ~ N (М, s2)
Мы будем рассматривать два исходных элемента: форму априорного распределения М и источник информации относительно М, который позволяет пересмотреть априорную оценку.
Начнем с формы априорной оценки. Ясно, что эта форма зависит от ожиданий индивида, формирующего эту оценку, т.е. от накопленных опыта и знаний. Поскольку переменная X непрерывна (это следует из (6.1)), то естественно предположить, что оценка М должна быть непрерывной, а не дискретной. Хотя методы, развиваемые в этом разделе, применимы к различным формам априорных распределений, мы ограничимся случаем, когда априорная оценка берется в форме нормального распределения. Предположим, что априорная оценка М нормально распределена со средней µ и дисперсией σ2. Чтобы выбрать подходящие значения µ и σ, мы поступим так же, как в разделе 5.2. Например, если наша оценка М такова, что мы считаем 100 наиболее вероятным значением и таким, что почти наверняка (с вероятностью 95,44%) значение М лежит между 80 и 120, то значениями µ и σ, отражающими такие априорные ожидания, будут соответственно 100 и 10. (Напомним, что нормально распределенная переменная попадает в интервал, границы которого удалены на 2 стандартных отклонения от средней, с вероятностью 95,44%.) Для случая, когда априорный 95,44-процентный вероятностный интервал для М задан в виде (100; 120), µ — значение априорной средней равно 110, а σ — значение априорной дисперсии равно 5.
Можно выразить предположение, в силу которого X ~ N (М, s2), в терминах априорной функции плотности вероятности для М (см. (2.29), где множитель σ–1 включен в коэффициент пропорциональности):
Перейдем теперь к вопросу о получении информации относительно М. Как и в гл. 5, существует естественный источник такой информации, а именно элементы рассматриваемой совокупности. Поскольку М — средняя значений X в рассматриваемой совокупности, естественно считать, что обследование элементов совокупности и выяснение соответствующих им значений X проливает свет на интересующее нас значение М. Вновь, как и в гл. 5, имеются две «крайние» возможности: мы можем обследовать все элементы совокупности или же обследовать только один ее элемент. Существует и «промежуточная» возможность — обследовать n элементов. Применим теперь процедуру, аналогичную использованной в гл. 5: сначала выясним, как воспользоваться информацией, полученной при обследовании одного элемента, а затем обобщим полученные результаты на случай, когда обследуют п элементов.
Как и в гл. 5, естественно выбрать наш единственный элемент (или произвести выборку объема 1) так, чтобы получить информацию об интересующем нас параметре. Это означает, что мы осуществляем наш выбор «правильно», т.е. обеспечивая каждому элементу совокупности равные шансы быть выбранным. Отсюда следует, что вероятностное распределение значений X среди выбранных элементов в точности такое же, как распределение значений X в совокупности. Поэтому, в силу (6.1), распределение значений X среди выбираемых элементов должно иметь вид N (М, s2). Ясно, что оно зависит от неизвестного значения M, удобнее всего выразить это так: условное распределение (значений X среди выбираемых элементов), когда дано, что М принимает значение m, имеет вид N (m, s2). Это можно записать с помощью условной функции плотности вероятностей (ср. (2.29), где мы включили множитель s–1 в коэффициент пропорциональности):
Это записано правдоподобие того, что для выбранного элемента значение X окажется равным х (или, короче, «правдоподобие наблюдения х»), если дано, что М принимает значение m. Теперь мы имеем возможность воспользоваться теоремой Байеса и, следовательно, получить апостериорную оценку М, учитывающую наблюдение х. Априорная оценка задана соотношением (6.2), правдоподобие — соотношением (6.3), и поэтому, воспользовавшись (4.23), мы получим для апостериорной оценки:
Заметим теперь, что выражение под экспонентой можно упростить, воспользовавшись следующим алгебраическим тождеством:
Теперь мы имеем дело с функцией плотности вероятностей нормально распределенной переменной (см. (2.29)) со средней ![]() и дисперсией
и дисперсией ![]() . Мы можем сформулировать следующий важный результат.
. Мы можем сформулировать следующий важный результат.
Первое, что следует отметить, анализируя этот результат: если априорной оценке соответствует нормальное распределение, то и апостериорной оценке также соответствует нормальное распределение. Значит, оценки остаются внутри семейства нормальных распределений. Второе, заслуживающее внимания обстоятельство касается характера воздействия новых наблюдений на среднюю величину оценки: как видно из (6.6), априорная средняя µ преобразуется в апостериорную среднюю:
которая является средневзвешенной величиной априорной средней (µ) и значения, полученного при наблюдении (х). Более того, априорная средняя входит в (6.7) с весом, пропорциональным s2, т.е. пропорциональным дисперсии X, а значение, полученное при наблюдении, — с весом, пропорциональным σ2, т.е. пропорциональным дисперсии М. Это означает, что с уменьшением σ2 (при прочих равных) увеличивается вес априорной средней, а с уменьшением s2 (при прочих равных) увеличивается вес наблюдения. Другими словами, чем больше вы доверяете своей априорной оценке M, тем меньший вес получит новая информация при формировании вашей апостериорной оценки, или чем более вероятно, что значение, полученное при наблюдении, близко к реальному значению m, тем больший вес вы присвоите наблюдениям. Все эти выводы интуитивно воспринимаются как вполне осмысленные.
Апостериорную среднюю (6.7) можно записать в альтернативном виде, разделив числитель и знаменатель на произведение дисперсий s2σ2 (очевидно, что обе формы записи эквивалентны, если σ ≠ 0, s ≠ 0):
В этой форме записи коэффициент при µ равен 1/σ2, а при х равен 1/s2. Конечно, отношение этих весов осталось прежним, т.е. равным отношению s2 и σ2, однако такая форма записи удобнее, поскольку при каждом из компонентов стоит характеристика его собственной «точности», и, кроме того, зависимости, о которых шла речь в предыдущем абзаце, становятся более явными. Так, коэффициент при значении априорной средней равен 1/σ2, т. е. является обратной величиной по отношению к априорной дисперсии; таким образом, чем меньше априорная дисперсия, тем больший вес соответствует априорной средней. Аналогично при значении, полученном в результате наблюдения, стоит коэффициент 1/s2, равный величине, обратной дисперсии наблюдаемых значений; таким образом, чем меньше дисперсия наблюдения, тем больший вес ему соответствует. В любом случае вес обратно пропорционален дисперсии. Поэтому полезно дать величине, обратной дисперсии, свое наименование и ввести для нее специальное обозначение. Назовем ее точностью этой переменной. Очевидно, чем меньше дисперсия, тем больше точность, и чем больше дисперсия, тем меньше точность; слово «точность» оказывается в данном случае вполне подходящим. Обозначим точность априорной оценки через p, а точность наблюдения — через р, т. е.
(6.9) p ≡ 1σ2, р ≡ 1/s2
Воспользуемся новыми обозначениями и перепишем выражение (6.8) для средней апостериорной оценки М:
Мы видим, что апостериорная средняя является средневзвешенной величиной априорной средней и значения, полученного при наблюдении, с весами, пропорциональными точности априорной оценки и точности наблюдения соответственно. Итак, чем больше точность априорной оценки, тем больший вес соответствует априорной средней; а чем больше точность значения, полученного при наблюдении, тем больше вес наблюдения.
Выясним теперь, как повлияет новая информация на дисперсию оценки и ее точность. Из (6.6) следует, что априорная дисперсия равна σ2, а апостериорная — равна ![]() . Это означает, что априорная точность 1/σ2 = p и апостериорная точность
. Это означает, что априорная точность 1/σ2 = p и апостериорная точность ![]() = 1/σ2 + 1/s2 = p + p. Таким образом, в результате учета информации, полученной при наблюдении, точность увеличилась с p до p + р: оценка после наблюдения становится более точной, чем до него, причем точность увеличивается на величину, равную точности наблюдения. Это с интуитивной точки зрения вполне осмысленный результат. С помощью введенного нами нового обозначения ключевой результат (6.6) можно записать в альтернативной, но алгебраически эквивалентной форме:
= 1/σ2 + 1/s2 = p + p. Таким образом, в результате учета информации, полученной при наблюдении, точность увеличилась с p до p + р: оценка после наблюдения становится более точной, чем до него, причем точность увеличивается на величину, равную точности наблюдения. Это с интуитивной точки зрения вполне осмысленный результат. С помощью введенного нами нового обозначения ключевой результат (6.6) можно записать в альтернативной, но алгебраически эквивалентной форме:
Обобщим полученные результаты. Если априорное распределение нормально, то и апостериорное распределение будет нормальным; апостериорная средняя является средневзвешенной априорной средней µ и значения х, полученного в результате наблюдения, причем веса пропорциональны априорной точности p и точности распределения наблюдаемых значений р соответственно; апостериорная точность равна сумме априорной точности и точности наблюдения.
Например, предположим, что нас интересует переменная Х, о которой известно, что она нормально распределена в некоторой совокупности, причем дисперсия распределения — s2 = 9, а ее средняя М неизвестна. Предположим, что наши ожидания относительно М можно описать посредством априорной оценки, имеющей нормальное распределение со средней µ = 100 и дисперсией σ2 = 16. Пусть случайно выбран один элемент совокупности, для которого переменная X принимает значение х = 112,5. Воспользуемся (6.6) или эквивалентной формой этого соотношения (6.11) и получим апостериорную оценку М (нормально распределенную) со средней
Это означает, что апостериорная дисперсия равна 144/25 и, следовательно, апостериорное стандартное отклонение равно: 12/5 = 2,4. Таким образом, апостериорная оценка имеет вид N [108, (2,4)2]. Обе оценки, априорная и апостериорная, изображены на рис. 6.1.
Рис. 6.1. Априорная и апостериорная оценки М (значение s2 известно). Априорно М удовлетворяет распределению N (100; 16); правдоподобие того, что средняя М переменной X равна m удовлетворяет распределению N (m; 9); апостериорная оценка М, учитывающая случайно выбранный элемент x = 112,5, удовлетворяет распределению N (108; 2,42)
Как видно из рис. 6.1, новая информация привела к смещению оценки средней М в сторону значения переменной Х, полученного при наблюдении (на величину, зависящую от отношения характеристик априорной точности и точности измерения), одновременно уменьшается разброс оценки, ее неопределенность. Этот эффект отражается на длине различных вероятностных интервалов. Например, априорный 95-процентный вероятностный интервал для М равен 100 ± 1,96*4 (92,16; 107,84); апостериорный 95-процентный вероятностный интервал для М равен 108 ± 1,96*2,4 (103,30; 112,70). Таким образом, априорная оценка и одно наблюдение х = 112,5 приводят нас к выводу, что с вероятностью 0,95 значение средней М лежит между 103,30 и 112,70. Длина 95-процентного вероятностного интервала в результате наблюдения уменьшилась с 15,68 до 9,41; это уменьшение служит мерой «ценности» новой информации. Заметим, что уменьшение вероятностного интервала не зависит от значения, полученного при наблюдении, поскольку длина 95-процентного вероятностного интервала зависит только от точности (дисперсии) соответствующего распределения, а, как мы уже видели, само значение, полученное при наблюдении, не влияет на апостериорную точность. Не появилось ли у вас желание обсудить интуитивную оправданность этих выводов?
До сих пор мы рассматривали случай выборки объема 1. Обобщим теперь наши результаты на случай выборки объема n. Будем, как обычно, считать, что выборка осуществлена «правильно», и каждому элементу совокупности обеспечены одинаковые шансы попасть в эту выборку. Отсюда следует, что условное распределение каждого значения X из выборки удовлетворяет соотношению (6.3). Это означает, что результат (6.11) справедлив и в этом случае и его можно использовать для определения воздействия, которое окажет на априорную оценку выборка, состоящая из n элементов. Будем учитывать влияние n наблюдений (обозначим соответствующие им значения переменной через х1, х2, …, хn) последовательно. Мы начали с априорного распределения N (µ, σ2) и после первого наблюдения х1 получили в соответствии с (6.11) апостериорное распределение
Схематически это можно представить следующим образом:
Теперь нам предстоит учесть информацию, появившуюся при втором наблюдении, когда мы выбрали элемент с соответствующим ему значением х2. Прежде чем информация о новом наблюдении поступила, наша оценка имела вид:
т. е. соответствовала априорному распределению в соотношении (6.11), а х2—информации, воздействие которой нужно учесть. Воспользоваться (6.11) мы можем, если известны «μ» и «π». Но, в частности, «μ» может принять значение (πμ + px1)/(π + р), а «π»— значение π + р. Подставим вместо π и μ эти значения в (6.11) и получим
Здесь апостериорная средняя является средневзвешенной соответствующей априорной средней ![]() и наблюдения х2 с весами, пропорциональными новой априорной точности π + р и точности наблюдения р. Апостериорная точность также равна сумме новой априорной точности π + р и точности наблюдения р. После упрощения выражения, стоящего в правой части, (6.13) можно записать так:
и наблюдения х2 с весами, пропорциональными новой априорной точности π + р и точности наблюдения р. Апостериорная точность также равна сумме новой априорной точности π + р и точности наблюдения р. После упрощения выражения, стоящего в правой части, (6.13) можно записать так:
Ясно, что (6.12) и (6.14) можно объединить и тогда
Этот процесс можно продолжить. Запишем результат для общего случая n наблюдений х1, x2, … xn:
Это выражение можно упростить, если обозначить через ![]() среднюю выборочных значений, т.е.
среднюю выборочных значений, т.е.
Из (6.20) следует, что х1 + x2 + … + xn ≡ n![]() , и поэтому (6.19) можно записать так:
, и поэтому (6.19) можно записать так:
Поскольку это чрезвычайно важный результат, перепишем его в форме (6.11).
Итак. Во-первых, если априорная оценка распределена нормально, то и апостериорное распределение будет нормальным независимо от объема выборки, т е. оценка остается в семействе нормальных распределений. Во-вторых, апостериорная средняя является средневзвешенной априорной средней и выборочной средней, причем веса равны π и nр соответственно. Таким образом, чем больше априорная точность (при прочих равных), тем больший вес имеет априорная средняя; чем больше объем выборки или больше точность каждого наблюдения, тем больший вес (при прочих равных) соответствует выборочной средней. Результат, как видим, вполне осмыслен интуитивно. В-третьих, апостериорная точность равна сумме априорной точности и произведения объема выборки на точность каждого наблюдения.
Из (6.22) следует, что апостериорная средняя зависит только от среднего значения ![]() наблюдений х1 + x2 + … + xn. Поэтому порядок, в котором появляются наблюдаемые значения, не существен, и каждое из них имеет одинаковый вес. Более того, поскольку наша оценка относится к М — среднему значению совокупности, вся информация, заключенная в наблюдениях х1 + x2 + … + xn, сосредоточена в значении выборочной средней
наблюдений х1 + x2 + … + xn. Поэтому порядок, в котором появляются наблюдаемые значения, не существен, и каждое из них имеет одинаковый вес. Более того, поскольку наша оценка относится к М — среднему значению совокупности, вся информация, заключенная в наблюдениях х1 + x2 + … + xn, сосредоточена в значении выборочной средней ![]() . Любая другая информация о наблюдениях в данном случае оказывается избыточной. Другими словам, знания значения
. Любая другая информация о наблюдениях в данном случае оказывается избыточной. Другими словам, знания значения ![]() достаточно, чтобы пересмотреть вероятностную оценку М.
достаточно, чтобы пересмотреть вероятностную оценку М.
Еще одно свойство, вытекающее из (6.22): апостериорная точность не зависит от значений х1 + x2 + … + xn, полученных при наблюдениях, а зависит только от параметров π, n и р. Тем самым имеется возможность обеспечить желаемое значение апостериорной точности путем соответствующего выбора объема выборки n. Эквивалентным образом это свойство можно сформулировать так: желаемую длину α-процентного вероятностного интервала (при заданном α) можно обеспечить, выбрав соответствующее значение n. Например, рассмотрим 95-процентный вероятностный интервал — он имеет длину, равную 3,92 апостериорным стандартным отклонениям. Предположим, нужно осуществить выборку (наименьшего) объема n так, чтобы эта длина не превышала некоторого заранее заданного значения w. Тогда нужно найти n, удовлетворяющее равенству
(поскольку точность распределения является обратной величиной его дисперсии). Это уравнение, если на время «забыть», что n — натуральное число, приводит к решению
В качестве n остается взять ближайшее натуральное число, не меньшее правой части равенства (6.23). Мы видим, что придется увеличивать объем выборки n, если меньше окажется точность априорного распределения, или меньше будет точность наблюдений, или уменьшится требуемая длина вероятностного интервала. Приведем простой числовой пример, с которым мы уже встречались в данном разделе. В этом примере π = 1/16 = 0,0625 и р = 1/9 = 0,1111. При подстановке в (6.23) w = 9,408 получим n = 1, что соответствует нашим ожиданиям и может служить проверкой правильности вывода (6.23). Другие примеры содержатся в таблице, где в качестве n указано ближайшее натуральное число, не меньшее правой части (6.23). Из таблицы видно, что за исключением малых значений n (когда априорная оценка доминирует над выборочной информацией) уменьшение вдвое длины вероятностного интервала требует четырехкратного увеличения объема выборки. Достаточно взглянуть на выражение (6.23), чтобы убедиться в общем характере этой зависимости при условии, что длина w достаточно мала в сравнении с π.
Прежде чем привести конкретный пример применения (6.22), посмотрим, что произойдет с нашей задачей, если полностью пренебречь априорными представлениями. Очевидный способ учесть указанное обстоятельство — принять точность априорного распределения равной нулю. Из (6.22) ясно, что тогда апостериорная оценка будет функцией только выборочной информации. Формально при π = 0 мы получим из (6.22) следующий результат.
Утверждение (6.24) можно записать в альтернативной и эквивалентной форме.
Этот простой, но весьма важный результат свидетельствует о том, что апостериорная оценка средней совокупности (когда априорные знания отсутствуют) нормально распределена вокруг выборочной средней, а дисперсия этого распределения пропорциональна дисперсии переменной X и обратно пропорциональна объему выборки. Апостериорные вероятностные интервалы для М легче получить с помощью (6.25) и формул в Excel. Например, 95-процентный вероятностный интервал для М равен ![]() ± 1,96 s/√n. Длина этого интервала 3,92 s/√n может быть сделана сколь угодно малой путем соответствующего выбора объема выборки n. Есть и еще одно свойство, вытекающее из (6.22) и (6.25), на которое следует обратить внимание: апостериорная дисперсия стремится к нулю при неограниченном увеличении объема выборки. Более того, апостериорная средняя либо равна выборочной средней (в случае (6.25)), либо стремится к ней при неограниченно увеличивающемся n (в случае (6.22)), а та в свою очередь стремится (при неограниченном увеличении n) к средней величине m для всей совокупности (апостериорная оценка средней для совокупности «стягивается» в вырожденное распределение у точки, соответствующей реальному значению средней для совокупности).
± 1,96 s/√n. Длина этого интервала 3,92 s/√n может быть сделана сколь угодно малой путем соответствующего выбора объема выборки n. Есть и еще одно свойство, вытекающее из (6.22) и (6.25), на которое следует обратить внимание: апостериорная дисперсия стремится к нулю при неограниченном увеличении объема выборки. Более того, апостериорная средняя либо равна выборочной средней (в случае (6.25)), либо стремится к ней при неограниченно увеличивающемся n (в случае (6.22)), а та в свою очередь стремится (при неограниченном увеличении n) к средней величине m для всей совокупности (апостериорная оценка средней для совокупности «стягивается» в вырожденное распределение у точки, соответствующей реальному значению средней для совокупности).
В заключение данного раздела проиллюстрируем ключевой результат (6.22) и его специальный случай (6.25) на одном примере. Предположим, нас интересует вес студенток Йоркского университета. Пусть нам удалось узнать (или мы готовы предположить), что характеристики их веса нормально распределены с известным стандартным отклонением в 14 фунтов, но неизвестной средней М. Чтобы получить информацию относительно М, мы можем осуществить случайную выборку среди студенток данного университета (отбирая их по фамилиям из списка всех студенток с помощью соответствующего механизма) и взвесить попавших в выборку студенток. Пусть вначале были выбраны 25 студенток и оказалось, что их средний вес равен 135 фунтам. Какой будет оценка М в свете полученной информации?
Апостериорная оценка зависит от априорной. Предположим вначале, что никаких априорных сведений у нас нет, т.е. что априорная оценка обладает нулевой точностью. Воспользуемся (6.25), положив х = 135, s = 14 и n = 25; мы найдем, что наша апостериорная оценка М нормально распределена со средней ![]() = 135 и дисперсией s2/n = 142/25 = 2,82, т.е. наша апостериорная оценка имеет вид N (135; 2,82). Это ее полная характеристика, и мы можем найти любые интересующие нас параметры. Например, апостериорный 95-процентный вероятностный интервал равен 135 ± 1,96×2,8, т.е. (129,51; 140,49). Итак, на основе выборочной информации мы можем заключить, что с вероятностью 0,95 М лежит между 129,51 и 140,49 фунтов.
= 135 и дисперсией s2/n = 142/25 = 2,82, т.е. наша апостериорная оценка имеет вид N (135; 2,82). Это ее полная характеристика, и мы можем найти любые интересующие нас параметры. Например, апостериорный 95-процентный вероятностный интервал равен 135 ± 1,96×2,8, т.е. (129,51; 140,49). Итак, на основе выборочной информации мы можем заключить, что с вероятностью 0,95 М лежит между 129,51 и 140,49 фунтов.
Пусть теперь мы хотим получить более точную оценку M, скажем, такую, что ее 95-процентный вероятностный интервал имеет длину не более 6 фунтов. Воспользуемся (6.23) при w = 6, π = 0, р = 1/s2 = 1/196 и вычислим соответствующее значение n; оно равно 84. Поскольку мы уже располагаем выборкой из 25 студенток, нужно дополнительно выбрать 59 студенток, чтобы достичь требуемой точности. Пусть среднее дополнительной выборки равно 138. Какой станет наша оценка теперь? Ответ можно получить двумя путями: либо рассмотрев дополнительную информацию в сочетании с полученной ранее оценкой для выборки из 25 студенток, либо сразу объединить обе выборки в одну большую выборку и учесть всю содержащуюся в этой выборке информацию в сочетании с начальной априорной оценкой (в таком случае априорной информации уже не будет). Рассмотрим каждый из этих путей.
Оценка, полученная на основе первоначальной выборки, как мы помним, имеет вид N (135, 2,82), а выборочная средняя для дополнительной выборки из 59 наблюдений равна 138. Подставим в (6.22) значения: μ = 135, π = 1/2,82, n = 59, р = 1/142 и ![]() = 138. Эта формула позволяет нам рассчитать среднее значение нормально распределенной апостериорной оценки, учитывающей дополнительную выборку:
= 138. Эта формула позволяет нам рассчитать среднее значение нормально распределенной апостериорной оценки, учитывающей дополнительную выборку:
Таким образом, наша апостериорная оценка такова: N (137,1; 2,333). Соответствующий 95-процентный вероятностный интервал определяется соотношением 137,1 ± 1,96√2,333, т.е. равен (134,1; 140,1). Его величина равна 6 фунтам, как и требовалось.
Предположим теперь, что две имеющиеся в нашем распоряжении выборки сразу же объединены в одну большую выборку, состоящую из 25 + 59 = 84 наблюдений. Средний вес студенток в этой новой выборке будет равен (25*136 + 59*138)/83 = 137,1, поскольку первые двадцать пять студенток вместе весят 25* 135 фунтов, а оставшиеся пятьдесят девять — 59* 138 фунтов. Остается объединить эту информацию с нашей исходной информацией, которая заключалась в полном пренебрежении априорными сведениями. Подставив в (6.25) значения ![]() = 137,1, s = 14 и n = 84, обнаружим, что апостериорная оценка М нормально распределена со средней
= 137,1, s = 14 и n = 84, обнаружим, что апостериорная оценка М нормально распределена со средней ![]() = 137,1 и дисперсией s2/n = 142/84 = 2,333, т.е. апостериорная оценка имеет вид N (137,1; 2,333). Это в точности (впрочем, вряд ли мы в этом сомневались) совпадает с оценкой, полученной выше другим способом.
= 137,1 и дисперсией s2/n = 142/84 = 2,333, т.е. апостериорная оценка имеет вид N (137,1; 2,333). Это в точности (впрочем, вряд ли мы в этом сомневались) совпадает с оценкой, полученной выше другим способом.
Рассмотрим теперь альтернативную ситуацию — мы в состоянии дать априорную оценку М. Конкретно будем исходить из того, что в силу имеющейся первоначальной информации М удовлетворяет распределению N (140,9) (ему соответствует 95,44-процентный вероятностный интервал (134; 146)). Подставим в (6.22) значения: μ =140, π = 1/9, n = 25, р = 1/142 и ![]() = 135. Это позволит получить апостериорную оценку М после того, как осуществлена первая выборка из двадцати пяти студенток. Оценка будет удовлетворять распределению N (137,33; 4,19), а соответствующий 95-процентный вероятностный интервал имеет вид (133,32; 141,34). Полезно сопоставить его с вероятностным интервалом, найденным ранее для случая нулевых априорных знаний: (129,51; 140,49). Первый из этих двух вероятностных интервалов уже и смещен вправо по сравнению со вторым — так отразилось влияние априорных сведений. Наконец, инкорпорируем информацию, заключенную во второй выборке, рассматривая полученную только что оценку в качестве априорной. Пользуясь первым из двух возможных способов, подставим в (6.22) значения: μ = 137,33, π = 1/4,19, n = 59, p = 1/142 и
= 135. Это позволит получить апостериорную оценку М после того, как осуществлена первая выборка из двадцати пяти студенток. Оценка будет удовлетворять распределению N (137,33; 4,19), а соответствующий 95-процентный вероятностный интервал имеет вид (133,32; 141,34). Полезно сопоставить его с вероятностным интервалом, найденным ранее для случая нулевых априорных знаний: (129,51; 140,49). Первый из этих двух вероятностных интервалов уже и смещен вправо по сравнению со вторым — так отразилось влияние априорных сведений. Наконец, инкорпорируем информацию, заключенную во второй выборке, рассматривая полученную только что оценку в качестве априорной. Пользуясь первым из двух возможных способов, подставим в (6.22) значения: μ = 137,33, π = 1/4,19, n = 59, p = 1/142 и ![]() = 138. Тогда апостериорная оценка М будет удовлетворять распределению N (137,7; 1,853), а соответствующий 95-процентный вероятностный интервал будет иметь вид (135,03; 140,37). Если этот вероятностный интервал мы сравним с полученным ранее для той же выборки из 59 наблюдений, но в предположении об отсутствии априорных сведений (134,1; 140,1), то убедимся, что эти два интервала почти одинаковы. Влияние содержащихся в выборке наблюдений на апостериорную оценку увеличилось, поскольку возросло число наблюдений в этой выборке (рис. 6.2).
= 138. Тогда апостериорная оценка М будет удовлетворять распределению N (137,7; 1,853), а соответствующий 95-процентный вероятностный интервал будет иметь вид (135,03; 140,37). Если этот вероятностный интервал мы сравним с полученным ранее для той же выборки из 59 наблюдений, но в предположении об отсутствии априорных сведений (134,1; 140,1), то убедимся, что эти два интервала почти одинаковы. Влияние содержащихся в выборке наблюдений на апостериорную оценку увеличилось, поскольку возросло число наблюдений в этой выборке (рис. 6.2).
Рис. 6.2. Последний пример раздела 6.2. Оценки М: (А) — априорная, (В) — с учетом первой выборки, (С) — с учетом второй выборки. Наблюдения (1) — средняя первой выборки, (2) — средняя второй выборки
Итак, мы рассмотрели случай 2 из таблицы, помещенной в конце раздела 6.1. Вы достаточно подробно познакомились с не совсем обычной ситуацией, когда значение средней предполагается неизвестным, в то время как дисперсия задана. Представить себе нечто подобное в реальной жизни нелегко, и поэтому придумать описанный выше пример было трудно. Более реалистичен случай 4, когда и средняя, и дисперсия неизвестны. Но прежде чем перейти к нему, рассмотрим в следующем разделе случай 3, когда средняя известна, а дисперсия неизвестна, тем. самым будет проложен путь к анализу случая 4 в разделе 6.4.
6.3. Вывод при неизвестной дисперсии и известной средней
К этому моменту нам удалось обсудить два примера статистического вывода, а именно: вывод относительно доли элементов совокупности, обладающих определенным свойством, и вывод о значении средней распределения при известной дисперсии. В каждом из этих примеров нам приходила на помощь относительно простая техника вывода, непосредственно ведущая к цели, а результаты вполне соответствовали интуитивным представлениям. Основное внимание мы уделяли обсуждению и интерпретации ключевых результатов. Надеемся, что к настоящему моменту читатель уже овладел базовыми процедурами и в состоянии самостоятельно ими пользоваться. Поэтому в дальнейшем изложение станет значительно «компактнее», поскольку мы опустим большую часть технических деталей. Читатель тем меньше в них нуждается, чем свободнее он владеет базовыми процедурами. Мы предлагали читателю принять на веру некоторые ключевые результаты, чтобы он мог сосредоточить все свое внимание на достижении интуитивного понимания как самих результатов, так и предпосылок, обеспечивающих их получение.
Ознакомившись с данной и последующими главами, мы убедимся, что, по мере того как приложения становятся все более реалистическими и полезными, сложность соответствующих им технических приемов также возрастает. Поэтому, а также имея в виду то, что встречающийся в литературе экономический анализ обычно ведется в предположении об отсутствии априорных знаний, мы отнесемся к этому специальному случаю очень внимательно. Даже рассматривая ситуацию с явно ненулевой априорной информацией, мы будем дополнительно анализировать в качестве предельного случай отсутствия априорных знаний. Тем самым мы сможем практически не рассматривать конкретные способы описания априорных оценок.
Обсудим теперь проблему статистического вывода в условиях, когда дисперсия неизвестна, а средняя фиксирована. Постановка задачи будет такой же, как в предыдущем разделе: нас интересует некоторая переменная X, нормально распределенная на некоторой совокупности. При этом мы предполагаем среднюю переменной X для данной совокупности известной, а дисперсию переменной X для той же совокупности неизвестной. В соответствии с нашей общей договоренностью относительно обозначений первую величину будем обозначать через m, а последнюю — через S2. Объединим сделанные предположения;
(6.26) X ~ N (m, S2)
Мы намерены показать, как информация, поступившая в форме наблюдений над переменной X, может быть использована для уменьшения имеющейся неопределенности относительно S2. Мы можем записать принятые предположения о поведении переменной X в альтернативной, но в точности эквивалентной (6.26) форме
(6.27) X ~ N (m, 1/P)
где Р ≡ 1/S2 есть точность переменной X, а поставленная нами задача состоит в демонстрации того, как наблюдения переменной X могут быть использованы для уменьшения неопределенности наших представлений относительно Р. (Здесь Р обозначает нечто, совершенно отличное от того, что обозначалось этой же буквой в гл. 5.) Благодаря альтернативной форме (6.27), как мы в этом вскоре убедимся, удается несколько уменьшить технические сложности, возникающие при преобразованиях.
Как обычно, исходным пунктом рассуждений будет утверждение относительно наших априорных ожиданий по поводу значения неизвестного параметра — в данном случае Р. Поскольку Р может принимать только неотрицательные значения и притом любые в промежутке от нуля до бесконечности, в качестве возможного способа описания априорной оценки можно воспользоваться гамма-распределением. (Нормальное распределение для этой цели не годится, поскольку не позволяет исключить отрицательные значения; бета-распределение также придется отклонить, ибо ему соответствуют значения из отрезка [0; 1].)
Среди рассмотренных ранее распределений гамма-распределение оказывается единственно подходящим и отвечающим целям нашего анализа. Таким образом, остановимся на предположении о том, что наши априорные представления о параметре Р можно описать с помощью гамма-распределения с параметрами α и β (см. раздел 2.4). В силу (2.31), это означает, что априорная плотность вероятностей переменной Р задается в виде
Посмотрим теперь, как скажется на этой оценке новая информация, заключенная в выборке объема 1. Если процесс извлечения выборки рандомизирован, то, как и в предыдущем разделе, распределение значений X для элемента выборки в точности совпадает с распределением X в исходной совокупности. Значит, в силу (6.27), для элемента выборки имеем X ~ N (m, 1 /Р), т.е. условное распределение X при данном Р = р есть N (m, 1/р). Правдоподобие х при данном Р = р будет выглядеть так:
(Сравнивая (6.З) и (6.29), можно обнаружить между ними различия, несмотря на то, что оба эти соотношения отражают один и тот же факт. Замена р ≡ 1/s2 объясняет не все различия между двумя указанными соотношениями; в (6.29) перед экспонентой появился множитель р1/2, которого не было в (6.3). Дело в том, что в предыдущем разделе нас интересовала средняя m, и потому можно было учесть не содержащие m компоненты в множителе пропорциональности соотношения (6.3). На этот раз нас интересует р, и теперь не содержащие р компоненты могут быть включены в множитель пропорциональности соотношения (6.29). Вот почему множитель р1/2 может быть исключен из (6.3), но его необходимо сохранить в (6.29).)
Воспользуемся теоремой Байеса (4.23). В силу (6.28) и (6.29), для апостериорного распределения Р, учитывающего одно наблюдение х, можно записать
Сопоставив это выражение с (2.31), приходим к выводу, что перед нами функция плотности вероятностей гамма-распределения с параметрами α + 1/2 и β + (x – m)2/2. Таким образом, получен важный результат.
Мы вновь столкнулись с ситуацией, когда оценка остается внутри своего семейства — в данном случае внутри семейства гамма-распределений. Можно было бы решить, что это случайность. Однако это не так. Мы просто соответствующим образом выбрали априорное распределение. При других априорных распределениях такой результат не был бы получен: например, если бы априорное распределение Р было бета-распределением, то апостериорное уже не было бы бета-распределением; точно так же при нормальном априорном распределении Р апостериорное распределение этого параметра нормальным уже не будет. С аналогичной ситуацией мы сталкивались в предыдущем разделе этой главы: если бы в качестве априорного для М было выбрано бета- (или гамма-) распределение, то апостериорное уже не было бы бета- (гамма-) распределением. Вы можете самостоятельно выяснить, почему это происходит.
Результат (6.31) можно обобщить, как это было сделано в предыдущей главе (см. (5.8)), где параметры распределения при появлении новых данных изменялись чрезвычайно просто. В данном случае из (6.31) следует, что с появлением одного наблюдения х первый параметр возрастает на 1/2, а ко второму прибавляется (х — m)2/2. Обобщение на случай n наблюдений х1, x2, … xn проводится непосредственно: каждое из наблюдений увеличивает первый параметр на 1/2; в результате i-го наблюдения второй параметр распределения увеличивается на (xi – m)2/2. Таким образом, нами получен следующий результат.
с той лишь разницей, что в первом выражении участвует средняя совокупности (m), а во втором — выборочная средняя ![]() . Воспользовавшись (6.33), переформулируем (6.32).
. Воспользовавшись (6.33), переформулируем (6.32).
В разделе 2.4 было показано, что гамма-распределение с параметрами α и β имеет среднюю α/β и дисперсию α/β2. Поэтому из (6.34) вытекает, что средние априорного и апостериорного распределений равны соответственно
соответственно. Из (6.35) вытекает, что независимо от значений α и β апостериорная средняя при неограниченном возрастании n стремится к 1/![]() 2. Аналогично из (6.36) получаем, что при этом дисперсия апостериорной оценки стремится к нулю. Объединяя эти два результата, мы обнаружим, что апостериорная оценка Р при неограниченном увеличении n «стягивается» к вырожденному распределению с центральным значением 1/
2. Аналогично из (6.36) получаем, что при этом дисперсия апостериорной оценки стремится к нулю. Объединяя эти два результата, мы обнаружим, что апостериорная оценка Р при неограниченном увеличении n «стягивается» к вырожденному распределению с центральным значением 1/![]() 2.
2.
Свойство (6.34) позволяет интерпретировать конкретную априорную оценку Р подобно тому, как это было сделано в гл. 5. Точнее, (6.34) свидетельствует об «эквивалентности» априорной оценки Р, заданной в виде G (α, β), наблюдению выборки объема 2α, в которой сумма квадратов отклонений наблюдавшихся значений от m равна 2β. Тем самым, кроме всего прочего, появляется возможность формально записать условие полного отсутствия априорной информации — положить значения α и β одновременно равными нулю. В рамках нашей интерпретации априорная оценка G (0, 0) «эквивалентна» наблюдению выборки нулевого объема (для которой, очевидно, сумма квадратов отклонений тоже равна нулю). Итак, из (6.34) можно вывести следующий важный результат.
С целью, которая вскоре станет ясна, мы придадим этому результату несколько иную форму. Вначале воспользуемся (2.31) и заметим, что если Р ~ G (n/2, n![]() 2/2), то соответствующая функция плотности вероятностей пропорциональна
2/2), то соответствующая функция плотности вероятностей пропорциональна
р(n/2) – 1 ехр (–ns2р/2).
Введем временно новую переменную Y, определяемую соотношением Y = n![]() 2P. Поскольку переменные Y и Р пропорциональны, их функции плотности вероятностей также пропорциональны, т.е. после некоторых простых преобразований мы убедимся в том, что функция плотности вероятностей переменной Y пропорциональна y(n/2) – 1 ехр (–y/2).
2P. Поскольку переменные Y и Р пропорциональны, их функции плотности вероятностей также пропорциональны, т.е. после некоторых простых преобразований мы убедимся в том, что функция плотности вероятностей переменной Y пропорциональна y(n/2) – 1 ехр (–y/2).
Это функция плотности вероятностей для переменной, удовлетворяющей гамма-распределению с параметрами n/2 и 1/2. В разделе 2.4 уже говорилось, что у этого специального случая гамма-распределения имеется свое собственное наименование — о такой переменной говорят, что она удовлетворяет распределению хи-квадрат с n степенями свободы. Таким образом, мы приходим к следующему выводу: переменной Р ~ G (n/2, n![]() 2/2) соответствует новая переменная n
2/2) соответствует новая переменная n![]() P, удовлетворяющая распределению хи-квадрат с n степенями свободы. Воспользуемся этим свойством и преобразуем (6.37).
P, удовлетворяющая распределению хи-квадрат с n степенями свободы. Воспользуемся этим свойством и преобразуем (6.37).
На первый взгляд утверждение (6.38) ничем не лучше утверждения (6.37). Однако преимущество (6.38) в том, что благодаря ему не нужна обращаться к неудобным таблицам гамма-распределения, а можно воспользоваться более простыми таблицами распределения хи-квадрат, которые есть почти во всех книгах по статистике. [7]
В этом разделе нам приходится иметь дело уже с более сложным формальным аппаратом: числовые примеры позволят проиллюстрировать некоторые ключевые результаты. Мы ограничимся рассмотрением случая, когда априорные знания отсутствуют. Предположим, вас заинтересовал вопрос, сколько денег тратят студенты в буфете (баре), находящемся на территории университетского городка, в течение недели.
Пусть вам известно или же вы готовы принять в качестве допущения, что переменная X (интересующая вас величина недельных расходов одного студента) нормально распределена со средней, равной 6 фунтам, — это значение было получено на основе анализа всех имеющихся счетов и суммарных поступлений. Предположим, вы не знаете дисперсии этих недельных расходов (измеряемой либо величиной самой дисперсии S2, либо характеристикой точности Р = 1/S2), но хотите иметь о ней представление. Для получения информации относительно Р (или S2) вы решили произвести рандомизированную выборку двенадцати студентов (это, конечно, не первые попавшиеся нам сегодня вечером двенадцать студентов!) и попросить их в течение предстоящей недели регистрировать все свои расходы на покупки в университетском буфете. Более того, вы убеждаете студентов в необходимости быть предельно честными и аккуратными, объясняете им, что факт наблюдения никак не должен влиять на обычный режим покупок. Если студенты последуют вашим советам, то полученные с их помощью двенадцать значений переменной X можно будет считать подходящей рандомизированной выборкой для последующего анализа. (Вы, вероятно, хорошо представляете себе, что получить несмещенную информацию о расходах, связанных с развлечениями, весьма трудно. В большинстве обзоров, в частности, в Обзоре семейных расходов —Family Expenditure Survey, — публикуются лишь такие отчеты о расходах, которые проходят определенную независимую проверку благодаря контролю за общей суммой расходов.)
Пусть в результате проведенных наблюдений вы получили следующие значения (фунты в неделю) для каждого из двенадцати студентов: 7,12; 5,62; 4,31; 8,22; 6,39; 5,91; 6,55; 5,25; 7,02; 4,99; 6,02; 7,00. Выборочная средняя равна 6,20, и мы с уверенностью можем сказать, что она не смещена вниз. Подставим в (6.33) соответствующие выборке значения наблюдаемых величин (при этом m = 6) и найдем, что ![]() 2= 1,1058. Предположим теперь, что в качестве исходной мы рассматриваем ситуацию, когда никакой априорной информации относительно Р нет. Тогда можно воспользоваться утверждением (6.38), в силу которого с учетом имеющихся в нашем распоряжении двенадцати наблюдений апостериорная оценка Р такова, что 13,2696 Р удовлетворяет распределению хи-квадрат с 12 степенями свободы (здесь n
2= 1,1058. Предположим теперь, что в качестве исходной мы рассматриваем ситуацию, когда никакой априорной информации относительно Р нет. Тогда можно воспользоваться утверждением (6.38), в силу которого с учетом имеющихся в нашем распоряжении двенадцати наблюдений апостериорная оценка Р такова, что 13,2696 Р удовлетворяет распределению хи-квадрат с 12 степенями свободы (здесь n![]() 2 = 12*1,1058 = 13,2696 и n = 12).
2 = 12*1,1058 = 13,2696 и n = 12).
Мы располагаем теперь полной характеристикой апостериорной оценки и можем найти некоторые обобщенные ее характеристики. Например, с помощью (6.39) и формул распределения хи-квадрат в Excel можно найти 95-процентный вероятностный интервал для Р. Будем считать, что с вероятностью 0,975 переменная 13,2696 Р должна быть не меньше некоторого числа и лишь с вероятностью 0,025 она превосходит некоторое другое число. Тогда в интервал между двумя найденными числами рассматриваемая нами переменная попадет с вероятностью 0,95. Pmin =ХИ2.ОБР(0,025;12) = 4,40, Pmax =ХИ2.ОБР(0,975;12) = 23,04. Таким образом, 95-процентный вероятностный интервал (но не минимальной длины) для переменной, удовлетворяющей распределению хи-квадрат с 12 степенями свободы, имеет вид (4,40; 23,03). Обращаясь теперь к (6.39), можем записать Р (4,40 ≤ 13,2696 Р ≤ 23,03) = 0,95. Чтобы преобразовать это в утверждение относительно переменной Р, мы просто разделим каждый член неравенства на 13,2696: Р (0,3316 ≤ Р ≤ 1,7355) = 0,95.
Опираясь на выборочную информацию, мы таким образом установили, что с вероятностью 0,95 точность переменной X лежит между 0,3316 и 1,7355. Соотношение S2 ≡ 1/P позволяет преобразовать интервал, определенный выше для значений точности, в интервал для значений дисперсии: Р (0,5762 < S2 < 3,0157) = 0,95.
Если необходимо, можно перейти к утверждению относительно величины стандартного отклонения S: для этого достаточно вычислить арифметическое значение квадратного корня для каждого из членов неравенства, стоящего под символом вероятности: Р (0,7591 < S < 1,7366) = 0,95.
Таким образом, мы приходим к выводу, что с вероятностью 0,95 стандартное отклонение для изучаемых нами недельных расходов студентов содержится в интервале между 0,7591 и 1,7366. Предположим теперь, что найденный интервал представляется нам излишне широким— это означает, что наша оценка неточна, и потому мы решили произвести дополнительную выборку, состоящую из восемнадцати студентов. Теперь в нашем распоряжении выборка объема 30 наблюдений. Из (6.38) следует, что для вычисления значения ![]() 2 потребуются все значения xi. Допустим, что мы произвели необходимые расчеты и получили
2 потребуются все значения xi. Допустим, что мы произвели необходимые расчеты и получили ![]() 2 = 1,3260 при n = 30. Подставим эти значения
2 = 1,3260 при n = 30. Подставим эти значения ![]() 2 и n в (6.38). С учетом всех тридцати наблюдений апостериорная оценка Р будет такой, что
2 и n в (6.38). С учетом всех тридцати наблюдений апостериорная оценка Р будет такой, что
(6.40) 39,78P удовлетворяет распределению хи-квадрат с 30 степенями свободы
Для новой выборки мы можем получить обобщающие характеристики распределения подобно тому, как это было только что сделано. В частности, 95-процентный вероятностный интервал для S: (0,92; 1,5392). Полученные вероятностные интервалы несколько уже в сравнении с теми, которые соответствовали лишь двенадцати наблюдениям.
При необходимости любых ссылок на характеристику точности можно избежать. Воспользуемся тем обстоятельством, что Р = 1/S2 и сформулируем ключевой результат (6.38) в альтернативной форме.
Кроме того, если n достаточно велико (скажем, больше 60), мы можем обращаться с распределением хи-квадрат, имеющим n степеней свободы, считая, что его средняя равна n, а дисперсия равна 2n, и оно хорошо приближается нормальным распределением, причем приближение тем лучше, чем больше число n. Таким образом, для достаточно больших n утверждение (6.44) можно уточнить: апостериорная оценка S такова, то n![]() 2/S2 приблизительно удовлетворяет нормальному распределению N (n, 2n). Теперь у вас имеется возможность исследовать, как «работает» подобное приближение для рассмотренного выше примера (хотя в нем n = 30, т.е. принятое ограничение, в силу которого n > 60, не удовлетворяется).
2/S2 приблизительно удовлетворяет нормальному распределению N (n, 2n). Теперь у вас имеется возможность исследовать, как «работает» подобное приближение для рассмотренного выше примера (хотя в нем n = 30, т.е. принятое ограничение, в силу которого n > 60, не удовлетворяется).
На этом анализ случая 3 завершен. Основные положения данного раздела практически те же, что в примерах из гл. 5 и разделе 6.2, а именно изменение априорной оценки некоторого параметра в результате инкорпорирования (с помощью теоремы Байеса) новой информации.
6.4. Вывод при неизвестной средней и неизвестной дисперсии
Мы изучим в данном разделе случай 4 (наиболее общий из тех, которые были названы в разделе 6.1), когда обе величины — и средняя, и дисперсия, характеризующие представляющую для нас интерес переменную, — неизвестны. Переменную по-прежнему будем обозначать через X, предполагая, что она нормально распределена на интересующей нас совокупности. Поскольку ни среднюю совокупности, ни ее дисперсию мы не знаем, воспользуемся для их обозначения буквами М и S2. В целом наши предположения относительно переменной X можно записать в виде
(6.45) X ~ N (М, S2) или (6.46) X ~ N (М, 1/Р), где Р = 1/S2 есть неизвестная характеристика точности.
В каждом из предыдущих случаев был только один неизвестный параметр. В данном разделе мы сталкиваемся с новой ситуацией: имеются два неизвестных параметра. Поэтому и априорная, и апостериорная оценки должны выражаться с помощью совместных распределений двух параметров М и Р (или, что эквивалентно, М и S2). Введенные в гл. 3 обозначения позволяют специфицировать априорную оценку в виде fMP (m, р) — совместной функции плотности вероятностей переменных М и Р. Мы зададим ее косвенным способом, что позволит построить эту функцию, опираясь на материал двух предыдущих разделов. В разделе 3.4 говорилось о свойстве, в силу которого совместная функция плотности вероятностей может быть записана как произведение подходящим образом выбранных условной и маргинальной функций плотности. В рассматриваемом нами случае
(6.47) fMP (m, р) = gM(m|p)*fP(p)
Материал раздела 6.3 подсказывает как «очевидного кандидата на роль» fP() — априорного маргинального распределения Р — гамма-распределение с параметрами σ и β. Оно приведено в (6.28). Далее, на основе раздела 6.2 мы можем взять в качестве gM(m|p) — априорного распределения — М при условии, что Р принимает значение р — нормальное распределение, имеющее среднюю µ и точность pр (или дисперсию σ2s2). Формально (см. (2.29)) получим
(6.48) gM(m|p) µ (pр )1/2ехр[ – pр (m – µ)2/2]
(Поскольку точность распределения М при условии Р = р пропорциональна р, распределение переменной X будет обладать тем большей дисперсией, чем с меньшим доверием вы относитесь к своей оценке средней величины переменной X.)
Объединяя (6.28) и (6.48), получим следующую априорную совместную оценку М и Р:
Как и ранее (см. разделы 6.2 и 6.3), информация поступает к нам в виде наблюдений над переменной X, удовлетворяющей распределению N (M, 1/Р). Начнем со случая выборки объема 1. Соответствующая функция правдоподобия имеет вид (6.29), и мы воспроизведем ее здесь, сделав необходимые изменения в обозначениях:
Апостериорная совместная оценка, как обычно, определяется с помощью теоремы Байеса, и применительно к данному случаю мы можем записать:
После вполне «обозримых» алгебраических упрощений (подобных тем, с которыми мы уже сталкивались в разделах 6.2 и 6.3) преобразуем соотношение к виду
Сформулируем теперь полученный результат.
Хотя это утверждение и выглядит весьма громоздким, суть его чрезвычайно проста: апостериорное распределение сохраняет ту же форму, что и априорное (т.е. оценка остается внутри того же семейства), но с параметрами, преобразованными с учетом новой информации так, как это показано в (6.53).
Уже привычным для нас способом мы можем обобщить полученный результат на случай n наблюдений. Однако необходимые при этом алгебраические преобразования громоздки, и мы их опустим. Если же подобные выкладки заинтересуют вас, то вы сможете самостоятельно убедиться в справедливости следующего утверждения.
(Сравнивая (6.53) и (6.56), мы видим, что выражения для µ’, p’ и α’ во второй группе формул представляют собой очевидные обобщения соответствующих выражений из первой группы. Этого нельзя сказать о выражениях для β’. Тому, кто попытается получить общий результат самостоятельно, следует вначале рассмотреть случай n = 2 и лишь после этого переходить к обобщению.)
В приведенных выше выражениях совместное распределение М и Р задавалось посредством маргинального распределения Р и условного распределения М при Р = р. Поскольку тем самым дается полная характеристика совместному распределению, имеется возможность получить дополнительно и маргинальное распределение М. Это можно сделать непосредственно с помощью методов из гл. 3, в частности, из раздела 3.4. Опустим довольно громоздкие выкладки и ограничимся формулировкой результата:
Этот результат позволяет в сочетании с (6.55) определить апостериорное маргинальное распределение М.
Как вы могли убедиться, материал данного раздела концептуально не отличается от материала двух предыдущих разделов. Единственное, с чем мы столкнулись, это громоздкость алгебраических преобразований. Чтобы упростить изложение, мы посвятим оставшуюся часть раздела рассмотрению случая, когда априорная информация отсутствует. Каким образом нам следует охарактеризовать этот случай, учитывая то, что мы уже знаем? Обратимся к разделу 6.2 (неизвестная средняя, известная дисперсия), где достаточно было просто положить n = 0, что означало постоянство априорной плотности М. (Это не совсем очевидно вытекает из (6.2). Однако достаточно установить, как ведет себя функция плотности нормального распределения при неограниченном возрастании дисперсии σ2, чтобы убедиться, что при этом n стремится к нулю. Кривая становится все более пологой и все теснее прилегает к горизонтальной оси, в пределе совпадая с ней.) Вспомним также, что в разделе 6.3 (известная средняя, неизвестная дисперсия) мы описали случай отсутствия априорной информации, положив α = 0 и β = 0; это означало, что априорная плотность распределения Р пропорциональна р–1 (см. (6.28). Результаты двух предыдущих разделов наводят нас на мысль, что в данном разделе (неизвестная средняя, неизвестная дисперсия) подходящей характеристикой для случая отсутствия априорной информации окажется пропорциональность плотности совместного априорного распределения произведению константы (раздел 6.2) и р–1 (раздел 6.3), т.е. плотность совместного априорного распределения должна быть пропорциональна р–1. Обращаясь к (6.49), мы видим, что подобные требования равносильны такому выбору параметров: p = 0, α = – 1/2, β = 0. (Если приведенные здесь весьма непростые аргументы вас не удовлетворили, то вам придется принять сказанное на веру. Строгий вывод мы здесь не приводим.)
Итак, возьмем (6.55) и положим p = 0, α = 1/2, β = 0, что приведет к результату (6.58).
По соображениям, которые станут ясны позднее, введем величину ŝ, определяемую равенством
Выражение (6.59) — почти выборочная дисперсия; различие состоит в том, что в знаменателе (6.59) вместо n стоит n – 1. Поэтому мы будем называть ŝ2 модифицированной выборочной дисперсией, a ŝ — модифицированным выборочным стандартным отклонением. Объединив теперь (6.58) и (6.57), получим весьма важный результат.
Вспомним результат, полученный непосредственно перед (6.38), в силу которого из условия Y ~ G(k/2, β/2) следует, что новая переменная βY удовлетворяет распределению хи-квадрат с k степенями свободы; объединяя этот результат с (6.58), получим важное утверждение.
Положив Р ≡ 1/S2, можно записать утверждение, эквивалентное (6.61).
Утверждения (6.60) и (6.61) или (6.62) чрезвычайно важны, взятые вместе, поскольку они полностью характеризуют апостериорные маргинальные распределения величин М и Р или S в случае, когда априорная информация отсутствует. Заметим, что вся информация, которая нам нужна о выборке, — это ее средняя ![]() и модифицированная дисперсия ŝ2.
и модифицированная дисперсия ŝ2.
В заключение приведем пример, иллюстрирующий применение ключевых результатов (6.60) и (6.61) или (6.62). Предположим, интересующая нас переменная X — индекс интеллектуального развития (IQ) студентов Йоркского университета. Пусть мы знаем или готовы предположить, что значения X нормально распределены по всей совокупности (всех студентов Йоркского университета). Но нам неизвестны ни средняя, ни дисперсия Х; к тому же нет никаких оснований для какого-либо априорного заключения об их возможных значениях. Чтобы узнать что-нибудь о средней и о дисперсии, мы можем сделать рандомизированную выборку из всей совокупности студентов (выбор осуществляется так, как это указано в разделе 6.2) и определить индекс IQ студентов, попавших в выборку. Пусть такая выборка объемом в 25 наблюдений осуществлена (рис. 6.3). Рассчитаем в Excel для этих данных выборочную среднюю ![]() =СРЗНАЧ(A1:E5) = 115,1; выборочную модифицированную дисперсию ŝ2 =ДИСП.В(A1:E5) = 23,205 и выборочное модифицированное стандартное отклонение ŝ =СТАНДОТКЛОН.В(A1:E5) = 4,817. Подставим найденные выборочные значения в (6.60):
=СРЗНАЧ(A1:E5) = 115,1; выборочную модифицированную дисперсию ŝ2 =ДИСП.В(A1:E5) = 23,205 и выборочное модифицированное стандартное отклонение ŝ =СТАНДОТКЛОН.В(A1:E5) = 4,817. Подставим найденные выборочные значения в (6.60):
(6.63) апостериорная оценка М такова, что величина (М – 114,14)/0,963 удовлетворяет t-распределению с 24 степенями свободы.
Аналогично после подстановки выборочных значений в (6.62) придем к выводу:
(6.64) апостериорная оценка такова, что величина 556,92/S2 удовлетворяет распределению хи-квадрат с 24 степенями свободы.
Рис. 6.3. Измерение IQ 25 студентов (А1:Е5) и некоторые параметры выборки (G1:J4)
Утверждение (6.63) полностью характеризует нашу апостериорную (маргинальную) оценку М. Утверждение (6.64) полностью характеризует нашу апостериорную (маргинальную) оценку S. Так же можно получить и другие обобщающие характеристики. Пусть, например, нужно найти наш апостериорный 95-процентный вероятностный интервал для М и для S. Можно сделать это следующим образом. Воспользуемся утверждением (6.63) и функцией Excel =СТЬЮДЕНТ.ОБР(). Pmin =СТЬЮДЕНТ.ОБР(0,025;24) = –2,064, а Pmax =СТЬЮДЕНТ.ОБР(0,975;24) = 2,064. То есть, переменная, удовлетворяющая t-распределению с 24 степенями свободы, с вероятностью 95 % лежит в интервале с концевыми точками ±2,064. Поэтому в соответствии с (6.63)
Таким образом, 95-процентный вероятностный интервал для М, основанный на выборочной информации, имеет вид (113,2; 117,1) — с точностью до первого десятичного разряда. Мы можем утверждать, что с вероятностью 0,95 средняя величина индекса IQ для студентов Йоркского университета находится между 113,2 и 117,1.
Чтобы найти 95-процентный вероятностный интервал для S, стандартного отклонения для того же индекса IQ, обратимся к (6.64) и формуле Excel для распределения хи-квадрат. Мы обнаружим, что переменная, удовлетворяющая распределению хи-квадрат с 24 степенями свободы, с вероятностью 0,95 лежит между Pmin =ХИ2.ОБР(0,025;24) = 12,4 и Pmax =ХИ2.ОБР(0,975;24) = 39,4. Поэтому, воспользовавшись (6.64), получим Р (12,40 ≤ 556,92/S2 ≤ 39,4) = 0,95. Путем несложных преобразований получим, что Р (3,8 ≤ S ≤ 6,7) = 0,95. Итак, (3,8; 6,7) — 95-процентный вероятностный интервал для S, найденный на основе выборочной информации. Мы можем сделать вывод, что с вероятностью 0,95 величина стандартного отклонения при определении индекса IQ среди студентов Йоркского университета лежит между 3,8 и 6,7.
6.5. Доверительные интервалы и критерии значимости
В байесовской статистике сделанное в текущий момент утверждение относительно вероятностного распределения значений интересующего нас параметра или переменной величины полностью характеризует текущие ожидания относительно этого параметра или этой переменной. Сказать больше об этих ожиданиях нельзя. Однако можно сказать меньше, просто указать определенные обобщающие характеристики имеющегося в текущий момент вероятностного распределения в зависимости от того, какие конкретные его свойства на этот раз представляют для нас интерес. Тем не менее, отвечая на вопрос: «что вы к текущему моменту знаете об этом параметре (об этой переменной)?», стремятся либо указать само распределение (в том виде, в каком его представляют себе), либо способ, позволяющий обобщить его наиболее важные свойства. Это все, что в данном случае требуется.
Однако сторонник классического подхода отнесется к подобным проблемам иначе. Как уже говорилось в разделе 5.6, основное различие между классическим и байесовским статистическими подходами состоит в том, что для первого вероятностные утверждения о фиксированных параметрах недопустимы, в то время как для второго они не только возможны, но и обязательны. В классической статистике имеются две различные, но связанные одна с другой задачи, решаемые в процессе основанного на выборочных наблюдениях статистического вывода относительно неизвестных параметров. Одна называется оцениванием, другая — проверкой гипотез. Первая из этих двух задач относится к использованию выборочных данных для получения оценок неизвестных параметров (характеризующих генеральную совокупность), а вторая — к использованию выборочных данных для проверки гипотез относительно неизвестных параметров (см., например, Проверка гипотез: одновыборочные критерии). Начнем с оценивания.
Мы уже ознакомились в разделе 5.6 с классическим подходом к оцениванию. Оценки бывают двух типов — точечные и интервальные; в первом случае в качестве оценки неизвестного параметра указывается лишь одно число, во втором — интервал и тем самым передается информация о точности оценки. При этом не объясняется, почему в качестве оценки выбраны определенная точка или определенный интервал. Мы посмотрим теперь, о каких оценках идет речь, и соотнесем их с байесовским анализом, проведенным в разделах 6.2–6.4.
Случай 2 (раздел 6.2): неизвестная средняя М и известная дисперсия s2. В этом случае обычная классическая точечная оценка М — выборочная средняя ![]() . Таким образом, статистик, стоящий на классических позициях, если его просят указать число, которое он считает в некотором смысле «лучшей оценкой» М, называет
. Таким образом, статистик, стоящий на классических позициях, если его просят указать число, которое он считает в некотором смысле «лучшей оценкой» М, называет ![]() . Для него интервальные оценки (об этом уже шла речь в разделе 5.6) задаются в форме α-процентных доверительных интервалов. В случае 2 обычный α-процентный доверительный интервал для М задается в виде
. Для него интервальные оценки (об этом уже шла речь в разделе 5.6) задаются в форме α-процентных доверительных интервалов. В случае 2 обычный α-процентный доверительный интервал для М задается в виде
Точная интерпретация α-процентного доверительного интервала (6.66) такова: «Если уже построены α-процентные доверительные интервалы (6.66) для неизвестной средней генеральной совокупности, то α процентов из них будут содержать неизвестную среднюю, в то время как оставшиеся 100 – α % не будут ее содержать. При этом неизвестно, попадет средняя в какой-либо конкретный доверительный интервал или нет».
Выражение (6.66) выглядит весьма привычно для нас. В самом деле, если мы вернемся к разделу 6.2, а именно к выражению (6.25), то обнаружим, что байесовский α-процентный вероятностный интервал, найденный при отсутствии априорной информации, задается соотношением
Выражение для вероятностного интервала алгебраически идентично (6.66). Таким образом, алгебраически наш байесовский α-процентный вероятностный интервал для М, соответствующий отсутствию априорной информации, идентичен классическому α-процентному доверительному интервалу для М. Конечно, концептуально они совершенно различны.
Случай 3 (раздел 6.3): неизвестная дисперсия S2 и известная средняя m. В этом случае обычной точечной классической оценкой S2 будет ![]() 2 (см. (6.33)), т.е.
2 (см. (6.33)), т.е.
Обычный классический a-процентный доверительный интервал для S2 можно записать в виде
(Yk удовлетворяет распределению хи-квадрат с k степенями свободы). Если вы обратитесь к (6.44), то убедитесь, что классический доверительный интервал (6.67) алгебраически идентичен байесовскому α-процентному вероятностному интервалу для S2, найденному при отсутствии априорной информации. Итак, вновь байесовский α-процентный вероятностный интервал, найденный при отсутствии априорной информации, и классический α-процентный доверительный интервал оказались алгебраически идентичными. (Впрочем, в этом нет ничего неожиданного, поскольку и в байесовском, и в классическом случае «ожидалось», что величина n![]() 2/S2 удовлетворяет распределению хи-квадрат с n степенями свободы; различие состоит в том, что с байесовской точки зрения — это утверждение относительно S2 при данном
2/S2 удовлетворяет распределению хи-квадрат с n степенями свободы; различие состоит в том, что с байесовской точки зрения — это утверждение относительно S2 при данном ![]() 2, а с классической — утверждение относительно
2, а с классической — утверждение относительно ![]() 2 при данном S2.)
2 при данном S2.)
Случай 4 (раздел 6.4): неизвестная средняя М и неизвестная дисперсия S2. В этом случае обычными классическими точечными оценками М и S2 будут ![]() и ŝ2 соответственно, причем последняя определяется (см. (6.59)) как
и ŝ2 соответственно, причем последняя определяется (см. (6.59)) как
(Тk удовлетворяет t-распределению с k степенями свободы). Обратившись к (6.60) и (6.62), вы убедитесь в алгебраической идентичности классических доверительных интервалов (6.68) байесовским α-процентным вероятностным интервалам для М и S2, найденным в предположении об отсутствии априорной информации.
Итак, во всех трех рассмотренных случаях байесовский α-процентный вероятностный интервал, найденный в предположении об отсутствии априорной информации, и классический α-процентный доверительный интервал алгебраически идентичны. При этом концептуально они совершенно различны, а факт их алгебраического совпадения делает эти различия несущественными для практика, поскольку в рамках байесовской статистики классический α-процентный доверительный интервал интерпретируется как байесовский α-процентный вероятностный интервал, полученный в предположении об отсутствии априорной информации. Наоборот, если сторонник классического подхода попросит вас указать α-процентный доверительный интервал для некоторого параметра, то вы просто рассчитаете байесовский α-процентный вероятностный интервал в предположении об отсутствии априорной информации.
Задача теории классического статистического вывода, известная как проверка гипотез, не имеет непосредственного аналога в теории байесовского вывода, хотя некоторая ее интерпретация может быть предложена. Чтобы на этот раз избежать повторений, сосредоточим внимание сразу же на случае 4 — все дальнейшие рассуждения можно без особого труда воспроизвести и для двух предшествующих ему случаев. Более того, мы ограничимся случаем проверки гипотез относительно М и сошлемся на возможность повторить все рассуждения для случая проверки гипотез относительно S2.
Проверка гипотез относительно М означает использование выборочных данных для проверки двух взаимоисключающих гипотез относительно (истинного, но неизвестного) значения М. Типичная пара таких гипотез задается в виде Н0 и Н1. Н0: М = m0, Н1: М > m0, где m0 — некоторое специфическое значение М. В результате проведения классической процедуры одна из этих гипотез в свете информации, содержащейся в выборке, должна быть принята, а другая — отвергнута. Ясно, что, вообще говоря, имеется возможность принятия «ложной» гипотезы. Поэтому проверку организуют таким образом, чтобы вероятность отклонения верной гипотезы Н0 (ее называют «нуль-гипотезой») равнялась некоторому заранее заданному, достаточно малому значению (обычно 5 или 1%). Эту величину называют уровнем значимости критерия. Запишем это определение более точно: если критерий определен так, что Р(Н0 отвергается |Н0 верна) = α/100, то его уровень значимости равен α%. Для данного конкретного примера можно показать, что подходящей процедурой проверки, указывающей на достижения α-процентного уровня значимости, будет контроль за выполнением одного из условий:
где величина tk,β была определена выше. Если в результате такой проверки принята гипотеза Н0, то говорят о незначимости критерия при α-процентном уровне, если же гипотеза Н0 отвергнута, то говорят о значимости критерия при α-процентном уровне. (Наряду с этим пользуются понятием, в силу которого ![]() — значимо или незначимо, смотря по обстоятельствам, отличается от m0.)
— значимо или незначимо, смотря по обстоятельствам, отличается от m0.)
Какой смысл заключен в такой процедуре для сторонника байесовского подхода? Как мы покажем, в результате подобной проверки он получит некоторую информацию относительно Р (М > m0). Заметим, что Р (М > m0) можно записать в виде
Аналогично, если критерий незначим при α-процентном уровне, то можно заключить, что Р (М > m0) ≤ (100 – α)/100.
Обобщим полученные результаты: сторонник байесовского подхода, осуществив проверку нулевой гипотезы Н0 (М = m0) против альтернативной гипотезы Н1 (М > m0) и отклонив гипотезу Н0 при α-процентном уровне значимости, делает вывод, что апостериорная вероятность истинности гипотезы H1 (в предположении об отсутствии априорной информации) превышает (100 – α)/100. Приведем числовой пример. Если гипотеза Н0 отвергнута при 5-процентном уровне значимости, то вероятность истинности гипотезы превышает 0,95, если же Н0 принимается (точнее, не отклоняется), то вероятность истинности гипотезы H1 меньше 0,95.
Итак, мы убедились в том, что классическое утверждение «гипотеза Н0 (М = m0) отвергается в пользу гипотезы Н1 (М > m0) при α-процентном уровне значимости» и байесовское утверждение «при отсутствии априорной информации вероятность истинности гипотезы Н1 превышает (100 – α)/100» алгебраически эквивалентны.
В заключение отметим тот существенный факт, что байесовская интерпретация классических понятий всегда основана на предположении об отсутствии априорной информации. Тем самым лишний раз подчеркивается то обстоятельство, что в классической статистике никакой роли априорной информации не отводится и потому все классические выводы базируются исключительно на выборочной информации. В этом смысле классический подход можно рассматривать как крайний и специальный случай байесовского подхода.
Резюме. В этой главе речь шла о статистических выводах относительно средней и/или дисперсии некоторой интересующей нас переменной, о которой известно, что она нормально распределена на рассматриваемой генеральной совокупности. При этом базовый принцип остался тем же, что и в предыдущей главе (а именно преобразование априорных ожиданий в свете новой информации, содержащейся в выборочных данных), хотя на этот раз потребовались более сложные алгебраические преобразования (особенно в разделе 6.4). Поэтому, чтобы избежать сложностей, мы рассматривали более простой случай вывода при отсутствии априорной информации. Ключевые результаты для этого случая приведены в (6.25), (6.44), (6. 60) и (6.62) и сведены в табл. 6.1, которая в сжатом виде содержит основные положения данной главы, что может оказаться полезным на практике.
Таблица 6.1. Статистический вывод о средней и/или дисперсии при отсутствии априорной информации. Источники. Случай 2 — результат (6.25), в силу которого M ~ N(![]() ,s2/n), после преобразования к стандартному нормальному распределению (см. раздел 2.4). Случай 3 — результат (6.44). Случай 4 — результаты (6.60) и (6.62).
,s2/n), после преобразования к стандартному нормальному распределению (см. раздел 2.4). Случай 3 — результат (6.44). Случай 4 — результаты (6.60) и (6.62).
Пожалуй, чаще всего приходится пользоваться результатами, относящимися к случаю 4, которые приведены в последней строке таблицы. Чтобы воспользоваться таблицей, достаточно вычислить лишь выборочную среднюю ![]() и модифицированную выборочную дисперсию ŝ2. После этого, вооружившись формулами t-распределения и распределения хи-квадрат, вы в состоянии дать полное описание апостериорных оценок средней М и дисперсии S2 рассматриваемой совокупности. Итак, несмотря на все технические сложности, с которыми пришлось столкнуться в этой главе, сам процесс построения статистического вывода при отсутствии априорной информации оказывается весьма «прозрачным» даже для наиболее трудного случая 4.
и модифицированную выборочную дисперсию ŝ2. После этого, вооружившись формулами t-распределения и распределения хи-квадрат, вы в состоянии дать полное описание апостериорных оценок средней М и дисперсии S2 рассматриваемой совокупности. Итак, несмотря на все технические сложности, с которыми пришлось столкнуться в этой главе, сам процесс построения статистического вывода при отсутствии априорной информации оказывается весьма «прозрачным» даже для наиболее трудного случая 4.
Главу завершает краткое изложение классического подхода статистического вывода. Показано, как классические процедуры оценивания и проверки гипотез интерпретируются в терминах байесовского подхода. Благодаря этому вы с одинаковым успехом сможете читать работы, посвященные анализу выборочных данных, как классического, так и байесовского направления.
Упражнения
6.1. Предположим, что доход X — нормально распределенная переменная с неизвестной средней М и известной дисперсией 100. В выборке содержатся следующие наблюдения над X: 24 26 28 29 22 21 25 26 24. (а) Найдите апостериорное распределение средней М и 95-процентный вероятностный интервал для М при каждом из следующих априорных распределений М: а) N (20, 9); б) N (30, 9); в) N (20, 16); г) N (20, ∞). (б) Найдите апостериорное распределение и 95-процентный вероятностный интервал средней М после следующих дополнительных девяти наблюдений переменной X: 29 26 28 22 21 24 24 25 26. Рассмотрите две выборки по отдельности и, последовательно изменяя оценки, найдите апостериорные оценки по мере поступления данных (первый способ); (в) Повторите задание (б), но теперь предварительно объедините обе выборки в одну, после чего определите влияние полученной таким образом выборки на исходную априорную оценку (второй способ).
6.3. Если ваши априорные знания относительно средней М нормально распределенной переменной X отсутствуют, то какого размера выборка вам потребуется, чтобы ваш апостериорный 95-процентный вероятностный интервал для М был не шире, чем 3,92? Дисперсия X равна: а) 100; б) 25.
6.5. Рассмотрите числовой пример из раздела 6.3. Пусть произведена дополнительная выборка, состоящая из десяти студентов (сверх тех двенадцати, которые были выбраны ранее). Соответствующие новой выборке значения X: 6,31; 5,29; 4,11; 8,23; 6,11; 5,93; 7,01; 6,22; 5,01; 6,50. Рассчитайте апостериорный 95-процентный вероятностный интервал для S в предположении, что априорная информация отсутствует, а выборочная содержится во всех 22 наблюдениях, результаты которых стали известны вам одновременно (будьте внимательны при расчете значения s̃2 для этой объединенной выборки).
6.6. Предположим, что доход X нормально распределен с неизвестной средней М и неизвестной дисперсией S2. Пусть выборка объема 9 содержит первое множество наблюдений из перечисленных в упражнении 6.1. Рассчитайте 95-процентные вероятностные интервалы для М и S при условии, что априорная информация отсутствует. Каким станет этот интервал после того, как будут учтены следующие девять наблюдений из того же упражнения 6.1?
6.7. Известно, что доходы в рассматриваемом регионе распределены нормально. Пусть у выборки, состоящей из 12 наблюдений, средняя ![]() равна 24,4, а модифицированное выборочное стандартное отклонение равно 10,388. Как вы относитесь, имея такую информацию, к утверждению, что средний доход в этом регионе меньше 32? Насколько правдоподобно, с вашей точки зрения, что стандартное отклонение дохода в данном регионе заключено между 5 и 15?
равна 24,4, а модифицированное выборочное стандартное отклонение равно 10,388. Как вы относитесь, имея такую информацию, к утверждению, что средний доход в этом регионе меньше 32? Насколько правдоподобно, с вашей точки зрения, что стандартное отклонение дохода в данном регионе заключено между 5 и 15?
6.8. Логарифм недельных доходов в домашнем хозяйстве удовлетворяет приблизительно нормальному распределению. Предположим, в результате контактов со случайно выбранными тридцатью шестью домашними хозяйками было обнаружено, что логарифм их выборочного дохода имеет среднюю 2,3 и стандартное отклонение 0,5. Оцените в свете этой информации гипотезу, в силу которой средняя величина недельного дохода в домашнем хозяйстве для изучаемой совокупности не превосходит 150 фунтов (априорная информация отсутствует; логарифмы взяты по основанию 10).
6.9. Пусть характеристика интеллектуальных возможностей студентов (индекс IQ) приблизительно удовлетворяет нормальному распределению. Проведено тестирование двадцати пяти случайно выбранных студентов Йоркского университета. Выборочная средняя значений IQ равна 115, а модифицированное стандартное отклонение равно 8. Какова в свете информации, содержащейся в этой выборке, вероятность того, что для среднего студента Йоркского университета значение IQ выше среднего значения этой характеристики для студентов всех университетов страны, которое равно 112? Можно ли считать разброс значений IQ для Йоркского университета необычайно низким, если стандартное отклонение для всех университетов равно 12? Решающий эту задачу не располагает собственной априорной информацией.
Решения
6.1. Воспользуемся формулой (6.22):
За расчетами лучше проследить по соответствующему листу Excel-файла. Как и следовало ожидать варианты А и Б дают одинаковый результат.
6.3. Воспользуемся формулой (6.23):
где π – априорная точность (величина обратная априорному стандартному отклонению), w – ширина апостериорного 95-процентного вероятностного интервала (если значение α ≠ 0,95; вместо коэффициента 3,92 будет использовано иное число), р – известная точность переменной Х.
Видно, что при прочих равных, чем ниже точность р (выше дисперсия s2) данных, тем больше требуется выборка, чтобы апостериорный 95-процентный вероятностный интервал всё еще попадал в заданные пределы w.
6.5. Воспользуемся формулой (6.33)
и возьмем в качестве xi значения 22 наблюдаемых величин, а m = 6 (см. рис. ниже). ![]() 2= 1,1241. Так как никакой априорной информации относительно Р (точности) [8] нет, можно воспользоваться (6.38)
2= 1,1241. Так как никакой априорной информации относительно Р (точности) [8] нет, можно воспользоваться (6.38)
в силу которого с учетом имеющихся в нашем распоряжении 22 наблюдений, апостериорная оценка Р такова, что 24,7302 Р удовлетворяет распределению хи-квадрат с 22 степенями свободы (здесь n![]() 2 = 22*1,1241 = 24,7302 и n = 22). Теперь с помощью формулы Excel =ХИ2.ОБР() найдем нижнее и верхнее критические значения, отвечающие 95-процентному вероятностному интервалу для Р. Pmin =ХИ2.ОБР(0,025;22) = 10,9823, Pmax =ХИ2.ОБР(0,975;22) = 36,7807. Таким образом, можем записать Р (10,9823 ≤ 24,7302 Р ≤ 36,7807) = 0,95, или Р (0,4441 ≤ Р ≤ 1,4873) = 0,95. Соотношение S2 ≡ 1/P позволяет преобразовать интервал, определенный выше для значений точности, в интервал для значений дисперсии: Р (0,6724 ≤ S2 ≤ 2,2518) = 0,95 или стандартного отклонения: Р (0,82 ≤ S ≤ 1,50) = 0,95. Таким образом, с вероятностью 0,95 стандартное отклонение для изучаемых нами недельных расходов студентов содержится в интервале между 0,82 и 1,50.
2 = 22*1,1241 = 24,7302 и n = 22). Теперь с помощью формулы Excel =ХИ2.ОБР() найдем нижнее и верхнее критические значения, отвечающие 95-процентному вероятностному интервалу для Р. Pmin =ХИ2.ОБР(0,025;22) = 10,9823, Pmax =ХИ2.ОБР(0,975;22) = 36,7807. Таким образом, можем записать Р (10,9823 ≤ 24,7302 Р ≤ 36,7807) = 0,95, или Р (0,4441 ≤ Р ≤ 1,4873) = 0,95. Соотношение S2 ≡ 1/P позволяет преобразовать интервал, определенный выше для значений точности, в интервал для значений дисперсии: Р (0,6724 ≤ S2 ≤ 2,2518) = 0,95 или стандартного отклонения: Р (0,82 ≤ S ≤ 1,50) = 0,95. Таким образом, с вероятностью 0,95 стандартное отклонение для изучаемых нами недельных расходов студентов содержится в интервале между 0,82 и 1,50.
6.6. Воспользуемся формулой (6.60) для расчета 95%-ного вероятностные интервалы для среднего значения совокупности – М:
Модифицированное выборочное стандартное отклонение ŝ найдем по формуле (6.59):
Воспользуемся формулой (6.61) для расчета 95%-ного вероятностные интервалы для стандартного отклонения совокупности – S:
Результаты расчетов приведены на рис. ниже. По результатам расчета для выборки 1 можно сказать, что с 95%-ной вероятностью среднее лежит в диапазоне 23,00…27,00, а стандартное отклонение в диапазоне 1,75…4,98. Если к тому же провести наблюдения и над второй выборкой, 95%-ный вероятностный диапазон для среднего значения совокупности М сузится до размеров 23,17…26,83, а 95%-ный вероятностный диапазон для стандартного отклонения совокупности S – до размеров 1,89…3,78.
6.7. Задача 6.7 является во многом обратной задаче 6.6. Мы также будем использовать формулы (6.60) и (6.61). Для начала преобразуем утверждение «М ≤ 32» в форму , удовлетворяющую t-распределению с 11 степенями свободы «(M — 24,4)/2,999 ≤ 2,5344». А затем найдем вероятность того, что это второе утверждение истинно, используя формулу =СТЬЮДЕНТ.РАСП(2,5344;11;ИСТИНА) = 0,9861. То есть, с вероятностью 98,6% можно утверждать, что средний доход в этом регионе меньше 32. Далее проведем последовательность преобразований для стандартного отклонения совокупности (см. Excel-файл и рис. ниже). Видно, что с вероятностью 92% стандартное отклонение дохода в данном регионе заключено между 5 и 15.
6.8. Задача аналогична предыдущей:
Можно утверждать, что гипотеза Н0: М ≤ 150 фунтов имеет мало шансов на успех – 7,3%.
6.9. Алгоритм поиска ответа на первый вопрос аналогичен предыдущему примеру (см. Excel-файл и рис. ниже). Можно утверждать, что с вероятностью 96,3% для среднего студента Йоркского университета значение IQ выше среднего значения этой характеристики для студентов всех университетов страны. Отвечая на второй вопрос, мы должны оценить вероятность того, что полученное по выборке из 25 студентов модифицированное стандартное отклонение (равное 8 ) меньше среднего стандартного отклонения для всех университетов страны (равного 12). Можно утверждать, что гипотеза Н0: Sдля Йорка = 12 почти не имеет шансов на успех, их не более 1%.
Глава 7. Элементарный регрессионный анализ
Изложенные в предыдущих главах общие методы можно применить теперь к задачам, представляющим для экономистов наибольший интерес, и заняться эмпирическим анализом экономических соотношений. Вы, наверное, не сомневаетесь в том, что выводы или прогнозы, сделанные на основе практически любой экономической теории, представимы в форме гипотетических соотношений между экономическими переменными. Например, опираясь на теорию спроса, можно предсказать количественный уровень спроса на некоторый товар в зависимости от цены на него, цен на другие товары и доходы потребителей; теория агрегированного потребления позволяет предсказать величину потребительских расходов в зависимости от дохода и нормы банковского процента и т.д. Цель этой и следующих двух глав — показать, как информация в форме наблюдений за соответствующими экономическими переменными может быть использована для уточнения наших знаний о подобных экономических соотношениях.
Как правило, в экономической теории можно указать ее отдельные составляющие, каждая из которых объясняет поведение одной экономической переменной. Эти отдельные составляющие теории обычно выражают в форме гипотетических соотношений вида
(7.1) Y = Н (X)
где Y — переменная, поведение которой объясняется, а X — вектор объясняющих переменных. Каждое из гипотетических соотношений принято сопровождать замечанием о его справедливости «при прочих равных условиях», характеризующим воздействие каких-либо неучтенных объясняющих переменных (не существенных, забытых или сознательно игнорируемых).
В зависимости от того, что представляет для нас интерес, гипотетические соотношения можно анализировать либо каждое в отдельности, либо группами, включающими от двух до нескольких сотен соотношений. Например, простейшая модель рынка состоит из функции спроса, функции предложения и условия равновесия. Аналогично в простейшую макроэкономическую модель входят агрегированная функция потребления и тождество, характеризующее распределение дохода. Более сложные макроэкономические модели содержат функцию потребления, инвестиционную функцию, функцию формирования основного капитала, функцию импорта, уравнения, описывающие изменения цен и заработной платы. Подобные модели из двух или более взаимосвязанных соотношений, называют моделями с одновременными уравнениями. К ним мы обратимся в гл. 9, а пока будем заниматься более простой задачей — анализом моделей, состоящих из одного уравнения, т.е. представимых в виде (7.1). Им посвящены гл. 7 и 8.
Общий случай модели, состоящий из одного уравнения (когда вектор X состоит из произвольного числа переменных, а функция Н () может принимать разные формы) изучается в гл. 8. Гл. 7 как бы прокладывает путь к этому общему случаю, знакомя читателя с важнейшим специальным случаем, позволяющим ввести необходимые концептуальные понятия и идеи. Это случай, когда X оказывается всего лишь скаляром (т.е. модель содержит лишь одну объясняющую переменную), а Н() — линейная функция. Тогда (7.1) можно записать в виде
(7.2) Y = А + ВХ
и мы получаем модель парной линейной регрессии, где А и В — ее параметры (в частности, А — точка пересечения прямой с осью ординат, В — тангенс угла наклона к оси абсцисс). Таким образом, (7.2) отражает гипотезу о линейной связи между Y и X, такой, что Y = А, когда X = 0, и увеличение значения переменной X на 1 приводит к увеличению переменной Y на величину В. Наиболее известным примером подобной модели является линейная агрегатная функция потребления, где Y — агрегированное потребление, X — агрегированный доход, В— предельная (тоже агрегатная) склонность к потреблению.
Как мы уже отметили выше, экономисты сопровождают гипотетические соотношения словами «при прочих равных условиях»; это служит сигналом того, что соотношение предполагается справедливым лишь при постоянстве всех остальных условий. Но чрезвычайно трудно обеспечить выполнение подобного требования на практике. Мы пользуемся данными, генерируемыми реально функционирующей экономической системой, а не появляющимися в таком контролируемом эксперименте, где, вообще говоря, можно обеспечить необходимое постоянство условий, не связанных непосредственно с проводимыми измерениями. Поэтому требование, чтобы все происходило «при прочих равных условиях», не может быть удовлетворено. Обычный выход из положения состоит в прибавлении к (7.2) члена, «улавливающего» все остальное, или остаточного члена. Тогда мы получим такое выражение для нашего гипотетического соотношения
(7.3) Y = А + ВХ + U
где U и есть остаточный член. Как только мы записали соотношение в форме (7.3), необходимость в оговорке «при прочих равных условиях» исчезла.
Остаточный член U содержит все факторы, отличные от X, которые влияют на Y. В противовес первым двум слагаемым А + ВХ, образующим детерминированную часть соотношения (7.3), третье слагаемое U называют его недетерминированной частью. Относительная роль недетерминированной части в (7.3) зависит от того, насколько существенна величина X при определении значения Y. В более общей формулировке: вид распределения переменной U зависит от конкретных особенностей задачи и от подхода к ее решению. Для полной спецификации соотношения (7.3) задание распределения переменной U столь же важно, как и спецификация вида функции, т.е. интересующих нас параметров А и В. Таким образом, нам предстоит на основе имеющейся информации уточнить наши представления, во-первых, о значении А, во-вторых, о значении В, в-третьих, о распределении переменной U. В данной главе будет показано, как наблюдения над X и Y позволяют решить эту задачу.
Из гл. 6 мы знаем, насколько упрощается использование информации, если нам известна форма распределения (или же мы готовы сделать по этому поводу какие-то предположения), т.е. можно конкретизировать задачу, указав, что распределение является равномерным, бета-распределением, нормальным или каким-либо еще. Целям данной главы соответствует предположение, в силу которого переменная U нормально распределена. Это наиболее общее предположение, и оно вполне приемлемо для большинства экономических приложений. К нему приводят и аргументы теоретического характера. Важнейший факт математической статистики — центральная предельная теорема — утверждает, что при определенных обстоятельствах переменной, являющейся суммой большого числа независимых переменных, свойственна тенденция к нормальному распределению ее значений. Поскольку U отражает влияние на Y, вообще говоря, бессчетного множества других переменных, то естественно предположить, что значения U распределены нормально (если нет конкретных указаний, позволяющих принять иную гипотезу). В дальнейшем мы будем придерживаться этого предположения.
Очевидно, что среднюю переменной U удобно принять равной нулю, ибо если она отлична от нуля, то можно скорректировать соответствующим образом параметр А (просто прибавив к нему значение средней). Таким образом, средняя (математическое ожидание) переменной Y при фиксированном X равна А + ВХ, т.е. U измеряет отклонение реально наблюдаемого (при данном X) значения Y от соответствующей этому X средней, или от математического ожидания. Разброс, как обычно, можно характеризовать величиной стандартного отклонения переменной U, которое, как это было принято в гл. 6, будем обозначать через S. Обобщая принятые предположения, можем теперь записать, что
(7.4) U ~ N (О, S2)
Соотношения (7.3) и (7.4) позволяют полностью специфицировать линейную модель парной нормальной регрессии. Этой модели и посвящена данная глава. Обобщим сказанное: в данной главе будет показано, как наблюдения над переменными X и Y позволяют получить информацию о соотношении, связывающем экономические показатели Y и X, причем относительно этого соотношения приняты следующие предположения:
(7.5) Y = А + ВХ + U
U ~ N (О, S2)
Предположения (7.5) и значения трех параметров А, В и S полностью специфицируют характер связи между X и Y. На протяжении данной главы будем предполагать, что форма связи (7.5) выбрана правильно, и нам остается определить ее параметры А, В и S. Чтобы отличать S2 — дисперсию переменной U — от параметров A и В, имеющих явный экономический смысл, будем называть А и В коэффициентами рассматриваемого соотношения (В — коэффициент при переменной X; А тоже можно считать коэффициентом, но при некоторой фиктивной переменной, всегда принимающей значение 1). Как и ранее, будем обозначать неизвестные параметры прописными буквами, а известные значения этих параметров — соответствующими строчными буквами. Следовательно, буквы a и b будут употребляться, когда коэффициенты известны, а буквы А и В — когда неизвестны; аналогично s2 — известное значение дисперсии, a S2 — значение, которого мы не знаем. Как и в гл. 6, могут иметь место четыре (основных) случая:
(Помимо основных случаев имеется еще несколько «подслучаев»: например, в случае 2 есть два подслучая, в каждом из которых один коэффициент известен, а другой неизвестен. Мы не будем рассматривать подобные конкретизации перечисленных здесь и в гл. 6 общих случаев.)
Как и в гл. 6, случай 1 тривиален: поскольку все о соотношении, связывающем интересующие нас переменные, известно, то нет предмета для обсуждения. Оставшиеся три случая нетривиальны и будут изучены в разделах 7.2–7.4. В разделе 7.5 (как и в гл. 6) результаты, полученные в предыдущих трех разделах, будут соотнесены с результатами применения классического подхода к решению тех же задач. Во всех случаях важно «качество» подгонки конкретных соотношений (вытекающих из экономической теории) к конкретным данным наблюдений, а также важна проблема относительности выбора эмпирического представления, отражающая разнообразие возможностей теоретического объяснения одной и той же переменной (раздел 7.6). Несколько подробных примеров регрессий содержит раздел 7.7, а в разделе 7.8 обсуждается применение эмпирического анализа для целей прогнозирования.
Важно все время помнить об основных целях данной главы. Во-первых, необходимо оценить значения параметров А, В и S2 в свете наблюдений над отвечающими характеру исследования экономическими показателями. Типичный вывод может выглядеть так: на основе 80 (квартальных) наблюдений над агрегированными показателями дохода и потребления в Великобритании мы полагаем, что с вероятностью 0,95 предельная (агрегированная) склонность к потреблению заключена между 0,59 и 0,63. Еще один пример: наблюдения за динамикой спроса на деньги и доходов позволяют считать, что вероятностью 0,73 эластичность спроса на деньги от дохода не меньше единицы. Во-вторых, требуется установить относительное правдоподобие конкурирующих теоретических объяснений. При этом формулировка типичного вывода может быть такой: по данным о размерах инфляции, о предложении денег и членстве в профсоюзах монетаристское объяснение инфляции представляется в три раза более правдоподобным, чем то, которое связывает ее с давлением со стороны профсоюзов.
Концептуально материал данной главы не сложнее материала предыдущих глав, однако его изложение требует преодоления ряда технических трудностей. Чтобы не останавливаться на деталях преобразований и доказательств, мы перенесем некоторые из них в приложения. Более того, мы ограничимся рассмотрением случая, когда вся априорная информация в расчет не принимается (т.е. либо отсутствует, либо мы ею пренебрегаем). Читатель, желающий познакомиться с более общей ситуацией, найдет в тексте ссылки на соответствующую литературу. Чтобы помочь читателю, мы будем проводить аналогии с материалом гл. 6. Содержание данной главы служит своего рода «естественным обобщением» результатов предыдущей главы, равно как содержание следующей главы обобщает то, что будет изложено в этой.
Представим теперь модель из гл. 6 в обозначениях данной главы. Напомним, что в гл. 6 относительно интересовавшей нас переменной X предполагалось, что она нормально распределена, т.е. X ~ N (М, S2). После замены X на Y, а М на А мы запишем модель в виде
Y ~ N (A, S2)
Перепишем это условие в эквивалентной и более простой форме:
(7.6) Y = А + U, U ~ N (O, S2)
Сравнив теперь (7.5) и (7.6), мы обнаружим, что последняя система условий является частным случаем первой: при подстановке В = 0 в (7.5) мы получим (7.6). Таким образом мы убеждаемся в том, что рассматриваемая в данной главе модель (7.5) служит «естественным обобщением» модели (7.6), которой по существу мы и занимались в гл. 6.
Представим далее в обозначениях гл. 7 табл. 6.1. В этой таблице, как вы помните, содержатся результаты случаев 2, 3 и 4 из гл. 6 для ситуации, в которой априорная информация игнорируется (в данной главе иная ситуация просто не рассматривается). Табл. 7.1 и есть преобразованная с учетом новых обозначений табл. 6.1. При этом произошла замена X на Y, М на А и некоторые другие небольшие изменения в обозначениях, что видно из самой таблицы.
Сопоставив табл. 6.1 и 7.1, вы легко убедитесь в том, что обе они на самом деле отражают одно и то же, но в различных обозначениях. Как будет показано в дальнейшем, результаты этой главы можно обобщить в таблице, полностью аналогичной табл. 7.1. Приступим теперь к нашему анализу и начнем со случая 2.
7.2. Вывод при неизвестных коэффициентах и известной дисперсии
В этом разделе мы рассмотрим случай вывода при неизвестных коэффициентах и известной заранее дисперсии. В соответствии с принятым нами соглашением параметры будем обозначать А и В, а дисперсию — через s2. Наша модель имеет вид (по сравнению с (7.5) произошло одно изменение S → s):
(7.7) Y = А + ВХ + U
U ~ N (О, s2)
Нас интересуют значения параметров А и В, а информация поступает к нам в форме пар наблюдений над значениями переменных X и Y. Поскольку мы хотим обеспечить информативность этих наблюдений в отношении А и В, мы должны, как и в гл. 5 и 6, получить эти наблюдения случайным (рандомизированным) образом или же, пользуясь терминологией двух предшествующих глав, обеспечить рандомизированную выборку из совокупности всех пар (X, Y). Вопрос о том, как получить подобную выборку (или о том, можно ли конкретную выборку рассматривать как полученную подобным образом), будет рассмотрен позже. В данный момент мы просто предположим, что наши наблюдения обладают необходимыми свойствами, т.е. выборка генерирована так, как это требуется. Пусть объем выборки равен n, а пары наблюдений мы обозначим следующим образом: (х1, у1); (х2, у2); …; (хn, уn).
Теперь, воспользовавшись теоремой Байеса, как мы делали это в гл. 5 и 6, можно вывести апостериорную оценку A и В при наличии некоторой априорной их оценки и множества полученных указанным выше образом наблюдений. Поскольку здесь участвуют два параметра, то и оценки, о которых идет речь, будут двумерными совместными оценками. Если отвлечься от некоторых технических сложностей, то рассматриваемая нами задача решается непосредственным применением теоремы Байеса. Однако мы не будем исследовать самый общий случай, что привело бы к громоздким выкладкам, и ограничимся случаем отсутствия априорной информации, который постараемся охарактеризовать в формальных терминах в точности так, как это было сделано в разделе 6.2. Отсутствие априорной информации о коэффициентах А и В можно выразить, предположив, что оба априорных маргинальных распределения, как для А, так и для В, являются нормальными и обладают бесконечной дисперсией. (По сути это означает, что функция плотности и для А, и для В равномерна от –∞ до +∞.) После того, как априорная оценка задана, апостериорная совместная оценка коэффициентов А и В выводится с помощью обычных преобразований. Детально вывод описан в приложении (в конспекте не приводится).
Ясно, что полученная таким образом апостериорная оценка будет иметь форму совместного распределения вероятностей для A и В, которое характеризуется совместной функцией плотности
fAB (а, b | ((х1, у1); (х2, у2); …; (хn, уn))
Тем самым совместная апостериорная оценка полностью специфицирована. Из разных ее характеристик, как правило, наибольший интерес представляют маргинальные распределения (для A и для В) в отдельности. Их можно получить из совместного распределения (см. раздел 3.3). Итак, мы приходим к важному результату.
Проиллюстрируем применение этого результата на простом примере. Как видно из (7.8), все, что необходимо сделать, это — воспользоваться наблюдениями для вычисления сначала ![]() и
и ![]() , а затем â,
, а затем â, ![]() , sA и sB. Эти величины используют для определения апостериорных (маргинальных) оценок для А и для В, из которых уже любая форма обобщающих утверждений может быть выведена обычным способом. Предположим, что мы располагаем рандомизированной выборкой из девяти наблюдений над (X, Y): (1, 6); (2, 9); (3, 12); (4, 15); (5, 12); (6, 18); (7, 18); (8, 21); (9, 24).
, sA и sB. Эти величины используют для определения апостериорных (маргинальных) оценок для А и для В, из которых уже любая форма обобщающих утверждений может быть выведена обычным способом. Предположим, что мы располагаем рандомизированной выборкой из девяти наблюдений над (X, Y): (1, 6); (2, 9); (3, 12); (4, 15); (5, 12); (6, 18); (7, 18); (8, 21); (9, 24).
Из табл. 7.2, содержащей все необходимые подготовительные вычисления, мы находим, что ![]() = 5, а
= 5, а ![]() = 15. Это позволяет преобразовать исходные данные наблюдений в отклонения от средних — столбцы Е и F табл. 7.2 (то, что сумма элементов в каждом из этих столбцов равна нулю, свидетельствует о безошибочности вычислений).
= 15. Это позволяет преобразовать исходные данные наблюдений в отклонения от средних — столбцы Е и F табл. 7.2 (то, что сумма элементов в каждом из этих столбцов равна нулю, свидетельствует о безошибочности вычислений).
Таблица 7.2. Последовательные вычисления для примера из раздела 7.2
Воспользуемся теперь соотношениями (7.9) и получим
и следовательно â = ![]() –
– ![]()
![]() = 15 – 2,05*5 = 4,75. Пусть теперь значение s (мы предполагаем его известным заранее) равно 1,5. Обратимся вновь к (7.9) и найдем:
= 15 – 2,05*5 = 4,75. Пусть теперь значение s (мы предполагаем его известным заранее) равно 1,5. Обратимся вновь к (7.9) и найдем:
(с точностью до третьего знака после запятой).
Если мы подставим найденные значения в (7.8), то придем к выводу, что при отсутствии априорной информации относительно А и В данные о девяти наблюдениях (приведенные выше) позволяют в качестве апостериорных оценок А и В выбрать такие распределения, что
Итак, апостериорные (маргинальные) оценки полностью определены. Если потребуется теперь рассчитать какие-либо соответствующие им обобщающие характеристики, то это можно осуществить обычным образом. Например, чтобы найти апостериорный 95-процентный вероятностный интервал для A и В, воспользуемся тем фактом, что для стандартного нормального распределения такой интервал определяется концевыми точками ± 1,96. Следовательно, для коэффициента А:
Итак, опираясь на девять приведенных выше наблюдений и на предположение об отсутствии априорной информации относительно коэффициентов А и В, мы можем сделать вывод, что с вероятностью 0,95 коэффициент A заключен между 2,61 и 6,89. Аналогично для коэффициента В
Р (1,67 ≤ В ≤ 2,43) = 0,95
Таким образом, коэффициент В с вероятностью 0,95 лежит между 1,67 и 2,43. Чтобы продемонстрировать возможности использования информации, заключенной в (7.10), предположим, что некто обратился к нам с просьбой оценить, насколько правдоподобно, что реальное значение В больше 2. Тогда нам придется рассчитать Р (В > 2). Это можно сделать, используя формулу в Excel =1-НОРМ.РАСП(2;2,05;0,194;ИСТИНА) = 0,6016
Приведенный пример показывает, что результат (7.8) можно применять непосредственно, и все приемы получения апостериорных оценок коэффициентов А и В хорошо нам знакомы. Единственное, что остается, — дать интерпретацию (7.8) на интуитивном уровне.
Рассмотрим вначале средние величины апостериорных оценок. Как следует из (7.8), обе величины (А – â)/sA и (В – ![]() )/sB удовлетворяют стандартному нормальному распределению, т.е. имеют нулевое значение средней; отсюда вытекает, что среднее значение коэффициента А равно â, а среднее значение коэффициента В равно
)/sB удовлетворяют стандартному нормальному распределению, т.е. имеют нулевое значение средней; отсюда вытекает, что среднее значение коэффициента А равно â, а среднее значение коэффициента В равно ![]() . Более того, поскольку стандартное нормальное распределение симметрично, то каждая из апостериорных оценок для А и для В тоже центрирована и симметрична (оценка коэффициента А — относительно â, а оценка коэффициента В — относительно
. Более того, поскольку стандартное нормальное распределение симметрично, то каждая из апостериорных оценок для А и для В тоже центрирована и симметрична (оценка коэффициента А — относительно â, а оценка коэффициента В — относительно ![]() ). Отсюда вытекает, что апостериорная оценка средней соотношения
). Отсюда вытекает, что апостериорная оценка средней соотношения
(7.11) Y = А + ВХ,
в свою очередь, центрирована и симметрична относительно своей средней
Возникает естественный вопрос: «Какой смысл имеют â и ![]() , а также со отношение Y = â +
, а также со отношение Y = â + ![]() Х?»
Х?»
Статистики а̂ и b̂ — выражения, полученные путем непосредственного применения теорема Байеса. Алгебраически â и ![]() задаются первыми двумя равенствами из (7.9). Однако ни один из этих факторов не поможет нам ответить на поставленный вопрос. Поэтому вернемся к иллюстративному примеру и изобразим на графике девять точек, соответствующих наблюдениям, и прямую Y = â +
задаются первыми двумя равенствами из (7.9). Однако ни один из этих факторов не поможет нам ответить на поставленный вопрос. Поэтому вернемся к иллюстративному примеру и изобразим на графике девять точек, соответствующих наблюдениям, и прямую Y = â + ![]() Х, рассчитанную на основе этих наблюдений (см. рис. 7.1).
Х, рассчитанную на основе этих наблюдений (см. рис. 7.1).
Рис. 7.1. Наблюдения и апостериорное среднее соотношение
Прямая Y = â + ![]() Х пересекает ось ординат в точке â = 4,75, и тангенс угла ее наклона к оси абсцисс есть
Х пересекает ось ординат в точке â = 4,75, и тангенс угла ее наклона к оси абсцисс есть ![]() = 2,05. Далее, поскольку â = ӯ –
= 2,05. Далее, поскольку â = ӯ – ![]()
![]() : (см. (7.9)), прямая Y = â +
: (см. (7.9)), прямая Y = â + ![]() Х проходит через точку средних значений для данных наблюдений, т.е. через точку (
Х проходит через точку средних значений для данных наблюдений, т.е. через точку (![]() , ӯ) (в нашем случае это точка (5,15)). Картина, изображенная на рис. 7.1, означает, что рассчитанное в соответствии с (7.9) соотношение (7.12) представляет собой прямую, которая действительно обеспечивает «подгонку» данных девяти наблюдений. Однако существует множество различных прямых линий, визуально примерно одинаково обеспечивающих «подгонку» наблюдений в указанном выше смысле. Чем же отличается полученная нами прямая от других? Быть может, ее особенность состоит в том, что она была «избрана» из более широкого множества благодаря теореме Байеса и представляет собой среднюю апостериорной оценки соотношения (7.7) при отсутствии априорной информации о значениях параметров?
, ӯ) (в нашем случае это точка (5,15)). Картина, изображенная на рис. 7.1, означает, что рассчитанное в соответствии с (7.9) соотношение (7.12) представляет собой прямую, которая действительно обеспечивает «подгонку» данных девяти наблюдений. Однако существует множество различных прямых линий, визуально примерно одинаково обеспечивающих «подгонку» наблюдений в указанном выше смысле. Чем же отличается полученная нами прямая от других? Быть может, ее особенность состоит в том, что она была «избрана» из более широкого множества благодаря теореме Байеса и представляет собой среднюю апостериорной оценки соотношения (7.7) при отсутствии априорной информации о значениях параметров?
Теперь мы можем ответить на этот вопрос. Выберем произвольно прямую линию Y = a + bХ и обозначим измеренное по вертикали отклонение от нее i-го наблюдения (хi, yi) через ei. Тогда
(7.13) ei = yi – a – bxi
В зависимости от значений а и b некоторые из ei могут оказаться положительными, а некоторые — отрицательными (не исключено и равенство отклонений нулю). По своему смыслу каждое еi указывает, как далеко отстоит конкретное наблюдение от данной линии. Сумма квадратов отклонений, рассчитанная по всем наблюдениям, служит агрегатной мерой того, как далеко отстоят наблюдения от рассчитанной линии.
Мы покажем ниже, что из всех возможных а и b значения â и ![]() , определяемые (7.9), таковы, что минимизируют сумму квадратов отклонений. Таким образом, линия Y = â +
, определяемые (7.9), таковы, что минимизируют сумму квадратов отклонений. Таким образом, линия Y = â + ![]() Х обеспечивает «наилучшую подгонку» наблюдений среди всех прямых линий в том смысле, что она минимизирует сумму квадратов отклонений наблюдений от прямой. Прежде чем продолжить обсуждение, убедимся в справедливости сформулированного утверждения.
Х обеспечивает «наилучшую подгонку» наблюдений среди всех прямых линий в том смысле, что она минимизирует сумму квадратов отклонений наблюдений от прямой. Прежде чем продолжить обсуждение, убедимся в справедливости сформулированного утверждения.
Рассмотрим задачу такого выбора а и b, при котором минимизируется сумма квадратов отклонений. Для ее решения нужно найти а и b, обеспечивающие минимальное значение выражения
Для этого придется приравнять нулю обе частные производные ∂D/∂a и ∂D/∂b. (Это хорошо известное условие, позволяющее находить минимальные и максимальные значения, если же вы не знакомы с ним, то примите окончательный результат на веру.) Несколько упреждая события, обозначим через а̂ и b̂ значения а и b, при которых ∂D/∂a = ∂D/∂b = 0. Из (7.14) получим
После упрощений это приводит к уравнениям
их можно решить относительно двух неизвестных â и ![]() . Из (7.15) после деления на n и перегруппировки получаем â = ȳ – b̂x̄, т.е. первое из уравнений (7.9). Воспользуемся этим уравнением и исключим â из (7.16), после чего разрешим полученное уравнение относительно
. Из (7.15) после деления на n и перегруппировки получаем â = ȳ – b̂x̄, т.е. первое из уравнений (7.9). Воспользуемся этим уравнением и исключим â из (7.16), после чего разрешим полученное уравнение относительно ![]() :
:
т.е. второе из уравнений (7.9). Таким образом, доказано утверждение, в силу которого прямая Y = â + ![]() Х обеспечивает «наилучшую подгонку» наблюдений в смысле минимизации суммы квадратов отклонений наблюдений от прямой линии. (Если вы вдруг усомнитесь в том, действительно ли мы обнаружили минимум, поскольку равенство частных производных нулю достигается и в точке максимума, то советуем вам обратить внимание на то, что максимуму соответствуют ситуации, когда либо а, либо b неограниченно возрастают по абсолютной величине.)
Х обеспечивает «наилучшую подгонку» наблюдений в смысле минимизации суммы квадратов отклонений наблюдений от прямой линии. (Если вы вдруг усомнитесь в том, действительно ли мы обнаружили минимум, поскольку равенство частных производных нулю достигается и в точке максимума, то советуем вам обратить внимание на то, что максимуму соответствуют ситуации, когда либо а, либо b неограниченно возрастают по абсолютной величине.)
Найденная прямая линия называется линией подгонки, полученной с помощью метода наименьших квадратов (иногда просто линией наименьших квадратов). После нескольких упражнений вы будете легко ориентироваться в процедуре ее построения. (Многие из современных электронных калькуляторов-рассчитают для вас значения â и ![]() после того, как вы введете в них значения наблюдений.)
после того, как вы введете в них значения наблюдений.)
Обобщим результаты обсуждения, накопившиеся к данному моменту: прямая Y = â + ![]() ̂Х, где â и
̂Х, где â и ![]() определяют из (7.9), является линией подгонки, полученной с помощью метода наименьших квадратов. Байесовская апостериорная оценка коэффициента А, постоянного свободного члена в соотношении (7.7), при отсутствии априорной информации о нем центрирована относительно â — свободного члена в уравнении прямой, найденной в результате подгонки наблюдений с помощью метода наименьших квадратов. Также байесовская апостериорная оценка коэффициента В, тангенса угла наклона для уравнения (7.7), при отсутствии априорной информации о нем центрирована относительно
определяют из (7.9), является линией подгонки, полученной с помощью метода наименьших квадратов. Байесовская апостериорная оценка коэффициента А, постоянного свободного члена в соотношении (7.7), при отсутствии априорной информации о нем центрирована относительно â — свободного члена в уравнении прямой, найденной в результате подгонки наблюдений с помощью метода наименьших квадратов. Также байесовская апостериорная оценка коэффициента В, тангенса угла наклона для уравнения (7.7), при отсутствии априорной информации о нем центрирована относительно ![]() — тангенса угла наклона в уравнении той же прямой. Однако важно представлять себе, что все это — результат непосредственного применения теоремы Байеса, а не проявления «магических» свойств метода наименьших квадратов. Итак, во-первых, â и
— тангенса угла наклона в уравнении той же прямой. Однако важно представлять себе, что все это — результат непосредственного применения теоремы Байеса, а не проявления «магических» свойств метода наименьших квадратов. Итак, во-первых, â и ![]() являются апостериорными средними оценок коэффициентов А и В соответственно; во-вторых, а̂ и b̂ — коэффициенты (свободный член и тангенс угла наклона к оси абсцисс) прямой, полученной при подгонке методом наименьших квадратов.
являются апостериорными средними оценок коэффициентов А и В соответственно; во-вторых, а̂ и b̂ — коэффициенты (свободный член и тангенс угла наклона к оси абсцисс) прямой, полученной при подгонке методом наименьших квадратов.
Перейдем теперь к характеристикам, связанным с дисперсией апостериорных оценок коэффициентов А и В. Из (7.8) следует, что апостериорное стандартное отклонение для А есть sА, а апостериорное стандартное отклонение для В есть sВ, где sA и sB определены в (7.9). Апостериорные α-процентные вероятностные интервалы для А и В задаются (в соответствии с (7.8)) в виде
соответственно, где zβ находят из условия Р (Z ≤ zβ) = β/100, a Z ~ N (0, 1). Отсюда следует, что длина каждого из этих интервалов прямо пропорциональна величине соответствующего апостериорного стандартного отклонения (sA и sB). В свою очередь, точность апостериорных оценок также определяется значениями sA и sB соответственно. Выражения для sA и sB приведены в (7.9), они получены непосредственным применением теоремы Байеса. Приведем некоторые интуитивные соображения, касающиеся величин sA и sB. Начнем с последней из них.
Из (7.9) нам известно, что sB — апостериорное стандартное отклонение коэффициента В — задается в виде
Преобразуем это выражение и введем с этой целью sx — выборочное стандартное отклонение переменной X:
С помощью (7.18) можно (7.17) записать в виде
В соответствии с этим выражением апостериорное стандартное отклонение коэффициента В прямо пропорционально зависит от s (стандартного отклонения переменной U), обратно пропорционально зависит, во-первых, от sX (выборочного стандартного отклонения переменной X) и, во-вторых, от квадратного корня из объема выборки n. В чем же содержательный смысл трех перечисленных свойств?
Обратимся к рис. 7.2, позволяющему провести попарные сопоставления, причем каждая из трех пар иллюстрирует связь между величиной sB и конкретным свойством диаграммы рассеяния. Прямая, обеспечивающая подгонку эмпирических данных и полученная методом наименьших квадратов, одна и та же на каждом из шести графиков (нас интересуют факторы, влияющие на дисперсию оценок, а не на их средние величины). Зададим себе по поводу каждой из трех пар вопрос: «В каком из двух случаев моя апостериорная оценка коэффициента В, характеризующего тангенс угла наклона прямой к оси абсцисс, заслуживает большего доверия?».
Рис. 7.2. Три парных сравнения (интерпретация трех свойств стандартного отклонения апостериорной оценки коэффициента В)
Начнем с пары, изображенной на рис. 7.2 (а): число наблюдений (n) одинаково для обоих случаев, как и разброс по оси X (т.е. sX); единственное различие заключено в характеристиках разброса вдоль вертикальной оси (s). Для правой диаграммы рассеяния величина s ощутимо больше, чем для левой. Теперь, скорее всего, в ответ на поставленный выше вопрос вы скажите: «Я буду больше доверять моей апостериорной оценке коэффициента В в случае, которому соответствует левая диаграмма». Таким образом мы проиллюстрировали тот факт, что с увеличением s увеличивается также SB — разброс апостериорной оценки коэффициента В, и получили интуитивную интерпретацию первого из трех свойств, выведенных из (7.19).
Перейдем теперь к рис. 7.2 (б): для этой пары число наблюдений (n) одинаково, разброс вдоль оси ординат (s) одинаков; единственное различие состоит в величинах sX, характеризующих разброс вдоль оси X. Для левой диаграммы разброс sX заметно больше, чем для правой. В этом случае на поставленный выше вопрос естественно получить такой ответ: «Я буду больше доверять моей апостериорной оценке коэффициента В в случае, которому соответствует левая диаграмма». Таким образом проиллюстрировано второе из свойств, выведенных из (7.19): с увеличением sХ значение SB — разброса апостериорной оценки коэффициента В — уменьшается.
Наконец рассмотрим последнюю пару, изображенную на рис. 7.2 (в): разброс в направлении вертикальной оси одинаков (s), равно как и разброс в горизонтальном направлении (sХ); единственное различие — число наблюдений (n). Для левой диаграммы n больше, чем для правой. Скорее всего, ваш ответ на поставленный выше вопрос в данном случае должен звучать так: «Я с большим доверием отнесусь к своей апостериорной оценке коэффициента В, полученной для левой диаграммы». Это означает, что с ростом n величина SB — разброс апостериорной оценки коэффициента В — уменьшается. Тем самым интуитивно проинтерпретировано и третье из свойств, выведенных из (7.19). Таким образом, каждый из факторов, определяющих точность апостериорной оценки коэффициента В, содержательно осмыслен.
Аналогичную интерпретацию можно дать результатам, относящимся к величине SA, однако основную часть рассуждений мы оставим читателю. Выражение для SA содержится в (7.9):
Воспользуемся (7.18) для sХ и заметим, что можно записать как n(sX2 + ![]() 2) (см. упражнение 7.5). Тогда для SA получим более «компактное» выражение
2) (см. упражнение 7.5). Тогда для SA получим более «компактное» выражение
Величина sA — апостериорное стандартное отклонение коэффициента А — зависит прямо пропорционально от s (стандартного отклонения переменной U) и обратно пропорционально квадратному корню из объема выборки n. Величина sA, кроме того, зависит обратно пропорционально от sX (выборочного стандартного отклонения переменной X) и прямо пропорционально величине ![]() (выборочной средней переменной X). Интуитивно приемлемая интерпретация каждого из первых трех свойств в точности такая же, что была дана выше для sB, и проиллюстрирована рис. 7.2. Однако четвертое свойство несколько отлично от остальных. Оставляем читателю возможность самостоятельно предложить содержательную и интуитивно приемлемую интерпретацию этого свойства (см. упражнение 7.4).
(выборочной средней переменной X). Интуитивно приемлемая интерпретация каждого из первых трех свойств в точности такая же, что была дана выше для sB, и проиллюстрирована рис. 7.2. Однако четвертое свойство несколько отлично от остальных. Оставляем читателю возможность самостоятельно предложить содержательную и интуитивно приемлемую интерпретацию этого свойства (см. упражнение 7.4).
Обобщим сказанное: стандартные отклонения sA и sB апостериорных оценок коэффициентов А и В (при отсутствии априорной информации) определены в (7.9). Как было сейчас показано, и sA, и sB будут тем меньше, чем меньше s (стандартное отклонение переменной U), чем больше sX (выборочное стандартное отклонение переменной X) и чем больше n (объем выборки); кроме того, sA будет тем меньше, чем меньше ![]() (выборочная средняя переменной X). Каждое из этих свойств хорошо интерпретируется на содержательном уровне.
(выборочная средняя переменной X). Каждое из этих свойств хорошо интерпретируется на содержательном уровне.
Смысл основного результата (7.8) раскрыт теперь достаточно подробно в отношении средних и стандартных отклонений апостериорных оценок коэффициентов. Осталось лишь упомянуть о форме распределения этих оценок. Из (7.8) известно, что апостериорная оценка каждого из коэффициентов нормально распределена. Это вытекает из предположения о нормальном. Мы получили полную аналогию с результатом для случая 2 из гл. 6.
На этом мы пока завершим изучение случая 2. Ключевой результат (7.8), определивший апостериорные оценки неизвестных коэффициентов A и В (в соотношении Y = А + ВХ + U), базируется на выборке из n наблюдений и на предположении об отсутствии априорной информации о значениях коэффициентов. Чтобы воспользоваться этим ключевым результатом, нужно просто рассчитать значения â и ![]() (это параметры прямой, полученной при подгонке наблюдений методом наименьших квадратов) и значения sA и SB (стандартные отклонения апостериорных оценок коэффициентов А и В). Эти значения подставляют затем в (7.8) и находят таким образом полную характеристику апостериорных оценок коэффициентов А и В.
(это параметры прямой, полученной при подгонке наблюдений методом наименьших квадратов) и значения sA и SB (стандартные отклонения апостериорных оценок коэффициентов А и В). Эти значения подставляют затем в (7.8) и находят таким образом полную характеристику апостериорных оценок коэффициентов А и В.
В данном разделе предполагалось, что значение s2 — дисперсия переменной U — известно. На практике подобный случай, как правило, не встречается. Поэтому мы приступим теперь к рассмотрению ситуации, когда величина S2 неизвестна. Раздел 7.3 мы начнем с простой задачи вывода относительно S2 при известных а и b, чтобы затем перейти к изучению более общего случая — статистического вывода относительно трех неизвестных параметров А, В и S2. Этому случаю посвящен раздел 7.4.
7.3. Вывод при известных коэффициентах и неизвестной дисперсии
В настоящем разделе мы рассмотрим случай статистического вывода при известных коэффициентах и неизвестной дисперсии. Будем по-прежнему обозначать известные коэффициенты буквами а и b, а неизвестную дисперсию через S2. Тогда наша модель (ср. с (7.5)) примет вид:
(7.21) Y = а + bХ + U,
U ~ N (0, S2).
Нам необходимо, пользуясь информацией в виде пар наблюдений над X и Y, составить определенное представление о параметре S. Мы уже знакомились с этой задачей в гл. 6 (случай 3). Действительно, поскольку а и b известны, а из (7.21) следует, что (известная) переменная величина (Y – а – bХ), представляющая собой линейную комбинацию данных наблюдений с фиксированными и известными параметрами, нормально распределена на некоторой совокупности, для которой средняя равна 0, а дисперсия S2 неизвестна. Следовательно, результат, полученный в разделе 6.3, можно непосредственно применить. Нужно только заменить в утверждении из гл. 6 переменную X переменной (Y – а – bХ) и учесть, что известное значение средней n равно 0. После n наблюдений над X и Y мы имеем n значений новой переменной: y1 – а – bх1, y2 – а – bх2, …, yn – а – bхn. Эти значения можно прямо использовать в (6.34) или (6.44). Поскольку в данной главе мы ограничиваемся рассмотрением случая, когда априорная информация отсутствует, можно воспользоваться результатом (6.44). Сформулируем его в терминах данной главы.
Выражению (6.33) также будет соответствовать свой аналог:
Установив соответствие между рассматриваемым случаем и случаем 3 из гл. 6, мы может на этом не останавливаться подробно. Все изложенное в разделе 6.3 справедливо и для ситуации из раздела 7.3. Однако лучше всего проиллюстрировать сказанное на конкретном примере. Возьмем пример из раздела 7.2, но только предположим, что параметры а и b известны, а информацией, заключенной в наблюдениях, воспользуемся, чтобы оценить неизвестную величину S2.
Пусть нам известно, что а = 5 и b = 2. Приведем еще раз наши девять наблюдений над переменными X и Y: (1, 6) (2, 9) (3, 12) (4, 15) (5, 12) (6, 18) (7, 18) (8, 21) (9, 24).
На графике рис. 7.3 нанесены точки, соответствующие девяти наблюдениям, и изображено подогнанное к ним соотношение Y = а + bХ, которое при данных а и b принимает вид Y = 5 + 2Х. Теперь воспользуемся ключевым для рассматриваемого случая результатом (7.22). Для этого нужно рассчитать ![]() 2. Но из (7.23) вытекает, что сначала придется составить множество значений yi – а – bxi при i = 1, 2, …, n. Выражение yi – а – bxi есть величина вертикального отклонения точки, соответствующей наблюдению (хi, yi), от рассматриваемой пря мой Y = 5 + 2X; это отклонение положительно, если точка, соответствующая наблюдению, находится выше прямой, и отрицательно, если эта точка находится ниже прямой (когда точка попадает на прямую, то отклонение, естественно, равно нулю).
2. Но из (7.23) вытекает, что сначала придется составить множество значений yi – а – bxi при i = 1, 2, …, n. Выражение yi – а – bxi есть величина вертикального отклонения точки, соответствующей наблюдению (хi, yi), от рассматриваемой пря мой Y = 5 + 2X; это отклонение положительно, если точка, соответствующая наблюдению, находится выше прямой, и отрицательно, если эта точка находится ниже прямой (когда точка попадает на прямую, то отклонение, естественно, равно нулю).
Рис. 7.3. Наблюдения и линейное соотношение с известными коэффициентами
На рис. 7.2 изображены точки, соответствующие i = 4 и i = 5. После подстановки значений (xi, уi) в выражение yi – 5 – 2xi получим девять отклонений: –1 0 +1 +2 –3 +1 –1 0 +1. Чтобы рассчитать s̃2, возведем величину каждого отклонения в квадрат, просуммируем полученные квадраты и разделим результат на 9. Получим, ![]() 2 =2. Если мы подставим теперь это значение
2 =2. Если мы подставим теперь это значение ![]() 2 в (7.22), то обнаружим, что апостериорная оценка S2 (дисперсии переменной U) при отсутствии априорной информации и с учетом девяти наблюдений будет такой, что 18/S2 удовлетворяет распределению хи-квадрат с девятью степенями свободы (обозначают χ2 (9)). Тем самым апостериорная оценка полностью определена. Различные обобщающие характеристики можно найти посредством обычных процедур. Например, 95-процентный вероятностный интервал для S можно найти, исходя из того, что переменная, удовлетворяющая распределению хи-квадрат с 9 степенями свободы с вероятностью 0,95, лежит между =ХИ2.ОБР(0,025;9) = 2,70 и =ХИ2.ОБР(0,975;9) = 19,02. Следовательно Р (2,70 ≤ 18/S2 ≤ 19,02) = 0,95 или Р (0,98 < S < 2,58) = 0,95. Таким образом, мы можем на 95% быть уверены, что стандартное отклонение переменной U лежит между 0,98 и 2,58. А теперь ответим на вопрос: насколько правдоподобно, что стандартное отклонение переменной U меньше 2,1? Нам придется просто рассчитать Р (S < 2,1), воспользовавшись тем, что 18/S2 ~ χ2 (9): =1-ХИ2.РАСП(18/2,1^2;9; ИСТИНА) = 0,906. Таким образом, имеется менее 1 шанса из 10, что значение S в нашем случае превзойдет 2,1.
2 в (7.22), то обнаружим, что апостериорная оценка S2 (дисперсии переменной U) при отсутствии априорной информации и с учетом девяти наблюдений будет такой, что 18/S2 удовлетворяет распределению хи-квадрат с девятью степенями свободы (обозначают χ2 (9)). Тем самым апостериорная оценка полностью определена. Различные обобщающие характеристики можно найти посредством обычных процедур. Например, 95-процентный вероятностный интервал для S можно найти, исходя из того, что переменная, удовлетворяющая распределению хи-квадрат с 9 степенями свободы с вероятностью 0,95, лежит между =ХИ2.ОБР(0,025;9) = 2,70 и =ХИ2.ОБР(0,975;9) = 19,02. Следовательно Р (2,70 ≤ 18/S2 ≤ 19,02) = 0,95 или Р (0,98 < S < 2,58) = 0,95. Таким образом, мы можем на 95% быть уверены, что стандартное отклонение переменной U лежит между 0,98 и 2,58. А теперь ответим на вопрос: насколько правдоподобно, что стандартное отклонение переменной U меньше 2,1? Нам придется просто рассчитать Р (S < 2,1), воспользовавшись тем, что 18/S2 ~ χ2 (9): =1-ХИ2.РАСП(18/2,1^2;9; ИСТИНА) = 0,906. Таким образом, имеется менее 1 шанса из 10, что значение S в нашем случае превзойдет 2,1.
Рассмотрение случая 3 на этом завершено. Как мы видели, с точностью до обозначений этот случай совпал со случаем 3 из гл. 6. Таким образом, все выводы раздела 6.3 оказались применимыми в рассматриваемой здесь ситуации. Дополнительно ничего не потребовалось. Перейдем теперь к случаю 4 — наиболее общему случаю в данной главе.
7.4. Вывод при неизвестных коэффициентах и неизвестной дисперсии
В этом разделе мы рассмотрим наиболее общий случай из всех, имеющих отношение к данной главе, а именно случай, когда все три параметра (два коэффициента и дисперсия) неизвестны. Модель будет иметь вид:
(7.24) Y = А + ВХ + U
U ~ N (0, S2)
Как и в двух предыдущих разделах, мы сосредоточим внимание на ситуации, когда отсутствует априорная информация об интересующих нас параметрах. Для характеристики этой ситуации мы обратимся к приему, которым пользовались в случае 4 из гл. 6 (см. раздел 6.4). Технические детали читатель найдет в приложении 4 (здесь не приводится). Как и в двух предыдущих разделах, мы будем считать, что информация поступает в форме рандомизированной выборки наблюдений (х1, у1); (х2, у2); …; (хn, уn) над (X, Y).
Нас интересует апостериорная совместная оценка трех неизвестных параметров А, В и S, опирающаяся на выборку из n наблюдений и полученная в предположении, что априорная информация об этих параметрах отсутствует. Мы вновь прибегнем к непосредственному применению теоремы Байеса. Чтобы не акцентировать внимание на сложных алгебраических преобразованиях, мы перенесли детальные выводы, касающиеся свойств апостериорной совместной оценки, в приложение. Здесь остановимся лишь на маргинальных распределениях этой совместной оценки, т.е. апостериорных маргинальных оценках параметров А, В и S. Ключевой результат, полученный в приложении, выглядит следующим образом.
Приведенные результаты не столь громоздки, как это может показаться на первый взгляд. Начнем с утверждения (7.25) об апостериорных оценках коэффициентов А и В и сравним его с утверждением (7.8) для соответствующих оценок в случае 2. Полезно заметить, что апостериорные оценки коэффициентов А и В остаются центрированными и симметричными относительно â и ![]() соответственно (как это имело место для первых двух выражений в (7.9) и, конечно же, справедливо для совпадающих с ними первых двух выражений в (7.27)). Итак, апостериорные оценки остаются центрированными относительно коэффициентов прямой, полученной при подгонке данных наблюдений с помощью метода наименьших квадратов. Далее, из (7.25) следует, что апостериорные α-процентные вероятностные интервалы для коэффициентов А и В определены соответственно как
соответственно (как это имело место для первых двух выражений в (7.9) и, конечно же, справедливо для совпадающих с ними первых двух выражений в (7.27)). Итак, апостериорные оценки остаются центрированными относительно коэффициентов прямой, полученной при подгонке данных наблюдений с помощью метода наименьших квадратов. Далее, из (7.25) следует, что апостериорные α-процентные вероятностные интервалы для коэффициентов А и В определены соответственно как
здесь tk,β определяется из условия Р (Tk ≤ tk,β) β/100, где Тk удовлетворяет t-распределению с k степенями свободы. Итак, длины апостериорных вероятностных интервалов для каждого из коэффициентов А и В пропорциональны ŝA и ŝB соответственно. В случае 2, когда значение S2 было известно, длины этих апостериорных вероятностных интервалов были пропорциональны sA и sB. Сравним теперь каждую из пар: sA и ŝA, sB и ŝB в соответствии с тем, как определяются эти величины соотношениями (7.9) и (7.27). Мы видим, что единственное различие состоит в участии s в выражениях для sA и sB, в то время как в выражениях для ŝA и ŝB участвует ŝ. (Этим объясняется необходимость использования различных обозначений.) В случае 4, которому посвящен данный раздел, значение s, конечно, неизвестно, и потому им невозможно воспользоваться в процессе вывода. Можно, правда, считать величину ŝ оценкой для s, так что ŝA и ŝB окажутся оценками sA и sB (ведь различие между соответственными элементами первой и второй пар состоит в употреблении в первом случае ŝ, а во втором s). Во всем остальном, однако, выражения для ŝA и sA, как и выражения для ŝB и sB, совпадают. Таким образом, наши интуитивные представления о факторах, определяющих sA и sB (и, следовательно, дисперсии апостериорных оценок коэффициентов А и В в случае 2), справедливы в отношении факторов, определяющих ŝA и ŝB (и, следовательно, дисперсии апостериорных оценок коэффициентов А и В в случае 4).
Обсудим теперь результат (7.26) для апостериорной оценки параметра S в случае 4 и сравним ее с аналогичной оценкой (7.22) в случае 3. В (7.26) утверждается, что величина (n – 2)ŝ2/S2 удовлетворяет распределению хи-квадрат, в то время как в (7.22) говорилось, что распределению хи-квадрат удовлетворяет величина n![]() 2/S2. Различие между этими величинами состоит, во-первых, в том, что в знаменателе выражения для ŝ2 стоит , в то время как в знаменателе для
2/S2. Различие между этими величинами состоит, во-первых, в том, что в знаменателе выражения для ŝ2 стоит , в то время как в знаменателе для ![]() 2 стоит , поскольку а и b предполагались известными в случае 3, а в случае 4 они неизвестны и потому заменены их оценками â и
2 стоит , поскольку а и b предполагались известными в случае 3, а в случае 4 они неизвестны и потому заменены их оценками â и ![]() . Во-вторых, сопоставляемые величины отличаются коэффициентами, характеризующими число степеней свободы: в (7.26) их n – 2, а в (7.22) было n. Мы обсудим причины, вызвавшие подобное расхождение, ниже, а пока попытайтесь сделать это самостоятельно. (Вернитесь к табл. 6.1 или «эквивалентной» ей табл. 7.1; возможно, это поможет вам найти правильный ответ. Обратите внимание, что число степеней свободы в оценке параметра S2 изменилось с n в случае 3 на n – 1 в случае 4.)
. Во-вторых, сопоставляемые величины отличаются коэффициентами, характеризующими число степеней свободы: в (7.26) их n – 2, а в (7.22) было n. Мы обсудим причины, вызвавшие подобное расхождение, ниже, а пока попытайтесь сделать это самостоятельно. (Вернитесь к табл. 6.1 или «эквивалентной» ей табл. 7.1; возможно, это поможет вам найти правильный ответ. Обратите внимание, что число степеней свободы в оценке параметра S2 изменилось с n в случае 3 на n – 1 в случае 4.)
Прежде чем продолжать разговор об общем содержании утверждений (7.25) и (7.25), приведем числовой пример. Вернемся к примеру из раздела 7.2, но предположим теперь, что параметры А, В и S неизвестны. Вновь выпишем данные о девяти наблюдениях: (1, 6) (2, 9) (3, 12) (4,15) (5, 12) (6, 18) (7, 18) (8, 21) (9, 24).
Как мы договорились, в данной главе будем исходить из отсутствия априорной информации о значениях интересующих нас параметров A, В И S. Тогда можно воспользоваться результатами (7.25) и (7.26), проведя все необходимые выкладки по формулам (7.27). Некоторые вычисления мы уже осуществили в разделе 7.2. В частности, мы знаем, что
Теперь основная задача — рассчитать ŝ. Для этого нужно найти значения yi – â – bxi, равные вертикальным отклонениям точек, соответствующих наблюдениям, от прямой, полученной в результате подгонки этих наблюдений с помощью метода наименьших квадратов. Проведем необходимые арифметические операции и получим следующие значения отклонений (они расположены в порядке возрастания i):
(7.28) –0,80 0,15 1,10 2,05 –3,00 0,95 –1,10 –0,15 0,80
Возведем каждое из отклонений в квадрат, просуммируем их и разделим полученную сумму на 7 (т.е. на n – 2); ŝ2 = 2,55, т.е. ŝ = 1,597. Подставим это значение наряду с найденными ранее в (7.27) и установим значения оставшихся выражений: ŝA = 1,160, ŝB = 0,206. Наконец, подставим все эти выражения в (7.25) и в (7.26) и получим соответствующие примеру апостериорные оценки:
Распределение каждой оценки полностью определено. Обобщающие характеристики могут быть найдены с помощью обычных процедур. Например, как вы можете убедиться самостоятельно (см. упражнение 7.6), апостериорные 95-процентные вероятностные интервалы для А, В и S равны соответственно (с точностью до второго десятичного знака): (2,01; 7,49) (1,56; 2,54) (1,06; 3,25).
В качестве дополнительного примера рассмотрим задачу определения (апостериорной) вероятности того, что коэффициент А положителен. Чтобы решить ее, используем формулу
=1-СТЬЮДЕНТ.РАСП(-4,75/1,16;7;ИСТИНА) = 0,9977. Т.е., с вероятностью 99, 77% можно утверждать, что А > 0. Аналогично Р (В > 0) =1-СТЬЮДЕНТ.РАСП(-2,05/0,206;7;ИСТИНА) = 0,99999. Таким образом, почти наверняка оба коэффициента А и В положительны.
В дальнейшем некоторые из реализованных здесь процедур будут обобщены, а сейчас рассмотрим два свойства прямой, полученной при подгонке методом наименьших квадратов, на которые до этого мы не обращали внимание. Оба эти свойства касаются (вертикальных) отклонений наблюдений от линии подгонки. Для нашего числового примера величины отклонений приведены в (7.28). Достаточно очевидное свойство состоит в том, что сумма всех вертикальных отклонений равна нулю. Является ли это свойство общим? Другими словами, если через ûi обозначить вертикальное отклонение i-го наблюдения от линии подгонки, найденной методом наименьших квадратов, т.е.
Еще одно, но уже не очевидное свойство величин ûi можно следующим образом продемонстрировать на числовом примере. Возьмем значения ûi из (7.28) и умножим каждое на соответствующее ему значение xi. Получим следующий «набор» величин ûixi: –0,80 0,30 3,30 8,20
–15,00 5,70 –7,70 –1,20 7,20. Просуммируем эти числа. Итогом будет нуль. И вновь это общий результат, который можно установить с помощью несложных выкладок. Из (7.29)
Последнее выражение в наших преобразованиях равно нулю в силу (7.16), т.е. в силу того, что коэффициенты а̂ и b̂ найдены методом наименьших квадратов:
Читателю полезно подумать об интерпретации этого свойства. Из (7.25) и (7.26) следует, что апостериорные оценки параметров A, В и S зависят от â, ![]() , ŝA, ŝB, ŝ и n. Мы достаточно подготовлены теперь, чтобы ввести ряд важных понятий, относящихся к этим рассчитанным на основе выборки величинам. Первые нам хорошо знакомы —это коэффициенты прямой, найденной методом наименьших квадратов и обеспечивающей подгонку данных, полученных при наблюдениях. Для краткости мы будем называть их коэффициентами наименьших квадратов. Следующая пара, ŝA и ŝВ, определяет величину апостериорных вероятностных интервалов для коэффициентов А и В. Для удобства мы последуем традиции классического подхода и будем называть ŝA и ŝB стандартными ошибками (коэффициентов) А и В. (Мы не придаем этому термину большого значения, не считая его ни эталонным, ни ошибочным, а ограничимся указанием на то, что он общеупотребителен при описании результатов статистического анализа.) Выражение для ŝ2 почти совпадает с выражением для дисперсии величин ûi (отклонений наблюдений от линии, полученной методом наименьших квадратов), различие состоит в появлении в знаменателе числа n – 2 вместо n. Поэтому мы будем называть ŝ2 модифицированной дисперсией остатков, a ŝ модифицированным стандартным отклонением остатков. Нередко можно встретить упоминание об ŝ как о стандартной ошибке регрессии — мы вновь не будем придавать большого значения тому, следует ли употреблять этот термин.
, ŝA, ŝB, ŝ и n. Мы достаточно подготовлены теперь, чтобы ввести ряд важных понятий, относящихся к этим рассчитанным на основе выборки величинам. Первые нам хорошо знакомы —это коэффициенты прямой, найденной методом наименьших квадратов и обеспечивающей подгонку данных, полученных при наблюдениях. Для краткости мы будем называть их коэффициентами наименьших квадратов. Следующая пара, ŝA и ŝВ, определяет величину апостериорных вероятностных интервалов для коэффициентов А и В. Для удобства мы последуем традиции классического подхода и будем называть ŝA и ŝB стандартными ошибками (коэффициентов) А и В. (Мы не придаем этому термину большого значения, не считая его ни эталонным, ни ошибочным, а ограничимся указанием на то, что он общеупотребителен при описании результатов статистического анализа.) Выражение для ŝ2 почти совпадает с выражением для дисперсии величин ûi (отклонений наблюдений от линии, полученной методом наименьших квадратов), различие состоит в появлении в знаменателе числа n – 2 вместо n. Поэтому мы будем называть ŝ2 модифицированной дисперсией остатков, a ŝ модифицированным стандартным отклонением остатков. Нередко можно встретить упоминание об ŝ как о стандартной ошибке регрессии — мы вновь не будем придавать большого значения тому, следует ли употреблять этот термин.
Чтобы воспользоваться основными утверждениями данного раздела, т.е. утверждениями (7.25) и (7.26), необходимо рассчитать значения выражений, содержащихся в (7.27), а именно коэффициенты наименьших квадратов, стандартные ошибки для А и В и модифицированное стандартное отклонение остатков. Эти вычисления можно провести с помощью Пакета анализа Excel (см., например, Простая линейная регрессия)
Остается подставить полученные значения в (7.25) и (7.26), что даст возможность определить апостериорные оценки, основанные на предположении об отсутствии априорной информации о параметрах А, В и S. Зная эти апостериорные оценки, нетрудно посредством стандартных процедур рассчитать различные обобщающие характеристики соответствующих распределений. Однако существуют альтернативные способы представления результатов «регрессионного анализа» (эти способы чаще применяют статистики классической школы), и весьма важно свободно ими владеть, чтобы адекватно воспринимать и интерпретировать содержащуюся в соответствующих работах информацию. Один из двух наиболее употребительных способов представления информации, полученной при регрессионном анализе, состоит в записи уравнения линии регрессии (полученной методом наименьших квадратов) с указанием в скобках под каждым из коэффициентов его стандартной ошибки. В общем виде это выглядит так:
Обычно приводят также число наблюдений, а иногда и значение ŝ. (Альтернативная статистика, R2, которая рассчитывается на базе ŝ, указывается значительно чаще; мы обсудим это в разделе 7.6.) Например, результаты анализа числового примера, рассмотренного в данном разделе, можно записать так:
Эта форма широко применяется, поскольку позволяет наглядно представить основные свойства, выявленные в ходе анализа. Она также удобна, если мы хотим получить выводы, сформулированные в (7.25) и (7.26), поскольку содержащуюся в (7.33) информацию можно сразу же преобразовать в утверждения байесовской статистики относительно апостериорных оценок, а именно записать, что обе величины (A – 4,75)/1,160 и (B – 2,05)/0,206 удовлетворяют t-распределению с 7 (= 9 – 2) степенями свободы, а величина 7*(1,597)2/S2 – распределению хи-квадрат также с 7 степенями свободы. Запись (7.33), очевидно, содержит всю необходимую информацию о регрессии.
Второй, столь же распространенный (альтернативный) способ представления результатов регрессионного анализа в основном идентичен (7.33). Различие в том, что вместо стандартных ошибок в скобках под каждым коэффициентом указывают соответствующее ему t-отношение. Мы обсудим этот способ в разделе 7.5 после того, как объясним, что такое t-отношение и какова его роль.
Мы завершаем данный раздел обобщающей таблицей, содержащей основные результаты данного и двух предшествующих разделов: в табл. 7.3 приводятся необходимые детали для расчета апостериорных оценок параметров A, В и/или S (в зависимости от контекста), когда априорная информация об оцениваемых параметрах отсутствует.
Таблица содержит практически все, что необходимо для анализа парной линейной регрессии с нормально распределенными остатками. Полезно тщательно изучить эту таблицу и, в частности, обратить внимание на то, что общего и что несхожего имеется в ней в сравнении с табл. 7.1.
Табл. 7.3. Статистический вывод для модели парной линейной регрессии с нормально распределенными остатками. Источники: для случая 2 – (7.8); для случая 3 – (7.22); для случая 4 – (7.25) и (7.26)
7.5. Доверительные интервалы и проверка значимости
В гл. 5 и 6 мы установили, что байесовский α-процентный вероятностный интервал для некоторого неизвестного параметра в предположении, что априорные сведения об этом параметре отсутствуют, алгебраически совпадает с классическим α-процентным доверительным интервалом для того же неизвестного параметра (при этом нужно иметь в виду, что интерпретации указанных интервалов существенно различны). Этим свойством мы воспользуемся при изложении материала данной главы. Чтобы избежать ненужных повторений, мы сосредоточим внимание на случае 4, поскольку и рассуждения, и проводимый ниже анализ в той же мере применимы к двум оставшимся случаям.
Из (7.25) следует, что α-процентные вероятностные интервалы для коэффициентов А и В, если априорная информация о них отсутствует, соответственно имеют вид:
где tk,β определяется из соотношения Р (Тk ≤ tk,β) = β/100, а Тk удовлетворяет t-распределению с k степенями свободы. Эти выражения в точности совпадают с выражениями для α-процентных доверительных интервалов коэффициентов A и В в классическом анализе. Аналогично из (7.26) следует, что α-процентный вероятностный интервал для параметра S (также при отсутствии о нем априорной информации) можно записать в виде
где yk,β определяется из условия Р (Yk ≤ yk,β) = β/100, a Yk удовлетворяет распределению хи-квадрат с k степенями свободы. Это выражение вновь алгебраически идентично записи классического α-процентного доверительного интервала, соответствующего параметру S. Можно с одинаковым успехом пользоваться как байесовским α-процентным вероятностным интервалом (полученным при условии отсутствия априорной информации об интересующем нас параметре), так и классическим α-процентным доверительным интервалом, учитывая только, что интерпретируются они по-разному.
Несколько сложнее дать байесовскую интерпретацию классической процедуры проверки гипотез, хотя, как мы видели в гл. 6, некоторый способ такой интерпретации вполне возможен. Вновь, чтобы избежать повторений, ограничимся случаем 4 и, в частности, проверкой гипотезы относительно коэффициента В (приводимые ниже рассуждения и анализ в равной мере применимы к другим параметрам и к другим случаям). Статистики классического направления чаще всего проверяют в отношении коэффициента В, имеющего определенное экономическое содержание, (нуль-) гипотезу Н0: В = 0 против альтернативной гипотезы Н1 : В > 0. Такая проверка представляется оправданной, если нужно убедиться в наличии (или отсутствии) эмпирического подтверждения теории, предсказывающей, что между переменными Y и X существует положительная связь. Например, это имеет место в случае теории агрегированного потребления, где Y — потребление, а X — доход. Наоборот, если проверяемая теория предсказывает отрицательную связь между Y и X, то гипотезу «Н1 : В > 0» придется заменить гипотезой «Н1: В < 0». В каждом случае «принятие» гипотезы Н1 означает «принятие» соответствующего теоретического положения.
В разделе 6.5 уже было показано, что базовая процедура классической статистики, состоящая в проверке гипотезы Н0 против гипотезы H1, представляет собой правило, позволяющее на основе выборочных данных определить, следует ли «принять» гипотезу Н0 (и «отвергнуть» H1) или «принять» Н1 (и «отвергнуть» Н0). Это правило (критерий) формулируется так, чтобы оставался достаточно малый шанс — меньший заранее определенного уровня в 5% или в 1% — «отвергнуть» гипотезу Н0, в то время как на самом деле она верна. Эта малая, заранее фиксированная вероятность называется уровнем значимости критерия.
Для проведения подобной проверки можно сформулировать критерий, указывающий на достижение α-процентного уровня значимости:
Если в результате проверки гипотеза Н1 принята (гипотеза Н0 отвергнута), то говорят, что критерий значим (при α-процентном уровне значимости); можно также сказать, что коэффициент ![]() значимо больше нуля (при α-процентном уровне значимости). Мы не намерены объяснять, почему в классической статистике утвердилась подобная процедура, эти объяснения имеются в любом курсе. Нас интересует лишь смысл, который эта процедура имеет с байесовской точки зрения.
значимо больше нуля (при α-процентном уровне значимости). Мы не намерены объяснять, почему в классической статистике утвердилась подобная процедура, эти объяснения имеются в любом курсе. Нас интересует лишь смысл, который эта процедура имеет с байесовской точки зрения.
Как было показано в разделе 6.5, способ придать рассматриваемой процедуре смысл в рамках байесовского подхода состоит в трактовке результата проверки как некоторого сообщения о Р (Н1 | наблюдения) — вероятности того, что гипотеза Н1 истинна в свете имеющихся наблюдений. (Для упрощения записи условие «| наблюдения» мы опускаем.) Итак,
Например, если критерий значим при 5-процентном уровне значимости, то мы можем заключить (при отсутствии априорной информации), что имеется более 95% шансов, что гипотеза Н1 окажется истинной.
С другой стороны, если критерий незначим при α-процентном уровне значимости, то Р (Н1) < (100 — α)/100. Мы приходим к выводу, что значимость или незначимость критерия содержит в себе некоторую информацию относительно Р (H1) ≡ Р (В > 0). (Полезно отметить, что результат проверки не дает сколько-нибудь существенной информации относительно Р (Н0) ≡ Р (В = 0), ибо эта вероятность непременно равна нулю, за исключением разве что совсем необычных обстоятельств.)
Обобщим сказанное: если статистик классической школы говорит, что «коэффициент b значимо отличается от нуля при α-процентном уровне значимости» (это является синонимом утверждения о значимости критерия или о том, что гипотеза Н0 отклонена в пользу гипотезы Н1,— все при α-процентном уровне значимости), то статистик байесовской школы может интерпретировать такое высказывание как свидетельство того, что апостериорная вероятность положительности параметра В (при отсутствии о нем априорной информации) не менее чем (100 – α)/100. Например, утверждение «коэффициент b значимо отличен от нуля при 1-процентном уровне значимости» означает, что Р (В > 0) не менее чем 0,99. Таким образом, утверждения о значимости равносильны ограничениям на некоторые вероятности.
В рамках байесовского подхода естественнее и проще вычислить Р (В > 0) непосредственно и затем уже пользоваться этой величиной. Так, если, например, Р (В > 0) = 0,98, то полезнее привести эту информацию в ее «первозданном» виде, нежели прибегать к окольным сравнениям сначала с величиной 0,95 («коэффициент b значимо отличен от нуля при 5-процентном уровне значимости»), а затем с величиной 0,99 («коэффициент b значимо отличается от нуля при 1-процентном уровне значимости»).
В классической статистике существует договоренность отмечать уровень значимости коэффициентов с помощью звездочек. Часто (но не всегда) одной звездочкой помечают коэффициент, значимый при 5-процентном уровне значимости, двумя звездочками – при 1-процентном и не ставят звездочек при остальных коэффициентах.
Из (7.36) следует, что ответ на вопрос, значим или незначим некоторый коэффициент, зависит от величины отношения ![]() /ŝB в сравнении с соответствующим (уровню значимости и числу степеней свободы) значением t-распределения, которое обозначают через tn–2,100–α. Поскольку это отношение играет в статистике очень важную роль, для него ввели специальный термин — его называют t-отношение для данного коэффициента. Будем обозначать t-отношение для коэффициента В через tB, а для коэффициента А — через tA, т. е.
/ŝB в сравнении с соответствующим (уровню значимости и числу степеней свободы) значением t-распределения, которое обозначают через tn–2,100–α. Поскольку это отношение играет в статистике очень важную роль, для него ввели специальный термин — его называют t-отношение для данного коэффициента. Будем обозначать t-отношение для коэффициента В через tB, а для коэффициента А — через tA, т. е.
В каждом случае t-отношение для данного коэффициента есть отношение значения самого коэффициента (найденного методом наименьших квадратов) к его стандартной ошибке. В конце предыдущего раздела мы отмечали, что при оформлении результатов регрессионного анализа часто приводят значения t-отношений (а не значения стандартных ошибок), указывая их в скобках под соответствующими коэффициентами. В соответствии с такой договоренностью результаты расчетов для примера из раздела 7.4 будут записаны (ср. с (7.33)) в виде
(в скобках указаны t-отношения). Обычно сопровождают запись результатов замечанием о том, какая величина содержится в скобках; иначе могут возникнуть недоразумения. Если n = 9, то соответствующие табличные значения t-распределения для проверки классического критерия (7.36) при 5-процентном и 1-процентном уровнях значимости равны =СТЬЮДЕНТ.ОБР(95%;9) = 1,895 и =СТЬЮДЕНТ.ОБР(99%;9) = 2,998 соответственно. Взглянув на (7.40), мы убеждаемся, что оба t-отношения превосходят эти значения, т.е. оба коэффициента а и b значимо отличаются от нуля при 1-процентном уровне значимости (и, конечно же, при 5-процентном тоже). В байесовской терминологии, как мы убедились выше, это означает, что и Р (А > 0), и Р (В > 0) превосходят 0,99. (Такой вывод подкреплен и прямыми вычислениями этих двух вероятностей, проведенными в разделе 7.4.)
Одно из преимуществ представления результатов регрессионного анализа в форме (7.40) — возможность сразу же рассчитать точные значения Р(A > 0) и Р (В > 0). Они равны для нашего примера Р (T7 < 4,09) и Р (Т7 < 9,94) соответственно. В общем случае эти вероятности определяют так:
7.5. Доверительные интервалы и проверка значимости
До сих пор в данной главе мы вели анализ в предположении, что потенциально неопределенными в модели являются только значения ее параметров А, В и S. В остальном форма модели была задана соотношениями (7.5) и потому предполагалась известной и определенной. В частности, мы предполагали определенно известным, какая переменная является (единственной) подходящей объясняющей переменной (в данном случае X), какими должны быть форма соотношения (линейной) и вид распределения остаточного члена U (нормальным). На практике могут встретиться случаи, когда некоторые, если не все, из перечисленных предположений не удается сделать с определенностью. Как же вести анализ в подобных обстоятельствах?
В принципе дополнительных концептуальных проблем здесь не возникает: мы просто перечисляем все возможные альтернативы, учитывая альтернативные объясняющие переменные и/или альтернативные формы функциональных связей, и/или альтернативные распределения остатков, и снабжаем каждую из них своей априорной вероятностью. Затем применяем теорему Байеса, чтобы получить соответственные апостериорные вероятности. Если не считать возможных технических осложнений, способ действий при появлении дополнительных неопределенностей хорошо нам знаком.
В данном разделе мы рассмотрим кратко процедуры, позволяющие преодолеть первую из трех дополнительных неопределенностей, а именно неопределенность, связанную с выбором подходящей объясняющей переменной. Вторая из дополнительных неопределенностей, а именно неопределенность в выборе подходящей функциональной формы связи между переменными, будет проанализирована в гл. 8. Изучение альтернатив, связанных с третьей из них — с неопределенностью вида распределения остаточного члена U, выходит за рамки этой книги.
Рассмотрим ситуацию, когда нам известно, что значения переменной Y генерируются моделью, которая определена соотношениями (7.5), однако у нас нет уверенности в том, какая из двух потенциальных объясняющих переменных Х1 или Х2 в действительности объясняет поведение Y. Перед нами две «конкурирующие» модели, М1 и M2, определенные (ср. с. (7.5)) следующим образом:
С моделями М1 и М2 должны быть соотнесены некоторые априорные вероятности, скажем, Р (М1) и Р (M2). Они отражают чьи-то априорные ожидания о «солидности» каждой из двух конкурирующих гипотез. Если другие модели не рассматриваются, то вполне возможно, что Р(М1) + Р(М2) = 1, и по сути самой задачи обе величины Р (M1) и Р (М2) отличны от нуля. В остальном задача решается так же, как и другие в этой главе. (Предлагаемый ниже подход к ее решению допускает непосредственное обобщение на случай трех и более конкурирующих гипотетических моделей.)
Конкретизируем задачу: пусть две наши модели отражают альтернативные объяснения уровня инфляции (Y): M1 связана с монетаристским объяснением (Х1 — темп изменения спроса на деньги); М2 — соотношения типа кривой Филлипса (Х2 — уровень безработицы или какой-либо иной индикатор избыточного предложения рабочей силы).
В каждой из сравниваемых моделей какие-то (а возможно, и все) параметры Аi, Вi и Si могут быть неизвестными, а остальные (возможно, и все) — известными; другими словами, для каждой модели может иметь место один из четырех случаев, рассмотренных в предыдущих разделах данной главы. Анализируемые далее методы с одинаковым успехом применимы к любой из возможных ситуаций, однако, желая избежать ненужных повторений, мы ограничимся рассмотрением наиболее общего варианта, когда для каждой из моделей имеет место случай 4. Таким образом, все параметры A1, В1, S1, A2, В2 и S2 предполагаются неизвестными. Однако у нас могут быть некоторые предварительные представления об этих параметрах, и мы, как обычно, выразим их в форме априорного вероятностного распределения. Наиболее естественно воспользоваться двумя совместными распределениями, условными по отношению к выбору соответственной модели. Точнее, речь идет о совместном распределении параметров А1, В1 и S1 условии, что верна модель М1 и о совместном распределении параметров A2, В2 и S2 при условии, что верна модель М2. Обозначим соответственные функции плотности через
Каждую из этих условных функций плотности можно умножить на соответствующую маргинальную вероятность, т.е. первую на Р (M1), а вторую на Р (М2), и получить функции плотности совместных априорных распределений для модели и ее параметров:
При наличии данных о выборочных наблюдениях над переменными Y, Х1 и Х2 мы можем с помощью теоремы Байеса уже известным нам способом получить совместную апостериорную оценку для моделей и параметров. Эту совместную оценку можно представить в виде произведения (имеющего форму, сходную с (7.42)) функции плотности условного распределения для параметров при условии, что данная модель верна, и маргинальной вероятности того, что эта модель верна:
Среди получаемых при этом результатов один из наиболее интересных — апостериорные вероятности для двух моделей:
Сравнение этих апостериорных вероятностей с априорными, т.е. с Р (Mj), j = 1, 2, показывает, как данные о наблюдениях повлияли на представления об относительном правдоподобии конкурирующих моделей. В общем случае выражение (7.44) зависит от ряда факторов, в том числе от априорных оценок параметров в двух рассматриваемых моделях. Несмотря на концептуальную ясность, общее выражение (7.44) очень трудно получить, и алгебраически оно будет выглядеть довольно громоздким. Однако существует важный частный случай, хорошо согласующийся с интуитивными представлениями. Предположим, что мы априорно рассматриваем М1 и М2 как одинаково правдоподобные, так что Р (М1) = Р (М2) = 1/2. Пусть, кроме того, априорная информация обо всех параметрах Aj, Вj и Sj (j = 1, 2) отсутствует. Тогда можно показать, что отношение апостериорных вероятностей для моделей определяется соотношением
Здесь ŝ1 и ŝ2 — модифицированные стандартные отклонения остатков соответственно для регрессии Y на Х1 и регрессии Y на Х2, рассчитанных методом наименьших квадратов. Следовательно, при имеющих место обстоятельствах модель М1 представляется более правдоподобной по сравнению с моделью М2 в свете имеющихся наблюдений, когда s1 меньше s2, и, наоборот, модель М2 будет казаться более правдоподобной, чем модель М1 когда ŝ2 меньше ŝ1. Если априорно обе модели рассматривались как одинаково правдоподобные, то апостериорная оценка позволяет считать ту из них более правдоподобной, которой соответствует меньшее стандартное отклонение остатков. Это простой и интуитивно ясный вывод.
Когда априорные вероятности Р (М1) и Р (М2) не равны, правую часть соотношения (7.45) нужно домножить на отношение Р (М1) к Р (М2). Хотя величина ŝ (модифицированное стандартное отклонение остатков) играет важнейшую роль при оценивании и сравнении моделей, ее сравнительно редко указывают при оформлении результатов регрессионного анализа, особенно в классической статистике. Обычно приводят значение статистики R2, которая связана с ŝ следующим образом:
Член в правой части (7.46), вычитаемый из 1, содержит в числителе (немодифидированную) дисперсию остатков регрессии наименьших квадратов, а в знаменателе — дисперсию наблюдений над переменной Y; таким образом, этот член представляет собой часть дисперсии переменной Y, которая не объясняется регрессией. Следовательно, величина R2 измеряет долю дисперсии переменной Y, объясняемой данной регрессией. Величина R2 может изменяться от 0 (регрессия ничего не объясняет) до 1 (вся дисперсия переменной Y объясняется данной регрессией). Ясно, что мы располагаем индикатором того, насколько хорошо с помощью линии наименьших квадратов осуществляется подгонка наблюдений: R2 = 1 свидетельствует о совершенной подгонке (все наблюдения лежат на линии регрессии); R2 = 0 — об отсутствии какой бы то ни было подгонки (линия регрессии горизонтальна); значения R2, лежащие между этими двумя крайними величинами, характеризуют различные уровни качества подгонки. Более подходящей для применения статистикой является скорректированное значение R2, обозначаемое ![]() 2 и определяемое следующим образом:
2 и определяемое следующим образом:
Мы вернемся к обсуждению этой статистики в гл. 8, когда сможем объяснить ее преимущества перед R2. По традиции либо R2, либо ![]() 2 (чаще, чем ŝ) приводят в качестве характеристики уравнения при оформлении результатов регрессионного анализа. Например, в нашем числовом примере из раздела 7.4 ŝ = 1,597 и
2 (чаще, чем ŝ) приводят в качестве характеристики уравнения при оформлении результатов регрессионного анализа. Например, в нашем числовом примере из раздела 7.4 ŝ = 1,597 и ![]() = 30; следовательно, R2 = 0,934 и
= 30; следовательно, R2 = 0,934 и ![]() 2 = 0,924; результаты регрессионного анализа обычно представляют (ср. с (7.33)) в виде
2 = 0,924; результаты регрессионного анализа обычно представляют (ср. с (7.33)) в виде
(в скобках указаны стандартные ошибки).
Ясно, что R2 (и, как мы увидим в гл. 8, ![]() 2) — полезная дескриптивная статистика. Ею широко пользуются в классической статистике, и потому необходимо хорошо понимать ее смысл. Однако при «уровне проникновения в суть проблем» статистического оценивания, достигнутом к этому моменту нашего курса, основная ценность такой статистики состоит в ее связи с ŝ2: как видно из (7.46), уменьшение ŝ ведет к увеличению R2. (Аналогично из (7.47) следует, что R2 и ŝ связаны обратной зависимостью.) Поэтому если сравнивают две регрессионные модели, априорные вероятности которых равны, то относительные апостериорные вероятности характеризуются значениями R2: уравнению с большим R2 соответствует более высокая апостериорная вероятность. Это позволяет осуществить выбор одной из альтернативных моделей (имеющих одну и ту же объясняемую переменную) в соответствии с величиной R2. Однако такой способ выбора оправдан лишь при определенных обстоятельствах.
2) — полезная дескриптивная статистика. Ею широко пользуются в классической статистике, и потому необходимо хорошо понимать ее смысл. Однако при «уровне проникновения в суть проблем» статистического оценивания, достигнутом к этому моменту нашего курса, основная ценность такой статистики состоит в ее связи с ŝ2: как видно из (7.46), уменьшение ŝ ведет к увеличению R2. (Аналогично из (7.47) следует, что R2 и ŝ связаны обратной зависимостью.) Поэтому если сравнивают две регрессионные модели, априорные вероятности которых равны, то относительные апостериорные вероятности характеризуются значениями R2: уравнению с большим R2 соответствует более высокая апостериорная вероятность. Это позволяет осуществить выбор одной из альтернативных моделей (имеющих одну и ту же объясняемую переменную) в соответствии с величиной R2. Однако такой способ выбора оправдан лишь при определенных обстоятельствах.
7.7. Примеры регрессий
Теперь продемонстрируем применение полученных в этой главе результатов. Ключевые результаты сведены в табл. 7.3. Мы проиллюстрируем их применение на двух примерах эмпирического исследования функций потребления. Они различаются по уровню агрегирования и типу данных, используемых при их исследовании. В первом примере агрегированная функция потребления для Великобритании построена на базе временных рядов, а во втором — функция потребления для домашних хозяйств опирается на данные «пространственного» типа.
Идея агрегированной функции потребления хорошо известна из курса макроэкономики. Почти всегда сначала рассчитывают линейную функцию, удовлетворяющую соотношениям (7.5), где Y — уровень потребления, а X —уровень дохода. (Мы пользуемся обозначениями данной главы вместо более привычных обозначений тех же переменных через С и Y, чтобы избежать возможных недоразумений.) Коэффициент В характеризует агрегированную величину предельной склонности к потреблению, а коэффициент А — уровень потребления при нулевом доходе. Обычно считают, что величина А положительна, а В лежит между 0 и 1. Выясним, имеет ли это место, пользуясь агрегированными данными для Великобритании.
Лучшим источником агрегированных статистических данных по Великобритании, несомненно, являются ежемесячные публикации Государственной статистической службой экономических трендов, которые затем объединяются в ежегодные издания. Последние содержат длинные ряды подробных данных об основных экономических агрегатах и об их составляющих. Последний год, за который мы имели данные об интересующих нас переменных, — 1981. Обратившись к названным выше публикациям, мы обнаружим, что существуют различные способы отражения теоретических представлений о функции потребления с привлечением доступных агрегатных экономических характеристик. Теория не дает нам определенных рекомендаций относительно того, какие из подобных агрегатов, будь то потребительские расходы или валовой внутренний продукт (ВВП), рассчитанный в текущих ценах, следует предпочесть в нашей конкретной ситуации. У нас имеется возможность выбора между годовыми и квартальными данными, а в отношении последних — между скорректированными с учетом сезонных колебаний (с элиминированной сезонностью) либо без корректировки; кроме того, можно воспользоваться данными в текущих или в постоянных (1975 г.) ценах. Чтобы сделать выбор в отношении последнего из указанных аспектов, следует учесть, что функция потребления обычно предназначена для учета связи между реальным (а не номинальным, т.е. стоимостным) потреблением и реальным (а не денежным) доходом. Поэтому данные в постоянных ценах больше подходят для такой цели. Если говорить о выборе между годовыми и сезонными данными, то он зависит в значительной степени от характера и целей проводимого исследования.
Остановимся на квартальных данных с элиминированной сезонностью, что позволит располагать значительным числом наблюдений и при этом не учитывать колебания сезонного характера. Выпишем для дальнейшей работы (из Economic Trends Annual Supplement. London. Government Statistical Service, 1982, №7, p. 17—19) данные о потребительских расходах и ВВП, полученные в рыночных ценах и переведенные затем в постоянные цены 1975 г., квартальные и с элиминированной сезонностью. Данные в источнике приведены за период с первого квартала 1955 по первый квартал 1981 г., т.е. всего 105 квартальных наблюдений. В идеале в расчеты следует включить как можно больше данных о наблюдениях, т.е. все доступные, при условии, что они генерируются одной и той же моделью; тогда надежность апостериорных оценок окажется наибольшей из возможных. Однако для наглядности при проведении последующих расчетов мы ограничимся лишь частью этих наблюдений, что позволит упростить арифметические выкладки. Мы возьмем период с 1971 по 1980 г. (включительно), который характеризуется сорока наблюдениями (поскольку дальнейшее расширение информационной базы модели может привести к смещению соотношения (7.5); напомним, что обсуждаемые в этой главе методы опираются на предположение о неизменности соотношения (7.5) для всех участвующих в анализе данных).
Данные о наблюдениях изображены на рис. 7.4 в виде диаграммы рассеяния, причем по оси Y отложены значения уровня потребительских расходов, а по оси X — соответствующие значения ВВП. Предположим, что мы не располагаем априорными сведениями о значениях трех интересующих нас параметров A, В и S, определяющих конкретную модель, форма которой предполагается выбранной правильно, и соотношение, связывающее Y (потребительские расходы) и X (ВВП в рыночных ценах), имеет (ср. с (7.5)) вид: Y = А + ВХ + U, U ~ N (0, S2).
Рис. 7.4. Квартальные данные о потреблении и доходе в Великобритании за 1971–1980 гг. По оси Y отложена величина потребительских расходов в млн. фунтов стерлингов, по оси X — величина ВВП в млн. фунтов стерлингов, которая взята в качестве характеристики дохода
Как было показано в разделе 7.4, апостериорные оценки в свете имеющегося множества наблюдений определяются утверждениями (7.25) и (7.26). Чтобы воспользоваться ими, нам придется сначала рассчитать различные выражения из (7.27), а для этого, в свою очередь, потребуется вычислить соответствующие суммы, суммы квадратов и суммы попарных произведений. Все вычисления проводятся непосредственно на базе исходных данных, взятых из упомянутого выше сборника:
Итак, линия наименьших квадратов, обеспечивающая подгонку данных наблюдений, имеет вид: Y = 2462 + 0,522 X. Она и изображена на рис. 7.4. Остается рассчитать
(см. (7.27)). Один способ — вычислить каждый из элементов yi – â – ![]() xi отдельно, а затем рассчитать их сумму квадратов и величину ŝ2. Однако это довольно долгий путь. Другой, более прямой способ основан на использовании следующего результата (см. упражнение 7.7):
xi отдельно, а затем рассчитать их сумму квадратов и величину ŝ2. Однако это довольно долгий путь. Другой, более прямой способ основан на использовании следующего результата (см. упражнение 7.7):
С его помощью и опираясь на вычисления, произведенные ранее, мы находим, что ŝ2 = 164846,6 и, следовательно, ŝ = 406. Из (7.27) получаем, что ŝA = 1158 и ŝB = 0,043. Выбрав одну из принятых форм представления результатов регрессионного анализа, мы можем записать:
(в скобках указаны стандартные ошибки параметров).
В предположении, что априорные сведения о параметрах А, В и S отсутствуют, на основе (7.25) и (7.26) мы можем построить апостериорные оценки этих параметров. Подставим â = 2462, ![]() =0,522, ŝA = 1158, ŝB = 0,043 в (7.25) и найдем, что обе величины (А – 2462)/1158 и (В – 0,522)/0,043 удовлетворяют t-распределению с 38 степенями свободы. После подстановки значения ŝ = 406 в (7.26) величина 6264171/S2 удовлетворяет распределению хи-квадрат также с 38 степенями свободы. Итак, получены полные характеристики апостериорных распределений. Различные обобщающие характеристики можно получить с помощью обычных вычислений. Например, 95-процентные вероятностные интервалы для коэффициентов А и В получают, основываясь на том, что переменная, удовлетворяющая t-распределению с 38 степенями свободы, с вероятностью 0,95 лежит в интервале с концами ±2,024. Следовательно,
=0,522, ŝA = 1158, ŝB = 0,043 в (7.25) и найдем, что обе величины (А – 2462)/1158 и (В – 0,522)/0,043 удовлетворяют t-распределению с 38 степенями свободы. После подстановки значения ŝ = 406 в (7.26) величина 6264171/S2 удовлетворяет распределению хи-квадрат также с 38 степенями свободы. Итак, получены полные характеристики апостериорных распределений. Различные обобщающие характеристики можно получить с помощью обычных вычислений. Например, 95-процентные вероятностные интервалы для коэффициентов А и В получают, основываясь на том, что переменная, удовлетворяющая t-распределению с 38 степенями свободы, с вероятностью 0,95 лежит в интервале с концами ±2,024. Следовательно,
95-процентные вероятностные интервалы для коэффициентов А и В равны (117; 4807) и (0,435; 0,609) соответственно. Опираясь на данные наблюдений, изображенные на рис. 7.4, можно с вероятностью 95% утверждать, что агрегированная предельная склонность к потреблению в Великобритании равнялась величине, заключенной между 0,435 и 0,609. То обстоятельство, что этот интервал весьма широк, связано с достаточно большой дисперсией исходных данных (см. рис. 7.4).
В экономической теории предполагалось, что значение А положительно, а значение В лежит между 0 и 1. Согласуется ли подобная гипотеза с фактами? Очевидный способ проверить это — рассчитать вероятности Р (A > 0) и Р (0 < В < 1) и убедиться в том, что они «достаточно велики». Наша апостериорная оценка коэффициента А: (A – 2462)/1158 ~ t(38), т.е. Р (A > 0) =
1-СТЬЮДЕНТ.РАСП(B18;38;ИСТИНА) = 0,97997. Аналогично Р (0 < В < 1) =1-СТЬЮДЕНТ.РАСП(-0,522/0,043;38;ИСТИНА) = 1. Итак, мы почти наверняка можем утверждать, что коэффициент А положителен (с вероятностью 98%) и с еще большей уверенностью что коэффициент В лежит между 0 и 1.
Наконец, для полноты картины рассчитаем t-отношения и значение R2:
Значение R2 говорит о том, что почти 80% дисперсии наблюдений над переменной Y «объясняется» регрессией. Теперь мы можем записать результаты регрессионного анализа в форме, альтернативной (7.50), но так же достаточно распространенной:
(в скобках указаны t-отношения для коэффициентов).
В качестве второго примера для демонстрации регрессионного анализа «в действии» мы также воспользуемся соотношением, связывающим потребление и доход, однако на этот раз мы воспользуемся не агрегатами, а данными о домашних хозяйствах и не временными рядами, а пространственными данными. Подобная информация может быть почерпнута из Family Expenditure Survey. («Обзоров семейных расходов») или же в обобщенном виде из General Household Survey («Общих обзоров домашних хозяйств»). Конкретные данные, исследованием которых мы займемся, взяты из издания за 1979 г., вышедшего в свет в 1980 г.: Family Expenditure Survey 1979. London, 1980, p. 169 (Appendix 8, Table А). В качестве данных, подходящих для эмпирических расчетов соотношения между потреблением и доходом, были выбраны средний недельный уровень потребительских расходов в домашнем хозяйстве и средний недельный уровень дохода в домашнем хозяйстве.
Усреднение проведено в обзоре для различных групп домашних хозяйств, различающихся по уровню дохода. В обзоре за 1979 г. таких групп было выделено шестнадцать, и потому мы располагаем шестнадцатью наблюдениями. Эти наблюдения отмечены на рис. 7.5, а.
Рис. 7.5. Потребление и доход в домашних хозяйствах Великобритании в 1979 г.: а) по вертикальной оси — средние потребительские расходы домашнего хозяйства за неделю, по горизонтальной оси — средний недельный доход домашнего хозяйства; б) X и Y — натуральные логарифмы величин, изображенных на диаграмме рис. а
Внимательное изучение диаграммы, образованной имеющимися в нашем распоряжении наблюдениями, позволяет обнаружить то, что вполне можно было предвидеть или предсказать исходя из теоретических соображений: интересующее нас соотношение не является линейным. Перед нами случай, когда отвечающая эмпирическим данным кривая должна иметь тем меньший тангенс угла наклона касательной к оси X, чем больше становится величина получаемого дохода. Это вполне согласуется с экономической теорией, которая предсказывает, что для пространственных микроэкономических данных, подобных нашим, предельная склонность к потреблению падает по мере роста дохода. Таким образом, становится ясно, что невозможно непосредственно воспользоваться линейной формой для моделирования рассматриваемой связи между экономическими переменными. Тогда возникает вопрос: какая форма функциональной связи окажется в данном случае приемлемой? Когда в экономической теории нет ответа на подобные вопросы, приходится искать его с помощью формальных процедур. Одна очевидная возможность — испытать в качестве формы связи линейную зависимость между логарифмами рассматриваемых переменных. Запишем модель в привычной для нас форме Y = А + ВХ + U, U ~ N (0, S2), но X здесь будет логарифмом среднего недельного дохода получаемого домашним хозяйством, a Y — логарифмом среднего уровня недельных расходов. Известно, что в подобных линейных соотношениях между логарифмами (их называют логлинейными) коэффициент В интерпретируется как эластичность. В нашем примере В есть эластичность потребительских расходов домашнего хозяйства по доходу .
На рис. 7.5, б представлена эмпирическая информация в логарифмическом масштабе по обеим осям. (Взяты натуральные логарифмы, хотя с тем же успехом можно было выбрать любое другое основание логарифмов.) Изучив этот рисунок, мы можем сделать вывод о том, что переход к логарифмам послужил таким преобразованием исходных данных, после которого гипотеза о линейной связи между переменными стала более приемлемой. Поэтому далее в этом примере мы будем подразумевать под данными наблюдений не сами исходные величины, а их логарифмы.
Как и в предыдущем примере из этого раздела, будем исходить из отсутствия априорных сведений об интересующих нас параметрах модели. Тогда результаты (7.25) и (7.26) применимы, но, прежде чем ими воспользоваться, придется произвести все необходимые расчеты по формулам (7.27). Прежде всего найдем необходимые для расчетов суммы, не забывая при этом, что теперь величины в формулах являются логарифмами:
С точностью до третьего знака после запятой подстановка полученных величин в соотношения (7.27) даст нам:
Вычисленная (в логарифмах) регрессия может быть представлена в форме:
(в скобках приведены стандартные ошибки параметров).
Рассчитанная линия наименьших квадратов изображена на рис. 7.5, б. Из (7.25) находим (при отсутствии априорной информации) наши апостериорные оценки коэффициентов А и В, которые таковы, что обе величины (А – 0,841)/0,071 и (В – 0,781)/0,015 удовлетворяют t-распределению с 14 степенями свободы. Следовательно, 95-процентные вероятностные интервалы для коэффициентов А и В равны (0,689; 0,993) и (0,749; 0,813) соответственно. На основе данных из «Обзора семейных расходов» мы можем быть уверены на 95%, что эластичность изменения среднего недельного уровня потребления в домашних хозяйствах в зависимости от изменения среднего недельного дохода, получаемого этими домашними хозяйствами, лежит между 0,749 и 0,813.
Чтобы записать результаты регрессионного анализа в альтернативной форме, рассчитаем значения t-отношений (они равны 11,8 и 52,1), а также значение R2 = 0,995. Тогда
(в скобках приведены t-отношения).
Значения t-отношений таковы, что Р (А > 0) и Р (В > 0) обе практически неотличимы от 1. Нам остается перейти от уравнения линейного в логарифмах к непосредственной связи между потреблением и доходом. Схематически полученное уравнение можно записать так: ln (потребление) = 0,841 + 0,781 ln (доход). Отсюда, учитывая, что е0,841 = 2,319, получим
Чтобы придать этому выражению содержательный смысл, рассчитаем с его помощью величину предельной склонности к потреблению (обозначим ее mpc в соответствии с начальными буквами ее английского наименования) для различных уровней дохода. Для этого достаточно продифференцировать (7.54) и учесть, что 2,319*0,781 = 1,811:
mpc = 1,811 доход–0,219
Пользуясь этой формулой, составим таблицу значений mpc при различных уровнях среднего недельного дохода в домашних хозяйствах.
Из таблицы видно, что предельная склонность к потреблению меняется с изменением уровня дохода, т.е. мы правильно отказались от обычной линейной формы связи между переменными.
На этом мы завершим анализ второго примера. Как мы убедились на примерах, результаты данной главы можно непосредственно применять к исходной статистической информации. При этом требуется (если исходить из отсутствия априорных сведений о параметрах А, В и S) по формулам (7.27) рассчитать â и ![]() (коэффициенты наименьших квадратов), ŝ (модифицированное стандартное отклонение остатков), а также ŝA и ŝВ (стандартные ошибки коэффициентов А и В). Значения найденных величин подставляют затем в (7.25) и (7.26) и получают апостериорные оценки параметров А, В и S. Затем результаты обобщают одним из принятых способов, вычисляя соответствующие характеристики. Вот и все, что требовалось для анализа парной линейной регрессии.
(коэффициенты наименьших квадратов), ŝ (модифицированное стандартное отклонение остатков), а также ŝA и ŝВ (стандартные ошибки коэффициентов А и В). Значения найденных величин подставляют затем в (7.25) и (7.26) и получают апостериорные оценки параметров А, В и S. Затем результаты обобщают одним из принятых способов, вычисляя соответствующие характеристики. Вот и все, что требовалось для анализа парной линейной регрессии.
7.8. Прогноз
С установлением апостериорных оценок параметров А, В и S интерес экономиста к анализируемым соотношениям обычно не исчезает. Он может воспользоваться полученными оценками для прогнозирования и определить значение Y, соответствующее некоторому данному значению X. Если быть точными, то можно сделать два прогноза: прогноз среднего значения Y, соответствующего конкретному значению X, и прогноз фактического значения Y, соответствующего конкретному значению X. Если заданное значение переменной X обозначить через х0, а соответствующие ему среднее и фактическое значения Y — через М0 и Y0 соответственно, то можно будет записать, что
Прописные буквы используются для обозначения обеих интересующих нас величин, поскольку мы исходим из того, что в общем случае обе они неизвестны. (В случае 3, рассмотренном в разделе 7.3, значения коэффициентов А и В известны, а потому известно и значение M0, т.е. проблем с его прогнозированием не возникает.)
Мы сосредоточим внимание на случае 4, которому посвящен раздел 7.4; соответствующие результаты могут быть получены и для других случаев. Из (7.25) нам известно, что апостериорные оценки обоих коэффициентов А и В имеют вид t-распределений. Более того, из (7.26) следует, что и U0 также удовлетворяет t-распределению с n – 2 степенями свободы. (Распределение U0 при заданном значении S = s является нормальным; в силу (7.26) маргинальное распределение S задается в форме распределения хи-квадрат; следовательно (см. гл. 6), маргинальное распределение U0 имеет форму t-распределения.) Существует хорошо известная теорема (ее подробное рассмотрение выходит за рамки нашей книги), утверждающая, что линейная комбинация переменных, удовлетворяющих t-распределению (с одинаковым для всех переменных числом степеней свободы), также удовлетворяет t-распределению. И для (7.55), и для (7.56) условия этой теоремы выполнены. Поэтому апостериорные оценки каждой из величин М0 и Y0 могут быть выражены в форме t-распределений. Приведем точную формулировку этого результата:
Из приведенных соотношений видно, что обе апостериорные оценки как для М0, так и для Y0 центрированы относительно m̂0 — точки, соответствующей X = х0 и лежащей на линии наименьших квадратов, которая обеспечивает подгонку данных наблюдений. Точность апостериорных оценок (отражаемая длиной апостериорных вероятностных интервалов) зависит от ŝM0, и ŝY0. Поэтому в обоих случаях точность будет увеличиваться с уменьшением ŝ, ростом n, приближением х0 к х, а также с увеличением выборочной дисперсии наблюдений над переменной X. Все эти свойства интуитивно ясны.
Проиллюстрируем использование результата (7.57) на первом примере из раздела 7.7, а именно в случае агрегированной функции потребления, построенной на основе временных рядов. Если вы обратитесь к Economic Trends Annual Supplement за 1982 г., то заметите, что нами использованы данные за 1971 – 1980 гг., но мы опустили наблюдения над значениями переменных в первом квартале 1981 г., хотя они были нам доступны. Величина ВВП в этом квартале (как следует из публикации) равнялась 28 188 млн. фунтов. Примем ее за х0 и получим прогноз соответствующих М0 и Y0. Если мы подставим в (7.58) значения различных переменных, рассчитанные в разделе 7.7, то найдем: m̂0= 17 181, ŝM0 = 85,7, ŝY0 = 415.
Следовательно, из (7.57) мы найдем характеристику наших апостериорных оценок для М0 и Y0; эти оценки таковы, что каждая из величин (M0 – 17 181)/85,7 и (Y0 – 17 181)/415 удовлетворяет t-распределению с 38 степенями свободы. Таким образом, получена полная характеристика апостериорных оценок. Соответствующие 95-процентные вероятностные интервалы будут равны (17007; 17 355) для М0 и (16 340; 18 021) для Y0. Первый из них, естественно, уже второго. У нас нет реальной возможности проверить первый из этих двух прогнозов, поскольку нам не известно среднее значение уровня потребления, отвечающее уровню ВВП в 28 188 млн. фунтов. Однако мы располагаем реальным значением, соответствующим потреблению в первом квартале 1981 г., когда ВВП был равен 28 188 млн. фунтам. Это реальное значение равно 17 886 фунтам. Как мы видим, оно лежит в нашем 95-процентном прогнозном (вероятностном) интервале для величины Y0. Этот результат укрепляет наше доверие к полученному соотношению как к средству прогнозирования.
Резюме. В данной главе рассмотрены основные положения эмпирического анализа экономических соотношений, имеющих форму линейной парной регрессии с нормально распределенными остатками. Эта модель определена в (7.5) и полностью описывается тремя параметрами: А и В — коэффициентами уравнения, S2 — дисперсией остаточного члена. Мы рассмотрели три случая: в одном коэффициенты были неизвестны, но известной была дисперсия, в другом — дисперсия неизвестна, но известны коэффициенты, в последнем — неизвестны и коэффициенты, и дисперсия. Мы сконцентрировали внимание на последнем (наиболее общем) случае и ограничились рассмотрением ситуации, когда априорная информация о значениях интересующих нас параметров отсутствует. Мы показали, что результаты данной главы представляют собой «естественное обобщение» результатов, полученных в гл. 6, где указанные случаи уже появлялись.
В табл. 7.3 сведены практически все существенные результаты. Наиболее важные относятся к случаю 4, поскольку этот случай чаще всего встречается на практике. Как показано в таблице, апостериорные оценки каждой из величин А и В задаются в форме t-распределения, а апостериорная оценка параметра S2 — в форме распределения хи-квадрат. Эти ключевые результаты можно использовать непосредственно. Все, что для этого требуется, – рассчитать значения â и ![]() (коэффициенты наименьших квадратов), ŝ (модифицированное стандартное отклонение остатков), ŝA и ŝB (стандартные ошибки коэффициентов А и В).
(коэффициенты наименьших квадратов), ŝ (модифицированное стандартное отклонение остатков), ŝA и ŝB (стандартные ошибки коэффициентов А и В).
В этой главе также говорится, как результаты классического анализа этой же задачи можно интерпретировать в терминах байесовского подхода. В частности, мы показали, что байесовские вероятностные интервалы, полученные при отсутствии априорной информации, и классические доверительные интервалы совпадают, а также, что классическая процедура проверки значимости параметра соответствует ограничению для определенного вероятностного утверждения по поводу этого параметра.
Приведены два примера подробного расчета регрессии между потреблением и доходом. Один из этих примеров использован в разделе 7.8 для иллюстрации процедуры прогнозирования.
Технически содержание данной главы сложнее содержания предыдущих глав, концептуально оно ничем принципиально новым не выделяется. В частности, утверждения относительно неизвестных параметров получены в результате применения общих положений байесовского подхода.
Упражнения
В каждом из приведенных здесь упражнений предполагается использование модели
Y = A + BX + U, U ~ N (0, S2)
параметры которой А, В и/или S2 либо все известны, либо все неизвестны (это указано в каждом конкретном случае). Наблюдения (х1, у1), (х2, у2), …, (xn, yn) над переменными (X, Y) получены в процессе рандомизированной выборки.
7.1. Пусть в результате шести наблюдений над (X, Y) мы имеем следующие пары чисел: (20,45) (10, 27) (14, 9) (38, 75) (22, 21) (16, 39).
а) Если s известно и равно 12, а коэффициенты А и В неизвестны, найдите апостериорные оценки коэффициентов A и В по данным наблюдений. Определите 95-процентные вероятностные интервалы для A и В, а также вероятности Р (А < 0) и Р (В > 0).
б) Если а = –4, b = 0, а параметр S неизвестен, вычислите апостериорную оценку для S по данным наблюдений. Определите 95-процентньш вероятностный интервал для S, а также Р (S > 12).
в) Если все параметры А, В и S неизвестны, найдите их апостериорные оценки по данным наблюдений. Рассчитайте 95-процентные вероятностные интервалы, а также Р (А < 0), Р (В > 0) и Р (S > 12).
г) Изобразите диаграмму рассеяния для данных наблюдений и проведите линию наименьших квадратов, обеспечивающую их подгонку.
7.2. Обратитесь к иллюстративному примеру, содержащему девять наблюдений, который был описан в разделе 7.2, а затем использован в разделах 7.3 и 7.4. Не прибегая к арифметическим выкладкам, определите воздействие, которое окажет на апостериорные оценки и соответствующие вероятностные интервалы информация о еще одном множестве из девяти наблюдений, в точности совпадающем с первоначальным множеством наблюдений.
7.3. Предположим, что каждое из n наблюдений лежит в точности на прямой линии. Покажите, что в этом случае ŝ = 0. Что это будет означать в случае 4 для апостериорных оценок A и В? Проинтерпретируйте свои выводы.
7.4. Объясните на интуитивном уровне, почему sA (и ŝA) являются возрастающими функциями от величины ![]() .
.
Решения
7.1. (а) Для расчета параметров распределения воспользуемся формулами (7.8) и (7.9) (см. лист Excel и рисунок ниже). 95%-ные интервалы для апостериорных коэффициентов: А (–25,52; 21,52) и В (0,83; 2,97). Вероятность того, что А < 0 составляет 56,6%; в то же время вероятность того, что В > 0 составляет 100%.
(б) Для расчета параметров распределения воспользуемся формулами (7.22) и (7.23) (см. лист Excel и рисунок ниже). 95%-ные интервал для S: (–29,11; 99,48). Вероятность того, что S > 12 составляет 100%.
(в) Для расчета параметров распределения воспользуемся формулами из табл. 7.3 (см. лист Excel и рисунок ниже). 95%-ные апостериорные интервалы: А (–31,61; 27,61), В (0,55; 3,25), S (9,05; 43,42). Р (А < 0) = 55,3%; Р (В > 0) = 99,7%; Р (S > 12) = 82,5%.
Я решил проверить правильность рассчитанных параметров, и запустил Пакет анализа (опцию Регрессия). Вот что получилось:
Видно, что параметры, полученные расчетом на основе формул и Пакетом анализа совпадают.
(г) Построив на основании данных (xi, yi) точечную диаграмму, можно увидеть, почему такие большие разбросы для параметров: данные не очень хорошо аппроксимируются линией. Коэффициент R2 показывает, что только 65,5% данных можно объяснить линейной зависимостью:
Глава 8. Развитие регрессионного анализа [9]
Глава 9. Модели с одновременными уравнениями
[1] Не все формулы, приведенные в книге я воспроизвожу в настоящей заметке, но чтобы не запутаться нумерацию я сохранил
[2] Разделы 3.5. Многомерные вероятностные распределения и 3.6. Обобщающие характеристики мне показался излишне сложным, поэтому я их пропустил.
[3] Напомню, что буквой U обозначается равномерное распределение на отрезке U [a, b], а N – нормальное распределение с параметрами N [µ, σ2]
[4] Оставшаяся часть раздела показалась мне слишком сложной для восприятия, поэтому я ее опустил
[5] Напомню, что книга издана на русском языке в 1987 г. Сегодня использование бета-распределения не вызывает трудностей благодаря функциям Excel =БЕТА.РАСП() и =БЕТА.ОБР()
[6] Напомню, что все эти ухищрения с использование аппроксимации бета-распределения нормальным распределением связаны с тем, что во времена написания книги не было замечательной программы Excel.
[7] С точки зрения Excel преимущество спорное, так как имеется как функция ХИ2.РАСП, так и ГАМММА.РАСП… 🙂
[8] К сожалению автор (или переводчик?) одной и той же буквой Р обозначает, и вероятность, и точность.
[9] Дальнейшее изложение показалось мне слишком специфичным, не добавляющим нового понимания по теме байесовской вероятности, поэтому оно опущено. В то же время именно эта часть книги может быть интересна тем, кто изучает эконометрику. В этом случае, вы легко найдете книгу в Интернете.

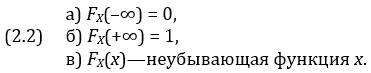
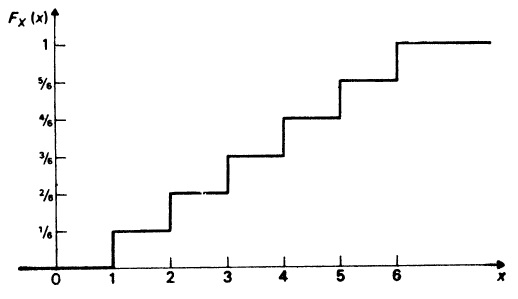
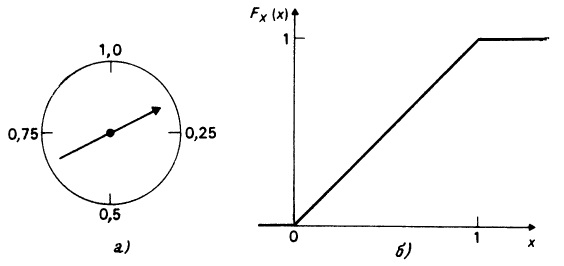



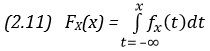
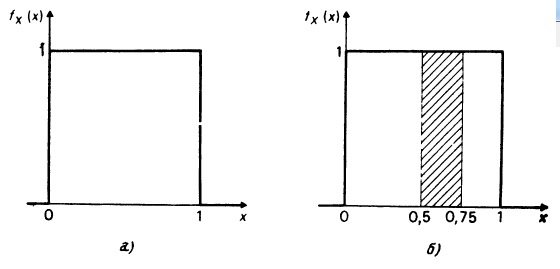
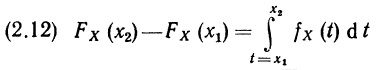
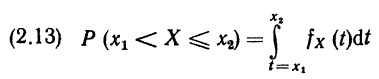
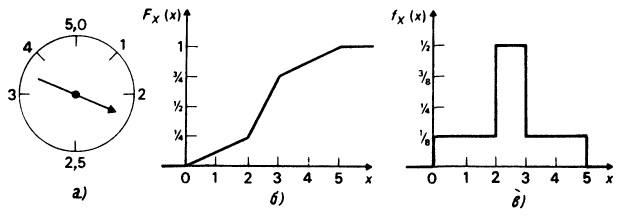

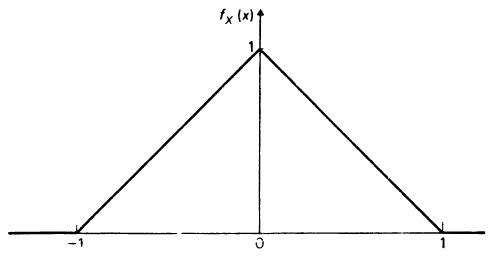
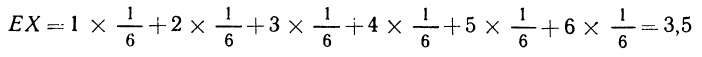

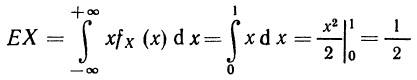
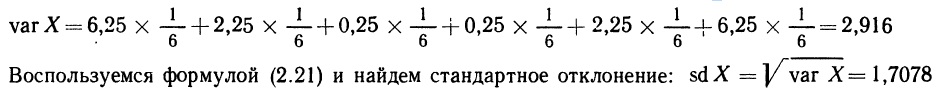
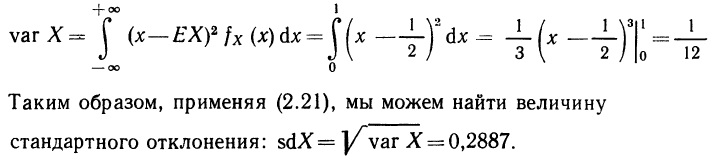
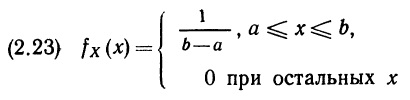
![Рис. 2.8. Равномерное распределение на отрезке [а; b]](https://baguzin.ru/wp/wp-content/uploads/2013/09/Рис.-2.8.-Равномерное-распределение-на-отрезке-а-b.jpg)