Жизненными циклами всего на свете – от растений и животных до городов, в которых мы живем, и компаний, в которых работаем – управляют универсальные законы. Об этих законах – законах масштабирования – рассказывает ученый-физик. Очень хорошо написанная книга, умная и увлекательная. Ссылку на нее я нашел у Нассима Николаса Талеба в книге Рискуя собственной шкурой.
Джеффри Уэст. Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний. – М.: Азбука-Бизнес, 2018. 512 с.
Скачать краткое содержание в формате Word или pdf (конспект составляет около 5% от объема книги)
Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon
Глава 1. Общая картина
В биологии управление ростом и жизнью, а также их поддержку обеспечивает процесс обмена веществ – метаболизм. Его численным выражением служит уровень метаболизма, то есть количество энергии в единицу времени, необходимое для поддержания жизни организма. Для человека он равен 2000 килокалорий в сутки. Таков наш биологический метаболизм, соответствующий существованию животного, развившегося естественным путем. Животному общественному, живущему теперь в городе, для выживания необходимы дома, отопление, освещение, автомобили, дороги, самолеты, компьютеры и т.д. В связи с этим для поддержания существования среднего жителя Соединенных Штатов требуется ошеломляюще большое количество энергии – 11 000 Вт.[1] Неудивительно, что нам грозят энергетические кризисы и нехватка природных ресурсов.
Поддержание порядка и структуры в развивающейся системе требует непрерывной подачи и использования энергии, побочным продуктом которых является возникновение беспорядка. Именно поэтому нам нужно есть, чтобы оставаться в живых, чтобы бороться с неизбежными, разрушительными силами производства энтропии. Энтропия убивает. В конечном счете на всех нас действуют «износ и амортизация» во всех своих многочисленных видах. Борьба с энтропией путем непрерывного потребления все новой энергии для роста, обновления, содержания и восстановления, которая становится все более и более трудной по мере старения системы, лежит в основе любого серьезного обсуждения старения, смертности, жизнестойкости и устойчивости, будь то в применении к организмам, компаниям или городам.
Принцип экономии на масштабе гласит, что чем больше размер, тем меньше ресурсов на душу населения (или, в случае животных, на клетку или на грамм массы тела) требуется для выживания.
Я не буду пытаться дать научное определение сложности, а опишу то, что я считаю существенными элементами типичных сложных систем. Такие системы состоят из великого множества индивидуальных составляющих, или агентов, которые, будучи собраны вместе, приобретают коллективные характеристики, обычно не проявляющиеся в свойствах самих отдельных компонентов и непредсказуемые на их основе. Например, вы – нечто гораздо большее, чем сумма составляющих вас клеток. А ваше сознание, ваша личность, ваш характер, – есть коллективное проявление множественных взаимодействий между нейронами и синапсами вашего мозга.
Аналогичным образом город – это нечто гораздо большее, чем простая сумма его зданий, дорог и жителей, компания – нечто гораздо большее, чем простая сумма ее сотрудников и продукции.
Коллективный результат, в котором система проявляет свойства, существенно отличные от получающихся при простом сложении отдельных вкладов всех составляющих ее элементов, называют эмерджентным поведением.
Самоорганизация – это эмерджентное поведение, в рамках которого составные части объединяются, образуя эмерджентное (вновь возникающее) целое.
В биологии сетевая динамика ограничивает темп жизни, заставляя его систематически снижаться с увеличением размеров в соответствии со степенными законами с показателями, кратными ¼. Напротив, динамика социальных сетей, лежащая в основе создания ценностей и инноваций, порождает противоположное поведение, а именно систематическое увеличение темпа жизни с увеличением размеров городов. Болезни распространяются быстрее, предприятия возникают и закрываются чаще, сделки проводятся с большей скоростью, и даже люди в большом городе ходят быстрее – и все это следует правилу приблизительно 15%-го увеличения. Все мы чувствуем, что жизнь в большом городе идет быстрее, чем в маленьком, и что ее темп повсеместно возрастает в течение нашей собственной жизни по мере увеличения городов и экономического роста.
Если сублинейное [медленнее, чем линейное] масштабирование уровня метаболизма приводит в биологии к ограничению роста, то суперлинейное [быстрее, чем линейное] масштабирование создания ценностей и инноваций (которое можно измерить, например, по числу выдаваемых патентов) приводит к неограниченному, часто превышающему экспоненциальный росту, согласующемуся с неограниченными экономическими системами.
Компании, подобно организмам и городам, также подчиняются простым степенным законам масштабирования. При этом их масштабирование в зависимости от размеров сублинейно. В этом отношении компании гораздо более похожи на живые организмы, чем на города. Степенной показатель масштабирования компании составляет около 0,9, в то время как для организмов он был равен 0,75.
Сублинейное масштабирование метаболизма организмов обеспечивает прекращение их роста и определяет их размер в зрелом состоянии, который остается приблизительно неизменным до самой их смерти. Сходная жизненная траектория действует и для компаний. В первые годы своего существования они быстро растут, но по мере приближения к зрелости этот рост замедляется, и, если компания вообще выживает, она рано или поздно перестает расти.
Глава 2. Мера всех вещей
Галилея часто называют «отцом современной науки», имея в виду его многочисленные фундаментальные вклады в физику, математику, астрономию и философию. Однако ему пришлось дорого заплатить за последовательное отстаивание гелиоцентрической гипотезы, вытекавшей из его наблюдений. В возрасте шестидесяти девяти лет, тяжелобольным, он предстал перед судом инквизиции, который признал его воззрения еретическими. Он был вынужден отречься от своих взглядов и после недолгого тюремного заключения провел остаток жизни (еще девять лет, в течение которых он ослеп) под домашним арестом.
Его книги были запрещены и попали в печально известный ватиканский «Индекс запрещенных книг». Лишь в 1835 г., более двухсот лет спустя, его работы были исключены из этого списка, и только в 1992-м – по прошествии почти четырех веков – папа Иоанн Павел II публично выразил сожаление по поводу обращения церкви с Галилеем. Мысль о том, что какие-то слова, написанные в незапамятные времена на еврейском, греческом и латинском языках, основанные на чьих-то личных мнениях, догадках и предрассудках, могли столь безапелляционно перевешивать результаты научных наблюдений и математическую логику, действует отрезвляюще. Как ни печально это признавать, мы и сегодня не можем похвастаться полной свободой от таких заблуждений.
Эйнштейн писал о Галилее: «Положения, полученные при помощи чисто логических средств, при сравнении с действительностью оказываются совершенно пустыми. Именно потому, что Галилей сознавал это, и особенно потому, что он внушал эту истину ученым, он является отцом современной физики и, фактически, современного естествознания вообще».
Галилей показал, что объем и вес увеличиваются пропорционально кубу линейного размера, а площадь, поперечное сечение и прочность – пропорционально квадрату линейного размера. Иначе говоря, по мере увеличения размеров последовательно уменьшается относительная прочность.
Бельгийский математик Адольф Кетле был классическим энциклопедистом, ученым универсалом, и внес свой вклад в множество разных научных дисциплин, в том числе в метеорологию, астрономию, математику, статистику, демографию, социологию и криминалистику. Но его главным наследием оказался индекс массы тела (ИМТ). Его определяют, как отношение массы тела к квадрату роста. Таким образом, он измеряется в фунтах на квадратный дюйм или килограммах на квадратный метр. Его идея сводится к предположению о том, что вес здорового человека масштабируется пропорционально квадрату роста, что противоречит тем выводам, которые мы сделали ранее из работ Галилея: тогда мы заключили, что масса тела должна возрастать гораздо быстрее, пропорционально кубу роста.
В середине XIX в. Уильям Фруд строил уменьшенные модели кораблей от метра до трех длиной, протягивал их через вытянутые бассейны, наполненные водой, и измерял их сопротивление потоку воды и характеристики их устойчивости. Благодаря своему математическому образованию он обладал техническим аппаратом, позволявшим ему масштабировать полученные результаты на случай крупноразмерных судов.
Он выяснил, что основная величина, определяющая характер относительного движения модели, – это параметр, который назвали впоследствии числом Фруда. Он определяется как отношение квадрата скорости судна к произведению его длины на гравитационное ускорение:
где v — характерный масштаб скорости, g — ускорение, характеризующее действие внешней силы, L — характерный размер области, в которой рассматривается течение. Например, если рассматривается течение жидкости в трубе в поле силы тяжести, то под величиной g = ускорению свободного падения (9,8 м/с2), v — скорость течения, L = длине трубы.
Это отношение играет ключевую роль во всех задачах, касающихся движения чего бы то ни было, от летящей пули и бегущего динозавра до летящего самолета и плывущего корабля. Основная суть открытия Фруда состояла в том, что, поскольку основные физические свойства остаются неизменными, объекты разных размеров, движущиеся с разными скоростями, ведут себя одинаково, если соответствующие им числа Фруда имеют одинаковое значение.
Развитие методики масштабирования превратило ее к настоящему времени в мощный и сложный элемент инструментария науки и техники, в высшей степени эффективно используемый для решения широчайшего спектра задач. В общем виде эта методика была формализована лишь в начале ХХ в., когда выдающийся специалист по математической физике лорд Рэлей опубликовал в журнале Nature важную статью под названием «Принцип подобия». Он подчеркивал ту важнейшую роль, которую играют в любой физической системе особые величины, обладающие свойством безразмерности.
Вероятно, самое знаменитое безразмерное число – это число пи (π), отношение длины окружности к ее диаметру.
Поскольку сущность любой измеримой величины не может зависеть от произвольного выбора единиц измерения, сделанного человеком, не могут от него зависеть и законы физики. Следовательно, все они – и вообще все научные законы – должны быть выражаемы в виде соотношений между масштабно инвариантными безразмерными величинами, даже если обычно мы записываем их в другой форме для собственного удобства. В этом состоял основной посыл эпохальной статьи Рэлея.
Глава 3. Простота, единство и сложность жизни
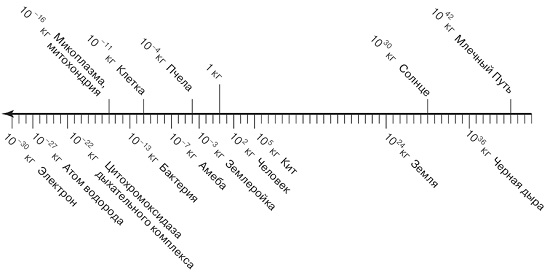
Все живые системы, от мельчайших бактерий до крупнейших городов и экосистем, являются, по сути, адаптивными сложными системами, действующими в широчайшем диапазоне множественных пространственных, временных, энергетических и массовых масштабов (рис. 1).
Рис. 1. Невероятный диапазон жизни, от сложных молекул и микробов до китов и секвой, в сравнении с галактическим и субатомным масштабами
Метаболизм – это огонь жизни… а пища – топливо жизни. Метаболическая энергия дает организмам энергию, необходимую для выживания, роста и воспроизводства, а также для отдельных процессов – например, кровообращения, сокращения мышц или нервной деятельности. Уровень метаболизма – это фундаментальный биологический параметр, задающий скорость почти всех жизненных процессов организма, от биохимических реакций, идущих внутри его клеток, до времени, необходимого для достижения зрелости, от скорости поглощения лесом углекислого газа до скорости разложения палой листвы. Уровень основного обмена среднего человека составляет всего около 90 ватт, что соответствует мощности обычной лампочки накаливания и эквивалентно ежедневному потреблению приблизительно 2000 пищевых калорий.
Уровень метаболизма всех организмов ведет себя с поразительной систематической регулярностью. Его зависимость от массы, построенная в логарифмическом масштабе, есть прямая линия, соответствующая простому степенному закону масштабирования. В современном виде этот закон сформулировал выдающийся физиолог Макс Клайбер в 1932 г. Применение логарифмической шкалы для представления подобных данных, охватывающих несколько порядков величины, не только удобно и наглядно, но и имеет более глубокие, концептуальные основания, связанные с идеей о том, что исследуемые структуры и процессы обладают свойствами самоподобия, математическим выражением которых являются простые степенные законы (рис. 2).
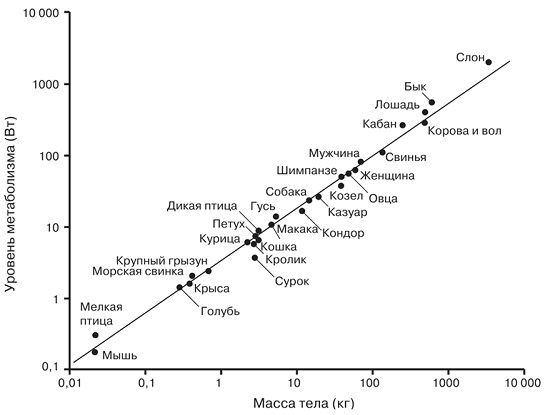
При увеличении массы на четыре порядка (по горизонтальной оси) уровень метаболизма возрастает всего на три порядка (по вертикальной оси), то есть наклон прямой равен ¾. Возьмем пример кошки, весящей 3 кг, что в 100 раз больше массы мыши, весящей 30 г. Уровень метаболизма кошки порядка 32 ватт, а для мыши – около 1 ватта. Таким образом, хотя кошка в 100 раз тяжелее мыши, уровень ее метаболизма больше лишь приблизительно в 32 раза, что дает нам яркий пример экономии на масштабе. Возьмем теперь корову, масса которой в 100 раз больше массы кошки. Уровень метаболизма коровы также в те же 32 раза выше, чем у кошки. А уровень метаболизма кита, еще в 100 раз более тяжелого, должен быть в 32 раза выше, чем у коровы.
Рис. 2. Уровень метаболизма у животных
В более общем случае, при увеличении массы в любое произвольное число раз на любом масштабе (в данном примере – в 100 раз) уровень метаболизма возрастает в одно и то же число раз (в данном примере – в 32 раза) независимо от величины исходной массы – то есть независимо от того, идет ли речь о мыши, кошке, корове или ките. Это замечательно систематически повторяющееся поведение называется масштабной инвариантностью или самоподобием и является неотъемлемым свойством степенных законов. Оно тесно связано с концепцией фрактала. Фрактальность, масштабная инвариантность и самоподобие в той или иной степени являются повсеместным свойством природы на всех ее уровнях, от галактик и облаков до клеток нашего тела, человеческого мозга, интернета, компаний и городов.
Существует более пятидесяти законов масштабирования, и – еще одна крупная неожиданность – соответствующие им показатели (аналоги ¾ из закона Клайбера) неизменно очень близки к числам, кратным ¼. Это число, по-видимому, играет некую особую, фундаментальную роль в определении многих измеримых характеристик организмов независимо от истории их развития. Если посмотреть на эту ситуацию через призму масштабирования, проявляется удивительная общая закономерность, свидетельствующая о том, что эволюция с высокой вероятностью определяется не только естественным отбором, но и другими, общими физическими принципами.
Дайте мне размер млекопитающего, и я, используя законы масштабирования, смогу рассказать вам почти все о средних значениях его измеримых характеристик: сколько пищи ему требуется в сутки, какова частота его сердцебиения, сколько занимает его взросление, длину и радиус его аорты, продолжительность его жизни, численность его потомства и так далее. Учитывая чрезвычайную сложность и многообразие форм жизни, это поистине поразительно.
С учетом столь выраженного разнообразия структур биологических сетей, явно контрастирующего с единообразием законов масштабирования, должен существовать общий набор сетевых свойств, действующих независимо от того, состоят ли такие сети из трубок (как в системах кровообращения млекопитающих), волокон (как в деревьях и других растениях) или диффузионных каналов (как в клетках).
Мы предложили следующий набор общих сетевых свойств, возникших, по нашему мнению, в результате процесса естественного отбора и порождающих законы масштабирования, математическое выражение которых дает степенные зависимости с показателями, кратными одной четверти.
Заполнение пространства. Сеть должна распространяться во все места системы, которую она обслуживает. Например, наша система кровообращения – это классическая разветвленная иерархическая сеть, в которой сердце прогоняет кровь через все многочисленные сетевые уровни: сначала через основные артерии, потом через сосуды все меньших и меньших размеров и в конце концов через капилляры, самые мелкие из сосудов, после чего кровь возвращается в сердце по венозной сетевой системе. Принцип заполнения пространства означает всего лишь, что капилляры, являющиеся концевыми модулями или последними ветвями сети, должны обслуживать все клетки нашего тела.
Неизменность концевых модулей. Этот принцип означает попросту, что все концевые элементы сетей данного типа, например, капилляры в системе кровообращения, имеют приблизительно одинаковые размеры и характеристики независимо от размеров организма. Такую неизменность концевых модулей можно объяснить экономностью естественного отбора. Аналогичным образом приблизительно неизменны концевые модули сетей, обслуживающих и поддерживающих существование зданий города, – скажем, электрические розетки или водопроводные краны. И в небоскребах, и в небольших зданиях установлены очень похожие розетки и краны. Основные концевые модули не изобретаются заново при проектировании каждого следующего здания независимо от того, где оно будет построено и какого оно будет размера.
Оптимизация. Последний постулат утверждает, что непрерывная работа многочисленных механизмов обратной связи и тонкой настройки, заложенных в постоянно продолжающихся процессах естественного отбора и действовавших в течение огромного времени, привела к «оптимизации» работы системы.
Все законы физики можно вывести из принципа наименьшего действия, утверждающего, грубо говоря, что из всех возможных состояний, в которых система может находиться – или которые она может принимать с течением времени, – физически реализуется то состояние, которое минимизирует действие системы. Практически все физически существующее определяется таким принципом оптимизации. Почему же жизнь должна быть исключением!?
Кислород играет ключевую роль в поддержании непрерывного снабжения молекулами АТФ, являющимися основным источником метаболической энергии, поддерживающей нашу жизнь. Мерой уровня метаболизма является скорость доставки кислорода в клетки, а также скорость циркуляции крови в сердечно сосудистой системе. Эти две системы находятся в тесном взаимодействии, и скорость течения крови, частота дыхания и уровень метаболизма пропорциональны друг другу. Сердце совершает около четырех сокращений на каждый вдох независимо от размеров млекопитающего. Именно такая тесная взаимосвязь между системами доставки кислорода обусловливает ту важную роль, которую свойства сердечно сосудистой и дыхательной сетей играют в определении и ограничении уровня метаболизма.
Скорость расходования энергии на прокачку крови по сосудам системы кровообращения называется выходной мощностью сердца. Эта энергия тратится на преодоление вязкого сопротивления, то есть трения, крови при течении по все более узким сосудам при ее перемещении по аорте, первой артерии, выходящей из сердца, и далее по множественным уровням сети вплоть до мельчайших капилляров, обеспечивающих питание клеток.
Один из основных постулатов нашей теории гласит, что получившаяся в результате эволюции конфигурация сети минимизирует мощность сердца, то есть энергию, необходимую для обеспечения циркуляции крови в системе.
В оптимизированной кровеносной системе сумма площадей поперечного сечения дочерних каналов, выходящих из разветвления, точно равна площади поперечного сечения исходного канала, разветвляющегося в нем. Т.е., радиусы последовательно расположенных сосудов должны масштабироваться регулярным самоподобным образом, уменьшаясь на каждом разветвлении в постоянное число раз, равное квадратному корню из двух.
Математики давно поняли, что существуют геометрии, лежащие за каноническими пределами классической евклидовой геометрии. Совершить фундаментальное открытие, показавшее, что свойства фрактальности повсеместно распространены в том сложном мире, в котором мы живем, выпало французскому математику Бенуа Мандельброту. Он показал, что степенные законы масштабирования – это математическое выражение самоподобия и фрактальности.
Мандельброт ввел понятие фрактальной размерности, равной сумме 1 и показателя степенного закона (то есть наклона прямой). Так, фрактальная размерность побережья Южной Африки равна 1,02, Норвегии – 1,52 и так далее. Смысл добавления единицы состоит в привязке идеи фракталов к общепринятой концепции обычной размерности. Размерность гладкой поверхности – 2, а размерность объема – 3. Таким образом, побережье Южной Африки очень близко к гладкой линии, так как его фрактальная размерность, 1,02, очень близка к 1, а побережье Норвегии сильно от нее отличается, поскольку его фрактальная размерность, равная 1,52, значительно больше 1.
В мире природы нет почти ничего гладкого: в нем по большей части встречаются объекты морщинистые, неправильные и зубчатые, и очень часто самоподобные. Почему же осознание столь фундаментального факта заняло более двух тысяч лет? По всей вероятности, это связано с тем, что человек постепенно разрывал тесные связи с миром природы. Когда мы начали изготавливать искусственные предметы, мы, по сути дела, изменили геометрию своего повседневного мира. Мы используем и ценим простоту прямых линий, гладких кривых и гладких поверхностей. Мы неизбежно приучились рассматривать мир сквозь линзу евклидовой геометрии, не видя беспорядочного, сложного, запутанного мира природы, из которого мы возникли.
Мандельброт обобщил эти иди на области гораздо более широкие. В число таких примеров входят наш мозг, шарики скомканной бумаги, молнии, речные системы и временные последовательности – например, электрокардиограммы (ЭКГ) или поведение фондового рынка. Выяснилось, что в течение одного часа торговли финансовые рынки испытывают в среднем такие же колебания, что и в течение суток, месяца, года или десятилетия. Рисунки этих колебаний оказываются попросту нелинейно масштабированными копиями друг друга (см. Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах).
Глава 4. Четвертое измерение жизни
Почти все сети, поддерживающие жизнь, представляют собой приблизительно самоподобные фракталы. Естественный отбор привел не только к минимизации потерь энергии, но и к максимизации метаболической способности, так как именно метаболизм производит энергетические и материальные ресурсы, необходимые для поддержания и воспроизводства жизни. Для этого была максимизирована площадь поверхностей, через которые эти ресурсы передаются. Эти поверхности составляют на самом деле суммарную площадь поверхности всех концевых модулей сети.
Биологические сети, побуждаемые силами естественного отбора к максимизации поверхностей обмена, достигают максимального заполнения пространства и, следовательно, масштабируются как трехмерные объемные тела, а не двумерные евклидовы поверхности. Это дополнительное измерение, возникающее из оптимизации производительности сети, приводит к тому, что организмы работают так, как если бы они действовали в четырех измерениях. В этом состоит геометрическая причина возникновения показателей, кратных одной четверти. Вместо показателей ⅓, которые действовали бы для гладких, нефрактальных евклидовых объектов, в их масштабировании работают показатели ¼. Хотя живые существа занимают трехмерный объем, их внутренняя физиология и анатомия ведут себя так, как будто они четырехмерны.
Биологи используют для обозначения процесса развития, происходящего во время роста особи, от оплодотворения яйцеклетки до рождения и далее до достижения зрелости, термин «онтогенез» (от греческого происхождение бытия).
Рис. 3. Символическое уравнение, представляющее энергетический баланс процесса роста, в котором метаболическая энергия распределяется между общим обслуживанием и новым ростом
Поскольку поступающая метаболическая энергия распределяется между обслуживанием уже существующих клеток и созданием новых, количество энергии, расходуемой на создание новых тканей, попросту равно разности между уровнем метаболизма и количеством, необходимым для обслуживания существующих клеток. Последняя величина прямо пропорциональна числу существующих клеток, а, следовательно, линейно возрастает при увеличении массы организма, в то время как уровень метаболизма возрастает сублинейно, по степенному закону с показателем ¾.
Предположим, что размеры организма удваиваются; тогда удваивается и количество клеток, в результате чего количество энергии, необходимое для их обслуживания, тоже увеличивается в два раза. Однако уровень метаболизма (то есть источник энергии) увеличивается всего лишь в 23/4 = 1,682… раза, что меньше двух. Таким образом, потребность в энергии растет быстрее, чем количество имеющейся метаболической энергии, в результате чего количество энергии, которое может быть выделено на рост, систематически уменьшается и в конце концов падает до нуля, что и приводит к прекращению роста. Другими словами, мы перестаем расти из-за несоответствия скоростей роста потребностей в обслуживании и поступлений энергии при увеличении размеров.
При рождении почти вся энергия уходит на рост, и лишь малая часть ее – на обслуживание, а после достижения зрелости вся она тратится на содержание, ремонт и замену. Рост останавливается. Сублинейное масштабирование и связанная с ним экономия на масштабе, порождаемые оптимизацией производительности сетевых систем, приводят к ограничению роста и систематическому снижению темпов жизни. Такое динамическое поведение является господствующим в биологии. Его преобразование в неограниченный рост и увеличение темпов жизни, а также его связь с огромным усилением нашего «социального» метаболизма будут основной темой глав 8 и 9.
Кривая выживаемости отражает вероятность достижения особью того или иного возраста и представляет собой зависимость доли некоторой популяции от возраста. Обратная ей кривая называется кривой смертности – на ней откладывается доля людей, умерших в определенном возрасте, что соответствует вероятности смерти человека в таком возрасте. Биологи, актуарии и геронтологи называют отношение числа смертей, происходящих в популяции в течение определенного времени (скажем, месяца), к числу оставшихся в живых смертностью или показателем смертности.
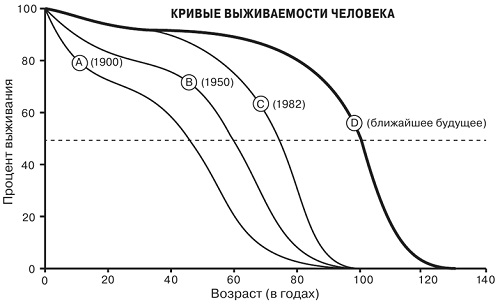
Один из наиболее удивительных результатов такого анализа состоит в том, что уровень смертности большинства организмов остается приблизительно неизменным независимо от возраста. Другими словами, доля особей, умирающих в течение некоторого периода времени, остается постоянной в любом возрасте. Например, если в возрасте от пяти до шести лет умирают 5% выжившей популяции, то те же 5% выжившей популяции умирают и в возрасте от сорока пяти до сорока шести лет, и в возрасте от девяноста пяти до девяноста шести. Постоянный уровень смертности означает, что число особей, умирающих в течение некоторого периода, прямо пропорционально числу доживших до этого времени. Выживаемость следует простой экспоненциальной кривой (рис. 4).
Рис. 4. Кривые выживаемости человека, отражающие быстрый переход от классического экспоненциального распада (с постоянным уровнем смертности), существовавшего до начала XIX в., к более прямоугольной форме по мере постепенного увеличения продолжительности жизни в связи с основными изменениями, обозначенными на графиках. Несмотря на этот прогресс, максимальная продолжительность жизни остается равной приблизительно 125 годам
Описывая распад радиоактивного материала, физики говорят о скорости распада. Скорость распада – это обычно постоянная величина, так что количество радиоактивного материала экспоненциально уменьшается в зависимости от времени, так же как уменьшается число особей во многих биологических популяциях. Физики также используют для описания распадов так называемый период полураспада: это время, необходимое для распада половины исходного числа атомов.
Эту терминологию можно использовать и в разговоре о смертности компаний. Данные показывают, что период полураспада американских компаний, котирующихся на фондовой бирже, составляет около десяти лет. Таким образом, всего через пятьдесят лет (пять периодов полураспада) продолжают торговаться на бирже лишь (½)5 = 1/32, то есть около 3% из них. Свидетельствуют ли общие черты смертности организмов, изотопов и компаний о действии одних и тех же, общих для них основополагающих динамических процессов?
Глава 5. От антропоцена к урбаноцену. Планета, на которой господствуют города
В качестве названия последней эпохи в истории нашей планеты, в течение которой деятельность человека стала существенно влиять на экологические системы Земли, был предложен термин «антропоцен». Мы начали значительно отличаться от преимущественно биологического вида и становиться видом преимущественно социальным, увеличивая тем самым эффективный уровень своего метаболизма. Также следует признать, что мы уже совершили резкий переход из чистого антропоцена в некую новую эпоху, характеризующуюся экспоненциальным ростом городов, которые господствуют теперь на нашей планете. Для обозначения этого гораздо более короткого и насыщенного периода, начавшегося вместе с промышленной революцией, я предлагаю особое название – «урбаноцен».
Лавры первого человека, осознавшего потенциальную угрозу, создаваемую неограниченным экспоненциальным ростом, и связавшего ее с проблемой ограниченности доступных ресурсов, принадлежат Томасу Роберту Мальтусу. Он утверждал, что население «умножается геометрически», то есть растет по экспоненциальному закону, в то время как возможности производства продовольствия и снабжения им – лишь «арифметически», то есть увеличиваются в гораздо более медленной линейной прогрессии, и рано или поздно численность населения должна превзойти имеющиеся продовольственные ресурсы, что приведет к катастрофическому краху.
Большинство авторитетов в области общественных наук и экономики подвергли идеи Мальтуса серьезной критике и отвергли их чуть ли не сразу после того, как он их высказал, – и, как мы увидим, небезосновательно.
В 1972 г., было опубликовано исследование «Пределы роста», которое выполнили в MIT Деннис Медоуз и Джей Форрестер (см. также Джей Форрестер. Мировая динамика). Эта работа была первой серьезной попыткой создать модель возможных сценариев глобальной устойчивости на основе имеющихся данных в сочетании с компьютерными моделями производства продовольствия, роста численности населения, индустриализации, использования невозобновляемых ресурсов и загрязнения окружающей среды.
Известный экономист Джулиан Саймон считал, что потрясающий рост, который мы наблюдаем в течение последних двухсот лет, продолжится «вечно» благодаря человеческой изобретательности и нашей неиссякаемой способности к инновациям. В книге Неисчерпаемый ресурс, вышедшей в 1981 г., Саймон утверждал, что большая численность населения – положительный фактор, так как она стимулирует появление еще большего числа технологических инноваций, изобретений и открытий, которые предоставляют нам новые возможности эксплуатации ресурсов и повышения уровня жизни.
Однако, у неограниченного экспоненциального роста есть темная сторона, выражающаяся в духе и сути Второго начала термодинамики и его проявлениях в виде роста энтропии. Какой бы замечательной ни была наша изобретательность, в конце концов все на свете приводится в действие и обрабатывается путем расходования энергии, а расходование энергии имеет неизбежные разрушительные последствия.
Когда человек еще был нормальной составной частью природного мира, действовал с энергопотреблением порядка нескольких сотен ватт и еще не изобрел сельского хозяйства, численность человечества во всем мире составляла всего лишь около 10 миллионов. Она выросла до нынешнего уровня за такое короткое время, что это вызвало серьезное нарушение динамического эволюционного равновесия природы и, таким образом, может привести к катастрофическим экологическим последствиям.
С точки зрения науки подлинно революционной чертой промышленной революции был резкий переход от открытой системы, получающей энергию от внешнего источника, Солнца, к системе замкнутой, источник энергии которой (ископаемое топливо) находится внутри ее самой. Такое фундаментальное системное изменение имеет огромные термодинамические последствия, так как в замкнутой системе неизбежно действует второе начало термодинамики, и, следовательно, происходит необратимое увеличение энтропии.
Наши социально экономические достижения, основанные на энергии ископаемого топлива, всего за двести лет превзошли все, что когда-либо удавалось совершить за столь короткое время естественному отбору, получающему питание непосредственно от Солнца.
С учетом того, какой огромный поток энергии неизменно поступает с Солнца на Землю каждый день, можно сказать, что энергетической проблемы вообще не существует. Суммарное количество энергии, передаваемой Солнцем на Землю, составляет около 1018 киловатт-часов в год, а наша потребность лишь 1014 киловатт-часов. Нам нужно вернуться к биологической парадигме, в которой большая часть наших энергетических потребностей удовлетворяется непосредственно Солнцем.
Глава 6. Прелюдия к теории городов
На мой взгляд, города представляют собой эмерджентные сложные адаптивные социально сетевые системы, возникающие в результате непрерывного взаимодействия их обитателей, которое усиливают и стимулируют механизмы обратной связи, создаваемые городской жизнью.
С рассмотрением городов через призму коллективной жизни их обитателей больше всех ассоциируется знаменитая писательница – теоретик урбанизма Джейн Джекобс. Ее основополагающая книга Смерть и жизнь больших американских городов оказала огромное влияние на представление о городах и решение задач «городского планирования» во всем мире. Почти пятьдесят лет спустя после того, как Джейн сформулировала свои гипотезы о первичной роли городов в национальной экономике, многие из тех, кто изучает города с самых разных точек зрения, приходят к тем или иным вариантам тех же выводов. Мы живем в эпоху урбаноцена, и в мировом масштабе оказывается, что судьбу планеты определяет судьба городов.
Известно, как трудно объективно оценить успешность города. При этом, выглядит бесспорным, что все распланированные города оказываются в той или иной степени бездушными и отталкивающими, лишенными жизненной энергии и культурной жизни и в целом бедными общественным духом. Однако города обладают поразительной жизнестойкостью и, будучи сложными адаптивными системами, непрерывно развиваются. Например, многие из нас считали Вашингтон «негородом». Сегодня он превратился в чрезвычайно многогранный и живой город, привлекающий множество энергичных и творческих молодых людей, завороженных его атмосферой активности и общности. Вашингтону понадобилось долгое время, чтобы стать «настоящим» городом.
Глава 7. К созданию научной теории городов
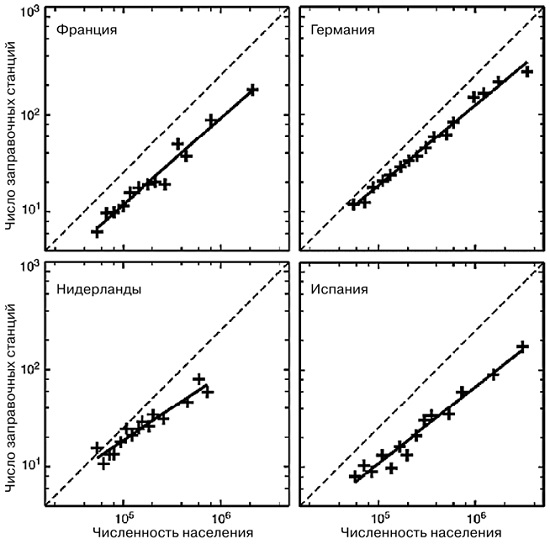
Изучая динамику городов, мы обнаружили, что число заправочных станций возрастает с увеличением численности населения в соответствии с простым степенным законом, очень напоминающим то, что мы наблюдали ранее в масштабировании биологических и физических величин (рис. 5). Более того, наклон этой прямой, соответствующий показателю степенного закона, составляет около 0,85, что говорит о наличии систематической экономии на масштабе. Другими словами, чем больше город, тем меньше заправочных станций требуется на душу его населения.
Рис. 5. Зависимости числа заправочных станций от размеров городов четырех европейских стран, представленные в логарифмическом масштабе, свидетельствуют о сублинейном масштабировании с близкими показателями. Штриховая линия имеет наклон, равный 1, и соответствует линейному масштабированию
Экономия на масштабе приводит к значительному сокращению выбросов и загрязнения окружающей среды. Соответственно, большие города в среднем оказываются более экологичными и имеют меньший углеродный след на душу населения.
Согласно нашим данным социально экономические величины, не имеющие аналогов в биологии, – например, средний размер зарплаты, число образованных работников умственного труда, число созданных патентов, уровень преступности, число ресторанов и величина валового внутреннего продукта (ВВП) города – также масштабируются удивительно регулярным и систематическим образом с одним и тем же показателем, близким к 1,15, независимо от того, о какой именно городской системе идет речь. В отличие от инфраструктурных параметров, которые масштабируются в зависимости от численности населения сублинейно, социально экономические величины – выражение самой жизни города – масштабируются суперлинейно, то есть систематически проявляют усиление на масштабе. Чем больше город, тем выше зарплаты, тем больше ВВП, тем выше уровень преступности, тем выше заболеваемость СПИДом и гриппом, тем больше в нем ресторанов, тем больше создается патентов и так далее на душу населения, и увеличение всех этих величин следует одному и тому же «правилу 15%».
Чем крупнее город, тем больше в нем создается инновационного «социального капитала», и, следовательно, тем больше имеет, производит и потребляет его средний житель, будь то товары, ресурсы или идеи. В этом состоит позитивная сторона городов и причина столь высокой их привлекательности.
Вспомним, что биологические сети имеют следующие общие свойства: 1) они заполняют пространство; 2) концевые модули должны быть неизменными; и 3) эволюция сетей стремится к их оптимизации. У всех этих свойств есть прямые аналоги в инфраструктурных сетях городов. Например, дорожные и транспортные сети должны заполнять пространство так, чтобы обеспечивать обслуживание всех локальных районов города, а неизменные концевые модули сети – это люди и их дома. Возникает один трудный и весьма интересный вопрос: что именно оптимизируется? Есть основания полагать, что эволюция инфраструктурных сетей способствует приближению к минимизации экономических и энергетических затрат.
Фрактальная природа городских и социальных сетей и протекающих в них потоков обеспечивает эффективное распределение энергетических и материальных ресурсов и порождает сублинейное масштабирование и экономию на масштабе.
На самом деле все обстоит несколько более сложным образом, так как города не однородны, но обычно содержат по нескольку локальных центров деятельности, работающих полуавтономным образом, хотя и образующих друг с другом иерархические связи. Такие центры часто называют «центральными местами» в соответствии с популярной моделью городской системы, известной под названием теории центральных мест. Она была предложена в 1930 х гг. немецким географом Вальтером Кристаллером и оказала на градостроителей и географов большое влияние.
В 1970 г. Стэнли Милгрэм опубликовал в журнале Science дискуссионную статью под названием «Опыт жизни в городах», которая заложила основы вновь зарождающейся дисциплины городской психологии. В больших городах мы постоянно сталкиваемся с таким количеством видов, звуков, «событий» и других людей, сменяющих друг друга с огромной скоростью, что мы просто не в состоянии переработать весь этот шквал информации, поступающей в наши органы чувств. Если бы мы пытались реагировать на каждый стимул, наши умственные и психологические контуры разрушились бы под этой нагрузкой, то есть у нас, как в перегруженной электрической схеме, просто вылетели бы предохранители. Милгрэм предположил, что те типы «антиобщественного» поведения, которые мы наблюдаем и с которыми сталкиваемся в больших городах, – это на самом деле адаптивная реакция на необходимость справляться с чувственной перегрузкой городской жизни, откуда следует, что без такой адаптации у всех нас вылетели бы предохранители.
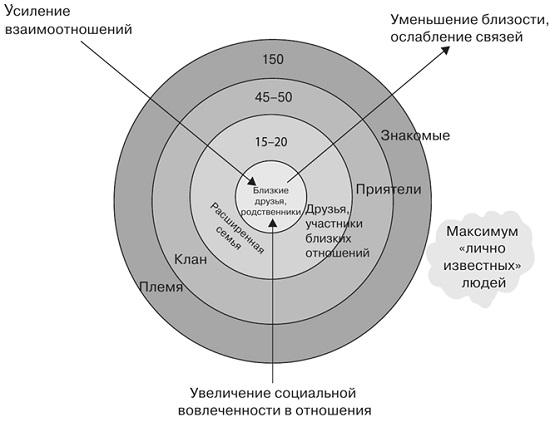
Эволюционный психолог Робин Данбар и его сотрудников предположили, что социальную сеть среднего человека можно разложить на иерархическую последовательность дискретных вложенных кластеров, размеры которых оказываются на удивление регулярными (рис. 6). Данбар вывел свою оценку идеальной численности социальных групп людей – число 150 – из корреляции с размерами мозга.
Рис. 6. Схема последовательности чисел Данбара, отражающая фракталоподобную иерархию модульной структуры социальных взаимодействий. Отметим, что интенсивность взаимодействия уменьшается с ростом размера модульной группы
Социально экономические параметры являются суммой взаимодействий или связей между людьми, а потому они зависят от степени коррелированности людей. Если все взаимодействуют со всеми, это дает суперлинейный степенной закон с показателем, равным 2. Однако в реальности интенсивность и количество взаимодействий каждого отдельного человека оказываются существенно ограничены, в результате чего значение показателя становится близким к 1,15.
Сублинейность масштабирования размеров инфраструктуры и энергопотребления точно равна величине, обратной суперлинейности масштабирования социально экономической деятельности. В этом и состоит гениальность городов. Неудивительно, что они привлекают к себе столько народа.
Глава 8. Следствия и предсказания
Увеличение размеров города приводит к образованию большего числа социальных взаимодействий на душу населения и в то же время к снижению их стоимости. Эта динамика порождает еще одну важную особенность современной жизни – непрекращающееся увеличение ее темпа. Ускорение времени есть эмерджентное явление, порождаемое механизмами непрерывной положительной обратной связи, заложенными в социальных сетях: по мере увеличения размеров социальные взаимодействия порождают новые взаимодействия, идеи стимулируют появление новых идей, а богатство приводит к появлению нового богатства.
Даже скорость пешей ходьбы возрастает с увеличением размеров города и приблизительно следует степенному закону, хотя его показатель несколько меньше канонического числа 0,15: он оказывается ближе к 0,10. Эта скрытая динамика нашла свое неожиданное выражение в недавно открытых в британском городе Ливерпуле дорожках для быстрых пешеходов. Оказалось, что пешеходы, идущие недостаточно быстро, так раздражали людей, что городу пришлось ввести специальные дорожки для быстрой ходьбы (рис. 7).
Рис. 7. Дорожки для быстрых пешеходов в английском городе Ливерпуле
Легкий доступ к дешевым многофункциональным смартфонам, подключенным к интернету, также внес большой вклад в ускорение темпов жизни и сжатие времени.
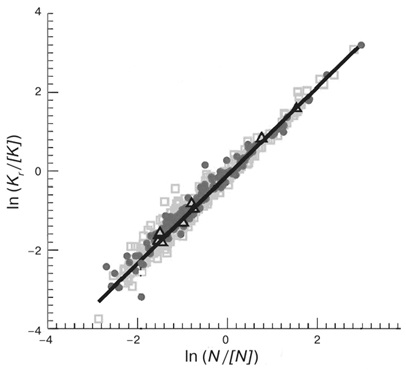
Как же измерить число взаимодействий между людьми? Традиционные методы основывались на использовании письменных опросов, что было делом долгим и трудоемким; к тому же они иногда страдали ошибками выборки, так как охват их по необходимости был ограничен. В то же время недавно появившиеся крупномасштабные наборы данных, собранных автоматически в сетях мобильной связи, которые охватывают значительные и репрезентативные части населения всего мира, открывают беспрецедентные возможности систематического изучения социальной динамики и организации всех городов (рис. 8). Этот результат дает подтверждение гипотезы о том, что в основе универсального масштабирования характеристик города действительно лежат социальные взаимодействия.
Рис. 8. Масштабирование степени связности между людьми, измеренной по числу взаимных телефонных вызовов между индивидуумами в городах Португалии и Великобритании, демонстрирует степенную зависимость
Глава 9. К созданию научной теории компаний
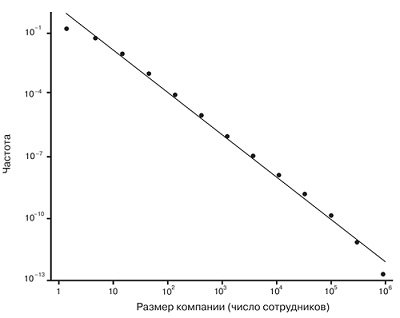
Распределение компаний по размерам подчиняется систематическому степенному закону, подобному закону Ципфа (рис. 9).
Рис. 9. Распределение американских компаний по размерам: по вертикальной оси отложен рейтинг компаний, а по горизонтальной – их размер (число сотрудников)
Очень редко принимается во внимание тот факт, что экономика представляет собой непрерывно эволюционирующую сложную адаптивную систему и что разбиение ее бесчисленных взаимозависимых составляющих на все более мелкие полуавтономные подсистемы может привести к ошибочным и даже опасным выводам, как хорошо видно из истории экономического прогнозирования.
Традиционные экономические теории сильно зависят от сохранения приблизительно равновесного состояния экономики. Способность предсказывать события, выходящие за обычные рамки, крупные изменения, поворотные моменты и разрушительные экономические ураганы и торнадо – гораздо более трудная задача, и с ее решением экономическая наука в большинстве случаев справлялась далеко не блестяще.
Нассим Талеб, автор приобретшего большое влияние бестселлера Черный лебедь, особенно резко высказывается об экономистах, несмотря на то – а может быть, именно потому – что сам он получил образование в области коммерции и финансов. Поэтому преимущество агентного моделирования состоит в возможности создания альтернативной основы для рассмотрения всей системы как единого целого, а не суммы неких идеализированных кусочков. Этот подход с самого начала признает, что экономика обычно представляет собой систему не равновесную, а развивающуюся и обладающую эмерджентными свойствами, которые порождаются взаимодействиями между ее многочисленными составляющими.
В применении к городам законы масштабирования показывают, что от 80 до90 % их измеримых характеристик можно определить, зная лишь численность их населения, а оставшиеся 10–20% являются мерой индивидуальности и уникальности каждого города. Рассуждая в том же духе, я хочу сейчас исследовать, насколько такая же система может быть использована для выявления эмерджентных законов, которым подчиняются компании.
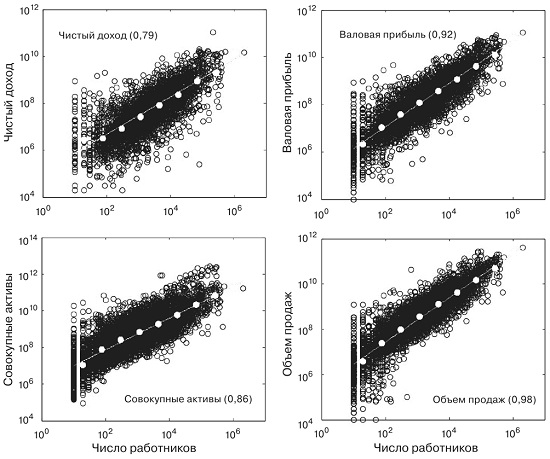
Компании действительно масштабируются в соответствии с простыми степенными законами (рис. 10). Эти результаты убедительно свидетельствуют о том, что компании, как и города или организмы, подчиняются универсальным динамическим принципам, не зависящим от их индивидуальных и даже уникальных черт, и что научное описание компаний, по меньшей мере в грубом приближении, действительно возможно.
Рис. 10. Зависимости доходов, прибылей, активов и объемов продаж 28 853 американских компаний, котировавшихся на бирже с 1950 по 2009 г., от численности их работников, построенные в логарифмическом масштабе, демонстрируют сублинейное масштабирование со значительным разбросом.
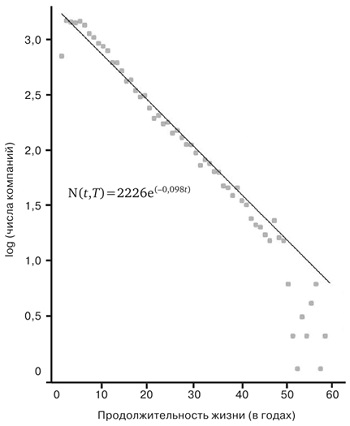
Важнейший аспект масштабирования компаний состоит в том, что многие из их ключевых параметров масштабируются сублинейно, как у организмов, а не суперлинейно, как у городов. Это заставляет предположить, что компании больше похожи на организмы, чем на города, и что господствующие в них тенденции должны быть связаны со своего рода экономией на масштабе, а не с усилением и инновациями. Это обстоятельство имеет важные последствия в том, что касается истории их существования и в особенности их роста и смертности. Сублинейное масштабирование порождает в биологии ограниченный рост и конечную продолжительность жизни (рис. 11), а суперлинейное масштабирование, свойственное городам (и экономическим системам), приводит к неограниченному росту.
Рис. 11. Зависимость логарифма числа выживших компаний от их возраста, демонстрирующая классическую картину экспоненциального распада, что свидетельствует о постоянном уровне смертности, как показывает прямая линия
Чем же таким особенным отличаются экспоненты, что они описывают распад такого множества никак не связанных друг с другом систем? Дело в том, что экспоненты возникают везде, где уровень смертности в каждый момент прямо пропорционален числу оставшихся в живых. Другими словами, процентная доля умерших за равные промежутки времени не изменяется со временем. То есть вероятность смерти компании не зависит ни от ее возраста, ни от ее размера. «Период полураспада» компаний, котирующихся на американских биржах (то есть время, за которое прекращает существование половина компаний, начавших свою деятельность в любой конкретный год), оказался близким к 10,5 года.
То, что компании масштабируются сублинейно, а не суперлинейно, как города, свидетельствует о существующем в них превалировании экономии на масштабе над инновациями и созданием новых идей. Несмотря на всю свою кажущуюся неповоротливость и неэффективность, города являются местами энергичной деятельности и проводниками перемен, а компании, за исключением молодых, по большей части производят впечатление застоя. Относительный объем средств, выделяемых на R&D, систематически уменьшается по мере роста компаний. Это означает, что при расширении компании поддержка инноваций отстает от роста бюрократических и административных расходов.
Труднейшая задача, которая стоит перед компаниями, заключается в нахождении равновесия между положительной отдачей от рыночных сил, которая побуждает оставаться с «надежной и испытанной» продукцией, и долговременной стратегической потребностью в исследовании новых областей и разработке новых продуктов, которые могут быть рискованными и не дают немедленных результатов. Компаниям по большей части свойственны близорукость, консервативность и нежелание поддерживать новаторские или рискованные идеи, стремление и дальше использовать, пока можно, крупные достижения своего прошлого, так как они «гарантируют» быстрый возврат средств. Поэтому компании склонны становиться все более и более одномерными. Сокращение многообразия – предвестник будущей катастрофы.
Глава 10. Перспективы теории Великого объединения устойчивости
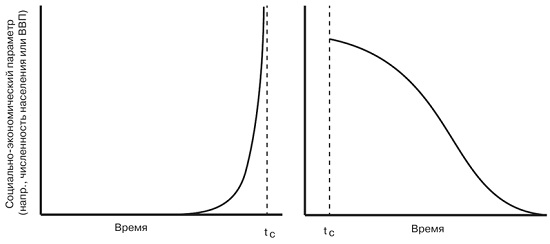
Суперлинейный рост с неизбежностью ведет к сингулярности конечного времени, которая является признаком неизбежных перемен и возможных крупных неприятностей в будущем (рис. 12).
Рис. 12. График, иллюстрирующий сингулярность конечного времени: представленная величина растет суперэкспоненциальным образом и становится бесконечно большой за конечное время tc, обозначенное вертикальной штриховой линией. После сингулярности наступает застой и крах
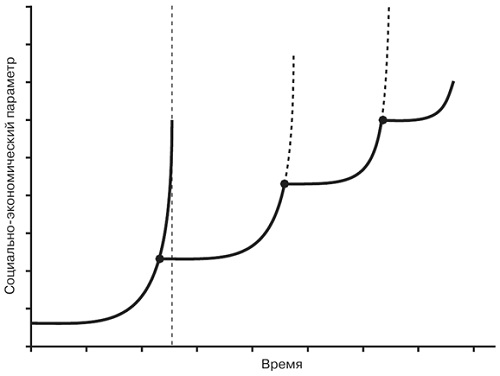
Для предотвращения краха необходима новая инновация, начинающая новый отсчет времени и обеспечивающая возможность продолжения роста без достижения приближавшейся сингулярности. После совершения перехода и «сброса отсчета времени», позволяющих избежать застоя и краха, процесс начинается заново с продолжением суперэкспоненциального роста, который рано или поздно приводит к новой сингулярности конечного времени, которую также необходимо будет обойти. Поддержка неограниченного роста в условиях ограниченности ресурсов требует непрерывного циклического появления инноваций, обеспечивающих смену парадигмы (рис. 13).
Рис. 13. График последовательных траекторий суперэкспоненциального роста, каждая из которых может привести к сингулярности конечного времени (обозначенной вертикальной штриховой линией) и последующему краху, как на рис. 77, если до наступления сингулярностей не появляются инновации (обозначенные черными точками), обнуляющие отсчет времени и начинающие новый цикл. Для ясности представления штриховые линии, обозначающие позднейшие сингулярности конечного времени, соответствующие черным точкам, не показаны.
Можно ли представить себе, что мы сумеем производить инновации, сравнимые по мощи и влиянию с изобретением интернета, каждые пятнадцать, десять или даже пять лет? Этот вопрос – пример классического доказательства методом reductio ad absurdum (доведение до абсурда), демонстрирующий, что, сколь бы изобретательны мы ни были, сколько бы мы ни создали чудесных устройств и приспособлений, мы попросту не сможем справиться с угрозой надвигающейся сингулярности, если будем продолжать действовать как обычно.
Непрерывный рост и связанное с ним все большее ускорение темпов жизни имеют важные последствия для всей нашей планеты, в особенности для городов, социально экономической жизни и процесса глобальной урбанизации. Сейчас молодые люди, начинающие свою трудовую деятельность, могут ожидать, что в течение их жизни произойдет несколько крупных перемен, которые с большой вероятностью приведут к резким изменениям их профессиональной карьеры.
[1] Интересно, это неточность перевода или автора? Нельзя же сравнивать мухи с котлетами!? Вт (ватт) – единица измерения мощности, а не энергии. Можно предположить, что речь идет о Вт*час. Тогда энергия равная 2000 ккал в сутки = 2000*4187 = 8,4Мдж. А 11 000 кВт*ч = 11 000*3 600 000 = 39 600МДж. Приблизительно в 5000 раз больше. – Прим. Багузина