В школе мы узнаем, что математика – скучный набор правил, который не поддается обсуждению. В книге «Как не ошибаться» Джордан Элленберг показывает, как узок подобный взгляд: математика – это не абстрактные идеи, далекие от реальной жизни. Математика пронизывает все, что нас окружает, и позволяет взглянуть за беспорядочную и хаотичную поверхность нашего мира, увидеть скрытые за ней структуры. Вооружившись математикой, мы можем видеть истинное значение информации, которую считали верной по умолчанию, и критически осмыслять все. Как рано нужно приезжать в аэропорт? Что именно отражает «общественное мнение»? Почему у высоких родителей невысокие дети?
По теме см. также Дэниел Левитин. Путеводитель по лжи. Критическое мышление в эпоху постправды, Дарелл Хафф. Как лгать при помощи статистики.
Джордан Элленберг. Как не ошибаться. Сила математического мышления. – М.: Манн, Иванов и Фербер, 2017. – 576 с.
Скачать конспект (краткое содержание) в формате Word или pdf (конспект составляет около 4% от объема книги)
Купить цифровую книгу в ЛитРес, бумажную книгу в Ozon или Лабиринте
Пролог. А мне это пригодится?
Во время второй мировой войны группа статистических исследований (Statistical Research Group, SRG) собрала крупнейших американских специалистов по статистике и использовала их возможности для решения военных задач. Военные представили на рассмотрение SRG следующую задачу: сколько брони, и в каких местах должно быть на истребителях, чтобы их было сложнее сбить, но они оставались маневренными.
Когда американские самолеты выходили из воздушных боев над Европой, они были покрыты дырами от пуль. Однако повреждения распределялись по корпусу самолета не равномерно:
Рис. 1. Статистика повреждения самолетов
Представители командования считали, что броню следует сделать толще там, где самолет получает больше всего пробоин. Броню следует укреплять не там, сказал Абрахам Вальд, где больше всего пробоин, а там, где их нет, то есть на двигателе. Причина, почему на двигателях уцелевших самолетах было меньше повреждений, только одна: в случае прямого попадания в двигатель самолет просто не возвращался из боя. Однако многие самолеты прилетали на базу с фюзеляжем, похожим на швейцарский сыр, — убедительный довод в пользу того, что корпус можно (а значит, и нужно) оставить без дополнительной брони.
Высшие чины американских военных ведомств всегда отдавали себе отчет, что страны побеждают в войнах не потому, что они храбрее противника или более независимы, или им чуть больше благоволит Бог. Как правило, победителем становится тот, у кого сбивают на 5% меньше самолетов, или кто использует на 5% меньше топлива, или кто обеспечивает пехоте на 5% более качественное питание.
Почему Абрахам Вальд увидел то, чего не смогли увидеть офицеры, обладающие более профессиональными знаниями и пониманием сути воздушного боя? Причина в аналитическом складе ума Вальда — так называемом математическом мышлении. Математик всегда ставит такие вопросы: «Из каких предположений вы исходите? Обоснованы ли эти предположения?».
В случае с авиационной броней офицеры, сами того не замечая, исходили из предположения, что вернувшиеся самолеты представляют собой случайную выборку всех самолетов. Но, как только вы осознаете, что в своих расчетах опираетесь на такое предположение, вам сразу станет понятно, насколько оно ошибочно: нет никаких оснований ожидать равной вероятности выживания всех самолетов независимо от того, в какую часть машины попадает огнестрельное оружие.
Глубинную структуру задачи с пробоинами в авиационной броне математики обозначают термином «систематическая ошибка выжившего». Такая погрешность часто возникает в самых разных ситуациях. Например, истории о том, что дельфины выталкивают тонущих людей на берег. На самом деле дельфины поддерживают тонущего на плаву, подталкивая в произвольных направлениях (что естественно для водных млекопитающих), но только выжившие — те, кого подтолкнули к берегу, — смогли рассказать о встрече с ними.
ЧАСТЬ I. ЛИНЕЙНОСТЬ
Глава первая. Стоит ли уподобляться Швеции
Несколько лет назад, в разгар дебатов вокруг «Закона о доступной медицинской помощи», Дэниел Митчелл из либертарианского Института Катона опубликовал в своем блоге статью с провокационным заголовком «Почему Обама пытается сделать Америку больше похожей на Швецию, тогда как сами шведы пытаются быть в меньшей степени шведами?». Ответ на этот вопрос требует построения в высшей степени научного графика. Вот как выглядит мир в понимании Института Катона:
Рис. 2. Линейная зависимость между благосостоянием и уровнем социальных льгот
Согласно этому графику, чем выше у вас мера шведскости, тем в худшей ситуации находится ваша страна. Шведы, люди далеко не глупые, поняли это и начали двигаться по графику в северо-западном направлении, к благосостоянию, которое обеспечивает свободный рынок. Однако Обама движется не в том направлении. Однако, с точки зрения людей, экономические взгляды которых ближе к мнению Обамы, а не Института Катона, график выглядит иначе:
Рис. 3. Нелинейная зависимость между благосостоянием и уровнем социальных льгот
Если это действительно так, тогда совершенно логично, что Обама увеличивает объем социального обеспечения, тогда как шведы сокращают его. Разница между этими двумя графиками сводится к различиям между линейностью и нелинейностью, одному из основных разграничений в математике. Мыслить нелинейно крайне важно, поскольку не все линии бывают прямыми. Нелинейное мышление означает следующее: какой путь выбрать, зависит от того, где вы находитесь. Часто оптимум находится где-то посередине.
Еще один пример нелинейной зависимости – хорошо известная в экономике кривая Лаффера:
Рис. 4. Кривая Лаффера
Глава вторая. Локально прямая, глобально кривая
Линейные рассуждения присутствуют повсюду. Вы прибегаете к ним каждый раз, когда утверждаете, что если хорошо иметь нечто, то лучше иметь этого еще больше. Почему вообще у кого бы то ни было может хотя бы на мгновение возникнуть мысль, что все линии прямые, когда совершенно очевидно обратное? Всё дело в том, что на ограниченном участке большинство линий прямые.
Ньютон сделал концептуальный скачок: уменьшайте поле зрения до тех пор, пока оно не станет бесконечно малой величиной — настолько малой, что она будет меньше любого размера, который вы можете назвать, но все же не равной нулю. В таком случае то, что было почти прямой линией, становится в точности прямой. Наклон этой кривой Ньютон называл флюксией, а мы называем производной.
Это и есть одна из причин, почему линейное мышление настолько естественно для нас: интуитивное восприятие времени и движения формируется у нас под воздействием явлений, которые мы наблюдаем в окружающем мире. Еще до того, как Ньютон сформулировал свои законы, мы, люди, в глубине души знали, что все вокруг нас стремится двигаться по прямой, если только нет причин двигаться иначе.
Глава третья. Поголовное ожирение
В журнале Obesity была опубликована статья, в заголовке которой был поставлен весьма неприятный вопрос: «Будут ли все американцы страдать избыточным весом и ожирением?». В статье дается ответ: «Да — к 2048 году». Спешу вас обрадовать. Не все из нас в 2048 году будут страдать ожирением. Почему? Потому что не все линии прямые. Тем не менее, как мы узнали от Ньютона, каждая линия достаточно близка к прямой. Эта идея лежит в основе линейной регрессии. Однако, вы можете применить этот метод, не задумываясь, действительно ли феномен, который вы пытаетесь моделировать, близок к линейному. Но вы не должны так делать.
Глава пятая. Когда пирог больше тарелки
В апреле 2012 года в ходе президентской избирательной кампании команда Митта Ромни, получив плохие результаты опросов среди избирателей женского пола, обнародовала такое заявление: «Администрация Обамы привела к тому, что для американских женщин наступили трудные времена. В период правления президента Обамы большому количеству женщин было крайне трудно найти работу — намного труднее, чем когда-либо за всю историю американского государства. На женщин приходится 92,3% от всех рабочих мест, потерянных при Обаме»10.
В каком-то смысле это заявление можно считать правильным. По данным Бюро трудовой статистики, в январе 2009 года общая численность работающих составляла 133 561 000 человек, а в марте 2012 года — 132 821 000 человек: на 740 тысяч рабочих мест меньше. Среди женщин были такие показатели: 66 122 000 и 65 439 000, а значит, в марте 2012 года работающих женщин было на 683 тысячи меньше, чем в январе 2009 года, когда Обама занял пост президента США. Разделите второе число на первое — и получите 92%. Создается впечатление, будто Обама ездил по стране и приказывал компаниям увольнять подряд всех женщин.
Но все не так. Эти числа представляют собой чистое сокращение рабочих мест. Мы не знаем, сколько рабочих мест было создано и сколько сокращено за эти три года; нам известно только то, что разность между двумя показателями составляет 740 тысяч. Показатель чистого сокращения занятости в одних случаях бывает положительным, в других отрицательным, поэтому брать от него процент — слишком опасное дело.
Интересную оценку показателю в 92,3%, приведенному командой Ромни, дали в Washington Post: «точный, но ложный». Задачу можно было бы сформулировать примерно так: «Сказался ли экономический спад и его последствия особенно тяжело на работающих женщинах, и если да, то в какой степени это является результатом политики администрации Обамы?» Какова форма кривой потери рабочих мест среди мужчин и женщин во время типичного экономического спада? Были ли у данного экономического спада заметные особенности в этом отношении? Какие именно места занимают преимущественно женщины? Какие решения Обамы негативно сказались на данном секторе экономики? Вы можете браться за калькулятор только после того, как сформулируете перечисленные вопросы. Но к данному моменту вся мысленная работа должна быть завершена. Деление одного числа на другое — просто расчеты; определение того, что на что следует делить, — это и есть математика.
ЧАСТЬ II. УМОЗАКЛЮЧЕНИЕ
Глава шестая. Библейский код и балтиморский фондовый брокер
Позвольте рассказать вам притчу. Однажды вы получаете от фондового брокера в Балтиморе новостной бюллетень; в нем идет речь о том, что вскоре курс определенных акций резко повысится. Проходит неделя, на протяжении которой, как и предсказывал балтиморский брокер, те акции действительно повысились в цене. На следующей неделе вы получаете еще одно письмо, причем на этот раз в нем содержится намек на акции, курс которых, по мнению этого брокера, вскоре упадет. И эти акции действительно резко упали в цене. Проходит десять недель подряд, и каждую неделю вы получаете очередную загадочную информационную рассылку с новым предсказанием, причем каждый раз это предсказание сбывается.
На одиннадцатой неделе вы получаете предложение инвестировать деньги через балтиморского фондового брокера, разумеется за изрядные комиссионные. На первый взгляд, как будто неплохая сделка, не так ли? Очевидно, что балтиморский фондовый брокер кое-что понимает — кажется совершенно невероятным, чтобы десять правильных прогнозов подряд о повышении и падении курсов акций сделал безнадежный дилетант без специальных знаний о рынке. На самом деле вы можете точно рассчитать шансы на успех: если дилетант дает правильный прогноз с вероятностью 50%, тогда вероятность 10 правильных прогнозов подряд составит (1/2)10 = 1/1024 = 0,1%.
Однако ситуация выглядит иначе, если описать ее с точки зрения балтиморского фондового брокера. В первую неделю он разослал 10 240 писем. Однако не все письма были одинаковыми. Половина писем были такими же, как и полученное вами письмо с прогнозом роста акций. В остальных письмах был прямо противоположный прогноз. Те 5120 человек, которые получили от брокера неправильный прогноз, больше не получали от него никаких писем. Однако вы и еще 5119 человек, которым пришло такое же письмо, что и вам, получили еще одну подсказку на следующей неделе. Из этих 5120 информационных писем в половине было сказано то же, что и в вашем письме, а в другой половине — прямо противоположное. После этой недели все равно оставалось 2560 человек, получивших два правильных прогноза подряд.
И так далее. После десятой недели останется десять счастливчиков (?), получивших от балтиморского брокера точные рекомендации по поводу выигрышных акций — независимо от того, что происходит на фондовом рынке. В любом случае существует десять получателей писем, в глазах которых он выглядит гением. Десять человек, с которых он рассчитывает собрать большие комиссионные. Десять человек, для которых прошлая результативность станет гарантией будущего успеха.
Глава седьмая. Есть ли у дохлой рыбы эмоциональная реакция
В современную эпоху, когда без труда получают огромные массивы данных, стандартные методы оценки результатов — то, как мы проводим грань между реальным явлением и случайной помехой, — оказались под большим вопросом. Если даже почивший навсегда лосось удачно проходит проверку на эмпатию, то необходимо срочно и очень серьезно задуматься: достаточно ли строгие критерии доказательства мы используем.
Существуют области математики (такие как геометрия и арифметика), которые наиболее отвечают нашей врожденной интуиции. Совсем другое дело — вероятность. Вот почему математическая теория вероятностей возникла на столь позднем этапе истории математики и почему она так поздно появляется в учебном плане по математике (об истории развития теории вероятностей см. Леонард Млодинов. (Не)совершенная случайность. Как случай управляет нашей жизнью).
Сценарий «не оказывает никакого воздействия» называют нулевой гипотезой. Нулевая гипотеза — это предположение о том, что изучаемое вами воздействие не имеет никаких последствий. Стандартную модель под названием «проверка значимости нулевой гипотезы» в наиболее распространенном виде разработал в начале ХХ столетия Рональд Эйлмер Фишер.
Процедуру опровержения нулевой гипотезы можно представить так.
- Провести эксперимент.
- Выдвинуть предположение, что нулевая гипотеза истинна, и обозначить символом p вероятность (согласно данной гипотезе) получения результатов со столь же крайними значениями, что были получены в результате наблюдений.
- Если это «p-значение» очень маленькое, радуйтесь — вы можете заявить, что ваши результаты статистически значимы. Если это число имеет большое значение, признайте тот факт, что нулевая гипотеза не была опровергнута.
Но насколько маленьким должно быть это «очень маленькое» значение? Нет принципиального способа провести четкое разграничение между тем, что является значимым, а что нет, но по традиции, которая началась еще со времен Фишера и которой принято придерживаться в настоящее время, в качестве пороговой величины используется значение p = 0,05.
Несмотря на то, что этот метод применялся как стандартный, находились люди, которые объявляли его огромной ошибкой. Что не так со значимостью? Прежде всего само слово. Лучше было бы объявить результат, прошедший проверку Фишера с p-значением меньше 0,05, «статистически заметным» или «статистически определимым», вместо того чтобы называть его «статистически значимым»! Эти термины были бы более близкими к сути данного метода, который просто говорит нам о существовании воздействия, но не позволяет определить размер или важность этого воздействия.
Глава восьмая. Доказательство от маловероятного
Я обратил внимание на такой факт: почти никто не знает, что такое логарифм. Позвольте мне исправить эту ситуацию. Логарифм положительного числа N, который обозначается как lg N, — количество цифр, из которых состоит это число.
Глава девятая. Международный журнал гаруспиции
Вот притча, которую я узнал от статистика по имени Козма Шализи1. Представьте, что вы гаруспик, то есть человек, который предсказывает будущие события по внутренностям принесенных в жертву овец. Вы и ваши коллеги отправляете материалы своей работы в рецензируемый журнал под названием «Международный журнал гаруспиции», чьи правила требуют, чтобы все без исключения опубликованные результаты прошли проверку на статистическую значимость.
Поскольку, в отличие от вас, я не верю в гаруспицию. Я считаю, что внутренности овцы ничего не могут предсказать, а когда данные совпадают, это просто дело случая. Иначе говоря, во всем, касающемся гадания на внутренностях животных, я сторонник нулевой гипотезы. Поэтому в моем мире успешное завершение любого эксперимента с гаруспицией весьма маловероятно. Насколько маловероятно? Стандартный порог статистической значимости, а значит, и критерий для публикации статьи в «Международном журнале гаруспиции» по соглашению установлен в виде p-значения, равного 0,05, или 1 из 20.
Если нулевая гипотеза всегда истинна (другими словами, если гаруспиция — это надувательство в чистом виде), тогда результаты только одного из двадцати экспериментов могут быть опубликованными. Тем не менее существуют сотни гаруспиков и тысячи овец со вспоротыми животами; при этом даже одна двадцатая предсказаний дает достаточно материала для заполнения каждого выпуска журнала новыми результатами, демонстрирующими эффективность этой методики.
Современная медицина и социология — отнюдь не гаруспиция. Тем не менее в последние годы многие ученые все громче бьют тревогу: возможно, в науке гораздо больше данных, полученных в духе гадания на внутренностях животных, чем нам хотелось бы признавать. Громче всех заявил об этом Джон Иоаннидис. В медицине большинство случаев вмешательства, которое мы предпринимаем, не обеспечивает требуемых результатов, а большинство связей, которые мы пытаемся обнаружить, отсутствуют.
Возьмем хотя бы связь генов с заболеваниями. Воздействие, о котором свидетельствуют результаты исследования, — это главным образом или всецело всего лишь шум в сигнале. Ученые называют эту проблему «проклятие победителя», и это одна из причин, почему при повторном проведении того же опыта впечатляющие, громко расхваливаемые результаты экспериментов зачастую не подтверждаются.
В значении 0,05 нет ничего особенного. Это абсолютно произвольное значение, чистая условность, которую выбрал Фишер. Однако условную границу, если придерживаться ее достаточно долго, можно ошибочно принять за то, что действительно происходит в реальном мире. Было бы ошибкой использовать р < 0,05 в качестве синонима определения «истинный» и p > 0,05 для обозначения понятия «ложный». Такое доказательство от маловероятного просто не работает в качестве принципа для выведения научной истины, лежащей в основе данных. Фишер писал: «В действительности ни у одного ученого нет фиксированного уровня значимости, в соответствии с которым он из года в год, при любых обстоятельствах отбрасывает гипотезы; скорее, он осмысливает каждую конкретную гипотезу в свете имеющихся доказательств и идей».
Глава десятая. Ты там есть, Бог? Это я, байесовский вывод
Многие опасаются эпохи больших данных. В какой-то степени страшит будущее: а вдруг начнут воплощаться пока еще туманные перспективы, что алгоритмы, обеспеченные достаточным объемом данных, начнут справляться с задачей логического вывода лучше самого человека (см. Педро Домингос. Верховный алгоритм).
Согласно модели будущего, Google должен знать вас: его центральное хранилище данных, обрабатывая миллионы микронаблюдений («Сколько времени он колебался, прежде чем щелкнуть на этом…», «Как долго его очки Google Glass задержались на том…» и так далее), начнет предвосхищать ваши поступки, предпочтения и даже мечты, особенно что касается покупок, которые вы захотите сделать, или вас убедят, что вы этого хотите.
Именно так все может быть! Но может и не быть. Существует множество математических задач, в которых обеспечение большего количества данных повышает точность полученного результата довольно предсказуемым способом. Например, чтобы предсказать траекторию движения астероида, необходимо измерить скорость его движения и определить местоположение, а также оценить гравитационное воздействие его астрономических соседей.
Однако некоторые задачи похожи скорее на прогноз погоды. Погода хаотична. Именно в процессе численного изучения погоды Эдвард Лоренц открыл математическую концепцию хаоса (см. Джеймс Глейк. Хаос. Создание новой науки). К чему ближе человеческое поведение — к астероиду или погоде? Как минимум в одном смысле поведение человека прогнозировать даже труднее, чем погоду. У нас есть очень хорошая математическая модель для погоды. В случае человеческого поведения у нас такой модели нет и, видимо, никогда не будет. Это делает задачу прогнозирования гораздо более трудной.
Проблема, с которой мы столкнулись, когда рассматривали доказательство от маловероятного; p-значение — это ответ на вопрос: «Вероятность, что наблюдаемый результат эксперимента будет иметь место при условии, что нулевая гипотеза правильна». Эта величина может быть довольно маленькой, например, р = 0,3.
Однако нам нужно знать другую условную вероятность: «Вероятность, что нулевая гипотеза правильна при условии наблюдения определенного результата эксперимента». Опасность возникает именно в случае, когда мы путаем вторую величину с первой. И такая путаница имеет место повсюду, не только в научных исследованиях. Когда окружной прокурор наклоняется к жюри присяжных и объявляет «Есть один шанс из пяти миллионов, повторяю, один шанс из пяти миллионов, что ДНК невиновного человека совпадет с ДНК, обнаруженной на месте преступления», он отвечает на первый вопрос: «Какова вероятность того, что невиновный человек выглядит виновным?» Однако работа жюри присяжных в том, чтобы найти ответ на второй вопрос: «Какова вероятность, что на первый взгляд виновный подсудимый невиновен?» На этот вопрос окружной прокурор уже не поможет им ответить.
Правило Байеса. Априорная вероятность описывает степень вашей уверенности в истинности теории до получения эмпирических данных, апостериорная вероятность характеризует степень уверенности после получения данных. При этом мы делаем байесовский вывод, поскольку переход от априорной к апостериорной вероятности основан на старой формуле теории вероятностей, которая называется теоремой Байеса.
Апостериорная вероятность зависит не только от эмпирических данных, которые вы получаете, но и от априорной вероятности. Это может показаться настораживающим. Разве наука не должна быть объективной? Вам хотелось бы заявить, что ваши убеждения основаны на одних только фактах, а не на каких-то априорных предубеждениях, с которыми вы вошли в эту дверь. Но давайте посмотрим правде в глаза: на самом деле ни у кого убеждения не формируются таким способом.
Если в результате эксперимента получены статистически значимые доказательства, что новая модификация существующего лекарственного препарата замедляет развитие некоторых разновидностей рака, скорее всего вы будете достаточно уверены в эффективности нового препарата. Но, если вы получите те же результаты, поместив пациентов в пластиковую модель Стоунхенджа, разве примете вы, пусть даже неохотно, вывод, что это древнее сооружение действительно фокусирует энергию колебаний Земли на организме человека и останавливает развитие опухоли? Нет, не примете, потому что это полная чушь. Вы подумаете, что, по всей видимости, Стоунхенджу просто повезло. У вас разные априорные оценки этих двух теорий, поэтому в итоге вы по-разному интерпретируете эмпирические данные, несмотря на то что в численном выражении они одинаковы.
Полагаться исключительно на проверку значимости нулевой гипотезы — это значило бы поступать совершенно не по-байесовски: строго говоря, такой подход предлагает нам относиться к лекарству от рака и к пластиковому Стоунхенджу с одинаковым уважением. В действительности специалисты по байесовской статистике зачастую вообще не думают о нулевой гипотезе.
Кстати, Фишер полностью отказался принять такой подход. Он безжалостно раскритиковал книгу Джона Мейнарда Кейнса «Трактат о вероятности», в которой говорится, что вероятность «измеряет “степень разумной убежденности”, которая приписывается теореме в свете представленных доказательств». На самом деле, теорема Байеса предоставляет в наше распоряжение правило относительно того, как следует корректировать степень своей уверенности в чем-то в свете новых наблюдений.
ЧАСТЬ III. ОЖИДАНИЕ
Г лава двенадцатая. Чаще опаздывайте на самолеты!
Лауреат Нобелевской премии по экономике за 1982 год Джордж Стиглер говорил: «Если вы никогда не опаздываете на самолет, значит, вы проводите слишком много времени в аэропорту». Каким бы необычным ни казалось утверждение Стиглера, вычисление ожидаемой ценности показывает, что оно абсолютно корректно.
Для того, чтобы сравнить разные события, нужна единая мера. Экономисты назвали ее полезностью и иногда измеряют в ютилях. Даниил Бернулли описал всё это в 1738 году, в труде Опыт новой теории измерения жребия: Петр бросает вверх монету, пока она не упадет лицевой стороной вверх; если это произойдет после первого броска, он должен дать Павлу 1 дукат, но, если только после второго — 2 дуката, после третьего — 4, после четвертого — 8 и так далее, так что после каждого броска число дукатов удваивается. Очевидно, что для Павла это достаточно привлекательный сценарий игры, за участие в которой он готов выложить какую-то сумму. Но какую именно?
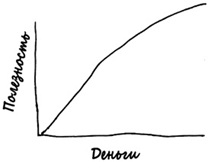
Бернулли утверждал: было бы ошибкой говорить, что дукат — это просто дукат. Дукат в руках богатого человека имеет иную ценность, чем дукат в руках крестьянина. В два раза больше дукатов не означает в два раза больше ютилей: не все линии прямые, а зависимость между деньгами и их полезностью отображается в виде одной из таких непрямых линий (рис. 5).
Рис. 5. Полезность каждой последующей единицы снижается
Принцип ожидаемой полезности притягательно прямолинеен и прост: при наличии ряда вариантов следует выбирать тот вариант, который имеет максимальную ожидаемую полезность. Пожалуй, этот принцип наиболее близок к математической теории индивидуального принятия решений из всего, что у нас есть. Кроме того, модель ожидаемой полезности охватывает многие аспекты того, как люди принимают решения, поэтому она остается основным количественным инструментом среди всех тех методов, которыми пользуются социологи. Свой трактат Опыт философии теории вероятностей, написанный в 1814 году, Пьер Симон Лаплас закончил такими словами: «Мы видим в этом эссе, что теория вероятностей есть в сущности не что иное, как здравый смысл, сведенный к исчислению: она заставляет оценивать с точностью то, что рациональные умы чувствуют, как бы инстинктом, часто не отдавая себе в этом отчета. …Она не оставляет места для сомнения в выборе мнений и решений; ее применение позволяет сделать самый правильный выбор».
Дэниел Эллсберг сформулировал головоломку. Предположим, у вас есть урна, внутри которой находится 90 шаров. Вам известно, что 30 из этих шаров красные, а про остальные 60 шаров вы знаете только то, что некоторые из них черные, а некоторые желтые. Ведущий эксперимента предлагает вам следующие четыре варианта действий:
- Красный. Вы получите 100 долларов, если следующий шар, который будет вынут из урны, окажется красным; в противном случае вы не получите ничего.
- Черный. Вы получите 100 долларов, если следующий шар окажется черным; в противном случае вы не получите ничего.
- Не красный. Вы получите 100 долларов, если следующий шар будет либо черным, либо желтым; в противном случае вы не получите ничего.
- Не черный. Вы получите 100 долларов, если следующий шар будет либо красным, либо желтым; в противном случае вы не получите ничего.
Какой вариант вы выберете?
Как скажет впоследствии Дональд Рамсфельд, есть известное неизвестное и есть неизвестное, и с ними необходимо вести себя по-разному. «Известное неизвестное» подобно варианту «красный»: мы не знаем, какой шар будет вынут, но можем определить вероятность, что это будет шар нужного нам цвета. С другой стороны, вариант «черный» подвергает игрока воздействию «неизвестного»: мы не только не уверены в том, что шар будет черным, но и не знаем, какова вероятность того, что он окажется черным. В книгах по теории принятия решений первый тип неизвестного называется риском, а второй неопределенностью. (см. Фрэнк Хейнеман Найт. Риск, неопределенность и прибыль).
Глава тринадцатая. Где пересекаются железнодорожные рельсы
Даниель Канеман и Амос Тверски выдвинули предположение, что люди в основном склонны придерживаться образа действий, отличающегося от того, что предписывает кривая полезности. Их работа о теории перспектив, за которую Канеман впоследствии получил Нобелевскую премию, рассматривается сейчас в качестве основополагающей в концепции бихевиористской экономики, чья задача состоит в создании максимально точной модели поведения людей: как они действуют на самом деле, а не как должны действовать согласно абстрактной концепции рациональности (см. Даниэль Канеман. Думай медленно… решай быстро). Теория Канемана—Тверски гласит: люди склонны придавать маловероятным событиям большее значение по сравнению с человеком, придерживающимся аксиом Неймана—Моргенштерна. Именно поэтому притягательность джекпота превосходит уровень, который можно было бы считать приемлемым согласно строгой оценке ожидаемой полезности.
Как насчет другого сравнения? Открытие магазина или продажа услуг — отнюдь не то же самое, что покупка лотерейных билетов. Ведя свой небольшой бизнес, вы в какой-то степени контролируете собственный успех. Однако у этих двух явлений есть нечто общее: для большинства людей открытие компании — это заведомо проигрышное дело. Не имеет значения, насколько вкусным будет ваш соус для барбекю, или насколько новаторским будет ваше приложение, или насколько жесткими будут ваши методы ведения бизнеса, — у вас гораздо больше шансов потерпеть неудачу, чем добиться успеха.
Такова природа предпринимательства, поскольку вы балансируете на грани между очень низкой вероятностью разбогатеть, довольно большой вероятностью зарабатывать на жизнь тяжелым трудом и существенно высокой вероятностью потерять все свои деньги. Если подсчитать цифры, для большой части потенциальных предпринимателей ожидаемая финансовая ценность, подобно ценности лотерейного билета, окажется меньше нуля. Обычные предприниматели (как и обычные покупатели лотерейных билетов) переоценивают свои шансы на успех. Даже бизнес, которому удается уцелеть, обычно приносит своим владельцам меньше денег, чем они получили бы в виде заработной платы в успешной компании. Однако полезность ведения бизнеса измеряется не только в ожидаемой денежной стоимости. Сам акт осуществления мечты или даже попытки ее осуществить — уже есть часть вознаграждения.
ЧАСТЬ IV. РЕГРЕССИЯ
Глава четырнадцатая. Триумф посредственности
Хорас Секрист был профессором статистики и руководителем отдела исследований в области ведения бизнеса Северо-Западного университета, специалистом по практическому применению методов количественного анализа в бизнесе, а также автором широко распространенного учебника по статистике для студентов и руководителей компаний. В 1933 году он опубликовал книгу «Триумф посредственности в бизнесе».
Для начала он разделил компании на группы, тщательно отделив успешные от неэффективных неудачников. Например, в 1916 году 120 магазинов одежды, которые изучал Секрист, сначала были упорядочены по отношению объема продаж к объему расходов, а затем разделены на шесть групп («секстили») по двадцать магазинов в каждой группе. Секрист считал, что со временем магазины из верхнего секстиля закрепят свой успех и займут еще более высокие позиции по мере совершенствования и без того хороших навыков работы на рынке. Но на самом деле он обнаружил нечто прямо противоположное.
Секрист сделал вывод, что причина заключалась в природе самой конкуренции, которая толкает успешные компании вниз и поддерживает их некомпетентных конкурентов: «Новые компании создаются людьми неподготовленными, во всяком случае неопытными. Пока конкуренция остается «свободной» не сможет устоять ни совершенство, ни несовершенство. Напротив, посредственность укрепит свои позиции. Господствует средний уровень интеллекта тех, кто занимается бизнесом, а методы, свойственные такому типу коммерческого мышления, становятся правилом».
Концепция регрессии Секриста восходит к идеям британского ученого XIX столетия Фрэнсиса Гальтона, разработавшего основы евгеники. Как было известно Гальтону, у высоких родителей обычно рождаются высокие дети. Вот в чем состоит удивительное открытие Гальтона: дети не всегда оказываются такими высокими, как их родители. Такая же закономерность имеет место и у низкорослых родителей, только в обратном направлении: их дети также будут иметь низкий рост, но не настолько, как у самих родителей. Гальтон открыл феномен, который сейчас называют регрессией к среднему значению. Отсутствие регресса теоретически возможно, но это привело бы к повышению изменчивости, а значит, в каждом поколении было бы больше очень высоких и очень низкорослых людей.
Гальтон считал, что то же самое должно касаться умственных способностей и интеллектуальных успехов: дети великого композитора, ученого или политического лидера зачастую добиваются какого-то признания в той же области, что их выдающиеся родители, но редко достигают, как они, высшей точки славы. Люди имеют высокий рост или по причине наследственной предрасположенности, или потому, что их росту способствуют внешние факторы, или по обеим причинам сразу. Чем выше человек, тем больше вероятность, что высокому росту способствуют именно обе причины.
Дети высоких людей унаследуют их гены, но нет никаких гарантий, что внешние факторы снова будут способствовать более высокому росту, чем рост, обусловленный наследственностью. Таким образом, в среднем дети будут выше обычного человека, но не такими высокими, как их родители. Именно это вызывает регрессию к среднему значению: не загадочная сила, которая благоволит посредственности, а просто воздействие наследственности в сочетании со случаем.
То же самое касается и бизнеса. Секрист не ошибался по поводу компаний, получавших самую большую прибыль в 1922 году: по всей вероятности, это были компании с самым эффективным управлением в своих секторах. Но им также сопутствовало везение. С течением времени руководство этих компаний вполне могло оставаться таким же мудрым и проницательным. Однако у компаний, которым повезло в 1922 году, было не больше шансов на такое же везение через десять лет, чем у любой другой компании.
На самом деле практически все жизненные обстоятельства, которые сопряжены со случайными колебаниями во времени, могут быть подвержены влиянию регрессии. Биологи искренне считают, что регрессия связана с биологией, специалисты по теории управления (такие как Секрист) предпочитают связывать ее с конкуренцией, литературные критики приписывают ее творческому истощению — но дело не в этом. Все дело в математике. Для отображения зависимости роста сына от роста отца Гальтон изобрел тип графика, который мы называем теперь диаграммой разброса (подробнее см. Джин Желязны. Говори на языке диаграмм). Диаграммы разброса особенно хорошо раскрывают взаимосвязи между двумя переменными.
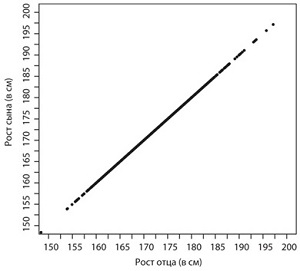
Предположим, например, что каждый сын и отец имеют одинаковый рост. Это ситуация, когда случай не играет никакой роли, а ваш рост целиком и полностью зависит от унаследованных от отца качеств (рис. 6).
Рис. 6. Рост сына полностью определяется ростом отца; случай не играет никакой роли
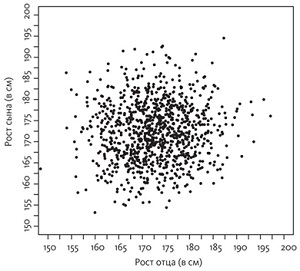
Когда рост сыновей никак не связан с ростом отцов, диаграмма разброса выглядит как на рис. 7. Это регрессия к среднему значению в самом выраженном виде: сыновья высоких отцов возвращаются к среднему росту, оказываясь в итоге не выше сыновей низкорослых отцов.
Рис. 7. Рост сына никак не связан с ростом отца; влияние оказывает лишь случай
Однако диаграмма разброса Гальтона не похожа ни на один из этих крайних случаев. Она выглядит иначе (рис. 8).
Рис. 8. На рост сына влияет как рост отца, так и иные факторы
Гальтон сразу заметил, что его диаграммы разброса в той или иной мере заключены в эллипс. Причина этого заключается в одном фундаментальном свойстве математики — в ней существует множество сложных объектов, но совсем немного простых. Следовательно, если у вас есть задача, решение которой допускает простое математическое описание, значит, существует только несколько вариантов такого решения. Таким образом, самые простые математические объекты широко распространены и выполняют множество обязанностей в качестве решений научных задач разных типов. Самые простые линии — прямые. Следующий тип простейших линий — линии, представленные квадратными уравнениями (в том числе, и эллипс).
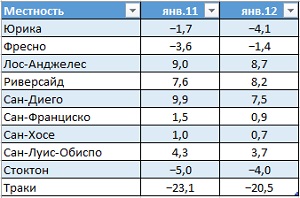
Что же такое корреляция с точки зрения геометра? Например, если необходимо изучить связь между показателями температуры за два разных года в 10 городах (рис. 9), можно построить вектор в десятимерном пространстве. Два столбца чисел можно представить в виде двух десятимерных векторов (рис. 10).
Рис. 9. Данные о температуре (условные единицы)
Рис. 10. Вектора в 10-мерном пространстве (для одного из векторов приведены все его 10 координат)
Корреляцию между этими двумя переменными определяет угол между двумя векторами. Точнее – косинус угла между векторами. Косинус угла равен 1, если угол равен 0 (то есть когда векторы указывают в одном направлении), и −1, если угол равен 180 градусам (векторы указывают в противоположных направлениях). Между двумя переменными имеет место положительная корреляция, когда соответствующие векторы образуют острый угол, и отрицательная корреляция в случае тупого угла.
Означает ли отсутствие корреляции, что переменные никак не связаны друг с другом? Совсем нет. Корреляция в понимании Гальтона ограничена в очень важном смысле: она обнаруживает линейные связи между переменными, когда увеличение одной переменной совпадает с пропорциональным увеличением (или уменьшением) другой переменной. Но, подобно тому как не все линии прямые, не всякая зависимость бывает линейной. Имейте это в виду, когда вам скажут, что два явления в природе или в обществе оказались некоррелированными. Это не означает, что между ними вообще нет связи; нет только связи того типа, которую должна обнаружить корреляция.
ЧАСТЬ V. СУЩЕСТВОВАНИЕ
Глава семнадцатая. Общественное мнение? Нет такого
Средний американец считает, что существует множество совершенно бесполезных федеральных программ, бросающих наши деньги на ветер, и готов урезать их, чтобы привести бюджет в равновесие. Проблема в том, что в обществе нет консенсуса по поводу того, какие программы бесполезны.
Система, которая опирается на принцип подчинения меньшинства большинству, довольно проста, изящна и, кажется, даже справедлива, но она эффективна только в том случае, если необходимо сделать выбор из двух вариантов. Если вариантов больше двух, в предпочтениях большинства начинают появляться противоречия (подробнее см. Парадокс Кондорсе, теорема Эрроу, или Как мы принимаем решения).
Во время президентских выборов 1992 года Билл Клинтон набрал 43% голосов избирателей, опередив Джорджа Буша-старшего, который набрал 38% голосов, и Росса Перо, получившего 19% голосов. Иначе говоря, большинство избирателей (57%) считали, что Билл Клинтон не должен быть президентом. С другой стороны, большинство избирателей (62%) считали, что Джордж Буш не должен быть президентом. А самое крупное большинство избирателей (81%) считали, что Росс Перо не должен быть президентом. Интересы каждого варианта большинства невозможно удовлетворить одновременно, а значит, в одном случае принцип большинства не будет выполнен.
Но давайте предположим, что 19% избирателей, отдавших свои голоса за Перо, разделились на 13% тех, кто считает Буша вторым лучшим кандидатом, а Клинтона худшим из всех кандидатов, и 6% тех, кто считает, что Клинтон лучший из двух кандидатов от основных партий. В таком случае, если вы зададите избирателям прямой вопрос: кого они хотят видеть президентом, Клинтона или Буша, — большинство (51%) отдали бы предпочтение Бушу.
Почему чувства избирателей по отношению к Россу Перо оказывают влияние на то, кто именно станет президентом — Буш или Клинтон? Думаю, правильный ответ состоит в том, что ответа просто нет. Такой штуки — общественного мнения — просто не существует. Точнее говоря, оно существует только в некоторых случаях, когда речь идет о вопросах, по которым у большинства есть однозначное мнение.
Глава восемнадцатая. «Я создал странный новый мир из ничего!»
Кондорсе считал, что на вопросы типа «Кто самый лучший лидер?» обязательно найдется какой-то правильный ответ, а граждане — что-то вроде прибора для научных исследований таких вопросов. В наше время мы уже так не говорим о демократии. Сегодня для большинства людей привлекательность демократического выбора состоит в его справедливости.
Это не просто дискуссия о политике — здесь вопрос фундаментальный, применимый к любой области психической деятельности. Мы пытаемся понять, что соответствует истине, или определить, какие умозаключения позволяют нам устанавливать существующие правила и процедуры. К счастью, эти понятия обычно приходят к соглашению, однако настоящие трудности, а вместе с ними и все самое концептуально интересное происходят там, где они расходятся.
Возможно, вы считаете очевидным, что именно поиск истины и есть то, чем мы должны заниматься. Однако так бывает не всегда и особенно в уголовном праве, где расхождения налицо: есть совершившие преступление обвиняемые, но им нельзя вынести приговор (хотя бы потому, что доказательства получены с нарушениями); есть невиновные, осужденные за преступление, которого они не совершали. Что можно считать справедливым в этом случае — наказать виновного и освободить невиновного или придерживаться принципов уголовного судопроизводства, к чему бы это ни привело?
Эта традиция обозначается термином «формализм». Именно об этом говорил Годфри Гарольд Харди, когда с восхищением отметил, что математики XIX столетия начали наконец спрашивать «как определить 1 − 1 + 1 − 1 +…», а не «что есть 1 − 1 + 1 − 1 +…». Это позволяло им избежать «ненужных затруднений», преследовавших математиков более ранних времен.
Величайшим сторонником формализма в математике был немецкий математик Давид Гильберт; его список двадцати трех проблем, представленный в Париже, на Международном конгрессе математиков в 1900 году, определил направление развития математики на большую часть ХХ столетия.
Значительное количество проблем Гильберта было вскоре решено; другие проблемы, например, под номером восемнадцать — о максимально плотной упаковке сфер, — были решены только недавно. Некоторые проблемы до сих пор остаются нерешенными. Минимум в одном случае великий Гильберт ошибся. В проблеме под номером десять он предложил найти алгоритм, позволявший взять любое уравнение и определить, есть ли у него решение, при котором все переменные принимают целочисленные значения, но в 1960–1970-е годы математики Мартин Дэвис, Юрий Матиясевич, Хилари Патнэм и Джулия Робинсон опубликовали ряд работ, в которых было доказано, что такого алгоритма не существует.
Вторая проблема в списке проблем, которые Гильберт представил перед собравшимися в Париже математиками, была сформулирована так: доказать, что аксиомы непротиворечивы, другими словами, — что конечное число основанных на них логических рассуждений не может привести к получению противоречивых результатов.
Однако Гильберта ждало разочарование. В 1931 году Курт Гёдель доказал свою знаменитую вторую теорему о неполноте, которая гласила, что не существует финитного доказательства непротиворечивости арифметики. Он погубил программу Гильберта одним ударом (см. Даглас Хофштадтер. Гедель, Эшер, Бах. Эта бесконечная гирлянда, Эрнест Нагель, Джеймс Рой Ньюмен. Теорема Гёделя).
Марк Твен сказал: «Требуется тысяча человек, чтобы изобрести телеграф или паровой двигатель, или фонограф, или телефон, или еще что-нибудь столь же важное, а мы приписываем изобретение последнему из них и забываем об остальных».
Эпилог. Как быть правым
Некоторых людей критикуют за их уклончивые формулировки типа: «Видите ли, с одной стороны, неопределенность могла бы быть подобна этому, но, с другой стороны, она вполне могла бы представлять собой и нечто такое…» Когда кто-то хочет осудить таких людей, он обычно приводит цитату из речи Теодора Рузвельта «Гражданство в республике», с которой он выступил в Сорбонне в 1910 году, вскоре после окончания своего президентского срока. Рузвельт говорит о том, что выживание цивилизации зависит от смелых, обладающих здравым смыслом, мужественных людей, — и лейтмотивом проходит мысль о торжестве сильных и бесстрашных над мягкими, размышляющими, бесполезными.
В речи Рузвельта были и такие слова: «Кабинетный философ, утонченный и культурный человек, который на основании своих книг говорит, как следует управлять людьми в идеальных условиях, совершенно бесполезен в реальной государственной работе». Читая эти слова, я думаю о Кондорсе, который проводил все свое время в библиотеке и который сделал для французского государства больше, чем большинство деловых и энергичных его современников.
Но есть и другие. В их понимании неуверенность — это качество сильного человека, а не слабака. И математика — один из элементов этого «неустойчивого равновесия». Математика еще и инструмент, с помощью которого мы можем рассуждать о неопределенности, приручая ее. Математика предоставляет нам возможность демонстрировать принципиальную неуверенность. Не просто всплескивать руками и говорить «ах», а занимать твердую позицию: «Я в этом не уверен, вот почему я в этом не уверен, и вот примерно в какой степени я в этом не уверен». Или того больше: «Я в этом не уверен, и вы тоже не должны быть уверены».
В наше время настоящим рыцарем принципиальной неопределенности является Нейт Сильвер, игрок в онлайновый покер, который стал знатоком бейсбольной статистики, а затем превратился в политического аналитика, публикации которого в колонке New York Times на тему президентских выборов 2012 года привлекли к методам теории вероятностей большее внимание общественности, чем когда бы то ни было (см. Нейт Сильвер. Сигнал и шум).






благодарю!
Присоединяюсь!
Огромное спасибо за публикацию книги в переводе.
Студент американского универа:-)
Специализация — political science.
Пишу проект, который включает рецензии на книги.
Элленберг в их числе. Перевод значительно облегчает мою задачу, помогает конкретнее сформулировать мысль. Спасибо!