Книга венгерского математика, содержащая собрание неожиданных выводов и утверждений из теории вероятностей, математической статистики и теории случайных процессов. Написана живо и увлекательно. Рассматриваются как классические парадоксы, двигавшие развитие науки, начиная с XVI в., так и современные проблемы теории вероятностей. Большинство аспектов вполне доступно, но отдельные вопросы требуют серьезной математической подготовки.
Габор Секей. Парадоксы в теории вероятностей и математической статистике. – М.: Мир, 1990. – 240.
Скачать конспект (краткое содержание) в формате Word или pdf
КЛАССИЧЕСКИЕ ПАРАДОКСЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Парадокс игры в кости. «Азартные игры» в мире физических частиц
Самой ранней книгой по теории вероятностей считается «Книга об игре в кости» (De Ludo Аlеае) Джероламо Кардано (1501–1576 гг.), которая в основном посвящена игре в кости. Итак, правильная игральная кость при бросании с равными шансами падает на любую из граней 1, 2, 3, 4, 5 или 6. В случае бросания двух костей сумма выпавших чисел заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2, …, 6 можно получить двумя разными способами: 9 = 3 + 6 = 4 + 5 и 10 = 4 + 6 = 5 + 5. Почему тогда 9 появляется чаще?
Объяснение. Задача настолько проста, что кажется странным, что в свое время ее считали трудной. Кардано отмечал необходимость учета порядка выпадения чисел. (В противном случае не все исходы были бы равновозможными.) 9 и 10 могут получаться следующим образом: 9 = 3 + 6 = 6 + 3 = 4 + 5 = 5 + 4 и 10 = 4 + 6 = 6 + 4 = 5 + 5. Это означает, что 9 можно «выбросить» четырьмя способами, а 10 – лишь тремя. Следовательно, шансы получить 9 предпочтительней. (Поскольку две кости дают 6*6 = 36 различных равновозможных пар чисел, шансы получить 9 равны 4/36, а для 10 —лишь 3/36.)
Парадокс де Мере
Существует старая история, впервые рассказанная, видимо, Лейбницем, о том, как известный французский игрок XVII века шевалье де Мере по дороге в свое имение в Пуату встретил Блеза Паскаля, одного из знаменитейших ученых XVII века. Де Мере поставил перед Паскалем две задачи, обе связанные с азартными играми. Обе задачи Паскаль обсуждал в 1654 г. в своей переписке с Пьером де Ферма, другим высокоодаренным ученым, жившим в Тулузе. Оба ученых пришли к одинаковому результату (подробнее см. Альфред Реньи. Письма о вероятности: письма Паскаля к Ферма).
При четырех бросаниях одной игральной кости вероятность того, что по крайней мере один раз выпадет 1, больше 1/2. В то же время при 24 бросаниях двух костей вероятность выпадения двух 1 одновременно (по крайней мере однажды) меньше 1/2. Это кажется удивительным, так как шансы получить одну 1 в шесть раз больше, чем шансы выпадения двух 1, а 24 как раз в 6 раз больше 4.
Объяснение. Если правильную игральную кость бросают k раз, то число возможных (и равновероятных) исходов равно 6k. В 5k случаях из этих 6k кость не ляжет на шестерку, и, следовательно, вероятность выпадения по крайней мере один раз 1 при k бросаниях равна (6k – 5k)/6k = 1 – (5/6)k, что больше 1/2, если k = 4. С другой стороны, величина 1 – (35/36)k, которая получается аналогично, все еще меньше 1/2 для k = 24 и превосходит 1/2, начиная с k = 25. Так что «критическое значение» для одной кости равно 4, а для пары костей равно 25. Это безусловно правильное решение на самом деле не удовлетворило де Мере, так как сам ответ он уже знал, но из решения так и не понял, почему ответ не согласуется с «правилом пропорциональности критических значений», утверждающим, что если вероятность уменьшается в шесть раз, то критическое значение возрастает в шесть раз (4:6 = 24:36). Абрахам де Муавр (1667–1754 гг.) в своей книге Доктрина шансов, опубликованной в 1718 г., доказал, что «правило пропорциональности критических значений» недалеко от истины, так как, если р — вероятность некоторого события (например, вероятность «выбросить» единицу есть р = 1/6), то критическое значение k можно найти, решая уравнение (1 – p)х = ½ (это уравнение имеет решение, если р заключено строго между 0 и 1). Критическое значение k есть наименьшее целое число, превосходящее х. Решение этого уравнения дается формулой:
(1) х = –ln2/ln(1 – p) = ln2/(p + p2/2 + …),
где ln – натуральный логарифм. Из вида решения ясно, что если р2 пренебрежимо мало, то р убывает почти пропорционально возрастанию критического значения, как де Мере и предполагал. Парадокс де Мере возникает потому, что для р=1/6 величина р2/2 (и другие слагаемые знаменателя в формуле 1) не настолько мала, чтобы ею можно было пренебречь. Таким образом, «правило пропорциональности критических значений» является правилом асимптотически верным, ошибка от его применения растет с ростом р. Это и есть настоящее решение данного парадокса.
Парадокс раздела ставки
Этот парадокс был впервые опубликован в Венеции в 1494 г. в обзоре средневековой математики. Автор Лука Пачоли (1445–1509 гг.) назвал свою книгу «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности» (имя Пачоли больше известно, как автора труда, в котором впервые изложена двойная запись в бухгалтерии; см. Лука Пачоли. Трактат о счетах и записях). Интересно отметить, что в Милане Пачоли близко подружился с Леонардо да Винчи, и благодаря этой дружбе Леонардо иллюстрировал работу Пачоли «О божественных пропорциях», опубликованную в Венеции в 1509 г. Недавно Эйштейн Оре обнаружил итальянскую рукопись, датированную 1380 г., в которой также упоминается парадокс раздела ставки. Многое указывает на арабское происхождение задачи или по крайней мере на то, что в Италию задача попала вместе с арабским учением. Как бы ни стара была проблема, фактом остается, что для ее правильного решения потребовалось очень много времени. Сам Пачоли даже не видел связи этой задачи с теорией вероятностей; он рассматривал ее как задачу о пропорциях. Неверное решение дал Никколо Тарталья (1499–1557 гг.), хотя он был достаточно гениален, чтобы в математической дуэли за одну ночь открыть формулу корней кубического уравнения. После нескольких неудачных попыток Паскаль и Ферма в конце концов в 1654 г. независимо друг от друга нашли правильный ответ. Это открытие было настолько важным, что многие считают этот год временем рождения теории вероятностей, а все предшествующие результаты относят к ее предыстории.
Два игрока играют в честную игру (т.е. у обоих шансы победить одинаковы), и они договорились, что тот, кто первым выиграет 6 партий, получит весь приз. Предположим, что на самом деле игра остановилась до того, как один из них выиграл приз (например, первый игрок выиграл 5 партий, а второй – 3). Как справедливо следует разделить приз? Хотя в действительности эта проблема не является парадоксом, безуспешные попытки некоторых величайших ученых решить ее, а также неверные противоречивые ответы создали легенду о парадоксе. Согласно одному ответу, приз следовало разделить пропорционально выигранным партиям, т. е. 5:3. Тарталья предложил делить в отношении 2:1. (Наиболее вероятно, что он рассуждал следующим образом: так как первый игрок выиграл на две партии больше, что составляет третью часть от необходимых для победы 6 партий, то первый игрок должен получить одну треть от приза, а оставшуюся часть следует разделить пополам.) На самом деле справедливым является раздел в отношении 7: 1, что сильно отличается от предыдущих результатов.
Объяснение. И Паскаль, и Ферма рассматривали эту проблему как задачу о вероятностях. Так что справедливым будет раздел, пропорциональный шансам первого игрока выиграть приз. Следуя идее Ферма, продолжим игру тремя фиктивными партиями, даже если некоторые из них окажутся лишними (т.е. когда один из игроков уже выиграл приз). Такое продолжение делает все 2*2*2 = 8 возможных исходов равновероятными. Поскольку только при одном исходе второй игрок получает приз (т.е. когда он выигрывает все три партии), а в остальных случаях побеждает первый игрок, справедливым является отношение 7:1.
Парадокс раздачи подарков
Несколько человек решили сделать друг другу подарки следующим образом. Каждый приносит подарок. Подарки складываются вместе, перемешиваются и случайно распределяются среди участников. Этот справедливый способ раздачи подарков применяется часто, так как считают, что для больших групп людей вероятность совпадения, т. е. получения кем-то собственного подарка, очень мала. Парадоксально, но вероятность по крайней мере одного совпадения намного больше вероятности того, что совпадений нет (кроме случая, когда группа состоит из двух человек, тогда вероятность отсутствия совпадений равна 50%).
Объяснение. Рассмотрим компанию из n человек, тогда число подарков также равно n. Подарки могут быть распределены n! различными способами. (Это общее число исходов.) Число исходов, в которых никто не получит свой собственный подарок, равно
так что отношение числа благоприятных исходов к общему числу исходов вычисляется по формуле
(3) рn = 1/2! – 1/3! + … +(–1)n/n!
и рn действительно меньше 1/2 при n > 2.
Когда собирается, к примеру, по крайней мере 6 человек (n ≥ 6), имеем рn ≈ 1/е ≈ 0,3679 с точностью до 4 знаков после запятой. Вероятность определенного совпадения, т.е. вероятность того, что конкретный человек получит свой собственный подарок, очевидно, равна 1/n, и 1/п стремится к 0 при увеличении n. Этот парадокс показывает «по капельке — море, по былинке— стог»: несмотря на малость вероятностей (1/n) определенных совпадений, вероятность того, что произойдет по крайней мере одно совпадение, приблизительно равна 2/3.
Санкт-петербургский парадокс
В начале XVII века Академия наук в Санкт-Петербурге опубликовала статью (на латинском языке), математические вычисления в которой казалось противоречили здравому смыслу. Статью написал Даниил Бернулли, и благодаря ему петербургский парадокс стал известен.
Единичное испытание в петербургской игре состоит в бросании правильной монеты до тех пор, пока не выпадет решка; если это произойдет при r-м бросании, игрок получает 2r долларов из банка. Таким образом, с каждым бросанием выигрыш удваивается. Вопрос в следующем: сколько следует заплатить игроку за участие в игре, чтобы игра стала безобидной? Безобидность петербургской игры рассматривается в классическом смысле: среднее значение (или математическое ожидание) чистого выигрыша должно быть равно 0. Однако, как ни удивительно, это естественное требование невыполнимо, какую бы (конечную) сумму денег игрок ни заплатил.
Объяснение. Потери банка имеют бесконечное математическое ожидание, так как вероятность окончания игры при k-м бросании равна 1/2k и в этом случае игрок получает 2k долларов. Тогда банк в среднем должен заплатить
долларов, что составляет бесконечно большую сумму денег, так что игра стала бы безобидной при бесконечном взносе. Хотя все математические вычисления корректны, результат неприемлем, поэтому некоторые математики предположили реализуемые модификации.
Бюффон, Крамер и другие предложили исходить из естественного предположения об ограниченности ресурсов (т.е. банк имеет лишь ограниченное количество денег). Пусть в банке есть миллион долларов. Тогда математическое ожидание выигрыша для игрока равно
(мы учли, что 220 > 106). Следовательно, при вступительном взносе игрока, равном 21 доллару, игра станет в некоторой степени выгодной для банка.
(На самом деле в своей статье Даниил Бернулли находит решение, на основе развиваемой им теории полезности; эта статья считается первой работой по теории риска; подробнее см. Даниил Бернулли. Опыт новой теории измерения жребия. – Прим. Багузина)
Парадокс смертности населения
Математические исследования по смертности населения и продолжительности жизни начались на раннем этапе развития капитализма благодаря потребностям страховых компаний. Эдмунд Галлей (открывший комету, названную его именем) опубликовал в 1693 г. статью о таблицах смертности, которая положила начало математической теории страхования жизни. Следующий парадокс (замеченный Даламбером) показывает одну из «зубодробильных» проблем новой теории.
По таблице Галлея средняя продолжительность жизни равна 26 годам и вместе с тем с равными шансами можно умереть до 8 лет и прожить больше 8 лет.
Объяснение. Действительно, согласно таблице Галлея, с равными шансами можно прожить больше 8 лет и умереть в возрасте до 8 лет, но если человек дожил до 8 лет, то он может прожить еще несколько десятилетий. Следовательно, неудивительно, что средняя продолжительность жизни намного больше 8 лет. Предположим, что среди тысячи человек лишь один достигает возраста Мафусаила (по легенде он прожил 969 лет). Тогда средний возраст значительно увеличится, но их вероятная продолжительность жизни (возраст, до которого они доживают с вероятностью 50%) существенно не изменится. Никакого парадокса нет, если обратить внимание, что среднее совсем не обязательно равно медиане.
Парадокс закона больших чисел Бернулли
В математике найдется немного законов, которые столь же часто понимались превратно, как законы больших чисел. (Не слишком широко известно даже то, что существует несколько законов больших чисел.) Первый закон больших чисел был доказан Якобом Бернулли (1654–1705 гг.) в его книге, названной «Ars conjectandi» («Искусство предположений»), которая была опубликована только после смерти автора в 1713 г. Сам Бернулли не использовал понятия «закон больших чисел»; это название ввел Пуассон лишь в 1837 г. По закону Бернулли, если правильную монету бросают n раз и при этом k раз выпадает герб, то при увеличении числа бросаний (n) отношение k/n (относительная частота выпадения герба) стремится к 1/2. Точнее, для произвольных положительных чисел ε и δ и достаточно большого n (зависящего от ε и δ) величина (k/n—1/2) меньше ε с вероятностью, превосходящей 1 – δ.
Игроки часто уверены, что если правильная монета много раз падает гербом, то, согласно закону больших чисел, вероятность выпадения решки с необходимостью возрастает. (В противном случае нарушалось бы то, что при очень большом числе бросаний выпадения герба и решки происходят приблизительно одинаково часто.) С другой стороны, у монет, очевидно, нет памяти, поэтому они не знают, сколько раз они уже выпадали гербом или решкой. По этой причине шансы выпадения герба при каждом бросании равны 1/2, даже если монета уже выпала гербом тысячу раз подряд. Не противоречит ли это закону Бернулли?
Объяснение. По закону Бернулли при очень большом числе бросаний герб выпадает приблизительно столько же раз, сколько и решка, но вся суть в том, что означает «приблизительно». Игрок, который полагает, что разность между числом выпадений герба и числом появлений решки должна быть очень мала, ошибается, так как закон Бернулли утверждает лишь, что отношение числа выпадений герба к общему числу бросаний приближенно равно 1/2 (с вероятностью, близкой к 1) или, что то же самое, отношение числа выпадений герба к числу появлений решки приблизительно равно 1. Другими словами, разность логарифмов этих чисел стремится к 0 (при увеличении числа бросаний). Если бы разность самих чисел была мала, то это противоречило бы отсутствию памяти у монет.
Какой максимальной длины серию из гербов мы можем ожидать? При n бросаниях, если n = 100, можно ожидать серию в 6–7 гербов подряд, если n = 1000, можно ожидать 9–10 гербов подряд, и 19–20 для n = 106. Следующую теорему доказали Паул Эрдеш и Альфред Реньи. При бросании монеты n раз серия из гербов длины log2n наблюдается с вероятностью, стремящейся к 1 при n–>∞. Этот факт очень полезен, когда нужно решить, описывает ли последовательность, составленная из двух символов, результаты бросания монеты или кто-то ее придумал, «тщательно» избегая включения длинных серий. Из-за широко распространенного неправильного понимания закона больших чисел Бернулли многие люди не будут повторять один и тот же знак 7 или более раз подряд в последовательности из 100 знаков.
Парадокс де Муавра
Одной из выдающихся фигур в теории вероятностей является Абрахам де Муавр (1667–1754 гг.). Этот математик, родившийся во Франции, после отмены Нантского эдикта (который предоставлял гугенотам свободу вероисповедания) переехал в Англию. Там в 1718 г. была опубликована его основная работа «Доктрина шансов» («The Doctrine of Chances»). В 3-м издании этой книги (1756 г.) де Муавр так писал о своем открытии мирового значения (о котором он сообщил некоторым друзьям еще в 1733 г.), содержащем в себе намного больше, чем закон больших чисел Бернулли: «…Возьму на себя смелость утверждать, что это труднейшая проблема о случайном…». Без сомнения, открытое де Муавром нормальное распределение, стало краеугольным камнем науки о случайном. (Де Муавр, как это ни странно, не включил свое открытие во 2-е издание книги в 1738 г.).
Согласно закону больших чисел Бернулли, вероятность того, что при бросании монеты число выпадений герба приблизительно равно числу появившихся решек, стремится к 1 при увеличении числа бросаний (приближенное равенство чисел означает, что их отношение стремится к 1). С другой стороны, вероятность того, что число гербов будет в точности равно числу решек, стремится к нулю. Например, при 6 бросаниях монеты вероятность выпадения 3 гербов равна 5/16; при 100 бросаниях вероятность выпадения 50 гербов равна 8%; при 1000 бросаний вероятность выпадения 500 гербов составляет менее 2%. В общем случае, когда монету бросают 2n раз, вероятность того, что герб выпадает ровно n раз, равна
и для достаточно больших n вероятность р приближенно равняется ![]() , что действительно стремится к нулю с ростом n. Суммируем сказанное: вероятность того, что число гербов приближенно равно числу решек, стремится к 1: в то же время вероятность того, что число гербов в точности совпадает с числом решек, стремится к 0. Разрыв между этими двумя фактами был окружен «атмосферой парадоксальности» до тех пор, пока де Муавр не построил над ним математический мост.
, что действительно стремится к нулю с ростом n. Суммируем сказанное: вероятность того, что число гербов приближенно равно числу решек, стремится к 1: в то же время вероятность того, что число гербов в точности совпадает с числом решек, стремится к 0. Разрыв между этими двумя фактами был окружен «атмосферой парадоксальности» до тех пор, пока де Муавр не построил над ним математический мост.
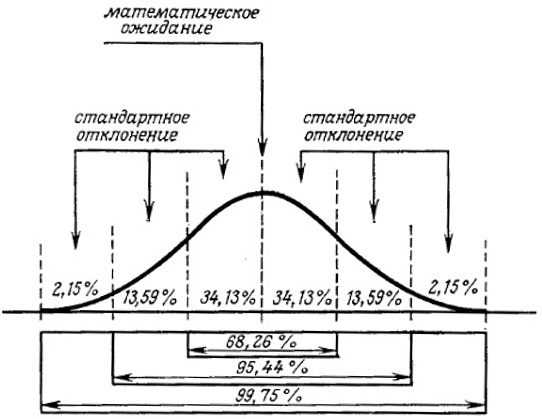
Объяснение. Пусть Нn и Тn обозначают число выпадений герба и решки соответственно при n бросаниях монеты. Согласно закону больших чисел Бернулли, вероятность того, что разность Нn – Тn становится пренебрежимо малой по сравнению с n, стремится к 1 (что совсем неудивительно). Однако де Муавр заметил, что величина |Нn – Тn|не является пренебрежимо малой по сравнению с ![]() . Он вычислил, например, что для n = 3600 вероятность того, что |Нn – Тn|не превосходит 60, равна 0,682688… (рис. 1; подробнее см. Нормальное распределение).
. Он вычислил, например, что для n = 3600 вероятность того, что |Нn – Тn|не превосходит 60, равна 0,682688… (рис. 1; подробнее см. Нормальное распределение).
Рис. 1. Нормальная плотность вероятности
Парадокс из теории игр
Хотя азартные игры в различных формах существуют со времен палеолита и математические исследования разных игр восходят к эпохе Возрождения, общая теория игр возникла лишь в XX веке (и лишь тогда была установлена ее связь с другими науками, например, такими, как экономика). В 1921 г. Эмиль Боре ль попытался создать математическую теорию игровых стратегий, однако принцип минимакса, фундаментальную теорему в теории игр, в 1928 г. доказал основоположник теории игр Джон фон Нейман. (Ранее даже Борель сомневался в ее справедливости.)
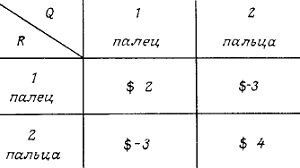
Двое детей R и Q играют в известную игру, которая состоит в следующем. Оба одновременно поднимают один или два пальца, если общее число поднятых пальцев четно, то Q платит R, и если оно нечетно, то R платит Q сумму, равную общему числу поднятых пальцев. Ниже в таблице (матрице выплат) указаны денежные суммы, которые Q должен заплатить R (рис. 2). Хотя многие считают эту игру справедливой (видимо потому, что числа в таблице при сложении дают 0, она такой вовсе не является: эта игра выгодна для Q.
Рис. 2. Матрица игры
Объяснение. Очевидно, если один из игроков все время поднимает один палец или всегда поднимает два, то второй игрок, заметив это, будет вести себя так, чтобы все время выигрывать. Следовательно, выгодными могут быть только «смешанные стратегии», т.е. при каждом испытании игрок случайно, но с фиксированными вероятностями, выбирает одну из двух возможностей (поднять один или два пальца). Предположим, что для обоих игроков мы уже нашли оптимальные стратегии, т.е. мы знаем, что лучшей стратегией для игрока R является то, что нужно поднять один палец с вероятностью р1 и поднять два пальца с вероятностью р2 (очевидно, p1 + р2 = 1), и аналогично для Q наиболее выгодно поднять один палец с вероятностью q1 и два пальца с вероятностью q2 (q1 + q2 = 1). Поскольку оба игрока принимают решения независимо друг от друга, сумма денег, которую Q в среднем выплатит R (если оба игрока применяют оптимальные стратегии), равна
(7) V = 2p1q1 – 3p1q2 – 3p2q1 + 4р2q2
Игра была бы справедливой, если бы V = 0. Однако мы покажем, что p1 = q1 = 7/12, p2 = q2 = 5/12, и тогда V =–1/12, что означает, что Q выигрывает в среднем 1/12 доллара после каждой игры даже в том случае, когда R применяет свою оптимальную стратегию.
Подставим q1 = 1, q2 = 0 в (7). Тогда V = Q1 = 2p1 – Зр2. Аналогично, если q1 = 0 и q2 = 1, то V = Q2 = –Зр1 + 4р2. В этих обозначениях имеем V = q1Q1 + q2Q2. Так как V — это средний проигрыш игрока Q, если он использует свою оптимальную стратегию, Q1 ≥ V и Q2 ≥ V, то V = q1Q1 + q2Q2 ≥ q1V + q2V = (q1 + q2)V = V.
Поскольку ни q1 ни q2 не могут быть равны нулю, из предыдущего соотношения вытекает, что V = Q1 = Q2, т.е. 2p1 – 3р2 = –3p1 + 4р2, поэтому (вспоминая, что p1 + p2 = 1) имеем p1 = 7/12, р2 = 5/12 и V = –1/12. Аналогично, 2q1 – 3q2 = –3q1 + 4q2 и, следовательно, q1 = 7/12, q2 = 5/12. Таким образом, доказано, что игра справедливой не является, и найдены оптимальные стратегии. Для обоих игроков выгодно поднимать один палец с вероятностью 7/12.
Подставляя в (7) 1 – p1 вместо р2 и 1 – q1 вместо q2, получаем V =12p1q1 – 7p1 – 7q1 + 4. Независимо от значения q1 при p1 = 7/12 имеем V = –1/12. Аналогично, независимо от значения p1 при q1 = 7/12 имеем V = –1/12. Таким образом, игроку все равно, как играть, если он знает, что его противник использует оптимальную стратегию.
Парадокс событий, происходящих почти наверно. Рассмотрим события, происходящие с вероятностями 0,99 и 0,9999 соответственно. Можно сказать, что обе вероятности практически одинаковы, оба события происходят почти наверно. Тем не менее в некоторых случаях разница становится заметной. Рассмотрим, например, независимые события, которые могут происходить в любой день года с вероятностью р = 0,99; тогда вероятность того, что они будут происходить каждый день в течение года, меньше, чем Р = 0,03, в то же время, если р = 0,9999, то Р = 0,97.
Парадокс вероятности и относительной частоты. Следующая история, принадлежащая Джорджу Пойа, показывает, как не следует интерпретировать частотную концепцию вероятности. Д-р Тел (доктор телепатии), закончив осмотр пациента, покачал головой. «Вы очень серьезно больны», — сказал он, — «из десяти человек с такой болезнью выживает только один». Пациента эта информация изрядно испугала, и д-р Тел начал его успокаивать: «Но Вам очень повезло, что Вы пришли ко мне, сэр. У меня уже умерли от этой болезни девять пациентов, так что Вы выживете».
Парадокс дня рождения. Если собираются вместе не более, чем 365 человек, то возможно, что все они имеют различные дни рождения. Однако среди 366 человек наверняка (100%) найдутся по крайней мере два таких, у которых дни рождения приходятся на один и тот же день в году. (Предположим, что мы здесь не рассматриваем високосные года.) Однако, если мы зададимся целью найти, сколько должно быть людей, чтобы с надежностью 99% Два из них имели один и тот же день рождения, то с удивлением обнаружим, что достаточно 55(!) человек. В то же время среди 68 человек с вероятностью 99,9 % по крайней мере два имеют одинаковый день рождения. Почти неправдоподобно, что такая малая разница между вероятностями 99% и 100 % может привести к столь большим различиям в числе людей. Этот парадоксальный случай иллюстрирует одну из главных причин, почему теория вероятностей применяется так широко.
Обозначим через n число дней в году, и пусть х (< n)— число людей в группе. Тогда вероятность того, что никакие два человека в этой группе не имеют одинаковых дней рождения, равна
(8) n (n – 1) (n – 2) … (n – х + 1)/nх.
Следовательно, если
(9) n (n – 1) (n – 2) … (n – х + 1)/nх = 1 – p
то р – вероятность того, что среди х людей найдутся имеющие один и тот же день рождения. Приближенное решение этого уравнения (при условии, что 0 < р < 1) равно:
Как играть в проигрышную игру. Предположим, что в некоторой игре число испытаний (n) всегда четно. Первый игрок А выигрывает очко с вероятностью р = 0,45; для В эта вероятность р = 0,55. Чтобы выиграть игру, игрок должен набрать больше половины всех очков. Если у А есть возможность выбирать число n, то, как ни странно, n = 2 не является лучшим выбором. (Это будет лучшим выбором, когда р очень мало, точнее, когда р меньше 1/3). Если р = 0,45 и n = 2, то вероятность выигрыша для А равна всего лишь 0,452 = 0,2025. Если же испытаний будет больше, то А окажется в лучшей ситуации. Легко доказать, что оптимальным является выбор n = 10. Такой результат на первый взгляд противоречит общему «принципу»: чем раньше мы прекратим проигрышную игру, тем лучше. Предположим, например, что нам нужно 20 долларов, а у нас есть только 10. Мы собираемся получить недостающую сумму, сыграв в рулетку. Поскольку рулетка — это проигрышная игра, рекомендуется, сделать наименьшее возможное число попыток, т.е. мы должны поставить сразу все наши деньги, например, на «красное». В этом случае шансы выиграть равны 18/38 (в американской рулетке есть два нуля: 0 и 00). С другой стороны, если мы каждый раз будем ставить лишь по одному доллару, то достигнем своей цели с вероятностью 0,11.
Абсурдный результат (Льюис Кэрролл). Следующие рассуждения также приводят к абсурдным результатам. Двое из трех заключенных, обозначаемых А, В и С, будут казнены. Они это знают, но не могут догадаться, кому же из них повезет. А рассуждает: «Вероятность, что меня не казнят, равна 1/3. Если я попрошу охранника назвать имя (отличное от моего) одного из двух заключенных, которых казнят, то тогда останется только две возможности. Либо другой, кого казнят, это я, либо нет, и поэтому шансы, что я выживу, увеличатся до 1/2». Однако также справедливо, что уже перед тем, как А спросит охранника, он знает, что одного из его компаньонов наверняка казнят, так что охранник не сообщит А никакой новой информации относительно его судьбы. Почему тогда вероятность казни изменилась?
Ответ очень прост: вероятность совсем не изменилась, она осталась равной 1/3. Заключенный упустил из виду, что охранник называет, например, В с вероятностью 1/2, если собираются казнить В и С, но эта вероятность равна 1, когда жертвами являются А и В. Следовательно, на самом деле шансы для А избежать казни равны отношению вероятности в последнем случае к сумме вероятностей в обоих случаях:
Этот парадокс лег в основу популярной в США телевизионной игры (см. Леонард Млодинов. (Не)совершенная случайность, глава 3).
ПАРАДОКСЫ В МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
Статистика стала наукой лишь в XVII веке. Ее основоположниками являются Джон Граунт (1620–1674 гг.) и сэр Уильям Петти (1623–1687 гг.). В книге Граунта «Естественные и политические наблюдения, сделанные над бюллетенями смертности» (1662 г.) исследовались вопросы народонаселения. В 1669 г. Гюйгенс на основе данных Граунта опубликовал таблицы смертности. В книгах Петти «Трактат о налогах» (1662 г.) и «Наблюдения над дублинскими записями смертности» (1681 г.) также использовались результаты и идеи Граунта. В работе Петти «Политическая арифметика», опубликованной в 1689 г. после смерти автора, Англия, Голландия и Франция сравниваются по их населению, торговле и судоходству. Термин «политическая арифметика» можно считать предвестником слова «статистика».
Парадокс Байеса
Томас Байес является одним из выдающихся основателей математической статистики. Его теорема, доказанная где-то около 1750 г. и опубликованная лишь после его смерти, стала источником некоторых разногласий в статистике. Жар споров до сих пор не утих. Более того, теоретическая пропасть между последователями байесовского и антибайесовского подходов продолжает увеличиваться. Простая формулировка теоремы Байеса заключается в следующем. Пусть X и Y — произвольные события, имеющие вероятность Р(X) ≥ 0 и Р(Y) > 0 соответственно. Обозначим через Р(X|Y) условную вероятность X, если известно, что Y уже произошло. Тогда
Следовательно, если X1 и X2 – непересекающиеся события, имеющие положительные вероятности, и одно из них происходит всегда, то
Это и есть формула Байеса. Она показывает, как по априорным вероятностям P(Yk) (вероятностям событий Yk до того, как событие X произошло) найти апостериорные вероятности (после того, как событие X произошло). Если рассматривать события Yk как причины, то формула Байеса представляет собой теорему о вероятностях причин. Сама по себе теорема бесспорна, но в большинстве ее применений вероятности P(Yk) неизвестны.
Незнание априорного распределения оказалось столь разрушительным для обоснованности статистических выводов из теоремы Байеса, что эта теорема была почти исключена из статистических исследований. Однако во второй трети XX века байесовский подход вновь получил некоторое развитие. Все более распространялась мысль о том, что последовательное применение формулы Байеса (когда после каждого наблюдения апостериорные вероятности пересчитываются и на следующем шаге они используются как априорные вероятности) снижает роль исходного априорного распределения, так как после многократного пересчета исходное распределение вряд ли оказывает влияние на заключительное апостериорное распределение.
Субъективный выбор априорных распределений порождает общий вопрос о том, можно ли вообще объективно определять неизвестные вероятности и вероятностные распределения независимо от наших наблюдений и измерений, или они имеют смысл только благодаря нашей субъективной информации. Бруно де Финетти, глава итальянской школы по теории вероятностей, в своей монографии утверждает, что вероятность, как и флогистон, не существует объективно в отличие от абсолютного пространства и времени или вселенной. «Объективная вероятность» является всего лишь попыткой выделить и материализовать наши вероятностные представления. По мнению Финетти любое событие (например, завтра пойдет дождь) либо произойдет, либо не произойдет (это объективно), и, опираясь на доступную информацию, мы можем посчитать «субъективную» вероятность события. Индивидуальная или субъективная вероятность отражает степень нашей уверенности в том, что событие произойдет. Мы можем говорить о субъективной вероятности, даже если «случайность» не объективна. Однако необходимо подчеркнуть, что значительно большая часть ученых утверждает, что объективная случайность и объективная вероятность существуют. Они убеждены в том, что объективные вероятности будущих событий заложены в современном состоянии мира. Так понимал объективное существование вероятности лауреат Нобелевской премии Макс Борн, который известен тем, что ввел объективную вероятность в квантовую физику.
Парадокс метода наименьших квадратов. Из-за неизбежных ошибок измерений часто кажется, что теоретические формулы и эмпирические данные противоречат друг другу. В начале прошлого века Лежандр, Гаусс и Лаплас предложили эффективный метод, позволяющий уменьшить влияние ошибок измерений. (Например, Лежандр разработал и применил его в 1805 г. для нахождения орбит комет.) Основоположниками этой теории были Галилей (1632), Ламберт (1760), Эйлер (1778) и другие. Новый прием, названный методом наименьших квадратов, детально исследован Гауссом в его работе «Теория движения небесных тел» (1809). Именно Гаусс указал также на вероятностный характер этого метода. (Хотя Лежандр обвинял Гаусса в плагиате, он не мог представить для этого достаточных оснований. Гаусс претендовал на приоритет лишь в использовании метода, а не его публикации.) Лаплас опубликовал свой основной труд по теории вероятностей в 1812 г., посвятив его «великому Наполеону» (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей). На протяжении всей четвертой главы его книги излагается исчисление ошибок. С того времени метод наименьших квадратов развился в новый раздел математики. Возможности метода порой переоценивают и часто используют тогда, когда другие методы были бы более подходящими. На эту проблему обращал внимание еще Коши во время «дебатов» с Бьенеме (в ходе диспута Коши использовал плотность вероятности 1/(π(1 + х2)), названную позднее его именем, хотя он и не был первым ученым, применившим «плотность Коши»).
Парадоксы корреляции. К последней трети прошлого века некоторые науки (например, молекулярная физика) достигли такого уровня развития, что стало необходимым использование в них теории вероятностей и математической статистики. В 1859 г. книга Дарвина произвела революцию в биологии, и вскоре после этого двоюродный брат Дарвина Фрэнсис Гальтон заложил основы генетики человека. (Исследования Менделя по генетике были заново «открыты» лишь на рубеже веков; слово «генетика» употребляется только с 1905 г., но результаты Гальтона привлекли всеобщее внимание уже в прошлом веке). Гальтон и его ученики (особенно Карл Пирсон) ввели такие важные понятия, как корреляция и регрессия, которые стали основными понятиями в теории вероятностей и математической статистике (а также в связанных с ними науках). Вес и рост человека, естественно, тесно связаны между собой, но они не определяют друг друга однозначно. Корреляция выражает эту связь одним числом, абсолютная величина которого не превосходит 1.
Абсолютное значение корреляции максимально (т.е. равно 1), когда между X и Y существует линейная зависимость, т.е. Y = аХ + b (где а ≠ 0). Если X и Y независимы (и их дисперсии конечны), то их корреляция равна 0, другими словами, они некоррелированы. В математической статистике оценкой для корреляции r, как правило, является выборочный коэффициент корреляции, который строится по независимой выборке (Х1, Y1), (Х2, Y2), …, (Xn, Yn) следующим образом:
В ряде случаев г хорошо характеризует связь между X и Y, но уже на рубеже веков вычислялись зависимости, лишенные смысла; например, корреляция между числом гнезд аистов и числом младенцев. Понятие корреляции постепенно мистифицировалось и некоторые «внутренние» (вообще говоря, случайные) связи стали считать существующими, если была велика корреляция (т.е. близка по абсолютной величине к 1). Вот почему возникли совершенно абсурдные результаты, и это чуть не дискредитировало всю статистику. Как правило, игнорировался тот факт, что большая корреляция для X и Y может быть результатом влияния какой-то третьей величины. Например, в Англии и Уэльсе заметили, что с увеличением числа радиослушателей возрастало число сумасшедших и умственно отсталых людей. Однако такая интерпретация совершенно ошибочна, так как нельзя психически заболеть от того, что слушаешь радио. Дело лишь в том, что с течением времени растет и число радиослушателей, и число случаев психических заболеваний, но между ними нет никакой причинной зависимости. К сожалению, неверные толкования не всегда столь очевидны, например, в технических или экономических приложениях. Сравнение вероисповедания и роста людей дает еще один пример надуманной зависимости, согласно которой при движении от Шотландии к Сицилии доля католиков в населении постепенно возрастает и в то же время средний рост людей убывает. Однако какая-либо причинная связь здесь совершенно невозможна. (В фашистской расовой теории еще более нелепые идеи провозглашались здравыми и даже научными.)
Пусть случайная величина X равномерно распределена на интервале (—1, 1) и Y= |Х|. Очевидно, что между X и Y существует тесная связь, однако их корреляция r(Х, Y)=0.
Объяснение. Если X и Y независимы, то r(X,Y) = 0, но обратное утверждение неверно. Некоррелированные случайные величины могут быть сильно зависимы, как в указанном выше примере, когда Y=|Х|. Поэтому «некоррелированность» не следует понимать, как независимость.
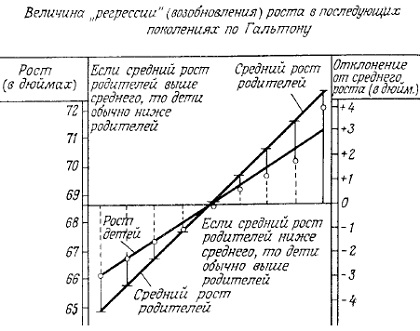
Парадоксы регрессии. Коэффициент корреляции описывает зависимость между двумя случайными величинами одним числом, а регрессия выражает эту зависимость в виде функционального соотношения и поэтому дает более полную информацию. Например, регрессией является средний вес тела человека как функция от его роста. Понятие «регрессии» ввел Гальтон, который в конце прошлого века сравнивал рост родителей с ростом их детей. Он обнаружил, что рост детей у высоких (или низких) родителей обычно выше (или ниже) среднего, но не совпадает с ростом родителей (рис. 3). Линия, показывающая, в какой мере рост (и другие характеристики, к которым мы позже вернемся) регрессируют (возобновляются) в среднем в последующих поколениях, была названа Гальтоном линией регрессии. Позднее регрессией стали называть любую функциональную зависимость между случайными величинами. Вначале регрессионный анализ применялся в биологии и важнейшим научным журналом, в котором освещалась эта тема, был журнал «Биометрика», выходящий с октября 1901 г. Между 1920 и 1930 гг. большое значение приобрело использование регрессионного анализа в экономике и возникла новая область науки: эконометрика (термин, принадлежащий Р. Фришу (1926), которому позднее была присуждена Нобелевская премия) со своим журналом «Эконометрика», впервые вышедшим в 1933 г. От изучения частных регрессионных задач исследователи постепенно перешли к регрессионному анализу структуры, присущей глобальным экономическим системам (Дж. Кейнс, Я. Тинберген и другие, например, Р. Клейн, которому в 1980 г. присуждена Нобелевская премия по экономике). Журнал «Технометрика» публикуется с 1959 г. и в основном посвящен техническим приложениям. Регрессионный анализ величины X, определяемой по другой величине Y, когда X измерить трудно, а Y достаточно легко, весьма важен. В настоящее время регрессионный анализ используется практически во всех областях пауки, что само по себе неплохо, но, к сожалению, регрессионный анализ иногда является одним из главных средств для достижения «громких научных успехов», для проведения небрежных исследований и замазывания (научных) проблем. Регрессия никогда не подменяет научных концепций и теоретических обоснований, хотя и облегчает их поиск.
Рис. 3. Линия регрессии Гальтона.
Парадокс интервальных оценок. Фишер (1890–1962 гг.) начал заниматься интервальными оценками немного раньше, чем Нейман (1894–1981 гг.). Фишер даже обвинил Неймана, который тогда работал в Польше, в присваивании и обобщении своих идей. В это время у Фишера уже были личные и профессиональные конфликты с другими выдающимися статистиками. Он ненавидел К. Пирсона (1857–1936 гг.) и поэтому не публиковался после 1920 г. в журнале «Биометрика» (ведущем периодическом журнале по статистике, среди основателей и редакторов которого был Пирсон). Фишер перенес свою антипатию, хотя и в ослабленном виде, на Э. Пирсона (1895–1980 гг.), сына К. Пирсона, и его друга Е. Неймана. Позднее Нейман стал одним из ведущих статистиков в США, и их личный спор перерос в спор англо-американский. Фишеру никогда не нравилась идея сведения статистических выводов к принятию решений с помощью функций потерь. (Это «американское» направление в статистике было разработано венгром Абрахамом Вальдом на основе теории игр Джона фон Неймана.) Главное противоречие выражалось в следующем: в Америке (в соответствии с прагматизмом Пирса) не важно, о чем вы думаете, а важно, что вы делаете. В Англии же—наоборот. Хотя рассуждения Фишера и не были всегда убедительными, он является одним из крупнейших (если не крупнейшим) статистиков, когда-либо живших. Поэтому странно, что он не стал профессором статистики. В действительности, в 1943 г. он-таки стал профессором Кембриджского университета, но по генетике. Между 1952 и 1954 г. он также был президентом Королевского общества.
Парадокс типичного и среднего. Понятие среднего, например, средняя зарплата, часто используется как синоним типичного. На самом деле если в некоторой стране есть всего лишь несколько очень богатых семей и большое количество бедных, чьи доходы соответственно огромны и малы, то арифметическое среднее их доходов вовсе нетипично. Например, медиана доходов дает более реалистичную картину, (Медиана означает такой доход, что число людей с большим доходом, равно числу людей, имеющих меньший доход.) Кроме средней зарплаты есть и другие средние характеристики, вводящие в заблуждение. «Средний человек» – одна из них. Неудивительно, что исследования бельгийского ученого Л. А. Ж. Кетле по этому вопросу стали источником горячих споров. Худшее в «среднем человеке» не его серость, а возникающие противоречия. Например, средний рост не соответствует среднему весу и т. д. Только по одной этой причине можно усомниться в справедливости слов Дж. Рейнольдса (первого президента Королевской академии художеств в Лондоне), когда он сказал, что в среднем источник прекрасного.
Несмотря на свою непоследовательность, книга Кетле (1835) рассматривается как веха, если вообще не как начало количественного анализа общественных явлений. Ф. Гальтон, С. Пирсон и Ф. Эджворт пенили Кетле как гениального первооткрывателя регрессионного подхода. Под влиянием его книги Гальтон занялся научными исследованиями. Однако у Кетле есть и другие заслуги перед наукой. В 1820 г. он основал Королевскую обсерваторию Бельгии и стал ее первым директором. Он был также великолепным организатором: в 1834 г. по его предложению было создано Статистическое общество в Лондоне, он был инициатором проведения Первого международного конгресса по статистике в Брюсселе в 1853 г.
Парадокс точности измерения. Предположим, что нам нужно найти длину двух различных стержней с помощью двух измерений. Прибор, которым мы можем измерять длину, дает результат со случайной ошибкой, имеющей стандартное отклонение ст. Парадоксально, но измерение каждого стержня в отдельности не является лучшим способом. Стандартное отклонение результата будет меньше, если сначала измерить общую длину Т стержней, приложив конец одного стержня к концу другого, а затем положить стержни рядом и найти разницу их длин D. Тогда приближенные длины стержней соответственно равны (Т + D)/2 и (Т – D)/2. Стандартное отклонение этих длин равно σ/√2, что действительно меньше, чем σ.
Парадоксальное оценивание вероятности. Оценкой для неизвестной вероятности обычно служит относительная частота. Например, если при ста бросаниях монеты решка выпала 47 раз, то оценкой для вероятности выпадения решки будет 47/100. Однако, если при 10 бросаниях более или менее правильной монеты решка ни разу не появилась, то нет оснований считать вероятность выпадения решки равной 0. При наличии некоторой априорной информации (например, что монета более или менее правильная) оценивание через относительную частоту, вообще говоря, не является лучшим способом. Наша априорная информация хорошо выражается через бета-распределение, зависящее от двух параметров а и b. Математическое ожидание бета-распределения: m = a/(a+b).
Наша априорная информация относительно m может быть выражена через а и b (например, если монета правильная, то m = 1/2, следовательно, а = b). Если априорное распределение является бета-распределением с параметрами (а, b), то по теореме Байеса апостериорное распределение также будет бета-распределением. (Это свойство объясняет широкую применимость бета-распределения.) Если в n экспериментах событие, имеющее неизвестную вероятность, произошло k раз, то параметрами апостериорного распределения будут (а + k, b + n – k), следовательно, апостериорное математическое ожидание запишется в виде: M = (a + k)/(a + b + n), что дает более содержательную и лучшую оценку для неизвестной вероятности, чем относительная частота k/n. Очевидно, при достаточно больших n величина М практически не отличается от относительной частоты, однако, например, когда n = 10, k = 0 и а = b = 100, имеем М = 100/210 ≈ 0,48; в то же время относительная частота равна 0, что совершенно нелепо.
Парадокс проверки независимости; являются ли эффективные лекарства эффективными? Ниже приведены три таблицы, в которых показано действие некоторого лекарства только на мужчин, только на женщин и, наконец, на больных обоего пола (объединенные результаты). Видно, что после приема лекарства доля выздоровевших больше как среди мужчин, так и среди женщин. С другой стороны, как это ни странно, из таблицы с объединенными результатами следует, что доля выздоровевших больше среди тех людей, которые лекарство не принимали. Следовательно, лекарство, показавшее свою эффективность как среди мужчин, так и среди женщин, дало отрицательный результат для смешанной группы мужчин и женщин. Аналогично, новое лекарство может оказаться эффективным в каждом из десяти различных госпиталей, но объединение результатов укажет на то, что это лекарство либо бесполезно, либо вредно.
Рис. 4. Результаты исследований эффективности лекарств
ПАРАДОКСЫ СЛУЧАЙНЫХ ПРОЦЕССОВ
Первые значительные результаты в теории случайных процессов или стохастических процессов, если воспользоваться словом греческого происхождения, появились лишь в прошлом веке. Благодаря успехам, достигнутым в классической механике, в XVII и XVIII веках главным образом изучались детерминистические процессы. В это же время в науке развился «механистический детерминизм», согласно которому случайность считалась чем-то несущественным и из основных наук ее следовало по возможности исключить. Однако со второй половины прошлого века математические исследования по случайным процессам получают все большее распространение в фундаментальных областях науки, в частности, в различных разделах физики: статистической физике, квантовой физике XX века, где случайные процессы играют главную роль. С углублением научного знания все очевиднее становилась необходимость в изучении стохастических процессов.
Парадокс ветвящихся процессов. В первой половине прошлого века было замечено следующее интересное явление: некоторые знаменитые аристократические и простые фамилии постепенно исчезали. Эту проблему с математической точки зрения изучали И. Ж. Бьенеме в 1845 г. и де Кондолье в 1873 г. В 1874 г. Гальтон и Ватсон опубликовали важнейшую статью, посвященную этому вопросу. Ветвящиеся цепочки фамилий стали первым примером случайного ветвящегося процесса. Процессы такого типа появляются в химии, физике и некоторых других областях. Например, процесс деления ядер, или цепная реакция, в ядерной физике хорошо моделируется случайными процессами. Поколения нейтронов сменяют друг друга чаще, чем поколения людей, однако в обоих случаях главный вопрос остается одним и тем же: при каких условиях процесс затухнет (фамилия исчезнет) или разовьется до бесконечности (бомба взорвется). Понятие ветвящегося процесса введено в 1947 г. А. Н. Колмогоровым и Н. А. Дмитриевым.
Красивые старые фамилии постепенно исчезают, и их место занимают более заурядные, например, Смит и т. д. Использование комбинаций из двух или трех фамилий не всегда позволяет избежать совпадения фамилий, иногда даже в одном учреждении. Предлагаемый ниже порядок присваивания фамилий представляется необычным, но разумным и не зависящим от пола. Каждый ребенок наследует две фамилии, одну от матери и другую от отца. Поскольку у каждого из родителей тоже по две фамилии, в качестве фамилий для ребенка можно взять более редкие (или более привлекательные). Кроме таких двойных фамилий у людей также будут и имена. При таком порядке мир фамилий стал бы более красочным и индивидуальным.
Марковские цепи и физический парадокс. Понятие марковской цепи принадлежит русскому математику А. А. Маркову, чьи первые статьи по этому вопросу были опубликованы в 1906–1908 гг. Марков использовал новое понятие для статистического анализа распределения букв в знаменитой поэме Пушкина «Евгений Онегин». «Цепь Маркова» (это название было предложено А. Я. Хинчиным) — важнейшее математическое понятие, возникшее (по крайней мере частично) при решении лингвистических проблем.
В наши дни цепи Маркова (и их обобщение на случай непрерывного времени и непрерывного фазового пространства — марковские процессы) играют в естественных и технических науках намного большую роль, чем в лингвистике, где они первоначально применялись. Проблема обратимости-необратимости — это интересный парадокс классической механики и термодинамики, и марковские цепи являются эффективным средством его анализа. Суть проблемы заключается в том, что законы классической механики обратимы и поэтому не могут объяснить, почему кусок сахара растворяется в чашке кофе, но мы никогда не наблюдаем обратный процесс. Необратимость нашего мира отражает второй закон термодинамики (впервые сформулированный Л. С. Карно). (Первый закон термодинамики — это закон сохранения энергии.) Спустя сорок лет Р. Клаузиус ввел математическое понятие энтропии, ставшее основным в теории необратимых процессов. (Согласно Клаузиусу слово «энтропия» происходит от греческого τροπη, означающего «поворот», «превращение».
Клаузиус утверждает, что он добавил «эн», чтобы слово звучало аналогично «энергии», однако греческое слово ἐντροπία имеет самостоятельное значение — «повернуть голову в сторону».) Используя понятие энтропии, второй закон термодинамики можно сформулировать следующим образом: в изолированной системе энтропия не может уменьшиться, обычно она возрастает. Л. Больцман пытался проверить этот закон с помощью кинематики атомов и молекул. (В то время идея Больцмана вовсе не выглядела естественной, так как многие физики сомневались в самом существовании атомов, например, М. Фарадей, Э. Мах или основатель «энергетизма» В.Ф. Оствальд.) Огромное влияние на Больцмана оказала работа Максвелла по динамической теории газов. В 70-е годы прошлого века Больцман обнаружил связь между энтропией и термодинамической вероятностью. Он показал, что необратимость не противоречит обратимой механике Ньютона- применение последней к большому числу частиц с необходимостью приведет к необратимости, так как системы, состоящие из миллионов молекул, стремятся перейти в состояние, имеющее большую термодинамическую вероятность. Это и есть «основная причина» распада, износа, старения (и, как утверждают некоторые, упадка нравов или цивилизации).
Статистический анализ текста «Евгения Онегина» не был единичным исследованием подобного типа. В конце прошлого века стало модным изучать частотное распределение слов в различных текстах (чтобы помочь в обучении иностранным языкам и стенографии). В 1898 г. Ф. Каэдиг опубликовал первый частотный словарь немецкого языка, который был основан на текстах, содержащих 11 миллионов слов. Во многом благодаря работам американского ученого Дж. Ципфа (1902–1950 гг.) применения математической статистики в лингвистике переросли в отдельное научное направление. Его книга «Человеческое поведение и принцип наименьшего усилия» содержит очень глубокие идеи (см. также Закон Ципфа и фрактальная природа социальных и экономических явлений).
Биржевый парадокс; мартингалы. Математические исследования, связанные с фондовой биржей, насчитывают почти столько же лет, сколько и сама биржа. Математический подход, видимо, использовался уже на бирже Грешема в XVI веке, однако основные методы теории вероятностей не применялись довольно долго. Характерно, что даже в 1900 г., когда в Париже Луи Башелье защищал докторскую диссертацию о связи между колебанием цен на фондовой бирже и броуновским движением (еще до того, как броуновским движением занялись физики), комиссия с трудом воспринимала его по существу новые идеи. Башелье создал общую математическую модель безобидных игр, так называемый мартингал.
Если ожидается, что какие-то акции принесут прибыль, то решение об их покупке кажется естественным, если же прибыли не будет, то надо их продавать. Столь же разумной представляется покупка на все деньги акций, от которых ожидается наибольшая прибыль. Все это верно, но на практике поступают иначе, так как хотя наша ожидаемая прибыль может возрастать (общий ожидаемый капитал будет стремиться к бесконечности), одновременно наше состояние будет убывать до нуля с вероятностностью 1. Так что действовать на фондовой бирже надо осторожно: акции, которые обещают принести прибыль, иногда следует продать.
Основная идея мартингальной системы заключается в удваивании ставки при проигрыше. Предположим, что мы играем в рулетку и всегда ставим на красное. Сначала поставим 1 доллар. Если выигрываем, то прекращаем игру; при проигрыше ставим в следующий раз 2 доллара. При выигрыше наш капитал увеличится на 1 доллар, и мы прекратим игру; при проигрыше мы теряем уже 1 + 2 = 3 доллара и ставим 4 доллара. При выигрыше наш капитал увеличится на 1 доллар, и мы прекратим игру; при проигрыше ставим в следующий раз 8 долларов и т. д. Если колесо рулетки хотя бы раз остановиться на красном числе, то при такой мартингальной системе игры мы покинем казино, став на 1 доллар богаче, чем, когда в него вошли. Поскольку красное в конце концов должно появиться, кажется, что эта система гарантирует успех. Однако предположим, что мы вошли в казино со 100 долларами, и 6 раз подряд выигрывало черное. Тогда мы проиграем 26 – 1 = 63 доллара и не сможем сделать следующую ставку в нужном размере – 64 доллара.
Парадокс ожидаемого времени разорения. Пусть А и В играют в орлянку. Если выпадает герб, то А платит В, если решка, то В платит А 1 доллар. Начальный капитал у А составляет 1 доллар, у В — 999 долларов; они играют до тех пор, пока один из них не разорится. У А, конечно, больше шансов первому остаться без денег. Если при первом бросании монеты выпадает герб, то А уже разорен. Как это ни удивительно, но ожидаемая продолжительность игры довольно велика: в среднем лишь после 999 подбрасываний монеты один из игроков разорится. Не является ли такая продолжительность намного больше того, что мы ожидали? В общем случае можно доказать, что если А имеет а долларов, и у его противника В есть b долларов, то средняя продолжительность игры составляет ab испытаний, в частности при а = b ожидаемая продолжительность игры равна а2.
Парадокс выбора. Нам часто нужно выбрать лучшее (с какой-то точки зрения) из некоторой совокупности людей или объектов (например, при покупке товаров или выборе будущего супруга). Для анализа этой проблемы предположим, что людей или объекты можно упорядочить по их достоинствам, т.е. сравнивая любые два из них, можно всегда сказать, какой из них лучше. Выбор лучшего не представляет трудностей, когда мы видим все объекты. Однако в большинстве случаев объекты или людей рассматривают последовательно и, раз что-то или кого-то отвергнув, мы к этому вернуться не можем. В дальнейшем будем предполагать, что если «кандидат» не выбран, когда подошла его очередь, то позднее мы не можем изменить наше решение. Но и в этом случае проблема не описана однозначно. Мы можем даже не знать общего числа объектов, из которых должны выбирать. (Как правило, нет такой информации при выборе будущего мужа или жены.) Предположим, что всего имеется n возможностей, точнее n лиц или объектов, проходящих мимо нас в произвольной последовательности (эти последовательности считаются равновероятными). Вопрос состоит в следующем. Исходя из какого метода выбирать лучшего кандидата, если любого из них можно сравнивать, естественно, только с предыдущими? Если всегда выбирать, например, третьего, то шансы выбрать лучшего равны 1/3. С ростом n величина 1/n стремится к 0 и поэтому при большом числе предложений вероятность выбора лучшего близка к 0. Удивительно, но есть метод, позволяющий выбирать лучшего кандидата с вероятностью близкой к 30% даже при больших значениях n. Метод состоит в следующем. После того, как пройдут первые 37% (точнее 100/e%) кандидатов, выбираем первого, кто окажется лучше всех предыдущих (если такого нет, то выбираем последнего). В этом случае шансы выбрать лучшего приблизительно равны 1/е, т.е. 37%, как бы ни было велико значение n.
Парадоксы голосования и выборов. Маркиз Кондорсе (один из друзей Вольтера) в 1758 г. привел следующий пример. Предположим, что в выборах участвовали три кандидата А, В и С, и они набрали соответственно 23, 19 и 18 голосов. Тогда кандидата A, как набравшего наибольшее число голосов, следует объявить победителем, но в действительности все 19 избирателей, голосовавших за В, возможно, предпочли бы С вместо А. В 1950 г. Кеннет Арроу (в 1972 г. ему присуждена Нобелевская премия по экономике) использовал этот пример, чтобы показать, что логически невозможно создать совершенно справедливую систему выборов. Таким образом, неудивительно, что нет единой системы выборов, принятой во всем мире.
ПАРАДОКСЫ В ОСНОВАНИЯХ ТЕОРИИ ВЕРОЯТНОСТЕЙ. РАЗНЫЕ ПАРАДОКСЫ
В 1900 г. на Международном математическом конгрессе в Париже Давид Гильберт среди 23 важнейших нерешенных проблем в математике назвал проблему построения оснований теории вероятностей.
Парадокс метода Монте-Карло
Метод Монте-Карло — численный метод, основанный на случайной выборке. При решении вычислительных задач часто можно найти подходящую вероятностную модель, в которую входит искомое неизвестное число. Затем для решения задачи много раз наблюдаются исходы случайных экспериментов, включенных в вероятностную модель, с тем чтобы с заданной точностью (на основе наблюденных значений) можно было оценить искомое число (см. Использование метода Монте-Карло для расчета риска). Хотя идея этого метода довольно стара, его настоящее применение началось лишь с появлением компьютеров, когда Е. Нейман, С. Улам и Э. Ферми использовали метод Монте-Карло для приближенного решения трудных вычислительных задач, связанных с ядерными реакциями во время Манхэттенского проекта. Название метода объясняется тем, что в нем применяются последовательности случайных чисел, в качестве которых могли бы выступать регулярно объявляемые результаты игр, проводимых в казино, например, в Монте-Карло (см. также Станислав Улам. Приключения математика).
В связи с методом Монте-Карло теория построения случайных чисел на компьютерах превратилась в важное направление в математике. Вместо настоящих случайных чисел (которые возникают в ходе случайных физических процессов, например, в ходе радиоактивного распада) популярными становятся псевдослучайные числа, конструируемые с помощью детерминированных вычислительных алгоритмов. В связи с псевдослучайными числами возникает следующий вопрос. В каком смысле их можно считать случайными, если они получены с помощью детерминированных (неслучайных) алгоритмов?
В 1965–1966 гг. Колмогоров и Мартин-Лёф представили понятие случайности в новом свете. Они определили, когда последовательность, состоящую из 0 и 1, можно считать случайной. Основная идея состоит в следующем. Чем сложнее описать последовательность (т.е. чем длиннее «самая короткая» программа, конструирующая эту последовательность), тем более случайной ее можно считать. Длина «самой короткой» программы, естественно, различна для разных компьютеров. По этой причине выбирают стандартную машину, называемую машиной Тьюринга (подробнее см. Чарльз Петцольд. Читаем Тьюринга). Мерой сложности последовательности является длина наиболее короткой программы на машине Тьюринга, которая генерирует эту последовательность. Сложность — мера иррегулярности. Последовательности, длина которых N, называются случайными, если их сложность близка к максимальной.
Таким образом, сложность и случайность тесно взаимосвязаны. Если программист собирается получить «настоящие» случайные числа, то в силу результатов Колмогорова и Мартин-Лёфа он может это сделать только с помощью достаточно длинной программы. В то же время на практике генераторы случайных чисел очень короткие.
Парадокс первой цифры
Приблизительно сто лет назад, в 1881 г., Саймон Ньюкомб в «Американском математическом журнале» обратил внимание читателей на один интересный эмпирический факт. Однако вскоре это открытие было забыто и сделано вновь спустя 60 лет физиком Фрэнком Бенфордом, работавшим в компании «Дженерал Электрик». Закон получил имя Бенфорда. (Ньюкомб — не единственный ученый, с которым обошлись несправедливо. Закон эпонимии саркастически утверждает, что ни одна теорема, ни одно научное открытие не были названы именем первооткрывателя; см. Джон Уоллер. Правда и ложь в истории великих открытий) У.Уивер в «Леди Удача» изложил историю Бенфорда: «Мне рассказали, что приблизительно двадцать пять лет назад один инженер, работавший в компании «Дженерал Электрик», по дороге на службу нес книгу, содержавшую подробную таблицу логарифмов. Он держал книгу сбоку корешком вниз. Взглянув на книгу, он заметил, что наиболее загрязнены края страниц в начале книги, затем они становятся чище— как будто чаще всего смотрят первые страницы, реже — страницы в середине книги и совсем редко — последние страницы, «Это странно, – подумал он. – Это означает, что людям чаще всего приходится искать логарифмы чисел, которые начинаются с 1, чуть реже — чисел, начинающихся с 2 и так далее и, наконец, реже всего — логарифмы чисел, начинающихся с 9. Но это совершенно невозможно, так как людям нужны значения логарифмов самых разных чисел, поэтому различные цифры должны быть представлены одинаково.»
Рассмотрим какую-нибудь таблицу, например, таблицу целых степеней двойки или любую таблицу физических постоянных или таблицы демографической статистики. Как правило, окажется, что первая цифра (≠0) чисел в таблице не будет равномерно распределена на множестве 1, 2, 3, …, 9. Цифра 1 встречается чаще всего, затем идет 2 и так далее, 9 будет самой редкой цифрой. Согласно закону Бенфорда относительная частота первых цифр, не превосходящих k, равна не k/9 (что означало бы равномерность распределения), a lg(k + 1). Следовательно, относительные частоты для 1, 2, …, 9 приблизительно равны 30%, 17%, …, 5%. Закон Бенфорда не утверждает, что 1 — наиболее часто встречающаяся первая цифра во всех таблицах (каждый может придумать таблицу, в которой единиц вообще не будет), но все-таки единица как первая цифра в таблицах появляется обычно чаще, чем, например, девятка.
Объяснение. Проанализируем таблицу степеней двойки. Первой цифрой числа 2n является 1, если существует такое целое число s, что 10s ≤ 2n < 2·10s. Если n (и, следовательно, s) достаточно велико, то s/n приблизительно равно lg2. Это означает, что среди первых n степеней двойки каждая Ig2-я начинается с 1. Аналогично, по закону Бенфорда доля степеней двойки, которые начинаются с цифры, не превосходящей k, приблизительно равна lg(k + 1). (См. также Закон Бенфорда или закон первой цифры.)
Парадокс поэзии и теории информации. В качестве последнего парадокса в этой книге приведу слова моего покойного учителя профессора Альфреда Реньи: «С тех пор, как я начал заниматься теорией информации, я часто размышляю над краткостью стихотворений; почему одна строка стихотворения содержит значительно больше «информации», чем очень короткая телеграмма такой же длины. Удивительное богатство значений в литературных трудах кажется противоречит законам теории информации. Ключом к этому парадоксу, я думаю, является понятие «резонанса». Писатель не только сообщает нам информацию, но и играет на струнах языка с таким мастерством, что наш разум и даже само подсознание резонируют. Поэт с помощью удачного слова может вызвать цепочку идей, эмоций и воспоминаний. В этом смысле труд писателя — волшебство.»
Библиография на русском языке
(несколько устаревшая, так как книга на венгерском языке была написана в середине 1980-х)
Березовский Б. А., Гнедин А. В. Задача наилучшего выбора проблем. — М.: Наука, 1984.
Больцман Л. Лекции по теории газов. — М.: Гостехиздат, 1956.
Вильямс Дж. Д. Совершенный стратег, или Букварь по теории стратегических игр. – М.: Советское радио, 1960.
Гиббс Дж. В. Термодинамика. Статистическая механика. — М.: Наука, 1982.
Гнеденко Б.В. Очерк истории теории вероятностей // В книге «Курс теории вероятностей. – М.: Наука, 1988.
Гуревич В., Волмэн Г. Теория размерности. — М.: Гос. изд-во иностранной литературы, 1948.
Дрейпер H., Смит Г. Прикладной регрессионный анализ. – М.: Статистика, 1973.
Дуб Дж. Л. Вероятностные процессы. — М.: ИЛ, 1956.
Дынкин Е. Б. Марковские процессы. — М.: Физматгиз, 1963.
Закс Ш. Теория статистических выводов. – М.: Мир, 1975.
Кендалл M., Моран П. Геометрические вероятности. — М.: Наука, 1972.
Кендалл M., Стьюарт А. Статистические выводы и связи. – М.: Наука, 1973.
Линник Ю. В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, изд. 2-е. — М.: Физматгиз, 1962.
Майстров Л.E. Развитие понятия вероятности. – M.: Наука, 1980.
Матерой Ж. Случайные множества и интегральная геометрия. — М.: Мир, 1978.
Мостеллер Ф. Пятьдесят занимательных вероятностных задач с решениями. – М.: Наука, 1985.
Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.
Окстоби Дж. Мера и категория. — М.: Мир, 1974.
Питмен Э. Основы теории статистических выводов. – М.: Мир, 1986.
Пойа Д. Математика и правдоподобные рассуждения. – М.: Наука, 1975.
Пуанкаре А. О науке. — М.: Наука, 1983.
Сантало Л. Интегральная геометрия и геометрические вероятности. — М.: Наука, 1983.
Синай Я. Г. Теория фазовых переходов: Строгие результаты. — М.: Наука, 1980.
Соболь И. M. Метод Монте-Карло. — М.: Наука, 1978.
Феллер В. Введение в теорию вероятностей и ее приложения. — М: Мир, 1984.
Харрис T. Теория ветвящихся случайных процессов. — М.: Мир, 1966.
Хьюбер П. Робастность в статистике. — М.: Мир, 1984.
Чжун Кайлай. Однородные цепи Маркова. — М.: Мир, 1964.
Шеффе Г. Дисперсионный анализ. — М.: ГИФМЛ, 1963.
По теме см. также:
Чарльз Уилан. Голая статистика
Левин. Статистика для менеджеров с использованием Microsoft Excel
Как с помощью диаграммы приукрасить действительность? или о факторе лжи Эдварда Тафти

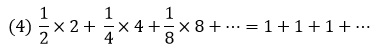
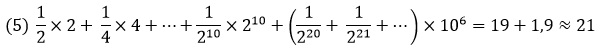
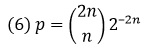
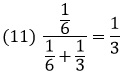
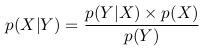
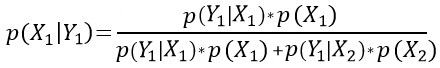
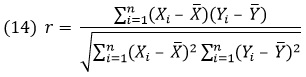

Отличная книга, но, как справедливо замечено, не всем будет понятно. С другой стороны, полезно будет понять хотя бы часть.
Вот хорошая подборка книг по статистике http://statanaliz.info/bibliotechka
Очень интересно, спасибо!
РЕШЕНИЕ ПАРАДОКСОВ:
1. «Что было раньше: яйцо или курица?»
Даются два понятия «ЯЙЦО» и «КУРИЦА» и в РЯДУ ПОСЛЕДОВАТЕЛЬНО РАЗВЁРТЫВАЕМЫХ ПОНЯТИЙ (РПРП) требуется найти понятия предшествующие к каждому из них.
В РПРП для «ЯЙЦА» предшествующим является «КУРИЦА», ибо понятием «эмбрион» (или другими ) не интересующим нас по постановке вопроса мы можем пренебречь.
В РПРП для «КУРИЦА» пренебрегаемым понятием является «цыплёнок», но не «треснувшееся яйцо (из которого старается вылупиться цыплёнок)», ведь в постановке вопроса не акцентировано внимание на обязательности рассмотрения лишь яйца целостного состояния, т. е. для «КУРИЦА» предшествующим является не то понятие на котором акцентирован вопрос, а его разновидность.
ВЫВОД: «КУРИЦА»
2. Даётся понятие «Недвижущегося (Ахиллес)» , который не состоит в РПРП и отсутствие динамического состояния у которого завуалировано перемещениями, которую следуя Зенону производим и мы переставляя это понятие на предыдущие позиции в РПРП понятия «Движущегося (черепаха)» — вот в этом и вся загадка этого апория Зенона. В такой постановке вопроса даже Усейну Болта не тягаться с черепахой…
Решение парадоксов (окончательная версия).
Когда не учитывается степень ПОЗИЦИОННОЙ ЗАВИСИМОСТИ (ПЗ-и) ВЕДОМОГО /понятия в пределах рассматриваемого вопроса/ к ВЕДУЩЕМУ /понятию в пределах этого же вопроса/ возникает парадокс.
ВЕДОМОЕ:
«Яйцо», полагаясь от ВЕДУЩЕГО «курица» в МАКСИМАЛЬНО ВОЗМОЖНОЙ
(МксВ-ой) ПЗ-и в обоих своих СОСТОЯНИЯХ (Сст-ях) /НАЧАЛЬНОМ (Нч)
как снесённое ею; КОНЕЧНОМ (Кн) как насиженное ею/, в ракурсе
вопроса «кто был раньше» выявляющим ВЕДУЩЕГО в МИНИМАЛЬНО ВОЗМОЖНОМ
(МнмВ-ом) числе понятий комбинационно годных для выбора искомого /в данном случае вариант с годным полагающимся в МксВ-ой ПЗ-и от этой роли и с не годным полагающимся вне ПЗ-и от этой роли/, невольно становится рассматриваемым на эту роль.
«Ахиллес» перемещающееся лишь на метку оставляемую ВЕДУЩИМ
«передвигающейся черепахой» естественно, что не догонит её полагаясь в
обоих Сст-ях в МксВ-ой ПЗ-и от неё;
«Я» Кн Сст-я, полагающееся от ВЕДУЩЕГО «ложь» в МнмВ-ой ПЗ-и,
рассматриваемое в МксВ-ой ПЗ-и Нч Сст-я становится поочерёдно
отрицаемым /в обоих Сст-ях/;
«Критянин» Кн Сст-я, полагающееся в МнмВ-ой ПЗ-и от ВЕДУЩЕГО «множества
критян не представленного этим критянином, как не лжецом»,
рассматриваемое в Нч Сст-и полагающимся в МксВ-ой ПЗ-и от иного
ВЕДУЩЕГО «множества критян представленного этим критянином не, как
не лжецом» становится поочерёдно отрицаемым /в обоих Сст-ях/;
«Брадобрея» в обоих Сст-ях полагающегося в МксВ-ой ПЗ-и от ВЕДУЩЕГО
«бреющих себя» и, соответственно, в МнмВ-ой ПЗ-и от иного ВЕДУЩЕГО
«не бреющих себя», рассматривают в ситуации смены степеней ПЗ-и от
ВЕДУЩИХ.
«Стрелу летящую (Сст-е движения)» полагающуюся в обоих Сст-ях /Нч – выхода из
Сст-я покоя; Кн – входа в Сст-е покоя/ в МнмВ-ой ПЗ-и от ВЕДУЩЕГО «Стрелы не летящей (Сст-е покоя)» стараются представить полагающейся в МксВ-ой ПЗ-и.
«Знание Сократа» полагается в МксВ-ой ПЗ-и от ВЕДУЩЕГО «познаваемого».