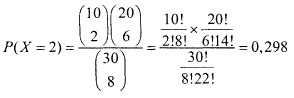Гипергеометрическое распределение, как и биномиальное, позволяет оценить количество успехов в серии из n испытаний. Разница между ними заключается в способе получения исходных данных. В биномиальной модели данные выбираются либо из конечной генеральной совокупности с возвращением либо из бесконечной генеральной совокупности без возвращения. В гипергеометрической модели данные извлекаются только из конечной генеральной совокупности без возвращения. [1] Таким образом, в то время как в биномиальной модели вероятность успеха р остается постоянной, а испытания не зависят друг от друга, в гипергеометрической модели эти условия не выполняются. Наоборот, в гипергеометрической модели каждый исход зависит от предыдущих исходов.
Гипергеометрическое распределение, описывающее вероятность X успехов при заданных параметрах n, N и А:
где Р(Х) — вероятность X успехов при заданных n, N и А, n — объем выборки, N — объем генеральной совокупности, А — количество успешных исходов в генеральной совокупности, N – A — количество неудачных исходов в генеральной совокупности, X — количество успехов в выборке, N – X — количество неудачных исходов в выборке.
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Количество успехов X в выборке не может превосходить количество успехов А в генеральной совокупности либо объем выборки n. Таким образом, диапазон значений, которые может принимать случайная величина, подчиняющаяся гипергеометрическому распределению, ограничен либо объемом выборки (как и диапазон биномиальной переменной), либо объемом генеральной совокупности.
Математическое ожидание гипергеометрического распределения:
(2) μ = E(X) = nA/N
Стандартное отклонение гипергеометрического распределения:
Выражение ![]() называется поправочным коэффициентом конечной генеральной совокупности. Он необходим, поскольку элементы выборки извлекаются из конечной генеральной совокупности.
называется поправочным коэффициентом конечной генеральной совокупности. Он необходим, поскольку элементы выборки извлекаются из конечной генеральной совокупности.
Например, предположим, что некая организация пытается создать группу из 8 человек, обладающих определенными знаниями о производственном процессе. В организации работают 30 сотрудников, обладающих необходимыми знаниями, причем 10 из них работают в конструкторском бюро. Какова вероятность того, что в группу попадут два сотрудника из конструкторского бюро, если членов группы выбирают случайно? Объем генеральной совокупности в этой задаче N = 30, объем выборки n = 8, а количество успехов А = 10.
Используя формулу (1), получаем:
Таким образом, вероятность того, что в группу попадут два сотрудника из конструкторского бюро, равна 0,298 (или 29,8%).
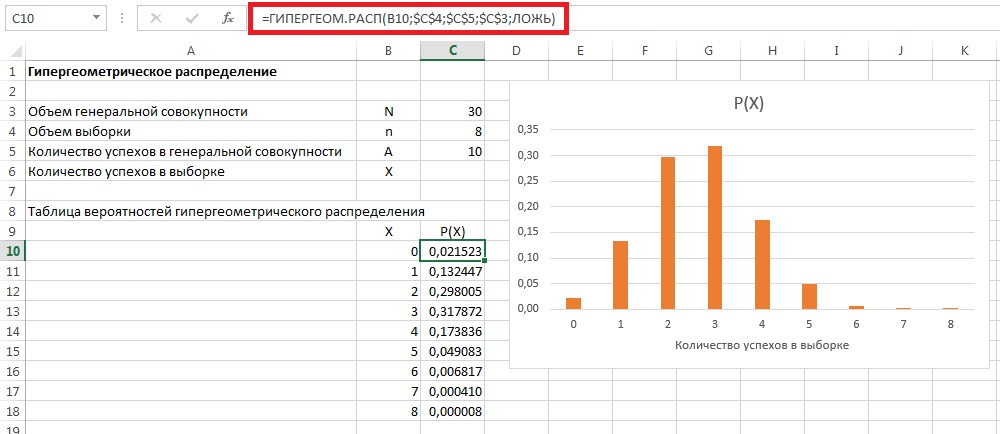
При увеличении генеральной совокупности и объема выборки вычисления гипергеометрического распределения становятся все более утомительными. Однако гипергеометрическое распределение можно вычислить с помощью функции Excel =ГИПЕРГЕОМ.РАСП() (рис. 1).
Рис. 1. Вычисление в Excel гипергеометрического распределение при N = 30, А = 10 и n = 8 (кликните на изображении, чтобы увеличить его)
Таким образом, в рамках рассмотренного выше примера, наиболее вероятно, что в группе из 8 сотрудников трое будут из конструкторского бюро.
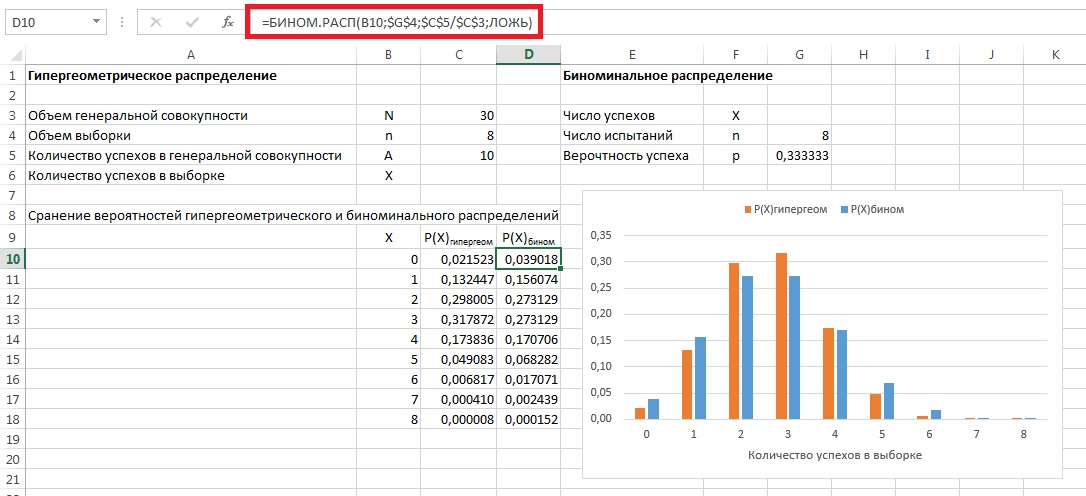
Видно (рис. 6), что гипергеометрическое и биномиальное распределения довольно похожи.
6. Сравнение гипергеометрического и биномиального распределений (кликните на изображении, чтобы увеличить его)
Предыдущая заметка Биномиальное распределение
Следующая заметка Распределение Пуассона
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 316–318