Функция МУМНОЖ используется в Excel для перемножения матриц. Матричная алгебра?! Я напрочь забыл университетский курс матричной алгебры! Хотя это верно для большинства из вас, рекомендую вспомнить, как умножать матрицы. Зачем? Умножение матриц имеет некоторые весьма практичные применения. В этой главе вы рассмотрите проблему вычисления суммарной стоимости, сначала решите ее методом «длинной руки», а затем используете функцию МУМНОЖ для выполнения той же задачи легче и быстрее.
Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Предыдущая глава Оглавление Следующая глава
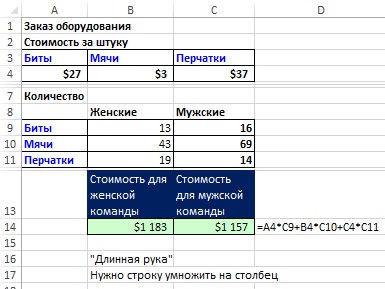
Рис. 18.1. Стоимость оборудования для мужской команды
Скачать заметку в формате Word или pdf, примеры в формате Excel
Используем МУМНОЖ для построения формулы общих издержек
На рис. 18.1 показано, как можно рассчитать общую стоимость оборудования для мужской команды. Обратите внимание, что вы сначала перемножаете, а затем суммируете ряд расходов (А4:С4) и столбец количеств предметов (С9:С11). Хотя вы получите правильные ответы с помощью этой формулы, есть лучший способ сделать это – воспользуйтесь функцией МУМНОЖ. Однако, прежде чем приступить, запомните два правила матричного умножения:
- Количество столбцов первого массива должно быть равно числу строк второго массива.
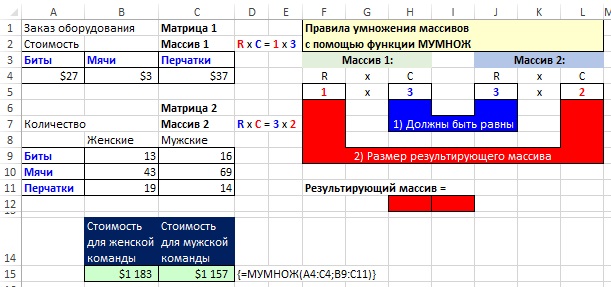
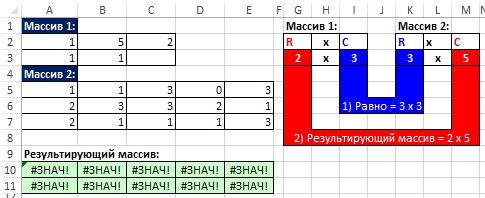
- Размер результирующего массива будет равен количеству строк первого массива, умноженному на число столбцов второго массива (рис. 18.3).
Рис. 18.3. Поскольку цель – вычислить две суммы (для женской и мужской команд), результирующий массив будет две ячейки в ширину; Чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
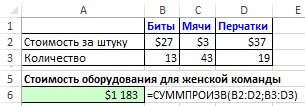
Почему нельзя было использовать функцию СУММПРОИЗВ? Дело в том, что два массива имеют разные размеры. Для сравнения на рис. 18.4 показано, как можно получить результат, если второй массив имеет тот же размер, что и первый.
Рис. 18.4. Если диапазоны ориентированы одинаково, можно применить функцию СУММПРОИЗВ
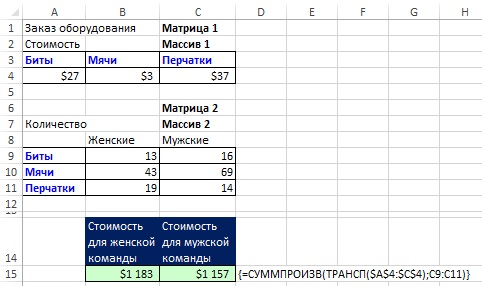
Справедливости ради заметим, что первый массив можно привести к той же размерности, что и второй, с помощью функции ТРАНСП (рис. 18.5).
Рис. 18.5. Формула с СУММПРОИЗВ и ТРАНСП всё же справится с задачей
Вот причины, по которым возможно использовать функцию МУМНОЖ (см. рис. 18.1 и 18.3):
- Поскольку число столбцов в массиве 1 (стоимость) равно числу строк в массиве 2 (Количество), разрешается выполнять матричное умножение.
- Цель – рассчитать общие затраты и вернуть массив размером 1*2; это означает, что результирующий массив, который получается путем умножения матрицы 1*3 на матрицу 3*2 как раз имеет размерность 1*2.
Чтобы воспользоваться функцией массива МУМНОЖ (см. рис. 18.3):
- Выберите область Стоимость (А4:С4) в качестве первого массива, а область Количество (В9:С11) – в качестве второго.
- Выделите область, в которой разместится результирующий массив – В15:С15.
- В строке формул наберите =МУМНОЖ(A4:C4;B9:C11).
- Введите формулу, нажав Ctrl+Shift+Enter.
Использование функции МУМНОЖ для расчета средневзвешенного значения
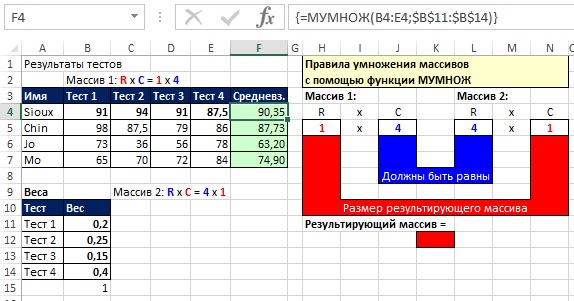
Как показано на рис. 18.7, вы можете использовать МУМНОЖ для расчета средневзвешенного значения, когда два массива имеют одинаковое количество элементов, но разные размеры (разную ориентацию). Массив 1 (значения тестов для Sioux, диапазон В4:Е4) имеет размерность 1*4 и массив 2 (веса тестов, диапазон $B$11:$В$14) имеет размерность 4*1. Введите формулу массива {=МУМНОЖ(B4:E4;$B$11:$B$14)} (см. рис. 18.7, строка формул) в ячейку F4 и скопируйте её вниз по столбцу.
Рис. 18.7. Использование функции МУМНОЖ для расчета средневзвешенного значения
Таблица умножения на основе функции МУМНОЖ
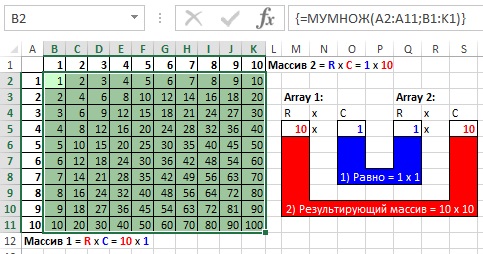
На рис. 18.8 показано как создать таблицу умножения. В качестве альтернативы можно использовать смешанные ссылки (подробнее см. Относительные, абсолютные и смешанные ссылки на ячейки в Excel).
Рис. 18.8. Таблица умножения на основе функции МУМНОЖ
Нахождение ожидаемой доходности портфеля акций
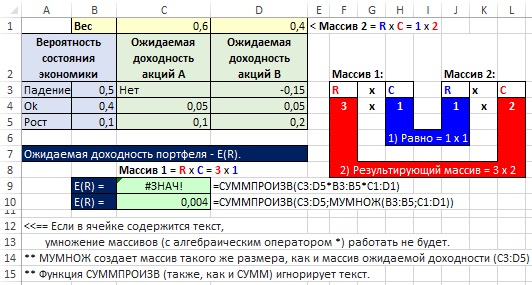
На рис. 18.9 показан тот же пример, что и в главе 10 для вычисления ожидаемой доходности портфеля акций. Цель формулы – перемножение трех диапазонов С3:D5, В3:В5 и С1:D1. В главе 10 вы узнали, как обойти требование функция СУММПРОИЗВ, чтобы все массивы имели один и тот же размер: нужно помещать каждый массив не в отдельный аргумент, а все массивы разместить в аргументе массив_1, перемножив их алгебраически. Однако, в этом случае, при наличии нечисловых данных в любом из массивов, функция СУММПРОИЗВ возвращает ошибку.
Функция МУМНОЖ умножает массив 1 (вероятность состояния экономики, диапазон В3:В5) на массив 2 (вес, диапазоне С1:D1), и создает результирующий массив того же размера, что и массив ожидаемой доходности (3*2, диапазон С3:D5). Теперь вы можете умножить эти два массива: =СУММПРОИЗВ({"Нет";-0,15:0,05;0,05:0,1;0,2};{0,3;0,2:0,24;0,16:0,06;0,04}), поместив их в отдельные аргументы функции СУММПРОИЗВ, и воспользоваться свойством функции СУММПРОИЗВ игнорировать текст.
Рис. 18.9. Ячейка D10 содержит надежную формулы для расчета ожидаемой доходности
Параметры функции массива МУМНОЖ:
- Синтаксис МУМНОЖ(массив1; массив2). Функция содержит ровно два аргумента.
"Массив1"и"массив2"могут быть заданы как диапазоны ячеек, константы массивов или ссылки.- Функция МУМНОЖ возвращает значение ошибки #ЗНАЧ! в следующих случаях:
- Если какая-либо ячейка пуста или содержит текст (рис. 18.10; ячейка С3).
- Если число столбцов в аргументе «массив1» отличается от числа строк в аргументе «массив2».
Рис. 18.10. Ячейку С3 пустая, и функция МУМНОЖ возвращает ошибку
Функции массива МОБР и МЕДИН
Эти функции понадобятся, если вы захотите решать системы уравнений с помощью матричной алгебры. Функцию МОБР (матрица обратная) вычисляет обратную матрицу. Функция МЕДИН (матрица единичная) возвращает единичную матрицу. Матрицы обычно обозначают прописными буквами, например, А. Обратной (А–1) называют матрицу, произведение которой на исходную матрицу A равно единичной матрице I (или, в русскоязычном обозначении – E; рис. 18.11). Обратная матрица существует только для квадратных матриц. В единичной матрице диагональные элементы равны 1, не диагональные элементы равны нулю.
Рис. 18.11. Матриц А, обратная матрица А–1, их произведение возвращает единичную матрицу (при условии, что обратная существует)
Чтобы рассчитать обратную матрицу A–1 выделите ячейки D2:E3, и в строке формул наберите =МОБР(A2:B3). Введите функцию массива нажав Ctrl+Shift+Enter. Единичная матрица в ячейках G2:H3 получена умножением матриц А и A–1 с помощью формулы массива {=МУМНОЖ(A2:B3;D2:E3)}.
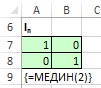
Единичная матрица нужной размерности, начиная с Excel 2013 может быть получена с помощью функции массива МЕДИН (рис. 18.12). Чтобы ввести функцию МЕДИН выделите квадратный диапазон, и в качестве аргумента функции укажите число строк (или столбцов) диапазона.
Рис. 18.12. Функция массива МЕДИН, появившаяся в Excel 2013
Решение систем уравнений с помощью функции МУМНОЖ
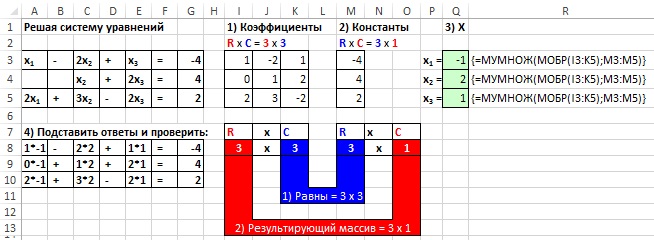
На рис. 18.15 представлена система из трех линейных уравнений с тремя переменными х1, х2 и х3. Поскольку, и уравнений, и переменных – три, можно использовать МУМНОЖ и МОБР для нахождения неизвестных. Выполните следующие действия:
- Разместить коэффициентов из уравнений в массиве 3*3 в диапазоне I3:К5.
- Константы из уравнений разместите в массиве 3*1 в диапазоне М3:М5.
- Выделите диапазон Q3:Q5 (3*1) и наберите в строке формул: =МУМНОЖ(МОБР(I3:K5);M3:M5). Введите формулу массива, нажав Ctrl+Shift+Enter.
- Подставьте найденные значения в уравнения и проверьте правильность решения.
Рис. 18.15. Решение системы уравнений с помощью функций МУМНОЖ и МОБР

2. Выделите область, в которой разместится результирующий массив – В15:С16
Возможно, опечатка, область ввода формулы — 2 ячейки: B15:C15
Спасибо. Поправил.
Здравствуйте, мне нужно найти сумму произведений переменных из одной таблицы, которые удовлетворяют одному критерию к переменной по второй таблице по второму критерию, но в первой таблице есть нулевые значения. И я не знаю, как это сделать