Это глава из книги: Майкл Гирвин. Ctrl+Shift+Enter. Освоение формул массива в Excel.
Предыдущая глава Оглавление Следующая глава
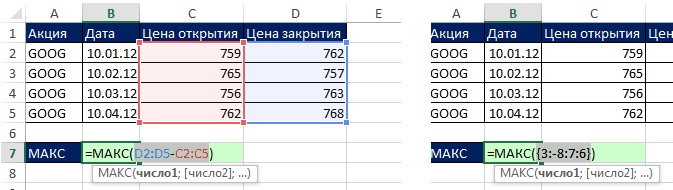
Ранее в этой книге вам неоднократно встречались массивы констант. Действительно, каждый раз, когда вы проводили оценку работы элементов формул, используя клавишу F9, вы видели пример массива констант. Например, в первой формуле массива, созданного в главе 2 (снова показан на рис. 7.1), вы можете выделить D2:D5-C2:C5, и нажав F9, увидеть результирующий массив {3;–8;7;6}. Однако, ранее, оценив массив, вы сразу же нажимали Ctrl+Z, чтобы оставить внутри формулы не жесткий код, а ссылку. Если бы вы не использовали Ctrl+Z, вы бы создали массив констант, который бы не изменялся при изменении исходных данных на листе. В этой главе вы узнаете о ситуациях, в которых использование массива констант дает преимущества.
Рис. 7.1. Выделите массив (слева), нажмите F9 (справа), и получите массив констант
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Рассмотрим синтаксис, используемый для создания массива констант, и примеры, иллюстрирующие три типа массива констант, с которыми вы можете столкнуться в Excel.
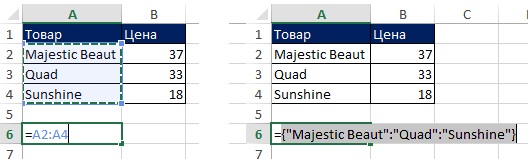
Вертикальный массива констант (рис. 7.2). В ячейке А6 создайте ссылку на массив =А2:А4, и нажмите F9. Вы увидите массив элементов, расположенный в фигурных скобках; текст всегда отображается в кавычках; двоеточие – разделитель, указывающий, что элементы расположены в столбце друг под другом.
Рис. 7.2. Вертикальный диапазон ячеек: выделите ссылку (слева) и нажмите F9 (справа)
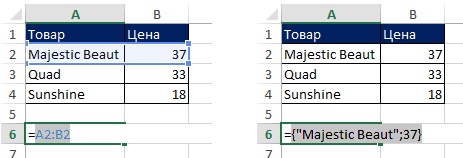
Горизонтальный массив констант (рис. 7.3). В ячейке А6 создайте ссылку на массив =А2:В2, и нажмите F9. Вы увидите массив элементов, расположенный в фигурных скобках; текст всегда отображается в кавычках; цифры отображаются просто цифрами; точка с запятой, – разделитель, указывающий, что элементы расположены в одном ряду, в соседних столбцах.
Рис. 7.3. Горизонтальный диапазон ячеек: выделите ссылку (слева) и нажмите F9 (справа)
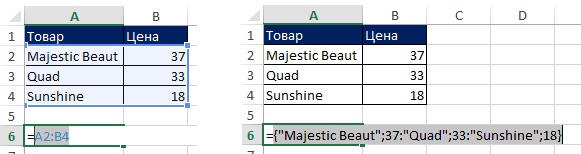
Прямоугольный массив констант (рис. 7.4). В ячейке А6 создайте ссылку на массив =А2:В4, и нажмите F9. Вы увидите массив элементов, расположенный в фигурных скобках; текст всегда отображается в кавычках; цифры отображаются просто цифрами; используются два разделителя: точка с запятой – для перехода к соседней колонке в той же строке, и двоеточие – для перехода в первую колонку новой строки.
Рис. 7.4. Прямоугольный диапазон ячеек: выделите ссылку (слева) и нажмите F9 (справа)
У вас может возникнуть вопрос, существуют ли ситуации, когда массив констант будет полезен? Не входит ли он в противоречие с золотым правилом Excel: если исходные данные могут измениться, разместите их на листе и сошлитесь на них внутри формулы; если исходные данные не изменятся, жестко закодируйте их в формуле. Польза от массива констант заключается в том, что формула с ним не требует нажатия Ctrl+Shift+Enter. Таким образом, если исходные данные не изменятся, используйте массив констант.
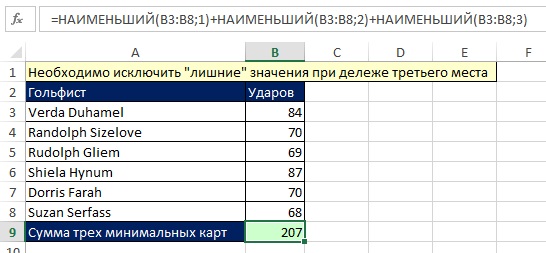
Рассмотрим пример из игры в гольф (рис. 7.5). Цель – найти сумму трех лучших (минимальных) результатов, при этом не учитывать 4-й и последующие результаты, если они равны третьему (видно, что в нашем примере как раз такой случай с числом 70). Для решения задачи отлично подойдет функция НАИМЕНЬШИЙ, аргумент k которой позволит выбрать требуемые значения: k = 1 даст минимальное значение, k = 2 – второе и т.д. Как видно на рис. 7.5, сумма трех наименьших при k = 1, 2, 3 дает правильный ответ. Отличная формула, имеющая, пожалуй, лишь тот недостаток, что потребует времени на написание, если вам нкжно отобрать, скажем, 10 минимальных значений.
Рис. 7.5. Аргумент k функции НАИМЕНЬШИЙ позволяет получить k-ое наименьшее значение
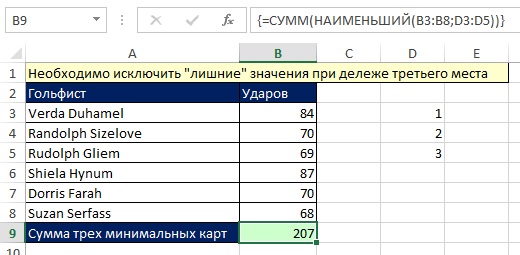
Чтобы создать более компактную формулу можно поместить массив в аргумент функции (рис. 7.6). И здесь вам пригодится массив констант {1,2,3}. Вы можете использовать жесткий код, поскольку число отбираемых значений меняться не будет. Поскольку аргумент k имеет три значения, функция НАИМЕНЬШИЙ также вернет три значения, которые и будут просуммированы. Чтобы убедиться в этом, выделите аргумент число1 функции СУММ и нажмите F9 (рис. 7.7). Видно, что, хотя третье наименьшее значение имеют два равных числа 70, функция НАИМЕНЬШИЙ(B3:B8;{1;2;3}) вернула только три числа.
Рис. 7.6. Массив констант помещен в k аргумент функции НАИМЕНЬШИЙ
Рис. 7.7. Функция НАИМЕНЬШИЙ возвращает три наименьших значения, исключая «лишние» 70
Примечание: не важно, зададите ли вы массив констант горизонтальным {1;2;3} или вертикальным {1:2:3}.
Для ввода формулы не потребовались Ctrl+Shift+Enter. Однако, если вы вместо массива констант в аргументе k, используете ссылку на диапазон (рис. 7.8), ввод формулы потребует нажатия Ctrl+Shift+Enter (в противном случае вы получите ошибку #ЗНАЧ!). Заметим, что Ctrl+Shift+Enter можно всё же избежать, если воспользоваться формулой: =СУММПРОИЗВ(НАИМЕНЬШИЙ(B3:B8;D3:D5))
Рис. 7.8. Использование ссылки на диапазон D3:D5 в аргументе k потребует Ctrl+Shift+Enter
Примечание: HELP функции НАИМЕНЬШИЙ не содержит упоминания, что аргумент k может быть представлен массивом констант. Это является очередным свидетельством того, насколько плохо задокументированы возможности Excel по работе с формулами массива. Я узнал об этом на форуме MrExcel и многолетних изысканий методом проб и ошибок.
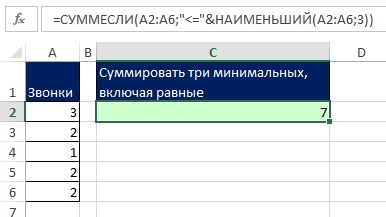
Если вам потребуется просуммировать все разделенные (ничейные) результаты, можно воспользоваться обычной функцией СУММЕСЛИ, а не формулой массива (рис. 7.9).
Рис. 7.9. Формула суммирует три минимальных балла, в том числе равные
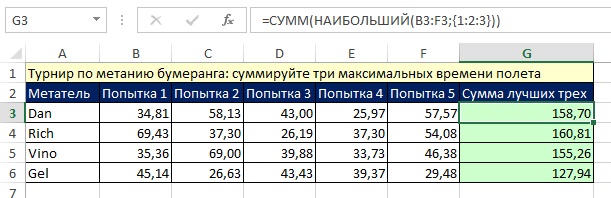
Следующий пример демонстрирует использование функции НАИБОЛЬШИЙ (рис. 7.10). Цель – суммировать три самых длительных полета бумеранга у каждого участника.
Рис. 7.10. Массив констант в аргументе k функции НАИБОЛЬШИЙ
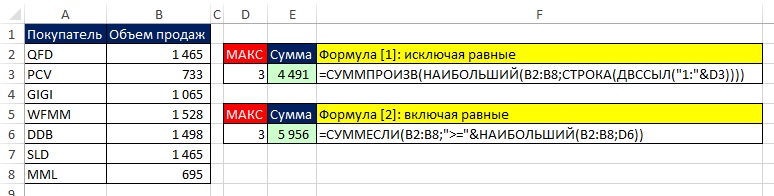
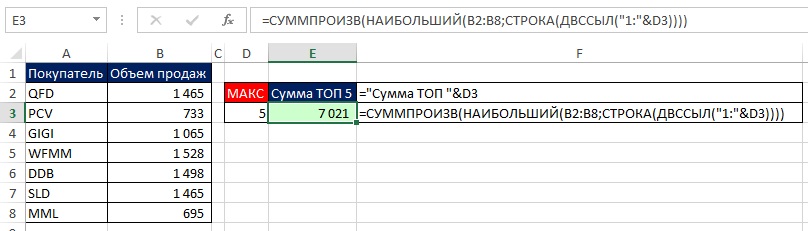
А что, если вы хотите, чтобы формула суммировала переменное число максимальных или минимальных значений? На рис. 7.11 приведены две формулы, которые суммируют три наибольших значения. Формула [1] исключает деленные третьи значения, формула [2] включает таковые. Отличие этих формул от рассмотренных ранее заключается в том, что число максимальных значений не жестко зашито в формулу, а определяется значениями в ячейках D3 и D6. При изменении чисел в ячейках D3 и D6, сумма в ячейках Е3 и Е6 будет изменяться. На рис. 7.12 показаны суммы для двух максимальных значений.
Рис. 7.11. Если изменить значения в ячейках D3 и D6, формула вернет новое значение
Рис. 7.12. Формулы 1 и 2 дают одинаковые результаты для двух максимальных значений, так как среди вторых значений нет одинаковых
Формула [2], наверное, проста для понимания, а вот формула [1] содержит элементы, с которыми вы ранее не встречались. Используя функции СТРОКА и ДВССЫЛ можно создать динамический массив переменной длины из последовательных чисел. Начните ввод формулы с функции ДВССЫЛ (рис. 7.13). ДВССЫЛ запрограммирована возвращать ссылку, заданную текстовой строкой. В нашем случае элемент аргумент ссылка_на_ячейку "1:"&D3 представляет собой ссылку на строки 1:3. Чтобы убедиться в этом, выделите этот элемент и нажмите F9.
Рис. 7.13. Конкатенация "1:" и D3 (слева) дает ссылку на строки "1:3" (справа)
Если вы захотите оценить, что возвращает формула =ДВССЫЛ("1:"&D3), выделите ее целиком и нажмете F9 (рис. 7.14), то получите ошибку «Формула слишком длинная. Ее длина не должна превышать 8192 знака».
Рис. 7.14. При оценке формулы =ДВССЫЛ("1:"&D3) возвращается ошибка
Ошибку вызвана тем, что ссылка на строки 1:3 содержит все ячейки в строках с 1 по 3. На листе Excel (начиная с версии 2007) 16 384 столбца, т.е. в трех строках содержится 49 152 ячейки. Сама по себе функция ДВССЫЛ не содержит ошибки, поэтому если поместить ее в качестве аргумента функции СТРОКА, вы получите требуемый результат (рис. 7.15). Заметим, что аргумент функции СТРОКА ожидает одно значение. Вы же «подсовываете» ему 49 152 ссылки на ячейки. Правда все эти ссылки относятся к строкам 1, 2 и 3. Так что функция СТРОКА вернет массив {1:2:3} (убедитесь в этом, выделив целиком функцию СТРОКА, и нажав F9). Обратите внимание, что поскольку речь идет о строках, в синтаксисе массива в качестве разделителя присутствует двоеточие.
Рис. 7.15. Функция СТРОКА возвращает номер строки аргумента ссылка; поскольку ДВССЫЛ возвращает ячейки, относящиеся к строкам 1, 2 и 3, функция СТРОКА возвращает массив {1:2:3}
Итак, с помощью конструкции СТРОКА(ДВССЫЛ(…)) вам удалось создать аргумент k функции НАИБОЛЬШИЙ (рис. 7.16). Этот элемент формулы является динамичным. Если в ячейке D3 ввести значение 2, массив для k вернет {1;2}, а если 5, то – {1;2;3;4;5}.
Рис. 7.16. Аргументом k функции НАИБОЛЬШИЙ получает массив, созданный конструкцией СТРОКА(ДВССЫЛ(…))
Вы можете закончить ввод формулы путем размещения функции НАИБОЛЬШИЙ в качестве аргумента массив1 функции СУММПРОИЗВ. Мне СУММПРОИЗВ нравится больше, чем просто СУММ, поскольку первая не требует нажатия Ctrl+Shift+Enter, а вторая – требует.
Рис. 7.17. Завершите ввод формулы путем размещения функции НАИБОЛЬШИЙ в качестве аргумента массив1 функции СУММПРОИЗВ
Мы только что разобрали трюк, который можно назвать «массив последовательных чисел переменной длины» (рис. 7.18).
Рис. 7.18. Формула мгновенно отработает, если в ячейке D3 ввести новое значение, например, 5
Примечание: функция ДВССЫЛ является летучей (англ. – volatile). Функции этого класса пересчитываются при любом изменении в Excel. Пересчет может быть запущен, например, вставкой новой строки или изменением формата ячейки (даже в другой книге). Для сравнения, функция СУММ пересчитывается только если изменилось какое-либо значение, на которое ссылается СУММ. Вследствие этого свойства волатильные функции увеличивают время расчета формул. Вы узнаете больше о пересчете формул в главе 13.
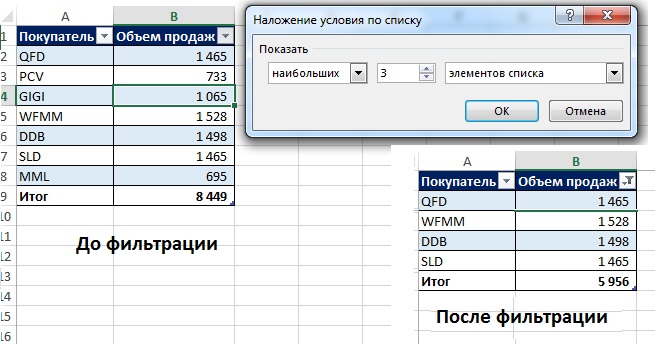
Прежде чем перейти к следующей формуле массива, хочу познакомить вас с инструментом Excel –Таблица (рис. 7.19). [1] Для создания таблицы встаньте на любую ячейку в диапазоне А1:В8 и пройдите по меню: Главная → Стили → Форматировать как таблицу (или нажмите Ctrl+T; Т – английское). Далее в меню Конструктор область Параметры стилей таблицы поставьте галочку напротив Строка итогов. Примените фильтр в колонке Объем продаж: Числовые фильтры → Первые 10, задайте 3 наибольших элемента списка. К сожалению, отфильтрованный список будет включать дубли, так как третье наибольшее значение представлено двумя строками.
Рис. 7.19. Использование инструмента Таблице для отбора трех максимальных значений
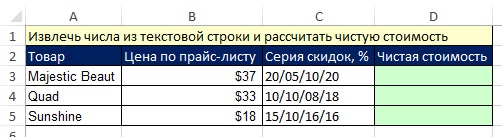
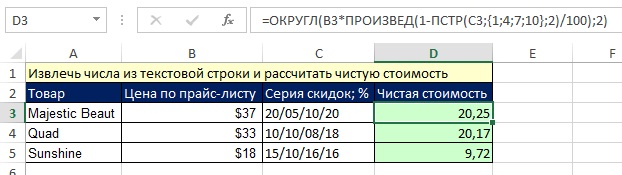
Рассмотрим еще один пример того, как можно использовать массив констант. В главе 3 мы вывели формулу для расчета стоимости товара с учетом скидок. При этом четыре значения скидок были размещены каждая в своей ячейке. Попробуем решить задачу, когда четыре значения скидок размещены в одной ячейке (рис. 7.20).
Рис. 7.20. Значения скидок размещены в одной ячейке в виде текстовой строки
В одной ячейке нужно последовательно:
| Извлечь числа из текстовой строки | {"20";"05";"10";"20"} |
| Разделить на 100 | {0,20;0,05;0,10;0,20} |
| Вычисление коэффициента | (1-0,20)*(1-0,05)*(1-0,10)*(1-0,20) |
| Вычисление коэффициента | 0,80*0,95*0,90*0,80=0,5472 |
| Чистая стоимость | $37*0,5472=$20,25 |
Чтобы одновременно извлечь четыре числа из текстовой строки, можно использовать массив констант в аргументе начальная_позиция функции ПСТР (рис. 7.21). Функция ПСТР возвращает заданное число знаков из строки текста, начиная с указанной позиции. Обычно аргумент начальная_позиция содержит один элемент. Например, если вы ввели формулу =ПСТР(C3;4;2), функция вернет два символа, начиная с 4-го из ячейки С3.
Рис. 7.21. Массив констант в аргументе начальная_позиция функции ПСТР
Однако, в нашем примере, вы вводите четыре значения в аргумент начальная_позиция. Поэтому функция ПСТР вернет четыре результата. Убедитесь в этом, выделив целиком функцию ПСТР и нажав F9 (рис. 7.22). Обратите внимание, что функция ПСТР возвращает текстовые элементы. Это не помешает нам, потому что на следующем шаге мы выполним с этим массивом математические операции, что автоматически приведет к преобразованию текста в числа.
Рис. 7.22. Убедитесь в том, что функция ПСТР возвращает массив, выделив ее и нажав F9
На следующем шаге разделите массив на 100, а затем вычтете результат из единицы (рис. 7.23). Поскольку деление будет выполняться первым, вам не нужны дополнительные скобки. Оцените получившуюся формулу, выделив ее и нажав F9.
Рис. 7.23. Деление на 100 преобразует текст, извлеченный функцией ПСТР, в число
Завершите ввод формулы, умножая элементы массива, полученного на предыдущем шаге, с помощью функции ПРОИЗВЕД; далее умножьте на цену по прайс-листу, и наконец округлите результат до двух знаков после запятой (рис. 7.24). Поскольку вы использовали массив констант в аргументе функции ПСТР, ввод формулы не требует Ctrl+Shift+Enter.
Рис. 7.24. Формула для вычисления чистой стоимости
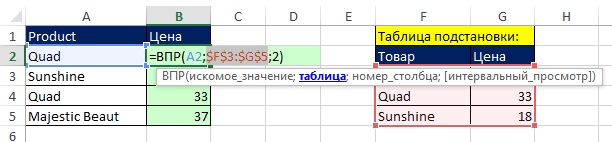
Использование массива констант в функции ВПР для экономии места. На рис. 25 показано типичное применение функции ВПР (первая колонка в таблице F2:G5 отсортирована, поэтому ВПР ищет лишь приблизительное совпадение). Если вы предполагаете, что данные в таблице подстановки (F2:G5) меняться не будут и вам неудобно, чтобы таблица занимала место на листе, вы можете ввести код таблицы жестко в формулу. Проблема с жестким кодированием массива констант в формуле ВПР заключается в относительно большом объеме ввода (массив нужно поместить в фигурные скобки, текст – в кавычки, а также ввести «тучу» разделителей). Можно использовать небольшую хитрость: если таблица у вас уже есть, создайте обычную ВПР, а потом выделите аргумент таблица и нажмите F9. Вы преобразуете ссылку на диапазон в массив констант (рис. 7.26). Вы можете затем скопировать формулу ВПР вниз по колонке и удалить таблицу подстановки.
Рис. 7.25. Если данные в таблице подстановки могут меняться, обычная ВПР со ссылками на ячейки – отличный выбор
Рис. 7.26. Выделите аргумент таблица и нажмите F9; вы преобразуете ссылку на диапазон в массив констант
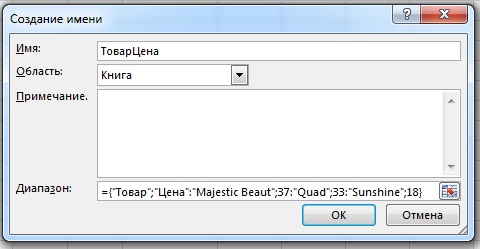
Еще одна возможность сэкономить пространство на листе – присвоить массиву констант имя, а затем использовать это имя в формулах. Чтобы поименовать массив констант, перейти на вкладку Формулы и щелкните Диспетчер имен (или нажмите Ctrl+F3), далее нажмите кнопку Создать. В открывшемся диалоговом окне Создание имени задайте имя, область применения имени и диапазон (в нашем случае, это не ссылка на ячейки, а массив констант). Можете воспользоваться хитростью, описанной выше, чтобы не набирать массив констант с клавиатуры (рис. 7.27).
Рис. 7.27. Присвоение имени массиву констант
Вы можете использовать это имя в качестве аргумента функции ВПР (рис. 7.28). Обратите внимание, что =ВПР(A2;ТоварЦена;2) не является формулой массива.
Рис. 7.28. Имя ТоварЦена содержит массив констант
Вы только что использовали два элемента (массив констант и определенное имя) в качестве аргумента Таблица функции ВПР. А как насчет других аргументов ВПР? Могут ли они содержать массив констант и/или операции с массивами? Как вы видели в главе 6, аргумент искомое_значение не может обрабатывать массивы. А аргумент номер_столбца? Может ли он обрабатывать массив?
На рис. 7.29 (диапазон А1:Н4) показана таблица подстановки с названиями товаров в первом столбце (отсортированы по алфавиту) и компонентами затрат в столбцах 2–8. Цель формулы – сложить затраты по столбцам 2, 4, 5, 7 и 8. Вы можете использовать массив констант в качестве аргумента номер_столбца функции ВПР, чтобы получить на выходе функции сразу пять значений затрат. Вы можете увидеть это, если выделите функцию ВПР и нажмете F9 (рис. 7.30).
Рис. 7.29. Поместите в аргумент номер_столбца функции ВПР массив констант номеров столбцов
Рис. 7.30. Так как аргумент номер_столбца содержит пять элементов, функция ВПР вернет пять значений
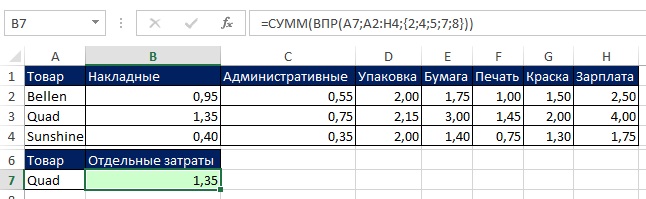
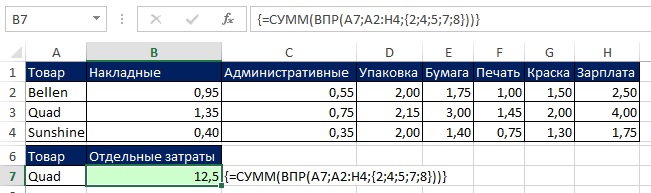
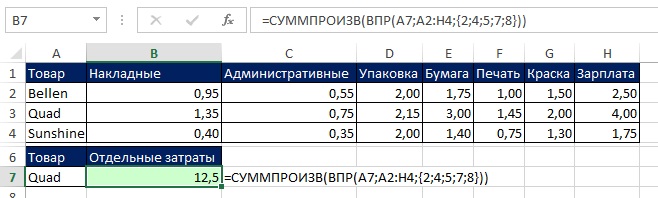
Если вы введете формулу =СУММ(ВПР(A7;A2:H4;{2;4;5;7;8})) простым нажатием Enter, то получите неверный ответ (рис. 7.31). Видно, что функция СУММ обработала только первый элемент массива {1,35;2,15;3;2;4}, возвращенный функцией ВПР. Чтобы получить корректный результат введите формулу в ячейку используя Ctrl+Shift+Enter (рис. 7.32). Если вам хочется сэкономить на нажатии трех клавиш, поместите ВПР внутрь СУММПРОИЗВ (рис. 7.33).
Рис. 7.31. Ввод формулы с помощь Enter дает ошибочный результат
Рис. 7.32. Независимо от того, содержит ли аргумент номер_столбца функции ВПР массив констант или ссылку на диапазон, ввод формулы требует нажатия Ctrl+Shift+Enter
Рис. 7.33. Когда вы помещаете ВПР внутрь СУММПРОИЗВ, вам не нужно нажимать Ctrl+Shift+Enter
Итак, получается, что некоторые аргументы функции, которые могут содержать массив констант, не требуют использования Ctrl+Shift+Enter (например, массив в НАИМЕНЬШИЙ и НАИБОЛЬШИЙ, текст в ДЛСТР, логическое_значение в ИЛИ), а некоторые – требуют (например, номер_столбца в ВПР).
До сих пор в этой главе вы использовали массивы констант в качестве аргументов функций. Массивы констант также могут использоваться в математических операциях и операциях сравнения массивов. При этом, если используется только массив констант, формула не требует нажатия Ctrl+Shift+Enter (рис. 7.34–7.36). Если также используется и массив в виде ссылок на диапазон, ввод формулы требует нажатия Ctrl+Shift+Enter (рис. 7.37).
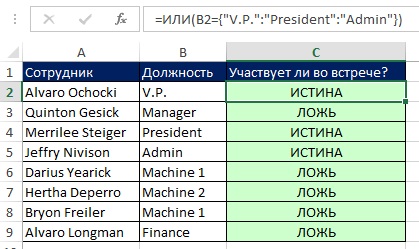
Рис. 7.34. Формула массива (в ячейке С2) спрашивает: «равно ли содержимое ячейки В2 одному из значений: V.P., President или Admin?»; операция сравнения включает в себя операцию с массивом констант в аргументе логическое_значение1 функции ИЛИ и не требует нажатия Ctrl+Shift+Enter
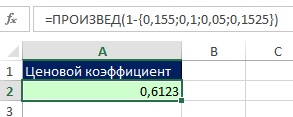
Рис. 7.35. Формула массива рассчитывает ценовой коэффициент [2] на основании значений отдельных скидок; выполнена математическая операция умножения с использованием массива констант в аргументе число1, что не требует нажатия Ctrl+Shift+Enter
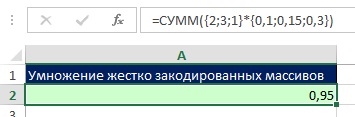
Рис. 7.36. Формула умножает два массива констант и затем суммирует результаты произведения (я не думаю, что вы будет использовать такую формулу, но я включил ее, чтобы проиллюстрировать работу массива констант); математическая операция с массивами констант помещена в аргумент число1 функции СУММ и не требует нажатия Ctrl+Shift+Enter
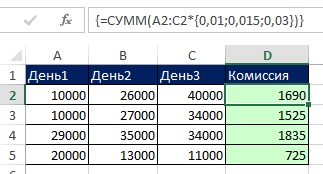
Рис. 7.37. Формула перемножает массивы ссылок и констант и затем суммирует результаты произведения (лучше использовать функцию СУММПРОИЗВ; я включил эту формулу, чтобы проиллюстрировать работу массива констант); математическая операция включает в себя не только массив констант, но и ссылку на диапазон ячеек, и она требует нажатия Ctrl+Shift+Enter
Резюме главы
- Массивы константы можно использовать, как в обычных, так и в формулах массива
- Синтаксис массивов констант: фигурные скобки в начале и в конце массива; точка с запятой разделяет элементы в строке, двоеточие – одну строку от другой; текстовые элементы помещаются в двойные кавычки, а числа, логические значения и значения ошибок – без кавычек
- Используются три типа массивов констант: вертикальные, горизонтальные, прямоугольные
- Массив констант не может содержать более 8192 символов
- Для ввода формулы массива:
- Если используется только массив констант, Ctrl+Shift+Enter не требуется
- Некоторые аргументы функций при размещении в них массива констант не требуют Ctrl+Shift+Enter (например, массив в НАИМЕНЬШИЙ и НАИБОЛЬШИЙ, текст в ДЛСТР, логическое_значение в ИЛИ, начальная_позиция в ПСТР, число1 в ПРОИЗВЕД и СУММ)
- Некоторые аргументы функций требуют нажатия Ctrl+Shift+Enter, если они содержат массив констант (например, аргумент номер_столбца в ВПР)
- Золотое правило Excel в отношении формул массива можно дополнить следующим:
- Если данные не будут меняться и вы экономите место на листе, используйте массив констант
- Поименуйте массив констант и используйте его имя в формулах









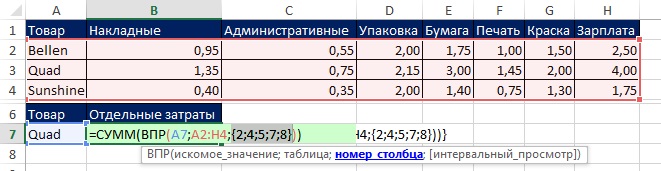

Здравствуйте! Подскажите, пожалуйста, как можно просуммировать диапазон с выбранным условием (то есть не один столбец, как это делает функция суммесли, а несколько, причем просуммироваться должны столбцы все, подходящие условию), пример такой же как у вас на рисунке 7,33, только если бы Quad повторялось много раз и просуммировать нужно было бы столбцы B-H (то есть все столбцы подряд)
Разобралась, спасибо!