Это вторая книга Ильи Пригожина в моей библиотеке (см. Порядок из хаоса). На самом деле, это серьезный труд физика (с применением математики), и вся книга целиком предназначена, конечно же, физикам. Но… словно предчувствуя (или понимая), что его теория выходит далеко за пределы физики, Илья Пригожин пишет главу, излагающую его выводы более-менее человеческим языком. Любопытно, что в философском словаре сына-студента о синергетике говорится, как о учении, расширяющем границы диалектики. [1] На мой взгляд, идеи, изложенные в книге, могут быть полезны менеджерам, поскольку формируют системный подход и способствуют преодолению детерминистского взгляда на происходящее, будущее, и, даже, прошлое.
Илья Пригожин. От существующего к возникающему. – М.: КомКнига, 2006. – 296 с. [2]
Скачать краткий конспект в формате Word или pdf
Глава 10. Необратимость и структура пространства и времени
Второе начало термодинамики как динамический принцип
Противоположность между существующим и возникающим, постоянством и изменением, детерминизмом и случаем давно привлекала и продолжает привлекать внимание философов и представителей естественных наук. Со времен Ньютона физика видит свою задачу в достижении не зависящего от времени уровня реальности, на котором не происходят истинные изменения, а лишь вполне детерминированным образом эволюционирует начальное состояние. Глубокий переворот в нашем мышлении, вызванный теорией относительности и квантовой механикой, по существу, не затронул основной установки классической физики. В динамике, будь то классическая, квантовая или релятивистская, время выступает лишь как некий внешний параметр, не имеющий выделенного направления. В динамике нет ничего такого, что позволяло бы отличать прошлое от будущего.
Энтропия есть «информация» о состояниях. В ходе динамической эволюции энтропия остается неизменной вследствие унитарного характера такой эволюции. Именно поэтому я считаю уместным назвать динамику физикой существующего. Термодинамику в отличие от динамики следовало бы назвать физикой возникающего. Второе начало термодинамики подтверждает реальность изменения и вводит физическую величину (например, энтропию), наделяющую время выделенным направлением, или, если воспользоваться выражением Эддингтона, задающую «стрелу времени». Энтропия устанавливает различие между прошлым и будущим. Кроме того, термодинамика приводит к новой концепции времени как внутренней переменной, присущей системе. Такое понимание времени позволяет считать более «старым» (по сравнению с другим) то из двух состояний, которому соответствует большее значение энтропии. Интерпретация времени как внутреннего свойства физической системы выходит за рамки традиционного физического описания системы.
Перед лицом вопиющего противоречия между динамическим описанием и формулировкой второго начала термодинамики физики обычно склонялись к принятию динамического описания в качестве фундаментального, а второе начало термодинамики считали проистекающим из приближенной процедуры, дополнительно налагаемой на динамику. Более того, некоторые физики склонны приписывать второму началу термодинамики субъективный или антропоморфный характер. Так, по утверждению Макса Борна «необратимость есть следствие неявного введения незнания в фундаментальные [динамические] законы», а Е. Вигнер пытается определять энтропию как меру «утилизуемого знания» о системе, которым мы располагаем.
Последние достижения в области физики и химии делают все более затруднительным принятие представлений о необратимости, выражаемых вторым началом термодинамики. С подобной точкой зрения можно было бы согласиться, если бы необратимость была специфической особенностью, присущей лишь крупномасштабным макроскопическим явлениям, например, диссипации [рассеивание] энергии вследствие трения, теплопроводности и т.п. Но, как теперь известно, необратимость играет важную конструктивную роль в процессах, представляющих первостепенный интерес для столь различных областей науки, как биология и космология. Возможность возникновения самоорганизации (так называемых диссипативных структур) в ситуациях, далеких от равновесия, осознание роли необратимости в эволюции всей Вселенной в целом, попытки найти формулировку второго начала термодинамики, позволяющую применять его к столь важным процессам, как гравитационный коллапс, — все эти неожиданные физические открытия, по-видимому, свидетельствуют о том, что второе начало термодинамики по своему характеру более фундаментально, чем принято считать.
В физике элементарных частиц необратимость также играет более существенную роль, чем отводилась ей до сих пор. Почти все так называемые элементарные частицы нестабильны и претерпевают распады. Правда, физики все еще надеются, что им удастся включить все эти явления в рамки унитарной схемы динамической эволюции. Однако становится все яснее, что традиционная схема унитарной динамической эволюции в конечном счете может оказаться неадекватной.
Изложенные выше причины побудили нас избрать подход к проблеме необратимости, в корне отличный от традиционного. В качестве фундаментального физического факта мы приняли закон возрастания энтропии и вытекающее из него существование «стрелы времени». Задачу удовлетворительной теории необратимости мы видим в изучении тех принципиально важных изменений в концептуальной структуре динамики, к которым приводит принятие второго начала термодинамики в качестве основного постулата.
Различие между нашим и традиционным подходами, возможно, лучше всего пояснит следующая историческая аналогия. В начале XX в., до появления специальной теории относительности Эйнштейна, было предпринято несколько попыток объяснить отрицательный результат эксперимента Майкельсона — Морли (постоянство скорости света с, не зависящее от движения системы отсчета). Эти теории не вносили сколько-нибудь заметных изменений в классическую ньютоновскую концепцию пространства-времени и исходили из существования абсолютной системы отсчета (эфира). Постоянство скорости света авторы теорий пытались объяснять, как кажущийся эффект, вызываемый реальным сокращением измерительных стержней, движущихся относительно эфира. Были предложены хитроумнейшие объяснения, связывающие сокращение с электромагнитным взаимодействием заряженных частиц, образующих измерительный стержень.
Эйнштейн поступил иначе: постоянство скорости света с он принял за фундаментальный физический факт и проследил, к каким изменениям в наших представлениях о пространстве, времени и динамике приводит принятие такого постулата. Аналогичным образом поступаем и мы, когда, не пытаясь объяснить второе начало термодинамики как кажущееся свойство, связанное с той или иной аппроксимацией (или вводимым в динамику тем или иным «незнанием»), постулируем второе начало как фундаментальный физический факт и пытаемся выяснить, к каким изменениям в наших представлениях о пространстве, времени и динамике приводит принятие такого постулата.
Намеченная нами программа очень далека от своего завершения; и предстоит еще много сделать, прежде чем мы сумеем до конца раскрыть все следствия, проистекающие из принятия второго начала термодинамики в качестве основного принципа. Но даже сейчас имеются веские основания утверждать, что принятие второго начала в качестве фундаментального постулата влечет за собой глубокие изменения в наших представлениях о пространстве, времени и динамике, а в конечном счете — в нашей оценке места, занимаемого человеком в природе, и старой философской проблемы существующего и возникающего.
Для принятия второго начала в качестве фундаментального постулата динамики необходимо ввести новые понятия: внутреннее время Т и микроскопический оператор энтропии. Прежде всего, заметим, что для включения второго начала термодинамики в качестве фундаментального постулата динамики, очевидно, необходимо потребовать существование подходящего механизма, который бы нарушал инвариантность обычного динамического описания относительно обращения времени. Интересующее нас нарушение симметрии должно быть внутренним, т.е. не связанным с существованием новых взаимодействий. В то же время оно должно быть универсальным, т.е. возможным во всех динамических теориях, будь то классическая механика, квантовая механика или теория относительности.
Такая общая и внутренняя разновидность нарушения симметрии может представиться, если по тем или иным причинам физически реализуются не все состояния или начальные условия, допустимые при динамическом описании, а лишь ограниченный набор состояний, обладающих асимметрией во времени требуемого типа. Приведем заимствованный у Поппера пример системы, в котором осуществляется односторонне протекающий процесс и, следовательно, возникает стрела времени.
Представим себе, что мы сняли на кинопленку обширный участок водной поверхности. Первоначально она покоилась, а затем в воду бросили камень. Просматривая фильм от конца к началу, мы увидим на экране сходящиеся круговые волны все возрастающей амплитуды. После того как в центре поднимется самая высокая волна, кольцо спокойной волны, окружающее возмущенный участок, сомкнется. Такую картину невозможно признать реализуемым физическим процессом. Для осуществления подобного процесса понадобилось бы расположить вдали от центра огромное количество источников волн. Для того чтобы их координация поддавалась объяснению, картина на экране должна быть такой, как если бы волны исходили из одного центра. Но тогда мы снова придем к той же трудности, с которой столкнулись в самом начале, если вздумаем просмотреть «исправленный» вариант фильма от конца к началу.
Итак, кратко суть интересующего нас типа нарушения симметрии состоит в том, что рассматриваемая нами симметрия нарушается вследствие асимметричной природы физически допустимых состояний. Именно такого рода нарушения симметрии мы имеем в виду, предлагая свою формулировку второго начала термодинамики в качестве динамического принципа. Опишем теперь более подробно, каким образом нам удается осуществить эту идею.
Наведение моста между динамикой и термодинамикой
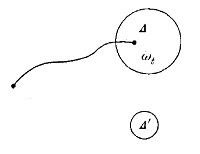
Прежде чем мы сформулируем второе начало термодинамики на языке внутренних нарушений симметрии между двумя размерностями времени, уместно кратко напомнить некоторые основные понятия классической динамики. Существуют два описания динамической эволюции классических систем. Одно из описаний состоит в прослеживании движения точек по траекториям в фазовом пространстве (рис. 1). Г — фазовое пространство, St — преобразование, отображающее точку ω в точку ωt. Другое описание (его можно назвать описанием Гиббса — Эйнштейна) вводит в фазовом пространстве функции распределения ρ. Поток в фазовом пространстве сохраняет объем (или меру).
Рис. 1. Фазовая траектория ω → ωt (где ωt = St*ω) в фазовом пространстве Г
Обратимся теперь к подходу, предложенному Больцманом. Чтобы получить необратимость, нам необходимо сопоставить динамике вероятностное описание — например, марковский процесс (см. гл. 6). Основной величиной при таком описании является вероятность перехода. Поскольку мы действуем в фазовом пространстве, необходимо рассматривать величину Р(t, ω, Δ), дающую вероятность перехода из точки ω в область Δ за время t. Она должна быть положительным числом, заключенным между нулем и единицей. Здесь мы сразу же сталкиваемся с основным различием по сравнению с теорией траекторий.
Предположим, что траектория идет из точки ω в точку ωt (рис. 2). Тогда:
Рис. 2. Вероятности перехода Р(t, ω, Δ) = 1, Р(t, ω, Δ’) = 0
Это крайне вырожденный случай, так как в цепи Маркова по крайней мере некоторые из вероятностей перехода не равны ни нулю, ни единице (в противном случае мы просто возвращаемся к детерминистскому описанию). Как и в проблеме необратимости, возможны два подхода: либо вероятности в конечном счете обусловлены нашим незнанием начальных условий (и, следовательно, траекторий), либо по крайней мере для определенных классов динамических систем существует альтернативное описание на языке траекторий в фазовом пространстве. Поскольку траектории соответствуют точечному преобразованию, альтернативное описание должно быть нелокальным в смысле, который мы обсудим ниже.
Ситуацию, с которой мы столкнулись, интересно сравнить с известным ожесточенным спором по поводу существования «скрытых переменных». Как известно, квантовомеханическая волновая функция представляет собой не что иное, как амплитуду вероятности. Отражает ли эта вероятность природу вещей, или ее появление обусловлено нашим незнанием — тем, что мы провели усреднение по каким-то скрытым параметрам? Ныне конфликт можно считать разрешившимся. Как показали эксперименты, вероятности присущи самой природе квантовой механики. С аналогичной проблемой мы сталкиваемся и в нашем случае: является ли необратимость следствием нашего незнания или отражением какой-то новой, глубоко лежащей нелокальности в структуре пространства-времени?
Второе начало термодинамики мы формулируем в виде двух утверждений. (1) Cуществуют два нарушающих симметрию преобразования Λ и Λ’, порождающих две различные полугруппы Wt и Wt’, одна из которых приводит к возрастанию энтропии в одном направлении времени, а другая — в противоположном направлении времени. (2) Существует некий принцип отбора, распространяемый динамикой, в соответствии с которым лишь одно из двух нарушающих симметрию преобразований Λ и Λ’ порождает физически реализуемые состояния и, следовательно, физически наблюдаемую эволюцию.
Системы, для которых существует оператор преобразования Λ, можно назвать «внутренне случайными». Именно для таких систем вероятность обретает внутренний смысл независимо от каких бы то ни было «скрытых переменных». Системы, для которых существует оператор Λ и, кроме того, выполняется принцип отбора, можно назвать внутренне необратимыми.
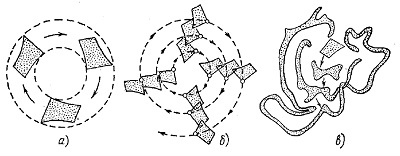
Обсудим подробнее те условия, которые налагает на динамику такая «двухступенчатая» формулировка второго начала термодинамики. Существование нарушающего симметрию преобразования Λ с указанными выше свойствами возможно лишь при условии, если динамическое движение сильно неустойчиво, или обладает высокой чувствительностью по отношению к начальным условиям. Если говорить точнее, то необходимым условием для существования преобразования Λ является перемешивание, а достаточным условием — К-поток, или поток с перемешиванием (рис. 3).
Рис. 3. Различные типы потоков в фазовых пространствах: а) неэргодический поток; б) эргодический поток без перемешивания; в) поток с перемешиванием.
Нарисовать сколько-нибудь простую схему такого потока — задача безнадежная, так как любые две точки, сколь бы мало ни было расстояние между ними в начальный момент, могут разойтись сколь угодно далеко. Даже начав с распределения очень простой формы, мы со временем получим «чудовище», как метко назвал объекты такой сложности Бенуа Мандельброт (см. также Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах). Возможно, пример из области биологии поможет читателю уяснить степень сложности «фигуры», возникающей в системах с перемешиванием: мы имеем в виду объем легкого и иерархию трахей и бронхов, из которых оно состоит (рис. 4).
Рис. 4. Модель легких
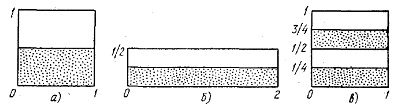
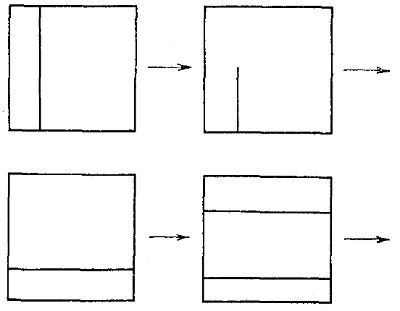
Не вдаваясь в математическое определение К-потоков, упомянем лишь о том, что такие динамические системы обладают важным свойством: в каждой точке фазового пространства существуют два многообразия (меньшей размерности, чем все фазовое пространство) — одно сжимается под действием динамического движения при возрастающих t, другое растягивается. Поведение сжимающихся и растягивающихся многообразий особенно наглядно можно проследить на преобразовании пекаря, являющемся к тому же простейшим математическим примером К-систем. Под действием преобразования пекаря (рис. 5) вертикальная линия все более и более сокращается (сжимающиеся слои), а длина горизонтальной линии при каждой итерации преобразования пекаря удваивается (растягивающиеся слои) (рис. 6).
Рис. 5. Преобразование пекаря. Сначала единичный квадрат (а) «раскатывается» в прямоугольник ½*2; (б), половина которого отрезается и кладется сверху на другую половину. Образуется новый единичный квадрат (в), в котором темные и светлые полосы делят его на четыре, а не на две, как в случае квадрата (а), отдельные области.
Рис. 6. Преобразование пекаря: сжимающиеся и растягивающиеся слои.
Ясно, что сжимающиеся и растягивающиеся многообразия в тех случаях, когда они существуют, заведомо обладают временной асимметрией. Сжимающееся многообразие движется в будущее в некотором смысле как единый объект. Всем его точкам в будущем уготована одна и та же судьба, но чем глубже мы будем уходить в прошлое, тем более различными окажутся их истории. С расширяющимися многообразиями все обстоит наоборот. Их точки в будущем ведут себя по-разному, но по мере углубления в прошлое их истории все более походят одна на другую.
Существование объектов со столь явно выраженной асимметрией во времени позволяет нам построить нарушающее симметрию преобразование Λ (или Λ‘), отводя неэквивалентные роли растягивающимся и сжимающимся многообразиям. Действительно, можно показать, что выбор преобразования Λ (порождающего эволюцию с возрастанием энтропии при t ≥ 0) как физически реализуемого преобразования, нарушающего симметрию, влечет за собой исключение (сингулярных) функций распределения, сосредоточенных на сжимающихся многообразиях, из числа физически реализуемых распределений. С другой стороны, если бы нарушение симметрии осуществляло преобразование Λ‘, то физически нереализуемыми считались бы состояния, связанные с растягивающимися многообразиями.
Вопрос о том, что физически реализуемо и что нереализуемо, эмпирический. Преимущество нашей формулировки второго начала в том, что она устанавливает взаимосвязь между вторым началом термодинамики и определяемой им «стрелой времени» с ограничением (на фундаментальном уровне) на приготовление начальных условий определенных типов. Интересно отметить, что в физически интересных моделях динамических систем типы начальных условий, исключаемые нарушающим симметрию преобразованием Λ, в точности совпадают с теми, которые на интуитивном уровне никогда не воспринимаются как реализуемые.
В этой связи интересно напомнить известную дискуссию между Эйнштейном и Ритцем. Ритц считал, что второе начало термодинамики выражает некий принцип, позволяющий исключать некоторые решения динамических уравнений, например, решения, выражаемые через опережающие потенциалы, из числа физически реализуемых. По мнению Эйнштейна, закон возрастания энтропии имеет лишь статистический смысл как эволюция от менее вероятных (упорядоченных) состояний к более вероятным состояниям. Эйнштейн считал также, что введение вероятностных соображений влечет за собой неполноту теоретического описания.
Примирить точки зрения Эйнштейна и Ритца оказалось невозможно из-за трудностей, с которыми столкнулись все попытки показать, каким образом абсолютный принцип запрета такого типа, как рассматривал Ритц, может привести к вероятностной интерпретации возрастания энтропии. Наша формулировка второго начала термодинамики включает в себя точку зрения Ритца, согласно которой второе начало термодинамики на фундаментальном уровне представляет собой ограничение на физически реализуемые состояния. Наш подход позволяет наглядно показать, что точки зрения Эйнштейна и Ритца не были непримиримыми. Их надлежит рассматривать как неполные и частные формулировки второго начала термодинамики. Недостающим звеном между точками зрения Эйнштейна и Ритца служит идея о внутреннем нарушении симметрии, которое действительно является ограничением. Наша формулировка второго начала термодинамики включает в себя и точку зрения Эйнштейна, так как приводит к переходу от детерминистской динамической эволюции к вероятностным процессам, эволюционирующим от более упорядоченных состояний к менее упорядоченным. Тем самым наш подход позволяет убедиться в том, что точки зрения Эйнштейна и Ритца были далеко по столь непримиримыми, как могло бы показаться, а лишь неполными и необщими формулировками двух аспектов второго начала. Недостающим звеном между точками зрения Эйнштейна и Ритца служит идея о внутреннем нарушении симметрии, с одной стороны, выражающем ограничение на физически реализуемые состояния, а с другой стороны, позволяющем осуществить переход от детерминистской динамики к вероятностному процессу.
Следует подчеркнуть, что наша точка зрения отличается от широко распространенного мнения, четко сформулированного Мартином Гарднером в замечательной книге «Этот правый, левый мир». По словам Гарднера, «некоторые события развиваются в одном направлении не потому, что не могут развиваться в противоположном направлении, а потому, что такое развитие было бы крайне маловероятно». Такое утверждение находится в противоречии с нашей формулировкой второго начала термодинамики: именно потому, что некоторые состояния строго запрещены и не могут быть ни обнаружены в природе, ни приготовлены нами, мы можем приписать разрешенным состояниям вероятностную меру.
Внутреннее время
Для того чтобы убедиться в осуществимости перехода от динамического описания к вероятностному с помощью преобразования Λ, необходимо прежде всего более подробно понятие внутреннего времени. Не подлежит сомнению, что обычный («внешний») временной параметр t не пригоден даже для формулировки асимметрии состояний во времени. Временная асимметрия может быть сформулирована на основе нового понятия времени, позволяющего говорить о (среднем) «возрасте» отдельных состояний. Таким понятием времени мы уже располагаем: оно введено оператором внутреннего времени Т.
т.е. средний возраст состояния ρ «идет в ногу» с внутренним временем или временем t, отсчитываемым по обычным часам.
Вместе с тем внутреннее время существенно отличается от внешнего времени, отсчитываемого нами по наручным часам. Оно соответствует скорее возрасту человека. Возраст не определяется какой-нибудь частью тела, изолированной от остального организма, а соответствует средней, глобальной оценке, относящейся ко всем частям тела. Наше понятие внутреннего времени весьма близко идеям, выдвинутым недавно географами, которые ввели понятие «хроногеографии». Рассматривая структуру города или ландшафта, мы наблюдаем временные элементы во взаимодействии и сосуществовании. Такие города, как Бразилиа или Помпеи, при таком сопоставлении соответствовали бы вполне определенному внутреннему возрасту, напоминающему в известной степени «возраст» разбиений при преобразовании пекаря. Наоборот, современный Рим, застройка которого производилась в различные периоды, соответствовал бы среднему времени, подобно тому, как произвольное разбиение допускает разложение на разбиения, соответствующие различным внутренним временам.
В квантовой теории нелокальность вводится постоянной Планка h. Самое удивительное, что неустойчивость движения, которой обусловлено существовапие внутреннего времени, служит еще одним источником нелокальности, возникающей уже в классической механике. Это обстоятельство приводит к далеко идущим следствиям, поскольку мы можем теперь легко построить нарушающее симметрию преобразование Λ, и выполнить переход от динамики — физики существующего — к термодинамике — физике возникающего.
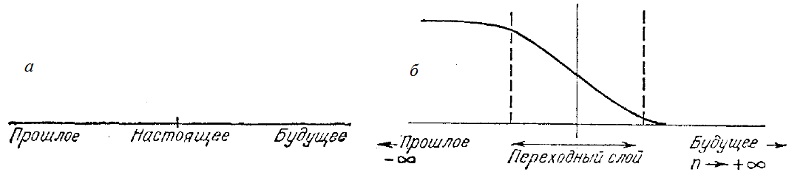
Описание внутреннего времени сильно отличается от традиционного представления о времени как о величине, изоморфной прямой (рис. 7а), идущей из далекого прошлого (t → – ∞) в далекое будущее (t → + ∞). Настоящее в таком представлении соответствует единственной точке, отделяющей прошлое от будущего. Настоящее возникает ниоткуда и исчезает в никуда. Стянутое в точку, оно бесконечно близко и прошлому и будущему. В традиционном представлении между прошлым, настоящим и будущим нет расстояний. В нашем представлении прошлое отделено от будущего интервалом, длина которого определяется характерным временем τс, и настоящее обретает продолжительность (рис. 7б).
Рис. 7. Представления о времени: (а) традиционное; (б) переход от прошлого (t → – ∞) к будущему (t → + ∞)
Интересно отметить, что многие философы, в том числе Бергсон и Уайтхед подчеркивали необходимость наделить настоящее такого рода «несжимаемой» продолжительностью. Именно к такому заключению, равно как и к новому типу нелокальности в пространстве, приводит принятие второго начала термодинамики в качестве динамического принципа.
Энтропийный барьер
В предыдущих разделах мы показали, что сильно неустойчивые динамические системы (например, системы, описываемые преобразованием пекаря) «внутренне случайны». Их эволюцию с помощью оператора Λ можно отобразить на вероятностный процесс. Сейчас нам необходимо обратиться ко второй части нашей задачи и от внутренне случайных систем перейти к системам, внутренне необратимым. Различие между двумя полугруппами наиболее наглядно проявляется в ограничениях, которые могут существовать, на тип физических состояний, доступных приготовлению или наблюдению в природе.
Выше мы уже ввели определение сжимающихся и растягивающихся слоев (см. раздел «Наведение моста между динамикой и термодинамикой»). Покажем теперь, что преобразование Λ порождает резкое различие между сжимающимися и растягивающимися слоями. Верно и обратное утверждение: выбор сжимающегося или растягивающегося слоя в качестве допустимого начального условия определяет тип полугруппы, которую мы получим.
Если бы мы выбрали преобразование Λ‘, которое порождает полугруппу, ориентированную в будущее, то нам пришлось бы признать приемлемыми сжимающиеся слои и отвергнуть как неприемлемые растягивающиеся слои. Следовательно, энтропия дает нам принцип отбора. По своему характеру этот принцип отбора новый: его нельзя вывести из динамики. Оп ограничивает класс функций, которые можно наблюдать или приготовить. Распространяет новый принцип отбора (поразительно напоминающий принцип запрета Паули в квантовой механике) динамика. Действительно, растягивающийся (или сжимающийся) слой навсегда остается растягивающимся (пли сжимающимся). Наоборот, имеются все основания ожидать, что второе начало термодинамики справедливо только для систем, в которых существуют состояния, переходящие при обращении времени в запрещенные.
Новая структура пространства-времени
Принятие второго начала термодинамики в качестве фундаментального динамического принципа приводит к далеко идущим следствиям в наших представлениях о пространстве, времени и динамике. Применение второго начала позволяет нам определить новое внутреннее время Т, которое в свою очередь дает возможность сформулировать нарушение симметрии, лежащее в основе второго начала. Введенное нами внутреннее время существует только для неустойчивых динамических систем. Его среднее 〈T〉 согласуется с динамическим временем в таких ситуациях, которые описываются, например, преобразованием пекаря. Но и в этом случае важно не смешивать Т и t. По своим наручным часам мы можем измерять свое среднее внутреннее время, но понятия внешнего и внутреннего времени совершенно различны. Динамическое время позволяет «маркировать» движение точки в классической механике или изменение волновой функции в квантовой теории. Но приписать таким системам внутреннее время мы можем лишь при гораздо более жестких условиях (таких, как неустойчивость движения).
Для того чтобы мы могли говорить об эволюции физических систем, необходимо либо приписать им производство энтропии в макроскопическом масштабе, либо, используя введенные в этой главе понятия, рассматривать эту эволюцию на микроскопическом уровне. Весьма часто элемент необратимости вводят в квантовую теорию через процесс измерения, однако представляется гораздо более удовлетворительным дать внутреннее описание необратимости путем отображения эволюции во времени на полугруппы. Роль второго начала термодинамики как принципа отбора должна представлять особый интерес для общей теории относительности, где второе начало должно привести к отбору физически реализуемых структур пространства-времени. Как известно, в основе общей теории относительности лежит понятие четырехмерного интервала ds2. Координаты в пространстве-времени, используемые для описания интервала ds2, считаются произвольными. Естественное дополнительное требование состоит в том, чтобы временная координата t была такой («тем временем»), в которой энтропия возрастает. Недавно на простом примере было показано, что в космологической модели с пространственными гиперповерхностями отрицательной кривизны можно ввести внутреннее время, тесно связанное с обычным космическим временем. Однако в общем случае такое утверждение неверно. Например, в знаменитой космологической модели Гёделя наблюдатель, следуя всегда в направлении возрастания времени, может вернуться в собственное прошлое.
Ранее мы упоминали о дилемме Эйнштейна — его отказе принять необратимость за фундаментальный физический факт. Однако в комментариях по поводу работы Гёделя, Эйнштейн высказал сомнения относительно того, что «безвременная» Вселенная Гёделя могла бы соответствовать Вселенной, в которой мы живем. «Мы не можем телеграфировать в наше время», — замечает Эйнштейн и добавляет: «Существенно, что посылка сигнала представляет собой (с точки зрения термодинамики) необратимый процесс, процесс, связанный с ростом энтропии (в то время как согласно нашим современным представлениям ), все элементарные процессы обратимы)».
Весьма интересно, что Эйнштейн не смог избежать рассмотрения необратимости как существенной составной части нашей картины мира. Мы надеемся в будущем вернуться к этим проблемам и подвергнуть их более детальному анализу. Еще на заре рационального мышления Аристотель различал время как «движение» (кинезис) и время как «рождение и гибель» (метаболе). Изучением первого аспекта занимается динамика, изучением второго — термодинамика. Мы ближе подходим к описанию, непротиворечиво сочетающему в себе оба аспекта. Это необходимо для описания основных процессов, таких, как самый акт измерения.
Процесс измерения можно рассматривать как особую разновидность взаимодействия человека с окружающим миром. Более подробный анализ такого рода взаимодействий должен учитывать, что живые системы, в том числе и человек, обладают временной асимметрией. Мы можем взаимодействовать с другими объектами (или живыми существами), также обладающими нарушенной временной симметрией, но точно так же можем вступать во взаимодействие с объектами, симметричными во времени. Например, мы можем приготовить жидкость в замкнутом объеме и подождать, пока эта система придет в состояние равновесия. Если считать, что достигается детальное равновесие, то у такой системы не может быть выделенного направления времени. Производя над системой различного рода действия (например, нагревая одну часть системы и охлаждая другую), мы можем нарушить временную симметрию и в некотором смысле передать системе присущую нам временную асимметрию.
Обычно говорят, что жизнь рождает жизнь. В том же смысле необратимость может передаваться через действия человека.
Микроскопическая теория необратимости приводит не только к лучшей интерпретации двух аспектов времени, связывая их с материей и с качественными изменениями, но и к пересмотру самой структуры пространственно-временного континуума. Обычные представления о траекториях в пространстве-времени при переходе к неустойчивым системам наталкиваются на значительные трудности. В этом нетрудно убедиться хотя бы на примере преобразования пекаря.
Поведение отдельных траекторий весьма чувствительно к начальным условиям. Нередко говорят об орбитальной стохастичности. Но если воспользоваться преобразованием Λ и перейти к нелокальному описанию, то основное внимание будет сосредоточено не на поведении точек, а на поведении «малых» областей. В отличие от описания на языке траекторий нелокальное описание устойчиво. Все области расщепляются на области все меньших размеров, которые в пределе покрывают все фазовое пространство.
Состояния и законы как результат взаимодействия существующего и возникающего
Перейдем теперь к рассмотрению еще одного изменения в понятиях динамики, к которому приводит микроскопическая формулировка второго начала термодинамики. В традиционном подходе существует различие между начальными условиями и законами эволюции. Начальные условия соответствуют заданию некоторого «состояния» (в классической механике — точки в фазовом пространстве, в квантовой механике — волновая функция, «точки» в гильбертовом пространстве), в то время как уравнение определяется «законом». Вместе с тем ясно, что между состояниями и законами существует взаимосвязь, поскольку состояния возникают в результате предшествующей динамической эволюции.
Состояния и законы находятся в тесной взаимосвязи. Существуют самосохраняющиеся формы начальных условий. В конечном счете начальное условие приходится на момент времени, выбираемый нами произвольно. Он не обладает никакими специфическими свойствами, которые выделяли бы его среди прочих моментов времени.
Именно это и позволяет прийти к заключению, которое я считаю наиболее поразительным выводом из нашей новой системы понятий: из существования законов, ориентированных во времени, таких, как возрастание энтропии по направлению к будущему, следует существование в такого рода системах состояний, ориентированных во времени.
Заключительные замечания
С точки зрения классической механики начальные условия произвольны, и только закон, связывающий начальные условия с конечным исходом, имеет внутренний смысл. Если бы это действительно было так, то проблема существующего была бы лишена любого смысла, кроме произвола, содержащегося в приготовлении существующего. Но произвол в выборе начальных условий соответствует сильно идеализированной ситуации, которую мы действительно в состоянии приготовить по своему усмотрению. Но стоит нам перейти к сложным системам (например, жидкости и тем более социальным структурам), как начальные условия перестают подчиняться нашему произволу, но возникают как исход предшествующей эволюции системы.
Вопрос об отношении существующего к возникающему обретает смысл только в таких ситуациях. Мы убедились в том, что можно определять состояния, симметричные во времени (если относить их к внутреннему времени), и состояния с нарушенной временной симметрией. Потребуем, чтобы состояния, которые можно наблюдать или приготовить, находились в согласии с законами, управляющими их эволюцией. Момент времени, когда производится наблюдение или приготовление, в действительности ничем не выделен. Следовательно, симметричное состояние должно возникать из другого симметричного состояния и со временем переходить в какое-то симметричное состояние. Аналогичным образом, состояние с нарушенной симметрией должно возникать из однотипного состояния и со временем переходить в какое-то состояние того же типа.
Инвариантность характера состояний приводит к тесной взаимосвязи состояний и законов или, если воспользоваться более философской терминологией, взаимосвязи существующего (бытия) и возникающего (становления). Существующее связано с состояниями, возникающее — с законами, по которым преобразуются состояния.
С логической точки зрения проблема существующего и возникающего допускает по крайней мере два возможных решения. В первом решении всякий внутренний временной элемент исключается, возникающее предстает всего лишь как развитие существующего. Второе решение вводит и в существующее, и в возникающее нарушенную временную симметрию. Однако решение проблемы существующего и возникающего выходит за рамки чистой логики: оно содержит элемент реального. Уже самый вопрос о смысле существующего или возникающего задает некую ориентацию во времени. Следовательно, нам не остается ничего другого, как избрать решение, связанное с нарушенной временной симметрией.
Подчеркнем, что такого рода отношение существующего к возникающему имеет смысл только в мире, в котором выполняется второе начало термодинамики. Как было показало, второе начало применимо только к системам, в значительной степени неустойчивым. Необратимость и неустойчивость тесно связаны менаду собой: необратимое, ориентированное время может появиться только потому, что будущее не содержится в настоящем.
Итак, мы приходим к выводу, что нарушенная временная симметрия является существенным элементом нашего понимания природы. Поясним смысл нашего утверждения на простом музыкальном примере. Сыграем некоторый набор звуков за данный временной интервал, например, в течение 1 с, начав с пиано и закончив фортиссимо. Сыграем затем те же звуки в обратном порядке. Ясно, что впечатление от проигрывания в первом и во втором случае будет совершенно различным. Несходство в восприятии допускает единственную интерпретацию: мы наделены внутренней стрелой времени, позволяющей нам отличать проигрывание первого ряда звуков от проигрывания второго. С точки зрения, изложенной в той главе, стрела времени не противопоставляет человека природе. Наоборот, она свидетельствует о том, что человек является неотъемлемой составной частью эволюционирующей Вселенной. В правильности подобного вывода мы убеждаемся на всех уровнях описания.
Время — не только существенная компонента нашего внутреннего опыта и ключ к пониманию истории человечества как на уровне отдельной личности, так и на уровне общества. Время — это ключ к пониманию природы. Наука в ее современном смысле насчитывает примерно трехвековую историю. Мы можем указать два момента, когда наука привела нас к определенной картине природы физического существования. В первом случае картину мира создал Ньютон — мира, образуемого неизменными субстанциями и состояниями движения. В ньютоновской картине мира материя, пространство и время разобщены: пространство и время выступают как пассивные «вместилища» материи.
Во втором случае картину мира создал Эйнштейн. Величайшим достижением общей теории относительности следует считать то, что пространство-время перестало в ней быть независимым от материи, оно порождается материей. Однако с точки зрения Эйнштейна идея локализации в пространстве-времени является важной составной частью теории.
Мы находимся на третьей стадии, когда само понятие локализации в пространстве-времени становится предметом тщательного анализа. Любопытно отметить, что интерес к микроскопической структуре пространства-времени стимулировали различные источники: квантовая теория и, как я пытался показать в этой монографии, микроскопическая теория необратимости. Кроме того, необратимость как деятельность, протекающая в пространстве-времени, приводит к изменению его структуры. На смену статического двуединства пространства и времени приходит более динамичное двуединство «овремененного» пространства.
Нельзя не отметить, сколь близки некоторые недавно полученные выводы к предсказаниям таких философов, как Бергсон, Уайтхед и Хайдеггер. Основное различие между их пророчествами и нашими заключениями состоит в том, что эти философы высказывали идеи, не связанные с развитием науки, в то время как мы прослеживаем генезис близких идей, так сказать, изнутри научного исследования.
В своей главной работе «Процесс и реальность» Уайтхед подчеркивает, что одной лишь простой локализации в пространстве-времени может оказаться недостаточно и что включение материи в общий поток может иметь решающее значение. По мнению Уайтхеда, никакие сущности, никакие состояния не могут быть определены без активности. Пассивная материя не способна порождать созидающую Вселенную.
Заголовок книги Хайдеггера «Бытие и время», оказавшей немалое влияние, сам по себе является своего рода девизом, подчеркивающим неприятие Хайдеггером безвременной концепции бытия, отвечающей духу основного течения западной философии со времен Платона. Суть книги изящно сформулировал Штейнер в своем комментарии к Хайдеггеру: «Человек и самосознание не являются центром, соучастниками бытия, Человеку отведена роль избранного слушателя, лишь реагирующего на бытие».
Я вполне сознаю, что моя книга не дает адекватного описания даже тенденций, наметившихся в последнее время. Необратимость существует не только на уровне динамических систем, но и на уровне макроскопической физики (например, в турбулентности), биологии или социологии. Следовательно, мы имеем дело с иерархией внутренних времен. С одной стороны, мы как сущности обязаны своим происхождением противоборству различных сил, но можем быть охарактеризованы одним внутренним временем. С другой стороны, как члены некоей группы мы принадлежим более высокому уровню внутреннего времени, в котором активно действуем. Весьма вероятно, что многие наши проблемы, ярко описанные Минковским, обусловлены конфликтом между масштабами внутреннего времени в нас самих и масштабами внешнего времени в окружающем нас мире.
Как бы то ни было, новая ситуация, возможно, поможет нам навести мосты между науками и другими видами культурной деятельности человека. Мир не является ни автоматом, ни хаосом. Наш мир — мир неопределенности, но деятельность индивидуума в нем не обязательно обречена на малозначимость. Наш мир не поддается описанию одной истиной. Мысль о том, что наука может помочь нам навести мосты и примирить противоположности, не отрицая их, доставляет мне глубокое удовлетворение.
[1] В качестве введения в эту тему рекомендую статью Сергея Остапенко Диалектика и синергетика. Понятие системы



Спасибо за обзор.