Кластерный анализ: сетевые графы и определение сообществ

Кластерный анализ используется для многих целей, но в этой заметке основное внимание будет уделено сегментации рынка. Ранее был рассмотрен кластерный анализ с использованием метода k-средних. Одна из проблем метода заключалась в выборе «правильного» k. Теперь задачу определения заинтересованных групп покупателей, основываясь на их заказах, мы будем решать с помощью сетевого графа, и значение k появится само собой. [1]

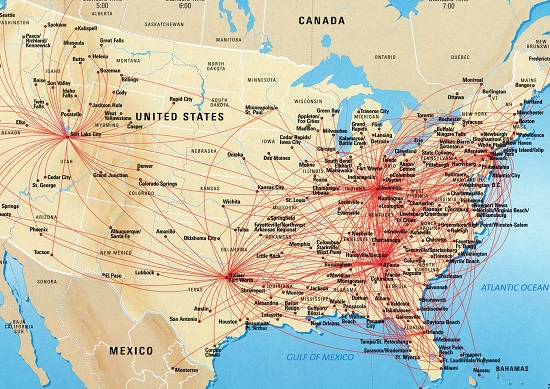
Сетевой граф — это набор предметов, называемых вершинами графа, которые соединены друг с другом ребрами (или связями). Социальные сети, такие как Facebook, содержат много данных, которые легко можно объединить в сетевой граф. Чтобы лицезреть классический сетевой граф, достаточно зайти на сайт любой авиакомпании (рис. 1). Удобный интерфейс для построения графов предоставляют, например, бесплатные сервисы DocGraph и NodeXL.

Рис. 1. Авиамаршруты компании Delta

Скачать заметку в формате Word или pdf, примеры в формате Excel: Друзья и Кластерный анализ

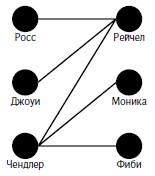
Сериал «Друзья» был одним из самых популярных комедийных шоу 1990-х и начала 2000-х годов. Действие разворачивается с участием шестерых друзей. Эти шестеро постоянно вовлечены в романтические отношения различного характера: настоящие романы, выдуманные романы, которые никогда ни к чему не приводят, романы на спор и т.д. (рис. 2).

Рис. 2. Диаграмма (псевдо)романов в сериале «Друзья»

Это неориентированный сетевой граф, потому что отношения обоюдны. А вот данные, например, из Twitter будут уже ориентированным графом: я могу подписаться на вас, но вы не обязаны подписываться на меня. Ребра ориентированного графа обычно изображаются стрелками. Один из минусов использования Excel для работы с сетевыми графами состоит в том, что, в отличие от разнообразных графиков и диаграмм, граф нельзя визуализировать встроенными в Excel средствами. Для визуализации графов в настоящей заметке будет использоваться Gephi.

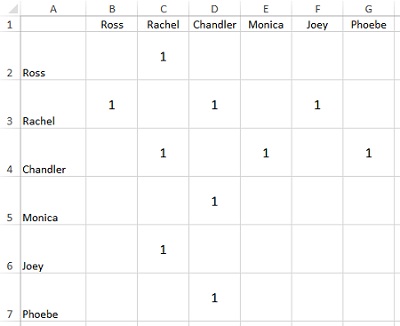
Кроме визуализации граф можно представить в виде матрицы смежности. Матрица смежности — это таблица вершин, заполненная 0 и 1, где 1 в конкретной ячейке означает «ребро», а 0 — «эти вершины не связаны» (рис. 3). Обратите внимание на симметричность матрицы по диагонали —граф неориентированный. Если бы отношения были односторонними, матрица бы получилась несимметричной. Ребрам можно добавить числовые значения, например, вместимость самолета.

Рис. 3. Матрица смежности для героев сериала «Друзья» (см. также Excel-файл)

Загрузите и установите Gephi (краткий справочник по инструментам Gephi вы найдете здесь). Подготовьте матрицу смежности для импорта в графическую форму. Для этого сохраните файл Друзья.xlsx в формате CSV (как обычный текст). [2] Откройте Gephi и, используя опцию Открыть файл с графом на стартовой странице (рис. 4), выберите файл Друзья.csv.

Рис. 4. Открытие файла Друзья.csv в Gephi (чтобы увеличить изображение, кликните на нем правой кнопкой мыши, и выберите Открыть картинку в новой вкладке)

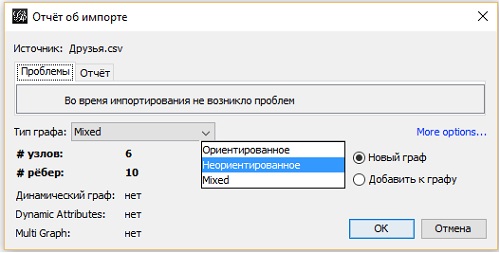
Появится окно Отчет об импорте (рис. 5). Обратите внимание: найдены шесть вершин и десять ребер. Поскольку матрица смежности симметрична, следовательно, все отношения продублированы. Чтобы избавиться от лишнего набора ребер, поменяйте тип графа с Mixed на Неориентированное. Нажмите ОК.

Рис. 5. Импорт графа Друзья

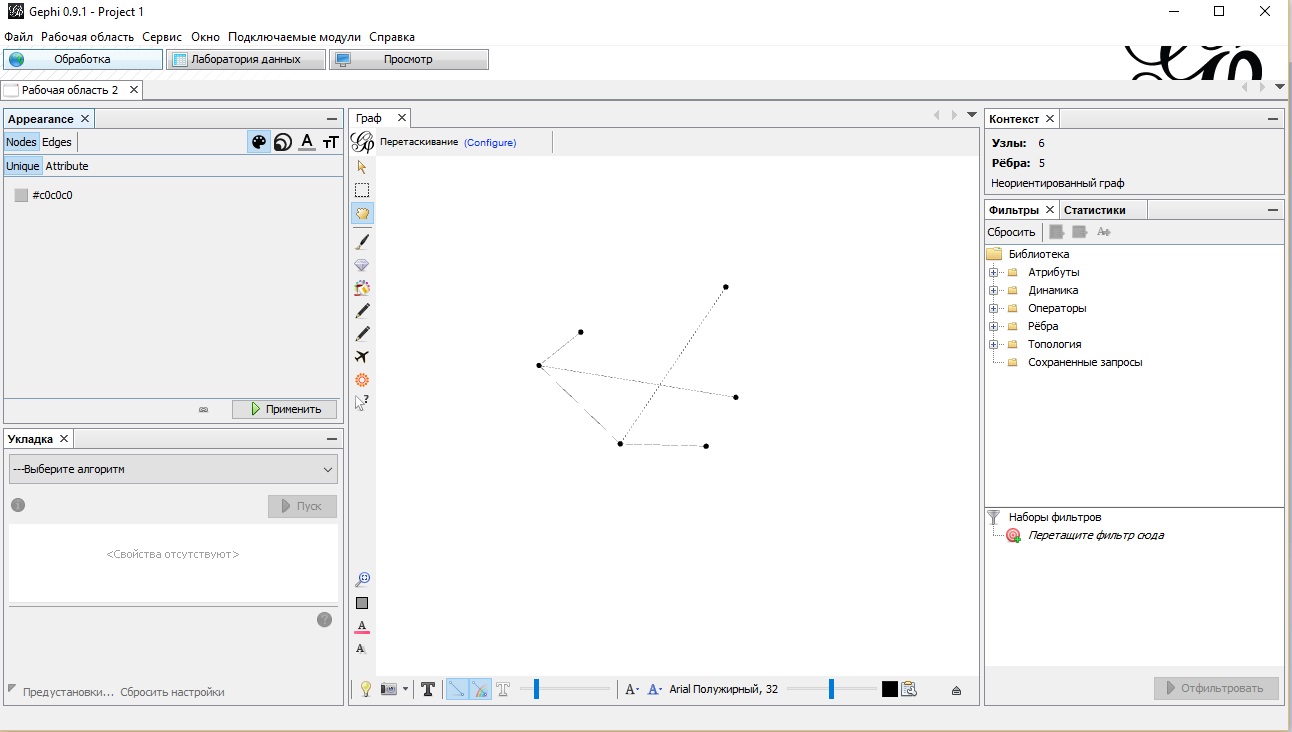
Ваш граф будет выглядеть, как на рис 6.

Рис. 6. Начальный вид графа Друзья

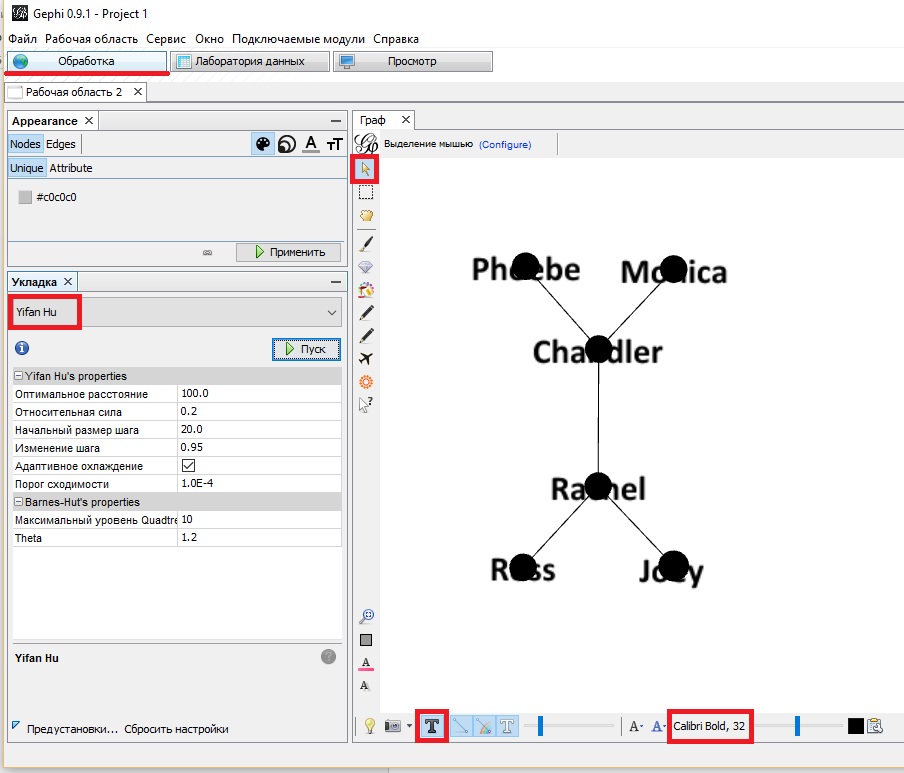
Удостоверьтесь, что в верхнем левом углу программы выбрана вкладка Обработка. Пока граф выглядит не очень интересно. Можно приблизить изображение, если выбрать инструмент Стрелка, и вращать колесиком мышки (рис. 7). Нажав на кнопку Т внизу окна просмотра, вы можете добавить названия вершинам графа.

Рис. 7. Граф после обработки

У Gephi есть пачка алгоритмов для придания графам хорошего внешнего вида (область Укладка). Некоторые из них используют такие средства, как гравитация между соединенными вершинами и отталкивание между несоединенными для более удачного расположения элементов. Поэкспериментируйте с алгоритмами. На мой взгляд, наиболее удачным оказался Yifan Hu.

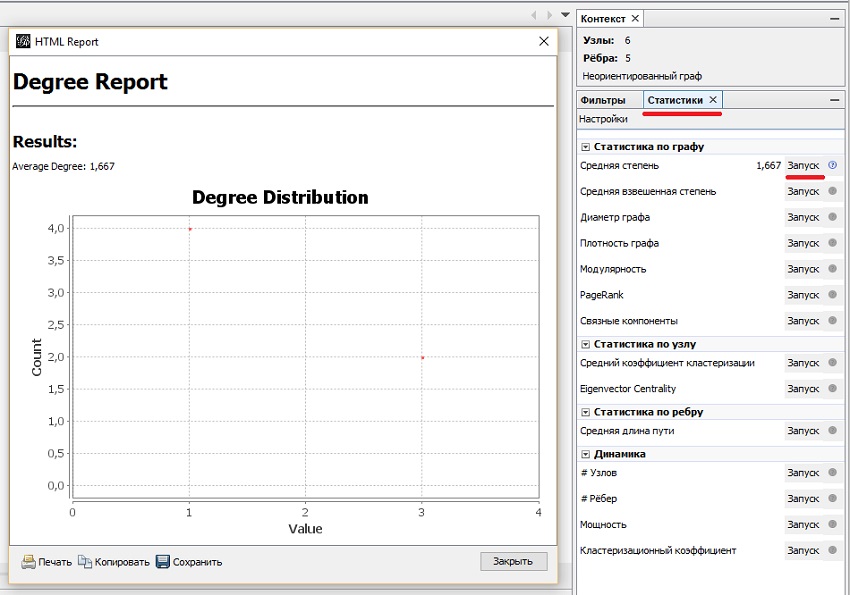
Степень вершины – количество ребер, связанных с вершиной. У Чендлера – 3, у Фиби — всего 1. Эти степени можно использовать в Gephi для изменения размера вершин. Чтобы вычислить среднюю степень графа, в правом окне перейдите на вкладку Статистики и кликните на кнопку Запуск в строке Средняя степень (рис. 8). Появится окно Degree Report. Средняя степень графа равна 1,667 при четырех вершинах со степенью 1 и двух — со степенью 3. Кликните Закрыть.

Рис. 8. Расчет средней степени графа

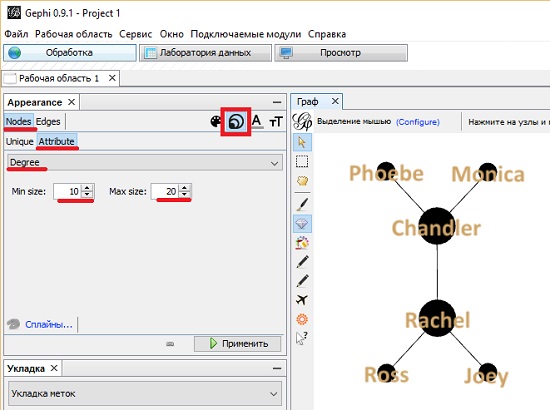
Переместитесь в область Appearance в левой верхней части окна (рис. 9). Выберите раздел вершин (Nodes), закладку Attribute и значок, который отображает изменение размера. В выпадающем меню выберите степень (Degree) и установите минимальный и максимальный размер вершин. Нажмите кнопку Применить. Gephi изменит размер вершин согласно степени их важности.

Рис. 9. Изменение размеров графа согласно степеням вершин

В ориентированном графе число ребер, подходящих к вершине, называется полустепенью захода. Количество же ребер, исходящих из вершины, – полустепенью исхода. Полустепень захода – как правило, это первое, на что обращают внимание пользователи Facebook или Twitter: «Ах, у них куча подписчиков… наверное, они очень крутые!» Google использует полустепень захода (для поисковой системы это количество обратных связей по ссылкам) в своем PageRank-алгоритме (подробнее см. Алгоритм ссылочного ранжирования PageRank и линейная алгебра).

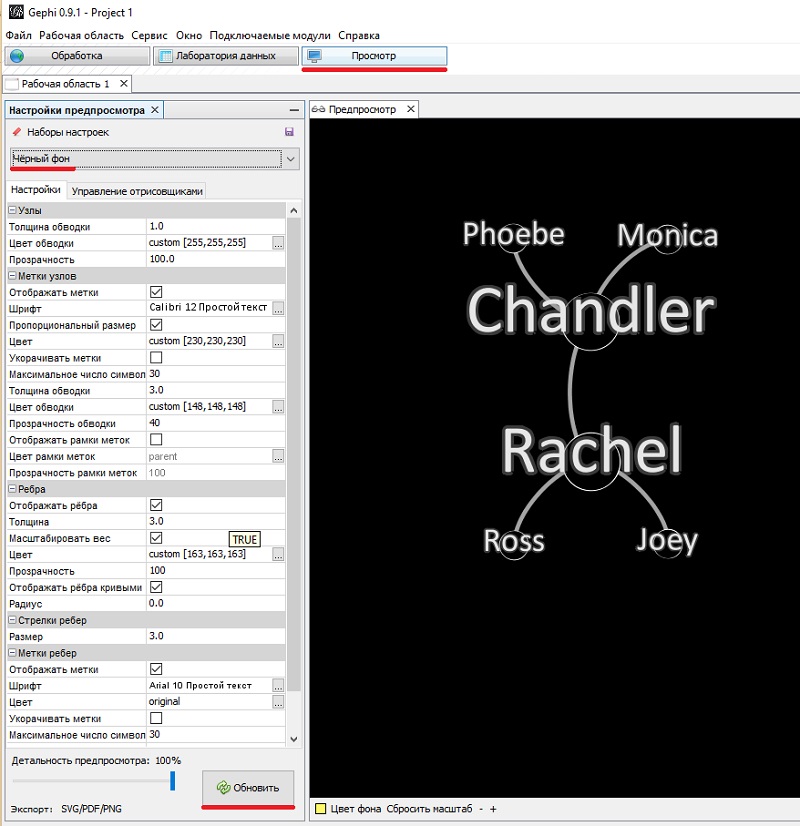
Чтобы подготовить граф к печати, перейдите на закладку Просмотр в верхней части экрана. В области Наборы настроек выберите Черный фон (рис. 10). Нажмите на кнопку Обновить в нижней части окна настроек. Обратите внимание, как вместе с самими вершинами изменились размеры подписей. Поэкспериментируйте с настройками, чтобы получить желаемый вид. Вы можете экспортировать это изображение в форматах svg, pdf, png, нажав кнопку Экспорт в левой нижней части окна.

Рис. 10. Настройка графа для печати или экспорта

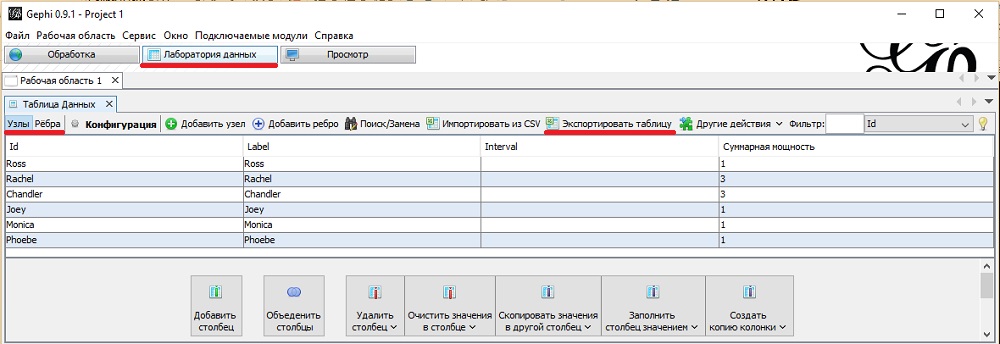
Заглянем внутрь Лаборатории данных, перейдя на соответствующую закладку. Обратите внимание, что разделов с данными два: Узлы и Ребра. В разделе Узлы можно увидеть шестерых участников с рассчитанной для них суммарной мощностью. Эти данные можно экспортировать в Excel-файл (в формате CSV).

Рис. 11. Информация о вершинах в разделе Лаборатория данных

Строим граф из данных об оптовой торговле вином

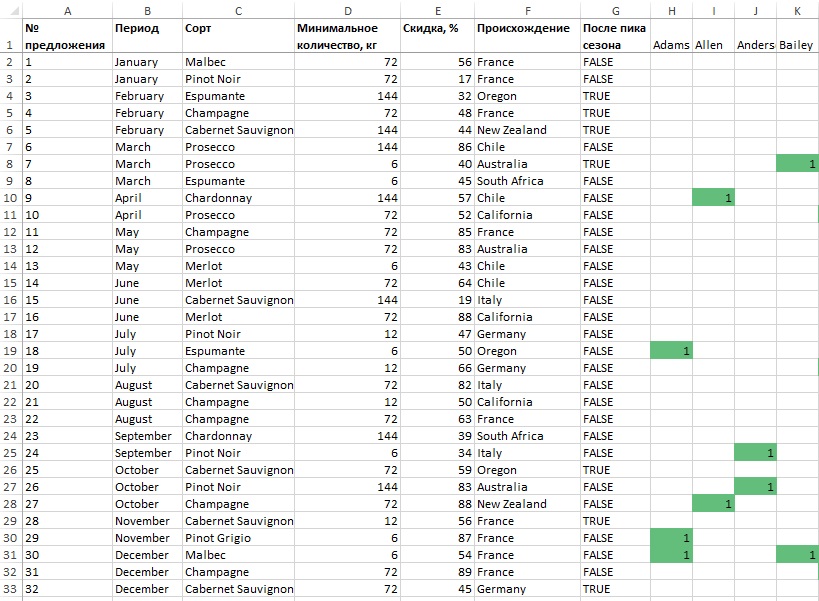
Ранее те же исходные данные были обработаны кластерным анализом с использованием метода k-средних (желательно прочитать упомянутую заметку; если вы хотите повторять манипуляции, представленные далее, скачайте Excel-файл). Напомню, что в примере вы продаете вина, и в течение года разослали 32 предложения (рис. 12). Если покупатель откликнулся на предложение, в соответствующей ячейки матрицы проставляется единица. Для наглядности эта область матрицы подсвечена условным форматированием.

Рис. 12. Матрица отклика покупателей на предложения

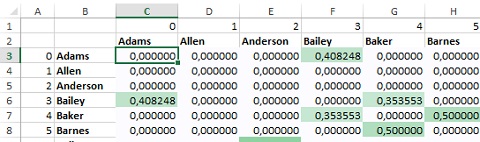
Теперь от этой матрицы вам нужно перейти к матрице близости различных покупателей между собой (рис. 13). И это будет выполнено на основании близости косинусов.

Рис. 13. Пустая таблица для матрицы близости косинусов

Напомним определение близости косинусов между бинарными заказами двух покупателей:

Количество совпадающих заказов по двум векторам, разделенное на произведение квадратного корня из количества заказов по первому вектору, умноженного на квадратный корень из количества заказов по второму вектору.

Так, для расчета близости косинусов в ячейке С3 (Adams–Adams) используется формула:

=СУММПРОИЗВ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!C$1);СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!$A3))/(КОРЕНЬ(СУММ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!C$1)))*КОРЕНЬ(СУММ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!$A3))))

В числителе формулы берется СУММПРОИЗВ из векторов заказа, которые вас интересуют, и рассчитывается количество совпавших заказов. В знаменателе перемножаются квадратные корни из количества заказов, сделанных каждым покупателем. Эта формула подготовлена для копирования на всю матрицу. Но это еще не все. Вы хотели создать граф покупателей, которые похожи друг на друга, но наверняка не задумались о диагонали матрицы. Да, Адамс идентичен сам себе и имеет близость косинусов, равную 1, но вам не нужен граф с ребрами, которые замыкаются на ту же вершину, от которой исходят, поэтому придется сделать все подобные значения равными 0. Добавьте условие ЕСЛИ:

=ЕСЛИ(C$1=$A3;0;СУММПРОИЗВ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!C$1);СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!$A3))/(КОРЕНЬ(СУММ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!C$1)))*КОРЕНЬ(СУММ(СМЕЩ(‘Рис. 12′!$H$2:$H$33;0;’Рис. 14’!$A3)))))

Вы построили матрицу близости косинусов, которая показывает, какие покупатели похожи. Как обычно, для наглядности добавьте условное форматирование (рис. 14).

Рис. 14. Заполненная матрица близости косинусов покупателей

С другой стороны, матрица близости – это граф со значениями. Каждая пара покупателей имеет между собой или 0, или ненулевое значение близости косинусов, которое отображает толщину ребра между ними. Если вы прямо сейчас экспортируете эти данные в файл *.CSV и далее импортируете в Gephi, то получите жуткую кашу из вершин и ребер. [3] Излишнее множество связей мешают алгоритму отображения правильно расположить вершины друг относительно друга (рис. 15). Вы заключили около 300 сделок и превратили их в тысячи ребер графа. Некоторые из них можно отнести к случайным. В самом деле, может, мы с вами совпали по одной сделке из десяти и у вас микроскопическая близость косинусов — так стоит ли проводить на графе это ребро?

Рис. 15. Месиво близости косинусов межпокупательского графа

Для придания данным осмысленности существуют две популярные техники удаления малозначимых ребер из сетевых графов:

• граф r-окрестности: оставляем только ребра определенной толщины; например, при г = 0,5 останутся только ребра со значениями больше или равно 0,5;
• граф k ближайших соседей: определяем максимальное число ребер, исходящих из одной вершины; например, при k = 5, при каждой вершине останется не более 5 ребер с наибольшими значениями.

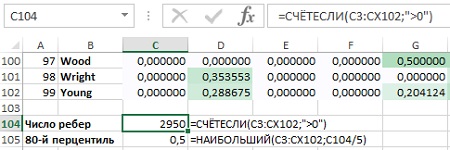
Априори нельзя сказать, какой метод лучше. Все зависит от ситуации. Далее будет рассмотрен метод r-окрестности (метод k ближайших соседей можно реализовать в Excel с помощью функции НАИБОЛЬШИЙ). Для начала нужно определить г. Воспользуемся принципом Парето: 20% связей определяют 80% сути графа. Используя в ячейке С104 формулу =СЧЁТЕСЛИ(C3:CX102,">0") определяем число ребер – 2950, созданных из исходных 324 сделок (рис. 16). Используя в ячейке С105 формулу =НАИБОЛЬШИЙ(C3:CX102;C104/5) определяем мощность ребра, соответствующую 80-ому перцентилю – 0,5. Т.е., 20% самых мощных ребер попадают в диапазон 0,5–1.

Рис. 16. Вычисление 80-го перцентиля из значений ребер

Таким образом, можно оставить 20% ребер с наибольшими значениями, просто отбросив все, значения близости косинусов которых меньше 0,5. Новую матрицу смежности (рис. 17) можно создать с помощью формулы: =ЕСЛИ(‘Рис. 14, 16′!C3>=’Рис. 14, 16’!$C$105;1;0).

Рис. 17. Матрица смежности r-окрестности = 0,5

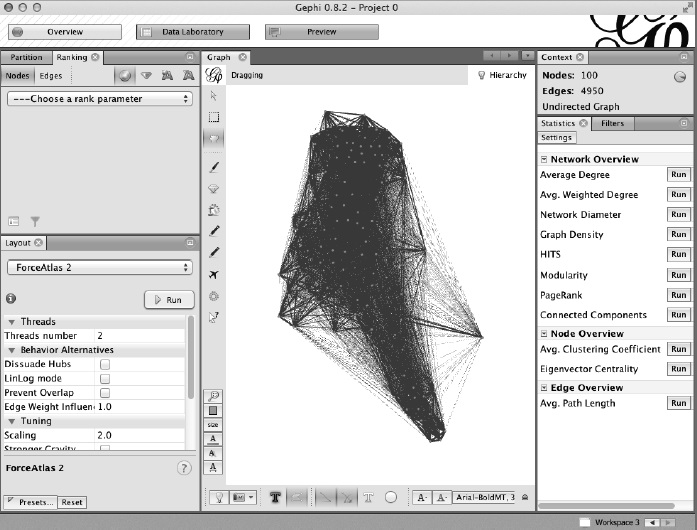
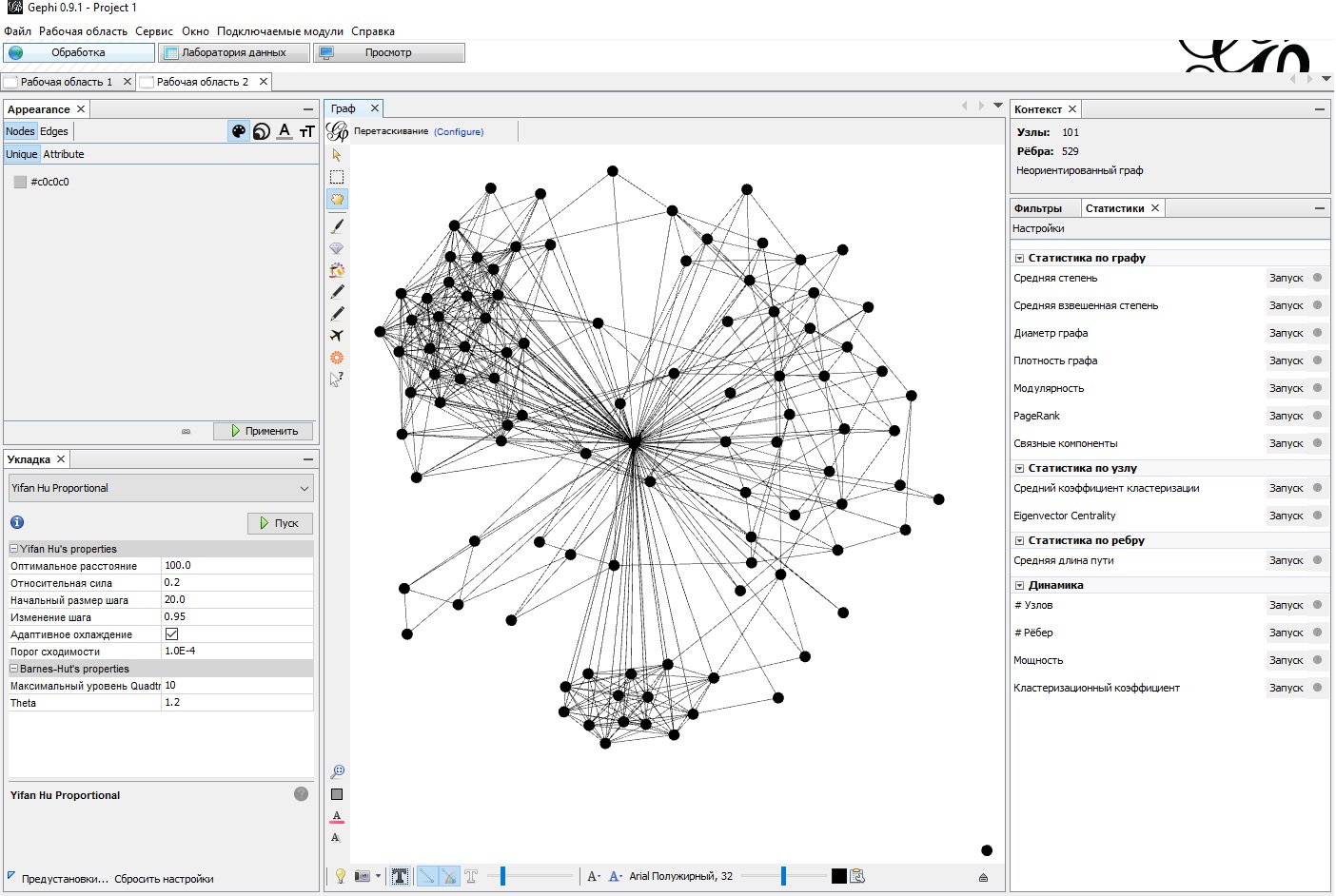
Экспортируйте матрицу смежности в CSV-файл и загрузите граф в Gephi. В графе (рис. 18) есть по меньшей мере два тесно связанных сообщества, что означает: интересы их участников отличны от остальных покупателей (первоначальную мешанину вершин и ребер мне удалось «укротить» с помощью алгоритма Yifan Hu Proportional). В правом нижнем углу можно увидеть одинокого Паркера, единственного покупателя, у которого не нашлось ребер с близостью косинусов большей или равной 0,5. Алгоритмы отображения стараются расположить его как можно дальше от связанной части графа.

Рис. 18. Визуализация графа с r-окрестностью = 0,5 в Gephi

Теперь у вас есть граф, который можно охватить взглядом, зрительно разделяя покупателей на группы. Сохраните проект, мы еще вернемся к нему позже.

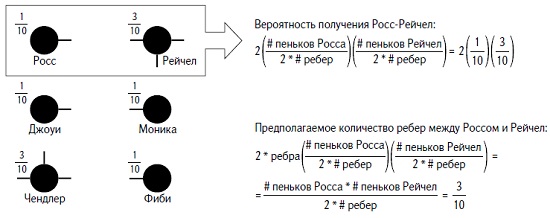
Можно еще улучшить ситуацию добавив модульную максимизацию. Алгоритм использует отношения между людьми на графе, чтобы делать предположения об их принадлежности к той или иной группе. Применяя модулярную максимизацию, вы даете себе одно «очко» каждый раз, когда группируете в один кластер две вершины, имеющие общее ребро в матрице. И получаете ноль очков, если группируете две несвязанные вершины. А также начисляется штраф. Модулярная максимизация основывает свои штрафы на следующем утверждении: Если взять граф и стереть на нем середины всех ребер (эти недоребра называются пеньками), а затем соединить их заново случайным образом несколько раз, сколько бы в этом случае ребер получилось между двумя вершинами?

Вот это предполагаемое число и есть «штрафное». Почему предполагаемое число ребер между двумя вершинами — это штраф? Да потому, что вы не собираетесь давать столько «очков» модели за группировку людей, основанную на отношениях, которые бы с большой вероятностью возникли и так, сами по себе. Так, например, Росс и Рейчел штрафуются на 0,3 (рис. 19).

Рис. 19. Предполагаемое количество ребер между Россом и Рейчел

Модулярность определения групп — это просто сумма всех очков (в том числе, и штрафных) для пар вершин, помещенных в одну и ту же группу, разделенная на общее количество «пеньков» в графе. Деление на количество «пеньков» сохраняет максимальную модулярность в пределах 1, вне зависимости от размеров графа, что облегчает сравнение разных графов между собой.

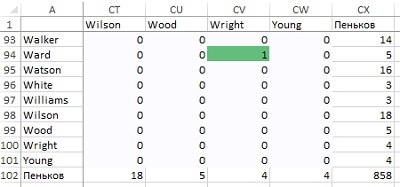
Вернемся к нашему примеру с продажами вина. Сосчитаем, сколько «пеньков» у каждого покупателя и сколько всего «пеньков» в графе. Обратите внимание, что количество «пеньков» покупателя — это просто степень его вершины. Всего в графе 858 «пеньков».

Рис. 20. Подсчет «пеньков» ребер на графе r-окрестности

Создайте еще одну пустую матрицу, и формулой извлеките значение из той же ячейки матрица смежности r-окрестности = 0,5 с рис. 17, но уменьшите его на размер «штрафа», вычисляемого по формуле, как на рис. 19:

вероятность покупателя А * вероятность покупателя В / общее количество «пеньков»

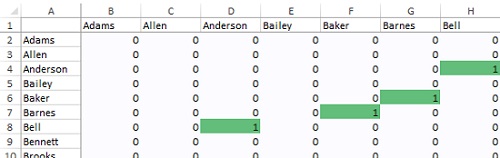
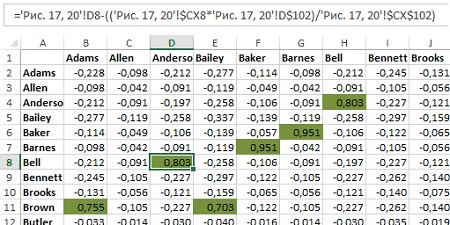
Для проверки обратимся к ячейке D8. В ней находится модулярность для кластеризации Bell/Anderson. Значение = 0,803. Bell и Anderson имеют общее ребро в матрице смежности, так что вы получаете 1 очко за их кластеризацию в одну группу (фрагмент ‘Рис. 17, 20’!D8 в формуле), но у Bell 13 «пеньков» (‘Рис. 17, 20’!$CX8), и у Anderson — тоже 13 (‘Рис. 17, 20’!D$102), так что их предполагаемое количество ребер равно 13 * 13 / 858 (‘Рис. 17, 20’!$CX$102) = –0,197. В итоге = 0,803.

Рис. 21. Таблица модулярностей

Теперь всё, что вам нужно сделать — это запустить оптимизационную модель, чтобы найти оптимальное распределение по группам. [4] Мы используем разделяющую кластеризацию. [5] Для начала необходимо найти наилучший способ разделения графа на две группы. Затем мы разделим эти группы на четыре, и т.д., до тех пор, пока «Поиск решения» не заключит, что наилучший способ максимизации модулярности — это перестать делить группы.

Создайте новый лист и вставьте покупателей в столбец А. Принадлежность каждого покупателя к группе будет обозначена в столбце Сообщество. Так как вы делите граф пополам, пусть этот параметр будет бинарной переменной (0 или 1) в Поиске решения.

Считаем принадлежность каждого покупателя к группе. В столбцах D и Е вычислим модулярность для каждого покупателя при отнесении его к соответствующей группе (рис. 22). Например, если вы поместите Адамса в группу 1, то вам нужно сложить все значения ячеек из строки 2 листа «Рис. 21», которые относятся к другим покупателям, также попавшим в группу 1. Так как мы присваиваем только 0/1, можно использовать СУММПРОИЗВ для умножения вектора группы на вектор модулярности и сложения результата.

Рис. 22. Лист, подготовленный к оптимизации

Поскольку значения модулярностей на листе «Рис. 21» расположены слева направо, а в оптимизационной модели они идут сверху вниз, придется использовать ТРАНСП (что, в свою очередь, означает использование формулы массива): {=СУММПРОИЗВ(B$2:B$101,ТРАНСП(‘Рис. 21’!B2:CW2))}. Формула умножает значения модулярности на значения принадлежности к группе. Остаются только те, которые относятся к членам группы 1, в то время как остальные обращаются в 0. СУММПРОИЗВ складывает их все.

Если Адамс был отнесен к группе 0, нужно всего лишь полученное значение вычесть из 1: {=СУММПРОИЗВ(1-(B$2:B$101),ТРАНСП(‘Рис. 21’!B2:CW2))}. Мы бы могли соединить эти две формулы с помощью функции ЕСЛИ, которая бы проверила принадлежность Адамса к той или иной группе, а затем использовала бы соответствующую формулу для сложения модулярностей тех или иных соседей. Но при использовании ЕСЛИ пришлось бы задействовать нелинейную модель в Поиске решения (подробнее см. Линейное программирование в Excel). В данном случае максимизация модулярности слишком тяжела для нелинейного Поиска решения, и он становится неэффективен. Следует сделать задачу линейной.

Обе предыдущие формулы линейны, так почему бы просто не установить переменную модулярности для Адамса – такую, чтобы она была меньше их обеих? Мы пытаемся максимизировать общую модулярность, поэтому модулярность Адамса будет стремиться вверх, пока не наткнется на меньшую из ограничивающих формул. Добавим в формулу вторую часть: {=СУММПРОИЗВ(B$2:B$101;ТРАНСП(‘Рис. 21’!B2:CW2))+(1-B2)*СУММ(ABS(‘Рис. 21’!B2:CW2))}

Если Адамс отнесен в группу 1, то эта часть формулы обращается в 0 (из-за умножения на 1-В2). В этом случае формула становится идентичной первой из рассмотренных выше формул. Но если Адамса отнесли в группу 0, то эта формула больше не подходит и ее нужно отключить. Поэтому часть формулы (1-B2)*СУММ(ABS(‘Рис. 21’!B2:CW2)) добавляет 1, умноженную на сумму всех абсолютных значений модулярности, которые Адамс может получить. Это действие гарантирует, что результат окажется выше, чем у ее перевернутой версии из соседней колонки: {=СУММПРОИЗВ(1-(B$2:B$101);ТРАНСП(‘Рис. 21’!B2:CW2))+B2*СУММ(ABS(‘Рис. 21’!B2:CW2))}

Все, что вы делаете — это заставляете модулярность Адамса быть меньше или равной правильному расчету и удаляете другую формулу из рассуждения, завышая ее значение. Это взломанная функция ЕСЛИ.

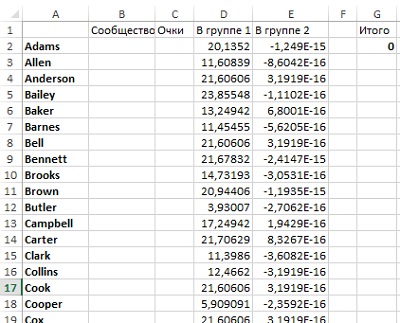
Таким образом, столбец С вы делаете столбцом модулярности, которая будет переменной решения, а в столбцы D и Е вставляете две формулы в качестве верхних границ модулярности. Складывая значения модулярности в столбце G2, получаем целевую функцию для максимизации: =СУММ(C2:C101)/’Рис. 17, 20′!CX102.

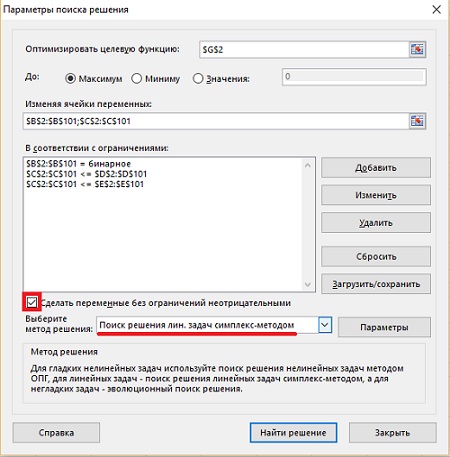
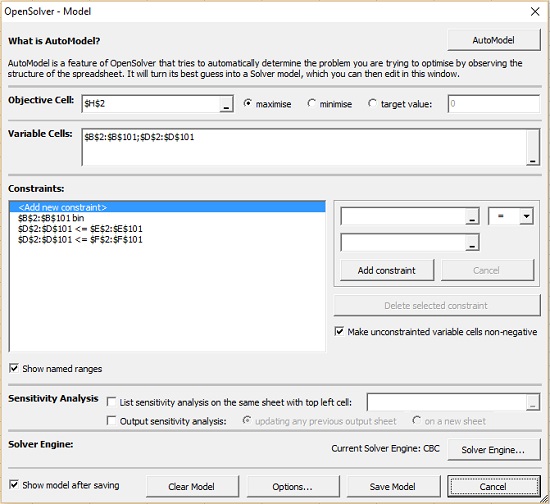
Кликните Поиск решения и отметьте, что вы максимизируете значение модулярности графа в ячейке G2 (рис. 23). Переменные решения — это значения принадлежности к группе в В2:В101 и значения модулярности в С2:С101. К значениям принадлежности к группе в В2:В101 нужно добавить условие бинарности. Также необходимо сделать переменные модулярности покупателей в столбце С меньше, чем обе верхние границы в столбцах D и Е. Также следует сделать все переменные неотрицательными, отметив галочкой эту опцию и выбрать Поиск решения линейных задач симплекс-методом. Кликните кнопку Параметры и установите Максимальное число подзадач на 15 000. Это гарантирует нам, что Поиск решения остановится минут через 20 после начала работы. Нажмите Ok, а затем Найти решение.

Рис. 23. Настройка симплексного алгоритма для первого деления графа на два кластера

К сожалению, Поиск решения не может решить эту задачу – слишком много переменных. Установите и запустите надстройку OpenSolver (подробнее см. Джон Форман. Много цифр: Анализ больших данных при помощи Excel, рис. 9). Перед запуском модели зайдите в параметры OpenSolver и установите ограничение времени 300 секунд. Когда алгоритм завершит работу согласно ограничению, созданному пользователем (рис. 24), он может сообщить вам, что нашел возможное решение, но оно не оптимальное. Это значит, что алгоритм просто не доказал оптимальность (точно так же на это не способны нелинейные алгоритмы), но не огорчайтесь: даже в этом случае можно быть уверенным, что решение не худшее.

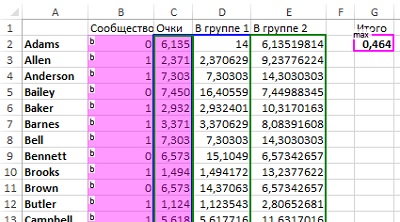
Рис. 24. Оптимальное решение для первого деления графа на два кластера

Мой поиск решения завершился на значении модулярности 0,464. У вас решение может быть иным. Просматривая столбец В, вы видите, кто оказался в группе 0, а кто — в группе 1. Теперь встает вопрос: окончательное ли это решение? Действительно ли группы всего две или больше? Чтобы ответить на этот вопрос, попытайтесь разделить эти группы пополам. Если дальнейшее разделение увеличит модулярность, то вы получите четыре кластера. Иначе, останетесь при своих.

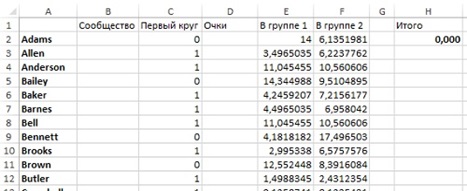
Создайте новый лист, и вставьте новый столбец после столбца Сообщество. Назовите его Первый круг, и скопируйте туда значения из столбца В (рис. 25). Теперь принадлежность к одной группе определяется парой значений в столбцах В и С. Кластеров может быть четыре: 0–0, 0–1, 1–0 и 1–1.

Рис. 25. Исходная модель для второго деления

Также необходимо поменять верхние границы расчета модулярности. В Е2 используется формула: {=СУММПРОИЗВ(B$2:B$101;ЕСЛИ(C$2:C$101=C2;1;0);ТРАНСП(‘Рис. 21’!B2:CW2))+(1-B2)*СУММПРОИЗВ(ЕСЛИ(C$2:C$101=C2;1;0);ТРАНСП(ABS(‘Рис. 21’!B2:CW2)))}. А в F2: {=СУММПРОИЗВ(1-(B$2:B$101);ЕСЛИ(C$2:C$101=C2;1;0);ТРАНСП(‘Рис. 21’!B2:CW2))+B2*СУММПРОИЗВ(ЕСЛИ(C$2:C$101=C2;1;0);ТРАНСП(ABS(‘Рис. 21’!B2:CW2)))}.

Логическое выражение ЕСЛИ(C$2:C$101=C2,1,0) предотвращает начисление «очков» Адамсу, пока его соседи не окажутся с ним в одном кластере после первого деления. Здесь можно использовать ЕСЛИ, потому что значения в столбце С больше не являются переменными. Вы можете настроить Поиск решения, а затем запустить OpenSolver. А можете сразу задать параметры в окне модели OpenSolver (рис. 26). Не забудьте ограничить работу OpenSolver 300 секундами.

Рис. 26. Настройка алгоритма для второго деления графа

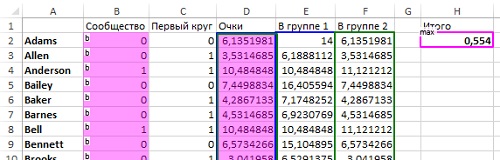
Модулярность возросла до 0,554 (рис. 27). Это значит, что второе деление было хорошей идеей.

Рис. 27. Оптимальное решение для второго деления

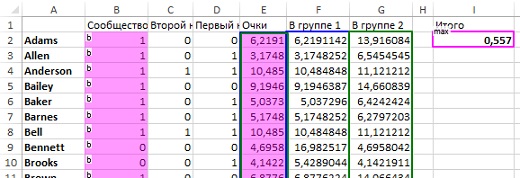
Стоит ли останавливаться на этом или продолжить? Единственный способ узнать ответ — поделить еще раз. Если результат не улучшится — значит третье деление было излишним. Создайте новый лист и модернизируйте его аналогично предыдущим манипуляциям (за формулами можно проследить в Excel-файле на листе «Рис. 28»). У автора книги никакого улучшения модулярности не произошло, а у меня значение выросло до 0,557 (рис. 28). Учитывая, что рост модулярности совсем незначителен, чтобы не усложнять, и продолжить следовать изложению Формана, допустим, что третье деление не повысило модулярность, и максимальный эффект был достигнут после второго деления. Таким образом, для дальнейшего изложения будем опираться на результаты рис. 27.

Рис. 28. Значение модулярности после третьего деления

Рассмотрим принадлежности к группам подробнее. Создайте новый лист, вставьте туда имена покупателей, и номера групп, преобразовав два бинарных столбца (В и С с рис. 27) в один десятеричный с помощью формулы: =ДВ.В.ДЕС(СЦЕПИТЬ(‘Рис. 27′!B2;’Рис. 27’!C2)) (рис. 29).

Рис. 29. Итоговые номера кластеров для модульной максимизации

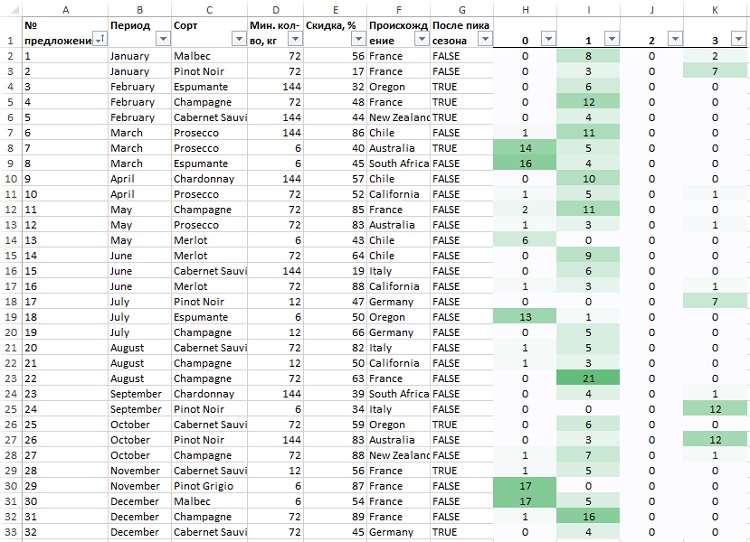
У нас получилось четыре кластера с ярлыками от 0 до 3. Чтобы проанализировать эти кластеры следует выделить наиболее характерные для них предложения (из 32). Возьмите часть таблицы с рис. 12 (диапазон А1:G33), добавьте столбцы Н:K, озаглавьте их по номерам кластеров – 0, 1, 2 и 3 (рис. 30). С помощью формулы {=СУММПРОИЗВ(ЕСЛИ(‘Рис. 29′!$B$2:$B$101=’Рис. 30’!H$1;1;0);ТРАНСП(‘Рис. 12’!$H2:$DC2))} сложите количество покупателей для каждого предложения.

Рис. 30. Распределение 32 предложений по кластерам

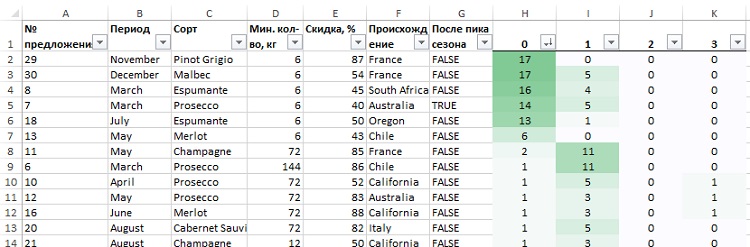
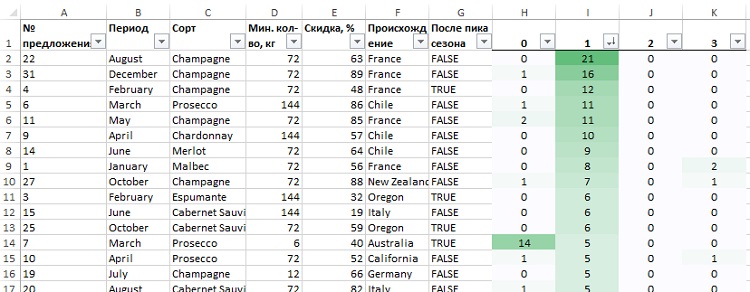
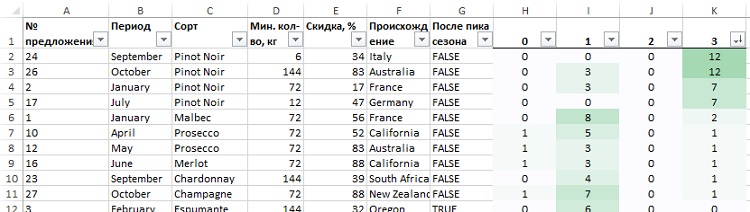
Примените к диапазону Н2:K33 условное форматирование, а также добавьте автофильтр, что позволит последовательно отсортировать наиболее популярные предложения в каждом кластере (рис. 31–33). Ваши результаты могут отличаться, и по порядку, и по составу. Кластер 2 оказался пустым (у Формана он содержал некоторые данные, правда, плохо структурированные). Обратите внимание, как похоже это решение на уже найденное нами ранее.

Рис. 31. Самые популярные предложения в кластере 0 – покупатели, предпочитающие партии минимального объема

Рис. 32. В кластере 1 покупатели предпочитают шипучие вина

Рис. 33. Кластер 3 – потребители, предпочитающие Pinot Noir

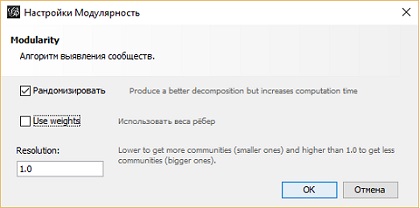
В заключение рассмотрим, как выполняется модулярная максимизация в Gephi. Откройте проект, сохраненный вами после обсуждения рис. 18. В правой части окна Gephi в разделе Статистика кликните на кнопку Запуск в строке Модулярность. В открывшемся окне настроек, вам не нужно использовать веса ребер, так как вы импортировали матрицу смежности, и все ребра имеют единичные значения (рис. 34).

Рис. 34. Настройки модулярности в Gephi

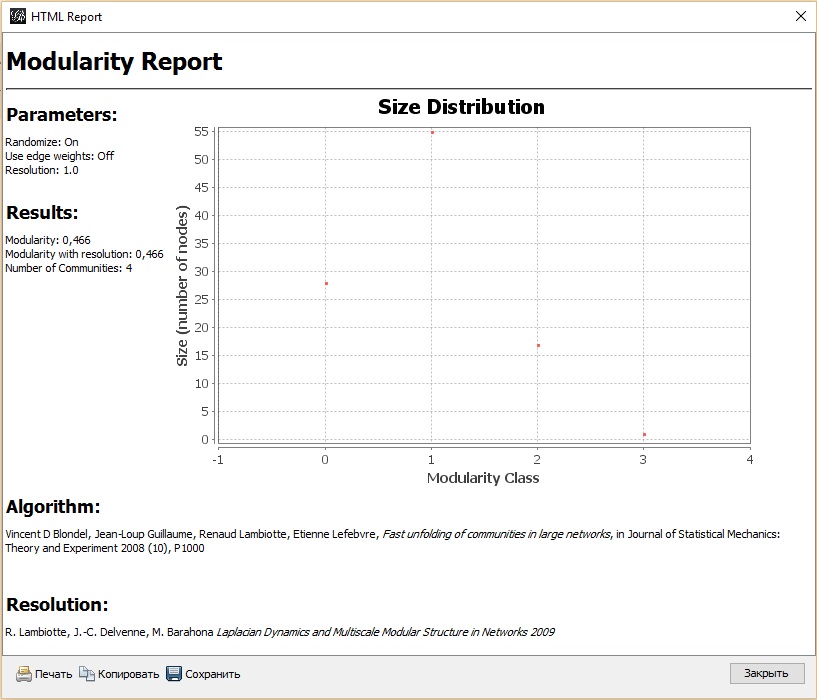
Нажмите ОК. Запустится оптимизация модулярности с использованием алгоритма приближения. Этот алгоритм выполняется существенно быстрее, чем в Excel. Появится отчет (рис. 35). Модулярность равна 0,466. Показаны размеры кластеров: нулевой – 28 вершин, 1-й – 55, 2-й – 17 и 3-й – 1. Обратите внимание: если вы запускаете этот алгоритм в Gephi, решение может оказаться другим, так как расчет рандомизирован.

Рис. 35. Отчет о модулярности в Gephi

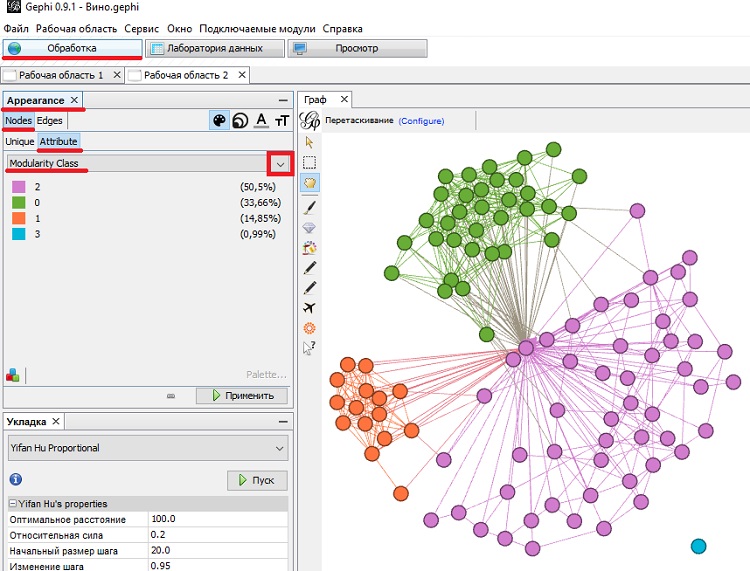
Получив в Gephi кластеры, можно подкрасить граф в соответствии с модулярностью. Проверьте, что вы на вкладке Обработка (рис. 36). В окне Appearance откройте раздел Nodes (вершины) –> Attribute. Выберите из выпадающего меню Modularity Class, подберите понравившуюся цветовую палитру и нажмите Применить. Вы видите два довольно компактных кластера, один – более аморфный и одинокого Паркера, который ни с кем не связан (на самом деле, он был совсем удален от кластеров, и я его подвинул, чтобы он поместился на рисунок).

Рис. 36. Подкрашенный граф покупателей, для выделения кластеров модулярности

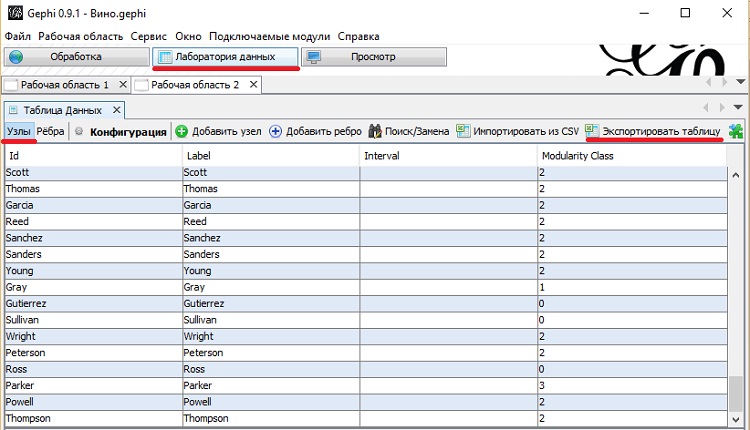
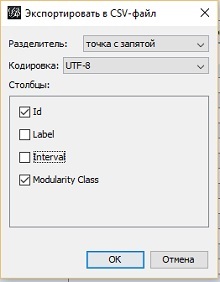
Информацию о модулярности вы можете экспортировать обратно в Excel. Это позволит вам сравнить результаты анализа в Excel и Gephi. Для этого перейдите на вкладку Лаборатория данных. Вы заметите, что классы модулярности (Modularity Class) уже заполнены в таблицы Узлы. Нажмите Экспортировать таблицу, установите параметры экспорта, и сохраните данные в файле CSV (рис. 38).

Рис. 37. Экспорт классов модулярности обратно в Excel

Рис. 38. Параметры экспорта в CSV-файл

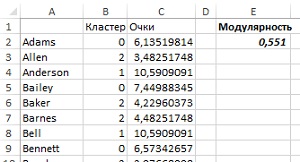
Откройте CSV-файл в Excel. Создайте в основном файле новый лист, куда перенесите данные из CSV-файла (рис. 39). Можно подсчитать итоговую модулярность для каждого покупателя с помощью следующей формулы для ячейки С2: {=СУММПРОИЗВ(ЕСЛИ($B$2:$B$101=B2;1;0);ТРАНСП(‘Рис. 21’!B2:CW2))}. Эта формула проверяет наличие покупателей в том же кластере, используя оператор ЕСЛИ, раздает им значения 0 или 1, а затем использует СУММПРОИЗВ для сложения их модулярностей. Сложив все значения в столбце С и разделив их на общее число «пеньков», вы получите в Е2 значение общей модулярности, равное 0,551. Это значение, полученное эвристикой Gephi сравнимо с эвристикой разделительной кластеризации Excel – 0,554.

Рис. 39. Модулярность кластеров, найденных Gephi

Хотя Gephi и является одним из лучших мест для подобного анализа, вам может потребоваться написание программного кода по данным графа, такое как библиотека igraph, которая имеет привязки к R и Python и великолепно подходит для работы с сетевыми графами. Также стоят упоминания базы данных графов Neo4J и Titan. Эти базы специально разработаны для хранения данных графов и последующих этапов доработки, независимо от сложности графа — интересует ли вас что-то простое, вроде «отображения любимых фильмов друга» или что-нибудь посложнее, вроде «нахождения кратчайшего пути на Facebook от одного знакомого к другому».

[1] Написано по материалам книги Джона Формана Много цифр: Анализ больших данных при помощи Excel. – М.: Альпина Паблишер, 2016. – С. 187–239

[2] Если вы используете английский Excel, то разделитель в CSV файле – запятая, а Gephi требует точку с запятой. Поэтому откройте файл в текстовом редакторе (например, в Блокноте) и замените все запятые на точки с запятой. Если у вас русский Excel, то разделитель в CSV файле – точка с запятой, и никакой дополнительной обработки не требуется.

[3] У меня Gephi вовсе отказался импортировать столь сложную матрицу.

[4] Нахождение оптимальных групп с помощью модулярности графа требует довольно сложной подготовки. Подобные задачи часто решаются сложной эвристикой, вроде популярного лувенского метода (подробнее см. здесь), но поскольку этот материал основан на работе в Excel (и Gephi) придется обходиться Поиском решения.

[5] Альтернативный метод – это агломеративная кластеризация. Если бы мы решали задачу таким методом, то каждый покупатель образовывал бы собственный кластер, а вы раз за разом объединяли бы по два ближайших кластера, пока цель не оказалась достигнутой.