Ранее мы построили весьма точную регрессионную модель для определения беременных покупателей супермаркета на основе данных об их покупках. А что, если построить несколько заведомо неказистых моделей и затем устроить голосование по поводу беременности покупательницы — а процент голосов использовать как единичный прогноз? Такой подход называется комплексным моделированием. Мы рассмотрим бэггинговые (bagging) одноуровневые деревья принятия решений. [1]
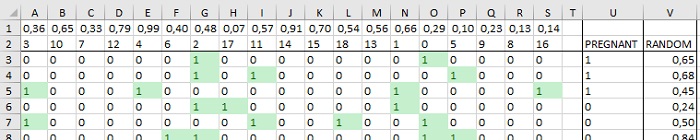
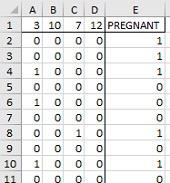
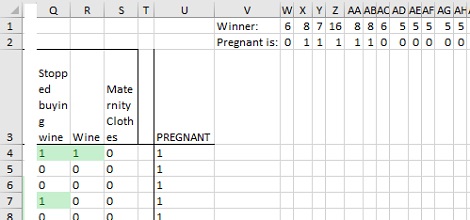
Excel-файл содержит обучающие данные из предыдущей заметки (это позволит сравнить модели). Фиктивными переменными (пол покупателей) уже настроенными. Отличительные признаки пронумерованы от 0 до 18 в строке 2 (рис. 1).
Рис. 1. Исходный набор обучающих данных; чтобы увеличить картинку, кликните на ней правой кнопкой мыши и выберите опцию Открыть картинку в новой вкладке
Скачать заметку в формате Word или pdf, примеры в формате Excel
Также в файле есть лист с тестовыми данными, по которым вам предстоит предсказать значения в столбце Pregnant с помощью данных слева от него, а затем проверить насколько данные прогноза совпали с фактическими.
В настоящем наборе данных нет пробелов. Для многих моделей, построенных на транзакционных данных бизнеса, это весьма актуально. Но иногда вы столкнетесь с ситуацией, когда в какой-нибудь строке данных не окажется элемента. Как же обучать модель, если некоторые графы пусты?
- Выкиньте строки с недостающими значениями. Если эти значения более или менее случайны, потеря пары строк обучающей последовательности не будет критичной.
- Если значения столбца числовые, пропущенные значения можно заменить средними по параметру. Если столбец категорийный, используйте самое популярное значение категории.
- Вы можете вставить рядом еще один столбец, заполненный нулями, пока не появится недостающее значение – в этом случае 0 становится 1. Таким образом вы заполняете пропущенные значения как можете, но рекомендуете модели не очень-то им доверять.
- Существуют и более сложные механизмы, использующие регрессионный анализ для заполнения пустот.
Бэггинг (метод случайных подвыборок) — это техника, которая используется для обучения нескольких классификаторов, но не на абсолютно одинаковых выборках. Если вы будете обучать классификаторы на одинаковых данных, они сами станут одинаковыми — но вам же нужно разнообразие моделей.
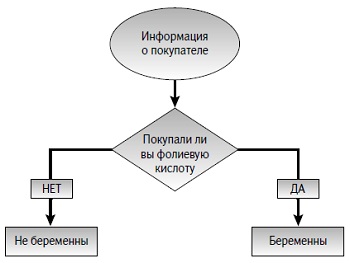
В модели бэггинга отдельные классификаторы будут одноуровневыми деревьями решений. Одноуровневое дерево решений — не более чем один вопрос, который вы обращаете к данным. В зависимости от ответа вы можете понять, ожидает ли семья ребенка или нет. Простые классификаторы вроде этого часто называют слабообучаемыми. Например, в обучающем наборе данных 104 «беременные» семьи (из 500) сделали такой заказ до рождения ребенка. С другой стороны, только двое «небеременных» покупателей заказали фолиевую кислоту. Так что между заказом препаратов фолиевой кислоты и беременностью, бесспорно, существует связь. Можно использовать эту простую зависимость для сборки такого слабообучаемого классификатора:
Покупали ли семьи фолиевую кислоту? Если да, то считать их «беременными». Если нет, то считать их «не-беременными» (рис. 2).
Рис. 2. Фолиевое одноуровневое дерево
Такое дерево решений делит выборку обучающих записей на две подвыборки. Вы, наверное, думаете, что это дерево имеет глубокий смысл? Что ж, в известной степени вы правы. Хотя смысл этот все-таки не настолько глубок, как вам кажется. В конце концов, в вашей обучающей выборке имеется 396 «беременных» семей, которые не покупали фолиевую кислоту и были неправильно классифицированы деревом решений.
Все равно это лучше, чем вовсе никакой модели, да? Несомненно. Но вопрос в том, насколько данное дерево лучше полного отсутствия модели. Один из способов оценить это — применить параметр под названием node impurity – загрязненность класса. Этим способом измеряется, как часто выбранная запись покупателя была неправильно классифицирована в качестве беременной или «не-беременной», если классификация производилась случайным образом, согласно распределению покупателей в своей подвыборке дерева решений.
К примеру, можно начать с отнесения всей тысячи покупателей в одну подвыборку, что является, скажем прямо, стартом без модели. Вероятность того, что вы выберете беременного покупателя из кучи, равна 50%. Классифицировав его случайным образом, исходя из соотношения 50/50, вы получите 50%-ный шанс правильно угадать класс. Таким образом, получается 50% х 50% = 25% вероятность выбора беременного покупателя и правильного угадывания факта беременности. Аналогично равна 25% вероятность выбора «не-беременного» покупателя и угадывания того, что он не является беременным. Все, что не относится к этим двум случаям — просто версии неверных догадок. Значит, у нас есть 100% – 25% – 25% = 50% шанс неправильного отнесения покупателя к классу.
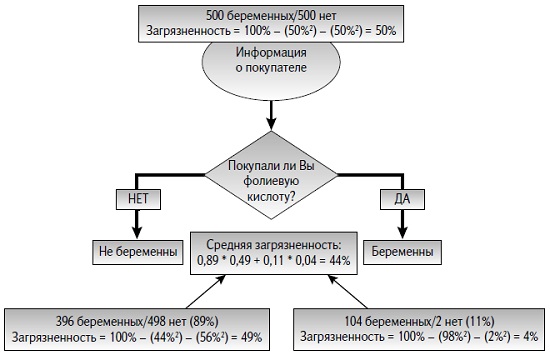
Дерево решений по фолиевой кислоте делит этот набор из 1000 записей на две группы — 894 человека, не купивших фолиевые препараты, и 106 купивших. У каждой из этих подвыборок своя собственная загрязненность, так что, усреднив загрязненность обеих подвыборок (принимая во внимание разницу в их размере), вы сможете узнать, насколько одноуровневое дерево исправило ситуацию. Из 894 покупателей, попавших в «не-беременную» корзину, 44% беременны, а 56% — нет. Загрязненность можно рассчитать, как 100% – 44%2 – 56%2 = 49%. Не такое уж большое улучшение.
Что касается тех 106 покупателей, которых мы поместили в «беременную» категорию: 98% из них беременны, и только 2% — нет. Загрязненность будет равна 100% – 98%2 – 2%2 = 4%. Усреднив общее значение загрязненности, получаем 44% (рис. 3). Это получше, чем бросать монетку!
Рис. 3. Загрязненность классов для фолиевого дерева
Одноуровневого дерева решений недостаточно. Представьте, что у вас огромное количество деревьев, каждое из которых обучено на разной части данных и загрязненность результатов каждого — меньше 50%? Почему бы не построить простые деревья решений по всеми остальными столбцами? У вас всего 19 признаков, и, честно говоря, некоторые из них, такие как адрес в виде дома или квартиры, несколько озадачивают. Так что вы имеете дело с 19 одноуровневыми деревьями сомнительного качества.
Но с помощью метода случайных подвыборок (бэггинга) можно «изготовить» сколько хотите деревьев. Бэггинг действует примерно таким образом:
- Для начала откусываем кусочек выборки. Стандартная практика — взять квадратный корень из количества признаков (четыре случайных столбца в нашем примере) и случайным образом две трети строк.
- Строим дерево решений для каждого из этих четырех выбранных вами признаков, с помощью случайно выбранных 2/3 данных.
- Из этих четырех деревьев выбираем наилучшее. Сохраняем. Перемешиваем все заново и обучает новое дерево.
- Когда у вас накопится куча деревьев, соберите их вместе, заставьте проголосовать и назовите их единой моделью.
Из обучающих данных вам нужно взять случайный набор строк и столбцов. Самый простой способ перемешать столбцы и строки – это добавить еще один столбец и одну строку, заполненные случайными числами (с помощью функции СЛЧИС(), рис. 4). Сортировка по случайным значениям слева направо и сверху вниз, а затем выбор нужного количества из верхнего левого угла таблицы дает вам случайный набор строк и признаков (подробнее о сортировке столбцов см. пояснения к рис. 2 в заметке Джон Форман. Много цифр: Анализ больших данных при помощи Excel).
Рис. 4. Добавление случайных чисел строку 1 и столбец V
Отсортируйте массив А1:S1002 по столбцам и массив А3:V1002 по строкам. Не обращайте внимания на то, что в результате сортировки случайные числа не выстроились по порядку – после сортировки они успели пересчитаться (рис. 5).
Рис. 5. Отсортированный случайным образом массив обучающих данных
Создайте новый лист и перенесите на него прямоугольник, образованный первыми четырьмя столбцами и первыми 666 строками с рис. 5. Для этого на новом листе укажите в ячейке А1: =’Рис. 4 и 5′!A2. А затем скопируйте эту формулу до D667. В ячейке Е1 укажите: =’Рис. 4 и 5′!U2. А затем скопируйте эту формулу до Е667. Теперь у вас на листе случайная выборка из обучающего массива (рис. 6). Поскольку данные отсортированы случайным образом, в конце концов у вас остается четыре разных столбца с признаками. Самое приятное то, что если вы вернетесь на лист «Рис. 4 и 5» и отсортируете все заново, этот образец обновится автоматически!
Рис. 6. Четыре случайных столбца и случайные 2/3 строк
Между любым одним признаком и зависимой переменной Preganant возможны 4 зависимости:
- признак может иметь значение 0, а Pregnant — 1;
- признак может иметь значение 0, а Pregnant — 0;
- признак может иметь значение 1, а Pregnant — 1;
- признак может иметь значение 1, а Pregnant — 0.
Вам нужно сосчитать количество обучающих строк, попадающих в каждый из этих случаев, чтобы построить дерево, аналогичное тому, что изображено на рис. 2. Для этого пронумеруйте четыре обозначенные комбинации нулей и единиц в G2:H5 (рис. 7). В диапазоне I1:L1 разместите порядковые номера из А1:D1. Заполните таблицу числом обучающих строк, значения которых совпадают с комбинацией прогноза (Predictor) и значением в столбце Preganant. Для этого, например, в ячейке I2 используется формула =СЧЁТЕСЛИМН(A$2:A$667;$G2;$E$2:$E$667;$H2).
Рис. 7. Четыре возможных варианта обучающих данных
Функция СЧЁТЕСЛИМН позволяет вам сосчитать строки, удовлетворяющие нескольким критериям. Первый критерий смотрит на значения признака номер 3 (в ячейках А2:А667) и проверяет их на равенство значению в ячейки G2 (0). Второй критерий проверяет значения Preganant (в ячейках Е2:Е667) и проверяет их на равенство значению в ячейки Н2 (1). Обратите внимание, что сочетание абсолютных и относительных ссылок в формуле подобрано таким образом, чтобы ее можно было скопировать в диапазон I2:L5.
Если бы каждый из этих признаков был деревом решений, то какое значение признака являлось бы индикатором беременности? Несомненно, значение с самой высокой концентрацией беременных покупателей в образце. В ячейке I6 для этого используется формула: =ЕСЛИ(I2/(I2+I3)>I4/(I4+I5);0;1).
Используя значения в строках со второй по пятую, вы можете рассчитать значения загрязненности для групп каждого дерева решений, которое вы выбрали для разделения по признаку. В ячейке I8 используется формула: =1-(I2/(I2+I3))^2-(I3/(I2+I3))^2. Среднее значение загрязненности в ячейке I10 вычисляется не как среднее значений I8 и I9, а как средневзвешенное по формуле: =(I8*(I2+I3)+I9*(I4+I5))/666.
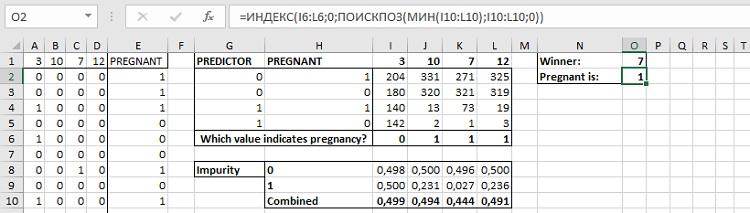
Ваши значения загрязненностей наверняка будут отличаться от моих — ведь мы пользовались генератором случайных чисел. В моем случае победителем является номер 7 (заглянув в лист «Рис. 1», можно увидеть, что это — фолиевая кислота) со значением 0,444 (выбирается минимальное из диапазона I10:L10).
Теперь нужно подготовить область О1:HG2 для записи большого числа победителей и предсказываемых ими значений Pregnant (0 или 1). В ячейке О1 укажите 7, а ячейке О2 – 1 (рис. 8). Вы также можете использовать в О1 формулу, чтобы она искала победителя: =ИНДЕКС(I1:L1;0;ПОИСКПОЗ(МИН(I10:L10);I10:L10;0)).
Рис. 8. Область для размещения победителей последующих итераций
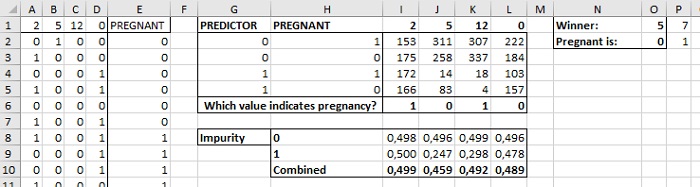
Если вы используете формулы в О1 и О2, перенесите значения из О1:О2 в Р1:Р2, чтобы сохранить их, как значения. Теперь, когда все формулы готовы, вам остается на листе «Рис. 4 и 5» повторно отсортировать массив А1:S1002 по столбцам и массив А3:V1002 по строкам. Перейдя на лист «Рис. 6-8» вы увидите нового победителя – 5. Вставьте столбец после О и впишите значения из О1:О2 в Р1:З2. И переходите к третьему «встряхиванию». И так еще 198 раз. Итого вы получите ансамбль из 200 моделей.
Рис. 9. При перемешивании данных появляется новое дерево
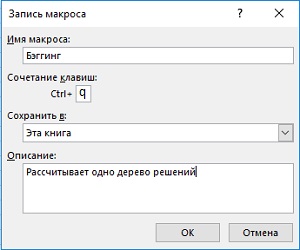
Подобные повторяющиеся действия отлично подходят для записи макроса. Если вы никогда этого не делали, не переживайте, это не сложно. Пройдите по меню Вид –> Макрос –> Запись макроса. Откроется окно, в котором вы сможете дать своему макросу название, например, Бэггинг. Для удобства запуска макроса свяжем его с комбинацией клавиш Ctrl+q (рис. 10).
Рис. 10. Окно записи макроса
Нажмите ОК, чтобы начать запись. Вот шаги, которые нужны для создания одноуровневого дерева решений:
- Нажать на лист «Рис. 4 и 5»
- Выделить столбцы А:S.
- Задать параметры сортировки по столбцам.
- Выделить диапазон А2:V
- Задать параметры сортировки по строкам.
- Переключиться на лист «Рис. 6-8».
- Кликнуть правой клавишей мышки на столбце Р и вставить новый пустой столбец.
- Выделить и скопировать выигрышное дерево из О1:О2.
- Вставить «Специальной вставкой» значения в Р1:Р2.
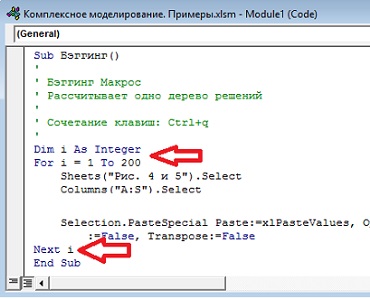
Пройдите по меню Вид –> Макрос –> Остановить запись. Теперь вы можете создавать новые деревья решений простым нажатием комбинации клавиш, активирующей макрос. Если вы добавите в макрос цикл, то сможете за один присест создать столько деревьев решений, сколько пожелаете. Пройдите по меню Вид –> Макрос –> Макросы. В открывшемся окне выберите макрос Бэггинг и кликните Изменить. В окне редактора VBA добавьте две начальные строки цикла и одну конечную (рис. 11).
Рис. 11. Добавления цикла позволяет запустить макрос для создания 200 деревьев решений
Вот это бэггинг! Все, что нужно сделать — это перемешать данные, взять подвыборку, обучить простой классификатор — и все по новой! Накопив в своем ансамбле 200 классификаторов, вы будете готовы делать прогнозы (рис. 12)
Рис. 12. 200 деревьев решений
Возьмите тестовые данные и добавьте к ним полученные 200 деревьев решений (рис. 13). Вы можете запускать по одной строке тестовых данных в каждое дерево. Начните с первой строки данных (строка 4) и первого дерева в столбце W.
Рис. 13. Деревья решений, добавленные к тестовым данным
Можете использовать функцию СМЕЩ, чтобы найти значение из столбца с деревом, записанное в W1. Если это значение равняется значению в W2, то дерево прогнозирует беременность покупателя. В противном случае прогноз дерева — покупатель не является беременным. Формула в ячейке W4: =ЕСЛИ(СМЕЩ($A4;0;W$1)=W$2;1;0). Скопируйте формулу на диапазон W4:HN1003. В столбце V вычислите среднее значение по всем деревьям решений, чтобы получить классовую вероятность для беременности. Например, в ячейке V4 используется формула: =СРЗНАЧ(W4:HN4).
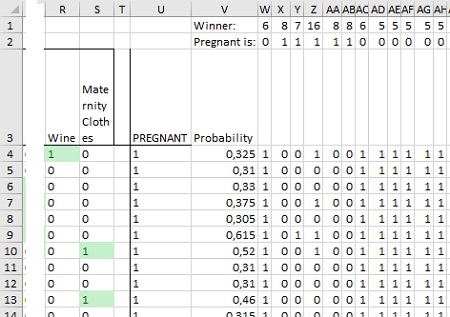
Рис. 14. Прогнозы для каждой строки
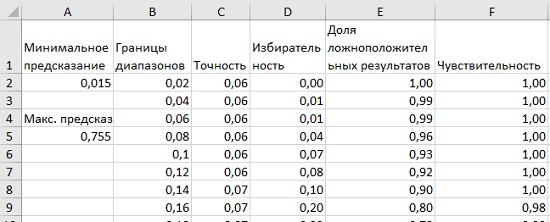
Вы можете оценить эти прогнозы, используя те же параметры оценки работы и расчеты, что и ранее. На новом листе в первом столбце найдите максимальный и минимальный прогнозы. Для моих 200 деревьев эти значения получились равными 0,015 и 0,755 (рис. 15). Поместите в столбец В серию граничных значений от минимума до максимума (в своем случае я сделал шаг равным 0,02). Точность, специфичность, доля положительных результатов и чувствительность вычисляются так же, как ранее. Обратите внимание на граничное значение прогноза 0,5 — при половине деревьев, проголосовавших за беременность, вы можете идентифицировать 33 беременных покупателя с одним лишь процентом ложноположительных результатов (напоминаю, что в вашем варианте это может быть совсем другое граничное значение — ведь мы используем случайные числа). Весьма неплохо для нескольких простых деревьев!
Рис. 15. Параметры качества работы модели бэггинга
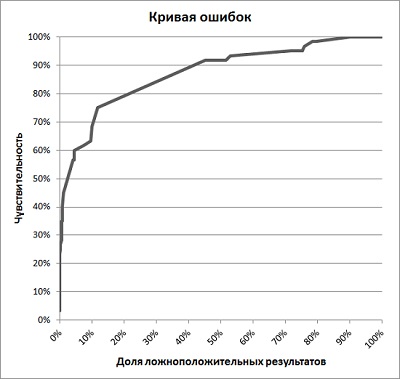
Также вы можете построить кривую ошибок, пользуясь долей ложноположительных и истинно положительных результатов или чувствительности (столбцы Е и F).
Рис. 16. Кривая ошибок бэггинга
Модели, используемые нами в MailChimp.com для предсказания спама и домогательств, — это модели случайного леса, которые мы обучаем параллельно с помощью примерно 10 миллиардов строк необработанных данных. Такое нельзя проделать в Excel. Я использую язык программирования R с пакетом randomForest.
[1] Написано по материалам книги Джона Формана Много цифр: Анализ больших данных при помощи Excel. – М.: Альпина Паблишер, 2016. – С. 293–314