Линейное программирование в Excel

Оптимизационные модели используются, чтобы найти ответы на вопросы типа:

• как составить расписание для сотрудников колл-центра, чтобы оно соответствовало их отпускным запросам, сбалансировало переработки и исключало круглосуточные дежурства?
• какие возможности бурения нефтяных скважин использовать для получения максимального дохода, держа при этом под контролем все риски?
• когда следует делать новые заказы в Китае и как их доставлять, чтобы минимизировать стоимость и соответствовать ожидаемому спросу?

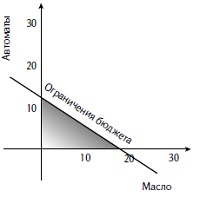
Рис. 1. Бюджетное ограничение делает область допустимых значений треугольной

Скачать заметку в формате Word или pdf, примеры в формате Excel

Целью оптимизации всегда является «максимизация» или «минимизация». Самая распространенная и понятная форма математической оптимизации — это линейное программирование, секретная разработка советских инженеров конца 1930-х годов, ставшая популярной в ходе Второй мировой войны. Кстати, слово «программирование» в данном словосочетании является пережитком военной терминологии того времени и не имеет ничего общего с компьютерным программированием. [1]

Начнем с любимого примера экономистов — пушек и масла. Идет 1941-й год, вы – хозяин французской молочной фермы. Днем вы доите коров и производите сливочное масло, ночью – собираете автоматы. Ваша цель – максимальная прибыль, чтобы как можно дольше производить автоматы. От посредника из Сопротивления вы получаете за каждый автомат по 195 денежных единиц (чтобы не напрягать Excel несуществующими франками, допустим, что это доллары). За каждую бочку масла на рынке вам платят по $150.

Условия и ограничения. Себестоимость одной бочки масла – $100, а одного автомата – $150. Месячный бюджет на производство — $1800. Вы храните продукцию в 21-кубометровом подвале. Автомат занимает ½ м³, бочка масла 1½ м³. Сколько автоматов и бочек масла вам нужно продать за месяц, чтобы получить максимальную прибыль?

Линейная программа определяется как набор решений, необходимый для оптимизации объекта в свете некоторых условий, где и объект, и условия линейны. Вы можете складывать, вычитать, умножать на константы, но не можете применять для решения нелинейные функции, например, перемножение переменных (нельзя автоматы умножить на масло), возведение в квадрат или логические циклы, такие как ЕСЛИ.

Представим области допустимых значений графически. Во-первых, количество пушек и бочек масла должно быть неотрицательным. Во-вторых, максимально можно произвести $1800/$150 = 12 автоматов или $1800/$100 = 18 бочек масла (рис. 1). Общее название этого треугольника – политоп – фигура с плоскими сторонами (например, бриллиант). В-третьих, подвал может вместить не более 21/(½) = 42 автоматов или 21/(1½) = 14 бочек масла (рис. 2).

Рис. 2. Ограниченный объем подвала отрезает кусок области допустимых значений

Чтобы найти идеальное соотношение автоматов и бочек введем в задачу понятие линии уровня функции. Такая линия в оптимизационной модели включает значения, приносящие одинаковую прибыль. Линию уровня можно задать уравнением:

(195 – 150) * N_{автоматов} + (150 – 100) * N_{бочек масла} = С,

где С – константа.

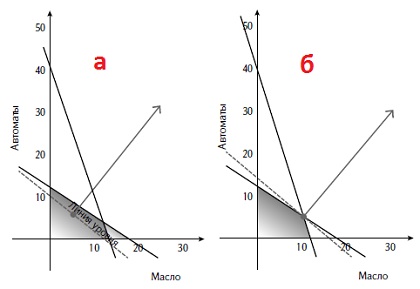
Например, при С = 450, линия будет проходить через координаты (0;10) и (9;0). Графически идея максимизации прибыли реализуется перемещением линии уровня параллельно самой себе в направлении увеличения значений по осям Х и Y (рис. 3). Любопытно, что для политопа оптимум всегда лежит в одной из вершин (или единственного решения не существует вовсе). На этом свойстве основан алгоритм симплексного метода. Решение задачи в Excel начинают с создания области модели (рис. 4). Формула целевой функции в ячейке В1 =СУММПРОИЗВ(C4:D4;C10:D10).

Рис. 3. Линия уровня и функция для оптимизации прибыли: а) некое произвольное начальное положение; б) линия уровня в оптимальном положении

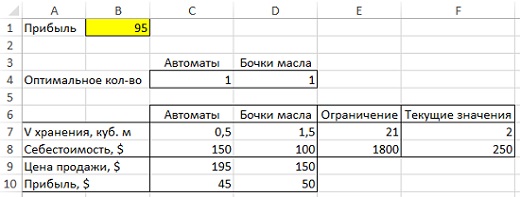
Рис. 4. Данные об автоматах и масле, помещенные в Excel

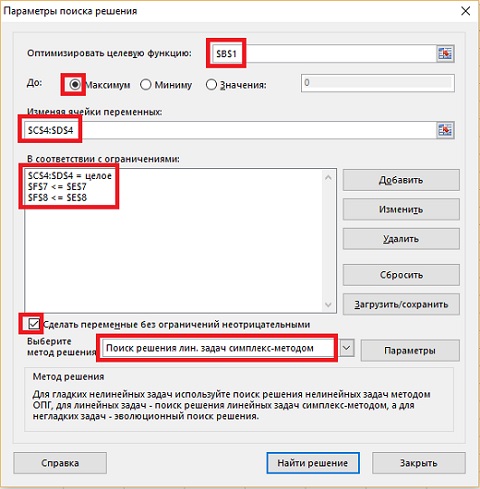
У вас всё готово, чтобы нажать кнопку ДАННЫЕ –> Поиск решения. (Если вы не видите этой кнопки, установите надстройку Поиск решения; см. Джон Форман. Много цифр: Анализ больших данных при помощи Excel, глава 1). В открывшемся окне Параметры поиска решения задайте выделенные опции и нажмите Найти решение.

Рис. 5. Окно Поиск решения

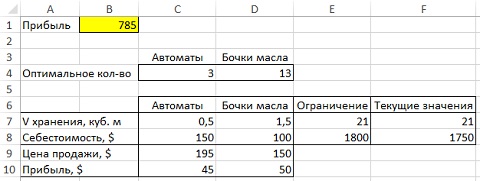
Excel обновит лист и внесет на него результаты расчета (рис. 6).

Рис. 6. Оптимизированная таблица автоматов и бочек масла

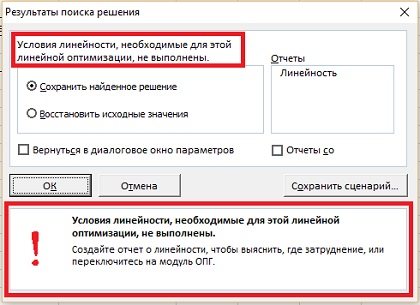
Что произойдет, если добавить нелинейность? Допустим ваш посредник предлагает $500, если число автоматов в месяц будет более 5. Просто добавьте функцию ЕСЛИ в ячейку с прибылью (В1). Теперь целевая функция выглядит так: =СУММПРОИЗВ(C4:D4;C10:D10)+ЕСЛИ(C4>5;500;0). Жмем Поиск решения. Неудача, Excel сообщает об ошибке – условия линейности не выполнены (рис. 7).

Рис. 7. Excel не дает вам использовать логические операторы в линейном алгоритме

Можно попробовать эволюционный алгоритм, лучше всего работающий с нелинейными моделями, и практически не ограничивающий вас в выборе функций. Работа эволюционного алгоритма в чем-то повторяет принципы работы биологической эволюции:

• генерирует пул исходных решений (что-то вроде генетического пула) разной степени вероятности;
• каждое решение имеет некий уровень пригодности к выживанию;
• решения размножаются перекрестным переносом, то есть их компоненты выбираются из двух или трех существующих решений и затем комбинируются;
• существующие решения мутируют в новые;
• имеет место локальный поиск, в процессе которого генерируются новые решения вблизи лучшего на данный момент решения в популяции;
• происходит отбор: случайно выбранные неуспешные кандидаты в решения выбрасываются из генетического пула.

К сожалению, с эволюционным алгоритмом все же возникают некоторые проблемы:

• Время работы существенно больше, чем при симплекс-методе
• Нет никакой гарантии, что он найдет оптимальное решение. Все, что в его силах — это контроль лучшего решения в популяции, пока не закончится время, либо популяция не изменится в достаточной степени для продолжения, либо вы принудительно не остановите «Поиск решения» нажатием кнопки ESC.
• Эволюционный поиск решения работает довольно медленно. А если области допустимых значений сложные, он часто ругается, не найдя даже места, с которого начать.
• Если вы хотите заставить эволюционный алгоритм хорошо работать в Excel, вам придется определить жесткие границы для каждой переменной решения. Даже если ваше решение более или менее неограниченное, вам все же нужны ограничения.

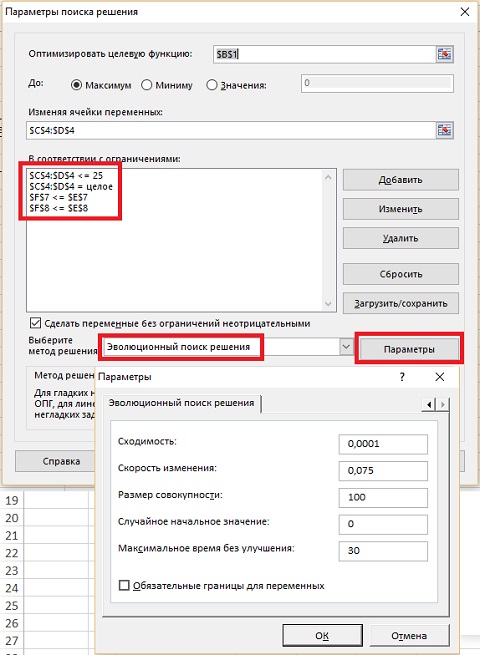
Принимая во внимание последний пункт, для решения задачи с автоматами и маслом вам нужно добавить ограничение, согласно которому оба решения не должны быть больше 25 (рис. 8). Установив основные параметры модели, кликните на кнопку Параметры. Проработав около минуты, эволюционный алгоритм выдал ожидаемое решение – 6 автоматов и 9 бочек масла. Поскольку без бонуса оптимально сделать лишь три автомата, а бонус выплачивается при производстве более 5 автоматов, очевидно, что оптимальным будет выбор 6 автоматов.

Рис. 8. Настройка эволюционного «Поиска решения»

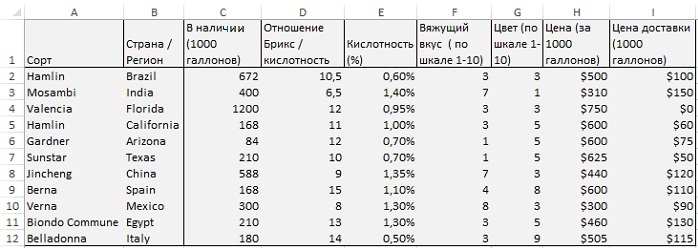
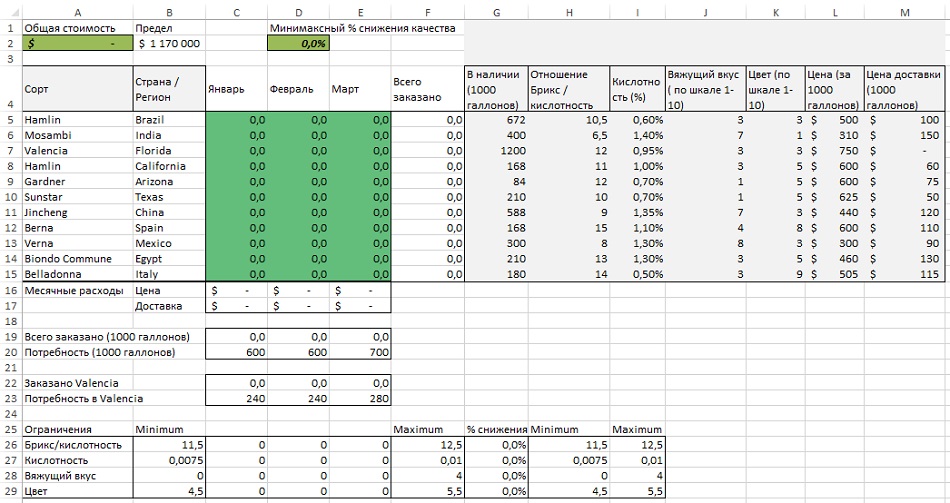
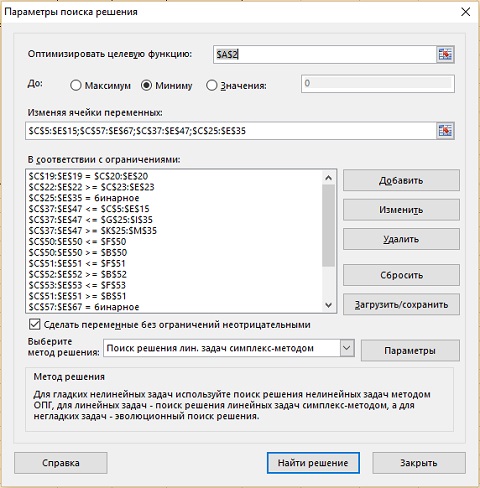
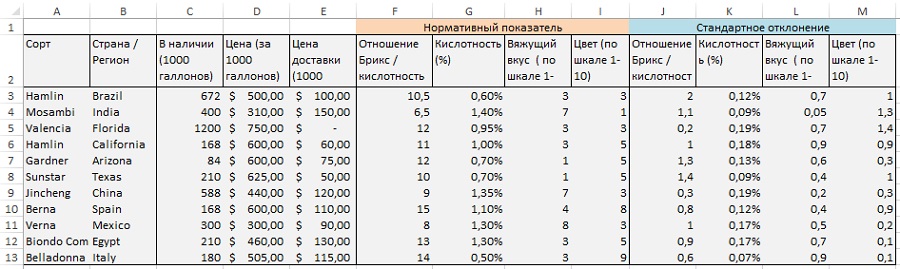
Рассмотрим теперь более сложный пример. Вы работаете в компании, которая производит апельсиновый сок, смешивая натуральные соки разных сортов (рис. 9). Чтобы ваш сок отвечал самым изысканным требованиям:

• отношение по шкале Брикс/кислотность должно оставаться в пределах 11,5–12,5;
• уровень кислотности должен оставаться между 0,75–1%;
• уровень вяжущего вкуса должен быть 4 или ниже;
• цвет должен находиться в рамках 4,5–5,5.

Шеф сообщил вам, что на январь и февраль он ожидает спросу на уровне 600 000 галлонов сока в месяц, а в марте – 700 000 галлонов. И еще, имеется договор со штатом Флорида, предоставляющий налоговые льготы при условии, что компания покупает не менее 40% сока каждый месяц у фермеров, выращивающих сорт Valencia. Договор следует соблюсти.

Рис. 9. Список характеристик для производства свежевыжатого апельсинового сока (чтобы увеличить изображение, кликните на нем правой кнопкой мыши, и выберите Открыть картинку в новой вкладке)

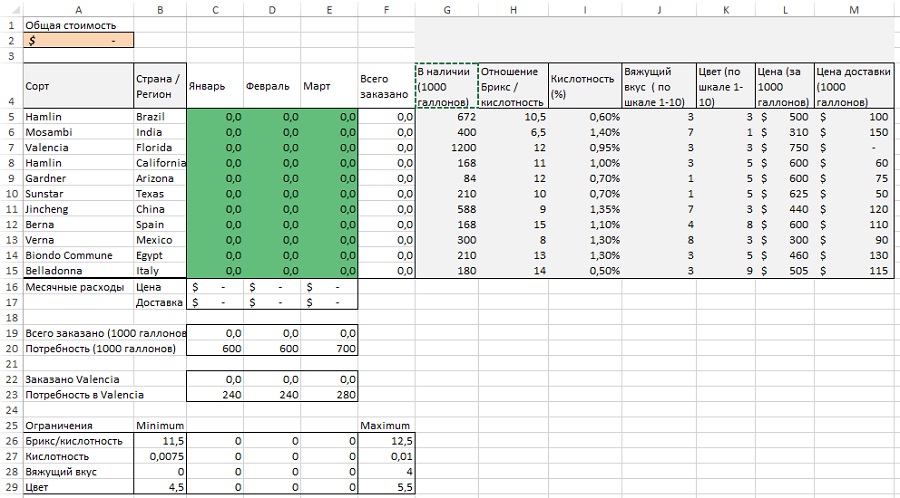
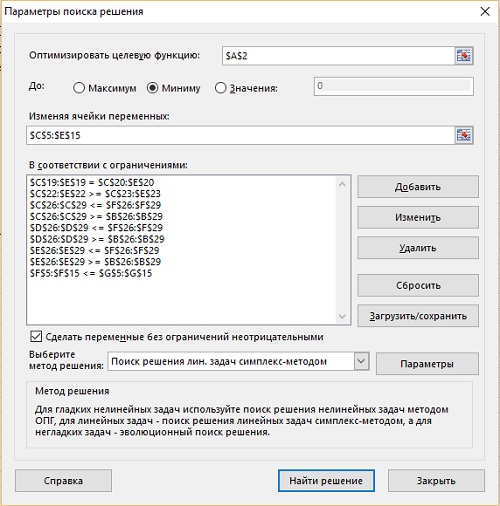
Создайте оптимизационную модель (рис. 10). Формулы можно изучить на соответствующем листе, приложенного Excel-файла. Кликните Поиск решения, и введите параметры (рис. 11). Нажмите Найти решение.

Рис. 10. Настраиваем таблицу смешивания

Рис. 11. Заполненное окно Поиск решения для задачи смешивания

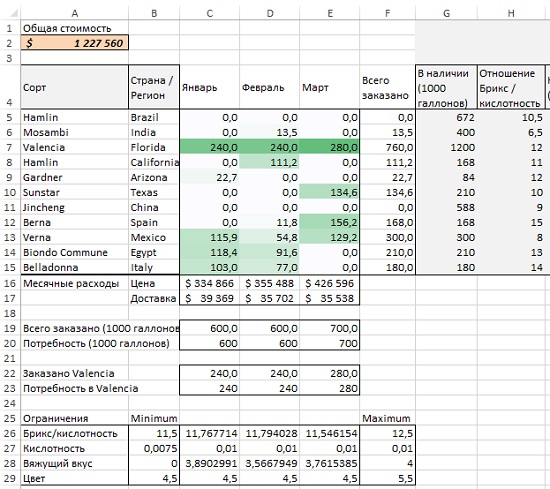
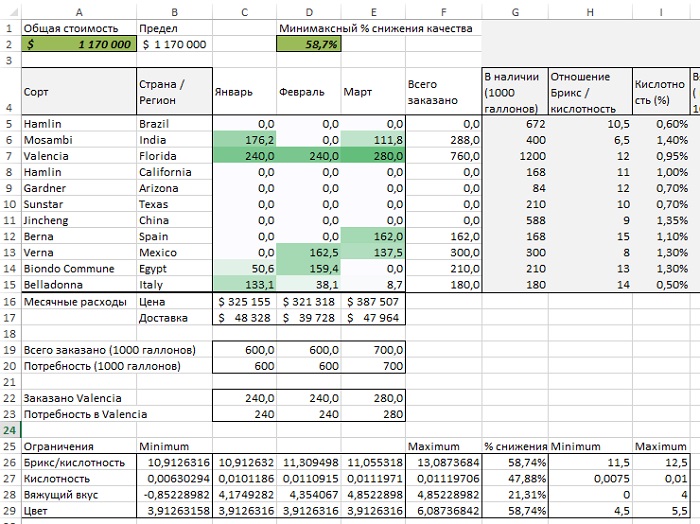
Запустив Поиск решения, вы находите оптимальную стоимость закупок — $1,23 млн. (рис. 12). Обратите внимание, что заказ флоридской Valencia проходит по нижней границе условия. Очевидно, эта сделка — не лучший вариант, но приходится смириться. Второй по популярности сорт — это Verna из Мексики, которая чертовски дешева, но ровно настолько же ужасна.

Рис. 12. Решение оптимизационной задачи по смешиванию апельсинового сока

Вы представляете результаты расчета шефу, но он остается недоволен, и говорит о том, что не хочет выходить за бюджет $1,17 млн. Вы возвращаетесь к компьютеру и начинаете понимать, что стоимость перестала быть целевой функцией. Теперь это условие! А какова цель? Вы можете снизить стоимость закупок только смягчив требования к качеству. Вы решаете сформулировать их в терминах процентного сокращения, и делаете новую модель (рис. 13).

Рис. 13. Модель с пониженным качеством

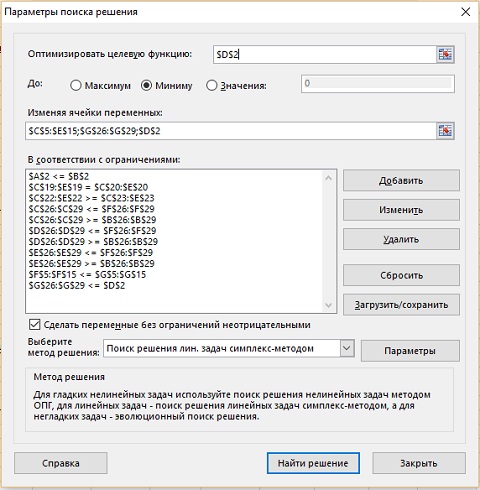
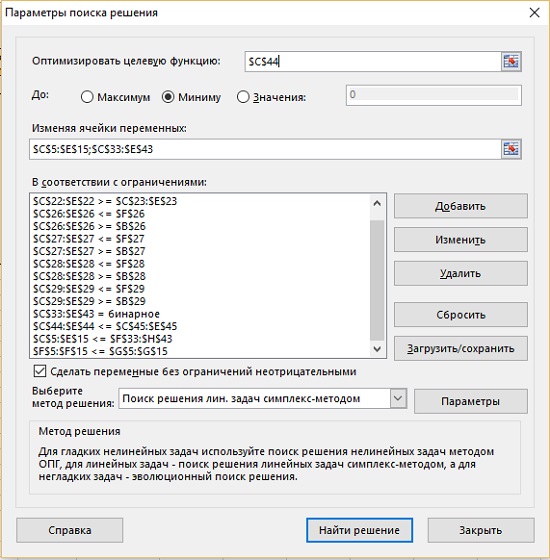
Обратите внимание, что в ячейках В26:29 и F26:F29 теперь не константы, а формулы. Ваша новая цель – минимизация процента снижения качества в ячейках G26:G29. Точнее, вы бы хотели минимизировать максимальное из значений в ячейках G26:G29. Однако, если в ячейку D2 поместить формулу =МАКС(G26:G29), модель не будет работать. Напоминаю, функция МАКС не является линейной. Здесь доступна маленькая хитрость – можно внести дополнительное условие в модель: $G$26:$G$29<=$D$2 (рис. 14), а ячейку D2 оставить пустой. Т.е., ячейка D2 будет оптимизироваться не благодаря наличию в ней формулы, а последовательными циклами, запускаемыми этим дополнительным условием.

Рис. 14. Параметры Поиска решения в модели с пониженным качеством

Нажмите Найти решение. Симплексный алгоритм будет пытаться приблизить D2 к 0 как целевую функцию модели, в то время как ограничения по вкусу и цвету будут пытаться увеличить ее насколько возможно, чтобы получить пригодную для работы смесь. Где же остановится значение D2? Самое меньшее из возможных значений — максимальный процент из четырех сниженных в диапазоне G26:G29. Мы видим (рис. 15, ячейки С26:Е29), что снижение расходов на 5% потребовало выйти за ограничения качества по всем четырем параметрам.

Рис. 15. Решение оптимизационной задачи с сокращением издержек на 5%

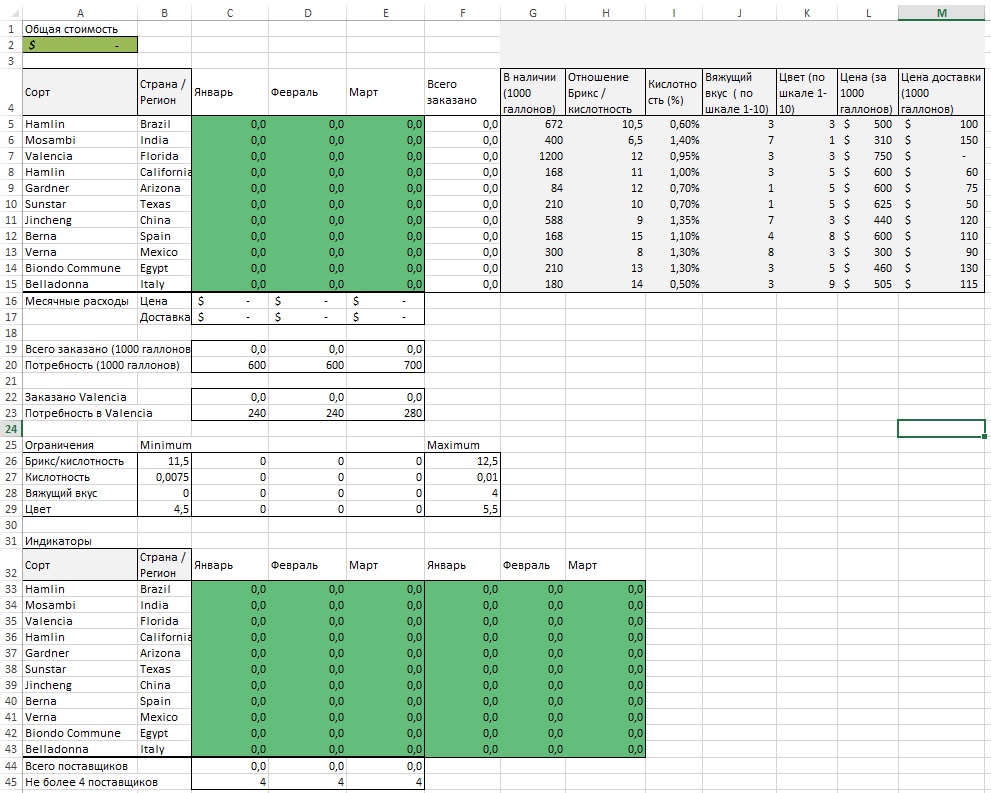
Вы представили данные шефу, который увидел, что сокращение расходов на 5% не стоит снижения качества сока, поэтому он согласовал ваш первый вариант. Но, когда вы принесли его в отдел снабжения, сотрудники возмутились. Как можно было так раздробить поставки!? Снабженцы настаивают, чтобы вы укрупнили партии: не более 4 поставщиков ежемесячно! И вы садитесь за новую модель. К сожалению, использовать функции ЕСЛИ или СЧЁТ вы не можете, так как хотите остаться в рамках линейной модели. Поэтому вам снова приходится прибегнуть к ухищрениям (рис. 16). Вы добавляете в модель область С33:Е43, которую определяете, как бинарную (значения в ней могут быть только 0 или 1), и оставляете ее пустой. А также область F33:H43, где каждая ячейка равна произведению значения из областей С33:Е43 на G5:G15. В параметры Поиск решения (рис. 17) вы добавляете еще одно условие $С$15:$Е$15 <= $F$33:$H$43 и еще одну область переменных – $C$33:$E$43.

Как в этом случае будет работать оптимизационный алгоритм? Когда он стартует все значения в областях С5:Е15, С33:Е43 и F33:H43 равны нулю. Допустим, что алгоритм пытается в ячейку С7 поместить значение 240. Сработает условие С7 <= F35, которое приведет к увеличению значения в F35, которое, в свою очередь, определяется формулой F35 = C35*$G7. Поскольку G7 – константа, а С35 – бинарная переменная, последней присваивается значение 1. Условие С7 <= F35 выполнено, т.к., 240 <= 1200. Таким образом вы моделируете неудобное условие «если… то»: «если заказ сделан, то бинарная переменная включается».

Рис. 16. Добавление индикаторов в модель

Рис. 17. Установка значений для условия «не более 4 поставщиков»

Нажмите Найти решение. Вы заметите, что решение задачи требует больше времени из-за добавления бинарных переменных. Если по какой-то причине Поиск решения слишком затянул свой поиск, вы всегда можете нажать ESC и увидеть лучшее из найденных решений на данный момент.

В принципе, вы уже довольно продвинутый специалист в области линейного программирования. Но, если вы вошли во вкус, и вам нравится разбираться с моделями всё возрастающей сложности, вот вам еще два зубодробительных примера.

Инженеры сообщили, что на производстве появились новые «снижатели кислотности». Данная технология способна нейтрализовать 20% кислоты в соке, протекающем через прибор. Это не только снижает процент кислоты, но и повышает индекс Брикс/кислотность на 25%. Но для «снижателя» нужна энергия и расходные материалы стоимостью $20 за 1000 галлонов сока. Не весь сок, поступающий от поставщиков, нужно прогонять через этот процесс, однако, если поставка по какому-нибудь заказу прогоняется через ионообменник, то должен быть обработан весь ее объем. Постройте модель с участием ионообменника для снижения стоимости.

Проблема с новым правилом заключается в том, что естественный способ его моделирования — нелинейный, что приведет к использованию медленного алгоритма оптимизации. Но, как и в предыдущем примере, можно ввести бинарную переменную в области С25:Е35, которая бы «включалась» при необходимости понизить кислотность партии (рис. 18). Поскольку, нельзя использовать произведение «индикатор понижения кислотности (бинарный) * объем партии», вы создаете область С37:Е47, которая вам пригодятся для уравнивания объемов, подлежащих снижению кислотности, без прямого участия в формулах самих этих объемов. Итак, области С25:Е35 и С37:Е47 не содержат формул. В области G25:I35 используются формулы =С25:Е35*G5:G15 (это ограничение партии общим доступным объемом сока), а в области К25:М35 =Е5:E15-GG5:15*(1-Е25:E35). Это условие заработает только если партия подлежит снижению кислотности.

Рис. 18. Область индикаторов в модели со «снижателем кислотности»

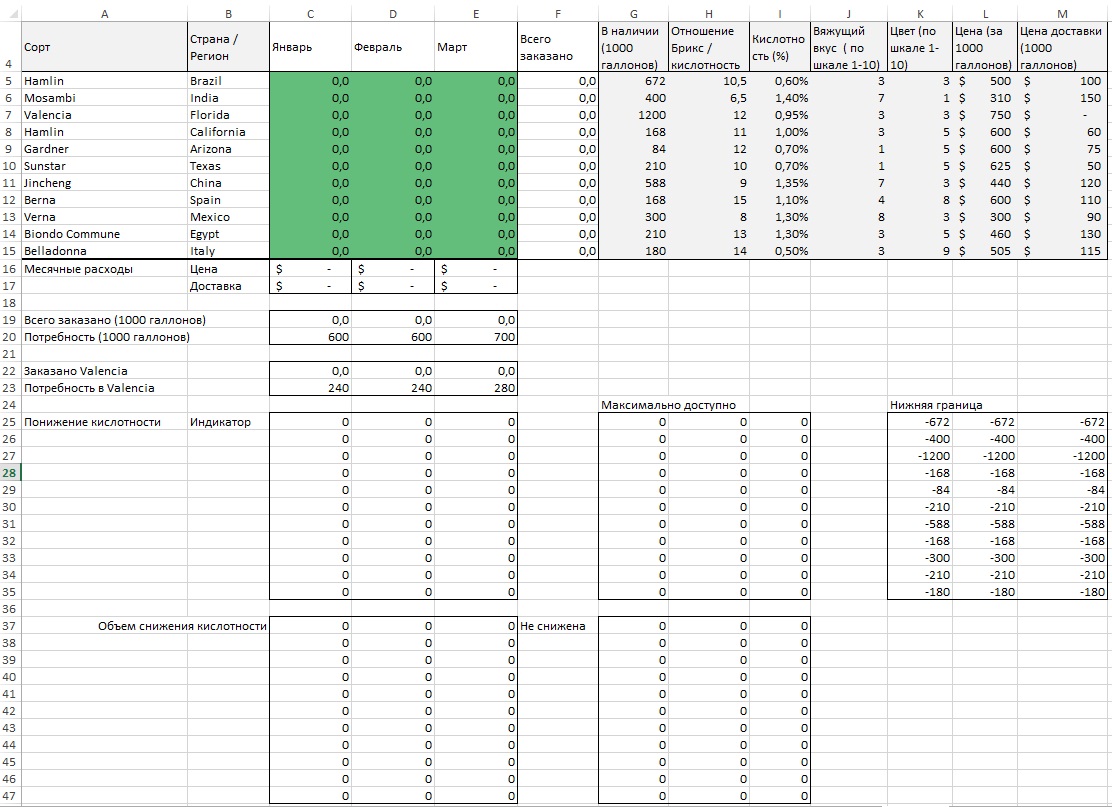
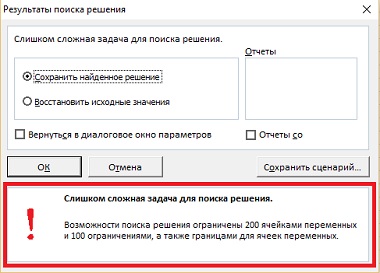
Также в модели со «снижателем кислотности» были изменены формулы в ячейках С16:Е16 (теперь они учитывают затраты на снижение кислотности по формуле «индикатор (бинарный) * объем партии * $20) и в ячейках С50:Е51 (теперь они учитывают повышение коэффициента Брикс/кислотность на 25% и снижение кислотности на 20% для обработанных партий). В параметрах Поиска решения появились новые переменные и дополнительные условие (рис. 19). К сожалению, нажав кнопку Найти решение, вы узнаете, что надстройка Поиск решения не может справиться с задачей (рис. 20). Модель стали слишком сложной.

Рис. 19. Параметры Поиска решения в модели со «снижателем кислотности»

Рис. 20. Поиск решения не справляется с задачей

Вам нужно загрузить и установить OpenSolver (как это сделать см. Джон Форман. Много цифр: Анализ больших данных при помощи Excel, глава 1). OpenSolver «подхватит» установки, введенные только что в окне Поиск решения. Поэтому просто нажмите кнопку Solver. Полученное решение – $1 235 927 более чем на $ 100 000 лучше предыдущего минимума – $1 338 913.

До сих пор мы считали, что поставляемая продукция имеет точно указанные параметры. Резонно предположить, что эти параметры подвержены вариации, характеризуемой среднеквадратичным отклонением (рис. 21; подробнее см. Определение среднего значения, вариации и формы распределения. Описательные статистики). Самое известное и широко используемое распределение случайной величины — это нормальное распределение, иначе называемое «колоколообразной кривой». Скажем, в случае с соком из Египта среднее значение отношения Брикс/кислотность будет 13, а среднеквадратичное отклонение (также называемой стандартным отклонением) — 0,9 (рис. 21). В данном примере 13 — это центр распределения вероятности, 68% заказов будут в пределах ±0,9 от 13, а 95% будут в пределах ±1,8 от 13.

Рис. 21. В параметры соков добавлено стандартное отклонение

Ваша цель — предложить план смешивания стоимостью меньше $1,25 миллиона, который наилучшим образом соответствует ожиданиям по качеству в свете вариабельности поставок.

Мы используем среднее и среднеквадратичное отклонение характеристик, чтобы применить имитационное моделирование по методу Монте-Карло (если вы слышите это название впервые, рекомендую Использование метода Монте-Карло для расчета риска). В этом методе вместо включения параметров распределения (среднего значения и среднеквадратичного отклонения) в модель напрямую, создается большое число сценариев, основанных на этих самых параметрах распределения.

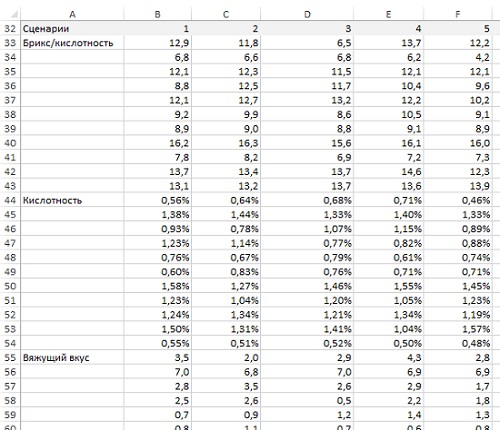
Сценарий — это один из возможных ответов на вопрос: «Если это — распределения, основанные на статистике, на что же будет похож конкретный заказ?» Каждый сценарий включает сорок параметров десяти сортов сока (рис. 22). Чтобы получить один такой параметр, воспользуйтесь функцией НОРМ.ОБР (подробнее о функции см. Нормальное распределение). Например, в ячейке В33 отношение Брикс/кислотность для сорта Hamlin определяется формулой =НОРМ.ОБР(СЛЧИС();H5;N5). Введите аналогичные формулы в область В33:СW76, сгенерировав 100 сценариев. Поиск решения не сможет работать с этими формулами, так как они нелинейны, поэтому скопируйте их в буфер и вставьте, но уже, как значения.

Рис. 22. Фрагмент сгенерированных сценариев характеристик соков

Далее для каждого сценария определяем 4 параметра по каждому месяцу (рис. 23).

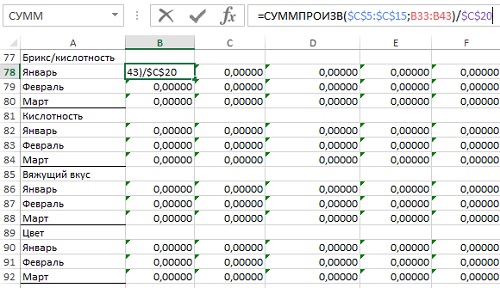
Рис. 23. Расчет характеристик для каждого сценария

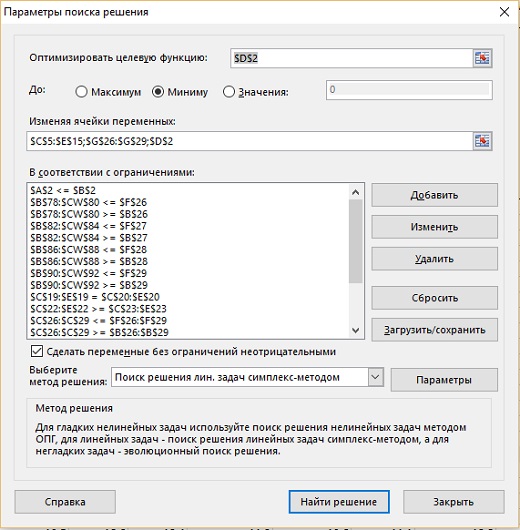
Цель минимизировать значение в ячейке D2. Т.е., найти решение, которое менее всего снижает границы качества для 100 сценариев. Как и в примерах на рис. 13–15, в ячейке D2 нет формулы. Оптимизация выполняется заданием параметров в окне Поиск решения. Все, что нужно — это поместить во все сценарии границы качества, а не просто ожидаемые значения характеристик. Таким образом, в отношение Брикс/кислотность вы добавляете условия B78:CW80 >= B26 и =< F26, затем проделываете то же самое с кислотностью, вяжущей составляющей вкуса и цветом (рис. 24). Нажмите Найти решение. Решение найдется довольно быстро. Если вы генерировали случайные значения сами, а не использовали те, что находятся в файле для загрузки, ваше решение может отличаться. Для моей сотни сценариев наилучшим показателем, который мне удалось получить, является изменение качества на 133%.

Рис. 24. Настройка Поиска решения для модели с вариабельностью характеристик

Если вы хотите расширить свои знания в области линейного программирования, рекомендую книгу The AIMMS optimization modeling book. Не пропустите две главы про трюки и подсказки – они поистине гениальны.

[1] Написано по материалам книги Джона Формана Много цифр: Анализ больших данных при помощи Excel. – М.: Альпина Паблишер, 2016. – С. 129–186. Насчет секретности разработки и Второй мировой – это, похоже, личное мнение автора книги. См. Википедию. – Прим. Багузина.