Мартин Гарднер. Путешествие во времени

Книга Мартина Гарднера Путешествие во времени – сборник эссе для любителей математики. Комбинаторные задачи с картами, танграмы, нетранзитивные парадоксы, магические квадраты, числа Каталана и многие другие. Рассчитана на любителей математики и не только.

Мартин Гарднер. Путешествие во времени. – М.: Мир, 1990. – 336 с.

Скачать краткое содержание в формате Word или pdf

На момент публикации заметки книга доступна только в букинистических магазинах.

Путешествие во времени

Признанный шедевр научной фантастики, небольшой рассказ Герберта Уэллса «Машина времени» – не первое литературное произведение о путешествии во времени. Одна из замечательных особенностей рассказа Уэллса – введение, в котором Путешественник во Времени объясняет теоретические основы своего изобретения. Время – это четвертое измерение. Мгновенный куб не может существовать. Тот куб, который мы видим, есть не что иное, как соответствующее текущему моменту времени сечение некоторого «фиксированного и неизменного» четырехмерного куба, обладающего длиной, шириной, высотой и продолжительностью. «Время ничем не отличается от любого из трех пространственных измерений, – сообщает Путешественник во Времени, – кроме того, что наше сознание движется во времени». Если бы мы могли взглянуть на какого-нибудь человека извне нашего пространства-времени, то увидели бы одновременно прошлое, настоящее и будущее этого человека так же, как в трехмерном пространстве мы единым взглядом охватываем все части волнистой линии.

Читая рассуждения Путешественника во Времени сегодня, можно подумать, что Уэллс был знаком с работой Германа Минковского по обоснованию специальной теории относительности Эйнштейна. Линия, по которой ползает наше сознание, – это наша «мировая линия» – линия, которую мы описываем в четырехмерном пространстве-времени Минковского. Но рассказ Уэллса появился в своем окончательном варианте за десять лет до того, как Эйнштейн опубликовал свою первую работу по теории относительности!

Когда Уэллс писал свой рассказ, он считал теории Путешественника во Времени несусветной наукообразной чепухой, которая понадобилась лишь для того, чтобы придать большее правдоподобие фантастическому замыслу. Но уже через несколько лет физики стали относиться к подобной «чепухе» со всей серьезностью. Понятие абсолютного космического времени с абсолютной одновременностью событий, происходящих в различных точках пространства, было изгнано из физики теорией относительности Эйнштейна.

Все современные физики сходятся во мнении, что если бы астронавт отправился в полет к далекой звезде и обратно на космическом корабле, летящем со скоростью, близкой к скорости света, то теоретически такой астронавт мог бы заглянуть на тысячи лет в будущее Земли. Курт Гёдель построил вращающуюся космологическую модель, в которой в принципе можно отправиться в любую точку как в прошлом, так и в будущем мира, хотя путешествия в прошлое отмечаются как физически невозможные. В 1965 г. Ричард Фейнман был удостоен Нобелевской премии по физике за развитый им пространственно-временной подход в квантовой механике, в рамках которого античастицы рассматривались как частицы, двигающиеся вспять во времени – в прошлое.

Танграмы

Китайская головоломка танграм, известная вот уже несколько тысячелетий, представляет собой квадрат разрезанный на семь частей. Игра заключается в том, что из семи элементов складывают различные фигурки. Таны получаются при разрезании квадрата на два больших, один средний, и два маленьких треугольника, квадрат и параллелограмм (рис. 1). Углы всех танов кратны 45°. Если сторону квадратного тана принять за единицу, то дли стороны любого другого тана выражается одним из четырех чисел: 1, 2,

Рис. 1. Таны

Игра в танграм распадается на три основные категории:

1. Поиск способов построения данного танграма (фигуры) или доказательство невозможности этого.
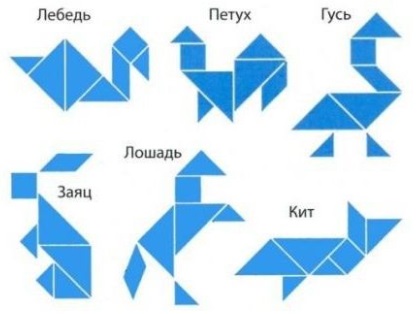
2. Изображение силуэтов животных, людей и других узнаваемых предметов с наибольшей выразительностью и юмором (рис. 2).
3. Решение различных задач комбинаторной геометрии.

Рис. 2. Танграмы животных

Нетранзитивные парадоксы

Широко распространенные игры изобилуют транзитивными правилами (например, в карточных играх, если карта А бьет каргу В, а карта В бьет карту С, то карта А бьет карту С), но встречаются также игры с нетранзитивными правилами. Взять хотя бы детскую игру, в которой но счету «три» показывают либо кулак («камень»), либо два раздвинутых пальца («ножницы»), либо все пальцы на руке («бумага»). Камень ломает ножницы, ножницы режут бумагу, бумага покрывает камень. В этой игре отношение победитель – побежденный нетранзитивно.

Самый старый и наиболее известный из нетранзитивных парадоксов – парадокс с голосованием на выборах, иногда называемый парадоксом Эрроу, в честь Кеннета Дж. Эрроу, сыгравшего решающую роль в формулировании и доказательстве «теоремы о невозможности идеальной избирательной системы», за которую ему других в 1972 г. была присуждена Нобелевская премия по экономике. В своей работе Коллективный выбор и индивидуальные ценности Эрроу выделил пять условий, которые, по всеобщему мнению, существенны для демократии, при которой социальные решения принимаются путем выявления предпочтений отдельных индивидуумов, определяемого по результатам голосования. Эрроу доказал, что эти 5 условий логически противоречивы: невозможно придумать избирательную систему, которая бы в некоторых случаях не нарушала по крайней мере одно из 5 существенных условий. Короче говоря, идеальная демократическая избирательная система в принципе невозможна.

Предположим, что 40% избирателей активно поддерживают кандидата А. Голоса оппозиции разделились: 30% поддерживают кандидата В и 30% – кандидата С. На выборах при таком распределении голосов побеждает кандидат А несмотря на то, что 60% избирателей настроены против него. Один из наиболее известных способов избежать столь нежелательных последствий разбиения голосов – ранжирование избирателями кандидатов по своему усмотрению. К сожалению, и этот способ также может порождать иррациональные решения.

Парадокс нетранзитивности был открыт маркизом Кондорсе и некоторыми другими авторами в конце XVIII в. и известен во Франции под названием эффекта Кондорсе (см. также Парадокс Кондорсе, теорема Эрроу, или Как мы принимаем решения). Льюис Кэрролл, который написал несколько памфлетов о выборах в Оксфордском университете, переоткрыл парадокс нетранзитивности. Многие из первых сторонников пропорционального представительства не подозревали о его ахиллесовой пяте. Эксперты и поныне еще далеки от единого мнения относительно того, от какого из пяти условий Эрроу следовало бы отказаться во имя усовершенствования системы голосования.

Парадокс с голосованием возникает в любой ситуации, в которой решение принимается на основе выбора одной из двух альтернатив, выбираемых из множества трех и более элементов.

Некоторые из парадоксов нетранзитивности лежат в основе малоизвестных пари, рассчитанных на простаков. Например, пусть есть три набора игральных карт (рис. 3). Каждый набор карт тасуется отдельно от другого и выкладывается на стол рубашкой вверх. Вы предлагаете партнеру вытянуть одну карту из любого набора, после чего вытягиваете карту из другого. Выигрывает тот, чья карта окажется старше. Нетрудно видеть, что независимо от того, из какого набора вытянет карту ваш партнер, вы можете из двух оставшихся выбрать «правильный» набор, позволяющий вам выиграть с шансами 5:4. Множество А «бьет» множество В, множество В «бьет» множество С, и множество С «бьет» множество А.

Рис. 3. Нетранзитивное пари, рассчитанное на простака и основанное на использовании магического квадрата: А -> В -> С-> А

В эту игру удобно играть, выбирая по 3 карты из трех различных колод с рубашками разного рисунка. Вы каждый раз тщательно тасуете колоду из 9 отобранных карт и раскладываете их в 3 множества по рисунку рубашек.

Индукция и вероятность

Представьте себе, что мы живем на ковре с необычайно сложным узором. Ковер может быть конечным, а может неограниченно простираться во все стороны. Одни фрагменты узора кажутся случайными, как абстрактная экспрессионистская живопись, другие – строго геометрические. Часть ковра может производить впечатление совершенно иррегулярной, но при рассмотрении ее в более широком обрамлении она оказывается фрагментом узора, обладающего тонкой симметрией.

Узоры реального мира в отличие от узоров воображаемого ковра непрестанно меняются. Тем не менее в общих чертах сравнение с ковром позволяет продемонстрировать некоторые трудности, с которыми сталкиваются при попытке понять эффективность естественных наук те, кто занимается философией науки.

Индукция – это процедура, с помощью которой «ковроведы», изучая отдельные части ковра, пытаются догадаться, как выглядят еще не обследованные его участки. Предположим, что ковер покрыт миллиардами крохотных треугольников. Всякий раз, когда встречается синий треугольник, у него в одном из углов оказывается красное пятнышко. Просмотрев тысячи синих треугольников и убедившись, что они все до единого помечены красным пятнышком, «ковроведы» высказывают гипотезу, согласно которой красное пятнышко есть у всех синих треугольников. Каждый вновь наблюдаемый синий треугольник с красным пятнышком подтверждает замеченную ими закономерность. В отсутствие контрпримеров убеждение «ковроведов» в правильности открытой ими закономерности растет по мере того, как увеличивается число подтверждающих примеров.

Переход от «некоторых» синих треугольников ко «всем» синим треугольникам, разумеется, является нарушением логики. Работая в рамках дедуктивной системы, невозможно быть полностью уверенным в том, как выглядит еще не обследованная часть ковра. С другой стороны, индуктивные умозаключения позволяют получать правильные выводы, и философы по-разному пытаются обосновать индукцию. Джон С. Милль обосновывает индукцию ссылкой на регулярность узоров ковра. Он сознает, что в его рассуждениях содержится круг, так как заключение «ковроведов» о том, что ковер покрыт узором, сделано на основании неполной индукции. Однако Милль не считает этот круг порочным, и многие современные философы придерживаются такого же мнения. Бертран Расселл в своем последнем большом труде пытался заменить расплывчатый тезис Милля об однородности природы чем-то более точным. Он сформулировал 5 постулатов о структуре мира, достаточных, по его мнению, для обоснования индукции.

Рудольф Карнап считает, что все способы обоснования индукции логически корректны, но тривиальны. Более интересная задача, подчеркивает Карнап, состоит в том, чтобы выяснить, возможно ли построить индуктивную логику. Построение индуктивной логики было надеждой и мечтой Карнапа. Он предвидел такое развитие науки в будущем, при котором ученый, работающий в области естественных наук, сможет излагать гипотезу вместе со всеми имеющимися у него экспериментальными или наблюдательными данными на формализованном языке. Затем, используя индуктивную логику, исследователь сможет сопоставить своей гипотезе некоторую вероятность, называемую степенью подтверждения.

Значение этой вероятности не может быть окончательным или заданным раз и навсегда: оно может увеличиваться, уменьшаться или оставаться неизменным по мере накопления новых данных. Карнап считает, что представители естественных наук уже мыслят в терминах индуктивной логики, но в терминах расплывчатых, не формулируя их явно. Однако по мере усовершенствования средств научного исследования значение степени подтверждения становится известным со все большей точностью. Возможно, что в конце концов нам удастся создать своего рода индуктивный анализ, который будет иметь практическое значение, облегчая нескончаемый поиск законов природы.

В своем труде «Логические основания теории вероятностей» Карнап пытался заложить основы индуктивной логики. Насколько ему удалось осуществить свой замысел, вопрос спорный. Некоторые философы (например, Дж. Кемени) разделяют взгляды Карнапа и продолжают развивать избранный им подход. Другие (главным образом Карл Поппер и Томас Кун) рассматривают весь проект как основанный на недоразумении.

Один из почитателей Карнапа К. Гемпель разумно заметил, что прежде чем мы попытаемся приписать подтверждениям какие-нибудь количественные величины, нам необходимо на качественном уровне понять, что именно следует понимать под «подтверждающим наблюдением». Именно здесь, при попытке придать точный смысл этому выражению, мы и сталкиваемся с наиболее серьезными трудностями.

Ситуация усугубляется тем, что существуют случаи, когда подтверждения делают гипотезу менее вероятной. Предположим, что вы выкладываете на стол карты из тщательно перетасованной колоды и переворачиваете их, чтобы подтвердить гипотезу, согласно которой карт зеленой масти не существует. Первые 10 карт оказываются обычными игральными картами, но затем вы неожиданно обнаруживаете карту синей масти. Это – одиннадцатый подтверждающий случай, но теперь ваша уверенность в правильности исходной гипотезы сильно поколеблена.

Подтверждения могут даже привести к опровержению гипотезы. Предположим, что 10 карт всех значений от туза до десятки перетасованы и выложены в ряд вверх рубашкой. Гипотеза состоит в том, что ни одна карта со значением n не находится на n-м месте от левого конца ряда. Вы переворачиваете первые 9 карт. Каждая перевернутая вами карта подтверждает гипотезу. Но если ни одна из 9 перевернутых карт не является десяткой, то, взятые вместе, эти 9 карт опровергают гипотезу.

Парадоксы подтверждения не являются, конечно, парадоксами в смысле противоречий. Перед нами парадоксы в более широком смысле – результаты и ситуации, противоречащие интуиции и делающие бессмысленными первые попытки Дж. Милля и других авторов дать определение того, что надлежит понимать под «подтверждающим примером». Философы, занимающиеся изучением парадоксов, знают о статистической теории отнюдь не понаслышке. Именно потому, что статистическая теория требует проведения столь многих тонких различий, задача формулировки индуктивной логики сопряжена со столь большими трудностями.