Недавно я прочитал книгу Филипа Тетлока и Дэна Гарднера. Думай медленно – предсказывай точно. Она посвящена различным аспектам прогнозирования. Для оценки точности прогнозов используется критерий Брайера. На русском языке статей по теме довольно мало, зато попалась любопытная заметка на английском – Ryan McGeehan. Scoring a risk forecast. Quantitative measurement of wrong-ness. Перед вами ее перевод от первого лица.
Я опишу несколько подходов, используемых для оценки прогнозов. Для простоты использую самый знакомый нам прогноз… – погода на завтра.
Пойдет ли дождь в центре Сан-Франциско завтра 19 июня 2019 г.?
Допустим, ваш прогноз, сделанный 18 июня, был 1% за то, что дождь пойдет. 19-го дождя не было. И мы оцениваем прогноз от 18-го, зная результат.
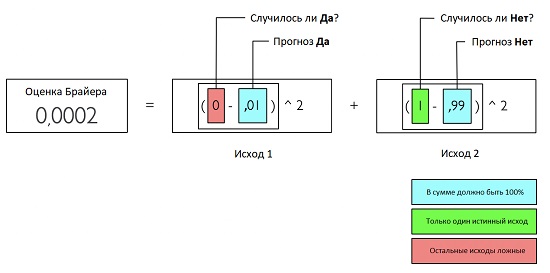
Рис. 1. Оценка Брайера
Скачать заметку в формате Word или pdf
Оценка Брайера
Оценка Брайера позволяет нам измерять и отслеживать погрешность наших прогнозов. Оценка Брайера BS (Brier score) — это аналог среднеквадратической ошибки для прогнозов:
BS оценивается разность между прогностической вероятностью события p и его частотой o, равной 0 или 1 в зависимости от того, было событие или нет. Чем меньше значение BS — тем лучше оценка прогноза.
Итак, в нашем прогнозе 1% за ответ «да» и 99% – «нет». Мы знаем, что «да» было ложным, потому что дождя не было. В оценке Брайера ИСТИНА кодируется как 1 и ЛОЖЬ – как 0. Наличие Да/Нет и ИСТИНА/ЛОЖЬ может привести к путанице, поэтому рассмотрим рис. 1. Уравнение должно содержать столько слагаемых, сколько возможно исходов.
Оценка Брайера и интуиция
Чем ниже оценка, тем лучше. Чем ошибочнее прогноз, тем выше будет оценка Брайера. Мы бы хотели так строить прогнозы, чтобы оценки Брайера от любого источника (человека или искусственного интеллекта) с течением времени уменьшались, демонстрируя улучшение наших методов. Идеальная оценка Брайера = 0. Полная неудача = 2.[1]
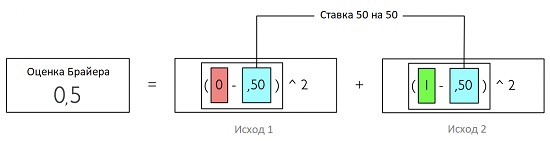
Первый ориентир – оценка лучше, чем случайное угадывание (подобно подбрасыванию монеты). Оценка Брайера для полностью неопределенной стратегии:
Рис. 2. Оценка Брайера в полностью неопределенной ситуации
В прогнозе с двумя исходами мы хотим, чтобы источник прогноза, по крайней мере, работал лучше, чем 0,5 балла в среднем. В противном случае следует положиться на монетку)). Критерий отличается в зависимости от количества исходов. Например, критерий безразличия при четырех исходах = 0,75.
Второй критерий – сравнение результатов с общепринятыми моделями, типа: «Всегда ставьте на хозяев поля», «Всегда ставьте на действующего политика», или «Вчерашняя погода – лучший прогноз на завтра».
Два источника прогноза можно сравнивать друг с другом, если они прогнозируют один и тот же сценарий. Например, вы не можете сравнить прогноз времени забега на 100 метров и марафона. Это два разных события.
Составляющие оценки Брайера
Оценку Брайера можно разложить на три составляющие, характеризующие различные аспекты системы:[2]
где вся выборка вероятностных прогнозов поделена на N+1 категорий (k = 1, 2, …, N+ 1), в каждой из которых содержится nk прогнозов с вероятностью рk; сk – частота наблюдаемого события в данной категории; с — частота наблюдаемого события по всей выборке.
Надежность — среднеквадратическая разность между прогностической вероятностью и наблюдаемой частотой в разных вероятностных категориях. Она означает способность системы прогнозировать точные вероятности. Например, явление наблюдалось в 30% случаев прогнозов с вероятностью 30%. Чем меньше значение этого члена — тем лучше.
Разрешение — это среднеквадратичная разность между наблюдаемой частотой в каждой категории и средней наблюденной частотой явления во всей выборке. Этот член означает способность прогностической системы разделять всю выборку прогнозов на подвыборки с различающимися наблюденными частотами явления.
Неопределенность зависит только от изменчивости наблюдений и характеризует трудность прогностической ситуации. Она не зависит от качества прогностической модели.[3]
Калибровка источника прогноза
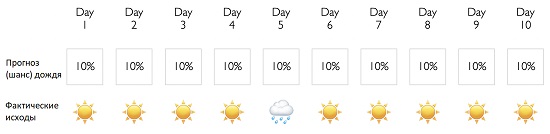
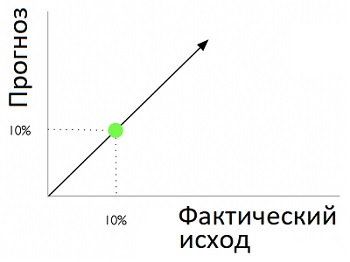
Калибровка показывает, насколько надежен источник прогноза. Калибровка возможна, если вы отслеживаете множество прогнозов и сравниваете их с фактическими результатами. Предположим, вы прогнозируете дождь 10 дней подряд. Каждый день вы даете 10% за то, что пойдет дождь.
Рис. 3. Прогнозные и фактические данные
В этом примере ваша калибровка идеальна. Когда вы уверены на 10%, вы на 10% правы.
На линейном графике идеальная калибровка – это точки на линии под углом 45°, когда прогнозы совпадают с историческими результатами:
Рис. 4. Идеальная калибровка
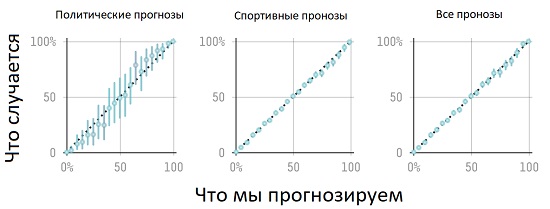
Если вы будете вести статистику, то с течением временем заметите отклонения от линии 1:1. Вот реальная калибровочная диаграмма (опубликованная в блоге 538[4]), в которой суммированы предсказания в течение десятилетия:
Рис. 5. Калибровка экспертов блога 538
Калибровка и интуиция
Для калибровочной диаграммы требуется много прогнозов. Вот почему обучение калибровке так полезно. Это заставляет прогнозиста давать большой объем прогнозов, необходимый для построения графика и наблюдения за отклонением точек от линии 1:1. Человек быстро калибруется, когда следит за таким графиком.
Ситуации прогнозирования, которые я обнаружил на практике, редко дают прогнозы в объеме, достаточном для калибровки. Я не встречал команды, которые использовали бы численный подход к калибровке. Наконец, точные прогнозы с использованием десятичных чисел от нуля до единицы, в принципе, встречаются редко. Большинство подходов к визуализации группируют прогнозы, округляя их или сглаживая.
Дополнение от 05.11.2022. Довольно ясное изложение идей оценки Брайера встретил в книге Дэвида Шпигельхалтер. Искусство статистики. Предлагаю вам соответствующий фрагмент.
Литература
Glenn W. Brier. Verification of Forecasts Expressed in Terms of Probability // Monthly Weather Review, 1950, v.78, # 1, pp. 1–3
А. Ю. Бундель. Оценка качества среднесрочных прогнозов количества осадков по данным ансамблевого интегрирования при помощи спектральной модели гидрометцентра России. Раздел «Оценка Брайера, диаграммы надежности и разрешения»
Дуглас Хаббард. Как измерить всё, что угодно. Оценка стоимости нематериального в бизнесе. – М.: Олимп-Бизнес, 2009. – 320 с.
[1] Если мы предсказали вероятность дождя 100%, а дождя не было, то BS = (0-1)2 + (1-0)2 = 2. – Здесь и далее Прим. Багузина.
[2] Этот раздел – фрагмент статьи А.Ю. Бундель. Оценка качества среднесрочных прогнозов… См. список литературы.
[3] Неопределенность = 0 для с = 0 и с = 1. Неопределенность максимальна для с = 0,5.
[4] 538 – число выборщиков президента США.
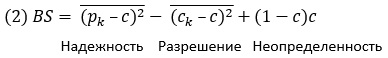
Я создала свои несколько сайтов и занимаюсь анализом продвижения, недавно нашла такой сервис https://ru.megaindex.com/ очень хороший ресурс для сошников, показывает точные результаты, и с его помощью становиться проще анализировать и продвигать сайт.