Книга посвящена одному из наиболее перспективных междисциплинарных подходов – теории самоорганизации, или синергетике. Известный физик и замечательный писатель Чарльз Сноу в середине XX века сетовал на опасную пропасть в науке, которая пролегла между естественно-научной и гуманитарной культурами. Одна из целей синергетики – перебросить мост через эту пропасть. Понятия, идеи, концепции синергетики сейчас все шире используются в экономике и социологии, в политике и бизнесе, в психологии и государственном управлении, оказывая тем самым влияние на наше мировоззрение.
Эту книгу хорошо дополняют: Илья Пригожин. Порядок из хаоса, Джеймс Глейк. Хаос. Создание новой науки, Илья Пригожин. От существующего к возникающему.
Безручко Б.П., Короновский А.А., Трубецков Д.И., Храмов А.Е. Путь в синергетику. Экскурс в десяти лекциях. – М.: Книжный дом «Либроком», 2010. – 304 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить бумажную книгу в Ozon
Лекция первая. Что такое «синергетика»?
Крестный отец синергетики — Герман Хакен в своей книге Синергетика пишет: «Синергетика занимается изучением систем, состоящих из многих подсистем самой различной природы, таких как электроны, атомы, молекулы, клетки, нейроны, механические элементы, фотоны, органы, животные и даже люди». Синергетика рассматривает, «каким образом взаимодействие подсистем приводит к возникновению пространственных, временных или пространственно-временных структур в макроскопических системах». В центре внимания синергетики находится согласованность взаимодействия отдельных частей при образовании структуры как единого целого.
Хакен обратил внимание на то, что кооперативные, взаимосогласованные явления наблюдаются в самых разнообразных системах: это и гидродинамические неустойчивости, и автокаталитические химические реакции, и динамика популяций, образование макромолекул и циклонов в атмосфере. Более того, при возникновении тех или иных структур в различных системах, все эти системы ведут себя схожим образом.
Г. Хакен не сделал никакого открытия: он не обнаружил нового эффекта, не построил никакой теории и даже не выдвинул никакой гипотезы. Он лишь обратил внимание научного сообщества на тот факт, что процессы самоорганизации и образования структур в самых различных системах имеют сходные черты.
Проблема синтеза знаний из различных областей науки, важность обобщенного способа изучения тех или иных научных проблем подчеркивалась еще известным философом Элвиным Тоффлером в его культовой книге Третья волна: «В начале 50-х годов, как раз тогда, когда биологи начали разгадывать генетический код, специалисты в области связи и теоретики из Лаборатории Белл, специалисты- компьютерщики из IBM, английские и французские специалисты в области теоретических научных исследований — все они начали интенсивную и увлекательную работу. Эти работы породили революцию в автоматике и во всех новых видах технологий… Однако вместе с оборудованием пришло и новое мышление. Ключом к революции в автоматике стал системный подход».
Синергетику, которая занимается поисками единого в самых разнообразных системах, можно рассматривать как науку, стремящуюся возвратить единство в разрозненную картину мироздания. Синергетика возникла не на ровном месте — она появилась как объединение на более высоком уровне знаний, идей и методов различных наук, у каждой из которых она заимствовала что-либо. Замысел профессора Хакена заключался в том, чтобы синергетика играла роль метанауки, которая подмечает и изучает общие закономерности различных систем, которые частные науки считали своими. (Заметим, что некоторое время тому назад на роль метанауки претендовала кибернетика. По Г. Хакену, коренное отличие синергетики и кибернетики в том, что «…кибернетика занимается регулированием и управлением, синергетика же – самоорганизацией».)
Отвлекаясь от изначальной природы изучаемой системы, синергетика сводит ее до модели, которая затем изучается методами синергетики (которые, в свою очередь, также привнесены в синергетику из других наук и переосмыслены ею). Оказывается, подчас системы совершенно различной природы с помощью синергетических методов могут быть сведены к одной модели, а тогда все результаты, являющиеся достоянием одной из наук, могут быть (с известной долей осторожности) перенесены в другую науку и сделаны доступными для специалистов этой науки.
Синергетику можно рассматривать как правоприемницу и продолжательницу многих естественно-научных дисциплин, и, пожалуй, в первую очередь (но не только) теории колебаний. С колебаниями – процессами или явлениями, обладающими той или иной степенью повторяемости — каждый из нас в своей жизни встречается постоянно. Колебания бывают самые разнообразные: это и переменный ток в наших домах, и биение нашего сердца, и музыка, звучащая из радиоприемника, и колебания температуры в течение суток, и колебания цен на рынке – все это различные виды колебаний. Разумеется, колебаниями электрического напряжения занимается физика, колебаниямисердца— физиология, колебаниями температуры – метеорология, а колебаниями цен – экономика. Каждая из этих наук объясняет эти колебания по-своему, с учетом сложившегося исследовательского аппарата, традиций и т. п. Но при таком подходе очень легко пройти мимо того очевидного факта, что все это — колебания, что они не просто похожи, но имеют общие закономерности. Именно исследованием общих закономерностей колебательных движений и занимается теория колебаний, отвлекаясь от частных черт изучаемых систем.
Логическим продолжением теории нелинейных колебаний является теория волновых процессов — развитие и распространение идей теории колебаний на распределенные системы. «Что такое распределенная система?» Если для вас оказывается существенной зависимость динамики системы от координат и времени (а не только от времени, как в теории колебаний) — вы изучаете систему с распределенными параметрами.
Из теории волновых процессов берет свое начало теория автоволновых процессов, также передавшая синергетике часть своего аппарата. Теория волновых процессов изучает пассивные системы, т. е. такие системы, в которых распространение волн может начаться только после того, как какой-либо внешний источник внес внешнее возмущение в систему, вывел ее из состояния равновесия. В то же время, существуют так называемые активные среды, в которых запасена энергия, необходимая для возникновения и распространения волн. Степь, покрытая сухой травой, по которой распространяется огонь, является автоволновой средой, само пламя — автоволной, а сам пример входит в число классических примеров как теории автоволновых процессов, так и синергетики.
Еще одна составляющая синергетики — теория динамического хаоса. Относительно простые системы, о «конструкции» которых все известно, могут демонстрировать непредсказуемое поведение. Несмотря на то, что мы знаем все уравнения, которые описывают систему, предсказать состояние системы через некоторый интервал времени мы не можем, а поведение таких систем внешне выглядит как беспорядочное и случайное.
К процессам самоорганизации, образования структур имеют самое непосредственное отношение теория диссипативных структур, основоположницей которой является бельгийская школа, возглавляемая выходцем из России, недавно ушедшим от нас лауреатом Нобелевской премии Ильей Пригожиным. В рамках этой теории самоорганизация и образование структур описываются с точки зрения термодинамического подхода. Нельзя обойти вниманием теорию фазовых переходов, изучающую переходы веществ из одних состояний в другие, теорию бифуркаций и катастроф, объектом исследования которых являются вопросы устойчивости (и неустойчивости). К синергетике можно отнести и изучение клеточных автоматов, с помощью которых моделируются процессы самоорганизации.
Лекция вторая. Моделирование — универсальный инструмент синергетики (или что общего у груза на пружинке с зайцами и лисами)
Понятие модели. Модель — нечто похожее по своим свойствам на оригинал, создаваемое и (или) используемое человеком для реализации своих целей. Выбор той или иной модели определяется целью моделирования.
Познавательная роль моделей. Модели играют роль «фотоаппаратов», «очков», «фильтров», через которые мы рассматриваем мир. Хорошей аналогией активной познавательной роли модели является фонарь, освещающий некоторую область в окружающей тьме.
Какие бывают модели и как они рождаются. По своему происхождению модели можно условно разделить на 4 группы:
- полученные интуитивно — из головы, например, придумыванием красивых уравнений;
- упрощением известного более общего — по принципу «от общего к частному», как деловое платье можно сконструировать из мудреного творения кутюрье, оторвав лишние рюшки и спрямив некоторые линии;
- по принципу от частного к общему — когда берут известные простые модели и объединяют их в ансамбль;
- непосредственно из данных эксперимента, наблюдения.
Модели могут иметь вид предметов, рисунков, формул, мыслимых образов. Мы ограничим рассмотрение лишь моделями, отражающими естественно-научное знание, а они, как правило, формулируются на языке математики. Но существуют и примеры изложения основ синергетики без формул, например, книга Н.Н. Моисеева Расставание с простотой.
Особая роль математических моделей. Математика — наука о количественных отношениях и пространственных формах действительного мира. Сначала она появилась как набор полезных правил и формул для решения практических задач, с которыми люди сталкивались в повседневной жизни. Ее создали цивилизации Древнего Египта и Вавилона около 3 тысячелетий до н. э. Но только приблизительно в VI веке до н.э. древние греки уловили возможность использования математики в качестве инструмента для получения новых знаний (подробнее см. Стивен Строгац. Удовольствие от х).
Математика как логический вывод и средство познания природы появилась в связи с тем, что к VI веку сложилось миропонимание, сводящееся к следующему: природа построена рационально, а явления протекают по точному плану, который в конечном итоге является математическим, человеческий разум всесилен, а поэтому этот план можно раскрыть и познать. В результате подобных наблюдений родились два основополагающих принципа:
- природа устроена на математических принципах;
- числовые соотношения — основа, единая сущность и инструмент познания порядка в природе.
В чем причина исключительной эффективности математики? Над этим задумывалось большое число мыслителей от древности до наших дней. По ответам их можно условно разделить на 2 группы. Первые считают, что математики подбирают аксиомы так, чтобы выводимые из них следствия согласовались с опытом, т. е. математика подстраивается под природу. Другими словами, всеобщие и необходимые законы опыта принадлежат не самой природе, а только разуму, который вкладывает их в природу. Вторые считают, что мир основан на математических принципах.
Что общего находит синергетика в системах различной природы? Например, колебания грузика на пружине, концентрации молекул в химической реакции или численность популяции одного биологического вида в условиях его конкуренции с другим видом при определенных условиях описывает одно и то же уравнение осциллятора:
где t — время, ω0 — коэффициент, имеющий смысл частоты собственных колебаний, а x в первом случае равно отклонению грузика от положения равновесия, во втором — отклонению концентрации молекул от равновесного значения, а в третьем — разности между численностью особей в популяции и ее равновесным (стационарным) значением.
Для всех перечисленных объектов и математической модели общим является повторяющийся через период Т = 2π/ω0 вид зависимости величины x от времени. Более того, можно указать даже форму колебаний, которая описывается функциями синуса или косинуса. Обогатившись математическим моделями, созданными исследователями различных природных и искусственных объектов и проанализированных поколениями математиков и естественников, синергетика рассматривает процессы самоорганизации — образования пространственных неоднородностей (структур) в системах, состоящих из большого числа элементов и их эволюции во времени.
Лекция третья. Математические понятия, без которых не обойтись
Почему в нашем курсе много физики и математики? Синергетика во многом «берет» свое начало из естественных наук. Кроме того, математический аппарат, который с успехом в них применяется, обеспечивает универсальность описания явлений различной природы.
Система — множество элементов, находящихся в отношениях и связях друг с другом, образующих определенную целостность, единство. В недавно вышедшей книге Д.М. Жилина Теория систем приведено такое определение: свойство совокупности, которое не является суммой или средневзвешенным свойством отдельных компонентов совокупности, называется эмерджентным свойством. Совокупность, обладающая эмерджентным свойством, называется системой.
Величины, которые можно измерить (сравнить с однородной величиной, принятой за единицу измерения), называют физическими. Отметим, что отнюдь не все величины можно измерить. Например, «красота» не имеет эталонов, с которыми можно было бы провести количественное сопоставление — измерить. Размеры (численные значения) величин, типичные для данной системы, будем называть характерными масштабами данной системы (рис. 3.1, 3.2).
Рис. 3.1. Характерные пространственные масштабы
Рис. 3.2 Характерные временные масштабы
Время, в течение которого протекают процессы, в физических системах существенно меньше, чем в системах социальных. Некоторые процессы в социальных системах могут иметь характерный временной масштаб, сопоставимый (или даже превышающий) время человеческой жизни. Поэтому для исследования подобных процессов в социальных системах может потребоваться время, равное времени жизни нескольких поколений. На таких временных масштабах очень сильно меняются методика сбора данных, подходы к их обработке и т.п. Все это очень затрудняет исследование социальных систем. Физические системы с этой точки зрения существенно более удобны — характерное время процессов, протекающих в таких системах, существенно меньше времени человеческой жизни, что позволяет исследователям проводить серии экспериментов за небольшой промежуток времени.
Воспроизвести по-новому еще раз ситуацию в социальной системе невозможно: если исследователя интересует какое-либо историческое событие (скажем, революция), то нельзя «вернуть» ситуацию «на исходные позиции» и после этого снова «запустить» процесс. Историк вынужден иметь дело с историческими документами, которые несут на себе отпечаток субъективных оценок; исторические документы могут быть искажены или даже фальсифицированы. Наконец, в физической системе можно спланировать и провести интересующий эксперимент, в то время как поставить эксперимент в социальной системе существенно более проблематично. Именно поэтому физические системы оказались более хорошо изученными как экспериментально с помощью хорошо развитого в физике инструментария и методик, так и теоретически с использованием математического аппарата; по ним накоплен большой объем данных.
Численные значения характеризующих систему величин. Переменные и параметры. Для того чтобы охарактеризовать систему, используется определенный набор величин. Все величины можно разделить на параметры и переменные. Переменные — это величины, которые могут изменяться при рассмотрении процесса, а параметры — это такие величины, которые в рамках рассматриваемой задачи могут считаться постоянными (такое деление в некоторой степени условно).
Переменные величины, в свою очередь, подразделяются на независимые переменные и зависимые (которые также называют функциями). Под независимыми переменными понимают такие переменные величины, которые в рамках данной задачи изменяются независимо от рассматриваемой системы. В качестве независимых переменных, как правило, выделяют время и пространственные координаты. Математиками найдено огромное число различных функций. К наиболее популярным относятся линейная, квадратичная зависимости, гармонические функции у = sin(х), у = cos(x) и экспонента у = ех.
Динамический и статистический подходы к описанию объектов и явлений. Динамический подход к описанию объектов и явлений является отражением детерминизма (учение о закономерности и причинной обусловленности всех явлений природы и общества). В рамках этого подхода предполагается, что если точно задать все начальные условия и указать все факторы, которые влияют на поведение рассматриваемой системы, то можно сколь угодно точно и однозначно предсказать все последующие состояния системы). Статистический (вероятностный) подход не претендует на точное описание и прогноз состояния системы. Центральным моментом здесь является понятие «вероятность», и описание системы сводится к заключению о том, что некоторое событие может произойти (а может и не произойти) с некоторой вероятностью.
Линейность и нелинейность. Функция является линейной, если ее графиком является прямая линия, а в формуле, задающей вид функции, отсутствуют нелинейные слагаемые (рис. 3.3).
Рис. 3.3. Примеры некоторых линейных и нелинейных функций
На одинаковые приращения независимой переменной линейная функция беспристрастно (т. е. независимо от значения независимой переменной) откликается одинаковыми приращениями. Это означает, что линейная зависимость не обладает избирательностью. Она не может описывать ни резонансных всплесков, ни насыщения, ни колебаний — ничего, кроме равномерного неуклонного роста или столь же равномерного и столь же неуклонного убывания.
Фракталы. Наряду с привычными геометрическими объектами – «прямая», «линия», «плоскость», «поверхность» – существует понятие «фрактал», с которым связано понятие фрактальной размерности. Под фракталами понимают множества, демонстрирующие на разных масштабах разрешения своей геометрической структуры свойства подобия в строгом или приближенном смысле, а также объекты в природе, обладающие этим свойством, хотя бы приближенно, в достаточно широком интервале масштабов. Понятие «фрактал» широко вошло в обиход благодаря математику Бенуа Мандельброту (подробнее см. Бенуа Мандельброт. (Не)послушные рынки: фрактальная революция в финансах). Ему принадлежит следующее определение: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому».
Пример фрактала — снежинка Коха (рис. 5). Ее построение начинается с равностороннего треугольника, затем на каждой стороне средняя треть заменяется ломаной линией, состоящей из двух отрезков такой же длины. Эта процедура повторяется до бесконечности, в результате чего получается область с фрактальной границей.
Рис. 3.4. Построение снежинки Коха
Еще один фрактальный объект — салфетка Серпинского. В его основе лежит равносторонний треугольник, который можно разбить на четыре одинаковых равносторонних треугольника и удалить центральный (рис. 3.5). То же самое проделывается с каждым оставшимся треугольником до бесконечности.
Рис. 3.5. Построение салфетки Серпинского
Фрактальные объекты часто встречаются и в природе (рис. 3.6).
Рис. 3.6. Лист папоротника, цветная капуста, структура ручья
Почему фрактальные объекты столь широко распространены в природе? Одной из причин является характерная особенность строения фракталов: фрактальный объект на плоскости занимает ограниченную площадь, в то время как его длина стремится к бесконечности. Аналогично, «объемные» фракталы характеризуются относительно малым объемом, но большой площадью поверхности. А это очень удобно для Природы! Действительно, какую функцию, например, выполняют легкие человека? Они должны обеспечивать эффективное взаимодействие между кровью и воздухом. Очевидно, что чем больше поверхность, на которой происходит такое взаимодействие, тем лучше. Аналогично, фрактальным образом устроена кровеносная система живых организмов (рис. 3.7), корневая система растений (здесь задача все та же — при малом объеме обеспечить большую поверхность соприкосновения) и пр.
Рис. 3.7. Фрактальная жизнь: строение кровеносной системы; нижний рисунок является увеличенным фрагментом верхнего
Лекция четвертая. Динамическая система
Что такое «динамическая система»? Динамическая система является моделью какой-либо реальной физической, химической, биологической, социальной или любой другой системы. Для того чтобы определить динамическую систему, необходимо:
- Задать набор величин (переменных), однозначно характеризующих состояние системы.
- Задать правило (оператор эволюции), по которому, зная текущее состояние системы, можно определить (предсказать) ее состояние в следующий момент времени.
Динамические системы являются видом математических моделей, отражающих мировоззренческий принцип детерминизма.
С понятием «динамическая система» тесно связаны понятия «фазовое пространство». Например, предположим, что нужно рассмотреть эволюцию системы домашняя кошка. В качестве переменных величин, характеризующих эту систему, выберем рост кошки и вес кошки. Сначала, будучи котенком, кошка имеет небольшой рост и вес (см. точку 0 на рис. 4.1). Затем, по мере взросления, рост и вес кошки увеличиваются (точки 1–4), и кошка достигает «расцвета сил» (точка 5). После этого рост кошки уже не изменяется, а вес уменьшается (точки 6–9).
Рис. 4.1. Зависимость роста и веса кошки от времени
Этот же самый процесс можно изобразить по-другому: отложить по одной оси рост, а по другой — вес кошки (рис. 4.2). Тогда каждая точка на плоскости (рост; вес) будет однозначно характеризовать состояние системы «домашняя кошка». Верно и обратное — каждое состояние рассматриваемой системы можно представить точкой на этой плоскости. Таким образом, имеет место взаимно однозначное соответствие между состоянием, в котором находится кошка, и точкой на плоскости (рост; вес). Такая плоскость, по осям координат которой откладываются переменные величины, характеризующие состояние системы, называется фазовой плоскостью. Если бы переменных величин, характеризующих состояние системы, было бы не две, а больше (скажем, три), то речь шла бы не о фазовом пространстве.
Рис. 4.2. Фазовая плоскость с фазовой траекторией для динамической системы домашняя кошка
Сначала, когда кошка является маленьким котенком, ее рост и вес невелики (точка 0 на рис. 4.1). На фазовой плоскости изображающая точка находится в этот момент времени около начала координат (точка 0 на рис. 4.2). Затем, когда кошка взрослеет, изображающая точка двигается по фазовой плоскости в сторону больших значений роста и веса (точки 2–5, рис. 4.2). Когда кошка начинает стареть, ее рост практически не изменяется, а вот вес уменьшается, поэтому изображающая точка двигается по фазовой плоскости так, что ее координата «рост» остается постоянной, а координата «вес» неуклонно уменьшается (точки 5–9, рис. 4.2). Линия, по которой двигается изображающая точка, называется фазовой траекторией. Таким образом, фазовая траектория характеризует эволюцию системы с течением времени, каждая точка фазовой траектории соответствует определенному состоянию системы в тот или иной момент времени. И если на графиках зависимости переменных, характеризующих состояние системы от времени, течение времени проявляется в том, что нужно рассматривать все большее значение по оси абсцисс (по горизонтальной оси), то на фазовой плоскости ход времени проявляется в движении изображающей точки по фазовой плоскости.
Среди динамических систем можно выделить два больших класса: динамические системы с дискретным и непрерывным временем.
Динамические системы с дискретным временем. Иногда достаточно знать состояние системы не в каждый момент времени, а только в некоторые определенные моменты времени. Например, вы положили в банк 10 тыс. руб. под 10% в месяц. Тогда, через месяц у вас на счету будет 11 тыс. руб., через 2 месяца — 12 100 руб. и т.д. В течение месяца сумма не изменяется. Следовательно, нет необходимости указывать сумму в каждый момент времени. Достаточно знать сумму на начало каждого месяца. Зависимость суммы вашего вклада S от времени t будет иметь вид, приведенный на рис. 4.3. Иными словами, для того, чтобы описать систему «счет в банке», необходимо указать сумму вклада лишь в определенные моменты времени. В этом случае время t не изменяется непрерывно, а принимает конечный набор значений t = 1 месяц, 2 месяца и т.д. Говорят, что время t принимает дискретный набор значений, оно (время) является дискретным. Системы, для описания которых используется переменная времени, принимающая дискретный набор значений, называются системами с дискретным временем.
Рис. 4.3. Зависимость суммы вклада от времени
Можно записать, что
где хn+1 — переменная величина, характеризующая состояние системы в n-й момент дискретного времени, f(x) — некоторая функция (оператор эволюции), которая позволяет по известному состоянию системы в n-й момент дискретного времени однозначно определить (предсказать) ее состояние в следующий (n + 1)-й момент дискретного времени.
Существует еще один способ графического представления того, как ведет себя переменная S. Для этого нужно отложить не зависимость суммы S от времени t, а зависимость суммы вклада в (n + 1)-й момент дискретного времени Sn+1 от суммы вклада в предыдущий n-й момент дискретного времени Sn. Фактически, нужно построить график функции f(S). Поведение системы с дискретным временем приведено на рис. 4.4.
Рис. 4.4. Диаграмма Ламерея для задачи о банковском счете: 1 – Sn+1 = f(Sn); 2 – Sn+1 = Sn (прямая, идущая под углом 45%)
Динамические системы с непрерывным временем. Такие динамические системы часто называют потоковыми системами. В этом случае значение переменной времени изменяется непрерывно, и в любой момент времени можно определить значения переменных величин, характеризующих динамическую систему. Для динамических систем с непрерывным временем оператором эволюции служат обыкновенные дифференциальные уравнения:
х — единственная переменная, которая характеризует рассматриваемую динамическую систему. Эта переменная изменяется с течением времени — в таких случаях говорят, что она зависит от времени t (t — независимая переменная), или что она является функцией времени x = x(t). Как быстро изменяется с течением времени переменная x, характеризуется производной:
Если переменная x увеличивается с течением времени, то значение производной x'(t) является положительным, если x уменьшается с течением времени — производная оказывается отрицательной. Чем быстрее изменяется переменная x с течением времени, тем больше по модулю оказывается значение производной.
На рис. 4.5 представлена зависимость величины x, характеризующей состояние системы, от времени t.
Рис. 4.5. Зависимость переменной x от времени имеет вид: x(t) = (t – 2)2/2 + 1. В различные моменты времениtпроизводная принимает различные значения
Дифференциальное уравнение «устроено» следующим образом: в него входят производные, а также переменные величины. Дифференциальное уравнение показывает, как связаны производные и их величины между собой. Простейшим дифференциальным уравнением является уравнение вида:
Если величина k в этом уравнении (являющаяся параметром системы) положительная, то, чем больше величина x, тем больше производная x'(t), и тем быстрее растет сама величина x(t) с течением времени t. В этом случае переменная x(t) неограниченно возрастает. В том случае, если параметр k отрицателен, величина x будет с течением времени уменьшаться и стремиться к нулю. И лишь в том случае, когда параметр kточно равен нулю, величина x не будет меняться с течением времени. Но малые «шевеления» параметра k приведут систему либо к состоянию неограниченного роста, либо к асимптотическому уменьшению величины x до нуля. Говорят, что ситуация k= 0 является вырожденной. Решение уравнения (4.4) в аналитической форме записи имеет вид x(t) = x0ekx, а его график приведен на рис. 4.6.
Рис. 4.6. Решение уравнения (4.4): 1– неограниченный (экспоненциальный) рост величины x при k > 0; 2 – экспоненциальное затухание (k< 0); 3 – постоянное значение величиныx (k = 0).
Любопытно, что к уравнению вида (4.4) приводят размышления, которые в 1798 году Томас Мальтус применил при описании роста численности народонаселения Земли. В этом случае x рассматривается как число людей, проживающих на Земле, t — время. Мальтус, использовавший уравнение (4.4) применительно к человеческому сообществу, пришел к выводу, что рост численности человеческого общества опережает темпы роста продовольственных запасов, а, следовательно, неизбежна жестокая конкуренция среди людей «за место под солнцем».
В реальной жизни никакая биологическая популяция не может расти неограниченно — экологическая система стабилизируется посредством ограничения природных ресурсов. Именно поэтому в 1838 году Ферхюльст предложил логистическую модель, которая более достоверно, нежели модель Мальтуса (4.4), описывает динамику популяций. Ферхюльст предположил, что ресурсы, необходимые для жизнедеятельности особей популяции, ограничены, и на рассматриваемом ареале могут одновременно проживать не более М особей. Величина М не зависит от времени и является параметром модели, который называется емкостью среды. Тогда коэффициент, отвечающий за скорость изменения численности популяции, должен зависеть от числа особей популяции x, причем при малых значениях x, когда численность популяции много меньше емкости среды (x≪М), ограниченность природных ресурсов не будет заметна, а значит и уравнение, и его решение должны очень мало отличаться от уравнения (4.4) и его решения. Следовательно, при малых x скорость изменения популяции должна быть близка к kх. С другой стороны, с увеличением численности популяции начинает сказываться ограниченность природных ресурсов, и коэффициент, ответственный за темп прироста популяции, должен уменьшаться, достигая нулевого значения при x=М. Уравнение, учитывающее все вышеизложенное, называется уравнением Ферхюльста (часто это уравнение также называют логистическим) и имеет вид:
Изначально, когда численность популяции мала (x≪М), уравнение (4.5) совпадает с (4.4), и численность популяции нарастает экспоненциально. Но по мере увеличения xначинает сказываться ограниченность природных ресурсов, скорость роста численности популяции уменьшается, и при t g ∞ численность популяции x стремится к М, а скорость роста популяции — к нулю (рис. 4.7).
Рис. 4.7. Решение логистического уравнения (уравнения Ферхюльста): 1 – экспоненциальное приближение при x≪М; 2 – решение логистического уравнения
Следует отметить, что уравнение Ферхюльста достаточно хорошо описывает динамику простых биологических систем типа колонии бактерий. Не менее хорошо ложатся на логистические кривые и данные, описывающие динамику развития сетей транспорта и коммуникаций в США (рис. 4.8).
Рис. 4.8. Динамика развития инфраструктуры США
Для линейных систем выполняется принцип суперпозиции. Это означает, что если, скажем, дифференциальное уравнение (4.7) является линейным (т.е. функция f(x), стоящая в его правой части, линейна), и х1(t), х2(t) – решения этого уравнения, то выражение a1х1(t) + a2х2(t), где a1, a2 — константы — также является решением этого уравнения. Поэтому, зная некоторый конечный набор решений, можно из них получить все множество возможных решений дифференциального уравнения (или системы дифференциальных уравнений), описывающего линейную систему. Для нелинейных систем принцип суперпозиции не выполняется.
Распределенные системы. До сих пор рассматриваемые динамические системы характеризовались переменной величиной х, зависящей только от времени (их называют сосредоточенными системами). Часто системы характеризуются не только временной, но и пространственной динамикой. В этом случае поведение систем будет характеризоваться некоторой величиной (или даже набором величин), зависящей не только от времени t, но и от пространственных координат. В простейшем случае поведение системы может зависеть только от одной пространственной координаты: х = x(t, z). Подобные системы, для описания которых необходима информация не только об их изменении с течением времени, но и о пространственной динамике, называются распределенными (иногда говорят о системах с распределенными параметрами).
Одна и та же система может (в зависимости от того, какие ставятся задачи) рассматриваться и как распределенная, и как сосредоточенная. В том случае, например, когда изучается вопрос о том, как изменяется численность населения Земли с течением времени, и исследователей не интересует, как это население расселено по государствам и материкам, система «население Земли» является системой со сосредоточенными параметрами. Если же основной интерес представляет плотность расселения людей и то, как она изменялась с течением времени, то система «население Земли» будет рассматриваться как система с распределенными параметрами.
Распределенные системы описываются дифференциальными уравнениями в частных производных. Частная производная обозначается ∂x/∂t, (символ ∂ говорит о том, что производная частная) и обозначает, что вычисляется производная от функции нескольких переменных x(t,z) по переменной t. Эта частная производная характеризует, как быстро изменяется величина х с течением времени в точке с координатой z. Если бы вычислялась производная по переменной z, то она характеризовала бы, как быстро меняется величина х вдоль пространственной координаты z в фиксированный момент времени t, и обозначалась бы ∂x/∂z.
Уравнения в частных производных часто используются синергетикой. В качестве примера приведем нелинейное уравнение диффузии, являющееся эталонным:
Иногда это уравнение называют уравнением Колмогорова—Петровского—Пискунова, которые впервые рассмотрели это уравнение применительно к задаче о динамике биологической популяции, распределенной по пространственному ареалу проживания. На рис. 4.9 приведен вид решения уравнения (4.6) для различных моментов времени. Видно, что для этого уравнения характерно решение в виде бегущей волны, распространяющейся по пространству вдоль оси z.
Рис. 4.9. Трансформация профиля бегущей волны плотности популяции с течением времени для нелинейного уравнения диффузии (4.6)
Лекция пятая. Колебания
Одной из задач синергетики является поиск общих закономерностей в процессах, протекающих в системах самой различной природы. Колебания — одно из таких самых общих явлений; их изучением и занимается теория колебаний. Теория колебаний устанавливает общие свойства на основе анализа некоторых эталонных математических моделей (например, гармонический, линейный, нелинейный осцилляторы), которые она конструирует и которые с завидным постоянством «обнаруживаются» везде, где есть колебания.
По определению, колебания — это изменение с течением времени какой-либо величины, обладающее той или иной степенью повторяемости.
Рассмотрим механический маятник (рис. 5.1а). Имеется подвес длиной l, закрепленный на неподвижном креплении. На подвесе закреплен груз массой m. Маятник находится в гравитационном поле Земли, ускорение свободного падения которого g. Если вывести маятник из состояния равновесия и отпустить, то он начнет совершать колебательные движения. Если трения (или, как говорят физики, диссипации) нет, то такое колебательное движение будет продолжаться вечно, причем система будет возвращаться в исходное состояние через один и тот же интервал времени. Этот интервал времени называется периодом колебаний. Он характеризует, как долго длится один цикл колебательного процесса. Здесь мы имеем дело с периодическими колебательными процессами, т.е. колебаниями, которые абсолютно точно повторяются во времени (рис. 5.1,). Максимальное отклонение положения системы от состояния равновесия называется амплитудой колебаний А. Величина амплитуды колебаний определяется величиной первоначального толчка или отклонения маятника от состояния равновесия. Если учесть наличие потерь энергии, которые всегда присутствует в реальных системах, то картина колебаний качественно изменится (рис. 5.1в): размах колебаний уменьшается с течением времени, и, в конце концов, колебания полностью прекратятся (или, как говорят физики, затухнут). Подобные колебания так и называются: затухающие колебания.
Рис. 5.1. Математический маятник: а) модель; б) вид периодических колебаний при отсутствии затуханий; в) вид затухающих колебаний
Отличительными свойствами линейных динамических систем является выполнение принципа суперпозиции и изохронность линейных колебаний. Что подразумевается под выполнением принципа суперпозиции? Давайте рассмотрим некоторую динамическую систему, о которой мы ничего не знаем, как некоторый «черный ящик» (рис. 5.2). Будем воздействовать на наш черный ящик сигналом f(t, Т1, Т2, …, Тn), в котором присутствует набор элементарных гармонических функций с различными временными масштабами Тi.
Рис. 5.2. К пояснению принципа суперпозиции колебаний: а) линейная; б) нелинейная системы
Понаблюдаем за откликом g(t) нашего черного ящика на такой сигнал. Если в отклике будут содержаться только те же самые временные масштабы, пусть даже и с другими амплитудами, то мы имеем дело с линейной системой (рис. 5.2а). А принцип суперпозиции означает, что между разномасштабными колебательными процессами отсутствует какое-либо взаимодействие. Поэтому для линейной задачи любое решение всегда можно сконструировать из определенного набора некоторых частных решений.
Если мы имеем дело с нелинейной системой, то отклик системы будет значительно более сложным. Он будет содержать сложную совокупность частот, являющихся суммами гармоник и субгармоник частот исходного сигнала. Более того, может оказаться, что выходной сигнал будет содержать непрерывный спектр частот.
Второе важное свойство линейных колебаний — это изохронность, под которой понимается постоянство периода колебаний. Свойство изохронности означает, что независимо от того, какую энергию сообщили линейной колебательной системе, период колебаний определяется только параметрами системы и не зависит от величины этой начальной энергии. Для нелинейных систем принцип изохронности не выполняется: колебания с различной амплитудой А будут происходить принципиально с разным периодом Т, т.е. период становится функцией амплитуды колебаний: Т = Т(А). Говорят, что нелинейные колебания неизохронны.
Явление резонанса. Рассмотрим линейную колебательную систему без трения, т.е. систему, описываемую моделью гармонического осциллятора. Пусть период колебаний нашей колебательной системы Т0. Будем воздействовать на нее внешним «негармоническим» периодическим сигналом f(t) с периодом Т (или круговой частотой ω = 2π/Т). Такую функцию можно записать в виде:
Здесь величина Fi имеет смысл амплитуды гармонической составляющей с частотой ωi = iω (i — целое). Это так называемое разложение периодической функции в ряд Фурье. Оказывается, что если одна из частот ωi сумме (5.1) близка к частоте собственных колебаний гармонического осциллятора (т.е. выполняется строгое условие ωi = ω0, либо более слабое условие ωigω0), то гармонический осциллятор начинает демонстрировать непериодические движения. Амплитуда колебаний растет со временем; темп этого нарастания зависит от величины амплитуды внешнего воздействия Fi (рис. 5.3). Это явление носит название резонанса. Физический энциклопедический словарь определяет явление резонанса как «резкое возрастание амплитуды установившихся вынужденных колебаний, которое имеет место при приближении частоты внешнего гармонического воздействия к частоте одного из собственных колебаний данной колебательной системы».
Рис. 5.3. Рост амплитуды колебаний гармонического осциллятора при явлении резонанса
Видно, что мы столкнулись с типичным проявлением неустойчивости, когда слабому внешнему возмущению соответствует на больших временах катастрофический размах амплитуды колебаний. Наша модель гармонического осциллятора «вышла из подчинения» и стала неверной. Неустойчивость — результат идеализации исходной системы. «Всякая идеализация, — по выражению Л. И. Мандельштама, — обладает способностью мстить за себя, обладает способностью создавать внутренние затруднения». Действительно, идеальная модель должна быть исправлена либо за счет диссипативных процессов (при этом она может остаться линейной), либо в ней должны быть учтены нелинейные эффекты.
При учете потерь в установившемся режиме в линейной колебательной системе имеют место незатухающие синусоидальные колебания с периодом внешней силы. Зависимость амплитуды таких колебаний от частоты вынуждающей гармонической силы носит название резонансной кривой (рис. 5.4). Из рисунка видно, что амплитуда колебаний максимальна, когда частота вынуждающей силы близка к частоте собственных колебаний, но не точно равна ей. Чем меньше потери, тем «острее» резонансная кривая. При отсутствии потерь амплитуда линейных колебаний уходит в бесконечность, и мы получаем «нефизический» результат.
Рис. 5.4. Резонансные кривые линейного осциллятора: кривые 1-3 соответствуют случаям со все уменьшающимися потерями; кривая 4 — потери равны нулю
Другой способ «подчинить модель» — учесть нелинейность. Действительно, при резонансе имеет место рост размаха колебаний, а линейные колебания, как мы уже обсуждали выше, — это колебания с малой амплитудой. Поэтому в какой-то момент при резонансе линейные модели должны «перестать работать», и необходим учет нелинейных эффектов, например, уже обсуждаемой выше зависимости собственной частоты колебаний от их амплитуды — неизохронности колебаний.
Нелинейные колебания. Наш мир так или иначе нелинеен, это мир нелинейных систем. Свойства нелинейных систем зависят от их состояния. Математическое поведение нелинейных систем описывается нелинейными уравнениями, содержащими изучаемые величины в степенях больше единицы или коэффициенты, зависящие от этих величин. Э.Петерс в своей книге Хаос и порядок на рынках капитала пишет: «Когда я был аспирантом-математиком, то мы изучали только линейные уравнения. Мы изучали их потому, что они имеют единственное решение. Они имели приложения в физике и технике. Они были аккуратны. Нелинейные дифференциальные уравнения выглядели бесполезными ввиду того, что имели множество решений, которые казались не относящимися к реальности. Они были сложны, беспорядочны и выглядели исключениями. Теперь мы знаем, что… эти уравнения полезны именно по тем причинам, по которым их стремились избегать раньше. Жизнь неупорядоченна. Она изобилует возможностями. Поэтому необходимы модели со множеством возможных решений» (см. также Эдгар Петерс. Фрактальный анализ финансовых рынков).
По И. В. Пригожину — одному из создателей науки о сложном — в дифференциальном уравнении, описывающем эволюцию нелинейной системы, меняется некоторый управляющий параметр. При определенном значении параметра возникают, по крайней мере, два пути эволюции системы. Говорят, что имеет место бифуркация (см. Илья Пригожин. Порядок из хаоса).
Ю.А. Данилов: «В физике нелинейность — это учет различного рода взаимодействий, обратных влияний и тонких эффектов, ускользающих от более грубых сетей линейной теории. В химии нелинейность отражает обратные связи в сокровеннейших механизмах реакций. В биологии нелинейность исполнена высокого эволюционного смысла: только сильная нелинейность позволяет биологическим системам «…услышать шорох подползающей змеи и не ослепнуть при вспышке близкой молнии. Те биологические системы, которые не смогли охватить диапазон жизненно значимых воздействий среды, попросту вымерли, не выдержав борьбы за существование. На их могилах можно было бы написать: „Они были слишком линейными для этого мира»».
В социальных и экономических системах нелинейность тоже проявляется в виде взаимодействия. Однако нелинейность таких систем очень сильно определяется психологией как отдельного индивидуума, так и социальных групп. Здесь интересно проследить крушение линейной парадигмы для описания процессов на финансовых рынках. До недавнего времени все подобные модели были линейны и базировались на двух основных предположениях.
- Модель рационального инвестора. Она предполагает, что инвесторы линейно реагируют на информацию, т. е. используют ее сразу после получения, а не ожидают ее накопления в ряде последующих событий. Это означает, что прошлая информация всегда учтена, найдя свое отражение в стоимости ценных бумаг на данный момент. С точки зрения математики это означает, что рациональный инвестор желает среднестатистической эффективности. Он оценивает потенциальную прибыль методом вероятностного взвешивания, который дает ожидаемую прибыль. Риск измеряется как стандартное отклонение прибылей. Инвесторы предпочитают стратегию, которые дают наивысшую прибыль при заданном уровне риска. Они не любят рисковать.
- Модель эффективного рынка. Цены отражают всю имеющуюся на данный момент информацию. Изменения в цене не соотносятся между собой. Стоимость определяется консенсусом большого количества участников рынка.
Оба этих предположения означают, что модели финансового рынка строятся на основе линейного подхода к обществу. Если следовать ему, то люди, получая информацию, немедленно ее используют. Можно показать, что в рамках линейной теории прибыли нормально распределены и приблизительно независимы. Однако доводы, лежащие в основе линейной модели рынка капитала, несостоятельны. Линейная модель должна быть заменена нелинейной. Где же в этой модели возникают нелинейные эффекты? Они в первую очередь лежат в психологии человека.
- Люди не реагируют на информацию сразу после ее получения. Они откликаются на нее некоторое время спустя, если она подтверждает изменение в недавнем тренде. Эта нелинейная реакция — противоположность линейной реакции гипотетического рационального инвестора.
- В психологии нет подтверждений тому, что люди являются более рациональными в совокупности, чем поодиночке. Доказательством этому служат социальные перевороты, преходящие увлечения и моды.
- Люди не всегда питают отвращение к риску и часто стремятся рисковать. Особенно если осознают, что они обречены на потери, если не будут этого делать (люди более склонны к риску ради избежания потерь, чем ради получения выгод; см. Даниэль Канеман. Думай медленно… решай быстро).
- Люди полны предубеждений в своих субъективных оценках. Так они уверены в своих предсказаниях всегда существенно больше, чем это оправдано имеющейся информацией.
Представление колебаний в фазовом пространстве. Эволюция динамических систем наблюдается в пространстве состояний системы или, как его еще называют, фазовом пространстве. Можно сказать, что фазовое пространство — это некоторое абстрактное пространство, по осям которого отложены переменные нашей системы. Поэтому, если нам известны все переменные системы, то графически обозреть динамику системы не представляет сложности. Мы просто наносим переменные на координатную плоскость. Если переменных всего две, то одну из них принимаем за х, другую — за у и вычерчиваем зависимость в декартовых координатах, т.е. наносим величину одной из них относительно значения другой в один и тот же момент времени. Это называется фазовым портретом системы — он вычерчивается в фазовом пространстве. Размерность фазового пространства зависит от количества переменных, характеризующих динамику системы. Если число переменных не более трех, то такой фазовый портрет можно наблюдать визуально. В противном случае размерность фазового пространства больше трех, и для визуального наблюдения нужно строить проекции или сечения фазового пространства.
Рассмотрим вначале самые простые линейные системы. В случае гармонического осциллятора фазовое пространство двумерно. Поэтому фазовый портрет колебаний «живет» на плоскости. Рассмотрим опять наш механический маятник. Переменными в такой системе выступают скорость и положение. Их и будем откладывать по осям нашего пространства. На фазовой плоскости линейного маятника без трения (гармонического осциллятора) есть единственная особая точка — начало координат (рис. 5.5). Эта особая точка характеризует изолированное состояние равновесия гармонического осциллятора и носит название центра. Центр соответствует поведению маятника, покоящегося в состоянии равновесия. Если теперь маятнику сообщить начальную энергию («просто» толкнуть), то он начинает раскачиваться, причем при отсутствии трения его энергия не уменьшается, как не уменьшается и размах колебаний, который полностью определяется величиной начального толчка. Все фазовые траектории в данном случае — эллипсы — замкнутые кривые. Такие траектории соответствуют периодическим движениям, поскольку фазовая точка движется по замкнутой фазовой траектории и, выйдя из какой-то точки фазовой плоскости, через некоторое конечное время вернется в нее же (система имеет то же самое положение и ту же самую скорость — процесс повторяется). Причем «время возвращения», или период колебаний, является конечным. Более того, этот период не зависит от того, по какой фазовой траектории движется система, т.е. период колебаний не зависит от амплитуды малых колебаний. Об этом свойстве изохронности мы уже упоминали выше.
Рис. 5.5. Фазовый портрет гармонического осциллятора
Фазовый портрет меняется, если мы вводим в осциллятор диссипацию. Пусть она будет малой. В этом случае первоначально сообщенная маятнику энергия рассеивается за счет трения и амплитуда колебаний становится все меньше и меньше. Если нарисовать одну из переменных в зависимости от времени, то результирующая волнистая линия будет постепенно уменьшать свою амплитуду до нуля — кривая становится прямой линией. В фазовом пространстве (координатах положение — скорость) мы получим спиральную линию, которая выходит из какой-то точки фазового пространства (которая характеризует начальное состояние системы) и заканчивается в начале координат, когда маятник останавливается. Если мы сообщим маятнику большую начальную энергию, то колебания будут продолжаться дольше и будут обладать большей начальной амплитудой, но тем не менее временной ряд придет к нулевому значению, а фазовый портрет — в начало координат. Можно сказать, что в этом случае в фазовом пространстве система «притягивается» к началу координат: где бы ни брала свое начало система, она приходит к началу координат — своему состоянию равновесия. Такое притягивающее множество, к которому сходятся все фазовые траектории из какой-либо области фазового пространства, называется аттрактором. Такой аттрактор называется фокусом и является простейшим примером аттрактора (рис. 5.6а). В случае большой диссипации состояние маятника также эволюционирует в фазовом пространстве к началу координат (положению равновесия), но теперь уже не колебательным образом. Фазовый портрет в этом случае представлен на рис. 5.7б, а сам аттрактор называется узлом. Заметим, что фазовые траектории, по которым движется гармонический осциллятор, не являются аттракторами, так как к ним не притягиваются никакие из траекторий. Гармонический осциллятор является консервативной системой (т.е. системой без диссипации), для которой в фазовом пространстве не существует аттракторов.
Рис. 5.6. Фазовые портреты линейного осциллятора: а) устойчивый фокус; б) узел; в) неустойчивый фокус
Важно то, что и узел, и фокус являются устойчивыми состояниями равновесия, т.е. малые отклонения фазовой траектории от них (например, вызванные либо искусственно, либо спровоцированные шумами) так и остаются малыми и имеют тенденцию уменьшаться. Узел и фокус являются примерами простых аттракторов. Однако возможна ситуация, когда диссипация отрицательна (такая ситуация возможна в экономическом маятнике). В этом случае состояние равновесия становится неустойчивым (неустойчивый фокус), и все спиральные траектории уходят из него. Такое неустойчивое состояние равновесия называют репеллером (рис. 5.7в).
Автоколебания и их свойства. Возникает вопрос: возможны ли периодические колебания, образом которых в фазовом пространстве являются замкнутые линии, в системах с трением? Оказывается, да, но системы должны быть принципиально нелинейными! Диссипативные системы, которые демонстрируют незатухающие колебания, называются автоколебательными. Простейшим примером автоколебательной системы являются колебания маятника в часах.
Автоколебания являются незатухающим колебательным процессом в диссипативной системе. Они не могут существовать, если нет какого-либо источника энергии и элемента, рассеивающего энергию (если нет диссипации энергии). Причем рассеивающий элемент должен взаимодействовать с источником энергии следующим образом: при установившихся периодических колебаниях энергия потерь в точности компенсируется в течение одного периода за счет источника, т.е. автоколебательная система непрерывно переводит энергию источника в энергию потерь (если, например, энергия теряется на трение, то энергия источника непрерывно переводится в тепло).
В линейной системе автоколебаний быть не может, даже если в ней имеет место отрицательное затухание. Для автоколебаний связь между источником энергии и колебательным элементом должна быть нелинейной. В простейших автоколебательных системах (автогенераторах), как правило, можно выделить колебательную систему с затуханием, усилитель и нелинейный ограничитель — звено «обратной связи».
Важное свойство автоколебаний — независимость вида и свойств автоколебаний от начальных условий. Если взять наш механический маятник, отвести его на некий угол и отпустить, то размах колебаний (при отсутствии потерь) будет как раз равен этой величине отклонения. Если отвести маятник на угол в два раза меньший, то и размах будет в два раза меньше. То есть для «обычных» колебаний амплитуда определяется начальными условиями. Для автоколебаний дело обстоит несколько иначе: их внешний вид определяется только свойствами самой автоколебательной системы и не зависит от начального состояния. Так маятник в ходиках можно отвести в начальный момент на любой угол, однако в установившемся режиме память об этом будет потеряна: автоколебания будут происходить с одной и той же амплитудой и частотой, независящими от начальной величины отклонения маятника.
Можно ли изменить характеристики (амплитуду, частоту, форму) автоколебаний? Да, но для этого надо изменять свойства самой автоколебательной системы. В случае ходиков частота автоколебаний изменяется путем изменения длины маятника (так и поступают с ходиками, когда они «спешат» или «отстают»).
В фазовом пространстве образом периодических автоколебаний являются предельные циклы Пуанкаре. Предельный цикл — замкнутая фазовая траектория, к которой стремятся все соседние траектории (рис. 5.7). Форма предельного цикла может быть различной. Главное, что предельный цикл, в отличие от фазовых траекторий гармонического осциллятора, является аттрактором, т.е. притягивает к себе траектории из других областей фазового пространства.
Рис. 5.7. Предельные циклы Пуанкаре в фазовом пространстве
В динамических системах автоколебания могут быть не только периодическими, но и квазипериодическими. Образом квазипериодических движений в фазовом пространстве является тор (рис. 5.8а). Он может реализоваться только в системе с фазовым пространством, размерность которого больше или равна трем. Особенностью аттрактора квазипериодических колебаний является то, что траектория нигде не замыкается, всюду плотно «наматываясь» на поверхность тора.
Рис. 5.8. Тор и странный аттрактор
Но и этим не ограничиваются возможные типы аттракторов в нелинейных системах. Последний тип аттрактора — хаотический или странный аттрактор. Он является образом хаотических автоколебаний (рис. 5.8б). Странные аттракторы — удивительные объекты. В системах, демонстрирующих хаотическую динамику, равновесие становится областью в фазовом пространстве — именно к этой области, называемой странным аттрактором, притягиваются все фазовые траектории, исходящие из других точек фазового пространства. Странные аттракторы демонстрируют фрактальные свойства своей структуры.
Примеры колебаний. В биологии классическим примером автоколебательной системы является сердце. С одной стороны, энергия, запасенная в клетках сердечной ткани, расходуется на сокращение сердечной мышцы (чтобы обеспечить перекачку крови по кровеносной системе) и на ее потребление клетками сердца для поддержания своей жизнедеятельности. С другой стороны, запас энергии пополняется при прокачке через сердце артериальной крови, богатой кислородом.
В экономической жизни автоколебания наиболее ярко иллюстрируются наличием долгосрочных циклов (с периодом 45-65 лет) периодического изменения различных экономических показателей. Такие экономические циклы связаны с именем выдающегося русского экономиста Н.Д. Кондратьева (1892–1938).
Еще один пример колебательных явлений — климатические изменения. Регулярная смена времен года, которая воспринимается нами как нечто само собой разумеющееся и привычное, — тоже колебания, как и суточные колебания температуры (днем температура выше, ночью ниже). Но речь пойдет не о столь привычных нам колебаниях, а о глобальных колебаниях, на первый взгляд незаметных, которые имеют другой временной масштаб — очень большую длительность, превышающую длительность человеческой жизни. Если на протяжении долгого времени проследить за значением средней температуры, то окажется, что эта величина также не была постоянной, а изменялась, совершая колебания, с чем связаны различные эпохи эволюционного развития нашей планеты (рис. 5.9).
Рис. 5.9. Колебания климата
Еще один пример колебательного поведения — динамика численности биологических популяций. Одним из факторов, позволяющих объяснить колебания численности популяций, является межвидовое взаимодействие особей двух популяций: так называемых «жертв», которые питаются природными ресурсами (различные растения), и «хищников», которые в основном питаются «жертвами».
Наблюдаются колебания и в химических системах. Впервые колебательную химическую реакцию, проявляющуюся в виде периодических вспышек при окислении паров фосфора, наблюдал Роберт Бойль в конце XVII века. Современная история исследований колебательных химических реакций в жидкой фазе началась в 1951 году, когда Б.П. Белоусов открыл колебания концентрации окисленной и восстановительной форм церия в реакции взаимодействия лимонной кислоты с броматом, катализируемой ионами церия. Позже в работах И. Р. Пригожина, бельгийского физика и химика, лауреата Нобелевской премии 1977 года за работы по термодинамике необратимых процессов, было показано, что колебательные химические реакции не только возможны, но и весьма вероятны вблизи стационарного состояния, достаточно удаленного от термодинамического равновесия.
В конце 1961 года работа Б.П. Белоусова была продолжена А. М. Жаботинским, который получил колебания при использовании в качестве восстановителя в реакции Белоусова не только лимонной, но и малоновой, а также яблочной кислот. Новость об этой удивительной реакции, которая в наше время носит название реакции Белоусова—Жаботинского, очень быстро обходит весь мир и начинает интенсивно изучаться во многих странах. Именно с реакции Белоусова—Жаботинского можно говорить о признании научным сообществом возможности колебательных химических реакций.
Наконец, говоря о колебаниях, оказывающих влияние на человеческую жизнь, нельзя не сказать несколько слов о землетрясениях — колебаниях земной коры, которые длятся, как правило, очень недолго, но по своим последствиям могут быть весьма серьезными. На рис. 5.10 статистические данные о землетрясениях представлены в виде графика, на котором по оси абсцисс отложена магнитуда М землетрясения, пропорциональная логарифму энергии Е землетрясения, а по оси ординат — число землетрясений с такой магнитудой. Видно, что распределение числа землетрясений N по их энергиям описывается с высокой степенью точности степенной зависимостью вида N(E) ~ НЕ–b.
Рис. 5.10. Распределение землетрясений разной силы во всем мире (с 1990 года), происходящих в среднем за год
Таким образом, следует сделать вывод о том, что колебания оказываются явлением, часто встречающимся в системах самой различной природы. Понятно, что разные системы изучаются разными науками: социальные системы исследуются историей, экономикой, социологией, политологией и т.д., механические или, например, электрические — механикой и физикой, земная кора — геологией, численность популяций — биологией, колебательные химические реакции — химией, изменения температуры или климата — метеорологией и т.п. Теория колебаний пытается взглянуть на разнообразные колебательные явления с единой точки зрения, выявить общие закономерности, свойственные колебательным системам.
В качестве подтверждения общности явлений в системах различной природы рассмотрим два графика (рис. 5.11), взятые из статьи Г. Г. Малинецкого Хаос. Тупики, парадоксы, надежды. На первом приведена зависимость индекса Доу-Джонса от времени перед Великой депрессией в США, а на втором — зависимость концентрации газа от времени перед землетрясением. Безусловно, эти две системы (человеческое общество и земная кора) совершенно различны, но, по всей видимости, существуют общие универсальные закономерности, обуславливающие одинаковый вид двух различных кривых перед событиями, качественно меняющими состояние систем. Синергетика стремится выявить подобные общие закономерности, возникающие в разных системах, и описывать их на своем языке, близком к языку математики.
Рис. 5.11. Колебания: а) логарифма индекса Доу-Джонса от времени перед Великой депрессией 1929 года; б) концентрации ионов хлора в родниках перед землетрясением в Кобе в 1995 году
Лекция шестая. Волны
Что такое волна? Волной называется явление распространения колебаний в пространстве. Физический энциклопедический словарь: волны — возмущения, распространяющиеся с конечной скоростью в пространстве и несущие с собой энергию… без переноса вещества (хотя последний может иметь место как побочное явление). Самое главное в этом определении то, что волны переносят энергию без переноса вещества.
Более общее определение понятия волны может прийти из рассмотрения нефизических ситуаций. Вот одна из страниц русской истории — 25 апреля 1742 года. В этот день состоялась коронация императрицы Елизаветы, дочери Петра I, на русский престол. Будущая императрица пожелала, чтобы момент возложения патриархом короны на ее голову был отмечен в новой столице России — Петербурге — выстрелом пушки Петропавловской крепости. Но по тогдашним законам коронация русских царей происходила в Москве в Успенском соборе. Радио и телевидения не было… Но способ реализации желания Елизаветы нашли. На всем примерно шестьсот пятидесяти километровом пути от собора в Москве до крепости в Петербурге на расстоянии прямой видимости (примерно сто метров) друг от друга выстроили солдат. Понадобилось приблизительно шесть тысяч пятьсот человек; в руке у каждого был флажок. В момент, когда корона коснулась головы Елизаветы, первый солдат взмахнул флажком, следующий повторил его действия, затем последовательно все остальные. Минут через десять-двадцать известие о коронации дошло до артиллериста в Петропавловской крепости, поскольку время реакции человека составляет десятые доли секунды. Спрашивается: что же переместилось из Москвы в Петербург?
Любой из солдат стоял на своем месте; правда, каждый взмахнул флажком. На языке науки действия солдата (поднял и опустил руку с флажком) означает изменение его состояния, или фазы. Именно это изменение состояния (фаза) и перемещалось вдоль цепи солдат. Тогда можно дать следующее весьма общее определение волны.
Перемещение в пространстве изменения состояния (фазы) называется волной.
Свойства волн.
- Перенос энергии. Волны, как и всякий движущийся объект, переносят энергию в процессе всего распространения.
- Волна обладает импульсом. Подобно движущимся частицам, волны обладают импульсом.
- Скорость волны. Поскольку волна распространяется в пространстве от одной точки к другой, то она обладает скоростью. В физике скорость характеризует быстроту изменения наблюдаемой величины и определяется отношением изменения этой величины к длительности отрезка времени, за которое это изменение произошло. Так, если речь идет о скорости движения точки вдоль некоторой оси координат X, изменение координаты ΔХ делят на время Δt и, устремляя величину Δt к нулю, находят скорость точки.
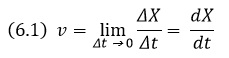
Но при рассмотрении волн не все так просто. Давайте рассмотрим фотографию волн от капли, упавшей в воду (рис. 6.1). От капли, возмущающей только очень малую область поверхности воды, начинают расходиться круги, а в центре быстро расширяющейся системы кругов образуется область спокойной воды. Для анализа этой сложной картины невозможно обойтись без рассмотрения волны, которой в чистом виде нет в природе. Это — бесконечная гармоническая волна, описываемая формулой:
где у — величина возмущения, распространяющегося в пространстве (для волны на поверхности воды – это отклонение точки поверхности по вертикали, для электромагнитной волны — интенсивность электрического или магнитного полей, для волны эпидемии — число заболевших и т.д.); а — постоянная амплитуда волны;(ωt – kx+ ϕ) – фаза волны; ω — постоянная частота (ω = 2π/Т, Т — период волны); k = 2π/λ — постоянное волновое число (λ — длина волны); ϕ — начальная фаза (рис. 6.2).
Рис. 6.1. Волны, расходящиеся от капли, упавшей на поверхность жидкости
Рис. 6.2. Изображение формы синусоидальной (гармонической) волны в пространстве «время — координата — размах колебаний». На рисунке показаны такие важные характеристики волны, как временной период (период колебаний Т), пространственный период (длина волны λ), амплитуда волны
Следуя физическому определению скорости (6.1), проведем следующие простые рассуждения. Пусть мы наблюдаем за распространением гармонической волны как на рис. 6.3, на котором показан профиль волны в два момента времени, разделенных интервалом Δt. Как видно из рисунка, волна распространяется вправо так, что за время Δt она прошла путь Δx. Начало и конец этого пути отмечен на рис. 6.3. стрелками (для удобства мы следили за распространением максимума волны). По аналогии с формулой (6.1) под скоростью волны можно понимать величину v = Δx/Δt.
Рис. 6.3. К введению фазовой скорости волны
Из рис. 6.3 следует, что значения функции у, описывающей профиль волны, одинаковы в начале и конце пути, следовательно, с учетом формулы (6.2) можно записать:
Последнее означает, что когда нас интересует скорость гармонической волны, то нас интересует выполнение условия постоянства фазы волны: wt – kx + ϕ = const. Дифференцируя в соответствии с определением (6.1) это выражение по времени, находим выражение для скорости гармонической волны:
Cкоростm волны (6.3) называется также фазовой скоростью vф.
Будут ли волны с разными частотами ω (разными длинами волн λ) распространяться с одной скоростью vф? Оказывается, что в зависимости от положительного или отрицательного ответа на данный вопрос мы имеем дело либо с отсутствием, либо, наоборот, с наличием дисперсии в среде, в которой распространяется волна. Дисперсию волн характеризует соотношение между частотой и волновым числом волны:
![]()
которое в теории волн принято называть дисперсионным уравнением. Если дисперсионное уравнение линейно, т.е. имеет вид:
(ω0 есть некоторая константа), то говорят об отсутствии дисперсии в среде. Очевидно, что в этом случае все волны распространяются с одной фазовой скоростью. Другое дело, если зависимость (6.5) нелинейная. Тогда говорят о наличии в среде дисперсии, и волны с разными частотами (длинами волн) распространяются с разной фазовой скоростью.
Определение скорости волны не ограничивается понятием фазовой скорости. Если дисперсионное уравнение волны таково, что вторая производная от функции ω = ω(k):
то вводят новую характеристику волнового движения, которую называют групповой скоростью:
Каков физический смысл понятия групповой скорости? Для ответа на этот вопрос рассмотрим суперпозицию двух гармонических волн со слабо отличающимися частотами и волновыми числами, но одинаковой амплитуды. График суммарной волны у, возникшей в результате сложения двух гармонических волн, показан на рис. 6.4. Из него видно, что результатом биений двух волн оказывается ряд периодически повторяющихся групп, причем такое повторение проявляется как во времени, так и по пространству. Каждая такая группа состоит из нескольких волн.
Рис. 6.4. Графическая интерпретация возникновения групп (биений) при сложении двух гармонических волн
Групповая скорость
Напомним, что фазовая скорость волны есть величина vф = ω/k. Поскольку и vф и vгр зависят от k, то понятно, что в случае, когда d2ω/dk2 ≠ 0, групповая скорость отличается от фазовой. При этом волны с различной длиной волны распространяются с различными групповыми скоростями. Как влияет дисперсия в системе на распространение возмущения, представляющего собой суперпозицию (сумму) ряда гармонических волн различной длины (волновой пакет)? Поскольку компоненты возмущения с различными волновыми числами (различными длинами волн) распространяются с различными скоростями, начальное возмущение через некоторое время растянется на некоторый пространственный интервал, который будет расти со временем. В этом случае мы имеем дело с диспергирующей волной. Если d2ω/dk2 = 0, то волна не диспергирующая и vф = vгр. В последнем случае при распространении волнового пакета искажение не наблюдается за счет того, что все волны, составляющие пакет, распространяются с одной скоростью.
Волны на воде. Океанские волны разделяют по их периоду.
Приливные волны, образование которых связано с притяжением Луны и Солнца, — самые длинные; их длина (теоретически) составляла бы половину окружности земного шара, если бы не мешали материки, а период этих волн от двенадцати до двадцати четырех часов. В открытом море это — линейные волны из-за большой длины, а нелинейность проявляется лишь у берега.
Цунами (рис. 6.5) — волны подводных землетрясений или извержений вулканов с периодом от десяти минут до часа. В открытом море цунами — линейная волна, но в береговой зоне высота волны возрастает иногда до десятков метров.
Бор (рис. 6.6) образуется при вхождении прилива в устье реки или пролив; передний склон волны представляет собой резкий перепад высотой до нескольких метров.
Ветровые волны – наиболее характерный тип движения на поверхности моря. В них выделяют зыбь с периодом 6–16 с, волнение с периодом 5–12 с и мелкие ветровые волны с периодом 1–4 с.
Наконец, капиллярные волны — рябь — имеют в воде длину, меньшую 1,7 см. На рис. 6.7 приведен спектр реального морского волнения.
Рис. 6.5. Пример волны цунами, возникающей в Тихом океане за счет извержения подводных вулканов
Рис. 6.6. Когда сильный прилив проходит много километров по мелководью, фронт приливной волны становится все круче. Он может образовывать бору, т.е. подвижную форму гидравлического прыжка. На левом рисунке показана бора на реке Цяньтан. На правом рисунке показана волновая бора на Амазонке.
Рис. 6.7. Спектр реального морского волнения
Океанологические эксперименты последних лет показали, что течений, которые рисуют на картах в виде широких рек, в действительности не существует. Основная кинетическая энергия океана сосредоточена в громадных медленно передвигающихся океанических вихрях, подобных циклонам и антициклонам в атмосфере. Правда, если усреднить все движения вихрей за много месяцев, то получится нечто вроде известных всем океанических течений.
Нелинейные волны. Выше мы рассматривали преимущественно линейные волны. Однако, как существуют нелинейные колебания, так существуют и нелинейные волны, поведение которых описывается нелинейными уравнениями. Мир нелинейных волн богат и разнообразен. Но и в нем есть свои эталонные модели, подобные эталонным моделям теории колебаний. Среди них — простые волны, ударные волны и уединенные волны — солитоны.
В линейной среде без дисперсии любая бегущая волна является стационарной, т.е. при распространении форма ее не меняется и она движется с постоянной скоростью. Причем все физические переменные в такой волне связаны алгебраически. Даже в слабо нелинейной среде при отсутствии дисперсии все гармоники, порождаемые нелинейностью, находятся в синхронизме с основной волной (все они распространяются с одинаковыми скоростями). Поэтому, спустя достаточно большое время, даже при очень слабой нелинейности, амплитуда их будет нарастать, что приведет к существенному изменению профиля волн, т.е. в нелинейных средах без дисперсии стационарных волн не бывает. На спектральном языке сказанное означает, что спектр исходного возмущения будет непрерывно расширяться в сторону больших частот. В результате в спектре волны появляются бесконечно высокие частоты, что и соответствует возникновению бесконечно быстрых перепадов на фронте волны.
Ударные волны. Обсудим теперь такое нелинейное волновое явление, как ударная волна. Об ударных волнах знают все, но подобно герою Мольера, не подозревают об этом. Проще всего ударную волну наглядно представить, как крутой и тонкий волновой фронт. «Тонкий» означает, что, например, на уровне моря его толщина в воздухе составляет порядка 0,025 мкм (для сравнения, длина световой волны в инфракрасной области составляет около 1 мкм). Когда в газообразном, жидком или твердом веществе внезапно высвобождается или вводится в него извне энергия, приводя к взрыву, возникает ударная волна. Рассмотрим в качестве примера динамику ударной волны при сферическом взрыве, когда химическая или ядерная энергия за милли- или микросекунды, т.е. по существу, внезапно, высвобождается в воздухе, в воде или под землей (см. рис. 6.8, на котором представлена фотография ядерного взрыва). При этом образуется сферический объем раскаленного газа, который находится под высоким давлением и, расширяясь, вызывает в окружающей среде ударную волну. Она движется наподобие приливной волны и практически мгновенно повышает давление, плотность и температуру среды. Кроме того, ударная волна создает поток вещества, следующий за ней. Охватывая все большие объемы вещества, сферическая ударная волна постепенно затухает, превращаясь в слабое возмущение или звуковую волну. Причем, вблизи от источника взрыва, когда давление, температура, плотность и скорость ударной волны велики, затухание происходит очень быстро. Затухание почти прекращается по мере превращения ударной волны в звуковой импульс. При распространении сильной ударной волны в невозмущенной среде давление, температура и плотность возмущенного состояния увеличиваются во много раз. Именно из-за этого гибнут попавшие в зону действия ударной волны люди и животные, под действием внезапного и сильного изменения давления рушатся различные сооружения. Большой ущерб всему живому и сооружениям может нанести ветер, возникающий благодаря скорости потока вещества.
Рис. 6.8. Первый подводный ядерный взрыв, произведенный в ходе испытаний ядерного оружия в акватории Новой Земли
Раскаты и грохот грома, особенно вблизи грозовых разрядов — одни из самых сильных звуков, известных в природе. Еще больше бед приносят землетрясения, во время которых из-за разрыва земной коры под действием сдвига внезапно высвобождается механическая энергия, что приводит к возникновению волн нескольких типов. Эти волны распространяются по поверхности земли и под землей.
Результатом подводного землетрясения являются цунами, вызывающие страшные разрушения. Цунами кажутся «безобидными» в открытом море, где их высота не превышает 30 см. Но расстояние между гребнями может достигать сотен километров, так что в цунами сосредоточена огромная масса воды, движущаяся иногда со скоростью 180 км/ч. Цунами замедляются на скалистой прибрежной отмели, их высота достигает несколько десятков метров.
Еще одно природное явление, порождающее ударные волны, — извержение вулканов. Канонический пример — извержение в 1883 году вулкана на необитаемом острове вулканического происхождения Кракатау, расположенном между Явой и Суматрой. Ударная волна трижды обогнула земной шар. Взрыв был слышен на расстоянии более чем 4 800 км от источника; в атмосферу было выброшено порядка 4,6 куб. км вулканического пепла и других продуктов извержения; энергия взрыва была эквивалентна энергии 250 тыс. бомб, сброшенных на Хиросиму.
Ударные волны возникают как на Земле, так и в воздухе, когда о землю ударяется метеорит. По одной из гипотез знаменитый Тунгусский метеорит, который в 1908 году взорвался над Сибирью, представлял собой ледяное ядро кометы. Оно распалось, не долетев до Земли. Но тем не менее ударная волна, возникшая, когда он входил в атмосферу Земли, привела к тому, что был повален и сгорел весь лес на площади около 2 000 км2.
Еще один вид ударной волны — звуковой удар, который мы слышим после пролета сверхзвукового самолета. При обычном разговоре увеличение давления по сравнению с атмосферным незначительно и составляет ~0,1 Па. В то время как звуковые удары, вызываемые современными сверхзвуковыми самолетами, во много раз сильнее и составляют ~100 Па. Когда самолет летит с дозвуковой скоростью, волны давления расходятся во всех направлениях. Их не услышишь — они слишком слабы. Ситуация соответствует картине концентрических кругов, расходящихся от места падения камешка в неподвижную воду. При переходе к сверхзвуковым скоростям слабые возмущения давления складываются, что и приводит к образованию двух конических ударных волн. У носовой части самолета находится вершина головной ударной волны, а у хвостовой части — хвостовая. Обе волны падают на поверхность Земли и отражаются обратно в атмосферу. Пространство перед головной волной не возмущено, и, следовательно, беззвучно. Сверхзвуковой самолет может быть виден, но звук от него не слышен до тех пор, пока конические ударные волны не достигли Земли и не отразились от нее. Мы слышим звуковой удар, когда самолет может уже скрыться из вида.
Уединенные волны (солитоны). Наблюдал и первым описал солитон великий инженер викторианской эпохи Джон Скотт Рассел более ста пятидесяти лет тому назад. И хотя это описание уже стало столь же распространенным, как и описание солдат, шагающих по мосту, оно столь поэтично и ярко, что трудно удержаться от его изложения. Вот какую картину рисует Рассел:
«Я полагаю, что наилучшее представление об этом явлении даст описание обстоятельств моего первого знакомства с ним. Я наблюдал за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась. Но масса воды, которую баржа привела в движение, не остановилась, а собралась у носа судна в состоянии интенсивного движения, затем неожиданно оставила его позади, катясь вперед с огромной скоростью и принимая форму большого одиночного возвышения, т.е. округлого, гладкого и четко выраженного водяного холма, который продолжал свой путь вдоль канала, не меняя своей формы и не снижая скорости. Я последовал за ним верхом и, когда нашел его, он по-прежнему катился вперед со скоростью приблизительно восемь или девять миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от одного до полутора футов. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала. Так в августе 1834 года мне впервые довелось столкнуться с необычайным и красивым явлением, которое я назвал уединенной волной трансляции; теперь это название общепринято» (рис. 6.9).
Рис. 6.9. Уединенная волна в канале Форз-Клайд (картинка найдена здесь).
Можно считать, что формирование солитона связано с конкуренцией между нелинейностью и дисперсией, которая приводит к формированию уединенной волны, форма которой не меняется по мере распространения в среде без диссипации. Солитон — это уединенная волна, сохраняющая свою форму и скорость после столкновения с другой такой уединенной волной.
В настоящее время исследование солитонов и связанных с ними задач выделилось в отдельное научное направление (солитонику). Исследователи в этой области решают широкий круг проблем, связанный не только с изучением фундаментальных свойств этого явления — возникновения уединенных волн на поверхности жидкости, но и в электродинамике, оптике, биофизике и т.п. Так, например, реализована на практике эффективная схема передачи больших объемов информации с помощью электромагнитных солитонов. Много интересного о солитонах можно найти в очень хорошей книге А.Ньюэлла Солитоны в математике и физике.
Лекция седьмая. Примеры процессов самоорганизации в различных системах
Синергетику чаще всего рассматривают как науку о самоорганизации. Центральным в теории самоорганизации является термин «структура», или «паттерн». Грею Уолтеру принадлежит такое определение: «Понятие паттерн подразумевает любую последовательность явлений во времени или любое расположение предметов в пространстве, которое можно отличить от другой последовательности или другого расположения или сравнить с ними… Вообще говоря, можно считать, что науки возникают в результате поиска паттернов, а искусства — в результате создания паттерна, хотя между поисками и созданием паттерна существует более тесная связь, чем обычно полагают».
По аналогии с колебаниями паттерны можно разделить на свободные, вынужденные и автопаттерны (рис. 7.1). Под автопатгернами будем понимать локализованные пространственные образования, устойчиво существующие в диссипативных неравновесных средах и не зависящие (в конечных пределах) от граничных и начальных условий. Самое главное в этом определении и раскрывающее смысл добавки «авто» к слову паттерн — независимость от изменения начальных и граничных условий. Также как и в случае автоколебаний, подобная независимость может быть только в средах с диссипацией, которая понимается весьма обще.
Рис. 7.1. Классификация структур (паттернов)
Поскольку образование автопатгернов — результат развития пространственно неоднородных неустойчивостей с их последующей стабилизацией за счет баланса между диссипативными расходами и поступлением энергии от источника неравновесности, то процесс образования автопаттерна похож на установление колебаний в распределенных автоколебательных системах (РАС). Для последних определение звучит так: РАС — неконсервативная система, в которой в результате развития неустойчивости возможно установление волновых или колебательных движений, параметры которых (амплитуда и форма колебаний и волн, частота, а в общем случае спектр колебаний) определяются самой системой и не зависят от изменения начальных условий.
Представим себе стоящие на ребре фишки домино. Такие фишки при малых их отклонениях от такого положения снова возвращаются в него. Другими словами, состояние в виде стоящей на ребре фишки устойчиво относительно малых возмущений. Но мы хорошо знаем, что если достаточно сильно толкнуть крайнюю фишку, то это приведет к самораспространяющейся волне последовательного падения фишек вдоль линии их построения (рис. 7.2). Причина этого явления связана с тем, что в исходном состоянии каждая стоящая фишка (по сравнению с лежащей) обладает потенциальной энергий W = mgh, где m — масса фишки, 2h — ее высота. Кроме того, и это существенно, соседние фишки, т.е. элементы системы, взаимодействуют между собой: каждая падающая фишка толкает соседнюю и роняет ее. В рассматриваемом случае самораспространяющаяся волна падения фишек представляет собой автоволну переключения системы из метастабильного состояния с потенциальной энергией W = mgh в более выгодное состояние с меньшей энергией W = 0. При таком переключении запасенная в фишках потенциальная энергия необратимо переходит в тепло, выделяющееся при падении фишек. Скорость и профиль такой автоволны переключения постоянны и не зависят от начального толчка первой фишки домино.
Рис. 7.2. Автоволна последовательного падения фишек домино. Внизу: профиль автоволны — положения центра тяжести фишек
Самым широким является определение самоорганизации как установления в диссипативной неравновесной среде пространственных паттернов (вообще говоря, эволюционирующих во времени), параметры которых определяются свойствами самой среды и слабо зависят от пространственной структуры источника неравновесности (энергии, массы и т.д.), начального состояния среды и условий на границах. Примеры самоорганизации, о которых далее пойдет речь, можно сказать, являются классическими — почти в каждой книге по самоорганизации этим примерам уделяется достойное место. Во многом, это объясняется тем, что в достаточно простых системах, которые мы и будем обсуждать, удается без различных ухищрений пронаблюдать образование структур возрастающей сложности.
Структуры Тьюринга. Тьюринг в 1952 г. попытался объяснить, почему некоторые живые организмы имеют близкое к периодическому строение. Сюда же примыкает задача о выяснении механизма возникновения пятен на шкуре животных. Тьюринг показал, что в первоначально однородной среде, в которой протекают химические реакции с диффузией, может установиться периодическое в пространстве и стационарное во времени распределение концентраций. Проблема морфогенеза — одна из центральных в исследовании самоорганизации. Главное в проблеме — ответить на вопрос: «Откуда первоначально недифференцированные клетки знают, где и каким образом дифференцироваться?» В отдельных клетках, как следует из экспериментов, такой информации нет. Находясь в ткани, клетка получает информацию о своем положении от других клеток, после чего идет дифференциация. Известно, что в экспериментах, произведенных на эмбрионах, клетка из центральной части тела после пересадки в головной отдел развивалась в глаз. В этих экспериментах доказано, что клетки не располагают информацией о своем последующем развитии, например, через ДНК, а извлекают ее из своего положения в клеточной ткани. Тьюринг предположил, что носителем такой «позиционной информации» служит химическая структура — «морфоген», возникающая благодаря совместному действию химических реакций и диффузии. Сейчас предполагается, что при достаточно высокой концентрации морфогенов в работу включаются гены, что и приводит к дифференциации клеток. Следует, правда, отметить, что существование морфогенов до настоящего времени окончательно не установлено, за исключением некоторых косвенных подтверждений (о Тьюринге см. Эндрю Ходжес. Игра в имитацию).
Одна из наиболее известных реакционно-диффузионных моделей морфогенеза принадлежит А. Гиреру и X. Мейнхардту (далее — модель ГМ). Модель ГМ основана на том, что все клетки развивающегося организма могут продуцировать два морфогена: активатор и ингибитор, которые могут диффундировать в другие клетки. Если диффузии нет (например, в случае идеального перемешивания), то в результате взаимодействия морфогенов система достигнет однородного стационарного состояния. Диффузия морфогенов с одинаковыми скоростями приведет к тому же: любое пространственное отклонение от стационарного состояния будет сглаживаться. К чему приведет разная скорость диффузии морфогенов? Малое пространственное возмущение может стать неустойчивым, и начинает расти пространственная структура, поскольку скорости реакции в любой заданной точке могут не успеть «подстроиться» друг к другу достаточно быстро. Такую неустойчивость называют диффузионной, а механизм образования структур — активаторно-ингибиторным.
Красивая аналогия, образно поясняющая активаторно-ингибиторный механизм образования структур в распределении концентрации морфогенов, дана в статье Марри: «Пусть имеется очень сухой лес, иными словами, есть все условия для лесного пожара. Чтобы свести к минимуму возможный урон, по всему лесу рассредоточены пожарные с противопожарным снаряжением и вертолеты. Теперь представим, что вспыхивает пожар (активатор). От мест воспламенения начинает двигаться фронт огня. Первоначально поблизости от места пожара недостаточно пожарных (ингибитора), чтобы погасить огонь. Однако с помощью вертолетов пожарные могут обогнать фронт огня и обработать деревья реактивами, которые не позволяют им загореться. Когда огонь достигнет обработанных деревьев, он погаснет. Фронт остановится. Если пожары спонтанно возникают в разных местах леса, то через какое-то время сформируются несколько распространяющихся фронтов огня (волн активации). В свою очередь, это заставит пожарных на вертолетах (волны ингибирования) обогнать каждый фронт и остановить его на некотором расстоянии от места воспламенения. Конечным результатом такого сценария будет лес с черными пятнами сгоревших деревьев, перемежающимися с пятнами зеленых нетронутых деревьев. В принципе полученная картина имитирует результат, даваемый реакционно-диффузионными механизмами, обусловленными диффузией».
Ячейки Бенара. Другим классическим примером самоорганизации являются ячейки Бенара. Слой жидкости (чаще всего силиконовое масло) находится в сосуде, обычно круглой или прямоугольной формы. На жидкость действует сила тяжести. Нижний слой жидкости подогревают, а верхнюю поверхность поддерживают при постоянной температуре (например, комнатной), которая ниже, чем температура нагревателя. Понятно, что устанавливается разность температур между верхней и нижней поверхностями жидкости (физики часто называют эту разность температур градиентом температуры), в результате чего возникает поток тепла снизу вверх. Так происходит всегда: теплота от более нагретых тел стремится перейти к менее нагретым.
Если градиент температуры мал, то перенос тепла осуществляется на микроскопическом уровне: из школьного курса физики известно, что теплота — это не что иное, как движение молекул жидкости. Чем больше температура, тем интенсивнее это так называемое тепловое движение молекул, тем больше скорость молекул. Молекулы жидкости сталкиваются между собой, и при столкновении «более быстрой» молекулы с «более медленной» первая молекула отдает часть энергии второй. Понятно, что в рассматриваемом слое жидкости в нижних слоях температура больше, соответственно, интенсивнее и тепловое движение молекул в этих слоях. В верхних же слоях меньше температура и менее интенсивное движение молекул. В результате взаимодействия «быстрых молекул» с «медленными молекулами» осуществляется передача тепла от нижних слоев к верхним без макроскопического движения жидкости. Под словами «макроскопическое движение жидкости» имеется в виду следующее: если мысленно выделить в жидкости некоторый малый объем и следить за всеми молекулами, заключенными в нем, то увидим, что все молекулы из этого объема, участвуя в хаотическом движении (т.е. двигаясь беспорядочно), наряду с этим совершают коллективное движение в некотором направлении, причем их перемещения оказываются много больше размеров молекул. И наоборот, когда говорим о «микроскопическом движении», то подразумеваем, что молекулы участвуют только в тепловом движении, и никаких направленных потоков жидкости нет.
Возрастая, градиент температуры достигает критического значения, и тогда внезапно (точнее говоря, лучше сказать «внешне внезапно») устанавливается макроскопическое движение жидкости, образующее четко выраженные структуры: на одних участках нагретая жидкость поднимается и затем охлаждается у верхней поверхности, на других — опускается (см. рис. 7.3). Именно в результате этого и возникает движение в виде цилиндрических или шестигранных ячеек. Эти ячейки, по внешнему виду напоминающие пчелиные соты, получили название ячеек Бенара.
Рис. 7.3. Возникновение шестигранных ячеек при конвекции Бенара в тонком слое жидкости. Сверху показаны линии тока жидкости в режиме Бенаровской конвекции. На нижнем кадре показан экспериментальный снимок конвекции Бенара. Снимок демонстрирует шестигранную конвективную структуру в слое силиконового масла глубиной 1 мм при равномерном нагреве снизу. Если верхняя граница свободна, то течение создается неоднородностями поверхностного натяжения, а не плавучестью. Свет, отраженный от алюминиевых хлопьев, демонстрирует подъем жидкости в центре каждой ячейки и ее опускание на краях
Рябь Фарадея. Если кювету, в которую налит слой жидкости с достаточно большой вязкостью (силиконовое масло) периодически «трясти» в вертикальном направлении, то на поверхности жидкости могут образовываться структуры, напоминающие по форме прямоугольники. Первым, кто наблюдал подобные структуры еще в 1831 году, был Майкл Фарадей.
Вихри за движущимся объектом. Говоря о самоорганизации в гидродинамике, стоит упомянуть еще один класс структур, имеющих важное практическое значение. Речь идет о вихрях, которые образуются при обтекании жидкостью или газом движущихся объектов, таких как самолеты, автомобили, суда. И здесь важное значение для образования структуры вихря имеет скорость движущегося объекта и его геометрия. Наблюдать подобные вихри легко можно в неглубоком слое жидкости: вам необходимо, опустив в воду какой-либо объект (например, кончик карандаша), двигать его в горизонтальном направлении с постоянной скоростью. При этом, при небольших скоростях будут наблюдаться два «уса» волн, двигающихся за карандашом. Угол между этими «усами» зависит от скорости его движения. С увеличением скорости ситуация изменяется: за движущимся объектом начинают образовываться вихри, которые затем отрываются от него, но еще некоторое время двигаются вслед за объектом по инерции. Оказывается, что критическое значение скорости, при превышении которого начинается процесс образования вихрей, зависит от геометрических размеров движущегося тела: например, чем больше диаметр движущегося объекта (если мы рассматриваем объект цилиндрической формы), тем при меньшем значении скорости движения начинают формироваться вихревые структуры. Это так называемая дорожка Кармана (рис. 7.4).
Рис. 7.4. Вихревая дорожка Кармана за круговым цилиндром
Процессы самоорганизации в человеческом обществе. Не стоит думать, что поле деятельности синергетики ограничивается только естественно-научным направлением. Процессы самоорганизации имеют место и в экологии, экономике, социологии, демографии и т.д. Например, задумывались ли вы над вопросом, почему на одинаковые товары устанавливается почти одинаковая цена? Вам кажется это само-собой разумеющимся? Но ведь продавцы могут устанавливать на свои товары свои цены, разные, их вроде бы никто не заставляет «держать» одинаковые цены. Тем не менее цена-то одинаковая. Это как раз пример процесса самоорганизации, который представляет интерес для синергетики.
Существует еще масса различных примеров, но мы остановимся лишь на одном. Оказывается, что «формирование общественного мнения» (которое можно, безусловно, определить по-разному) — коллективное явление. Один из его механизмов, имеющий, по-видимому, фундаментальное значение, был обнаружен в результате опытов Соломона Эша. Основная идея этих экспериментов заключалась в следующем: группе, состоявшей примерно из десяти «испытуемых», предлагалось ответить на простой вопрос, например, указать, с какой из трех различных по длине линий совпадает предъявленный отрезок (рис. 7.5). За исключением одного настоящего испытуемого, все остальные члены группы были помощниками экспериментатора, о чем испытуемый, естественно, не подозревал. В первом опыте помощники давали правильный ответ, и испытуемый, естественно, тоже. В последующих опытах помощники давали неверные ответы, и 60% испытуемых также давали неверные ответы. Это свидетельствует о том, что мнение остальных членов группы явно влияет на мнение индивидуумов. Последний эффект известен в психологии как проявление комфортности к мнению незнакомых людей и должен обязательно учитываться, например, при опросе свидетелей при судопроизводстве и т.п. Заметим, что так как в процессе формирования общественного мнения индивидуумы оказывают друг на друга взаимное влияние, то и это явление может быть проанализировано методами синергетики.
Рис. 7.5. Схема опыта С.Эша. Участники эксперимента должны были выбирать на карточке Б линию, которая совпадает по длине с линией на карточке А. Во время исследований испытуемый сталкивался с тем, что все остальные участники единодушно оценивали линию 1 на карточке Б как равную линии-образцу
Интересно то, что формирование структуры в опытах Эша можно сравнительно легко разрушить. Давайте представим себе, что одинокий испытуемый получил бы небольшую поддержку, т.е. еще один человек высказал бы мнение, противоречащее неверной оценке большинства. Что тогда? Эш провел эксперимент, когда один из его помощников отклонился от общей тенденции в ходе одного из исследований и открыто выразил несогласие с большинством. При соблюдении этого условия настоящие испытуемые проявили конформизм только в 6% случаев. Степень комфортности снижалась и в тех случаях, когда испытуемый получал возможность отвечать в частном порядке, т.е. вне пределов слышимости большинства исследуемой малой группы. С другой стороны, комфортность увеличивается, если группа оказывается привлекательной для индивида. Если вам нравятся люди, которые составляют большинство, вы просто обречены на большую комфортность, поскольку вы хотите им понравиться и не оказаться отверженными. Все вышеперечисленное может рассматриваться как некоторые управляющие параметры подобной социальной системы, хотя их формализованная формулировка, а не интуитивное понимание, оказывается достаточно сложным, а может быть и невозможным. Это тот случай, когда гуманитарные науки привносят в синергетику новые примеры и заставляют искать исследователей новые методы описания наблюдаемых «нефизических» явлений. Очевидно, что из анализа таких простых экспериментов становятся более понятными многие мотивы поведения людей, что определяет важность подобных исследований, в том числе и с применением аппарата синергетики.
Много интересных примеров образования подобных структур в малых социальных группах описано в книге Роберта Чалдини Психология влияния. В этой же книге подробно обсуждаются механизмы, приводящие к образованию подобных структур в общении людей, например, психологические методики и стратегии, позволяющие влиять на субъектов общения и навязывать то или иное мнение и индивидуальное поведение людям, подобно тому как это имело место в опыте С. Эша. Так Чалдини утверждает, что во многом такое влияние возможно благодаря определенным паттернам поведения и реакции людей. В частности, он пишет следующее: «Этологи, исследователи, которые изучают поведение животных в естественном окружении, обратили внимание на то, что в поведении представителей многих видов животных часто имеют место жесткие автоматические модели. Называемые жестко фиксированными моделями (паттернами) поведения, эти автоматические последовательности действий заслуживают особого внимания, поскольку они имеют сходство с определенным автоматическим… реагированием людей. Как у людей, так и у животных данные модели, как правило, приводятся в действие каким-то одним элементом информации. Это единственная специфическая черта играет роль спускового крючка, она часто оказывается очень ценной, поскольку позволяет индивиду принимать правильное решение без тщательного и полного анализа всех остальных элементов информации в конкретной ситуации. Преимущество такого стереотипного реагирования заключается в его эффективности и „экономичности»; автоматически реагируя на несущую основную информацию черту — „спусковой крючок», индивид сохраняет свое время, энергию и умственный потенциал…»
Все эти механизмы уступчивости или влияния основаны на определенных паттернах (или, как часто говорят психологи, стереотипах, или казуальных схемах) поведения, «зашитых» в психологию человека, который склонен в большинстве случаев автоматически, не раздумывая реагировать на внешнюю информацию в соответствии с заранее усвоенными причинно-следственными связями.
Лекция восьмая. Бифуркации
Во многих областях знаний (биология, география, педагогика) термин «бифуркация» обозначает «раздвоение», «разделение». В нелинейной динамике термин «бифуркация» трактуется более широко — это качественное изменение состояния системы при малом изменении управляющих параметров. Определение из Универсальной энциклопедии» Кирилла и Мефодия: Бифуркация, приобретение нового качества в движениях динамической системы при малом изменении ее параметров. Основы теории бифуркации заложены А. Пуанкаре и А. М. Ляпуновым в нач. XX века, затем эта теория была развита А.А. Андроновым и учениками. Знание основных бифуркаций позволяет существенно облегчить исследование реальных систем (физических, химических, биологических и др.), в частности предсказать характер новых движений, возникающих в момент перехода системы в качественно другое состояние, оценить их устойчивость и область существования.
В качестве примера рассмотрим простую механическую систему: шарик, катающийся по желобу, профиль которого определяется с помощью соотношения:
(8.1) у(х) = х4 + ах2 + bх
Соответствующий график, поясняющий рассматриваемую систему, представлен на рис. 8.1. Здесь х — переменная, которая однозначно определяет местоположение шарика (а, следовательно, состояние системы в рассматриваемый момент времени), а и b — управляющие параметры, определяющие профиль рассматриваемого желоба. При изменении величин управляющих параметров а и bизменяется профиль желоба, что влечет за собой изменение состояния системы — меняется местоположение равновесного состояния, шарик смещается в новое положение равновесия (происходит изменение величины переменной х). Таким образом, меняя управляющие параметры а и b, мы можем изменять состояние системы.
Рис. 8.1. Шарик в потенциальной ямке (а = –0,8; b = 1). Координата х0 определяет местоположение шарика, параметры а и b — профиль желоба
Все возможные значения управляющих параметров можно представить себе, как плоскость (а,b), называемую плоскостью управляющих параметров. Любая точка на этой плоскости однозначно соответствует одному, вполне определенному виду профиля желоба, по которому катается шарик. И наоборот, любой желоб вида (8.1) может быть поставлен в соответствие точке на плоскости (а,b). Если бы управляющих параметров было не два, а больше (например, три), то речь бы шла о пространстве параметров. Вернемся, однако, к понятию «бифуркация». Речь идет о том, что при малых изменениях значений управляющих параметров происходит качественное изменение состояния системы. Подчеркнем два важных момента: малые изменения значений управляющих параметров и качественное изменение состояния системы. Иными словами, всякое (малое) изменение управляющих параметров, конечно же, приводит к изменению состояния системы, но если отличия между начальным и конечным состояниями качественным образом не отличаются, то нельзя говорить о бифуркации.
Поясним сказанное на примере шарика в потенциальной ямке. На рис. 8.2 приведена плоскость управляющих параметров (а,b), и в некоторых точках показан профиль желоба, по которому может кататься шарик. Из рисунка видно, например, что в точках 3 и 4 плоскости параметров профили желоба, конечно же, отличаются друг от друга, но это отличие носит количественный, а не качественный характер. Качественно же оба эти профиля подобны: они имеют один минимум, а, следовательно, одно состояние устойчивого равновесия. В то же самое время, на плоскости параметров существует область (ограниченная пунктирными линиями), в которой желоб имеет три состояния равновесия. Желоб имеет три точки, в которых шарик может находиться в состоянии равновесия; два из этих состояний устойчивы, а одно — неустойчивое.
Рис. 8.2. Плоскость управляющих параметров (а,b) и вид потенциальной ямы в некоторых точках плоскости параметров
Если шарик будет находиться в состоянии неустойчивого равновесия (рис. 8.3), то любые сколь угодно малые воздействия на него (а такие воздействия рано или поздно обязательно реализуются) выведут шарик из этого состояния равновесия, и он скатится в одну из ямок — либо левую, либо правую. И в левой, и в правой ямках шарик будет находиться в состоянии устойчивого равновесия сколь угодно долго. В какую из двух этих ямок шарик попадет — определяется волей случая. Подобные системы, в которых возможно несколько устойчивых состояний (из которых реализуется, естественно, только одно), называются мультистабильными, а само явление — мультистабильностью.
Рис. 8.3. Система, находящаяся в состоянии неустойчивого равновесия. Незначительные воздействия на систему извне с неизбежностью приведут к тому, что система перейдет в устойчивое состояние равновесия
Понятно, что желоб с двумя ямками (и тремя состояниями равновесия) качественно отличается от желоба с одним состоянием равновесия. Переход от одного состояния к другому, качественно иному, как нетрудно догадаться, осуществляется на пунктирных линиях (см. рис. 8.2). Если на плоскости управляющих параметров достаточно близко «подойти» к пунктирной линии, то затем, слегка изменив управляющий параметр, можно пересечь эту линию, что приведет к качественной перестройке всей системы. Произойдет то, что и называется бифуркацией: качественное изменение состояния системы при малом изменении управляющих параметров. Линию, при пересечении которой происходит бифуркация, называют линией бифуркации, а значения параметров, при которых наблюдается бифуркация — бифуркационными параметрами.
Рассмотрим теперь суть происходящих явлений с точки зрения шарика, который находится в желобе. Пусть управляющие параметры а и bмедленно изменяются в соответствии с тем, как это показано стрелкой на рис. 8.4. В соответствии с изменением управляющих параметров, профиль желоба непрерывно изменяется. В точке 1 плоскости параметров желоб имеет одно устойчивое состояние равновесия, в котором и находится шарик. При пересечении пунктирной линии в точке 2 у желоба возникает еще один минимум и один максимум, т.е. появляются еще два состояния равновесия, одно из которых устойчивое (минимум), а другое — нет. По мере дальнейшего движения по плоскости параметров по указанному маршруту второй минимум становится все более глубоким (точка 3) и при достижении точки 4 глубина обеих ямок желоба оказывается одинаковой. В этом случае оба состояния равновесия «равноправны». Заметим, однако, что шарик до сих пор даже «не заметил» появления второго состояния равновесия, в котором он вполне мог бы находиться. Для шарика почти ничего не изменилось: он как находился в ямке, так и продолжает там оставаться. Да, с изменением управляющих параметров изменяется координата х0 равновесного состояния, а, следовательно, и координата местонахождения шарика, но это изменение столь незначительное, что шарик не придает ему особого значения. Плавные, малые изменения незаметны и кажутся неважными.
Рис. 8.4. Изменение состояния системы при движении по плоскости параметров в направлении, показанном стрелкой
Действительно, задумываемся ли мы каждое утро над тем, что стали на день старше? Обращаем ли мы внимание на то, что 15 января продолжительность дня была 7 ч 39 мин, а 16 января — 7 ч 42 мин? Замечаем ли осенним днем, что листья стали еще чуть-чуть желтее, чем были накануне? Так незаметно накапливаются малые изменения, на которые мы не обращаем внимания. Малое изменение координаты состояния равновесия от точки к точке при движении по плоскости управляющих параметров — вещь столь незначительная и неважная, что шарик не обращает на это никакого внимания. Наверное, шарику вполне могло бы показаться интересным и важным появление второго возможного состояния, в котором он мог бы находиться, но это второе состояние остается невидимым для шарика, оно скрыто от него высокими стенками желоба, и шарик о его существовании просто-напросто не догадывается.
Продолжим движение по плоскости управляющих параметров. В точке 5 глубина второго, «альтернативного» минимума превосходит глубину того минимума, в котором находится шарик, да и ширина второго минимума тоже больше, чем ширина первого. Понятно, что второе устойчивое состояние равновесия теперь уже более предпочтительно, нежели первое. Тем не менее, шарик по-прежнему «живет» в первом состоянии равновесия, и для него по-прежнему, по большому счету, ничего не изменилось. Второе состояние равновесия по-прежнему для него невидимо. Хотя теперь шарик может, если обратит внимание, по косвенным признакам определить, что в системе что-то изменилось: стали не столь крутыми стенки ямки, в которой он находится, да и глубина ямки, кажется, стала поменьше. Но сможет ли шарик за этими незначительными изменениями (которые являются предвестниками дальнейших событий) увидеть нечто более серьезное, чем некоторое изменение окружающей его среды, сможет ли он понять, что его теперешнее состояние равновесия находится под угрозой, зависит от его, шарика, «прозорливости». В подобной простой механической системе, наверное, это не очень сложно, особенно если у шарика есть некоторый опыт, т.е. если он несколько раз уже бывал в подобных ситуациях. Ведь еще небольшое движение, незначительное изменение управляющих параметров, и состояние равновесия, в котором очень долгое время находился шарик, исчезнет (точка 6), и шарик будет переброшен в совершенно иное состояние.
Приведем другой классический пример бифуркации, рассмотренный еще великим Эйлером. Нам понадобится измерительная линейка, тонкий столовый нож, полотно от ножевки, длинная пластмассовая расческа и т.п. Поставьте ее вертикально на твердое основание, а сами, обезопасив руку от травмы, начинайте давить на нее вниз (рис. 8.5). Увеличивая усилие F, вы обнаружите, что при F больших некоторого значения Fb полоска не сохраняет первоначальную прямолинейную форму (рис 8.5а) — это состояние теряет устойчивость, а вместо него возможно одно из двух других состояний (1 или 2 на рис 8.5б), когда полоска искривлена. Причем, какое состояние установится, зависит от разных незначительных факторов (первоначальной деформации полоски, отклонением от вертикали приложенной силы, вибрациями и т.п.). Здесь F — управляющий параметр, Fb — его бифуркационное значение.
Рис. 8.5. Опыт с линейкой: а) состояние линейки до бифуркации (величина F меньше бифуркационного значения); б) два возможных устойчивых состояния, в которые переходит система при превышении силой F бифуркационного значения Fb; в) соответствующая бифуркационная диаграмма
Происходящее в рассмотренной системе удобно иллюстрировать с помощью графиков (рис. 8.5в, где х — отклонение средней точки полоски от вертикали) — бифуркационных диаграмм. На рисунке по горизонтали отложены значения параметра, а по вертикали соответствующие им значения переменной, установившиеся в системе (т.е. это — и не фазовая плоскость и не плоскость параметров, а нечто комбинированное). На диаграмме видно, что вместо одного состояния, отмеченного цифрой 0, после бифуркации существуют и могут быть реализованы на практике состояния 1 и 2. Что касается состояния 0, то оно продолжает в принципе существовать и при значениях F, больших бифуркационного, но не может быть практически реализовано из-за его неустойчивости.
Понятно, что события, подпадающие под определение «бифуркация» (качественное изменение состояния системы при малых изменениях управляющих параметров), вполне можно отыскать и в социальных системах. Примером может служить революция, коренным образом перестраивающая привычную жизнь человеческого общества. Возможны и менее «глобальные» примеры. Человек работает-работает где-либо, и вдруг ни с того ни с сего, вроде бы из-за пустяка говорит: «А гори она огнем, вся эта шарага» и пишет заявление об увольнении. Система переходит в другое, качественно иное состояние.
Следует, однако, отметить следующий аспект: социальные системы чрезвычайно сложны, и поэтому следует помнить о том, что применять существующие в нелинейной динамике понятия к подобным системам (в том числе и понятия «бифуркация», «мультистабильность») следует с осторожностью, памятуя о том, что простой механический перенос может привести к ошибкам, а порой и к фальсификации. Когда речь идет о шарике в потенциальной яме, совершенно понятно, о каких возможных состояниях системы идет речь, какие из них устойчивые, какие нет, наконец, какое состояние реализуется в настоящий момент времени. Но что понимать под возможными состояниями социальной системы? Реализующееся состояние в данный момент времени — единственное, про остальные состояния, «существуют» они (точнее говоря, могли ли они осуществиться вместо теперешнего) или нет, остается только гадать, и наши догадки останутся догадками, о достоверности которых мы тоже можем делать свои заключения, но не более. Понятие «мультистабильность», по всей видимости, может быть применено к социальными системам, но вот «экспериментально» проверить существование мультистабильности в социальных системах, наверное, невозможно. Невозможно показать, что для какого-либо фиксированного момента времени (например, сегодняшнего) помимо того состояния, которое реализуется, «существует» еще одно (или несколько) альтернативных состояний, каждое из которых могло с той или иной вероятностью реализоваться. Предполагать это можно, но экспериментально проверить — нет. И конечно, «увидеть», «почувствовать», что социальная система приближается к точке бифуркации, за которой возникнет качественно другое состояние, существенно сложнее. И если мы видели, что шарик, находящийся в потенциальной ямке, практически до самого последнего момента не «видит» надвигающейся бифуркации (и перехода системы в иное состояние), что говорить о людях и о социальных системах. Н.С. Хрущев, например, не заметил приближение системы к точке бифуркации, отправляясь из отпуска на Пленум ЦК в октябре 1964 года, по результатам которого он был освобожден от должности Первого секретаря ЦК и выведен из состава Президиума, а на следующий день — от должности Председателя Совета Министров СССР. И Гай Юлий Цезарь в 44 году до н.э. также не заметил надвигающейся бифуркации, за что поплатился жизнью.
Обратим внимание еще на один важный аспект, связанный с понятием «бифуркация». В тот момент, когда система (по параметрам) находится вблизи точки бифуркации, очень большую роль начинают играть малые возмущения. Эти возмущения могут носить случайный характер или могут быть целенаправленными, но их роль существенно возрастает. Вернемся к шарику в потенциальной ямке и рассмотрим два состояния системы: вдали и вблизи от точки бифуркации (рис. 8.6). Видно, что когда система находится вдали отточки бифуркации, малые воздействия на нее не приводят к существенным изменениям ее состояния: шарик остается в том же самом положении, как и раньше. Для того чтобы «перебросить» систему в другое возможное состояние, необходимо приложить гораздо большие усилия. В то же самое время, когда система находится вблизи точки бифуркации, даже малого воздействия (которого раньше система просто-напросто не заметила бы) достаточно, чтобы перевести систему из одного состояния в другое.
Рис. 8.6. Система «шарик в потенциальной ямке» вдали и вблизи от точки бифуркации
Итак, вблизи точки бифуркации малые воздействия на систему могут привести к несоизмеримо большим «откликам». Еще одним фактором, который может привести к изменению состояния системы, является малое изменение управляющих параметров. Если система близка к точке бифуркации, то легкое «шевеление» управляющих параметров может привести к тому, что система окажется уже за границей бифуркации (как говорят, в закритической области), и система сама, уже безо всяких внешних воздействий, перейдет в новое состояние. На примере шарика в желобе, после пересечения бифуркационной линии в точке 6 (см. рис. 8.4), устойчивое состояние равновесия, в котором до этого момента находился шарик, сливается с неустойчивым и исчезает, а, следовательно, шарику ничего более не остается, как «перейти» к другому состоянию равновесия.
Примеров подобному поведению систем вблизи линии бифуркации много. По всей видимости, ряд операций на финансовых и фондовых рынках также можно использовать в качестве примера. Организованные действия группы лиц, заинтересованных в проведении той или иной финансовой операции, проведенные в нужный момент, приводят к тому, что либо на систему, находящуюся около состояния бифуркации, оказывается воздействие, выводящее ее из состояния равновесия, либо происходит малое шевеление управляющих параметров, и система оказывается в закритической области. В результате происходит переход системы в новое состояние, например, контрольный пакет акций оказывается у заинтересованного лица. Но если подобную операцию проводить в тот момент, когда система далека от состояния бифуркации, можно затратить большие средства, но желаемого результата не достичь.
Таким образом, воздействуя на систему, находящуюся вблизи бифуркационного состояния, можно добиться кардинальных изменений. Другое дело, что социальные системы — это не шарик в желобе. Определить, когда система приближается к точке бифуркации — сложная задача. Но не менее сложная и не менее важная задача, если возникает желание управлять подобным образом социальными системами, — это определить, в какое состояние перейдет система после того, как она покинет состояние равновесия.
Не стоит, однако, думать, что бифуркация — это всегда какое-либо резкое изменение, когда система изменяется до неузнаваемости. Пример бифуркации с сосуществующими положениями равновесия, описанный выше — один из самых простых. Вообще, в теории бифуркаций существует достаточно большое число различных типов бифуркационных ситуаций. Так, например, различают бифуркации и катастрофы; существует даже теория катастроф. Следует подчеркнуть, что бифуркации могут происходить плавно, подчас незаметно. Пересечение пунктирной линии в точке 2 на рис. 8.4 приводит к тому, что система качественно изменяется (меняется число возможных устойчивых состояний равновесия в системе), следовательно, происходит бифуркация. Однако, как уже говорилось, шарик, находящийся в другой ямке, не замечает произошедшей бифуркации. Другой пример с той же самой системой приведен на рис. 8.7. При движении по плоскости управляющих параметров вдоль линии b = 0 в точке a = 0 происходит бифуркация, состояние системы качественно изменяется, однако это изменение происходит плавно, без «катаклизмов». Шарик может заметить, что в системе что-то изменилось, поскольку его координата х0 вначале (до бифуркации) была равна нулю, а затем стала отличной от нуля. Однако это изменение произошло очень плавно, и ему можно не придать значение.
Рис. 8.7. Изменение состояния системы при движении по плоскости параметров вдоль линии b = 0 в направлении, указанном стрелкой
Но и в этом случае вблизи точки бифуркации малые воздействия на систему играют значительную роль. Именно эти воздействия определяют, в какую из ямок (левую или правую) попадет шарик. Именно эти ничтожные воздействия определяют, по большому счету, дальнейшую судьбу системы. В ситуации, изображенной на рис. 8.7, малые воздействия привели к тому, что шарик оказался в правой ямке. Если, после того как система уйдет от точки бифуркации, потребуется изменить состояние системы, потребуется перебросить шарик в другую ямку, то придется приложить усилия, несоизмеримо больше тех, которые в точке бифуркации определили выбор дальнейшей эволюции системы. Примером такой «мягкой», но заметной бифуркации могут являться демократические выборы. До того момента, пока не прошло голосование, на судьбу дальнейшего развития страны могут повлиять самые незначительные факторы (может быть, вплоть до прически кандидата). После того, как выборы состоялись, изменить что-либо гораздо сложнее.
Недавно опубликована статья И.Пригожина Кость еще не брошена. Послание будущим поколениям. В частности, он пишет следующее. «Будущее не дано нам заранее. Великий французский историк Фернанд Бродель однажды заметил: „События — это пыль». Правильно ли это? Что такое событие? Сразу же приходит аналогия с „бифуркациями», которые изучаются прежде всего в неравновесной физике. Эти бифуркации появляются в особых точках, где траектория, по которой движется система, разделяется на „ветви». Все ветви равно возможны, но только одна из них будет осуществлена. Обычно наблюдается не единственная бифуркация, а целая последовательность бифуркаций… С этой точки зрения история оказывается последовательностью бифуркаций».
Далее И. Пригожин подчеркивает, что за выбор ветви, которая возникает после точки бифуркации, отвечают флуктуации на микроскопическом уровне (они определяют событие, которое произойдет). В применении к обществу (по Пригожину такое применение — метафора) событие представляет собой возникновение новой социальной структуры после прохождения бифуркации, а флуктуации — следствие индивидуальных действий. Таким образом, событие имеет микроструктуру. В качестве примера И. Пригожин рассматривает революцию 1917 года в России, указывая, что конец царского режима мог принять различные формы. Он считает, что ветвь, по которой пошло развитие, была результатом действий «флуктуации», связанной с отсутствием дальновидности у царя, непопулярностью его жены, слабостью Керенского, насилием Ленина. Эта микроструктура и обусловила все последующие события.
«Мое послание будущим поколениям состоит, стало быть, в том, что кость еще не брошена, что ветвь, по которой пойдет развитие после бифуркации, еще не выбрана. Мы живем в эпоху флуктуаций, когда индивидуальное действие остается существенным… Я верю в возникновение необходимых флуктуаций, посредством которых те опасности, которые мы ощущаем сегодня, могли бы быть успешно преодолены».
Лекция девятая. Клеточные автоматы
Клеточные автоматы были задуманы в конце сороковых годов нашего столетия Дж. фон Нейманом и К. Цусе как универсальная вычислительная среда для построения алгоритмов. Клеточный автомат представляет собой некоторое дискретное пространство, на котором происходит эволюция, и набор правил, по которым эта эволюция осуществляется. Самым знаменитым клеточным автоматом является так называемая игра Жизнь, предложенная в 1970 году математиком Джоном Конуэем. Можно считать, что игра «Жизнь» описывает популяцию неких вымышленных организмов, развивающуюся во времени и пространстве в соответствии с заданными законами размножения и вымирания. Исследуя эволюцию этих организмов, можно отчетливо наблюдать процессы самоорганизации и структурообразования.
Пространством, на котором происходит эволюция, в игре «Жизнь» является плоскость, разделенная на квадратные ячейки. Размеры доски (количество ячеек по вертикали и горизонтали) могут быть различными — читатель может экспериментировать на обычной шахматной доске размером 8×8 клеток, хотя предпочтительнее, разумеется, отслеживать эволюцию с помощью компьютера. В дальнейшем будем рассматривать бесконечные доски, т. е. доски с таким большим числом клеток, что границы доски не достигаются, а, следовательно, не играют существенной роли.
Будем называть клетку «живой», если на ней находится фишка, в противном случае будем считать ее «мертвой» или «пустой». Время в игре «Жизнь» дискретно и измеряется в поколениях: каждый момент дискретного времени соответствует одному поколению. Существует набор простых правил, описывающих рождение и гибель клеток от поколения к поколению:
- Каждая живая клетка, у которой имеется две или три живые соседние клетки, выживает и переходит в следующее поколение.
- Каждая живая клетка, у которой оказывается меньше двух живых соседей, в следующем поколении погибает от одиночества.
- Каждая живая клетка, у которой оказывается больше трех живых соседей, в следующем поколении погибает от перенаселенности.
- В каждой пустой клетке, у которой оказывается ровно три живых соседа, в следующем поколении рождается новая жизнь.
Набор эволюционных правил очень прост, а эволюция живых клеток из поколения в поколение может быть очень сложной и красивой. Именно поэтому игра «Жизнь» завоевала широкую известность и стала классическим объектом той части синергетики, которая связана с самоорганизацией и структурообразованием. Рассмотрим эволюцию триплета (в игре «Жизнь» триплетом называется любая конфигурация из трех живых клеток), изображенного на рис. 9.1а. Как нетрудно видеть, из набора эволюционных правил игры «Жизнь» следует, что верхняя и нижняя клетки конфигурации погибают от одиночества (на рис. 9.1б они зачеркнуты). Центральная же клетка имеет двух живых соседей, поэтому она выживает и переходит в следующее поколение. Кроме этого, на двух клетках, прилегающих к триплету, рождается в следующем поколении новая жизнь (см. рис. 9.1б). Особо следует отметить, что гибнущие клетки погибнут только в следующем поколении, а, следовательно, в настоящий момент времени (несмотря на то, что они в следующий момент времени погибнут) эти клетки продолжают оказывать влияние на эволюцию системы. Точно также рождающиеся клетки появятся на игровом поле лишь в следующем поколении, и значит, в текущем поколении они никакого влияния на эволюцию системы не оказывают.
Рис. 9.1. Эволюция триплета «мигалка»: а) начальная конфигурация в первом поколении; б) то же самое первое поколение, с указанием гибнущих и рождающихся клеток; в) конфигурация «мигалка» во втором поколении
Таким образом, в следующем, втором поколении начальная конфигурация из трех вертикальных клеток превращается в три живые клетки, расположенные горизонтально (рис.9.1в). Нетрудно понять, что в следующем (третьем) поколении конфигурация будет полностью повторять первоначальную. Иными словами, исходная конфигурация оказывается периодической с периодом 2 (воспроизводит себя на втором ходу) — она попеременно превращается то в вертикальный, то в горизонтальный ряд из трех живых клеток. За свое поведение этот триплет был назван «мигалкой» или «семафором».
Другой триплет, показанный на рис. 9.2а, в следующем поколении превращается в устойчивую конфигурацию под названием «блок» — нетрудно видеть, что любая клетка из этой конфигурации имеет трех живых соседей, а следовательно, переходит в следующее поколение. Подобные стационарные структуры довольно часто появляются в ходе эволюции. Конуэл называет их «любителями спокойной жизни».
Рис. 9.2. Исходный триплет (а); тот же самый триплет с указанием рождающейся клетки (б) и второе поколение — устойчивая конфигурация «блок» (в)
Нетрудно видеть, что остальные триплеты, отличные от только что описанных (разумеется, не считая тех триплетов, которые совпадают с вышеописанными при повороте или зеркальном отражении) быстро погибают в ходе эволюции. На рис. 9.3 приведены еще несколько часто встречающихся стационарных конфигураций, а на рис. 9.4 — две периодические конфигурации. Первая из них (рис. 9.4а) называется «опрокидывателем», поскольку каждые семь поколений верх и низ у этой конфигурации меняются местами, а конфигурация, приведенная на рис. 9.4б, имеет период, равный четырем.
Рис. 9.3. Некоторые стационарные структуры, возникающие в игре «Жизнь»: а) бадья; б) лодка; в) корабль; г) каравай
Рис. 9.4. Периодические конфигурации игры «Жизнь»
Таким образом, уже из рассмотрения простейших конфигураций можно сделать вывод о том, что в игре «Жизнь» возможны следующие виды эволюционного развития популяции:
- Популяция полностью вымирает через конечное число поколений.
- Популяция с течением времени превращается в стационарную структуру, которая больше не изменяется.
- Из первоначальной популяции возникает периодически изменяющаяся во времени структура.
Следует отметить, в игре «Жизнь» существуют конфигурации, называемые «долгожителями» — это конфигурации, состоящие менее чем из десяти живых клеток, у которых устойчивое состояние не достигается в течение по крайней мере пятидесяти поколений. Несколько таких долгожителей представлены на рис. 9.5. Конфигурация, представленная на рис. 9.5а, носит название «r-пентамино», а ее эволюция оказывается несколько более длительной, чем эволюции конфигураций, рассмотренных до этого. Сам Конуэй проследил эволюцию «r-пентамино» до четыреста шестидесятого хода и описывает достигнутую конфигурацию следующим образом: «…от фигуры осталось множество мертвых (не изменяющихся) обломков и лишь несколько малых областей, в которых все еще теплилась жизнь, так что отнюдь не очевидно, что процесс эволюции должен происходить бесконечно долго».
Рис. 9.5. Конфигурации в игре «Жизнь», названные «долгожителями»
Однако эта конфигурация эволюционирует еще некоторое время и превращается в периодически пульсирующую конфигурацию с периодом 2 лишь после 1 103 поколений. Конфигурация, изображенная на рис. 9.5б, носит название «ворота» (Конуэй называет эту конфигурацию «прописная буква π»). Время жизни этой конфигурации оказывается существенно меньше, чем у «r-пентамино» — после всего лишь 173 поколений она распадается на пять «мигалок», шесть «блоков» и два «пруда». Наконец, «долгожитель», приведенный на рис. 9.5в, превращается в устойчивую конфигурацию, состоящую из шести «блоков», двенадцати «мигалок» и одного «каравая» в 609-м поколении.
Но оказывается, возможные сценарии эволюции не ограничиваются приведенными выше. Существует еще один класс структур в игре «Жизнь», которые эволюционируют периодически не только во времени, но и в пространстве. На рис. 9.6 приведена простейшая пространственно-временная периодическая структура, называемая «глайдером» (от англ. to glide — скользить). Подобные перемещающиеся конфигурации называются «космическими кораблями» (рис. 9.7). «Глайдер» считается «космическим кораблем» легчайшего веса, так как все остальные космические корабли состоят из большего числа живых клеток. Во время полета «космических кораблей» (исключая «глайдер») из них вылетают «искры», которые тут же гаснут при дальнейшем движении «кораблей». «Космические корабли» не могут занимать в длину более шести клеток, в противном случае на доске начинают появляться различные мелкие конфигурации, препятствующие дальнейшему движению «космического корабля», что ведет, в конце концов, к его разрушению и гибели. Однако, как выяснил Конуэй, таким «космическим кораблям» (их называют «сверхтяжелыми») необходим эскорт из двух или большего числа «кораблей» меньших размеров. Эскорт не дает возникать различным препятствиям на пути «сверхтяжелого космического корабля».
Рис. 9.6. Глайдер (пространственно-временная периодическая структура, которая воспроизводит себя через четыре хода, сдвигаясь на одну клетку вниз и вправо)
Рис. 9.7. Космические корабли
Таким образом, к возможным видам эволюционного развития, описанным выше, следует добавить:
- Популяция развивается в течение длительного интервала дискретного времени, не погибая и не повторяя себя в своем развитии.
- Популяция является периодической пространственно-временной структурой, периодически изменяющейся во времени и передвигающейся по эволюционному пространству.
- Популяция является неограниченно растущей, на бесконечном эволюционном пространстве ее численность растет неограниченно.
Любая конфигурация порождает в игре «Жизнь» только одну конфигурацию-наследника, а вот конфигураций-родителей может быть несколько. Иными словами, зная текущую конфигурацию живых клеток, можно однозначно определить конфигурацию, которая появится в следующем поколении, но вот однозначно определить конфигурацию, существовавшую на эволюционном пространстве в предшествующий момент дискретного времени, невозможно, поскольку текущая конфигурация в общем случае может быть порождена несколькими различными конфигурациями. С другой стороны, существуют такие конфигурации, у которых нет «конфигураций-родителей». Такие конфигурации называются «садами Эдема». Понятно, что «сад Эдема» не может появиться в результате эволюционного развития, а должен быть искусственно привнесен извне. Другим интересным моментом является то обстоятельство, что хотя эволюционные правила известны и их число невелико, предсказать заранее (как говорят, a priori) результат эволюции невозможно, пока последовательно не будут пройдены все поколения от начальной конфигурации до искомой.
Если вообразить достаточно большое количество «первичного бульона» из хаотически распределенных живых клеток, то можно ли ожидать появление в эволюционном пространстве каких-либо самовоспроизводящихся существ, а также того, что наиболее приспособленные из них к выживанию будут благополучно здравствовать дольше других. Поиграть в «Жизнь» можно здесь.
Искусственная жизнь. Перейдем теперь от клеточных автоматов к рассмотрению направления, связанного с исследованием эволюционных процессов, называемого Artificial Life (AL) — искусственная жизнь. В основе этого направления лежит чрезвычайно смелая (наверное, можно даже сказать, дерзкая) идея перенести эволюционные процессы в другую, неуглеродную среду. Подобной средой может стать оперативная память компьютера. Речь не идет о моделировании каких-либо процессов биологических объектов, реально существующих в нашем мире, с помощью электронных вычислительных машин. Компьютер выступает в этом случае не как средство моделирования, а скорее, как среда обитания, в которой могут существовать «цифровые организмы», живущие и эволюционирующие по другим законам цифрового мира.
Еще один вопрос, связанный с цифровой эволюцией, — вопрос о возможности возникновения «цифрового интеллекта». Эта тема является благодатной почвой для научно-фантастических произведений. В настоящее время трудно сказать по этому поводу что-либо определенное, но если возникновение «цифрового разума» и возможно, то, по всей вероятности, он может существенно отличаться от разума «биологического», поскольку ход эволюционного развития цифровой жизни происходит по другим законам, нежели развитие биологической жизни. С другой стороны, возможно существование общих закономерностей эволюционного развития, свойственных самым различным формам жизни, а, следовательно, и «цифровой разум» (конечно, если его возникновение возможно) может быть похож на разум биологический. Но пока все это остается лишь на уровне гипотез, и дать ответы на поставленные вопросы может лишь время (отдаленное от нас, а может быть и не очень).
Что могут дать человечеству исследования в области искусственной жизни. С одной стороны, эти исследования могут служить ключом к пониманию наиболее общих закономерностей эволюционного развития. С другой стороны, если люди научатся понимать эти закономерности, то, вмешиваясь в естественный ход эволюции цифровой жизни, внося изменения в структуру организмов, проводя селекцию организмов с нужными свойствами, может быть, удастся «вырастить» программные продукты (например, операционные системы, которые управляют работой компьютеров) с такими возможностями, которые сегодня даже трудно себе и представить. Понимание же наиболее общих закономерностей эволюционного развития может быть использовано и при селекции новых биологических видов.
Клеточные автоматы и моделирование динамики биологических популяций. У читателя вполне может сформироваться впечатление, что клеточные автоматы — это не более чем забавная игрушка. Однако это совершенно неверное представление. Научные исследования с использованием клеточных автоматов на сегодняшний день привлекают к себе все большее внимание ученых в самых различных областях науки. Во многом этому способствует бурное развитие вычислительной техники, без которой изучение моделей типа клеточных автоматов было бы практически невозможно.
Особенно интересен вопрос о возможности моделирования динамики различных биологических популяций с помощью клеточных автоматов. Рассмотрим клеточный автомат, с помощью которого удалось объяснить некоторые закономерности динамики численности народонаселения земного шара в тех или иных локальных областях. Такой клеточный автомат, подчиняющийся своим правилам (похожим, но не идентичным правилам в игре «Жизнь»), называют решеточным газом.
«Решеточный газ есть набор „атомов», положение в пространстве каждого из которых может принимать только дискретные значения. Это дискретное положение атома на каждом последующем дискретном шаге во времени определяется геометрией решетки, которая в свою очередь определяется ближайшими γ соседями каждой клетки решетки. В каждой клетке может находиться не более одного атома…»
Оказывается, эволюция числа клеток описывается хорошо известным в математической экологии уравнением Ферхюльста (логистическим уравнением). Интерес к модели решеточного газа и результатам, полученным с помощью нее, объясняется возможностью качественного описания особенностей пространственно-временной динамики численности «реальных» популяций. Обсудим в этом контексте некоторые проблемы демографии и, в частности, динамику численности народонаселения тех или иных локальных областей, используя результаты, полученные с помощью решеточного газа. В качестве примера приведем некоторые демографические данные численности населения США за последние 200 лет, которые были получены из базы данных университета Вирджинии.
Если рассмотреть динамику численности населения различных американских штатов, то можно заметить, что наблюдается разделение штатов на две большие основные группы (см. Короновский А. А., Лопатников Д. И., Храмов А. Е. Некоторые аспекты изменения численности народонаселения США с точки зрения нелинейной динамики). У первой группы, в которую были включены штаты, входившие в состав США с самого момента образования (данные территории начали заселяться с самого начала колонизации американского континента), — Флорида, Алабама, Южная и Северная Каролина, Нью-Йорк, Коннектикут и др., численность населения как функция времени хорошо описывается логистической кривой (см. рис. 9.8а, на котором представлена зависимость численности населения штата Нью-Йорк). Заметим также, что у этих штатов наибольшая плотность населения, и, как следствие, наиболее однородное распределение населения по территории.
Рис. 9.8. Динамика численности народонаселения штатов: а) Нью-Йорк и б) Миннесота. Пунктиром показаны соответствующие логистические кривые, наилучшим образом аппроксимирующие демографические данные. Здесь кружки — демографические данные начиная с 1780 года и интервалом в 10 лет
Другую группу составляют штаты, присоединенные к США существенно позже. Это внутренние территории, которые вначале были свободными (на них проживали индейские племена), затем начиналась их колонизация, на них появлялись переселенцы, земли получали статус территорий, на которые правительство США заявляло свои претензии, и затем соответствующие территории получали статус штатов. Это штаты Айова, Миннесота, Колорадо, Канзас, Оклахома и т.д. Для этих штатов типична динамика численности населения, приведенная на рис. 9.8б (он соответствует штату Миннесота, который до 1849 года был так называемой неорганизованной территорией, затем получил статус территории и только в 1858 году стал полноправным штатом). Для этих штатов, для которых характерно постепенное заселение (с одной стороны, здесь играли роль большое число переселенцев, с другой стороны — имело место коренное население), численность населения сначала обгоняла соответствующую логистическую кривую, а затем отставала от нее.
Интересно, что динамика решеточного газа, описывающего распространение «клеточной» популяции на территорию, на которой уже есть население, демонстрирует аналогичную динамику численности популяции. На рис. 9.9 приведена зависимость числа активных клеток решеточного газа N от дискретного времени. Начальные условия выбраны так, что имеется небольшая область с высокой плотностью активных клеток, а остальная область моделирования заполнена равномерно небольшим числом клеток. Сравнивая рис. 9.8б и 9.9, видно, что динамика обеих систем качественно подобна. Итак, следует признать, что «клеточная» (или «решеточная») популяция может оказаться весьма эффективным инструментом для исследования различных задач в биологии, экологии и даже демографии и социологии.
Рис. 9.9. Динамика численности «клеточной» популяции, распространяющейся на территорию, где уже есть население с небольшой плотностью расселения. Кривая 1 соответствует решеточному газу, 2 — уравнению Ферхюльста (сравни с рис. 9.8б)
Лекция десятая. Динамический хаос
Как возникает случайность в динамической системе? Главная сила науки состоит в возможности предсказывать. Скажем, затмения можно предсказать на тысячу лет вперед на основе законов гравитации. Однако почему-то нельзя точно предсказать погоду, хотя атмосферные течения подчиняются физическим законам столь же строго. Нельзя точно предсказать течение горного ручья и рассчитать траекторию шара в биллиарде. В чем же дело? Почему в указанных явлениях теряется четкая связь между причиной и следствием? Пьер Симон Лаплас считал, что законы природы подразумевают полную предсказуемость и строгий детерминизм, а случайность — порождение несовершенства наблюдений (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей). И более ста лет казалось, что в принципе он прав. Применение лапласовского детерминизма к социальным явлениям привело к известному философскому выводу об отсутствии свободной воли людей, о предопределенности их поведения.
Ощутимый удар лапласовскому детерминизму нанес Гейзенберг, который сформулировал принцип неопределенности в квантовой механике. Этот принцип утверждает, что нельзя одновременно точно измерить положение и скорость частицы. В частности, на основе этого принципа объясняется, почему процессы, происходящие в ядре (например, радиоактивный распад), принципиально нельзя предсказать, сколько бы информации о нем не собрали. Но, когда речь идет о непредсказуемости поведения крупномасштабных систем, принцип неопределенности ни при чем. Нужно искать другие объяснения.
Как может появиться случайность, а, следовательно, и непредсказуемость в детерминированной системе? Может ли динамическая система, описываемая уравнением вида
в которые не входят случайные функции, давать такое решение хi = xi(t), что при произвольном выборе хiполучаем случайную последовательность цифр? Не противоречит ли это известной теореме существования и единственности решения, которая гарантирует при заданных начальных условиях однозначное детерминированное поведение?
Если система обладает большим числом степеней свободы (например, газ в сосуде), то ситуация ясна: систему можно описать динамическим способом, но решение задачи становится нереальным. Дело в том, что мы не сумеем задать точно начальные координаты и скорости, допустим 1019 молекул, находящихся в 1 см3 газа. И если даже зададим, то ЭВМ не под силу рассчитать траектории такого числа частиц с учетом их столкновений друг с другом. Но как может появиться случайность в системе с небольшим числом степеней свободы, например, в идеализированном биллиарде, в котором шары катятся по столу и сталкиваются без потери энергии?
Дело в неустойчивости всех или почти всех траекторий системы. Игрок ударяет кием по шару, что приводит к серии столкновений. Предположим, что он полностью контролирует свой удар и хочет предсказать траекторию шара, по которому ударил. Так вот, если он пренебрежет даже гравитационным притяжением электрона на краю Галактики (очень слабое воздействие!), то его прогноз будет неправильным уже через минуту. Это объясняется тем, что шары не идеальны и малые отклонения от идеальной траектории, возникающие при каждом столкновении, нарастают, причем рост происходит экспоненциально. Таким образом, даже самое малое воздействие достигает макроскопических размеров. Это одно из основных свойств хаоса. Наиболее четко эту мысль выразили Н.С. Крылов, а затем Макс Борн. Определение детерминированности, данное М. Борном.
Каждое физическое состояние системы измеряется всегда с малой, но конечной неточностью ε. Поэтому оно определяется не числом, а некоторым вероятностным распределением. Задача состоит в том, чтобы на основе известного начального распределения предсказать распределения в момент времени t. Если данное решение устойчиво (начальное возмущение не нарастает), то любое последующее состояние предсказуемо, и система может считаться детерминированной. Такое определение детерминированности по М. Борну отличается от традиционного определения изменением последовательности предельных переходов при εg 0 и tg∞. Обычно сначала область начального рассеяния стягивается в точку, а затем смотрится поведение при tg∞. Конечно, получается полная предсказуемость. Этот путь является нефизичным и заменяется другим: сначала при заданном ε определяется поведение траекторий и область конечного рассеяния при любом t, в том числе область рассеяния при tg∞, а затем уже начальное рассеяние устремляется к точке. Если область конечного рассеяния при tg∞ нарастает, то поведение системы непредсказуемо. Экспоненциальная неустойчивость траекторий, характерная для хаотической динамики, нанесла второй удар по детерминизму Лапласа. Существование хаоса гарантирует быстрое превышение пределов предсказуемости и опрокидывает «лапласовские надежды», что ошибки останутся ограниченными или будут хотя бы медленно расти, допуская в конечном счете долгосрочный прогноз.
Для возникновения хаоса в динамической системе необходимо, чтобы в фазовом пространстве системы:
- все (или почти все) соседние траектории внутри некоторой области разбегались; т.е., малый разброс начальных отклонений ε вел к тому, что при достаточно большом t уже нельзя было точно определить состояние системы, которая может находиться в любой точке области σ (рис. 10.1);
- все траектории оставались внутри ограниченного фазового объема.
Рис. 10.1. Эволюция начального распределения на фазовой плоскости в случае неустойчивого состояния равновесия
Для консервативных динамических систем (т.е. систем без потерь), для которых их фазовый объем (с некоторой плотностью) по определению сохраняется справедлива теорема Пуанкаре о возвращении, которая гласит, что почти каждая точка любой области фазового пространства, двигаясь по траектории, вернется в эту область.
В трехмерном пространстве траектории могут разбегаться по двумерной поверхности, а возвращаться, выйдя в пространство. Траектория при этом может выглядеть, например, как раскручивающаяся плоская спираль, хвост которой, возвращаясь к ее началу, и вновь раскручивается (рис. 10.2 см. также рис. 5.8б). Располагаясь таким образом, траектория заполняет весь аттрактор, нигде не замыкаясь, и ведет себя сложно и запутанно.
Рис. 10.2. Пример возвращающейся неустойчивой траектории, представляющей собой раскручивающуюся плоскую спираль, хвост которой, загибаясь к ее началу, и вновь раскручивается
Объект в фазовом пространстве, к которому стремятся все или почти все траектории и на котором они неустойчивы, называется странным аттрактором, в отличие от простых — состояний равновесия и предельных циклов. Странный аттрактор – объект, в котором траектории по одним направлениям разбегаются, по другим – притягиваются. Может быть, удивление подобным поведением и породило прилагательное «странный»? Ведь в простых аттракторах есть только притяжение. Как пишет Д.Рюэль в книге Случайность и хаос, странные аттракторы не являются гладкими кривыми или поверхностями, но имеют «не целую размерность», т.е., являются фрактальными объектами. Далее, и это еще более важно, движение на странном аттракторе выказывает чувствительную зависимость от начальных условий. И, наконец, при том, что странные аттракторы имеют лишь конечную размерность, временной анализ частот выявляет континуум частот… Возникла новая парадигма, которая получила имя — хаос, — данное ей Джимом Йорке, прикладным математиком, работающим в Университете Мэриленда. То, что мы сейчас называем хаосом, является временной эволюцией с чувствительной зависимостью от начальных условий.
Сценарии перехода к хаосу. В 1976 году американский специалист в области математической и теоретической физики Митчел Фейгенбаум сделал открытие, состоящее в том, что сценарий перехода к хаосу через бесконечный каскад бифуркаций удвоения периода универсален для большого класса динамических систем.
Что уже было известно к этому времени и могло стать источником вдохновения для Фейгенбаума? Во-первых, еще в 1971 году было обнаружено интересное свойство решений уравнений типа xn+1 = λf(xn): при изменении параметра λ существующее периодическое решение, имеющее период Т, теряет устойчивость, а устойчивым становится решение с периодом 2Т, затем 4Т и т.д. Интервал изменения параметра λ, в пределах которого цикл периода 2n устойчив, быстро сужается. Все значения λ, в которых происходит бифуркация удвоения периода, сгущаются к некоторому значению λ = λкр. Как только λ становится больше λкр внутри некоторой области фазового пространства, оказывается бесконечное число неустойчивых циклов. Вслед за этим сложным образованием сразу появляется хаотический (странный) аттрактор.
Во-вторых, к этому времени появились сомнения в сценарии возникновения турбулентности по Ландау. В работе Д. Рюэля (Франция) и Ф.Такенса (Нидерланды) возникновение турбулентности связывалось с появлением странного аттрактора, который возникал после небольшого числа (трех) бифуркаций. Разумеется, появилась идея связать непрерывный переход к турбулентности с возможностью реализации в течении бесконечного каскада бифуркаций удвоения периода. М. Фейгенбаум анализировал логистическое уравнение xn+1 = λxn(1 – xn). Он хотел изучить комплексные аналитические свойства функций, порождаемых таким отображением. Уравнение аналитически не решалось, и Фейгенбаум занялся численными расчетами значений параметра λ, при которых происходило каждое удвоение. Фейгенбаум заметил, что значения параметров λ, соответствующие каждому удвоению, сходятся как геометрическая прогрессия. Это было удивительно: каждый последующий шаг можно было считать аналитически. Знаменатель прогрессии теперь носит название постоянной Фейгенбаума, его обозначают буквой δ, он равен 4,6692016…
В дальнейшем оказалось, что последовательность удвоений обладает свойством универсальности, которое не зависит от конкретных особенностей системы, а во многих случаях и от размерности фазового пространства. В чем же заключается эта универсальность? В том, что Фейгенбаум «выудил» геометрическую прогрессию: расстояние между значениями параметра λn, при котором рождается цикл периода 2n, и значением λкр, вслед за которым в системе возникает хаос, удовлетворяет условию (λкр – λn) = const δn. Полученный Фейгенбаумом результат, в частности, означал, что если в эксперименте обнаружены несколько первых удвоений, то можно предсказать значение λкр, после достижения которого рождается хаос.
Рис. 10.3. «Поваленное фиговое дерево» (бифуркационная диаграмма) для логистического уравнения
Получается, что между хаосом и порядком существует глубокая внутренняя связь: непериодический случайный процесс получается, как предел рождения периодических структур, т.е. согласно сценарию Фейгенбаума, хаос есть цикл S2∞. Независимо от конкретного вида системы, от степени ее сложности, теория Фейгенбаума дает вполне определенные количественные предсказания. Интересно, что по этому же сценарию (сценарию Фейгенбаума или, как его еще называют «переход к хаосу через каскад удвоений периода») возникает хаос и в нелинейных динамических системах, описываемых дифференциальными уравнениями, причем в таких системах опять появляются картины, аналогичные рис. 10.3, на котором показано «поваленное фиговое дерево».
Другие сценарии возникновения хаоса: перемежаемость и разрушение квазипериодических колебаний. Наиболее часто встречающийся в приложениях переход к хаосу — перемежаемость, который впервые описали французские физики П. Манневиль и И. Помо в 1980 году. На осциллограмме перемежаемость выглядит как постепенное (при изменении параметра) исчезновение периодических колебаний за счет их прерывания хаотическими всплесками (рис. 10.4).
Рис. 10.4. Зависимость переменной х от дискретного времени n для логистического отображения при переходе от цикла периода 3 к хаосу по сценарию перемежаемости с уменьшением управляющего параметра λ
Если в системе возник хаос, то возникает вопрос: «Насколько она хаотична?» Статистической характеристикой хаоса служит размерность странного аттрактора, которая отличается от привычной размерности линии, плоскости, объема. Оказывается, что странные аттракторы демонстрируют фрактальную структуру, и, соответственно, их размерность, является дробной.
На этом хочется поставить точку в обсуждении весьма непростых вопросов, касающихся сложного нерегулярного поведения детерминированных динамических систем (явления динамического или детерминированного хаоса). Для тех, кто захочет более глубоко и подробно познакомиться с этими вопросами, можно порекомендовать курс лекций профессора С.П. Кузнецова Динамический хаос.
Рекомендуемая литература
- Андронов А. А., Витт А. А., Хайкин С. Э. Теория колебаний. М.: Наука, 1981.
- Арнольд В. И. Теория катастроф. М.: URSS, 2009.
- Берже П., Помо И., Видаль К. Порядок в хаосе. О детерминистическом подходе к турбулентности. М.: Мир, 1991.
- Ван-Дейк М. Альбом течений жидкости и газа. М.: Мир, 1986.
- Вартофский М. Модели. Репрезентация и научное понимание / Пер. с англ. М.: Прогресс, 1988.
- Гласс И. Ударные волны и человек. М.: Мир, 1977.
- Глейк Дж. Хаос. Создание новой науки. СПб.: Амфора, 2001.
- Данилов Ю.А. Лекции по нелинейной динамике. М.: 3-е изд. М.: Книжный дом «Либрокомл/URSS, 2010.
- Данилов Ю.А., Кадомцев Б.Б. Что такое Синергетика? // Нелинейные волны. Самоорганизация. М.: Наука, 1983; С. 5–16.
- Данилов Ю.А. Роль и место синергетики в современной науке // Онтология и эпистемология синергетики. М.: ИФ РАН, 1997. С. 5–11.
- Жилин Д.М. Теория систем. Опыт построения курса – М.: Либроком, 2004. – 176 с.
- Зарубин В. С. Математическое моделирование в технике. М.: МГТУ им. Н.Э. Баумана, 2001.
- Иванов Б.Н. Мир физической гидродинамики. М.: URSS, 2002.
- Капица С. П., Курдюмов С. П., Малинецкий Г. Г. Синергетика и прогнозы будущего. М.: Наука, 1997; 3-е изд. М.: URSS, 2003.
- Климонтович Ю.Л. Введение в физику открытых систем. М.: Янус-К, 2002.
- Князева Е. Н., Курдюмов С. П. Основания синергетики. М.: Книжный дом Либроком/URSS, 2010.
- Кондратьев Н.Д. Большие циклы конъюнктуры и теория предвидения. – М.: Экономика, 2002. – 768 с.
- Короновский А. А., Трубецков Д. И. Нелинейная динамика в действии. Саратов: Изд-во ГосУНЦ «Колледж», 2002.
- Крайтчфилд Д. П., Фармер Дж. Д., Паккард Н.Х., Шоу Р. С. Хаос // В мире науки. 1987. №2. С. 16-28.
- Краснощеков П. С., Петров А. А. Принципы построения моделей. М.: Изд-во МГУ, 1983.
- Кузнецов С. П. Динамический хаос. М.: Физматлит, 2001.
- Кузнецов А. П., Кузнецове. П., Рыскин Н. М. Нелинейные колебания. М.: Физматлит, 2002.
- Малинецкий Г.Г, Потапов А. Б. Современные проблемы нелинейной динамики. М.: URSS, 2002.
- Мандельброт Бенуа. Фрактальная геометрия природы. – Ижевск: Институт компьютерных исследований, 2010. – 676 с.
- Математическое моделирование / Под ред. Дж. Эндрюса и Р. Мак-Лоуна; Пер. с англ. М.: Мир, 1979.
- Моисеев Н.Н. Математика ставит эксперимент. М.: Наука, 1979.
- Моисеев Н.Н. Расставание с простотой. – М.: Аграф, 1998. – 480 с.
- Мун Ф. Хаотические колебания. М.: Мир, 1990.
- Мышкис А. Д. Элементы теории математических моделей. М.: Книжный дом Либроком/URSS, 2009.
- Неймарк Ю. И. Математические модели естествознания и техники. Н. Новгород, Вып. 1. 1994; Вып. 2. 1996; Вып. 3. 1997.
- Николис Г., Пригожим И. Познание сложного. М.: Издательство ЛКИ/URSS, 2008.
- Ньюэлл А. Солитоны в математике и физике. – М.: Мир, 1989. – 326 с.
- Общероссийский естественно-научный журнал «Изв. высш. учеб. заведений. Прикладная нелинейная динамика».
- Пайтген Х.-О., Рихтер П.Х. Красота фракталов. Образы комплексных динамических систем. М.: Мир, 1993.
- Петерс Э. Хаос и порядок на рынках капитала. – М.: Мир, 2000. – 336 с.
- Постон Т., Стюарт И. Теория катастроф. М.: Мир, 1980.
- Рыскин Н. М., Трубецков Д. И. Нелинейные волны. М.: Физматлит, 2001.
- Рюэль Д. Случайность и хаос. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 192 с.
- Синергетическая парадигма: Многообразие поисков и подходов. М.: Прогресс-Традиция, 2000.
- Синергетическая парадигма: Нелинейное мышление в науке и искусстве. М.: Прогресс-Традиция, 2002.
- Синергетическая парадигма: Человек и общество в условиях нестабильности. М.: Прогресс-Традиция, 2003.
- Сноу Ч. П. Две культуры. М.: Прогресс, 1973.
- Соросовский образовательный журнал
- Стасенко А.Л. Волны на воде и «Заморские гости» Рериха // Квант. 1972. № 9. С. 10. (Статья повторно напечатана в журнале: Квант. 1990. № 1. С. 24-29, 62).
- Тарасенко В. Фрактальная логика. М.: Книжный дом Либроком/URSS, 2009.
- Тоффлер Э. Третья волна. – М.: АСТ, 2002. – 784 с.
- Тоффоли Т., Марголус Н. Машины клеточных автоматов. М.: Мир, 1991.
- Трубецков Д.И., Мчедлова Е. С., Красичков Л. В. Введение в теорию самоорганизации открытых систем. М.: Физматлит, 2002.
- Трубецков Д. И., Рожнев А. Г. Линейные колебания и волны. М.: Физматлит, 2001.
- Трубецков Д.И. Введение в синергетику. Колебания и волны. М.: URSS, 2003.
- Трубецков Д.И. Введение в синергетику. Хаос и структуры. М.: URSS, 2004.
- Трубецков Д.И. Колебания и волны для гуманитариев. Саратов: Изд-во ГосУНЦ «Колледж», 1997.
- Федер Е. Фракталы. М.: Мир, 1991.
- Фейнберг Е. Л. Две культуры. Интуиция и логика в искусстве и науке. Фрязино: «Век2», 2004.
- Филиппов А.Т. Многоликий солитон. М.: Наука, 1990.
- Хакен Г. Синергетика. Иерархия неустойчивостей в самоорганизующихся системах и устройствах. М.: Мир, 1985.
- Хакен Г. Тайны природы. Синергетика: наука о взаимодействии. – Ижевск: Институт компьютерных исследований, 2003. – 320 с.
- Хорафас Д.Н. Системы и моделирование. М.: Мир, 1967.
- Шустер Г. Детерминированный хаос. М.: Мир, 1988.
- Эткинс П. Порядок и беспорядок в природе. М.: Мир, 1987.

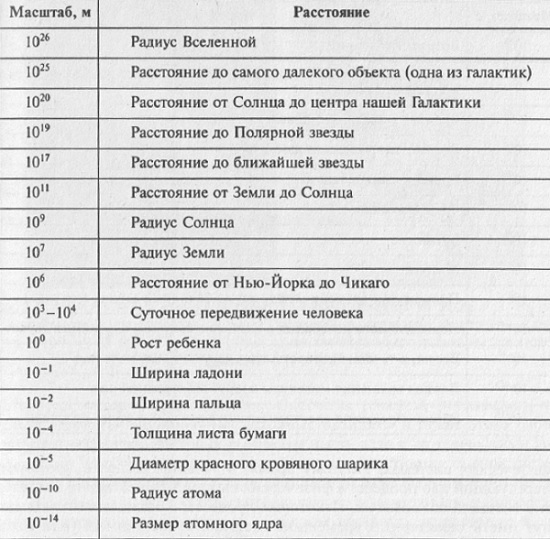


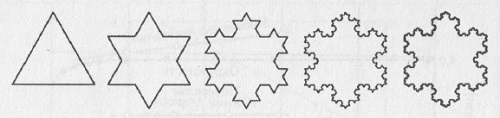

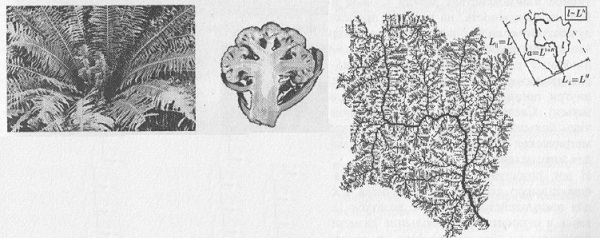
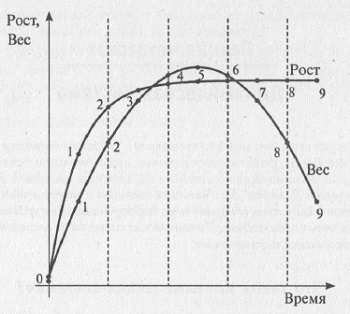
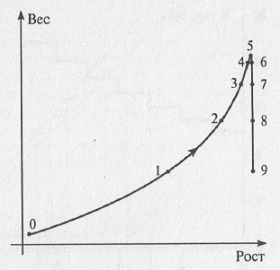

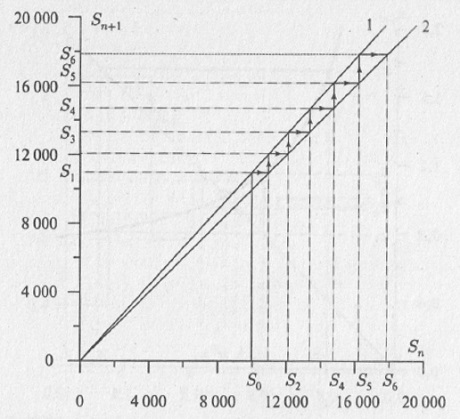
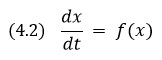
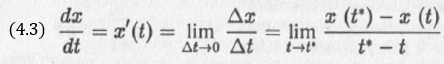
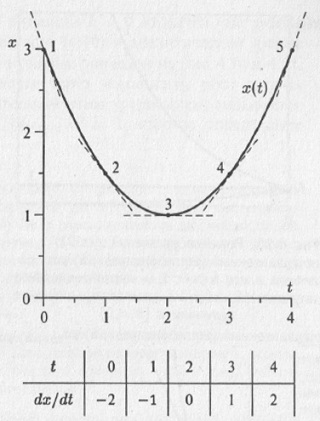
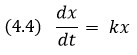
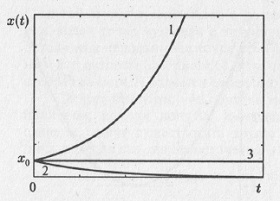
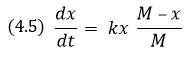
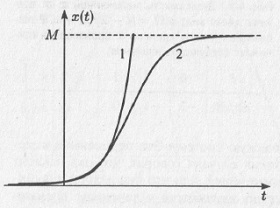
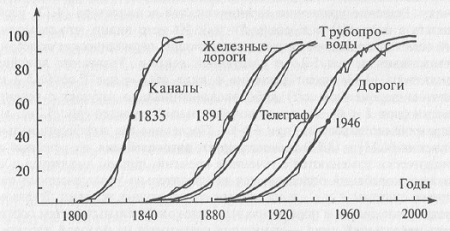
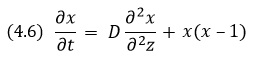
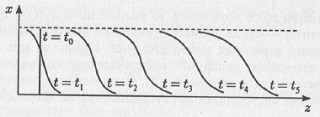
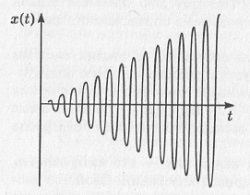
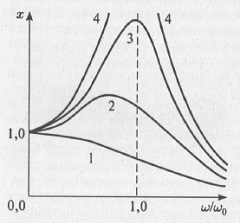
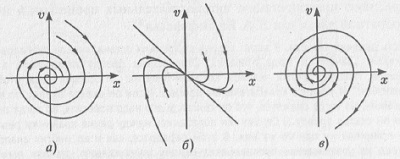
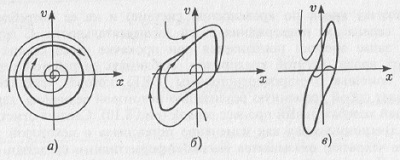

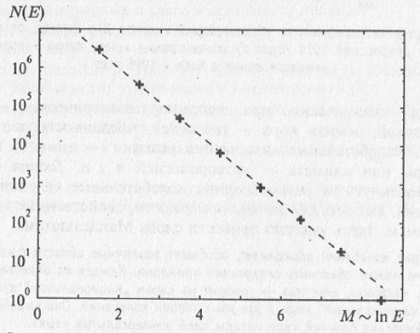
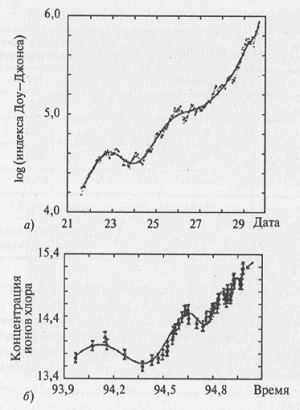

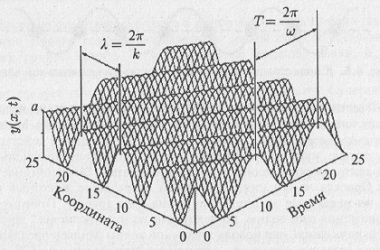
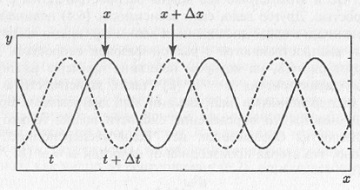
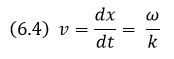
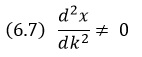
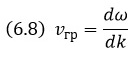
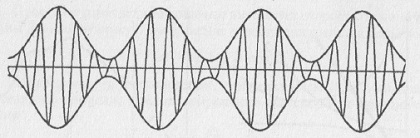



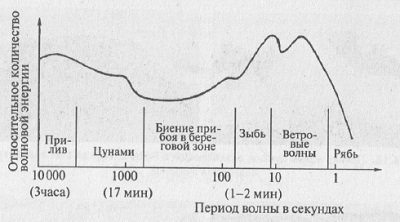


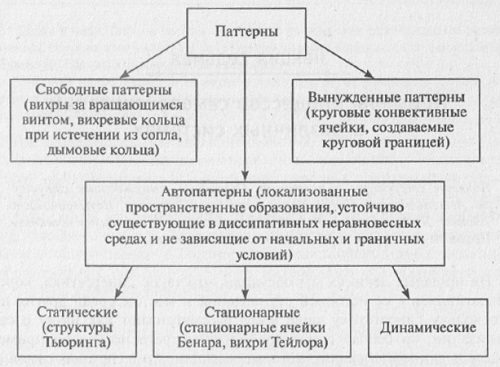
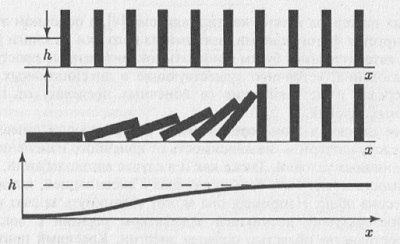
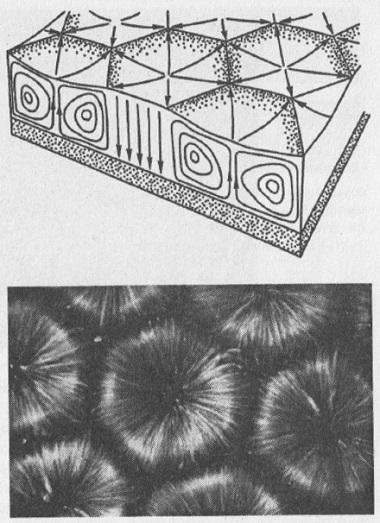

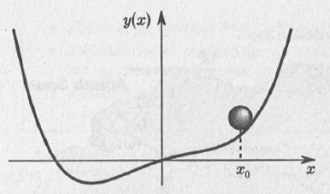

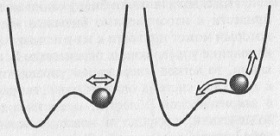
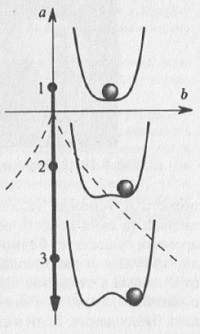
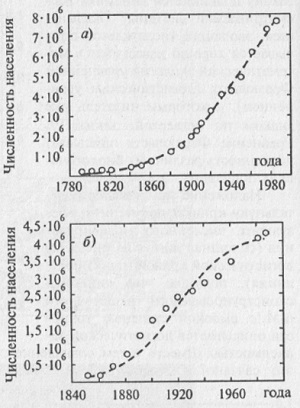
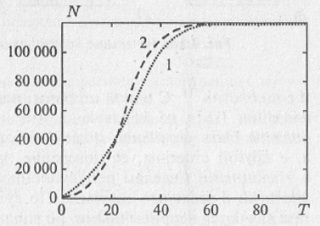
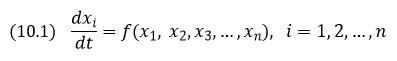
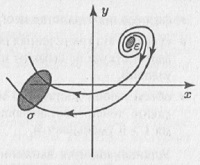
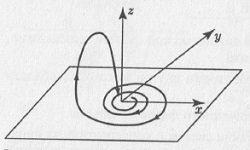
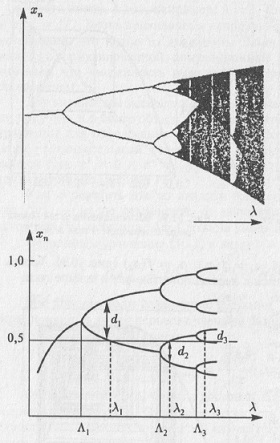
Добрый день!
Какие из этих книг, Вы планируете прочитать?
Карьера:
Инна Кузнецова. Вверх! Практический подход к карьерному росту
Дэвид Новак. Как я стал боссом
Ричард Боллс. Какого цвета ваш парашют?
Марк Гоулстон. Ментальные ловушки на работе
Мировая экономика:
Андрей Паршев. Почему Россия не Америка
Хазин. Закат империи доллара и конец
Pax AmericanaГуриев Сергей. Мифы экономики
Хэзлитт. Типичные ошибки государственного регулирования экономики
Алан Гринспен. Эпоха потрясений
Пол Кругман. Великая ложь
Пол Кругман. Выход из кризиса есть
Майкл Льюис. Бумеранг. Как из развитой страны превратиться в страну третьего мира
Джим Роджерс. Будущее глазами одного из самых влиятельных инвесторов в мире
Джим О’Нил. Карта роста. Будущее стран БРИК и других развивающихся рынков
Энергетические ресурсы:
Константин Симонов. Сжиженный газ — будущее мировой энергетики
Дэниел Ергин. Добыча. Всемирная история борьбы за нефть
Джеймс Хавард Кунстлер. Что нас ждет, когда закончится нефть, изменится климат и разразятся другие катастрофы XXI века
Ораторское искусство:
Уинстон Черчилль. Лучшие речи Черчилля
Ричард Доуиз. Утерянное искусство красноречия
Джерри Вайсман «Мастера слова»
Джеймс Хьюмс. Секреты великих ораторов
Саймон Себаг Монтефиоре. Речи, которые изменили мир
Контент-маркетинг:
Денис Каплунов. Контент, маркетинг и рок-н-ролл
Дмитрий Кот. Копирайтинг
Халилов. Маркетинг в социальных сетях
Уильям Зинсер. Как писать хорошо
Бизнес:
Михаил Дашкиев «Построй свой бизнеc»
Александр Прохоров. Русская модель управления
Довгань. Опыт предпринимателя
Рон Рубин. Бизнес в стиле дзен
Стэнли Маркус. Секреты идеального магазина
Крис Гильбо. Стартап за $100
Эрик Рис. Бизнес с нуля
Андрей Парабеллум. 100% стартап
Майкл Делл. От Dell без посредников
Егор Шестеренкин. Малый бизнес с нуля
Стив Бланк. Стартап. Настольная книга основателя
Гербер. Малый бизнес- от иллюзии к успеху
Крок. Как создавалась империя Макдональдс
Котин.И ботаники делают бизнес
Билл Гейтс. Дорога в будущее
Олег Тиньков. Я такой как все
Акио Морита. Сделано в Японии
Управление проектами:
Элияху Голдратт. Критическая цепь
Фергус О`Коннэл. Как успешно руководить проектами
Том Демарко. Человеческий фактор
Стратегия:
Сунь-Цзы. «Искусство стратегии»
Личная эффективность:
Игорь Манн. Номер 1
Робин Шарма. Путь к величию
Робин Шарма. 200 уроков жизни
Стивен Кови. Главное внимание главным вещам
Бизнес-романы:
Теодор Драйзер. Финансист
Айн Рэнд. Источник
Финансы:
Мэри Баффет. Баффетология
Карен Берман. Финансы для нефинансовых менеджеров
Алексей Герасименко. Финансовая отчетность для руководителей и начинающих специалистов
Дэвид Кларк. Уоррен Баффет рекомендует
Роберт Хагстром. Уоррен Баффет. Как 5 долларов превратить в 50 миллиардов
Куртис Фейс. Путь Черепах
Бенджамин Грэхем. Разумный инвестор
Майкл Льюис. Покер лжецов
Александр Элдер. «Как играть и выигрывать на бирже»
Мэри Баффет. Новая баффетология
Скотт Паттерсон. Кванты. Как волшебники от математики заработали миллиарды и чуть не обрушили фондовый рынок
Бартон Биггс. Вышел хеджер из тумана
Эрик Найман «Малая энциклопедия трейдера»
Джесси Ливермор. Как торговать акциями
Марк Дуглас. Зональный трейдинг
Лоренс Каннингем. Эссе об инвестициях
Роджер Ловенстайн. Когда гений терпит поражение. Взлет и падение компании Long-Term Capital Management, или Как один небольшой банк создал дыру в триллион долларов
Майкл Льюис. Большая игра на понижение
Аллен. Миллионер за минуту
Менеджмент:
Питер Друкер. Энциклопедия менеджмента
Ричард Кох. Принцип 80/20
Александр Шумович. Великолепные мероприятия
Кеннет Бланшар. Одноминутный Менеджер
Психология:
Шэрон Мельник. Стрессоустойчивость
Пол Экман. Психология лжи
Дэвид Майерс. Социальная психология
Карен Прайор. Не рычите на собаку
Юлия Гиппенрейтер. Общаться с ребенком
Хенрик Фексеус. Искусство манипуляции
Михаил Литвак. Командовать или подчиняться
Экономика предприятия:
Джеймс Вумек. Бережливое производство
Элия Голдратт. Процесс непрерывного улучшения. Цель-2
Дэвид Майер. Практика дао Toyota
Персонал:
Грабс-Уэст. Сотрудники на всю жизнь
Бизнес-процессы:
Майкл Хаммер. Реинжиниринг корпорации
Память:
Джошуа Фоер. Эйнштейн гуляет по Луне
Артур Думчев. Помнить все
Дэвид Рок. Мозг Инструкция по применению
Джейми Наст. Эффект визуализации
Роджер Сайп. Развитие мозга
Владимир Васильев. Суперпамять для всех
Денис Букин. Развитие памяти по методикам спецслужб
Консалтинг:
Марвин Бауэр. «Создание управленческого консалтинга»
Дэвид Майстер. «Истинный профессионализм»
Итан Расиел. Инструменты McKinsey
Итан Расиел. Метод McKinsey
МБА:
Джош Кауфман. Сам себе MBA Самообразование на 100%
Кен Робинсон. Образование против таланта
Барри Пирсон. MBA в кармане
Стивен Силбигер. МВА за 10 дней
Андрей Парабеллум. Прорыв в бизнесе
Переговоры:
Джордж Росс. «Переговоры в стиле Трампа»
Другие:
Дэн Бюттнер. Правила долголетия
Дмитрий Чернышев. Чем заняться вечером с семьей на даче без интернета
Это внутренняя кухня автора, как учит нас Стивен Кови. Зачем ему мешать?
Спасибо автору за обзор.