Заметка посвящается Тиму Злотову (шефу и другу), которому сегодня исполнилось бы 52 года.
Где-то в середине 2000-х я обсуждал с Тимом вопросы взаимодействия с одним моим коллегой. Я говорил, что мне с ним непросто, что он не организован, может не выполнить обещание, непредсказуем. На что Тим заметил, что мы очень хорошо дополняем друг друга. На одном полюсе он – создатель хаоса, на другом я – творец порядка. А в результате получается сотрудничество полное жизни. Об этом и представляемая сегодня книга.
Так же на эту тему вас может заинтересовать:
Гараедаги. Системное мышление. Как управлять хаосом и сложными процессами
Нассим Николас Талеб. Антихрупкость. Как извлечь выгоду из хаоса
Илья Пригожин. Порядок из хаоса
Джеймс Глейк. Хаос. Создание новой науки
Давид Рюэль. Случайность и хаос
Сергей Деменок. Просто хаос. – СПб.: ООО «Страта», 2013. – 232 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить бумажную книгу в Ozon
Настоящая книга представляет собой упрощённое изложение основных представлений теории динамического хаоса. Она не предназначена для специалистов в этой области. Эта книга для дилетантов в теории хаоса для тех, кто живёт в самой гуще интенсивного настоящего и вынужден динамично и адекватно реагировать на тенденции и тренды, просматривая следующие за ними метаморфозы реальных событий. Чтобы несколько скрасить сухость изложения на многих рисунках в книге присутствует черт (рисунки выполнены Т.В. Ковалевой).
Введение. Связность совершенно различных вещей и явлений, выраженная в математических отношениях, стала основой картезианской парадигмы: Вселенная подобно часовому механизму строго и точно подчиняется божественным законам – законам, открытым Ньютоном. Картезианская парадигма более трехсот лет служила основанием «здравому смыслу». Она обеспечила появление и рост промышленного производства, сформировала индустриальный капитализм и стимулировала каскад научно-технических революций. Однако нечто важное случилось в конце XX века. По всему фронту человеческой деятельности началось изменение понятий и представлений об окружающем мире. Хаос теперь не на периферии, но в самой сердцевине окружающей нас реальности. Хаос не противостоит, но сопутствует порядку Каждый фрагмент порядка погружён в хаос. Между любыми фрагментами порядка всегда есть область хаоса, в которой непременно найдётся фрагмент порядка.
I. РЕГУЛЯРНЫЙ ХАОС
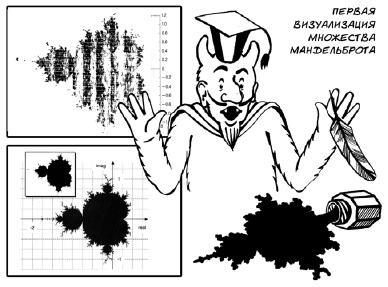
Георг Кантор (1845–1918) – немецкий математик, известный ка создатель теории множеств, построил так называемую шкалу трансфинитных чисел. Это такие отрезки, которые, с одной стороны, имеют бесконечно малую длину, а с другой стороны, их бесконечное суммирование даёт конечное число. Курьёзы теории множеств привели и совсем скоро к геометрии таких структур, как фракталы. Стоит ли удивляться, что символом фрактальной геометрии стало нечто, напоминающее чернильное пятно, – фрактал Мандельброта (рис. 1).
Рис. 1. Фрактал Мандельброта
Напомним средневековую притчу. В ответ на вопрос о доказательствах существования Бога Рабби Акива показал свиток чудесной каллиграфии и заявил, что этот свиток возник оттого, что он вчера разлил чернила, и чернильная клякса чисто случайно образовала данный текст. Понятно, что ему не поверили и сказали, что свиток исполнил искусный каллиграф. «Точно так же, ответил Акива, существование сложного прекрасного мира доказывает, что у него есть Творец».
Сегодня мы всё чаще слышим обратное. Модный эффект самоорганизации состоит, по-видимому, в том, что «чернильное пятно превращается в свиток чудесной каллиграфии». Такое магическое превращение уже стало не просто реальностью, но реальностью осмысленной, математически точно описанной и обозначенной термином «регулярный» или «динамический хаос».
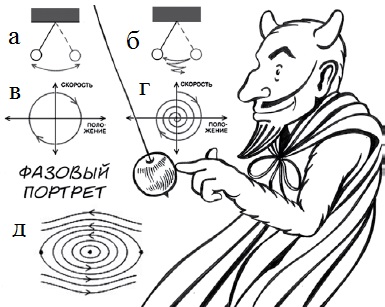
ФАЗОВЫЙ ПОРТРЕТ. Идея фазовой траектории проста. Пусть перед нами маятник. Слабый толчок и перед нами линейный гармонический осциллятор (рис. 2а). Такой режим выполняется при малой амплитуде колебаний до тех пор, пока можно считать, что отклонение от оси маятника пропорционально углу этого отклонения (sinx ≈ х), и пренебрегать трением. В координатах «скорость угол отклонения» такой осциллятор отображается как окружность (рис. 2в). От трения колебания затухают. Окружность трансформируется в спираль (рис. 2г).
Рис. 2. Движение маятника в фазовом пространстве
При увеличении силы исходного толчка поведение маятника становиться нелинейным: окружность трансформируется в эллипс. Если силу толчка увеличить ещё больше, то маятник станет вести себя как пропеллер и эллиптическая орбита вырождается в волнистые линии (рис. 2д). Мы можем фиксировать движение маятника в координатах скорости шара ν по одной оси и угла отклонения хорды от вертикали φ. В этих координатах возможные траектории маятника по мере увеличения угла φ изменяются от окружностей к овалам и далее, с потерей замкнутости, к волнистым линиям. [1]
ДИНАМИЧЕСКАЯ СИСТЕМА. Динамической называется такая система, в которой каждое значение параметра в любой последующий момент времени получается из исходного набора параметров по определённому правилу. Это правило задаёт оператор эволюции динамической системы. Оператор эволюции может быть описан дифференциальным уравнением, если система ведёт себя как поток, или рекуррентным отображением, если система ведёт себя как каскад. В первом случае траектория системы есть непрерывная линия в фазовом пространстве. Во втором случае фазовой траекторией динамической системы является дискретная последовательность точек в фазовом пространстве.
Классическая физика занималась такими динамическими системами, которые можно было не только выделить, но и отделить, изолировать от окружающей среды. В модели изолированной динамической системы её энергия сохраняется. Такие системы называют консервативными. В частности, маятник, совершающий колебания без трения, представляет собой консервативную динамическую систему. В реальности механическая энергия не сохраняется, а постепенно рассеивается (диссипирует) и переходит в тепло, т.е. в энергию микроскопического движения молекул, составляющих систему и её окружение. Такая модель называется диссипативной динамической системой. Строго говоря, в этом случае временная эволюция должна определяться не только состоянием самой системы, но и её окружением. При этом оператор эволюции может обусловливать деградацию системы и её «тепловую смерть», но может приводить к усложнению и развитию динамической системы.
Пусть в некотором фазовом пространстве есть кластер динамических систем, которые подчиняются единому оператору эволюции. Динамические системы кластера отличаются друг от друга только начальными параметрами. С течением времени каждая точка кластера перемещается в фазовом пространстве, как предписано оператором системы, так что форма кластера и его размеры будут меняться. Может случиться, что фазовый объём кластера в процессе временной эволюции будет оставаться постоянным. Это характерно для консервативных систем.
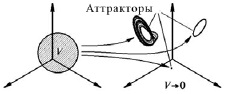
Кластер диссипативных систем ведёт себя иначе (рис. 3). С течением времени он «съёживается» и концентрируется в итоге на одном или нескольких аттракторах подмножествах фазового пространства нулевого или ограниченного объёма. Т.е., система, предоставленная самой себе, с течением времени «забывает» своё начальное состояние и принимает состояние аттрактора.
Рис. 3. Кластер диссипативных систем
ФРАКТАЛЫ. Мандельброт обнаружил, что в природе почти повсеместно присутствует одно общее свойство – самоподобие на разных масштабах. Дерево состоит из веток и веточек, облако из меньших облачков, заливы из бухт, и так много раз, почти бесконечно. Структуры, состоящие из частей, которые «в каком-то смысле подобны целому», Бенуа Мандельброт назвал фракталами (подробнее см., например, Сергей Деменок. Просто фрактал). Таким образом, есть «дикий хаос» совершенно безумный и недоступный никакому описанию хаос, и есть «ручной хаос», поддающийся изучению и описанию благодаря фракталам. Фрактал демонстрирует возможность сочетания сложности формы с простотой операции его построения. Он иллюстрирует то, как хаос и сложность могут возникать в результате действия простых законов и правил.
ДИНАМИЧЕСКИЙ ХАОС. Успехи классической механики в XVII–XIX вв. были столь впечатляющими, что стало казаться возможным представлять себе всю Вселенную как одну гигантскую динамическую систему. Эта доктрина – лапласовский детерминизм – исходила из полной предсказуемости поведения детерминированной динамической системы в той мере, в которой известны начальные условия и законы эволюции динамической системы (подробнее см. Пьер Симон Лаплас. Опыт философии теории вероятностей). На смену детерминизму Лапласа пришла новая парадигма, сформулированная в 1903 году Анри Пуанкаре: может случиться, что малые различия в начальных условиях вызовут очень большие различия в конечном явлении. Это ведет к потере предсказуемости. Поэтому динамическая система, будучи полностью предопределённой, ведёт себя непредсказуемо.
II. ХАОС – СУТЬ ДЕЛА
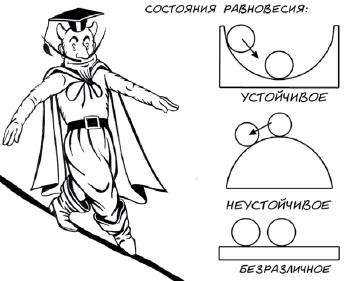
УСТОЙЧИВАЯ НЕУСТОЙЧИВОСТЬ. Во времена Галилея и Ньютона стали различать понятия равновесия и устойчивости. Поместим маленький шарик в нижнюю точку внутри полой сферы. Слегка толкнём его и понаблюдаем за движением. После совершения нескольких затухающих колебаний шарик вновь займёт положение на дне сферы. В этом случае положение равновесия устойчиво: малые возмущения исходного состояния затухают во времени. Если мы поместим шарик на вершину сферы (снаружи), то реакция на малое возмущение будет иной: при любом сколь угодно малом отклонении шарика от состояния равновесия он скатывается с вершины. Это положение равновесия неустойчиво: малые возмущения исходного состояния нарастают во времени. Наконец, шар на плоскости демонстрирует так называемое безразличное равновесие (рис. 4).
Рис. 4. Состояния равновесия
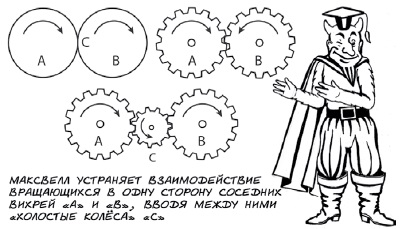
ТУРБУЛЕНТНОСТЬ И КОГЕРЕНТНОСТЬ. В XIX веке британский физик Джеймс Клерк Максвелл интерпретировал электромагнетизм в русле идей Декарта. Он представлял себе среду, охваченную вихревым движением. Вихри так малы, что умещаются внутри молекул. Вращающиеся «молекулярные вихри» производят магнитное поле. Направление осей вихрей совпадает с силовыми линиями, а сами они могут быть представлены как тоненькие вращающиеся цилиндрики. Скорость вращения вихрей определяет величину магнитной силы.
И тут возникала трудность чисто механического порядка. Внешние, соприкасающиеся части вихрей должны двигаться в противоположных направлениях, то есть препятствовать взаимному движению. Это напоминало такое положение, как если бы конструктор механизма поместил в непосредственной близости две шестеренки, вращающиеся в одну сторону. У них непременно должны были бы переломаться все зубья!
Чтобы избежать этого, Максвелл решил использовать «холостые колёса». Как можно обеспечить вращение двух рядом расположенных шестерёнок в одну сторону? Нужно поместить между ними небольшие передаточные шестерёнки, «холостые колёса». Максвелл предположил, что между рядами молекулярных вихрей помещён слой мельчайших шарообразных частичек, способных к вращению. Теперь вихри взаимодействовали между собой и вращались в одном направлении. Максвелл называет эти «холостые колёса», «смазочные шарики» между цилиндрами «частичками электричества», а движение их «поток частичек электричества» электрическим током (рис. 5). Так удачная модель стимулирует новое направление мысли. Позднее были открыты электроны.
Рис. 5. Модель электромагнетизма Максвелла
БИФУРКАЦИИ. Собственно, слово «бифуркация» происходит от французского слова bifurcation раздвоение, ветвление. Термин был введен Пуанкаре в 1885 году. Бифуркация представляет собой шаг на пути от порядка к хаосу. Для перехода от порядка к хаосу иногда достаточно одного шага (рис. 6).
Рис. 6. Два возможных пути эволюции системы – бифуркация
Переход динамической системы из одного устойчивого состояния в другое происходит под влиянием окружающей среды. Такие переходы могут осуществляться плавно, мягко, а могут происходить скачкообразно. При том, что одни параметры системы изменяются скачкообразно, другие могут эволюционировать плавно. Например, при прохождении температуры через ноль градусов по Цельсию вода изменяет свою молекулярную структуру. Процесс оледенения шёл постепенно, по мере отвода теплоты. Но температура при этом не изменялась. Обычно температура служит мерой теплоты, но во время «фазового перехода» она перестает отражать запас теплоты в системе.
При изменении «фазового состояния» многие параметры системы ведут себя аналогичным образом изменяются скачком. И это отражает факт перехода системы к новому устойчивому состоянию. В точке перехода система может находиться в одном из двух состояний. При нулевой температуре вода может быть в жидкой или в твёрдой фазах. В таком состоянии система как бы раздваивается. Если управляющий параметр фиксировать в «точке бифуркации», то система будет находиться в «неопределённом состоянии» сколь угодно долго. При этом малейшее изменение управляющего параметра или внешнее воздействие заставят систему принять один из двух фазовых портретов. Эта внезапность оттого, что молекулам воды не надо изменяться, меняются лишь правила внутренних связей.
Томас Мальтус в 1798 году издал короткую книгу «Эссе о законах населения, как оно влияет на будущее улучшение общества». Основным тезисом Мальтуса была идея, что рост населения имеет тенденцию к опережению производства продуктов питания. В своём эссе он представил её в довольно жесткой форме, утверждая, что население увеличивается в геометрической прогрессии (то есть экспоненциально, как числа 1, 2, 4, 8, 16…), а производство продуктов питания растет лишь в арифметической прогрессии (то есть линейно, как числа 1, 2, 3, 4, 5…).
В 1845 г. бельгийский социолог и математик Пьер Франсуа Ферхюльст изменил уравнение Мальтуса, допустив, что популяция рассматриваемого поколения зависит от популяции предыдущего поколения. В результате этого модель динамики популяции становилась нелинейной, что коренным образом изменило её характер. Ферхюльст предположил уменьшение фактора роста заменой r на r*(1 – xn). Очевидно, величина 1 – xn пропорциональна количеству имеющейся пищи. Иными словами, по мере того, как популяция xn приближается к единице, количество пищи постоянно сокращается и параметр роста стремится к нулю. В результате получаем закон роста популяции, называемый квадратичным отображением, или логистической параболой (от франц. прилагательного logistique, относящегося к тыловым службам, занимающимся расквартированием и снабжением войск):
xn + 1 = r(1 – xn)*xn
На самом деле природа не терпит и не совершает скачков – natura non facit saltus – природа ничего не делает резко, или: природа не делает скачков (лат.). Это наблюдение своими истоками восходит к Аристотелю. В XVIII веке Лейбниц его повторил: Nullam transitionemfieri per saltum никакой переход не случается скачкообразно (лат.). Анализ механизма бифуркации подтверждает этот принцип. Бифуркация является следствием непрерывной трансформации, которая происходит в области мнимых чисел, где шаг за шагом подготавливается внезапный переход на оси действительных чисел. Именно такой эффект имел в виду французский математик-универсал Жак Адамар, говоря: «Кратчайший путь между двумя истинами в вещественной области проходит через комплексную область».
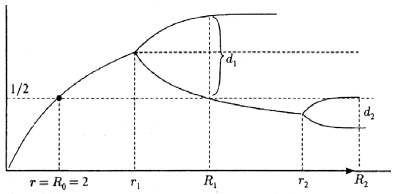
УНИВЕРСАЛЬНОСТЬ ФЕЙГЕНБАУМА. Наиболее впечатляющим в динамике логарифмического уравнения Ферхюльста является не хаос как таковой, а сценарий, по которому порядок трансформируется в хаос. При точном анализе точек бифуркации в процессе Ферхюльста обнаруживается закономерность, имеющая исключительное значение в мире нелинейных явлений. Закономерность касается длин интервалов значений параметра, при которых устойчивым является периодическое движение с некоторым определённым периодом. Эти интервалы сокращаются при каждом удвоении периода, причём множитель, характеризующий скорость перехода к хаотическому режиму, в пределе при n g ∞ приближается к универсальному значению:
δ = rn + 1/rn = rn/rn–1 = 4,669
Это число, первые десятичные знаки которого были опубликованы Гроссманном и Томэ в 1977 г., появляется снова и снова во многих других процессах. Оно является такой же характеристикой для сценариев удвоения периодов, как число π для отношения длины окружности к её диаметру.
Это число называют теперь числом Фейгенбаума. В 1978 г. Митчел Фейгенбаум проделал вычисления на своём калькуляторе в Лос-Аламосе для целого ряда различных процессов и получил в каждом случае один и тот же множитель. Он открыл универсальность этого числа. Это открытие вызвало невероятную активность учёных во многих областях науки. Было поставлено огромное число экспериментов, показавших, что сценарий удвоения периода действительно наблюдается во многих естественных системах. Это и начало турбулентности в потоке жидкости, и нелинейные колебания в химических или электрических сетях, и даже переход нормального ритма сердца в угрожающую жизни фибрилляцию.
Второй инвариант Фейгенбаума задаёт коэффициент уменьшения масштабов расстояний по оси ординат на бифуркационной диаграмме логистического отображения (рис. 7): расстояние dn от точки с ординатой 1/2 до ближайшей к ней точки цикла f(n). Он определяется в пределе n g ∞ так:
α = dn/dn+1 = 2,503
Рис. 7. Сценарий Фейгенбаума
Можно изучать самые разные явления, писать разные уравнения и получать один и тот же такт перехода от порядка к хаосу. Это поразительно. Фейгенбаум не имел ни малейшего представления о том, почему возникает эта регулярность. Он предположил, что его численные функции выражают законы природы, применимые к системам в точке перехода от порядка к турбулентности. Это не объясняло явления, но фиксировало его.
III. ГЕОМЕТРИЯ СВЁРНУТОГО, СМЯТОГО И СКРУЧЕННОГО
Сформулировано три взаимосвязанных признака регулярного, динамического, или детерминированного хаоса: существенная зависимость от начальных условий; квазипериодическое повторение; равномерное перемешивание.
Пьер-Симон Лаплас в 1776 г. написал: «Физическая астрономия, область знания, которая делает величайшую честь человеческому уму, даёт нам представление, хотя и неполное, чем был бы такой разум. Простота законов, по которым движутся небесные тела, и соотношения между их массами и расстояниями позволяют проанализировать их движение до определённой точки, и, чтобы определить состояние системы этих крупных тел в прошлых или будущих веках, математику достаточно того, чтобы их положение и скорость были получены из наблюдений в любой момент времени. Человек обязан этим мощности приборов, которыми он пользуется, и небольшому числу соотношений, которые он применяет в своих расчётах. Однако незнание различных причин, вызывающих те или иные события, а также их сложность в сочетании с несовершенством анализа мешает нам достичь той же уверенности по отношению к огромному большинству явлений. Таким образом, существуют вещи, которые для нас неопределённы, вещи, более или менее вероятные, и мы стараемся компенсировать невозможность их узнать, определяя различные степени их достоверности. Получается, что слабости человеческого разума мы обязаны появлением одной из самых тонких и искусных математических теорий науки о случае, или о вероятности».
В конце XIX начале XX веков Анри Пуанкаре радикально изменил воззрения на отношения случайности и предопределённости. В линейной системе близко расположенные точки фазового пространства остаются близкими в процессе эволюции системы. Такие системы предсказуемы: начальное измерение содержит информацию, которой можно воспользоваться для прогноза будущего поведения системы. Но большинство систем нелинейны: сколь угодно близко расположенные точки в фазовом пространстве расходятся в процессе эволюции.
В середине XX века в известных лекциях по физике Ричард Фейнман [2] пишет: «Обычно думают, что индетерминизм – это особенность квантовой механики. Но аналогичные представления следуют из классических законов. Конечно, с точки зрения классики, узнав местоположение и скорость всех частиц в мире, можно точно предсказать, что будет дальше. В этом смысле классический мир детерминирован. Но представьте теперь, что наша точность ограничена и что мы незнаем точно положение только одного из атомов; знаем, скажем, его с ошибкой в одну миллиардную. Тогда, если он столкнётся с другим атомом, неопределённость в знании его координат после столкновения возрастёт. Следующее столкновение ещё сильнее увеличит ошибку. Так что если сначала ошибка и была еле заметной, то всё равно вскоре она вырастает до огромнейшей неопределённости. Правильнее будет сказать, что для данной точности (сколь угодно большой, но конечной) можно всегда указать такой большой промежуток времени, что для него становится невозможным сделать предсказания. И этот промежуток (в этом вся соль) не так уж велик».
Американское издание фейнмановских лекций вышло в 1963 г. В том же году в Journal of the Atmospheric Sciences появилась статья американского метеоролога Эдварда Лоренца, положившая начало новому направлению в естествознании – исследованию хаоса в детерминированных системах.
СИМВОЛИЧЕСКАЯ ДИНАМИКА. Символы играют столь важную роль в описании поведения динамических систем, что появился раздел динамики – символическая динамика. Неустойчивость динамической системы приводит к сложному, запутанному их поведению и делает малопригодными классические методы анализа. Жак Адамар одним из первых попытался описать эту запутанность простейших динамических систем типа xn+1 =f(xn). Адамар обнаружил совершенно новый механизм неустойчивости. Развивая идеи Адамара, американский математик Марстон Морс первым ввёл в обиход термин «символическая динамика» в 1920-х годах. Он исследовал одну последовательность, которую ещё в 1906 году опубликовал норвежский математик Аксель Туэ. Сегодня она известна как последовательность Морса–Туэ.
Её построение начинается с нуля. На каждом следующем шаге к набору нулей и единиц, уже имеющемуся на предыдущем шаге, справа приписывается его дополнение набор знаков, в котором каждый нуль заменен единицей, а каждая единица заменена нулем 0 —> 01, 1 —> 10,
1 шаг 0
2 шаг 01
3 шаг 0110
4 шаг 01101001
5 шаг 0110100110010110
6 шаг 01101001100101101001011001101001 и т.д.
Отображение Морса–Туэ обладает свойством самоподобия содержит фрагменты, которые при надлежащем «растяжении» воспроизводят всю последовательность. В качестве примера рассмотрим шестой шаг построения. Начав с первого члена, выберем каждый второй член последовательности. Нетрудно заметить, что выбранные члены образуют снова последовательность Морса–Туэ 0110100110010110.
ГЕОМЕТРИЯ НА РЕЗИНОВОМ ЛИСТЕ. Топология – своего рода «геометрия на резиновом листе». Тополог имеет дело с простыми замкнутыми кривыми. «Простая» означает, что она не пересекает саму себя. При этом любую фигуру тополог может согнуть и свернуть, скомкать и смять, сжать и растянуть, скрутить и… делать с ней что угодно, только не разрывать и не склеивать. От геометрии Евклида осталась лишь одно качество непрерывность. Это единственное ограничение, наложенное на топологическую трансформацию, пространство нельзя разрывать. Иными словами, две близкие точки в процессе трансформации остаются близкими точками.
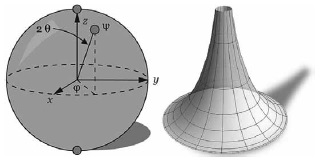
Термин «топология» впервые появился в работе ученика Гаусса Иоганна Листинга в 1847 году. Становление топологии совпало со знаковым сдвигом в познании мира. Изменился горизонт интересов. К началу XX века учёные приступили к исследованию того, что невидимо: структур микромира, с одной стороны, и строения Вселенной, с другой стороны. К этому времени уже разработаны геометрии Лобачевского и Римана (подробнее см. Леонард Млодинов. Евклидово окно). Отправным пунктом этих геометрий послужил V постулат Евклида, суть которого в том, что через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её. Лобачевский в работе «О началах геометрии» (1829) заявил, что допущение, противоположное постулату Евклида, позволяет также построить геометрию, столь же согласованную и непротиворечивую, как и евклидова. Допущение Лобачевского можно сформулировать так: через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её. Итальянский математик Эудженио Бельтрами в 1868 году заметил, что геометрия на куске плоскости Лобачевского совпадает с геометрией на поверхностях постоянной отрицательной кривизны, простейший пример которых представляет псевдосфера (рис. 8). Если геометрия Евклида реализуется на поверхностях с постоянной нулевой кривизной (на плоскости), Лобачевского с постоянной отрицательной кривизной (на псевдосфере), то геометрия Римана реализуется на поверхностях с постоянной положительной кривизной (на сфере).
Рис. 8. Сфера и псевдосфера
Топология изучает топологические свойства (или топологические инварианты) форм и фигур, которые не изменяются при гомеоморфных отображениях, т.е. отображениях, которые взаимно однозначны и взаимно непрерывны. Термин «гомеоморфизм» был введен Пуанкаре в 1895 г. Наглядно гомеоморфизм можно представить себе, как такое отображение одного множества на другое, которое происходит и без разрывов, и без склеивания. Например, будем считать, что фигуры А и Б «изготовлены» из очень прочного и эластичного материала, и будем допускать возможность любых растяжений и искривлений этого материала без разрывов и без образования складок и склеек; если мы сможем при этих условиях «наложить» фигуру А на фигуру В, то, значит, они гомеоморфны. Так, контур любого многоугольника гомеоморфен окружности. Поверхности шара, куба, цилиндра гомеоморфны между собой. Однако они не гомеоморфны тору, который можно наглядно представить себе, как поверхность баранки или автомобильной камеры. С топологической точки зрения бублик ничем не отличается от чашки для чая, зато их не спутаешь с яблоком или бананом, которые между собой топологически также неразличимы. При этом морской узел отличается от узла, который мы завязываем на ботинках.
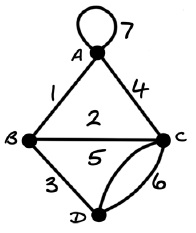
Ещё в эпоху Ришелье и д’Артаньяна Рене Декарт (1639) заметил неожиданное общее свойство всех правильных многогранников: для любого из них соотношение между числом вершин (V), рёбер (Е) и граней (F) может быть описано простой формулой: V – Е + F = 2. В следующем столетии Леонард Эйлер показал, что в обобщённом смысле многоугольник есть множество вершин, попарно соединённых ребрами, – граф (рис. 9). Эйлер ввёл инвариант χ = В – Р + Г, который стал называться «эйлеровой характеристикой» поверхности.
Рис. 9. Граф
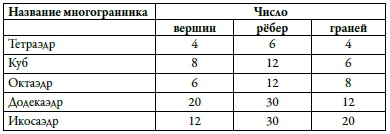
В таблице представлены данные для пяти правильных многогранников. Из неё ясно, что для каждого правильного многогранника имеет место соотношение В – Р + Г = 2, где В – число вершин, Р – число рёбер, Г – число граней многогранника. И для всех их χ = 2 (рис. 10).
Рис. 10. Параметры правильных многогранников, эйлерова характеристика которых равна 2
ДИСКРЕТНАЯ МАТЕМАТИКА: ТЕОРИИ ГРАФОВ И УЗЛОВ. На пересечении дискретной математики и топологии появилась теория графов. Графами можно назвать сети, в которых выделены только вершины и рёбра. Структурные элементы больших размерностей, в т.ч. грани, не рассматриваются. Даже объект графа «ребро» не имеет внутренней структуры это просто связь двух точек. С этой точки зрения графы являются линейно-точечными топологическими объектами. Единственное, что можно определить на ребре, в отличие от сетки, – указать направление. Направление – это ещё один топологический признак.
В теории графов комбинаторика соединения дискретных точек имеет топологическую интерпретацию. На практике этой теорией пользуются инженеры при проектировании схемы дорог, газопроводов, тепло и электросхем, химики при анализе валентных связей в сложных молекулах, историки при построении родственных связей в генеалогических деревьях, социолог при анализе иерархии подчинённости в огромных корпорациях, военачальники при разработке логистических потоков войск, провизии и информации. В каждом из этих примеров фигурирует схема, состоящая из точек, соединённых между собой линиями.
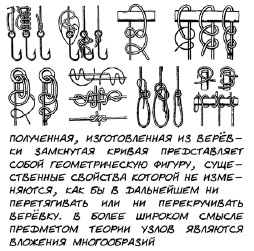
Давно известны морские и рыболовецкие узлы, которые используются для соединения двух концов верёвок или для крепления снастей: беседочный, шкотовый, кошачьи лапки. Подобные узлы и оказались в поле внимания топологов. Узел образуется, когда из отрезка верёвки делают петли, затем сквозь них пропускают концы верёвки и, наконец, два конца соединяют вместе. Полученная, изготовленная из верёвки замкнутая кривая представляет собой геометрическую фигуру, существенные свойства которой не изменяются, как бы в дальнейшем ни перетягивать или ни перекручивать верёвку. В более широком смысле предметом теории узлов являются вложения многообразий (рис. 11).
Рис. 11. Теория узлов
В математике узел – это некая абстракция: рассматривается не верёвка и не шнур, а бесконечно тонкая, гибкая и растяжимая нить. Кроме того, рассматривая математический узел, нужно либо как-то зафиксировать его концы (обычно говорят, что один конец уходит в бесконечность «вверх», а другой – в бесконечность «вниз»), либо просто соединить их. В последнем случае модель узла – замкнутая несамопересекающаяся кривая в пространстве.
ГЕОМЕТРИЯ СФЕР. Исследуя геометрию фигур на сфере, Риман заметил интересный факт: окружности наибольшего радиуса играют на сфере ту же роль, что и прямые на плоскости. Отрезок большой окружности является кратчайший линией, соединяющей две точки на сфере (более подробно см. Леонард Млодинов. Евклидово окно, часть 3. История Гаусса). Однако, в отличие от прямых на плоскости, любые две окружности наибольшего радиуса обязательно пересекаются в двух точках.
Возьмите любой неустойчивый режим. Если система линейна, то неустойчивость режима ведёт к неограниченному росту возмущений. Динамическая система «уходит на бесконечность». Однако большинство реальных систем ограничены в запасах энергии и не могут обеспечить неограниченный рост возмущений. Преодолеть энергетический «холм» в фазовом пространстве может не всякая динамическая система.
Алиса из книжки Льюиса Керолла «Алиса в Зазеркалье» не смогла. Если представить, что Алиса попала в фазовое пространство, то многие странности становятся интуитивно очевидными. Например, Алисе не под силу пересечь путь стремительной Красной Королевы, двигаясь ей навстречу. Но, повернув назад, обратив время вспять, она встречает Королеву, ведь Королева много раз в прошлом проходила вблизи дома, у которого кружила Алиса.
Посредством инверсии отображенное становиться отображаемым и в тот момент, когда оригинал и образ встречаются у зеркальной поверхности. В силу инверсии оригинал и образ меняются местами и, пройдя зеркальную поверхность, продолжают путь.
Механизм инверсии был известен математикам благодаря работам немецкого математика Людвига Иммануэля Магнуса, который в 1831 году впервые стал рассматривать отображение, превращающее внутреннюю область окружности во внешнюю и обратно. Пусть в евклидовой плоскости задана некоторая окружность с центром О (называемым полюсом или центром инверсии, эта точка «выколота», т.е. не учитывается) и радиусом R (рис. 12). Инверсия точки Р относительно окружности есть точка Р’, лежащая на луче ОР такая, что |ОР’|*|ОР| = R2.
Рис. 12. Инверсия относительно окружности
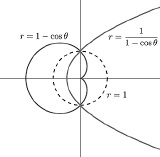
Очевидно, что любая точка, лежащая на окружности, относительно которой производится преобразование инверсии, при отображении переходит в себя же. Любая точка, лежащая внутри окружности, переходит во внешнюю область, и наоборот. Считается, что центр окружности переходит в бесконечно удалённую точку (∞), а бесконечно удалённая точка наоборот, в центр окружности: (О)’ = ∞, (∞)’ = О. Ясно, что повторное применение преобразования инверсии обращает первое её применение – все точки возвращаются обратно: (P’)’ ≡ P. Инверсия делает бесконечность обозримой. Как, например, инверсия параболы с уходящими «на бесконечность» ветвями есть обозримая сразу целиком и полностью кардиоида (рис. 13). Математические изыскания на тему инверсии оказались очень полезными в инженерной практике.
Рис. 13. Кардиоида – инверсия параболы
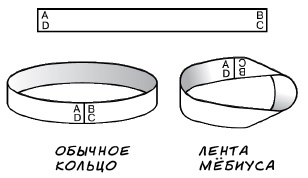
Мы ещё не знаем, какова структура нашей Вселенной. Она может иметь форму трёхмерной сферы, рожка или горна, но в любом случае она достаточно замысловато свёрнута и ограничена. При этом в каких-то её местах «встречаются области, где можно увидеть собственный затылок». При таком положении дел следует тренировать своё воображение для начала на самых простых из всех замысловатых форм, изучаемых топологией, таких, как лента Мёбиуса и бутылка Клейна.
ЛЕНТА МЁБИУСА И БУТЫЛКА КЛЕЙНА. Лист Мёбиуса получается следующим образом. Ленту прямоугольной формы один раз перекручивают и затем её концы склеивают (рис. 14). Лист Мёбиуса имеет лишь одну сторону. Например, зарегистрировано немало изобретений, в основе которых лежит односторонняя поверхность. После появления магнитофона нашлись умельцы, придумавшие особые кассеты, где магнитофонная лента соединяется в кольцо и перекручивается. Время непрерывного звучания увеличилось вдвое.
Рис. 14. Лист Мёбиуса
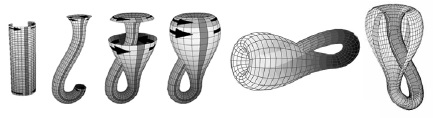
Бутылка Клейна – это своего рода трёхмерный лист Мёбиуса. Название, по-видимому, происходит от неправильного перевода немецкого слова Flӓche – поверхность, которое в немецком языке близко по написанию к слову Flasche – бутылка. Феликс Клейн [3] в 1882 году создал такую бутылку, у которой нет «внутри» и нет «снаружи», но в ней можно хранить вино. В трёхмерном пространстве она неизбежно самопересекается, но в четырёх измерениях она подобна листу Мёбиуса. Эта поверхность одновременно замкнута, как сфера и тор, и односторонняя, как лист Мёбиуса. В отличие от обычной бутылки, она не имеет края, а её поверхность нельзя разделить на внутреннюю и наружную. Та поверхность, которая кажется наружной, непрерывно переходит в ту, которая кажется внутренней, как переходят друг в друга на первый взгляд различные стороны листа Мёбиуса (рис. 15).
Рис. 15. Преобразование цилиндра в бутылку Клейна
РАЗМЕРНОСТЬ – НИТЬ АРИАДНЫ. В XX веке размерность оказывается в центре внимания научной мысли. От Евклида до Пуанкаре размерность объекта определяли, мысленно разделяя его поверхностями, сечениями, кривыми и точками путем индуктивного логического заключения. И если мыслителей с древних времён заботили размерности, то ремесленников больше заботили размер, площадь, объём. Так, испокон веков для измерения площади фигуры сложной формы ремесленники использовали палетку. Палетка – это прозрачная пластина, на которой нанесена сетка с квадратными ячейками, стороны которых одинаковы и равны некоторой величине δ. Если такую сетку наложить на карту Великобритании и подсчитать количество клеток, попавших в область объекта измерения, то можно оценить его площадь, которая пропорциональна количеству ячеек, попавших в его границы. Точность оценки возрастает с уменьшением шага сетки. Оказалось, что этот подход открывает новый путь к определению размерности.
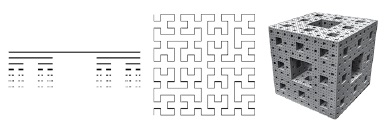
Математики давно заметили геометрические формы, топологическая размерность которых не отражает их сложности. Это, например, пыль Кантора, линия Гильберта или губка Менгера. Если перед вами точка, вы сразу присвоите ей нулевую размерность, если перед вами линия вы сразу скажете, что ее размерность равна единице. Но если перед вами губка Менгера, линия Гильберта или пыль Кантора, то вы испытаете затруднения с ответом на вопрос, какова их размерность (рис. 16).
Рис. 16. Пыль Кантора, линия Гильберта и губка Менгера
При увеличении масштаба измерения длина береговой линии растёт без ограничений, стремясь к бесконечности. Возьмите, например, карту Норвегии. Вычислите длину побережья в самом грубом масштабе. Теперь учтём изгибы основных фьордов. Полученный результат изменится. Приглядевшись поближе, мы увидим, что эти фьорды содержат ещё более мелкие фьорды и т.д. Мы всегда сможем найти ещё более точную длину, если будем огибать маленькие бухточки и мысочки, затем валуны, камни и гальку…
Посмотрите на облако. Оно имеет форму, хотя и бесформенно. Бенуа Мандельброт охарактеризовал созданную им фрактальную геометрию как морфологию безрельефного, бесформенного, облачного, аморфного: «облака не сферы, горы не конусы, береговые линии не окружности, древесная кора не гладкая, молния скользит не по прямой». Такая геометрия стоит очень близко к хаосу, ведь «хаос всё оформляет, но сам бесформен».
Обычно фрактальная размерность множества больше его топологической размерности и является дробным числом, заключённым между 1, 2 или 3.
[1] На мой взгляд, лучше всего новичкам знакомиться с понятием фазового пространства по книге Путь в синергетику. Экскурс в десяти лекциях. Лекция 4. Динамическая система.
[2] О Ричарде Фейнмане см., например, Леонард Млодинов. Радуга Фейнмана. Поиск красоты в физике и в жизни.
[3] Феликс Христиан Клейн (1849–1925) – немецкий математик и педагог. Клейну принадлежит идея алгебраической классификации различных отраслей геометрии (евклидова, сферическая, гиперболическая, проективная, аффинная, риманова, многомерная, комплексная и т.д.) в соответствии с теми классами преобразований, которые для этой геометрии несущественны. Более точно выражаясь, один раздел геометрии отличается от другого тем, что им соответствуют разные группы преобразований пространства, а объектами изучения выступают инварианты (неизменные свойства) таких преобразований.