Большинству из нас хорошо знакома колоколообразная кривая нормального распределения. Она отлично работает, когда выборки большие, но занижает значения на «хвостах», когда выборки малые. Для описания статистики малых выборок была разработана t-статистика Стьюдента. Она также симметрична и подчиняется колоколообразному распределению, но дает лучшую оценку для малых выборок. В отличие от нормального распределения t-статистика не одна, а представлена целым семейством распределений. Дополнительный параметр – размер выборки или число степеней свободы.
Рис. 1. Нормальная кривая и кривые t-распределения; df – число степеней свободы (от англ. degrees of freedom); gif-файл создан с помощью бесплатного сервиса ezgif.com, на который меня навела Евгения Крюкова
Скачать заметку в формате Word или pdf, примеры в формате Excel
Подход пивовара
В начале XX века Уильяму Сили Госсету, химику и статистику ирландской пивоваренной компании Guinness, потребовалось установить, какой из двух сортов ячменя дает лучшее пиво с большим выходом.[1] Ранее была разработана статистика нормального распределения, позволяющая находить доверительный интервал на основе случайной выборки, состоящей из не менее чем 30 объектов. К сожалению, у Госсета не было возможности протестировать большое число партий пива, изготовленных из каждого сорта ячменя. Однако он не отказался от своей затеи измерить то, что как будто не поддавалось оценке, и решил вывести новый вид распределения для крайне малых выборок. К 1908 г. Госсет разработал новый эффективный метод, который назвал t-статистикой, и захотел опубликовать результаты своей работы.
Однако у Guinness уже были проблемы с разглашением коммерческой тайны, и служащим компании было запрещено публиковать любую информацию о бизнес-процессах. Госсет понимал значение своей работы. Ему сильнее хотелось рассказать о своей идее, чем добиться немедленного признания. Поэтому он опубликовал статью под псевдонимом Стьюдент. И хотя истинный автор давно известен, практически во всех работах по статистике метод называется t-статистикой Стьюдента.
От физических значений к z-статистике
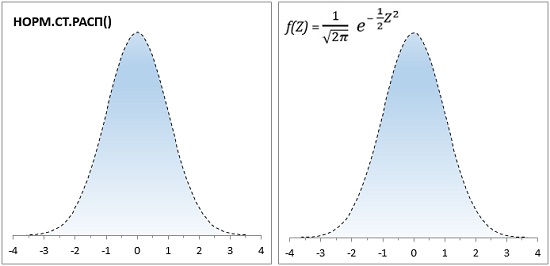
Колоколообразная кривая нормального распределения описывается формулой:
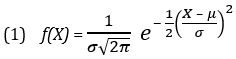
где f(X) – вероятность значения Х; f(X) откладывается по оси ординат; е — основание натурального логарифма; μ — математическое ожидание генеральной совокупности, σ — стандартное отклонение генеральной совокупности, X — произвольное значение непрерывной случайной величины; X откладывается по оси абсцисс; –∞ < X < +∞ (о вычислении μ и σ подробнее см. Определение среднего значения, вариации и формы распределения. Описательные статистики).
Формула (1) довольно сложная, и в докомпьютерную эру статистики использовали заранее рассчитанные таблицы. Поскольку составление таблиц для всего разнообразия Х, μ и σ дело неподъемное, была придумана стандартизация, которая состоит в приведении физических величин к z-единицам, путем простой арифметической подстановки
В этом случае всё многообразие нормальных кривых сводится к единому стандартизованному распределению:
где математическое ожидание (среднее) стандартизованного нормального распределения μ = 0, а стандартное отклонение σ = 1. Фактически, z – это десятичное число, для которого σ = 1, μ = 0.
Сейчас функция в Excel НОРМ.РАСП(x;среднее;стандартное_откл;интегральная) значительно упростила работу с формулой (1). Однако, заложенная традиция сохранилась, и статистики обсуждают особенности распределения, критические границы и т.п. в терминах стандартного нормального распределения (рис. 2). Для последнего в Excel используется функция НОРМ.СТ.РАСП(z;интегральная).
Рис. 2. Формула (3) реализована в Excel с помощью функции НОРМ.СТ.РАСП(); по оси абсцисс – z-единицы, по оси ординат – вероятность.
Для перехода от стандартного распределения к физическим величинам нужно применить обратное преобразование:
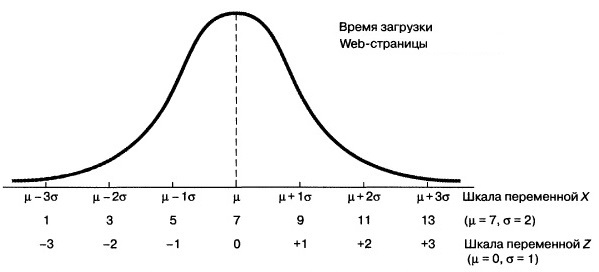
Допустим вы изучаете время загрузки некой Web-страницы, и выясняете, что оно распределено нормально, причем математическое ожидание равно μ = 7с, а стандартное отклонение σ = 2с. Как показывает рис. 3, каждому значению переменной X соответствует нормированное значение Z, полученное с помощью формулы преобразования (2). Следовательно, время загрузки, равное 9с, на одну стандартную единицу превышает математическое ожидание: Z = (9 – 7) / 2 = +1, а время загрузки равное 1с на три z-единицы (стандартных отклонения) меньше математического ожидания: Z = (1 – 7) / 2 = –3.
Рис. 3. Преобразование физических значений в z-значения для μ = 7, σ = 2
Описанные выше z-единицы используют для индивидуальных оценок, т.е. для измерений, приписываемых отдельным элементам выборки (например, рост каждого ученика школы). Если в качестве точек кривой нормального распределения берутся средние значения выборок (например, средний рост учеников различных классов), используют термин z-значение или z-статистика:[2]
где X̅ – среднее значение выборки (средний рост учеников 5А класса), μ – среднее значение генеральной совокупности (средний рост всех учеников школы), ![]() – стандартная ошибка средних (стандартное отклонение среднего роста учеников отдельных классов от среднего роста всех учеников школы). Последняя рассчитывается по формуле:
– стандартная ошибка средних (стандартное отклонение среднего роста учеников отдельных классов от среднего роста всех учеников школы). Последняя рассчитывается по формуле:
где σ – стандартная ошибка индивидуальных значений, n – размер выборки (число учеников в классе).
t-значение
Допустим, вы предполагаете, что дизельные двигатели автомобилей определенной модели выбрасывают в атмосферу больше оксида азота, чем заявлено в рекламных объявлениях. Вы знаете, что стандарт устанавливает ограничение на выбросы – не более 0,4 грамма на милю пробега. Вы хотели бы сравнить эмпирически полученные результаты не со средним по генеральной совокупности, а с этим стандартом – 0,4 г/милю. Это целевое значение, а не параметр генеральной совокупности. Вы тестируете пять автомобилей данной модели и измеряете уровень выброса оксида азота в дорожных условиях. Далее вы вычисляете среднее количество выбросов оксида азота для пяти автомобилей и находите стандартное отклонение. Наконец, вы находите величину:
где X̅ – средний уровень выбросов диоксида азота для пяти автомобилей; μ = 0,4 – установленный стандартом граничный уровень выбросов оксида азота;[3] s — стандартное отклонение уровня выбросов оксида азота по результатам для пяти автомобилей.
Это отношение очень похоже на формулу (2) для z-значения, но в действительности это t-значение. z- и t-значения отличаются тем, что для нахождения t-значения используется стандартное отклонение, полученное на основе выборочных результатов s, а не известное значение параметра генеральной совокупности σ. Использование латинской буквы s вместо греческой буквы σ для обозначения стандартного отклонения напоминает о том, что в данном случае значение стандартного отклонения является выборочной оценкой (статистикой), а не известным параметром.
Плотность распределения t-значений рассчитывается не с помощью формулы (3), а существенно сложнее. Я не привожу её здесь, поскольку сейчас в лоб ее никто не считает. Все используют готовые функции в статистических пакетах.
В Excel есть ряд функций, работающих с t-статистикой (рис. 4). Функции, имена которых включают часть РАСП, принимают t-значение в качестве аргумента и возвращают вероятность. Функции, имена которых включают часть ОБР, принимают значение вероятности в качестве аргумента и возвращают t-значение. Две последние функции на рис. 4 устарели и оставлены для обратной совместимости с более ранними версиями Excel.
Рис. 4. Семейство функций в Excel, работающих с t-статистикой Стьюдента
Степени свободы
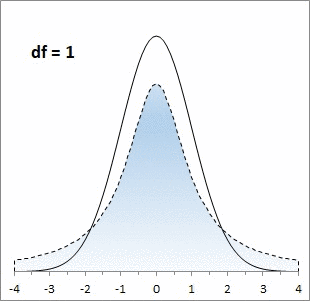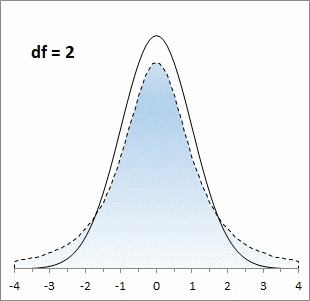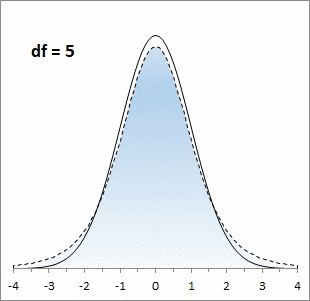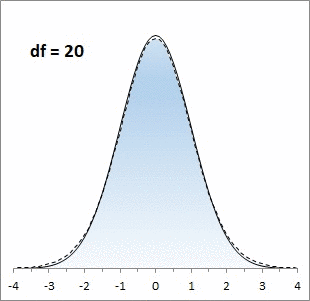
Кривая t-распределения аналогична стандартной нормальной кривой, но ее форма немного меняется в зависимости от количества наблюдений, использованных для ее построения. В общем случае количество степеней свободы df = n – k, где n — количество наблюдений в выборке, а k — количество статистик, фиксированных для выборки. Например, если мы просто изучаем выборку, то k = 1, так как мы зафиксировали только среднее значение выборки. Если мы изучаем регрессионную зависимость от одной переменной, то k = 2; зафиксированы две статистики: среднее по выборке и наклон регрессионной кривой. Каждая дополнительная независимая переменная в регрессионной зависимости уменьшает число степеней свободы на единицу.
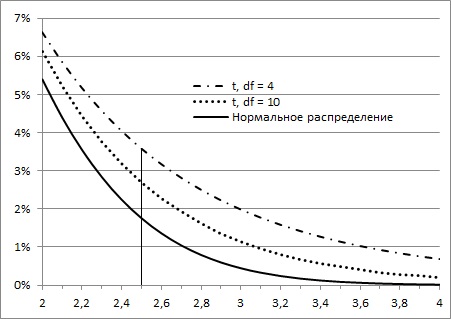
Во все функции Excel, предназначенные для работы с t-распределением, вторым аргументом входит количество степеней свободы df. Этот параметр необходим Excel для того, чтобы правильно вычислить форму кривой плотности t-распределения и вернуть корректное значение вероятности t-значения, заданного с помощью первого аргумента. Так для одного и того же z-значения = t-значению = 2,5 вероятность встретить его зависит от размера выборки (числа степеней свободы; рис. 5).
Рис. 5. Вероятность появления z- или t-значения зависит от того, какое распределение используется
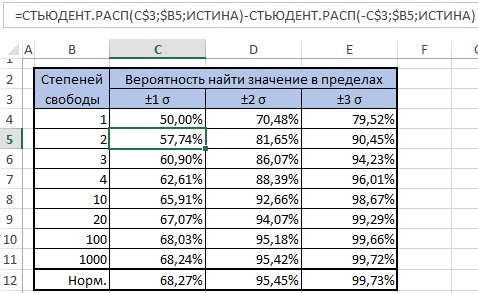
То, насколько толстыми или тяжелыми являются хвосты t-распределения можно выразить количественно (рис. 6). Так, например, в пределах одного стандартного отклонение от среднего при нормальном распределении находится 68,27% значений. Для t-распределения с двумя степенями свободы такая вероятность существенно меньше – 57,74%.
Рис. 6. Сравнение нормального и t-распределений
Функции Excel для работы с t-распределением
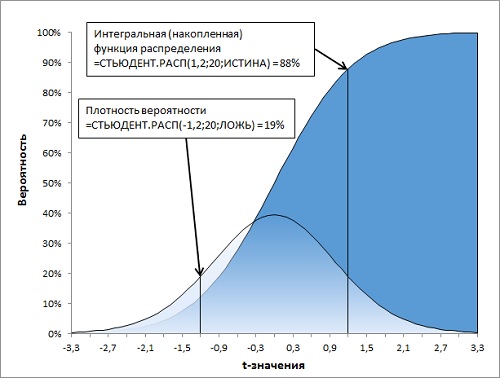
Рассмотрим работу функций Excel подробнее. Функция =СТЬЮДЕНТ.РАСП(t-значение;df;интегральная) возвращает левостороннее t-распределение Стьюдента (рис. 7). t-значение должно быть стандартизовано согласно формуле (7), т.е., выражено в долях стандартного отклонения σ при математическом ожидание генеральной совокупности µ = 0. Последний аргумент функции СТЬЮДЕНТ.РАСП() является логическим значением. Если он равен ЛОЖЬ, возвращается функция плотности распределения, т.е., вероятность для одного t-значения – Р(Х=t). Если он равен ИСТИНА, функция возвращает интегральное (накопленное) значение, т.е., вероятность попасть в интервал от минус бесконечности до t-значения – Р(Х≤t).
Рис. 7. Левостороннее t-распределение Стьюдента, функция Excel СТЬЮДЕНТ.РАСП()
Если функцию СТЬЮДЕНТ.РАСП() дополнить простыми арифметическими действиями, можно решить множество задач, связанных с t-распределением. Некоторые из них представлены ниже (рис. 8; во всех случаях df = 20):
- какова вероятность найти значение за пределами диапазона ±2,4σ от среднего значения Р(|Х|≥2,4)? =СТЬЮДЕНТ.РАСП(-2,4;20;ИСТИНА)*2
- какова вероятность найти значение внутри диапазона ±1,8σ от среднего значения Р(|Х|≤1,8)? =СТЬЮДЕНТ.РАСП(1,8;20;ИСТИНА)-СТЬЮДЕНТ.РАСП(-1,8;20;ИСТИНА) или, учитывая симметричность t-распределения, =(0,5-СТЬЮДЕНТ.РАСП(-1,8;20;ИСТИНА))*2
- какова вероятность найти значение справа от 2σ Р(Х≥2)?
=1-СТЬЮДЕНТ.РАСП(2;20;ИСТИНА) - какова вероятность среднего значения Р(Х=0)?
=СТЬЮДЕНТ.РАСП(0;20;ЛОЖЬ)
Рис. 8. Функция Excel СТЬЮДЕНТ.РАСП() позволяет решать основные задачи с t-распределением
Функция СТЬЮДЕНТ.РАСП.ПХ() возвращает правостороннее t-распределение, причем только интегральное. Т.е., она показывает накопленную вероятность, начиная с правой точки +∞ при движении влево – Р(X≥t).[4] У функции только два аргумента: t-значение и число степеней свободы. Она чуть более удобна, чем СТЬЮДЕНТ.РАСП() в задачах, где нас интересует вероятность обнаружить то или иное значение правого хвоста. Для примера (в) выше (см. также рис. 8в) формула будет такой: =СТЬЮДЕНТ.РАСП.ПХ(2;20).
Функция СТЬЮДЕНТ.РАСП.2Х() возвращает двустороннее t-распределение Стьюдента – P(|X|≥t) или P(X≥t или X≤-t). Как и функция СТЬЮДЕНТ.РАСП.ПХ(), она имеет два аргумента (t-значение и число степеней свободы), и возвращает только интегральное значение. Функция СТЬЮДЕНТ.РАСП.2Х() показывает накопленную вероятность для двух симметричных хвостов. Она чуть более удобна, чем СТЬЮДЕНТ.РАСП() в задачах, где нас интересует вероятность обнаружить два хвоста сразу. При этом задать нужно t-значение правого хвоста (отрицательные t-значения функция не принимает). Для примера (а) выше (см. также рис. 9а) формула будет такой: =СТЬЮДЕНТ.РАСП.2Х(2,4;20).
t-критерий
Одно из важных применений t-статистики связано с ответом на вопрос, насколько выборка характерна для генеральной совокупности? Например, если в генеральной совокупности среднее μ, а в выборке – х̅, какова вероятность, что выборка сделана из этой генеральной совокупности, а не из другой?
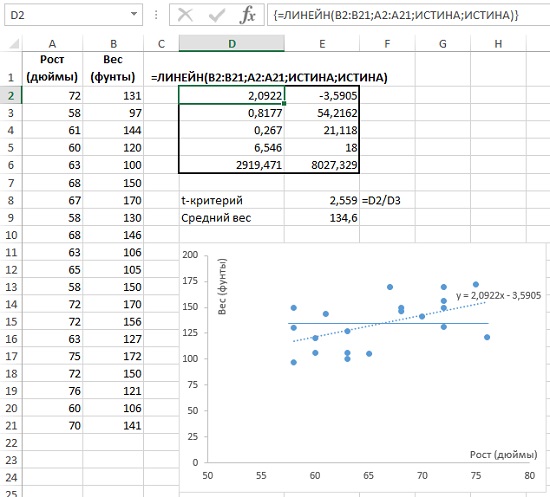
Рассмотрим пример (рис. 9). Исследуется зависимость веса от роста. Функция массива ЛИНЕЙН() (ячейки D2:E6), возвращает, в частности, наклон регрессионной кривой, он же коэффициент регрессии (ячейка D2) и стандартную ошибку коэффициента регрессии (ячейка D3). На рис. 9 данные роста и веса помещены на точечную диаграмму. На ней изображена регрессионная прямая (пунктирная линия; чтобы вывести ее, кликните в области диаграммы правой кнопкой мыши, и выберите опцию Добавить линию тренда…). Выведена также и формула регрессионной кривой y = 2,0922x – 3,5905 (естественно, коэффициент при х равен значению в ячейке D2).
t-критерий параметра = значение параметра, деленное на стандартную ошибку параметра
В нашем случае t-критерий коэффициента регрессии = коэффициент регрессии / стандартная ошибка коэффициента регрессии = 2,0922 / 0,8177 = 2,559 (ячейка Е8).
Рис. 9. Коэффициент регрессии = 2,0922 и t-критерий коэффициента регрессии = 2,559
Допустим, в генеральной совокупности вес не зависит от роста (нулевая гипотеза; на рис. 9 изображена сплошной прямой). Это значит, что коэффициент регрессии генеральной совокупности равен 0. В нашей выборке из 20 человек, мы обнаружили линейную зависимость веса от роста с коэффициентом регрессии (коэффициентом при х) = 2,0922. Если нормировать эту величину на стандартную ошибку, мы получим безразмерную величину = 2,559. Т.е., подсчитанный нами коэффициент регрессии в выборке на 2,559 сигм отстоит от нуля.
Насколько невероятно (или вероятно) получить такое отклонение в выборке, если в генеральной совокупности коэффициент регрессии = 0? Можно ли дать определение того, какое событие можно считать «невероятным». Считать ли его таковым, если оно происходит один раз в серии из 20 испытаний? Или в серии из 100 испытаний? А может быть, из 1000 испытаний? Как правило, событие считают «невероятным», если оно может произойти не чаще, чем в одном случае из двадцати.
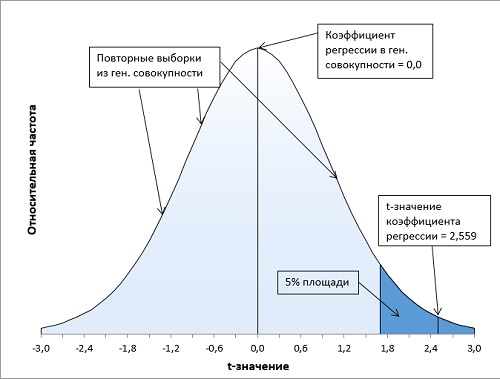
Итак, в качестве нулевой гипотезы можно принять, что вес не зависит от роста. В качестве альтернативной гипотезы мы предположим, что вес положительно коррелирован с ростом (чем больше рост, тем больше вес). Мы отклоним нулевую гипотезу, только если t-значение коэффициента регрессии попадет в правый хвост распределения в область, соответствующую 5% всей площади под кривой (α = 0,05). Это, как раз, произойдет не чаше, чем один раз на двадцать выборок (рис. 10).
Рис. 10. Расположение t-значения коэффициента регрессии (2,559) на кривой t-распределения Стьюдента (df = 18) показывает, что его вероятность около 1% не превышает α-уровень = 5%. Нулевая гипотеза может быть отвергнута. Статистики выборки говорят о зависимости веса от роста.
Расчет t-значения, соответствующего заданному уровню значимости
Проблема выбора «уровня невероятности», т.е. уровня статистической значимости, или α-уровня, десятилетиями будоражила статистиков. Найти ответы на подобные вопросы зачастую очень трудно, и многие исследователи лишь пожимают плечами и выбирают для альфа-уровня одно из общепринятых значений: р < 0,05 или р < 0,01. Почему именно такие значения?
Главная причина — это то, что в течение многих лет исследователи должны были полагаться на справочные таблицы, позволяющие найти такое t-значение, которое можно было бы считать «статистически значимым» на уровне 0,05 или 0,01 (таблиц для других α-значений практически не было). В наше время определение критического значения t-статистики при любом заданном уровне значимости не составляет труда.
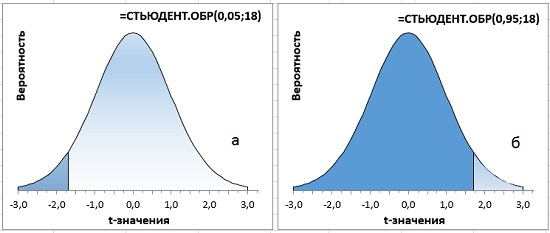
В Excel есть две функции для расчета t-критерия по уровню значимости (вероятности). СТЬЮДЕНТ.ОБР(вероятность;степени_свободы) возвращает левостороннее обратное t-распределение. В качестве первого аргумента функция принимает накопленную вероятность, начиная с –∞. Как правило, используется для односторонних тестов. В случае использования в двустороннем тесте α-значение следует разделить на 2. Например, t-значение для 5%-ного уровня значимости на рис. 10 можно найти с помощью формул =–СТЬЮДЕНТ.ОБР(0,05;18) или =СТЬЮДЕНТ.ОБР(1–0,05;18). В обоих случаях ответ 1,7341. В первом случае СТЬЮДЕНТ.ОБР(0,05;18) возвращает значение –1,7341, соответствующее 5%, накопленным от –∞ до –1,7341 (рис. 11а). Для получения окончательного ответа нужно воспользоваться свойством симметрии кривой распределения, и добавить знак минус перед функцией. Во втором случае СТЬЮДЕНТ.ОБР(1–0,05;18) возвращает значение 1,7341, соответствующее 95%, накопленным от –∞ до 1,7341 (рис. 11б).
Рис. 11. Односторонний t-критерий с уровнем значимости α = 5%
Вторая функция =СТЬЮДЕНТ.ОБР.2Х() используется в двусторонних тестах, когда мы допускаем, что исследуемое значение может отклоняться в обе стороны от среднего. В формулу следует подставить α-уровень значимости, функция сама разобьет его на две части и вернет значение, соответствующее двум симметричным хвостам (рис. 12; сравните с рис. 11а).
Рис. 12. Двусторонний t-критерий с уровнем значимости α = 5%
Ошибка первого рода
Предположим, перед вами стоит задача увеличить трафик нескольких веб-сайтов. Вы договариваетесь с владельцем популярного рекламного сайта о том, чтобы на его страницах отображались ссылки на 16 сайтов, случайным образом выбираемых из списка сайтов, контролируемых вашей компанией. Другие ваши 16 сайтов, также выбираемые случайным образом, не будут продвигаться в течение месяца.
Вы намереваетесь сравнить между собой средние показатели посещений сайтов, ссылки на которые специально продвигаются поставщиком рекламных услуг, и остальных сайтов. Вы останавливаете свой выбор на направленной гипотезе с альфа-уровнем 0,05: только если специально продвигаемые сайты характеризуются большим средним количеством посещений и только если различие между двумя группами сайтов настолько велико, что при многократном повторении данного испытания оно может случайно встретиться не чаще, чем в одном случае из 20, вы будете отбрасывать гипотезу о том, что специальное продвижение сайта не влияет на среднее количество его посещений.
Через месяц вы получаете свои данные и обнаруживаете, что средний показатель для вашей контрольной группы – сайтов, не получающих специального продвижения, – составляет 45 посещений в час, а для продвигаемых сайтов – 55 посещений в час. Стандартная ошибка среднего равна 5.
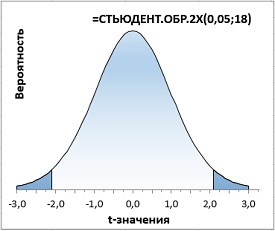
Итак, у нас имеется контрольная группа из 16 сайтов (df = 15), правосторонний однонаправленный тест с α-уровнем = 0,05. t-значение определяется по формуле =-СТЬЮДЕНТ.ОБР(0,05;15) и равно 1,7531. Критическое значение посещаемости определяется по формуле (4) и равно: t-значение * стандартное отклонение выборки + среднее по выборке = 1,7531 * 5 + 45 = 53,8. Среднее по экспериментальной группе (55) больше критического t-значения (55 > 53,8). Мы можем отвергнуть нулевую и принять альтернативную гипотезу – продвижение сайтов влияет на посещаемость (рис. 13).
Рис. 13. Попадание среднего значения внутрь α-уровня позволяет отвергнуть нулевую гипотезу
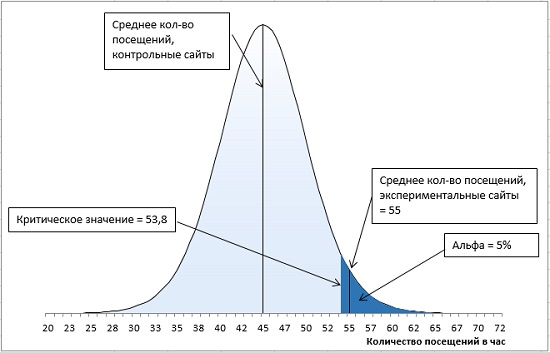
Но, значение альфа-уровня полностью контролируется нами — это наше правило принятия решений. Если бы мы установили для альфа-уровня значение 0,01, мы бы не отвергли нулевую гипотезу (рис. 14). Мы могли бы сказать, что среднее экспериментальной группы происходит из той же генеральной совокупности, что и среднее контрольной группы. Итак, статистическая ошибка I рода: мы отвергаем нулевую гипотезу, когда она верна.
Рис. 14. Для α-уровня = 0,01 среднее экспериментальной группы не позволяет отвергнуть нулевую гипотезу
Что же мешает установить α-уровень достаточно маленьким, и не отвергать нулевую гипотезу, когда она верна? …Ошибка II рода, заключающаяся в том, что мы не принимаем альтернативную гипотезу, хотя она верна.
Ошибка второго рода
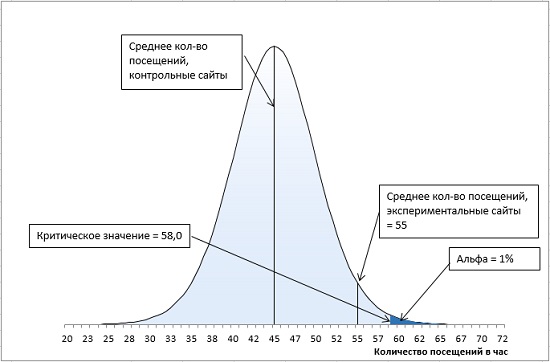
Представьте, что существуют две генеральные совокупности: одна из них состоит из сайтов, не получающих специального продвижения, вторая — из сайтов, получающих продвижение. Если вы повторите свое месячное исследование сотни или даже тысячи раз, то, возможно, получите две колоколообразные кривые (рис. 15).
Рис. 15. Ошибка второго рода при α-уровне = 0,05
Иногда среднее значение экспериментальной группы будет происходить из правого хвоста левой кривой распределения исключительно из-за выборочной ошибки. Поскольку в данном случае среднее экспериментальной группы превышает среднее контрольной группы более чем на 1,75 стандартной ошибки (попадает в область α-уровня = 0,05), вы должны отвергнуть нулевую гипотезу, даже если обе генеральные совокупности в действительности имеют одно и то же среднее. Такое неверное отбрасывание нулевой гипотезы, когда в действительности она является истинной, мы назвали ошибкой I рода. В терминах рис. 15 ошибка I рода – приписывание среднего результата экспериментальной выборки, равное 55, правой кривой, а не хвосту левой кривой.
Кривая слева представляет генеральную совокупность веб-сайтов, не получающих специального продвижения. На протяжении месяца частота посещений для некоторых из этих сайтов (очень немногих) составит всего 25 посещений в час, тогда как для других, столь же немногочисленных, – 62 посещения в час. Но 90% всех средних показателей выборок лежат в диапазоне 36,2–53,8 посещений в час.
Кривая справа представляет специально продвигаемые сайты. Как правило, показатели для них примерно на 10 посещений в час выше, чем для сайтов, представленных кривой слева. Их общее среднее составляет 55 посещений в час. Однако большая часть этой информации скрыта от вас. У вас отсутствуют данные о генеральной совокупности, и вы располагаете только результатами двух извлеченных вами выборок, но и этого вам будет вполне достаточно.
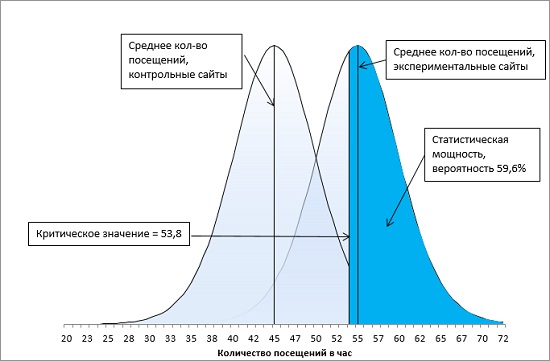
Рассмотрим правую кривую на рис. 15. Площадь под этой кривой от минимальных до критического значения (равного 53,8) выделена ярко голубым. Она определяет вероятность ошибки II рода. Средние выборок, проистекающие из этой области, мы относим к левой кривой, а не к правой. Для количественной оценки вероятности ошибки II рода найдем t-значение границы для правой кривой по формуле (7):
Вероятность того, что значение относится к правой кривой и лежит в диапазоне t-значений от –∞ до –0,247 определяется формулой =СТЬЮДЕНТ.РАСП(-0,247;15;ИСТИНА) = 0,404. Т.е., при выбранном нами α-уровне = 0,05 с вероятностью 40,4% мы отклоним альтернативную гипотезу, хотя она верна!
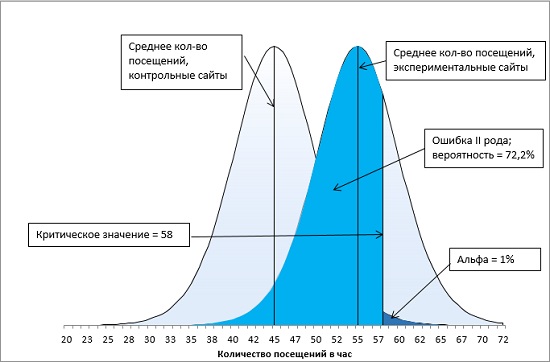
Что произойдет, если мы выберем α-уровень = 0,01, как на рис. 14? Вероятность ошибки II рода увеличится до 72,2% (рис. 16).
Рис. 16. Ошибка второго рода при α-уровне = 0,01
Статистическая мощность
Вероятность, количественно определяющую величину ошибки второго рода, называют β (на рис. 16 β = 72,2%). А вероятность р = (1 – β) – статистической мощностью (рис. 17).
Рис. 17. Статистическая мощность исследования при α-уровне = 0,05
Чем выше статистическая мощность, тем больше вероятность того, что мы отклоним нулевую гипотезу и примем альтернативную гипотезу. На мощность влияют четыре основных фактора:
- Тип теста (переход от двунаправленного теста к однонаправленному увеличивает мощность).
- Уровень α, то есть вероятность ошибки I рода: более высокая α увеличивает мощность.
- Разница между средними значениями выборок (мощность выше при большей разнице).
- Стандартная ошибка среднего (чем ниже ошибка, тем мощность выше).
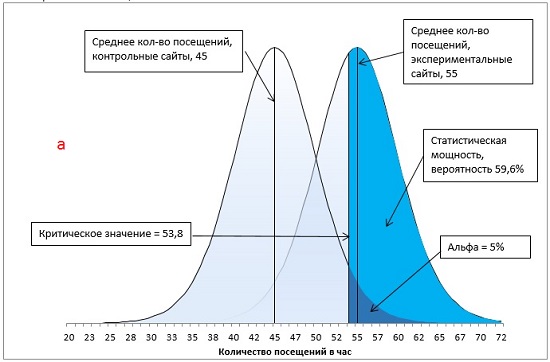
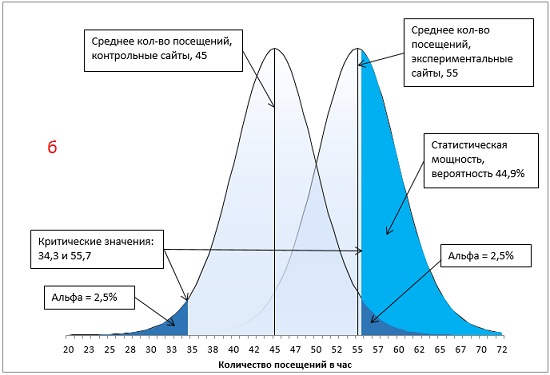
Давайте на нашем примере рассмотрим, как каждый из указанных факторов изменяет мощность, считая, что факторы меняться по одному (рис 18; расчеты и формулы можно найти в файле Excel).
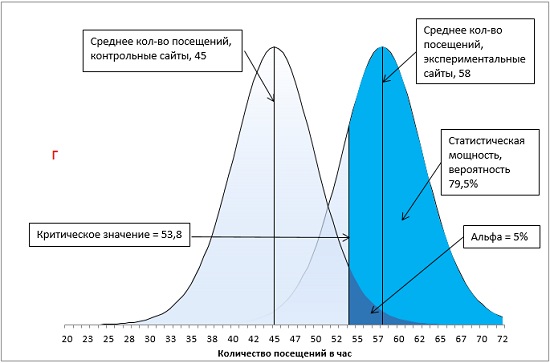
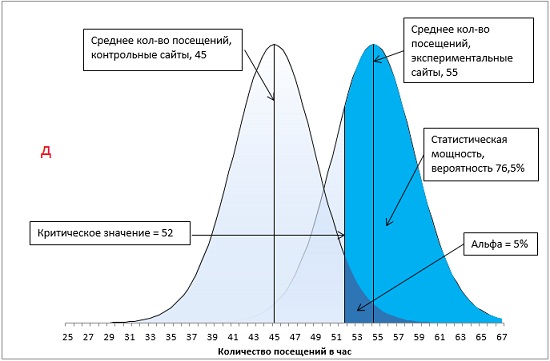
Рис. 18. Методы увеличения статистической мощности: а) базовый вариант; б) ненаправленная гипотеза; в) увеличение α с 0,05 до 0,1; г) увеличение разницы между средними экспериментальной и контрольной групп с 10 до 13 посещений в час; д) увеличение размера групп с 16 до 24 сайтов.
Первый метод повышения статистической мощности связан с подготовкой эксперимента. Если вместо ненаправленной гипотезы (двуххвостовой тест) использовать направленную (однохвостовой тест), вся величина α-уровня отнесется к одному хвосту распределения (сравните рис. 18а и 18б). В результате критическое значение сместится в сторону среднего значения распределения. Чем ближе критическое значение к среднему, тем более вероятно, что вы получите результат, превышающий критическое значение, что увеличивает статистическую мощность тестов. В нашем примере, мощность возрастет с 44,9% до 59,6%.
Второй метод повышения мощности теста предлагает ослабить α-уровень. Например, увеличивая α от 0,05 до 0,10, вы увеличиваете вероятность совершения ошибки I рода, но уменьшаете вероятность совершения ошибки II рода (сравните рис. 18а и 18в). В нашем примере, мощность возросла с 59,6% до 74%.
Оставшиеся два метода повышения статистической мощности основаны на формуле расчета t-статистики:
где t – t-значение для среднего выборки (а не для индивидуального значения), X̅ – среднее значение выборки, μ – среднее значение генеральной совокупности (или среднее значение контрольной выборки), ![]() – стандартная ошибка средних по выборкам (а не индивидуальных значений), равная:
– стандартная ошибка средних по выборкам (а не индивидуальных значений), равная:
где s – стандартная ошибка индивидуальных значений, n – размер выборки.
Для увеличения t-статистики (и, как следствие, статистической мощности) нужно, либо увеличить числитель, либо уменьшить знаменатель в формуле (8). Для увеличения разности X̅ – μ требуется внесение изменений в проведение эксперимента. Как это сделать, непростой вопрос, решаемый в каждом конкретном случае. В нашем примере, увеличение X̅ с 55 до 58 посещений в час при неизменном μ = 45, приведет к росту статистической мощности с 59,6% до 79,5% (рис. 18г).
И, наконец, уменьшение величины знаменателя тестовой статистики в формуле (8), есть не что иное, как уменьшение стандартной ошибки . Одним из способов уменьшения стандартной ошибки является увеличение размера выборки, n. В соответствии с формулой (9), чем больше n, тем меньше . В нашем примере, при неизменной стандартной ошибке индивидуальных значений s, увеличение контрольной и экспериментальной групп с 16 до 24 сайтов приведет к уменьшению с 5 до 4,1 и росту мощности с 59,6% до 76,5% (рис. 18д).
Один из хороших способов познакомиться с влиянием разных факторов на мощность – это поэкспериментировать с графическим калькулятором мощности, например, здесь.
Основные положения заметки
t-статистика Стьюдента используется вместо нормального распределения: а) для малых выборок; б) если стандартное отклонение генеральной совокупности σ не известно.
t-распределение представлено семейством распределений; дополнительный параметр – размер выборки или число степеней свободы.
Число степеней свободы равно размеру выборки минус число фиксированных статистик выборки (среднее, коэффициент регрессии, …)
Чем больше степеней свободы, тем ближе t-распределение к нормальному.
Функции в Excel, имена которых включают часть РАСП, принимают t-значение в качестве аргумента и возвращают вероятность. Функции, имена которых включают часть ОБР, принимают значение вероятности в качестве аргумента и возвращают t-значение.
Для подстановки в функции Excel значения предварительно должны быть стандартизованы.
Ошибка I рода: отбрасывание нулевой гипотезы, когда в действительности она является истинной. Ошибка II рода: не принятие альтернативной гипотезы, хотя она верна. Чем больше ошибка первого рода, тем меньше ошибка второго рода.
Критерий отнесения события к маловероятному является произвольным. Традиционно маловероятным считают событие, происходящее не чаще, чем 1 раз из 20 попыток.
Один из основных методов уменьшения ошибки второго рода – увеличение элементов в выборке.
[1] При написании замети использованы материалы книг: Дуглас Хаббард. Как измерить всё, что угодно, Левин и др. Статистика для менеджеров, Сара Бослаф. Статистика для всех, Конрад Карлберг. Регрессионный анализ в Microsoft Excel.
[2] На самом деле, можно встретить довольно много различных терминов в отношении нормированных значений z. Ориентируйтесь не на названия, а на суть понятий.
[3] Могут высказать справедливое замечание, что не следует обозначать граничный уровень так же, как и математическое ожидание генеральной совокупности µ. Соглашусь, но всё же использую обозначение, поскольку, в иных задачах здесь часто фигурирует именно математическое ожидание генеральной совокупности µ.
[4] Некоторые авторы указывают знак меньше или равно для левостороннего распределения Р(Х≤t), и больше для правостороннего Р(X>t). Однако, для t=0 значения СТЬЮДЕНТ.РАСП(0;df;ИСТИНА) = СТЬЮДЕНТ.РАСП.ПХ(0;df) = 0,5 для любого значения df. На мой взгляд, Excel при интегральном расчете трактует границу, как исчезающе малую. Поэтому, нет разницы, использовать знак ≥ или >.
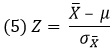



Классная статья для общего понимания!
Но замечание: разве в формуле (1) сигма в знаменателе не должна быть вынесена из-под корня?
Спасибо. Поправил.