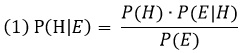На мой взгляд, на русском языке выходит недостаточно книг по байесовскому подходу, поэтому «я делаю стойку» при виде любого издания по этой теме. Научный вывод Виктора Светлова – это действительно научный труд из области математической логики, но я думаю, что мне удалось некоторые идеи изложить в популярном виде. Раздел, посвященный введению в байесовский метод, мне очень понравился. То ли я по прочтении десятка источников поднаторел в этом вопросе, то ли действительно изложено кратко и понятно. Книга содержит критику философии Карла Поппера, хотя она и сложновата для неспециалистов. В целом, книга посвящена современному этапу формирования байесовской парадигмы научного вывода. Подробно анализируется байесовский вариант решения проблем абдукции, индукции и научного прогресса.
Виктор Светлов. Научный вывод: Байесовская парадигма. – М.: Ленанд. URSS, 2017. – 200 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу в Ozon
Теорема Байеса как универсальная парадигма научного вывода
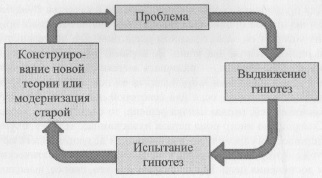
Абдукция, дедукция и индукция — методы, используемые во всех науках. Поэтому самый перспективный путь – синтез этих и, возможно, других методов в одной модели получения нового знания, называемой научным выводом. Процесс научного познания основан на регулярно повторяющемся цикле (рис. 1).
Рис. 1. Основной цикл научного познания
В общем случае решение научной проблемы означает логическое обоснование новой теории или модернизацию старой и требует совершения определенных познавательных шагов как от частного знания к общему, так и обратно. Ни один из этих шагов не является самоочевидным (особенно шаг от частного знания к общему), о чем среди прочих свидетельствует следующее известная оценка А. Эйнштейна сущности гипотетико-дедуктивного метода (ГДМ) в науке: «Для применения своего метода теоретик в качестве фундамента нуждается в некоторых общих предположениях, так называемых принципах, исходя из которых он может вывести следствия. Его деятельность, таким образом, разбивается на два этапа. Во-первых, ему необходимо отыскать эти принципы, во-вторых — развивать вытекающие из этих принципов следствия».
Научная проблема = противоречие между теорией (известным знанием) и аномальным фактом (неизвестным знанием).
Цикл научного исследования направляется и контролируется методологическими предписаниями, которые в зависимости от стадии научного исследования делятся на правила абдукции (изобретения) гипотез, дедукции необходимых и проверяемых следствий, индукции (обоснования гипотезы). Стадия открытия нового знания, которую вслед за Чарльзом Пирсом принято называть абдукцией, преследует цель – изобретение новой истины, т.е. потенциально, предлагает лучшее объяснение причины исследуемого факта.
Правило абдукции. Гипотеза Н представляет новое объяснение аномального факта Е, если и только если ее правдоподобие относительно этого факта больше правдоподобия всех ее альтернатив вместе взятых.
Правдоподобием гипотезы Н относительно аномального факта Е принято называть функцию Р(Е/Н). Читается «вероятность наступления факта Е если гипотеза Н истинна. Эта функция представляет из себя условную вероятность наступления Е при наступлении Н. Чем выше значение Р(Е/Н), тем более правдоподобно, что Н наиболее вероятная причина Е.
Правило абдукции объясняет творческий (интуитивный) характер большинства научных открытий. Истина открывается не в результате постепенного накопления знаний или механической дедукции из принятых аксиом, а в результате неожиданного «прозрения», указывающего, какая из гипотез представляет лучшее объяснение рассматриваемого факта.
Абдукция не обладает свойством открывать необходимые истины. Посылки абдуктивного рассуждения могут быть истинны, а заключение, тем не менее, ложно. Плодотворность абдукции заключается в том, чтобы изобрести новую и потенциально самую информативную истину. Но насколько она реально соответствует этим признакам, решается в специальном акте обоснования, называемом индукцией.
Вывод необходимых следствий из новой гипотезы, называемый дедукцией, проводится для: (1) развития ее содержания; (2) объяснения с ее помощью аномальных фактов; (3) извлечения решающих для ее эмпирического обоснования предсказаний.
Правило дедукции. Высказывание Е представляет необходимое (логическое, законное, общезначимое) следствие гипотезы Н тогда и только тогда, когда выполняется любое из трех эквивалентных условий:
- если Н истинна, всегда истинно Е;
- отрицание Е несовместимо с истинностью Н;
- если Е ложно, всегда ложно Н.
Правило индукции. Гипотеза Н получает независимое подтверждение в качестве новой истины, если и только если подтверждение решающего предсказания О, не совпадающего с объясняемым (аномальным) фактом Е максимизирует разность Р(Н|O) – Р(Н).
Вероятность Р(Н), которую принято называть априорной вероятностью гипотезы Н, обратно пропорциональна степени ее начальной информативности. Чем меньше значение Р(Н), тем более информативна гипотеза Н. Наоборот, чем выше значение вероятности Р(Н), тем она менее информативная. Вероятность Р(Н|О), которую принято называть апостериорной вероятностью гипотезы Н на основании факта О, измеряет степень эмпирической поддержки Н как возможной причины предсказываемого события О. Чем выше значение Р(Н|О), тем больше эмпирическая поддержка гипотезы Н от подтверждения предсказания О.
Абдукция имеет дело с аномальными фактами, требующими объяснения; индукция — с фактами, подтверждающими или опровергающими гипотезу и независимыми от объясняемых фактов. Если объясняемые факты задаются исследователю объективно, независимо от его воли, то подтверждающие и опровергающие факты конструируются, отыскиваются, собираются им, как правило, специально. Здесь уместна аналогия с криминальным происшествием. Преступление — факт, требующий объяснения с помощью абдукции. Выдвинутая гипотеза указывает на подозреваемого. Поиск улик, изобличающих подозреваемого или, наоборот, оправдывающего его невиновность, — сбор фактов, необходимых для индуктивного подтверждения или опровержения абдуктивной гипотезы.
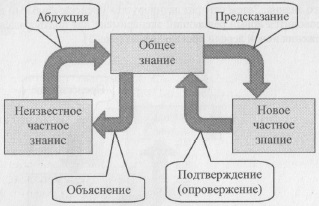
Синтез абдукции (открытия нового общего знания), дедукции (объяснения и предсказания) и индукции (подтверждения, опровержения) рождает новое качество научного вывода. То, что не свойственно по определению ни одному из перечисленных методов в отдельности, оказывается присуще их особому объединению, называемому научным выводом (рис. 2). Феномен (неизвестное частное знание) с помощью прозрения рождает гипотезу (общее знание), которая дедуктивно объясняет этот феномен. С другой стороны, из гипотезы дедуктивно следуют предсказания (новое частное знание), которые способны подтвердить или опровергнуть гипотезу.
Рис. 2. Целостная структура научного вывода; слева – объяснительный цикл научного вывода, справа – предсказательный
Научный вывод — совокупность методов и предписаний, регулирующих и контролирующих процесс открытия новой истины (функция абдукции), логического развития истины (функция дедукции) и коррекции результатов открытия и развития истины (функция индукции).
Теорема Байеса: основная идея и ее формализация
Наш мозг представляет байесовское устройство, познающее окружающий мир путем предсказаний и поиска причин наших ощущений.
Крис Фрит. Мозг и душа. Как нервная деятельность формирует наш внутренний мир.
Теория вероятностей допускает прямое и обратное применение. Прямое: если известна причина (ее объективная вероятность), всегда можно узнать ее следствие — предсказываемую вероятность ее наблюдаемого проявления, т.е. фиксируемое в опыте значение относительной частоты. Обратное: если известны вероятности следствий, можно вычислить вероятности их предполагаемых причин.
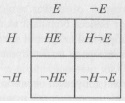
Пусть Н обозначает гипотетическую причину некоторого события Е. ¬Н – дополнение Н (множество возможных причин события Е, несовместимых с причиной Н); ¬Е — дополнение Е (множество событий в качестве возможных следствий причины Н, несовместимых с событием Е). Тогда НЕ обозначает: причина Н действует и событие Е происходит; Н¬Е — причина Н действует, но событие Е не происходит; ¬НЕ — причина Н не действует, но событие Е наступает; ¬Н¬Е — ни причина Н не действует, ни событие Е не происходит (рис. 3).
Рис. 3. Полное поле возможных результатов действия причины Н и реализации ее следствия Е
Вероятность Р(Н), измеряющую степень доверия исследователя к истинности гипотетической причины Н, независимой от планируемого опыта, принято называть априорной (доопытной) вероятностью Н. Вероятность Р(Н|Е) принято называть апостериорной вероятностью причины Н относительно происшедшего события Е. Сравнение априорной и апостериорной вероятностей одной и той же гипотезы Н дает информацию о влиянии происшедшего события на возможное изменение степени доверия исследователя к анализируемой причине.
Простейший вариант теоремы Байеса:
Ее основная идея состоит в том, что апостериорная вероятность Р(Н|Е) гипотезы Н всегда является частью абсолютной вероятности Р(Е) происшедшего события Е и совпадает с ней только в том случае, если ее дополнение ¬H несовместимо с Е (так как в этом случае имеет место Р(¬HЕ) = 0). Тем самым теорема Байеса доказывает, что апостериорная вероятность произвольной гипотетической причины Н представляет отношение вероятности ее совместной истинности с событием Е к сумме аналогичных вероятностей для Н и ¬Н относительно события E.
Допустим, подбрасывается монета, вероятность выпадения герба которой не известна и ограничена значениями 1/2 или 1. Соответственно в качестве гипотетических причин выступают предположения: Н1 = {Р(Г) = 1/2} и Н2 = {Р(Г) = 1}. Априорные вероятности гипотез одинаковы: Р(Н1) = Р(Н2) = 1/2. В первом опыте выпал герб: Е1 = Г1. Спрашивается, какая из указанных гипотез наиболее вероятна на основании Е1?
Перепишем равенство (1) с учетом начальных условий. Это позволит вычислить апостериорные вероятности гипотез Н1 и Н2 после выпадения герба в первом подбрасывании, т.е. после реализации события Е1:
Мы видим, что P(H1) = 1/2 > Р(H1|E1) = 1/3, но Р(Н2) = 1/2 < Р(Н2|Е2) = 2/3, что говорит о том, что выпадение герба в первом подбрасывании уменьшает доверие к гипотезе H1, как истинной причине события Е1 и увеличивает аналогичные шансы гипотезы H2.
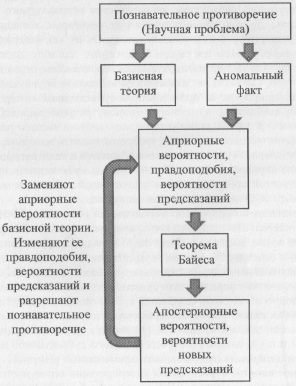
Вычисление апостериорных вероятностей возможных причин наблюдаемых событий составляет первую часть применения теоремы Байеса. Вторую часть образует вычисление вероятностей предсказаний новых событий на основании вычисленных априорных вероятностей. Обе части применения теоремы Байеса образуют цикл все более точного познания (объяснения и предсказания) вероятностей причин и их следствий с любой желаемой степенью (рис. 4).
Рис. 4. Цикл применения теоремы Байеса для объяснения и предсказания наиболее вероятных причин и следствий
Формула (1) вместе с обосновывающими их логико-математическими и методологическими положениями образуют концепцию индуктивной вероятности — логико-методологическое ядро обратного применения теории вероятностей. Основное допущения индуктивной концепции вероятностей: вероятности гипотез и совершаемых на их основе предсказаний имеют сложную концептуальную природу, так как зависят от наблюдаемых частот, логических особенностей языка, личной веры исследователя в правоту или ложность рассматриваемой гипотезы одновременно. Будучи чувствительными к концептуальным допущениям, индуктивные вероятности могут отражать влияние не только непосредственно наблюдаемых факторов, но и более фундаментальных факторов, скрытых, как правило, от наших глаз. Сила индуктивных вероятностей состоит также в том, что они представляют собой гибкий инструмент познания. Изменяясь в соответствии с накапливаемыми данными, индуктивные вероятности позволяют успешно учиться на опыте и, что самое главное, исправлять допущенные ранее ошибки и неточности.
Кроме математического значения, теорема Байеса имеет фундаментальный теоретико-познавательный смысл, который станет более очевиден при анализе фундаментальных и дискуссионных проблем индукции, абдукции и формализации основных паттернов научного вывода.
Проблема индукции и научный вывод
Индуктивная концепция вероятностей предполагает использование в научном выводе четырех видов вероятностей: априорных и апостериорных вероятностей гипотез, правдоподобий гипотез и вероятностей предсказаний. Теорема Байеса связывает их все в один самокорректирующийся механизм познания (рис. 5).
Рис. 5. Теорема Байеса в структуре научного вывода
Субъективная вероятность — это степень личной уверенности индивида в наступлении какого-либо события. Для Б. де Финетти вероятность, приписываемая субъектом некоторому событию, всегда «обнаруживается с помощью тех условий, при которых он мог бы заключить пари на это событие».
Субъективная вероятность должны быть когерентна, или непротиворечива. Это означает: если некоторый индивид верит с субъективной вероятностью 0,8, что событие Е наступит, то он обязан верить с субъективной вероятностью 0,2, что Е не наступит. В терминах шансов эквивалентно получаем, что индивид, заключивший пари с шансами 8 к 2 в пользу Е, обязан с такой же степенью готовности заключить пари с шансами 2 против 8, что Е не наступит.
Необходимым и достаточным условием когерентности является требование:
(2) Р(Е) + Р(¬Е) = 1
Благодаря требованию когерентности теория субъективных вероятностей превращается в особую интерпретацию обычного исчисления вероятностей, в сферу которого попадает такая, казалось бы, недоступная для строгого анализа область, как субъективные мнения, оценки, суждения.
Для решения проблемы связи субъективных вероятностей и частот де Финетти считает, что неясное и неудовлетворительное определение «независимых событий с фиксированной, но неизвестной вероятностью» должно быть заменено понятием «эквивалентные события». Требования эквивалентности достаточно, чтобы объяснить, почему «богатый опыт всегда заставляет нас считать вероятные будущие частоты или распределения близкими к тем, которые мы уже наблюдали». Эквивалентность позволяет отказаться от использования в науке понятия объективной вероятности, а также от гипотез об этих вероятностях.
Концепция субъективных вероятностей, как одна из возможных интерпретаций исчисления вероятностей, обладает, по мнению де Финетти, двумя важными достоинствами. В терминах этой концепции впервые получает экспериментальное определение понятие вероятности и впервые доказывается его субъективная природа. Частотная интерпретация, считает де Финетти, не предлагает первого и полностью исключает второе. С другой стороны, субъективная интерпретация предлагает «исключительно безупречное с операциональной точки зрения» определение вероятности в терминах «прямого экспериментального, измерения степени сомнения относительно реализации данного события».
Научный вывод в байесовской интерпретации объединяет процессы:
- асимптотического перехода от состояния начальной неопределенности, выражаемой некоторым множеством альтернативных гипотез, к состоянию полной определенности и достоверности, когда только одна гипотеза истинна;
- замещения априорных вероятностей, выражающих начальную установку на предмет исследования и основанную на эмпирических и теоретических данных, полученных до проведения научного исследования, на апостериорные вероятности, характеризующие результат изменения этой установки под влиянием исходов проведенных испытаний;
- фальсификации ложных гипотез и верификации истинной гипотезы.
Среди прочего это означает также решение проблемы индукции в обычном смысле — открытие с большой степенью надежности нового общего знания на основании известного частного знания.
Проблема абдукции и научный вывод
Форма абдуктивного вывода такова. Наблюдается удивительный (аномальный, опровергающий некоторое убеждение) факт С; если бы гипотеза А была истинна, факт С воспринимался бы как само собой разумеющийся; следовательно, имеется основание считать гипотезу А истинной.
Допустим, десять раз подбрасывалась монета. Если при этом имело место десятикратное выпадение герба, то такое событие является аномальным фактом, потому что оно опровергает наше интуитивное убеждение, что монета симметричная. Если выдвинуть альтернативную гипотезу, что монета несимметричная и вероятность выпадения ее герба равна 1 или близка к этому значению, данный факт перестает быть аномальным.
Чарльз Пирс требует от принимаемой гипотезы большего правдоподобия — более вероятного объяснения фактов при допущении ее истинности. Правдоподобие гипотезы, отстаивающей симметричность монеты, несмотря на десятикратное выпадение герба, равно 1/210 = 1/1024 ≈ 0,001. Правдоподобие альтернативной гипотезы, утверждающей, что вероятность выпадения герба равна 1, равно 1. Согласно требованию большей простоты, предпочтение должно быть отдано второй гипотезе. Более простая гипотеза всегда имеет большее правдоподобие, чем все ее конкуренты вместе взятые. Тем самым она отнимает у своих соперниц шанс быть более предпочтительными до нового испытания.
Связь абдукции Пирса с байесовской интерпретацией научного вывода станет более очевидной после определения необходимых условий ее законности. Абдукция представляет вывод от наблюдаемого аномального факта Е к объяснительной гипотезе Н только тогда, когда
- Н объясняет факт Е;
- Н — самая простая гипотеза (не существует оснований для принятия какой-либо иной альтернативы) из множества всех допустимых;
- Н готова к испытанию в опыте (имеет эмпирическое содержание).
В терминах байесовского научного вывода степень простоты гипотезы прямо пропорциональна степени ее правдоподобия. Для любых двух конкурирующих гипотез Н1, и Н2, исчерпывающих объяснение одного и того же аномального факта Е, можно сформулировать следующее полезное правило: Гипотеза Н1 лучше объясняет аномальный факт Е, чем кон курирующая гипотеза H2, настолько, насколько правдоподобие Н1 больше правдоподобия Н2: Р(Е|H1) > Р[Е|H2).
Конраду Лоренцу, известному австрийскому этологу, однажды потребовалось объяснить факт неожиданной вспышки агрессии глухих со дня рождения индюшек по отношению к своим только что вылупившимся птенцам (см. Конрад Лоренц. Так называемое зло). Пусть Е обозначает аномальный факт агрессии глухих индюшек и Р(Е) > 0. Общепринятое предположение, что «Индюшка, пока она сидит на гнезде, должна быть постоянно готова с максимальной энергией нападать не только на мышей, крыс, хорьков, ворон, сорок и т. д., но и на своих сородичей … потому что они также опасны для ее выводка, как и хищники» не объясняет указанный факт, так как очевидно, что дети индюшек не могут быть объектами агрессии своих матерей. Обозначим Н1 = «дети индюшек не могут быть объектом агрессии своих матерей» как общепринятую гипотезу. Так как гипотеза Н1 не объясняет факт Е, ее правдоподобие равно нулю, Р(Е|H1) = 0.
Для объяснения аномалии сотрудники Конрада Лоренца были вынуждены разработать более правдоподобную гипотезу. «Если не предполагать, что у индюшки повреждено что-то еще, кроме слуха, то такое поведение можно объяснить одним: у нее нет ни малейшей врожденной информации о том, как должны выглядеть ее малыши. Она клюет все, что движется около ее гнезда, если оно не настолько велико, чтобы реакция бегства у нее пересилила агрессию. Только писк индюшонка — и ничто больше — посредством врожденного механизма включает материнское поведение, одновременно затормаживая агрессию».
Пусть H2 = «дети глухих индюшек могут быть объектом агрессии своих матерей» обозначает новую гипотезу сотрудников Лоренца. Учитывая ее успех в объяснении аномального факта Е, правдоподобие H2 можно приравнять к единице: Р(Е|H2) = 1.
Научный вывод как доказательство
Обозначим символами Е и Н свидетельство и гипотезу соответственно. Возможны три исхода влияния свидетельства Е на вероятность гипотезы Н:
- свидетельство Е подтверждает гипотезу Н, если Р(Н|Е) > Р(Н);
- свидетельство Е опровергает гипотезу Н, если Р(Н|Е) < Р(Н);
- свидетельство Е индуктивно нейтрально по отношению к гипотезе Н, если Р(Н|Е) = Р(Н).
Допустим, имеется несколько альтернативных гипотез, образующих полное множество, т.е. такое множество, которое необходимо содержит истинную гипотезу. Пусть каждая гипотеза из этого множества имеет некоторое логическое следствие. Как изменится правдоподобие гипотез, если правдоподобие следствия одной из гипотез будет больше правдоподобия следствий всех остальных гипотез? Ответ на этот вопрос дает следующее умозаключение.
Дано: Н1 и Н2 образуют полное множество.
Р(Н1) + Р(Н2) = 1.
Из Н1 следует Е1, Р(Н1¬Е1) = 0.
Из Н2 следует Е2, Р(Н2¬Е2) = 0.
Начальная вероятность E1 больше начальной вероятности Е2, Р(Е1) > Р(Е2) ≥ 0,
Следовательно: правдоподобие гипотезы Н1, относительно свидетельства Е1 больше правдоподобия гипотезы Н2 относительно свидетельства Е2, Р(Н1|Е1) > Р(Н2|Е2).
Это умозаключение характеризует одну из самых распространенных ситуаций вероятностного вывода. С логической точки зрения оно представляет индуктивный вариант закона исключенного третьего дедуктивной аргументации: из нескольких взаимоисключающих гипотез та подтверждается сильнее, которая имеет более правдоподобное свидетельство. Умозаключение интересно тем, что объединяет две важнейшие индуктивные стратегии — подтверждение истинной гипотезы и опровержение (исключение) ложных гипотез.
Приведем пример использования этого умозаключения из художественной литературы.
— Вот что, Ватсон, — промолвил Шерлок Холмс. — мы оставим вопрос, кто убил Стрэкера, и будем думать, что произошло с лошадью. Предположим, Серебряный в момент преступления или немного позже ускакал. Но куда? Лошадь очень привязана к человеку. Предоставленный самому себе, Серебряный мог вернуться с Кингс-Пайленд или убежать в Кейплтон. Что ему одному делать в поле? И уж, конечно, кто-нибудь да увидел бы его там. Теперь цыгане, — зачем им было красть его?.. Украсть ее — большой риск, а выгоды — никакой. Это – вне всякого сомнения.
— Где же тогда Серебряный?
— Я уже сказал, что он или вернулся в Кингс-Пайленд или поскакал в Кейплтон. В Кингс-Пайленде его нет. Значит, он в Кейплтоне. Примем это за рабочую гипотезу и посмотрим, куда она нас приведет. Земля, как заметил инспектор, высохла и стала тверже камня, но местность слегка понижается к Кейплтону, и в той лощине ночью в понедельник, наверное, было очень сыро. Если наше предположение правильно, Серебряный скакал в этом направлении, и там нужно искать его следы.
Беседуя, мы быстро шли вперед и через несколько минут спустились в лощину. Холмс попросил меня обойти ее справа, а сам взял левее, но не успел сделать и пяти—десяти шагов, как он закричал мне и замахал рукой. На мягкой глине у его ног виднелся отчетливый конский след. Холмс вынул из кармана подкову, которая как раз пришлась по отпечатку.
— Вот что значит воображение, — улыбнулся Холмс. — Мы представили себе, что могло бы произойти, стали проверять предположение, и оно подтвердилось» (Конан Дойль А. Серебряный // Из досье Шерлока Холмса. М., 1991. С. 129)
Рассмотренный пример показывает, что знаменитый «дедуктивный метод» Шерлока Холмса на самом деле представляет вариант обычного гипотетико-дедуктивного метода, широко известного во времена А. Конан Дойля. Этот метод может использоваться как для объяснения уже существующих фактов, так и для поиска новых. На этом основании мы должны отклонить обвинение, что Шерлок Холмс был против современной логики. Наоборот, именно ей он обязан своими поражающими открытиями и проницательными догадками (см. также Индукция и дедукция. Какой тип умозаключений мы используем чаще?).
Стандартная модель научного вывода и ее проблемы
Стандартная модель научного вывода — гипотетико-дедуктивный метод научного исследования (ГДМ). Если логико-математическое знание истинно благодаря введенным определениям и принятым конвенциям, эмпирическое знание истинно благодаря прямому соответствию опыту, то благодаря чему истинно теоретическое знание? Ведь его прямая верификация в опыте невозможна и, кроме того, оно не является конвенциально истинным.
В качестве решения возникшей проблемы были разработаны три программы эмпирической значимости теоретического знания — научной систематизации, устанавливаемой теорией, Карла Гемпеля (1905–1997), подтверждения законов в формализованных языках Рудольфа Карнапа (1891–1970) и глобального преобразования ГДМ в дедуктивистскую модель научного знания Карла Поппера (1902–1994; подробнее см. Карл Поппер. Логика научного исследования).
Все три программы были построены в терминах формального анализа основных понятий ГДМ (объяснение, предсказание, подтверждение и опровержение гипотез). Развитие каждой из них быстро выявило существенные ограничения позитивистской интерпретации ГДМ. Поппер, например, решил превратить ГДМ в чисто дедуктивный метод и на этом основании полностью исключить индуктивные связи теории с опытом, что привело его ко многим нелепостям и ошибкам.
С именем Карла Поппера связана одна из самых грандиозных попыток обосновать дедуктивистскую модель науки, полностью исключающую какие-либо индуктивные отношения между теорией и опытными данными. Резко отрицательное отношение Поппера к положительному решению проблем верификации, подтверждения и индукции положило начало острому антагонизму между ним и Карнапом. Но хотя Поппер и противопоставлял себя членам Венского кружка, объективно его методологическая концепция полностью соответствует основным допущениям и целям неопозитивистской философии и методологии науки. Как и их, его интересует только проблема эмпирической значимости научного знания, которую он называет проблемой демаркации.
Дедуктивистская модель науки Поппера основывается на трех связанных друг с другом тезисах. Первый утверждает, что фальсифицируемость является единственным отличительным признаком научного знания и существует принципиальная асимметрия между верификацией и фальсификацией. Второй доказывает, что теории с высоким информативным содержанием не могут иметь высокой апостериорной вероятности, и поэтому вероятностная концепция индукции логически абсурдна. Третий тезис утверждает, что рациональный теоретический и прагматический выбор среди теорий возможен только на основании сравнения их правдоподобия как близости к истине, отождествляемого с истинным логическим содержанием, т.е. сугубо внутренней характеристикой этих теорий. Последние два тезиса исключают влияние каких-либо внешних, прежде всего эмпирических, факторов на прогресс научного знания.
Можно выделить следующие части дедуктивистской модели науки Поппера: 1) концепцию демаркации (эмпирической значимости, фальсифицируемости); 2) концепцию подкрепления; 3) специальные аргументы против вероятностной теории индукции; 4) концепцию правдоподобия и научного прогресса.
В соответствии с основными допущениями своей дедуктивистской модели науки Поппер утверждает, что испытанию следует подвергать только высокоинформативные, т. е. маловероятные, смелые, рискованные гипотезы. Испытание именно таких гипотез гарантирует приближение к истине. «… Я вполне готов согласиться с тем, что фальсификационисты, подобные мне, гораздо охотнее предпочтут попытку решить интересную проблему посредством смелого предположения, даже (и особенно) если оно вскоре окажется ложным, любому перечислению не относящихся к делу тривиальностей. Мы предпочитаем этот путь, потому что убеждены в том, что именно так мы можем учиться на наших ошибках; обнаруживая ложность наших предположений, мы больше узнаем об истине и все больше приближаемся к ней». Опровержение таких гипотез дает максимум научной информации и по этой причине составляет единственную цель научного познания. Несмотря на кажущуюся очевидность, данное утверждение тем не менее ложно.
Чем более смелую гипотезу мы опровергаем, тем меньшую информацию мы приобретаем; чем более вероятную гипотезу мы отвергаем, тем большую информацию мы получаем. Учитывая сказанное, ученый должен стремиться опровергать высоковероятные, пользующиеся максимальным доверием научного сообщества гипотезы, так как, только в этом случае он приобретает максимум научной информации. И он не должен стремиться, как утверждает Поппер, опровергать смелые гипотезы, так как это приносит ему минимальную информацию. Наоборот, подтверждать следует стремиться смелые гипотезы, так как в случае успеха ученый получает максимум информации. Подтверждение высоковероятных гипотез приносит минимальную информацию.
Причина всех неудовлетворительных следствий попперовской концепции правдоподобия — отождествление близости к истине с логическим содержанием теорий и полное игнорирование эмпирических и теоретических характеристик этого понятия. Более общей причиной является, конечно, антииндуктивизм Поппера, a priori исключающий любые индуктивные связи теории с опытными данными.
Гипотетико-индуктивная модель научного вывода
Первая половина XX столетия была временем триумфа стандартной концепции научного метода. Ситуация начала меняться во второй половине XX века, когда критике были подвернуты все ее основные положения. В результате была разработана теория гипотетико-индуктивного вывода (ГИВ).
Идея прогресса — детище Нового времени, означает постепенное и неуклонное движение от менее совершенных социальных форм существования к более совершенным. Гипотетико-дедуктивный метод выражает эту идею в методологических терминах. Стандартная схема научного прогресса, восходящая к Ф. Бэкону и Р. Декарту, основана на допущении постепенного индуктивного или дедуктивного накопления неизменяемых далее и тем самым окончательных истин. Считается, что все истинные теории связаны друг с другом отношением дедуктивного обобщения (подчинения). Единственное различие между двумя истинными теориями, Т и Т’ одна из которых более прогрессивна, чем другая, состоит в степени универсальности: старая теория Т должна быть частным случаем новой более универсальной теории Т’. Иными словами, научный прогресс представляет последовательность истинных и все более универсальных теорий такую, что каждый ее член — дедуктивное следствие всех последующих теорий, которые будут открыты в будущем, и вся последовательность конвергирует к абсолютной истине ТА как своему пределу.
Конечно, в науке периодически происходит смена одних истинных теорий другими истинными, но логически более сильными теориями. Но подобные концептуальные сдвиги не выражают всех альтернатив научного прогресса. Любая теория, кроме истинного содержания, включает и ложное. Откуда следует, что научный прогресс возможен не одним, а тремя способами: (1) за счет увеличения истинного содержания теорий при сохранении в неизменности их ложного содержания; (2) за счет уменьшения ложного содержания теорий при сохранении в неизменности их истинного содержания; (3) за счет комбинации первого и второго способов таким образом, что каждая новая теория более правдоподобна, чем все ей предшествующие.
Стандартная концепция символизирует только первый вариант. Поэтому неудивительно, что она была подвергнута во второй половине XX столетия ожесточенной критике и существенной ревизии. Доказывалось, в частности, что теории, связанные прогрессивным шагом, несоизмеримы в значениях своих базисных терминов, а при объяснении одной и той же предметной области они часто несовместимы. Каждая новая теория отвергает, заменяет или заново интерпретирует ранее полученные результаты. Смена одной теории другой представляет концептуальную революцию, существенно меняющую онтологию, методологию и аксиологию исследования. Никакой единой общей истины, к которой якобы неуклонно движется наука, не существует. Соответственно отношение дедуктивного следования нельзя было более считать базисным отношением научного прогресса.
Реалистическая концепция прогресса должна преодолеть ограничения, свойственные классической (дедуктивистской и индуктивистской версии) концепции научного прогресса. Для этого она должна быть связана с идеей о том, что первостепенной задачей науки является получение истинной информации о действительности и формирование адекватного представления о мире. Реалистическая теория научного прогресса признает истину в качестве ведущей, но не единственной цели исследования, преследуемой учеными. Ученых интересует не просто истина, а информативная истина, не абсолютная истина обо всем мире, а истина, зависящая от конкретных условий и задач исследования. Все тавтологии — истины, но их информативность равна нулю. Поэтому они никогда не станут целью научного исследования. Большая информативность теории позволяет ставить больше проблем, находить больше верных решений создавать более универсальные и логически более сильные теории.