Ноябрь 2022
Стандартное отклонение и стандартная ошибка
Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения – чем стандартное отклонение отличается от стандартной ошибки, и в каких случаях, применять ту или иную статистику. А недавно в книге Искусство статистики Дэвида Шпигельхалтера я узнал про бутстрэппинг, и понял, как объяснить различия стандартного отклонения и стандартной ошибки.
Для начала зададим 100 значений стандартной нормально распределенной случайной величины. В этом контексте стандартная означает, что ее матожидание μ = 0, а среднеквадратичное отклонение σ = 1. Поскольку значения в Excel получены с помощью волатильной функции СЛМАССИВ(), после любого действия они пересчитываются. Поэтому диаграммы в заметке и в файле будут отличаться.
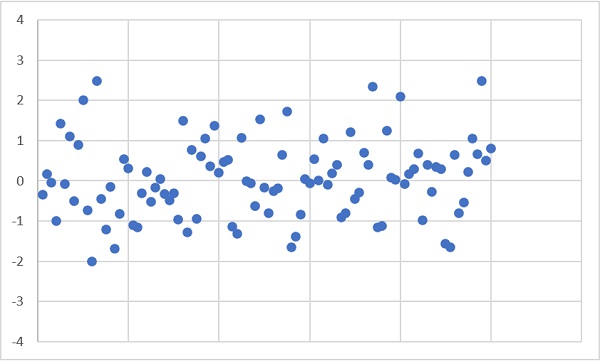
Рис. 1. Нормально распределенная случайная величина
Нетривиальный Байес
Недавно прочитал Искусство статистики Дэвида Шпигельхалтера. На тему байесовской вероятности очень понравился пример с монетами. Сначала – фрагмент книги, а затем небольшая модель в Excel.
У вас в кармане три монеты: на одной два орла, на другой две решки, третья обычная. Вы наугад вытаскиваете монету, подбрасываете ее, и выпадает орел. Какова вероятность, что на другой стороне монеты тоже орел? Дайте свой ответ, прежде чем читать далее.

Рис. 1. Три монеты
Дэвид Шпигельхалтер. Искусство статистики. Как находить ответы в данных
Статистика играла ключевую роль в научном познании мира на протяжении веков, а в эпоху больших данных базовое понимание этой дисциплины и статистическая грамотность становятся критически важными. Дэвид Шпигельхалтер приглашает вас в не обремененное техническими деталями увлекательное знакомство с теорией и практикой статистики.
Эта книга предназначена как для студентов, которые хотят ознакомиться со статистикой, не углубляясь в технические детали, так и для широкого круга читателей, интересующихся статистикой, с которой они сталкиваются на работе и в повседневной жизни. Но даже опытные аналитики найдут в книге интересные примеры и новые знания для своей практики.
Дэвид Шпигельхалтер. Искусство статистики. Как находить ответы в данных. – М.: Манн, Иванов и Фербер, 2021. – 448 с.

Подробнее »Дэвид Шпигельхалтер. Искусство статистики. Как находить ответы в данных
Центральная предельная теорема
Я часто сталкиваюсь с ситуацией, когда интересные научные концепции не используются на практике из-за сложности их представления. Одним из таких понятий является Центральная предельная теорема. Вот, что сказано в Википедии:
Центральные предельные теоремы – класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Звучит абстрактно… по крайней мере для меня. Переформулирую:
Центральная предельная теорема: независимо от формы распределения случайной величины средние выборок достаточного размера распределены нормально.
Если и эта формулировка мало что вам прояснила, не отчаивайтесь, изучите два примера.
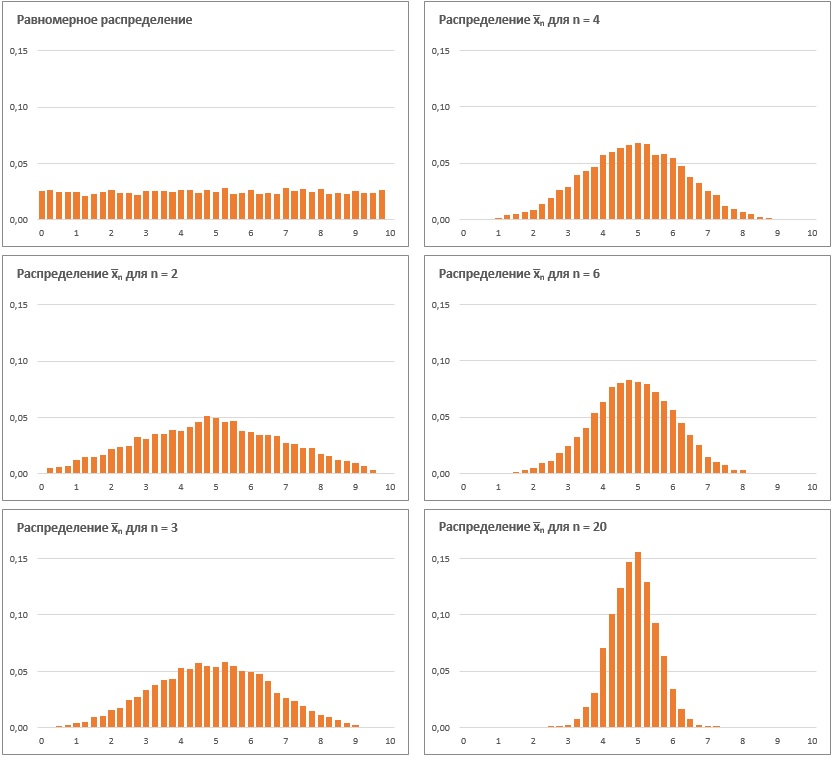
Рис. 1. Равномерное распределение случайной величины и распределение средних значений выборок разного размера
