Алексей Васильев. Числовые расчеты в Excel

Книга посвящена методам решения вычислительных задач с помощью Excel: алгебраические уравнения и системы, интерполирование и аппроксимация функциональных зависимостей, дифференцирование и интегрирование, решение дифференциальных и интегральных уравнений. В книге также описываются основные приемы работы с Excel, обсуждаются способы организации документов, анализируются методы ввода и редактирования данных, изучаются возможности применения форматов и стилей, иллюстрируются принципы использования встроенных вычислительных утилит, а также даются основы программирования на VBA. Ранее по теме я опубликовал Вильям Дж. Орвис. Excel для ученых, инженеров и студентов.

Алексей Васильев. Числовые расчеты в Excel. — СПб.: Издательство «Лань», 2022. — 600 с.

Скачать краткое содержание в формате Word или pdf (конспект составляет около 3% от объема книги), примеры в архиве (внутри файл Excel с поддержкой макросов)

Купить книгу в Ozon или Лабиринте

Главная идея книги — это адаптация стандартных (или «классических») алгоритмов решения задач вычислительной математики для реализации в приложении, имеющем «ячеечную» структуру, т.е. структуру электронной таблицы. Автор использует среду Excel 2013, самой свежей версии на момент выпуска книги. Я же использую Excel 365.

Глава 5. Методы вычислений и обработка данных

Числовые формулы и циклические ссылки

Эффектный механизм вычислений основан на использовании циклических ссылок. Циклическая ссылка – это ссылка в формуле на ячейку, которая содержит формулу (т.е. ссылка в ячейке на эту же ячейку). По умолчанию такая ситуация считается ошибочной, поскольку означает, что для вычисления значения ячейки по формуле с циклической ссылкой необходимо использовать значение этой ячейки. Круг замкнулся!

Для использования циклических ссылок пройдите Файл –> Параметры –> Формулы. Устанавливаем флажок Включить итеративные вычисления.

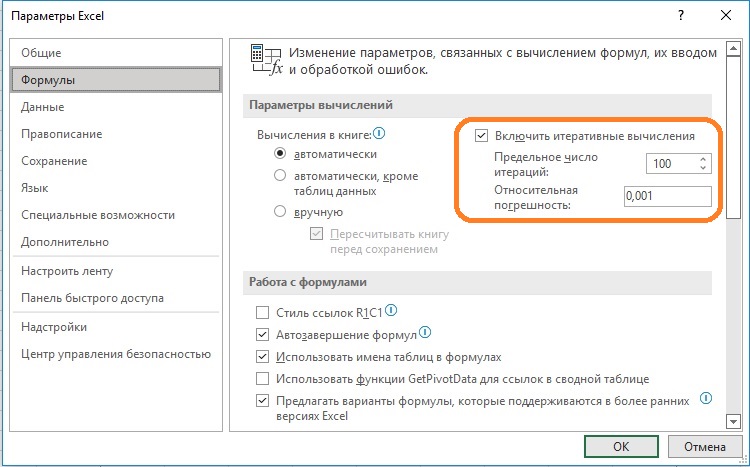
Рис. 1. Переход в режим использования циклических ссылок (итеративных вычислений)

В итерационном процессе начальное значение ячейки всегда равно нулю. Это нулевое значение используется в циклической ссылке для вычисления значения ячейки для первой итерации. Значение ячейки для первой итерации используется для вычисления значения ячейки для второй итерации и т.д. Предельное количество итераций определяется значением поля Предельное число итераций. Вычисления также заканчиваются, если относительная погрешность вычислений становится меньше того значения, что указано в поле Относительная погрешность.

Метод последовательных итераций может применяться для решения алгебраических уравнений вида х = f(x). Например, найдем корни уравнения х² — 6х + 5 = 0. У него два корня х = 1 и х = 5.

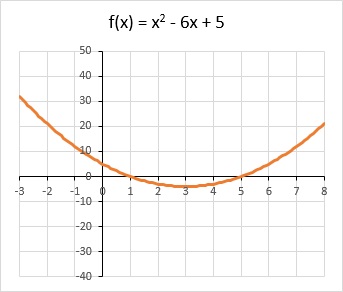
Рис. 2. График функции у = х² — 6х + 5

Представим уравнение в виде

В ячейку А1 введите формулу =(А1^2+5)/6

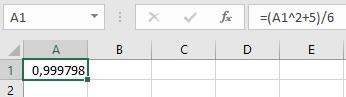
Рис. 3. Нахождение корня уравнения итерационным методом

Точность решения определяется настройками Параметров Excel (см. рис. 1). Если точности не хватило, нажмите <F9>. Итерационный процесс продолжится с текущего числового значения ячейки.

Одна из проблем итерационного процесса заключается в том, что он всегда стартует с нулевого значения в ячейке. Например, чтобы найти второй корень уравнения, его следует представим в виде…

Но… при х = 0 под корнем отрицательное значение. Поэтому если в ячейку А1 ввести формулу =КОРЕНЬ(6*А1-5), получим сообщение об ошибке:

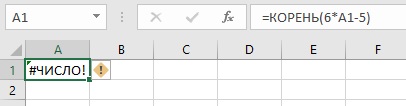
Рис. 4. Ошибка из-за того, что начальное выражение под корнем отрицательное

Изменим начальное значение. Идея состоит в том, чтобы ввести новую переменную z = х – а или х = z + а. И решить новое уравнение z = f(z + a) – a. Для переменной z начальное значение по-прежнему нулевое. В ячейку А2 введите начальное приближение для корня, а в ячейку А1 – формулу =КОРЕНЬ(6*(А1 +А2)-5)-А2.

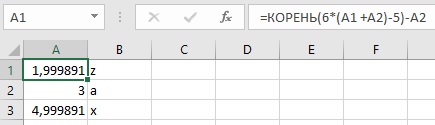
Рис. 5. Начальное значение для итерационных вычислений задается в явном виде

В результате решения уравнения z = f(z + а) — а находим корень для z. При этом х = z + а.

Чтобы метод итераций работал нужно, чтобы в области поиска корня функции f(x) ее производная по модулю была меньше единицы.

Как минимум, это условие должно выполняться в точке начального значения поиска корня.

Утилита подбора параметра

Большинство расчетных возможностей Excel реализуется через встроенные функции. Но иногда удобнее использовать специальные утилиты или надстройки. Так, например, назначение утилиты Подбора параметра состоит в том, чтобы подобрать значение в какой-то определенной ячейке такое, что значение в другой ячейке примет нужное значение.

Чтобы запустить утилиту пройдите Данные –> Прогноз –> Анализ «что если» –> Подбор параметра. Решим с помощью этой утилиты рассмотренное выше уравнение.

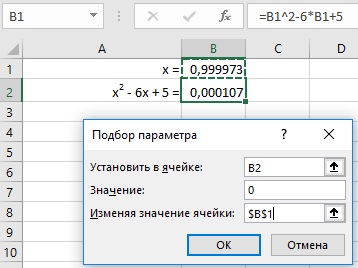
Рис. 6. Решение уравнение с помощью утилиты Подбор параметра

Найден один из двух корней уравнения. Второй корень х = 5 можно найти, если изменить начальное значение в ячейке ВЗ. Например, на 8. В реальной жизни угадать, как начальное приближение влияет на результат подбора параметра, бывает крайне сложно. Еще одна проблема заключается в том, что варьируется всего одна ячейка. В этом отношении более гибкой является надстройка Поиск решения, используемая в оптимизационных задачах.

Глава 7. Избранные вычислительные задачи

Решение дифференциального уравнения

Дифференциальным называется уравнение вида F(x, y, y’, y’’, … y⁽ⁿ⁾) = 0, связывающее аргумент х, неизвестную функцию у(х) и ее производные. Порядок дифференциального уравнения определяется порядком старшей производной. Задача – найти функцию.

Рассмотрим уравнение первого порядка у'(х) = f(x, у(х)). Чтобы найти решение уравнения в числовом виде, необходимо указать начальное условие – значение функции у(х) в точке х₀, т. е. указать числовое значение у₀ такое, что y(x₀) = y₀. Дифференциальное уравнение и начальные условия – это задача Коши. Для решения дифференциального уравнения используем не самый точный, но весьма простой метод Эйлера. Чтобы найти значение функции у(х) интервал значений аргумента от х₀ до х разбивается на N одинаковых частей так, что x_k = х₀ + kΔx, где Δx = (х – х₀)/N. k = 0, 1, …, N.

Для вычисления значения y(x_N) последовательно вычисляем значения y(x_k) в узловых точках x_k. При этом используем рекуррентное соотношение y_k+1 = y_k + Δx*f(x_k,y_k) с начальным приближением у₀ = у(х₀). Эту итерационную процедуру реализуем в Excel для уравнения у'(х) = у(х)*sinx с начальным условием у(π/2) = 10. Эта задача имеет «точное» аналитическое решение

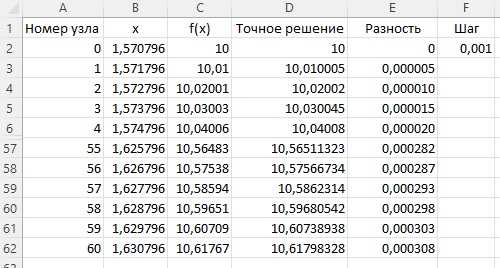
Рис. 7. Результат решения дифференциального уравнения в числовом виде

Здесь в столбце А — номер узла; В — значение аргумента в узле; С — значение искомой функции; D — точное решение уравнения; Е — разность точного и приближенного решений. В ячейке F2 указано значение для шага приращения по аргументу. Формулы см. в приложенном Excel-файле. Часть строк на рис. 7 скрыта.

Вычисление интегралов

Рассмотрим задачу о вычислении интеграла вида

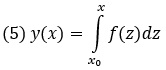
Для интегрирования используем метод трапеций. Интервал интегрирования разбиваем на N частей и выбираем узловые точки x_k = х₀ + kΔx, где Δх = (х — x₀)/N, а индекс k = 0, 1, …, N. Воспользуемся тем обстоятельством, что числовое значение интеграла равно площади под графиком функции на интервале интегрирования. Разобьем область под кривой на трапеции, с основаниями в узловых точках. Ребро трапеции в точке х_k равняется f(x_k). Тогда площадь области под кривой равняется (примерно) сумме площадей таких трапеции. А площадь одной трапеции равна

Таким образом, в качестве оценки для значения интеграла получаем выражение

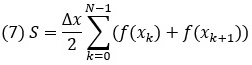
Воспользуемся этой формулой для вычислений в Excel интеграла

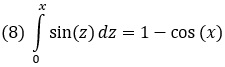
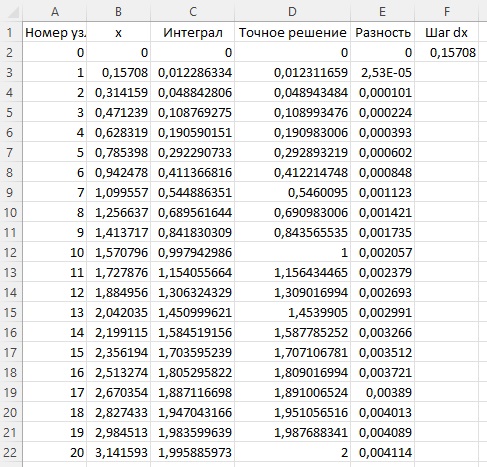
Рис. 8. Результат вычисления интеграла (формулы см. в приложенном Excel-файле)

Глава 8. Диаграммы

Параметрическая кривая

Под параметрической подразумевается кривая, уравнение которой задано в параметрическом виде. Идея определения в параметрическом виде зависимости у от х состоит в том, что задается зависимость каждой из этих переменных от параметра t. А если заданы зависимости х = f₁(t) и у = f₂(t), то система из этих двух уравнений определяет (неявно) зависимость у(х). Такая зависимость называется параметрической. Если в системе уравнений х = f₁(t) и у = f₂(t) путем алгебраических преобразований удается исключить параметр t, получают явное соотношение между переменными х и у. Для построения графика для зависимости у(х) нужно предварительно вычислить координаты точек (x_k, y_k) (k = 0, 1, 2, …, n). Это делают, используя соотношения: x_k = x(t_k) = f₁(t_k) и y_k = y(t_k) = f₂(t_k).

Мы построим график функции, которая в полярных координатах задана соотношением r = sin(5φ). Здесь r и φ – полярные координаты – радиус и полярный угол. Полярный угол φ может принимать значения от 0 до 2π, а радиус должен быть неотрицательным. Полярные координаты связаны с декартовыми х и у соотношениями х = rсоs(φ) и у = rsin(φ). В роли параметра выступает φ. Действительно, декартовы координаты точек на кривой определяются соотношениями x(φ) = r(φ)cos(φ) и y(φ) = r(φ)sin(φ ф), где r(φ) = sin(5 φ). Если результат, возвращаемый формулой r(φ) = sin(5 φ), меньше нуля, то присваиваем r значение 0 (r по определению неотрицательна).

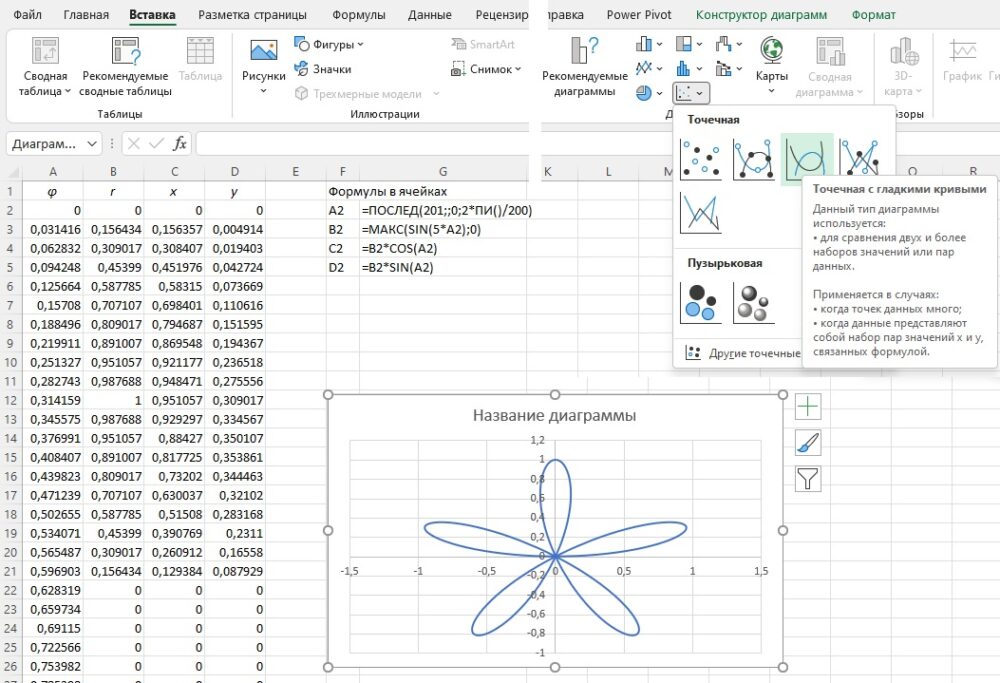
Рис. 9. Параметрическая кривая; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

Выделите диапазон C2:D202, пройдите Вставить –> Диаграммы –> Точечная и выберите тип Точечная с гладкими кривыми.

Глава 10. Основы программирования в VBA

Код процедуры, демонстрирующий использование конструкции With … End With

Пример использования конструкции If … Then … Else

Пример использования оператора выбора Case и цикла For Each … Next

Глава 11. Создание форм и обработка событий

Чтобы создать форму в VBE пройдите Insert –> UserForm. Добавьте в форму два текстовых окна и одну кнопку.

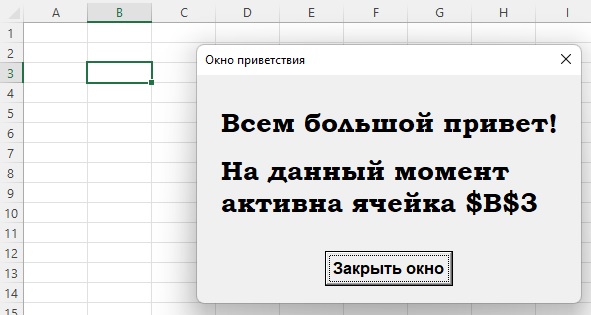
Рис. 10. Пользовательская форма

С формой связан код в отдельном Module2:

Свой код связан с кнопкой «Закрыть окно». Чтобы увидеть его дважды щелкните на кнопке:

Ключевое слово Private означает, что процедура доступна только для внутреннего вызова – вызвать эту процедуру как макрос из Excel не получится.

Обработка событий

Рассмотрим на примере формы для заполнения ячеек числами Фибоначчи. Первые два числа равны единице, а каждое следующее равно сумме двух предыдущих: 1, 1, 2, 3, 5, 8, 13, 21, …

Код макроса для заполнения ячеек числами Фибоначчи разместим в Module3

В макросе всего одна команда, которая отображает окно формы. Основной код связан с элементами формы.

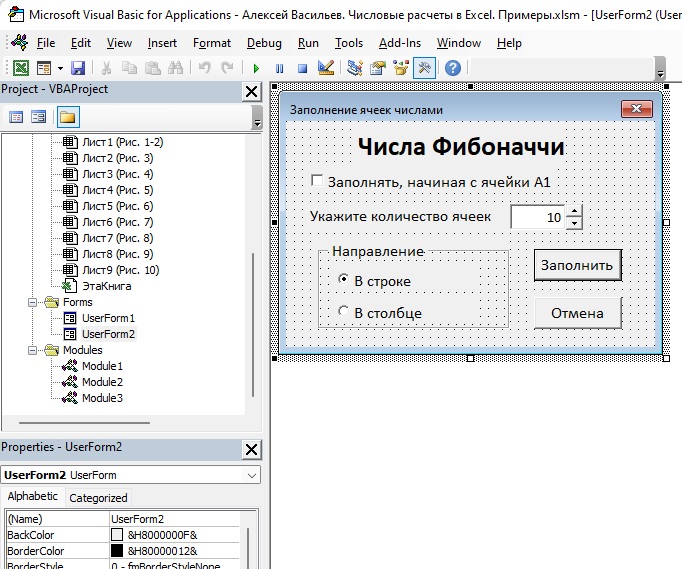
Рис. 11. UserForm2

Рассмотрим элементы формы. Свойство Caption UserForm2 = Заполнение ячеек числами. Текстовая метка Label1: Caption = Числа Фибоначчи. Далее следует элемент CheckBox1. Свойство Caption = Заполнять, начиная с ячейки А1. Свойство Value оставляем False (оно такое по умолчанию). Свойство Caption текстовой метки Label2 = Укажите количество ячеек. Справа от нее расположены элементы TextBox1 (Value = 10, Text Align = З-fmTextAlignRight) и SpinButton1 (Value = 10, Min = 3, Max = 20). Далее Frame1. Свойство Caption = Направление. Внутри два переключателя: OptionButton1 (Caption = В строке, Value = True) и OptionButton2 (Caption = В столбце, Value = False). Справа две кнопки: CommandButton1 (Caption = Заполнить, Default = True) и CommandButton2 (Caption = Отмена, Default = False).

Теперь перейдем к программированию кнопок. Начнем с самого простого кода для кнопки закрытия окна формы. Для этого дважды кликните на ней. И введите код:

Далее щелкните на числовом переключателе – SpinButton1:

При щелчке на пиктограмме числового счетчика, в зависимости от того, какая из двух стрелок «щелкнута», значение переключателя (значение свойства Value) увеличивается/уменьшается на величину, определяемую свойством SmallChange (в нашем случае это единица) — если новое значение не выходит за допустимые пределы (задаются свойствами Мах и Min). Процедура-обработчик запускается каждый раз при щелчке на счетчике. Поэтому, если мы изменяем состояние счетчика, это автоматически скажется на состоянии текстового поля.

Обработчик для текстового поля по умолчанию реагирует на событие/процедуру TextBoxI_Change. Нам это не подходит. Мы не хотим считать событием любое изменение содержимого поля (в процессе редактирования содержимого). Нас интересует ситуация, когда пользователь закончил редактировать поле. На этот случай предусмотрена процедура с ключевым словом AfterUpdate:

На момент начала редактирования текстового поля свойство Text текстового поля TextBox1 и свойство Value числового счетчика SpinButton1 одинаковы. Следующий шаг— пользователь ввел в текстовое поле новое значение – теперь это значение свойства Text объекта TextBox1. Мы его проверяем, и, если оно попадает в допустимый интервал значений, присваиваем соответствующее значение свойству Value числового счетчика SpinButton1. Если же новое значение в текстовом поле не попадает в допустимый интервал значений, в текстовое поле необходимо вернуть старое значение. Про это значение «помнит» свойство Value числового счетчика SpinButton1. Здесь действие обратное – свойству Text текстового поля TextBox1 присваивается значение свойства Value числового счетчика SpinButton1.

В теле процедуры TextBoxI_Afterllpdate() объявляется целочисленная переменная num, которой затем командой num = Val(TextBox1.Text) присваивается значение. Мы использовали функцию Val(), которой в качестве аргумента передается текстовое представление числа, а функция в качестве результата возвращает реальное число. Текстовое представление числа считывается инструкцией TextBox1.Text из текстового поля. Таким образом, в переменную num записано новое значение в текстовом поле. Затем на сцену выходит условный оператор, в котором проверяется условие принадлежности значения переменной num интервалу от SpinButton1.Min до SpinButton1.Мах. При этом мы использовали логический оператор And. Если условие выполнено, свойству SpinButton1.Value присваивается значение num. В противном случае свойству TextBox1.Text присваивается значение SpinButton1.Value.

Код кнопки CommandButton1:

В коде важный идеологический момент связан с тем, что мы сначала создаем массив из чисел Фибоначчи, а затем копируем числа из массива в ячейки рабочего листа. Поэтому предварительно определяются размеры массива (количество заполняемых ячеек), и этот массив заполняется числами. Затем мы определяем начальную ячейку заполнения и «направление» заполнения — в строке или в столбце.

Целочисленная переменная N объявляется для записи в нее размера массива. Целочисленная переменная I объявляется для использования в качестве счетчика цикла. Командой Dim F() As Integer объявляется динамический массив F() целых чисел. Затем из текстового поля инструкцией N = Val(TextBox1.Text) считывается количество заполняемых ячеек (размер массива). Чтобы выделить место под массив соответствующего размера, выполняем инструкцию ReDim F(1 То N).

Существует два типа массивов – статические и динамические. Размер статического массива должен быть известен на момент компиляции кода. Размер динамического массива определяется в процессе выполнения программы. Мы имеем дело со вторым случаем. С практической точки зрения разница между статическим и динамическим массивами в том, что размеры статического массива – константы. Например, командой Dim MyArray(1 То 100) As Integer объявляется целочисленный массив МуАггау из 100 элементов (индексы элементов массива изменяются от 1 до 100). Мы же сначала инструкцией Dim F() As Integer декларируем, что F – это массив из целых чисел, неизвестно пока какого размера. А командой ReDim F(1 То N) подтверждаем, что массив из N элементов. Предварительно, разумеется, мы присваиваем значение переменной N.

Командами F(1) = 1 и F(2) = 1 заполняются первые два элемента массива. Для заполнения прочих элементов массива используем оператор цикла с командой F(i) = F(i-1)+F(i-2) (i – индексная переменная) в теле оператора цикла (каждый следующий элемент равен сумме двух предыдущих).

Следующий этап связан с определением начальной ячейки. Для этого командой Dim StartCell As Range мы объявляем переменную StartCell типа Range. Это будет ссылка на начальную ячейку. В условном операторе проверяем, установлен ли флажок опции CheckBox1 (значение свойства Value равно True или False). В зависимости от результата проверки выполняется команда Set StartCell = Range(«A1») (начальная ячейка А1) или Set StartCell = ActiveCell (начальная ячейка – активная на момент запуска макроса). При присваивании значений объектным ссылкам используется ключевое слово Set.

Направление заполнения определяем путем проверки значения свойства OptionButtonl1.Value (выясняем, установлен переключатель OptionButton1 или нет). Если переключатель установлен, то запускается оператор цикла с командой StartCell.Offset(0,i-1).Value = F(i) в теле цикла. В противном случае запускается другой оператор цикла, в котором выполняется команда StartCell.Offset(i-1,0).Value = F(i). Этими командами ячейки рабочего листа заполняются значениями из массива F.

Метод Offset() вызывается из объекта ячейки и имеет два аргумента: смещение вдоль столбца и вдоль строки. В качестве результата возвращается ссылка на соответствующую ячейку. Так, например, инструкция StartCell.Offset(2,5).Value ссылается на ячейку, которая находится на 2 строки вниз и 5 столбцов вправо по отношению к ячейке StartCell. Функция Offset() в VBA подобна функции СМЕЩ в Excel.

Выгрузка формы из памяти осуществляется командой Unload UserForm2. Проверяем, как работает форма.

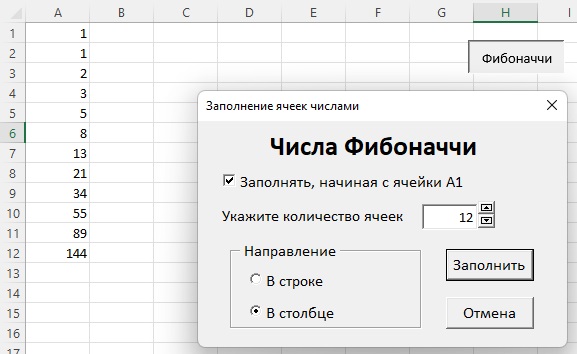
Рис. 12. Числа Фибоначчи

Глава 12. Решение алгебраических уравнений и систем

Показано, как использовать методы половинного деления (этот метод я изложил подробнее в отдельной заметке), хорд, касательных, последовательных приближений, Ньютона, градиентного спуска, а также методы линейной алгебры.

Глава 13. Интерполирование и аппроксимация

Представлены интерполяционный полином Лагранжа (см. подробнее), интерполяционный полином Ньютона, полиномиальная интерполяция, интерполяция набором функций, интерполяция сплайнами, а также методы аппроксимации.

Методы аппроксимации. Теория

Задача аппроксимирования близка по постановке к задаче интерполирования. В обоих случаях по набору «экспериментальных» данных необходимо восстановить «наилучшее» функциональное выражение между зависимой и независимой переменными. Отличие между этими задачами состоит в том, что в задаче интерполирования накладывается условие совпадения в узловых точках табличных значений и значений интерполяционной функции. При аппроксимировании параметров для варьирования недостаточно для того, чтобы аппроксимирующая функциональная кривая в каждой узловой точке принимала предопределенное значение. Ищется функция, которая будет иметь «наименьшее отклонение» от значений в узловых точках. При этом необходимо задать «метрику», через которую определяется «цена» отклонения от значения в узловой точке. В качестве метода оптимизации часто используют метод наименьших квадратов.

Предположим, имеется выражение F(x, а₁, а₂, …, а_m), на основе которого мы хотим аппроксимировать зависимость, заданную значениями у₁, у₂, …, у_m в узловых точках х₁, х₂, …, х_m. Задача состоит в том, чтобы на основе критерия вычислить параметры оптимизации а₁, а₂, …, а_m, которые входят в выражение для функции F(x, а₁, а₂, …, а_m).

В данном случае важно то, что количество m варьируемых параметров в аппроксимирующей функции не превышает количество n узловых точек, т.е. m ≤ n. Причем, если имеет место равенство m = n, то речь идет о задаче интерполирования.

В качестве критерия мы будем использовать метод наименьших квадратов. Для этого построим функцию, определяемую как сумма квадратов разности «экспериментальных» и «теоретических» значений в узловых точках:

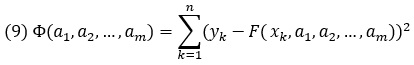
Суть метода состоит в том, чтобы подобрать такие параметры а₁, а₂, …, а_m, при которых значение выражения Φ(а₁, а₂, …, а_m) будет минимальным. В результате получаем систему из m алгебраических трансцендентных уравнений, решая которую, находим параметры а₁, а₂, …, а_m.

Если учесть явное выражение для функции Φ(а₁, а₂, …, а_m), уравнения системы для определения оптимизационных параметров могут быть записаны как

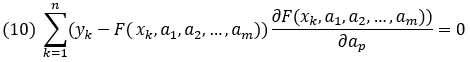
Индекс p = 1, 2, …, m.

Часто аппроксимирующая функция представима в виде линейной комбинации базисных функций, и оптимизация выполняется по коэффициентам этой линейной комбинации — имеется в виду, что функция F(x, а₁, а₂, …, а_m) = a₁f₁(x) + a₂f₂(x) + … + a_mf_m(x), где базисные функции f₁(x), f₂(x), … f_m(x) известны и определены однозначно.

Нередко задачу с нелинейной по параметрам оптимизации аппроксимирующей функцией удается свести к линейному случаю. Например, если по точкам (x_k, y_k) (k = 1, 2, …, n) мы пытаемся вычислить оптимальные параметры для функции F(x, A, b) = Аехp(bx), то можем рассмотреть набор точек (x_k, In(y_k)) и аппроксимировать эту зависимость линейной функцией ln(F(x, А, b)) = lnA + bx.

В этом случае мы можем значительно продвинуться в вопросе выбора оптимальных параметров а₁, а₂, …, а_m. В частности, несложно понять, что

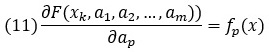
Тогда система для определения оптимизационных параметров записывается как

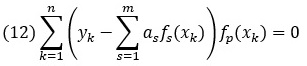
для индексов р = 1, 2, …, m. После преобразований эти уравнения можем записать в виде

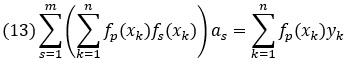
Относительно параметров a_s (индекс s = 1, 2, …, m) — это линейная неоднородная система алгебраических уравнений, которая достаточно легко решается, в том числе и в Excel. Ее удобно записать в матричном виде. Для этого введем ряд обозначений: вектор значений табулированной функции в узловых точках

… матрица F̂ размерами mхn (m строк и n столбцов) значений базисных функций в узловых точках с элементами F_ij = f_i(x_j) (индексы i = 1,2, …, m и j = 1, 2, …, n). Тогда систему уравнений для определения оптимизационных параметров можно в матричном виде записать как

где через

обозначен вектор, составленный из параметров оптимизации. Решение этой системы можем записать в виде

где индекс -1 обозначает обратную матрицу.

Аппроксимация в Excel

Реализуем описанную выше схему на листе Excel. Оттолкнемся от исходных данных (область В2:К3) и построим аппроксимирующую зависимость на основе полиномиального выражения второй степени. Аппроксимирующая функция имеет вид F(x) = а₁ + а₂х + а₃х², и задача состоит в определении по исходным данным параметров а₁, а₂ и а₃).

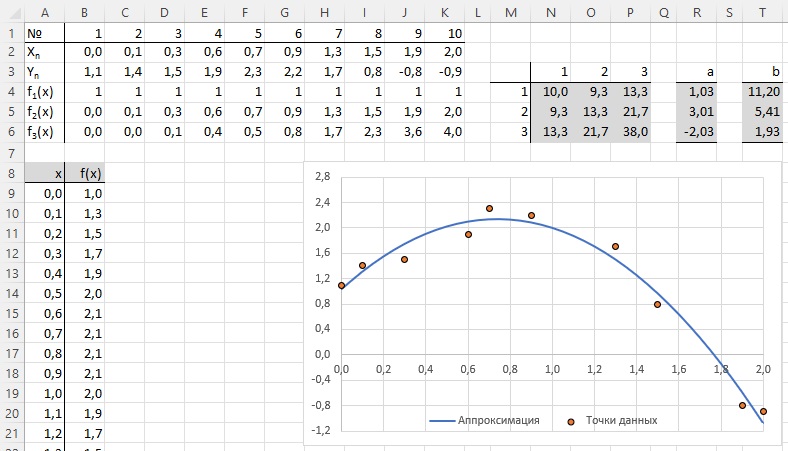
Рис. 13. Построение аппроксимирующей зависимости

Построим матрицу, составленную из значений базисных функций в узловых точках. Учитывая вид аппроксимирующей функции F(x) = а₁ + а₂х + а₃х², понятно, что базисными функциями являются f₁(x) = 1, f₂(x) = х и f₃(x) = х². Значения этих функций в узловых точках вычислено в ячейках В4:К6. Это и есть та матрица, на основе которой вычисляются параметры аппроксимирующей функции. Выполним промежуточные расчеты:

• в ячейках N4:P6 введем формулу массива =МУМНОЖ(В4:К6;ТРАНСП(В4:К6)). Результатом вычислений является матрица 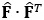коэффициентов линейной системы уравнений;
• в ячейках Т4:Т6 введём формулу массива =МУМНОЖ(В4:К6;ТРАНСП(ВЗ:КЗ)). Результатом является произведение 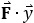, представляющее собой вектор правой части линейной системы уравнений.

Для вычисления параметров аппроксимирующей функции в ячейки R4:R6 вводим формулу массива =МУМНОЖ(МОБР(N4:P6);T4:T6). Этой формулой реализуется выражение (17). Получаем вектор-столбик с коэффициентами а. Теперь значение аппроксимирующей функции в любой точке х можно вычислить по формуле F(x) = 1,03 + 3,01х – 2,03х² (диапазон А8:В29).

Глава 14. Дифференцирование и интегрирование

Рассмотрено: вычисление производной в узловых точках. Общие подходы к числовому интегрированию. Метод Чебышева. Метод Гаусса. Вычисление несобственных интегралов. Вычисление повторных интегралов.

Глава 15. Решение дифференциальных и интегральных уравнений

Метод последовательных приближений. Метод степенных рядов. Метод Рунге–Кутты. Метод Адамса. Метод Милна. Системы дифференциальных уравнений. Интегральные уравнения.

Глава 16. Вместо заключения

Рассмотрен бесплатный аналог Excel – приложением Open Office Calc.