Чуть более года назад я впервые прочитал книгу Млодинова (Не)совершенная случайность. Как случай управляет нашей жизнью. Книга мне очень понравилась, так что по ее следам я написал одну заметку Закон Бенфорда или закон первой цифры, и запланировал еще несколько. Поэтому, когда я увидел, что в издательстве Livebook вышло еще две книги Млодинова, я не задумываясь их приобрел.
Млодинов знакомит читателей с непростыми научными понятиями через истории людей – великих математиков, философов, физиков с Древней Греции и до наших времен. Эти истории настолько захватывают, что вызывают желание узнать об отдельных персонажах подробнее.
«Евклидово окно» посвящено развитию наших представлений о пространстве. Автор начинает изложение с доевклидовых воззрений на геометрию, подробно останавливается на «Началах» Евклида, далее знакомит с геометрией Римана и Гаусса (последняя у российских читателей больше ассоциируется с именем Лобачевского), открытиях Эйнштейна и заканчивает современной теорией струн.
Леонард Млодинов. Евклидово окно – М.: Livebook, 2013. – 384 с.
Скачать краткий конспект в формате Word или pdf
Часть 1. История Евклида
Греки первыми осознали, что природу можно постичь, применив математику, а геометрия может не только описывать, но и объяснять. Развивая геометрию от простых описаний камня и песка, греки извлекли понятия точки, линии и плоскости. Мысль об осуществлении операций с числами доходила гораздо медленнее, поскольку занятия арифметикой подразумевают некоторую степень абстракции. Антропологи сообщают: если два охотника выпустили две стрелы, завалили двух газелей и заработали две грыжи, волоча добычу к стоянке, во многих племенах все эти «два» и «две» могли быть разными понятиями в каждом случае. В таких цивилизациях нельзя было складывать яблоки с апельсинами. На понимание того, что все это частные случаи одного и того же понятия — абстрактного числа 2, — потребовались тысячи лет.
Налоги первыми потребовали развития геометрии, чтобы «справедливо» взымать налоги с земли.
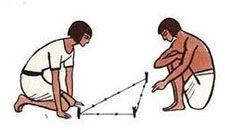
Чтобы строительство пирамид шло по плану, египтяне подключали специалиста, называвшегося гарпедонаптом, буквально — «натягивателем веревок» (рис. 1). Например, если натянуть веревку с узлами на 30-м, 40-м и 50-м ярдах, между сторонами в 30 и 40 ярдов получится прямой угол. (Слово «гипотенуза» по-гречески исходно означала «растянутая напротив».)
Рис. 1. Гарпедонапты с помощью веревки с узлами доказывают теорему Пифагора
О египетской математике мы знаем в основном из двух источников — из Папируса Ринда, названного в честь Александра Г. Ринда, передавшего этот документ в Британский музей, и из Московского папируса, находящегося в Музее изобразительных искусств в Москве.
Вавилоняне уравнений писать не умели. Все их расчеты выражались словесными задачами. Старейшее известное использование символа «плюс» появляется в одном немецком манускрипте 1481 года. Несмотря на достижения египтян и сообразительность вавилонян, их вклад в математику свелся к обеспечению греков собранием проверенных математических фактов и общих правил. Хоть обе цивилизации и знали теорему Пифагора, ни та, ни другая не вдумалась в общую закономерность, которую мы сегодня записываем как а2 + b2 = с2. Они, похоже, никогда не задавались вопросом, почему такое соотношение вообще существует или как его применить, чтобы получить большее знание.
Открытие того, что математика — нечто большее, нежели алгоритмы расчетов объемов грунта или размеров налогов, принадлежит одинокому греческому купцу, ставшему философом; его звали Фалес, и свершилось это открытие 2500 лет назад. Фалес сохранил для своей математики египетское название — «измерение земли», — однако перевел его на родной язык, и получилась «геометрия». Когда Фалес превратился в немощного старца он встретил самого важного предтечу Евклида — Пифагора Самосского.
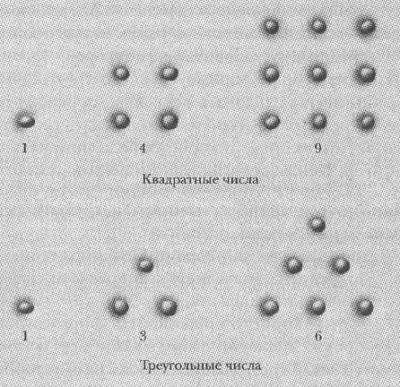
Для Пифагора и его последователей главной интригой математики виделись разнообразные численные закономерности. Пифагорейцы представляли себе числа как камешки или точки, выложенные в определенный геометрический узор. Они обнаружили, что некоторые числа можно сложить, разместив камешки на равном расстоянии в два столбика по два, в три по три и т.д. — так, чтобы получался квадрат (рис. 2). Пифагорейцы называли любое количество камешков, которые можно выложить таким способом, «квадратным числом», поэтому и мы зовем их до сих пор квадратами: 4, 9, 16 и т.д. Другие числа, как выяснили пифагорейцы, можно выложить так, чтобы получались треугольники: 3, 6, 10 и т.д.
Рис. 2. Пифагоровы фигуры из камешков
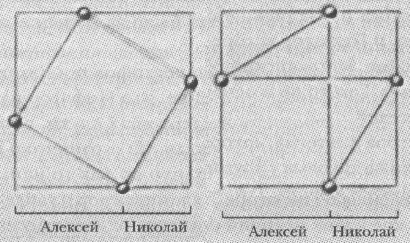
Теорему Пифагора можно доказать геометрически. Для доказательства потребуется знать всего один расчетный факт: площадь квадрата равна квадрату длины его стороны. Чтобы все упростить, дадим сторонам треугольника имена (рис. 3) [1]. В одном случае выйдет квадрат, чьи стороны равны гипотенузе, и еще четыре треугольника-«обрезка». В другом получится два квадрата, чьи стороны равны Алексею и Николаю, а сверх того – два прямоугольника – обрезка, которые можно рассечь по диагонали и получить четыре треугольника, в точности равных тем, что у нас получились в обрезках в первом случае. Остальное – дело счета. У двух построенных квадратов площади одинаковые, поэтому если выкинуть площади четырех треугольников-обрезков из обоих построений, оставшиеся площади недвижимости равны между собой.
Рис. 3. Геометрическое доказательство теоремы Пифагора
Один из учеников Пифагора написал, что «не будь чисел и их природы, ничто существующее никому не было бы ясно». Пифагорейцы отразили основы своей философии в термине «математика» — от греческого «матема», т.е. «наука», «знание».
Пифагорейцы доказали, что диагональ квадрата со стороной 1 не может быть простой дробью. Обозначим длину диагонали как с и начнем с допущения, что с можно выразить в виде дроби — скажем, m/n, в которой у m и n нет общих делителей, и они ни в коем случае не четные одновременно. Доказательство производится в три этапа. Первый: заметим, если с2 = 2, значит, m2 = 2n2. Словами: m2 — четное число. Поскольку квадраты нечетных чисел — нечетные, значит, и m само по себе должно быть четным. Второй: поскольку m и n не могут быть оба четными, значит, n должно быть нечетным. Третий: взглянем на уравнение m2 = 2n2 с другой стороны. Поскольку m — четное, его можно записать как 2q, при любом q. Если заменить m в m2 = 2n2 на 2q, получим 4q2 = 2n2, что то же самое, что 2q2 = n2. Это означает, что n2, а, следовательно, и n – четное.
Мы только что доказали, что если с можно записать как с = m/n, то m есть нечетное, а n— четное. Получается противоречие, а значит, исходное допущение, что с можно записать как с = m/n, — ложное. Такого рода доказательства, когда мы допускаем отрицание того, что стремимся доказать, а потом показываем, что отрицание ведет к противоречию, называется reductio ad absurdum. Это одно из изобретений пифагорейцев, и поныне полезное для математики.
Пифагор отошел от своей весьма перспективной практики ассоциировать геометрические фигуры с числами и заявил, что некоторые длины не могут быть выражены через числа. Пифагорейцы назвали такие длины алогонами, «неразумными», ныне мы называем их иррациональными. Сопротивление иррациональному продолжалось еще тысячи лет. В конце XIX века, когда одаренный немецкий математик Георг Кантор создал революционный труд, в котором попытался как-то укоренить эти числа.
Приблизительно в 300-е годы до н.э. на южном побережье Средиземного моря, чуть левее Нила, жил в Александрии человек, чья работа может потягаться по влиятельности с Библией. Имя этого человека — Евклид. О его жизни нам неизвестно почти ничего. Его знаменитая работа, «Начала», — одна из самых читаемых «книг» всех времен. История «Начал» заслуживает детективного романа не хуже «Мальтийского сокола». Во-первых, это не книга в буквальном смысле, но собрание из тринадцати свитков папируса. Первые четыре свитка написал Гиппократ (не врач) в 400-х годах до н.э. Евклид никак не претендовал на авторство этих теорем. Свою задачу он видел в систематизации греческого понимания геометрии. Он стал архитектором первого осмысленного отчета о природе двухмерного пространства, созданного одной лишь силой мысли, без всяких отсылок к физическому миру.
Во-первых, Евклид объяснил все термины введением точных определений, гарантирующих понимание всех слов и символов. Во-вторых, он прояснил все понятия, предложив для этого прозрачные аксиомы или постулаты (эти два термина взаимозаменяемы), и отказался от применения неустановленных выводов или допущений. И наконец, он выводил логические следствия всей системы лишь с использованием правил логики, примененной к аксиомам и ранее доказанным теоремам.
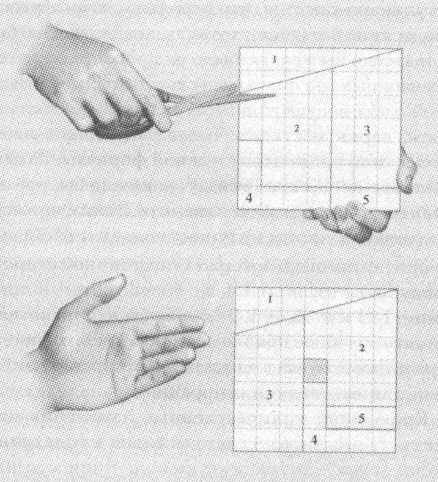
Некоторые могут возразить, зачем такое занудство? Точность очень часто играет решающую роль. Трюк, изобретенный фокусником-любителем Полом Карри (рис. 4), жившим в Нью-Йорке, — отличный геометрический пример. Возьмем квадратный лист бумаги и нарисуем на нем сетку из меньших квадратов семь на семь. Разрежем лист на пять частей и переложим их так, как показано на рисунке. В результате получим «квадратный пончик» — квадрат того же размера, что и исходный, однако по центру не будет хватать одного квадратика. Куда подевался этот квадратик? Мы что же, доказали теорему о том, что цельный квадрат равен по площади пончику?
Фокус состоит в том, что при пересборке квадрата фрагменты ложатся чуточку внахлест, и фигура в результате получается слегка жульнической — или, скажем так, приблизительной. Второй сверху ряд клеток получается чуть-чуть выше, а весь квадрат — на 1/49 длиннее по вертикали, чем должен быть, и этого как раз достаточно, чтобы набралась площадь недостающего квадратика. Но если бы нам доступно было измерение длин с точностью лишь до 2%, мы бы не уловили разницу между этими двумя фигурами и впали бы в искушение сделать мистический вывод, что площади квадрата и «квадратного пончика» равны друг другу.
Рис. 4. Фокус Пола Карри
Целью Евклида было построить систему так, чтобы в ней не оставалось места для нечаянных допущений, основанных на интуиции, угадывании или приблизительности. Он ввел двадцать три определения, пять геометрических постулатов и пять дополнительных постулатов, которые он назвал «Общими утверждениями». На этом фундаменте он доказал 465 теорем — практически все геометрическое знание его времени. Евклид дал определения точке, линии (которая, согласно определению, может быть искривленной), прямой линии, окружности, прямому углу, поверхности и плоскости.
Геометрическая суть евклидовой геометрии покоится на пяти постулатах. Первые четыре просты и могут быть сформулированы не без изящества. В современных терминах они звучат так:
- От всякой точки до всякой точки можно провести прямую.
- Ограниченную прямую можно непрерывно продолжать по прямой.
- Из всякого центра всяким раствором может быть описан круг.
- Все прямые углы равны между собой.
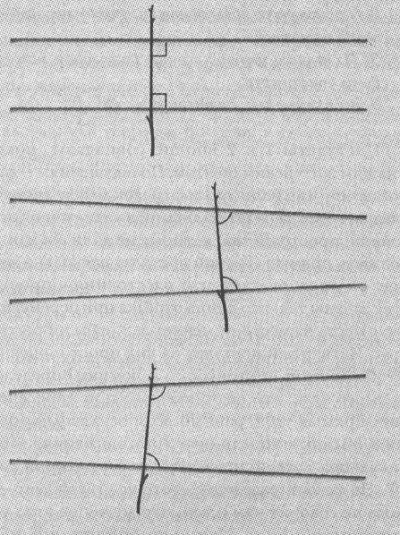
Пятый же постулат Евклида, называемый постулатом параллельности, не настолько очевиден. Евклиду формулировка постулата не нравилась:
5. Если прямая, пересекающая две прямые, образует внутренние односторонние углы, меньшие двух прямых, то, продолженные неограниченно, эти две прямые встретятся с той стороны, где углы меньше двух прямых (рис. 5).
Рис. 5. Евклидов постулат параллельности
Существует множество разных, но эквивалентных друг другу формулировок постулата параллельности. Например,
Если есть прямая и не лежащая на ней точка, то через эту точку можно провести одну и только одну прямую (в той же плоскости), параллельную данной.
Постулат параллельности может быть нарушен в двух случаях: несуществование параллельных прямых вообще или существование более чем одной линии, проведенной через данную точку параллельно данной прямой.
С падением Рима (около 476 года н.э.) Европе достались огромные каменные храмы, театры и особняки, современные городские удобства типа уличного освещения, проточной горячей воды и канализации, но очень мало чего из достижений ума. К 800 году сохранились лишь фрагменты перевода Евклидовых «Начал» на латынь. Греческая традиция абстрагирования и доказательства, казалось, утеряна навсегда. Блистательная исламская цивилизация процветала, а Европа скатывалась в глубокую интеллектуальную пропасть. Этот период европейской истории получил соответствующее название: Темные века. Но все же греческую мысль воскресили. В период позднего Средневековья группа философов создала пространство мысли, в которой процветали великие математики XVI века — Ферма, Лейбниц, Ньютон. Один из таких мыслителей оказался в центре следующей революции геометрии и нашего понимания пространства. Имя ему Рене Декарт.
Часть 2. История Декарта
Всю свою жизнь Декарт относился к работам греков весьма критически, однако геометрия раздражала его пуще прочего. Сравним для примера определение круга Евклидом (часть I «Начал») и Декартом — и убедимся в успехах последнего:
Евклид: Круг есть плоская фигура, содержащаяся внутри одной линии [которая называется окружностью], на которую все из одной точки внутри фигуры падающие [на окружность круга] прямые равны между собой.
Декарт: Круг есть все х и у, удовлетворяющие уравнению х2 + у2 = r2 для заданного значения r.
Декарт перевел язык пространства на язык чисел и, что еще важнее, применил этот перевод к перефразированию геометрии в алгебру. Декарт начал свой анализ с превращения плоскости в подобие графика, изобразив горизонтальную прямую и назвав ее осью х, а вертикальную — осью у. Любая точка на этой плоскости описывалась теперь двумя числами: вертикальным расстоянием до горизонтальной оси, обозначенным у, и горизонтальным расстоянием до вертикальной оси, обозначенным х. Точки на плоскости с тех пор записываются в виде упорядоченных пар (х; у). Эту систему обозначения принято называть декартовыми координатами. (На самом деле примерно тогда же аналогичное открытие сделал Пьер Ферма, однако если за Декартом водилась дурная привычка ни на кого не ссылаться в своих публикациях, Ферма имел худшую склонность — не публиковать свои работы вообще.)
Подлинное новаторство идей Декарта применительно к координатам состояло не в них самих, а в том, что Декарту удалось из них извлечь. Изучая классические греческие кривые, манеру определения которых Декарт столь глубоко презирал, он, тем не менее, обнаружил удивительные закономерности. Например, он изобразил несколько прямых и выяснил, что для любой прямой координаты х и у любой точки на ней всегда связаны простым отношением. Алгебраически эту связь можно выразить уравнением вида ах + by + с = 0, где а, b и с — постоянные, т.е. обычные числа вроде 3 или 4 1/2, и зависят они лишь от того, какую прямую в данный момент мы рассматриваем.
Декарт предложил современный вид записи с применением последних букв алфавита для обозначения неизвестных переменных и первых — для обозначения постоянных. До Декарта язык алгебры не блистал изяществом. К примеру, Декарт записал бы 2х2 + х3, а до него то же выражалось так: «2Q плюс С», где через Q обозначали квадрат (саrrе), а через С— куб. Он смог классифицировать алгебраические выражения согласно типу кривой, которую они представляли. Например, он опознал уравнения Зх + 6у – 4 = 0 и 4х + 7у + 1 = 0 как представляющие прямые, которые он изучил в общем случае ах+ bу + с = 0. Таким образом, он преобразовал алгебру из науки, изучающей мешанину отдельных уравнений, в дисциплину оформленных классов уравнений.
Часть 3. История Гаусса
Неизвестно, вскинул бы Евклид бровь-другую, узнай он, что его «Начала» еще 2000 лет останутся непреложны. Но за это у математиков развилась поголовная непереносимость к пятому постулату Евклида — о параллельности.
Подростка по имени Карл Фридрих Гаусс в 1792 году посетило озарение. С открытием искривленных пространств возник естественный вопрос: евклидово ли наше пространство — или, может, оно иное? Именно этот вопрос произвел переворот в физике. Но и математику он поверг в недоумение. Если евклидова структура не есть простая абстракция, описывающая истинное устройство пространства, то что же она такое? Если можно усомниться в постулате параллельности, как же тогда быть с остальными евклидовыми построениями? Вскоре после открытия искривленного пространства вся евклидова геометрия рухнула, а за нею и вся остальная математика. Когда же пыль осела, в новой эпохе очутились не только теория пространства, но и вся физика с математикой.
К концу XVIII века, если бы математики взглянули на свои открытия по-другому, они бы заключили, что неевклидовы пространства существовать могут, а если так, у них могут быть кое-какие странные свойства. Однако вместо этого математики продолжили огорчаться из-за невозможности доказать, что эти странные свойства приводят к противоречиям, а значит, пространство — все-таки евклидово.
В двенадцать лет Гаусс взялся критиковать евклидовы «Начала». Он сосредоточился, как и прочие до него, на постулате параллельности. Но критика Гаусса оказалась свежее и еретичнее. В отличие от своих предшественников, Гаусс не пытался ни нащупать более удобоваримую формулировку постулата, ни признать его необязательность путем доказательства через другие постулаты. Возможно ли, думал Гаусс, что пространство на самом деле искривлено?
К пятнадцати годам Гаусс стал первым математиком в истории, принявшим идею, что может существовать логически непротиворечивая геометрия, в которой постулат параллельности недействителен. Между 1813 и 1816 годами, уже преподавая математическую астрономию в Гёттингене, Гаусс наконец произвел решительный прорыв, которого ждали со времен Евклида: он составил уравнения, описывающие части треугольника в новом, неевклидовом, пространстве, чью структуру мы теперь называем гиперболической геометрией.
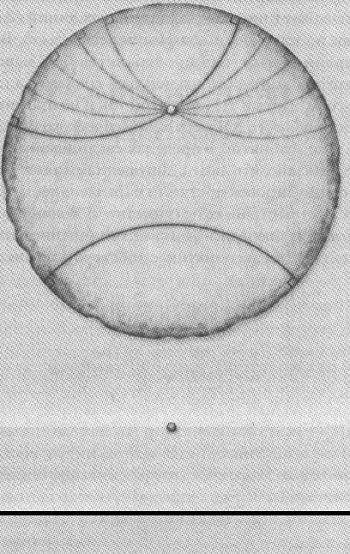
Гиперболическое пространство, открытое Гауссом, Бойяи и Лобачевским получается, если заменить постулат параллельности допущением, что для любой данной прямой есть не одна, а несколько параллельных прямых, проведенных через ту или иную точку, не лежащую на данной прямой. Одним из следствий этого является то, что сумма всех углов в треугольнике всегда меньше 180° на величину, которую Гаусс назвал угловым дефектом. Вроде бы малое изменение простой аксиомы — постулата параллельности, однако его хватило, чтобы породить волну, прокатившуюся по всему корпусу евклидовых теорем и поменявшую каждую, что описывала форму пространства. Словно Гаусс вынул стекло из евклидова окна и заменил его на искажающую линзу.
Ни Гауссу, ни Лобачевскому, ни Бойяи не удалось выработать простой способ наглядно иллюстрировать этот новый вид пространства. Это получилось у Эудженио Бельтрами и — попроще — у Анри Пуанкаре. Вот как устроена Вселенная Пуанкаре (рис. 6): вместо бесконечной плоскости — конечный диск, вроде блина, но бесконечно тонкий и с идеальной круговой кромкой. «Точки» — такие штуки, которые считались точками со времен Декарта. Линии Пуанкаре — «любые дуги окружностей, пересекающие границу диска под прямыми углами».
Модель Пуанкаре приводит к непротиворечивому определению фундаментального геометрического понятия, необходимого для определения гиперболического пространства. Постулат параллельности выглядит так:
В плоскости через точку, не лежащую на данной линии Пуанкаре, можно провести множество других линий Пуанкаре, не пересекающих данную.
Модель Пуанкаре — не просто модель гиперболического пространства. Это и есть гиперболическое пространство (в двух измерениях). На языке математики это означает, что ученые доказали: все мыслимые математические описания гиперболической плоскости — изоморфны, или, говоря нашим с вами языком, одинаковы. Если наше пространство гиперболическое, оно поведет себя в точности как модель Пуанкаре (но только в трех измерениях).
Рис. 6. Параллельные линии в гиперболическом и евклидовом пространствах
Десять лет, начиная с 1816 года Гаусс руководил огромной работой по изучению местностей в Германии; ныне мы называем такие работы геодезической съемкой. Перед исследователями стояла задача измерения расстояний между городами и другими точками на местности и создания соответствующих карт. Гаусс разработал ключевую для современной теории вероятности и статистики идею — теорему, согласно которой случайные погрешности распределяются относительно среднего значения в виде колоколообразной кривой (подробнее см., например, Нормальное распределение; российским читателям Гаусс, скорее всего, известен, именно как автор колоколообразной кривой, а не как разработчик неевклидовой геометрии).
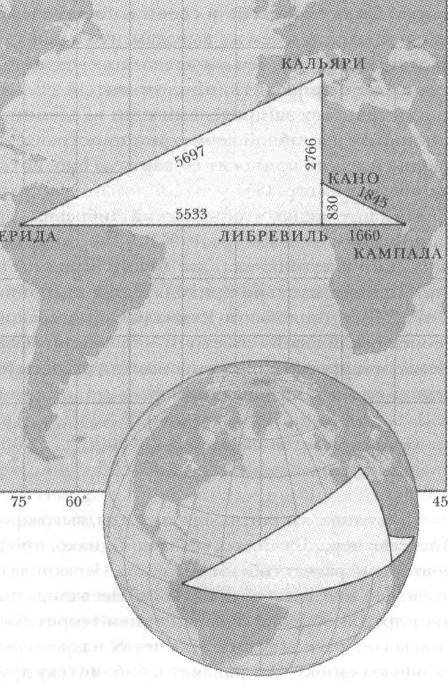
В гауссовой геометрии теорема Пифагора неверна. На карте (рис. 7) видно, что Либервиль, итальянский Кальяри (39° СШ) и колумбийская Лерида (71° ЗД) образуют прямоугольный треугольник. Этот треугольник тоже отображен на карте. Но сумма квадратов катетов – 38 264 845 – не равна квадрату гипотенузы – 32 455 809.
Рис. 7. Треугольники на карте и на глобусе
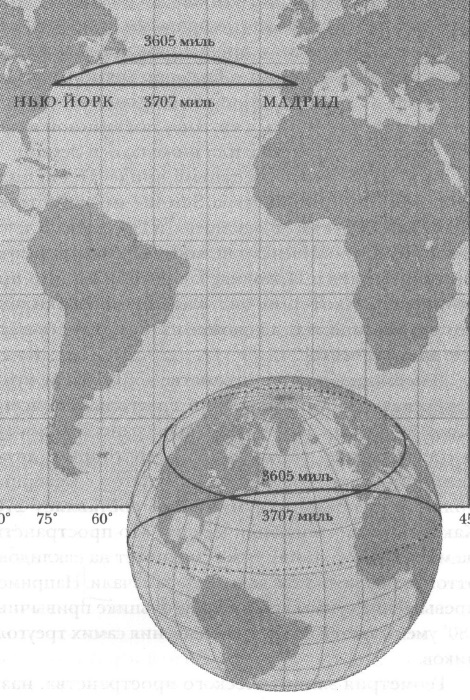
Если плыть по прямой от Нью-Йорка до Мадрида, т.е. строго вдоль линии широты, выйдет ли маршрут кратчайшим? Нет. Оказывается, нужно плыть вдоль странной кривой, обозначенной на карте (рис. 8). Кратчайшая траектория между Нью-Йорком и Мадридом — или между любыми другими двумя точками на земном шаре — кривая, называемая большим кругом (это круг на земном шаре, центр которого совпадает с центром Земли; это самые большие окружности, какие на земной поверхности, отсюда и название). [2]
Рис. 8. Кратчайшая траектория между Нью-Йорком и Мадридом
Для человека, живущего в плоскости, «центра Земли» не существует и Гаусс доказал, что такое возможно. «Плоский» человек заключил бы, что пространство, в котором он живет, — неевклидово: не гиперболическое, а похожее на поверхность шара, т.е. эллиптическое. В таком неевклидовом пространстве все большие круги пересекаются. Суммы углов в треугольнике всегда больше 180° (в гиперболическом пространстве — меньше).
В треугольнике, образованном экватором и двумя линиями долгот, соединяющих экватор с Северным полюсом, к примеру, сумма углов составляет 270°. Как и в случае гиперболического, это пространство на малых расстояниях тоже смахивает на евклидово, оттого отклонения так долго и не замечали.
Георг Риман в 1954 г. выступил с показательной лекцией, являвшейся ступенькой к получению им должности профессора. Риман представил свою лекцию в контексте дифференциальной геометрии, сосредоточившись на свойствах бесконечно малых областей поверхности, нежели на ее общих геометрических свойствах. По сути, Риман неевклидову геометрию как таковую ни разу и не помянул. Но последствия его работы были очевидны: Риман объяснил, каким образом сферу можно интерпретировать как двухмерное эллиптическое пространство.
Подобно Пуанкаре, Риман дал свою интерпретацию понятий «точка», «прямая» и «плоскость». В качестве плоскости он выбрал поверхность сферы. Его точки, как и у Пуанкаре, были местоположениями — в том же смысле, в каком Декарт имел в виду пары чисел, они же координаты (по сути — широта и долгота той или иной точки). Линиями Римана оказались большие круги — геодезические линии сферы.
Работа Римана в дифференциальной геометрии стала краеугольным камнем общей теории относительности Эйнштейна. Но еще до начала переворота труды Римана по эллиптическим пространствам произвели не менее мощное действие на мир математики. Необходимость видоизменять не только постулат параллельности, но и прочие, оказалась равносильна перетиранию прядей в веревке — и веревка вскоре лопнула. И лишь тогда математики осознали, что на этой веревке висела не только геометрия, но и вся математика.
Лекция Римана 1854 года дождалась публикации лишь в 1868-м. Последствия наработок Римана мало-помалу показали, что Евклид совершил ошибки нескольких разновидностей: он сделал множество негласных допущений, другие толком не доформулировал, а кроме того, попытался определить больше, чем было возможно.
Поскольку любое слово в словаре определяется другими, подмена понятий происходит практически с любым определением. Единственный способ избежать логического круга — допустить существование в конечном языке неких словарно неопределимых понятий. Ныне мы понимаем, что и математические системы обязаны включать подобные неопределимые понятия, и стараться включать минимальное их число, необходимое для того, чтобы система оставалась осмысление
Часть 4. История Эйнштейна
Гаусс и Риман показали, что пространство может искривляться, и разработали математику, необходимую для описания этого явления. Далее встал вопрос: а в каком пространстве обитаем мы? Или — еще глубже: что определяет форму пространства? Изящный и точный ответ, данный Эйнштейном в 1915 году, на самом деле впервые в общих чертах был предложен еще в 1854-м самим Риманом:
Вопрос обоснованности геометрии… связан с вопросом внутренней причины метрических взаимоотношений пространства… нам следует искать причину этих метрических взаимоотношений вне самого пространства, во внешних силах, воздействующих на него…
Если ньютоновы представления о пространстве и времени верны, легко увидеть, чего не может быть. Во-первых, не может быть пределов у скорости, с которой один объект приближается к другому. Чтобы в этом убедиться, вообразим, что такая предельная скорость существует; назовем ее с. Теперь представим, что объект приближается к нам с этой скоростью. Давайте (в научных целях) плюнем в этот объект. Если вся эта драма разворачивается в осязаемой среде под названием «абсолютное пространство», легко заметить, что этот объект приближается к вашей слюне быстрее, чем к вам. Закон предельной скорости нарушен. Во-вторых, скорость света не может быть постоянной. Точнее, свет должен достигать разных наблюдателей с разной скоростью. Если поспешите свету навстречу, он доберется до вас быстрее, а если будете удирать от него — медленнее.
Если существует объективное устройство пространства, эти две истины самоочевидны. И все-таки эти две «истины» ложны. Вот оно, основание специальной теории относительности, компонент, которого не доставало в первых рассуждениях о физике искривленного пространства.
Электромагнитная теория Максвелла считается краеугольным камнем современных механики, теории относительности и квантовой теории. Интересующиеся математикой, вот вам математические уравнения Максвелла для свободного пространства: ∇ * Е = 4πρ; ∇ * В = 0; ∇ * В – ∂Е/∂t = 4πj; ∇ * Е + ∂В/∂t = 0, где ρ и j — источники, а Е и В — поля (в Википедии формулы немного иные).
В специальной теории относительности Эйнштейн применил подход Евклида. Он основывал свои рассуждения на двух аксиомах о пространстве:
- Невозможно определить, не прибегая к сопоставлению с другими телами, покоитесь ли вы или находитесь в равномерном движении.
- Скорость света не зависит от скорости его источника и одинакова для всех наблюдателей во Вселенной.
Часто говорят, что в теории относительности движущиеся объекты воспринимаются как сжатые в направлении их движения. Это означает, что объект, измеряемый наблюдателем, считающим объект движущимся, будет воспринят как более короткий, нежели в случае наблюдателя, который считает объект неподвижным. Эйнштейн обнаружил аналогичные аномалии и в поведении времени. Движущиеся относительно друг друга наблюдатели не договорятся о длинах или интервалах времени или о том, сколько времени прошло. Подобно пространственным, и временные промежутки не имеют абсолютного значения.
Время, которое наблюдатель отмеряет между двумя событиями, находясь на одном месте, — что в его системе отсчета есть фиксированная точка пространства, — называется собственным временем. Любой другой наблюдатель, находящийся в движении (с постоянной скоростью) относительно первого, воспримет временной интервал между двумя событиями как больший. Поскольку относительно себя самих мы всегда находимся в покое, время нашей жизни, измеряемое другими, всегда дольше, нежели его воспринимаем мы сами.
Что это означает применительно к законам движения? В специальной теории относительности объекты все еще подчиняются первому закону Ньютона: они движутся по прямой, если на них не действует внешняя сила. Наблюдатели могут не соглашаться в том, какой длины тот или иной сегмент этой самой прямой, — но не в том, что она, в принципе, прямая. Однако это пока и не «релятивистская формулировка» первого закона: в теории относительности для разных наблюдателей пространство и время по-разному взаимодействуют друг с другом. Для того, чтобы и пространство, и время оказались охвачены одной теорией, понятия геометрии необходимо видоизменить.
Вместо точек в пространстве и времен событий нам придется формализовать понятие события, иными словами — ввести точки в четырех измерениях пространства-времени. Мы теперь говорим не о траекториях в пространстве, а о мировых линиях в пространстве и времени. Отныне у нас не расстояния, а комбинация временного интервала и пространственных расстояний между событиями. А вместо прямых — геодезические линии, определяемые как кратчайшие или длиннейшие мировые линии, соединяющие два события.
Первый закон Ньютона можно сформулировать в терминах новой геометрии так:
Если на объект не действует внешняя сила, он всегда перемещается вдоль мировой линии от одного события к другому так, что время, прошедшее по часам этого объекта (т.е. собственное время) максимально.
Поддержка Планком теории относительности — ирония судьбы: он с большим трудом принял ранние работы Эйнштейна по фотоэффекту — новую интерпретацию его же, Планка, квантовой теории. Но вот поди ж ты: в части теории относительности Планк оказался человеком широких и гибких взглядов — он немедленно воспринял ее как верную. В 1906 году Планк стал первым человеком после Эйнштейна, опубликовавшим статью по теории относительности. В той статье он первым же и применил относительность к квантовой теории.
Бывший преподаватель Эйнштейна по Политехникуму Герман Минковский, находившийся тогда в Гёттингене, оказался еще одним поборником теории относительности — из тех немногих, кто внес в нее важный вклад еще на заре ее существования: он устроил коллоквиум, на котором ввел в теорию относительности геометрию и понятие о времени как о четвертой координате. В лекции 1908 года Минковский сказал: «Таким образом пространство само по себе и время само по себе обречены отойти в мир теней, и лишь союз этих двух сохранит независимое существование».
Невзирая на поддержку маститых физиков — преимущественно в Германии, — широкого признания специальной теории относительности пришлось дожидаться. Но пока физическое сообщество не спеша раздумывало над идеями Эйнштейна, он уже принялся за работу над следующей, еще более великой революцией.
Как потом рассказывал сам Эйнштейн, в ноябре 1907 года, он сидел в кресле в патентном бюро в Берне и вдруг возникла мысль: «если человек свободно падает, он не чувствует собственного веса». Эйнштейн говорил, что это осознание «поразило» его; оно стало откровением, приведшим ученого к его величайшему достижению. Падающий человек Эйнштейна стал эйнштейновым яблоком. Эйнштейн искал нечто подобное с 1905 года — новый принцип, могущий стать путеводным в поисках лучшей теории относительности. Он понимал, что исходная теория неполна. Даже с учетом всех следствий субъективности пространства и времени, его специальная теория все равно оставалась лишь новой кинетикой.
Она описывала, как тела реагируют на воздействие определенных сил, но она их не определяла. Ясное дело, специальная теория относительности задумывалась так, чтобы идеально стыковаться с теорией Максвелла, поэтому загвоздка состояла не в электромагнитных силах. Силы гравитации же — совсем другое дело.
Единственной на 1905 год теорией тяготения оставалась ньютонова. Ньютон был не дурак: он дал такое описание гравитационным силам, чтобы оно увязывалось с его же кинетикой, т.е. с его законами движения. Поскольку специальная теория относительности заменила ньютоновские законы новой кинетикой, неудивительно, что Эйнштейн счел гравитационную теорию Ньютона неподходящей. Вспомним формулировку закона всемирного тяготения:
Сила тяготения между двумя материальными точками в любой момент времени пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними в данный момент времени.
Этот закон был немил самому открывателю: Ньютон находил мгновенную передачу силового воздействия подозрительной. В теории относительности подозрение переросло в обвинение: ничто не может передаваться быстрее скорости света. Но и это еще не все. Задумаемся над оборотом «в данный момент». В теории относительности, как мы успели заметить, это субъективная категория. Если две массы находятся в движении друг относительно друга, события, кажущиеся одной из этих масс одновременными, другой массой будут восприняты как произошедшие в разное время. Ну и к тому же, как обнаружил Лоренц, они не договорятся ни о показателях масс, ни о значениях расстояний.
Озарение, посетившее Эйнштейна – «если человек свободно падает, он не чувствует своего веса» – в более широкой формулировке стало принципом эквивалентности, или третьей аксиомой Эйнштейна:
Невозможно различить вне сопоставления с другими телами, движется ли данное тело с постоянным ускорением или покоится в равномерном гравитационном поле.
Иными словами, гравитация — фиктивная сила. Ее можно считать всего лишь декоративным элементом выбранной нами системы отсчета и устранить, выбрав другую.
Эйнштейн впервые выдвинул соображение, что гравитация влияет на ход времени, в 1907 году. Из специальной теории относительности нам известно, что пространство и время взаимосвязаны. Сколько понадобилось времени техническому эксперту, чтобы осознать: присутствие гравитации меняет и форму пространства? Пять лет. Стоит это запомнить — на случай, когда вдруг проглядите что-нибудь, что впоследствии покажется вам очевидным. Эйнштейн говорил: «Если б мы знали, что именно делаем, это не называлось бы исследованием, правда?» Эйнштейн совершил логический переход к искривленному пространству летом 1912 года в Праге. Шел шестой год размышлений над созревающей теорией относительности. Эйнштейн заключает, что евклидову геометрию необходимо отставить. Остается единственный вопрос: в пользу чего?
Ломать — не строить. Эйнштейну для построения новой физики требовалась новая геометрия, которая описывала бы искажение пространства. К счастью, Риман (и несколько его последователей) уже все придумали. К несчастью, Эйнштейн не слыхал о Римане — как, впрочем, и почти все остальные. Зато Эйнштейн еще как слыхал о Гауссе.
25 ноября 1915 года Эйнштейн представил работу под названием «Уравнения поля тяготения» Прусской научной академии. В ней он объявил: «Наконец общая теория относительности завершена как логическая структура». Эта работа содержала уравнение, описывающее распределение материи в пространстве (и времени) в связи с метрикой четырехмерного пространства-времени. Поскольку метрика определяет геометрию, уравнения Эйнштейна определяют форму пространства-времени. В теории Эйнштейна масса не производит гравитационного воздействия, а меняет пространство-время.
Можно суммировать вклад Эйнштейна в геометрию его же прозаическими словами. О своей революционной работе он писал: «Когда слепой жук ползет по поверхности шара, он не сознает, что его путь искривлен. Мне повезло это заметить».
Часть 5. История Виттена
Есть ли связь между природой пространства и законами, которым это пространство подчиняется? Эйнштейн показал, что присутствие материи влияет на геометрию, искажая пространство (и время). Однако в новой физике пространство может отыграться на материи гораздо больше. Согласно этим теориям, самые основные свойства пространства — например, его размерность — определяют законы природы и свойства материи и энергии, из которых состоит наша Вселенная.
В рамках теории струн существуют настолько малые дополнительные измерения пространства, что свободное место в них невозможно наблюдать в современных экспериментальных условиях (хотя косвенно, вполне вероятно, нам это вскоре удастся). Они, может, и крошечные, однако своей топологией, т.е. свойствами, обусловливающими их форму, — к примеру, плоскости, сферы, кренделя или бублика, —определяют, что внутри них существует (например, мы с вами). Сверни мы эти крошечные бубличные измерения в крендель и — пшик! — электроны (и, как следствие, люди) могут перестать существовать. Более того: струнная теория, по-прежнему плохо понятая, развилась в другую, М-теорию, о которой мы знаем еще меньше, но она, похоже, ведет нас к следующему заключению: пространство и время на самом деле не существуют, а являются лишь аппроксимациями чего-то более сложного.
С явлением струнной теории физики вновь вернулись к партнерской дисциплине — математике, абстрактной науке, занятой со времен Гильберта правилами, а не реальностью. Теория струн и М-теория пока движимы не традицией озарения физиков и не экспериментальными данными, которых не хватает, но открытиями их математической структуры. Неслучайно Эдвард Виттен, ныне главный идеолог новой теории, получил не Нобелевскую премию, а медаль Филдза — математический эквивалент Нобелевки. Поскольку геометрия и материя — отражения друг друга, так же должны быть связаны между собой и их современные исследования. Виттен идет еще дальше: он утверждает, что струнная теория должна стать новой ветвью геометрии.
На дворе стоял 1981 год. Джон Шварц услышал в коридоре знакомый голос. «Эй, Шварц, ты нынче в скольких измерениях?» Это Фейнман, в те времена еще не «открытый», — культовая фигура лишь в разреженных сферах физики. Фейнман считал теорию струн сумасбродной. Шварц не возражал. Он уже привык, что к нему не относятся серьезно.
Шварц пытался решить задачу, о которую преткнулся Эйнштейн и все остальные после него: согласование квантовой теории с относительностью. И простого решения не предвиделось. В отличие от теории относительности, первая обобщенная квантовая теория не рождалась десятки лет после открытия Планком квантования энергетических уровней. Все изменилось в 1925-1927 годах благодаря усилиям австрийца Эрвина Шрёдингера и немца Вернера Гейзенберга (я недавно прочитал Эрвин Шредингер. Что такое жизнь с точки зрения физика? Рекомендую). Независимо друг от друга они открыли — возможно, точнее будет сказать «изобрели» — элегантные теории, объяснявшие, как заменить ньютоновы законы движения другими уравнениями, включавшими принципы квантовой теории, выведенные за последние несколько десятилетий. Две новые теории получили названия волновой механики и матричной механики соответственно. Как и в случае специальной теории относительности, следствия квантовой теории были заметны лишь в отрыве от повседневной жизни, на сей раз — не из-за бешеной скорости, а из-за малости размеров. Поначалу не только связь между двумя теориями и теорией относительности оставалась невнятной, но и их отношения между собой. Математически они выглядели столь же разными, сколь их первооткрыватели.
Эквивалентность волновой механики Шредингера и матричной механики Гейзенберга вскоре доказал английский физик Поль Дирак. Единая теория, которую они представляли, получила нейтральное название квантовой механики. Дирак также расширил квантовую механику и включил в нее принципы специальной теории относительности (и разделил Нобелевские премии за квантовую механику 1932 и 1933 годов). Дирак, однако, общую теорию относительности в свои рассуждения не включил. И на то есть причина: сделать это невозможно.
Эйнштейн, родитель обеих теорий, отчетливо видел конфликт между ними. Хотя общая теория относительности глубоко ревизовала взгляды Ньютона на Вселенную, она сохранила одну из «классических» догм: определенность. Располагая нужной информацией о системе — хоть о вашем теле, хоть обо всей Вселенной, — вы могли бы, согласно парадигме Ньютона, рассчитать события будущего. А вот по квантовой теории это не так.
Именно это Эйнштейн терпеть не мог в квантовой механике. Сила чувства привела его к отвержению этой теории. Последние тридцать лет жизни он пытался расширить общую теорию относительности так, чтобы она включала все силы природы, и надеялся, что в процессе ему удастся разобраться с противоречием между теорией относительности и квантовой теорией. Не удалось. Через тридцать лет после смерти Эйнштейна Джон Шварц почуял, что нашел ответ.
Неопределенность в квантовой механике — дело принципа. Принципа неопределенности. Согласно ему, некоторые характеристики систем, количественно описанные ньютоновскими законами движения, не могут быть описаны бесконечно точно. Этот предел определенности в природе вдохновил Эйнштейна на знаменитое высказывание: «Квантовая механика действительно впечатляет. Но внутренний голос говорит мне, что это еще не настоящий Иаков. Эта теория говорит о многом, но все же не приближает нас к разгадке тайны Всевышнего. По крайней мере, я уверен, что Он не бросает кости».
Статистические различия (среднее, дисперсия) случайной величины – не принцип неопределенности. Квантовый принцип неопределенности идет дальше; он гласит, что определенные качества образуют комплементарные пары — пары, у которых есть определенное ограничение: чем точнее измерено одно качество, тем менее точно удастся измерить другое. Согласно квантовой теории, значение этих комплементарных свойств за пределами ограничивающей точности неопределенно, а не просто за пределами возможностей нашего оборудования.
Математика принципа неопределенности утверждает: результат неопределенности двух комплементарных членов пары должен равняться числу, называемому постоянной Планка. Местоположение — часть одной из комплементарный пар принципа неопределенности. Ее напарник, импульс. Погрешность одного меняется в обратной пропорции к точности второго. Постоянная Планка — малюсенькое число. В противном случае мы бы заметили квантовые эффекты гораздо раньше (если бы в таком мире вообще могли существовать).
Квантовой механике в формулировке Гейзенберга и Шрёдингера удалось весьма успешно описать явления и атомной, и даже ядерной физики своего времени. Но применение принципа неопределенности к гравитации в описании теории Эйнштейна приводит нас к довольно диковинным выводам о геометрии пространства.
Конфликт между общей теорией относительности и квантовой механикой становится очевиден лишь в областях настолько малых, что даже в наши дни нет никакой надежды наблюдать их впрямую. Для приверженцев строгих цифр: это расстояние порядка 10–33 сантиметра, и называется оно планковской длиной. Для любителей зрительных образов: если увеличить планковскую длину до диаметра яйцеклетки человека, обычный детский игральный шарик раздулся бы до размеров наблюдаемой Вселенной.
В царстве ультрамикроскопичности есть, судя по всему, другие измерения, свернутые в себе самих, настолько малые, что, как и квант в 1899 году, остаются незамеченными. Они и есть ключевой ингредиент в спасительном снадобье для общей теории относительности. Именно о них размышлял, но позднее отбросил десятки лет назад сам создатель теории относительности.
Теодор Калуца в письме предложил Эйнштейну, как можно объединить электромагнитные силы с гравитационными. У этой теории была одна маленькая странность. Эйнштейн написал в ответ: «Идея создания [объединенной теории] посредством пятимерного цилиндрического мира никогда не приходила мне в голову…»
Калуца задался вопросом: если формально расширить эйнштейново поле до пяти измерений, какие уравнения получатся для дополнительных g-факторов? Ответ ошеломительный: выходят уравнения Максвелла для электромагнитного поля! Начиная с пятого измерения электромагнетизм вдруг возникает в теории гравитации. Эйнштейн сомневался в теории Калуцы, однако чуть погодя все же передумал и в 1921 году помог Калуце опубликовать его теорию.
Главный способ изучения элементарных частиц физиками таков: физики разгоняют частицы до бешеных скоростей и энергий, после чего вляпывают их друг в дружку и смотрят, какие именно дребезги полетят во все стороны. При этом успешной квантовой теории создания и исчезновения элементарных частиц не существовало. S-матрица являла собой черный ящик, в который можно было что-нибудь засунуть — определения сталкивающихся частиц, их импульсов и т.д. — и получить на выходе аналогичные данные, но для вновь возникших частиц. Для построения матрицы рассеяния, т.е. внутренностей черного ящика, вообще говоря, требовалась теория взаимодействия частиц.
Что же у черного ящика внутри? В 1970 году Ёитиро Намбу из Университета Чикаго, Хольгер Нильсен из Института Нильса Бора и Леонард Сасскинд из Университета Иешивы, ответили на вопрос: нужно моделировать элементарные частицы не как точки, а как малюсенькие колеблющиеся струны. Намбу с коллегами открыли струнную теорию практически в том же смысле, что Планк когда-то — квантовую. Оба набрели на идею: энергетические уровни можно представить количественно, а частицы можно представить, как струны; в обоих случаях ни подлинное значение, ни широта охвата этих идей не были поняты, а на формирование осмысленной теории потребовались годы. Оба набрели на то, что могло быть новым законом природы — или просто математической ужимкой. И лишь годы усилий могли определить, что есть что. В случае с квантовой теорией потребовалось 25 лет — от Планка до Гейзенберга и Шрёдингера. Струнная теория уже проскочила этот рубеж.
В марте 1995 года Эдвард Виттен говорил о струнной теории на конференции в Университете Южной Калифорнии. Со времен суперструнной революции Шварца прошло одиннадцать лет, и для многих теория струн постепенно разваливалась. Речь Виттена все изменила. Он объяснил еще одно математическое чудо: все пять различных струнных теорий, по его утверждению, — лишь разные приблизительные формы одной и той же масштабной теории, ныне именуемой M-теорией. Согласно М-теории, струны являются не фундаментальными частицами, а примерами более общих объектов — бран (сокращение от мембран). Браны — версии струн в измерениях высоких порядков, тогда как сама струна — одномерный объект. Мыльный пузырь, например, — 2-брана. Согласно М-теории, законы физики зависят от более сложных колебаний этих более сложных сущностей. И в М-теории есть одно дополнительное свернутое измерение — итого получается одиннадцать, а не десять измерений. Но самое странное в этой теории вот что: пространство и время в некотором фундаментальном смысле не существуют. Со времен Евклида это — самое глубинное изменение в понимании пространства.
М-теорию понять еще сложнее, чем струнную. Идеи, порожденные М-теорией, уже привели к поразительнейшему намеку на то, что есть что-то в этой самой идее струн: к предсказанию, связанному с физикой черных дыр. Черные дыры — одно из явлений, предсказанных общей теорией относительности. Их характерная особенность заключается в их черноте (для физиков это означает, что никакой свет или иное излучение не могут из них вырваться). В 1974 году Стивен Хокинг сказал: р-р-р-р, неправильный ответ! С учетом законов квантовой механики приходится заключить, что черные дыры — не вполне черные. А все оттого, что, по принципу неопределенности, пустое пространство не вполне пусто: оно заполнено парами частица- античастица, которые существуют лишь краткий миг, после чего самоуничтожаются в ничто. Согласно очень хитроумным вычислениям Хокинга, когда это происходит совсем рядом с черной дырой, та может всосать одного члена пары, а второго выкинуть в космос — и вот их-то можно наблюдать как излучение. Значит, черные дыры светятся. Это к тому же означает, что в них ненулевая температура, в точности так же, как свет от углей указывает на некоторое количество тепла.
Надежда на экспериментальное свидетельство М-теории жива — по двум причинам. Первая — возможное открытие в следующем десятилетии суперсимметричных частиц. Это может произойти в Большом адронном коллайдере в женевском ЦЕРНе. Вторая проверка на реальность — поиск отклонений от закона тяготения.
Природа развивается по своему внутреннему порядку. Математика являет его нам. Станет ли М-теория дивным учебником завтрашних студентов колледжей — или всего лишь примечанием к лекции по истории науки под названием «Тупики»? Ныне целое поколение исследователей смотрит на природу и видит ее струны. И по-старому смотреть на мир уже вряд ли получится.