Александр Альбов. От абака до кубита

Нам кажется невероятным, что вавилоняне четыре тысячи лет назад умели решать кубические уравнения, не имея понятия о формулах, выражающих корни через коэффициенты… Однако было бы ошибкой считать математику «мертвой» наукой с раз и навсегда заданной схемой вычислений. Известные нам математические образы прошли долгую эволюцию — миновали века, прежде чем вырабатывался тот или иной удобный для счета символ, та или иная формула. Когда и почему возникли современные символы математики? Математическая истина не имеет границ, поскольку математика — это искусство называть разные вещи одним и тем же именем. Основные фрагменты истории этой науки будут любопытны и полезны каждому.

Александр Альбов. От абака до кубита. – СПб.: ООО «Страта», 2015. – 296 с.

Скачать конспект (краткое содержание) в формате Word или pdf

На момент публикации заметки книга представлена только в Интернет-магазине Лабиринте

Глава 1. Математические символы древности

В математике принято символы, участвующие в записи числа, называть цифрами. Первое научное определение числа дал древнегреческий математик Евклид в своих «Началах» (ок. 300 до н.э.).

Системы счисления делятся на непозиционные и позиционные. В непозиционной системе значение цифры постоянно и не зависит от её места в записи числа. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. В позиционных системах счисления одна и та же цифра в записи числа имеет различные значения в зависимости от того места (разряда), где она расположена. Вторая величина, которая характеризует позиционную систему счисления, — основание системы. Эта как правило, целое число, выражающее количество цифр в данной системе. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам.

В этой связи замечательно высказывание математика Николая Николаевича Лузина (1883–1950): «Преимущества десятичной системы счисления не математические, а зоологические. Если бы у нас на руках было не десять пальцев, а восемь, то человечество пользовалось бы восьмеричной системой счисления».

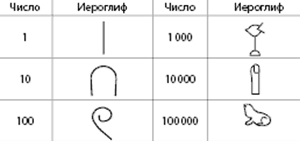
Древний Египет. В древнем Египте применялась непозиционная десятичная система счисления и были известны лишь два арифметических действия — сложение и вычитание. Египтяне обозначали узловые числа иероглифами (рис. 1).

Рис. 1. Числа-иероглифы Древнего Египта

С помощью этих знаков число 45386 запишется в аддитивном представлении следующим образом: 10000 + 10000 + 10000 + 10000 + 1000 + 1000 + 1000 + 1000 + 1000 + 100 + 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 + 1 + 1 (рис. 2).

Рис. 2. Иероглифическая запись число 45 386

Вавилония. Вавилонская система счёта была позиционной, что давало ей огромное преимущество перед египетской. В основании вавилонской системы счисления не десять, как в привычной нам, а шестьдесят. Натуральные числа от 1 до 59 записывали по десятичной системе. Форма знаков была следующей: единица изображалась вертикальным клином , а десятка — скобкой . Так, числа 3, 20, 32 записывались следующим образом: 

Начиная с 60, способ записи чисел меняется. Шумеры пользовались одним и тем же символом, но указывали его значение его положением. Например, число 169 (т. е. два «шестидесятка» и 49 единиц) обозначается «цифрами» 2 и 49, т. е. запись имеет вид .

Ряд элементов вавилонской системы используется до сих пор. Именно вавилоняне разделили сутки на 24 часа, час— на 60 минут, а минуту— на 60 секунд. Именно они разделили окружность на 360 градусов, а это значит, что угловые меры тоже введены вавилонянами.

Для вычисления квадратного корня применялся алгоритм половинного деления, известный как метод Ньютона. Пусть имеется число n, из которого нужно извлечь квадратный корень. Выберем два числа A и B, квадраты которых больше и меньше n. Рассчитывается C = (A + B)/2. Если квадрат C больше n, то A заменятся на C; если квадрат C меньше n, то B заменятся на C. Процесс повторяется до тех пор, пока не найдена величина, квадрат которой равен n или является близким приближением к n.

Главной и самой удивительной чертой вавилонской математики является стремление сформулировать любую задачу, арифметическую или геометрическую, в виде уравнений, то есть в алгебраической форме. Вот типичный пример: «Площадь участка равна сумме двух квадратов и составляет 1000. Сторона малого квадрата равна 2/3 стороны большего квадрата, уменьшенного на 10. Найти стороны квадратов».

Если обозначить стороны большого и малого квадратов через x и y, задача сведётся к решению системы уравнений:

Подставив в первое уравнение y, получим:

Положительный корень этого квадратного уравнения x = 30. Отсюда следует, что y = 10.

Помимо алгебраической направленности другая важная черта математики Двуречья заключается в полном отсутствии доказательной базы. Понятия о теоремах и необходимости доказывать их логическим путём, опираясь на некие аксиомы, впервые появляются в греческой математике. Наиболее чётко этот универсальный метод сформулирован в «Началах» Евклида в третьем веке до н.э.

Древняя Греция. В древнейшее время в Греции была распространена так называемая аттическая нумерация. Числа 1, 2, 3, 4 обозначались чёрточками I, II, III, IIII. Число 5 записывалось знаком  (древнее начертание буквы «пи», с которой начинается слово «пенте» — пять); числа 6, 7, 8, 9 обозначались . Число 10 обозначалось Δ (начальной буквой слова «дека» — десять). Числа 100, 1000 и 10 000 обозначались Н, X, М — начальными буквами соответствующих слов. Числа 50, 500, 5000 обозначались комбинациями знаков 5 и 10, 5 и 100, 5 и 1000, а именно: . Числа записывались следующим образом:

В Египте и Вавилонии способы вычислений носили утилитарный характер, отвечая на вопрос «как?»; у греков же постановка вопроса была гораздо глубже — их интересовало «почему?». Попытки ответа порождали новую математику, пронизанную мыслью о логическом доказательстве, но не только её — не менее важным было появление многочисленных философских систем. На этой ниве трудились мистик Пифагор, рационалист Демокрит, Зенон, Фалес Милетский, Анаксимандр, Диоген, Эмпедокл, Гераклит, Платон, Аристотель, Сократ.

Евклид стал первым математиком Александрийской школы. Его историческая заслуга состоит в том, что в тринадцати книгах своих «Начал» он собрал достижения предшественников — Фалеса, Пифагора, Демокрита, Гиппократа, Евдокса и других, упорядочил их и привёл геометрические знания прошлого в стройную систему. Это сделано им столь тщательно и искусно, что на протяжении двух с лишним тысяч лет «Начала» остаются лучшим изложением элементарной геометрии. Многие учебники являются лишь переработкой этого классического трактата.

Славянская нумерация. Славянская кириллическая нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой ионийской записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию (рис. 3).

Рис. 3. Славянская нумерация

Запись числа, использованная славянами, аддитивная, то есть в ней используется только сложение:  Для того, чтобы не перепутать буквы и цифры, использовались титла — горизонтальные чёрточки над числами.

В России славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления (арабские цифры). В «Арифметике» Магницкого (1703) номера листов даны ещё в славянской нумерации, что естественно, ведь новым, «арабским», цифрам эта книга только учила.

Рим. Для расчётов римляне использовали абак — металлическую или деревянную пластину с желобками, в которых размещались камешки. Эти камешки стали самым большим вкладом Рима в математику — на латыни «камень» — «calx», а «маленький камешек» — «calculus». От этого слова произошли термины «калькуляция» и «калькулятор». Как и греки, римляне использовали десятичную непозиционную систему, которую, вероятно, позаимствовали у этрусков. В этой нумерации используется всего семь знаков:

Порядок записи — слева направо, от старших разрядов к младшим (например, сотни-десятки-единицы). Цифра, которая стоит справа от основной, увеличивает её, а стоящая слева — уменьшает. Например, IL = 49, LI = 51. Рассмотрим число CXLVIII. Первой будет C = 100, но следующую цифру X = 10 нельзя добавлять к сотне, так как за X стоит большая цифра L = 50, и это значит, что X нужно вычесть из L и получить 40. В последней совокупности V больше, чем стоящее справа III, и к пятёрке нужно добавить тройку. Получаем: CXLVIII = 148.

Индия и арабские страны. Самым важным вкладом древних индийских математиков является система нумерации (включающая ноль), которую мы теперь называем арабской. Центром научной мысли стран ислама долгое время являлся Багдад, где халиф аль-Мамун учредил в начале IX века «Дом мудрости». В 827 году по его повелению (и при его финансировании) были проведены градусные измерения дуги меридиана в долине Синджар, осуществлён перевод труда Птолемея на арабский язык («Альмагест»), благодаря чему этот труд дошёл до Европы. В 829 году в Багдаде основана астрономическая обсерватория.

Мухаммед ибн Муса аль-Хорезми много лет возглавлял «Дом мудрости» и создал здесь труд своей жизни «Хисаб аль-джабр ва-ль мукабала». Арабский оригинал этой книги утрачен, но имеется латинский перевод XII века «Algorizmi de numero Indozum» («Об индийском числе, сочинение Алгоризми»). В других переводах аль-Хорезми именовался Algorismus, и в результате в математику вошёл термин «алгоритм» (латинизированное имя автора), а «аль-джабр» превратилось в «алгебру».

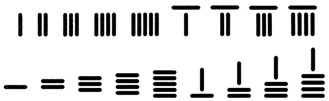
Китай. Древнейшая китайская счётная система датируется IV веком до н. э. Счёт производился с помощью бамбуковых палочек «цзе», или «суаньчоу», которые располагались на дощечке, затем этот способ заменил абак. Палочки соответствовали цифрам от 1 до 9, причём имелись два возможных варианта их расположения, вертикальный и горизонтальный (рис. 4).

Рис. 4. Китай. Вертикальное и горизонтальное расположение счётных палочек для цифр от 1 до 9

Вертикальный вариант был предназначен для указания единиц, сотен и т. д., горизонтальный — для десятков, тысяч и т. д., так что в представлении числа в виде набора цифр эти способы расположения чередовались. Отсутствие значимой цифры (т.е. ноль) обозначалось пустым местом. Число 4508 в данной системе счёта выглядело так:

Со II столетия н. э. цифры от 1 до 9 обозначались иероглифами:

Для обозначения порядка числа использовались особые иероглифы:

Была разработана своеобразная запись чисел с помощью цифр от 1 до 9 с указанием их порядков — иероглиф порядка следовал за цифрой. Фактически это уже десятичная позиционная система — например, число 10 563 представлялось в ней так:

В начале мы видим горизонтальную чёрточку, цифру 1, за которой идет знак порядка «десять тысяч»; затем следует иероглиф для цифры 5 и знак порядка «сотня»; затем иероглиф для цифры 6 и знак порядка «десяток»; затем иероглиф для цифры 3 (без знака порядка). Это эквивалентно записи: 1 х 10000 + 5 х 100 + 6 х 10 + 3 = 10 563.

В 1983 г. китайские археологи вскрыли захоронение, которое датируется 186 г. до н.э. В нём были обнаружены 190 бамбуковых полосок с математическими задачами. После реставрации этой находки появилась возможность ознакомиться с текстом «Математики в девяти книгах». Среди задач, приведённых в них, есть связанные с решением уравнений. Иногда такие задачи формулируются в виде забавных историй. Например, имеется 5 воробьёв и 6 ласточек, их взвесили на весах. Вес всех воробьёв тяжелее веса всех ласточек. Если переместить одну ласточку и одного воробья, то вес будет одинаковым Общий вес ласточек и воробьёв— один цзинь. Спрашивается, сколько весят ласточка и воробей. Если обозначить вес воробья через х, а вес ласточки — через у, задача сведётся к решению линейной системы:

5х + 6у = 1

4х+ у = х + 5у

Отсюда х = 2/19 цзиня, у = 3/38 цзиня. Эта задача демонстрирует, что в I тысячелетии до н.э. китайские математики умели решать системы линейных уравнений и работать с дробями.

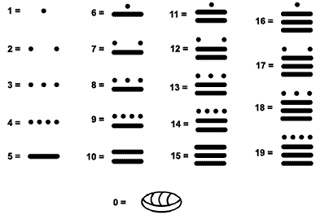
Индейцы Майя. Среди трёх великих индейских цивилизаций, которые испанцы застали в Новом Свете, майя безусловно были самыми искусными математиками. Система счисления майя была позиционной двадцатеричной. Цифры у майя обозначались самым простым способом: точки (единицы) и тире (пятёрки). Единственным сложным для изображения знаком, входившим в нумерацию, был ноль, похожий на рисунок раковины (рис. 5).

Рис. 5. Цифры майя

Числа майя записывались не горизонтально, а вертикально, как бы строя башенку из этажей-цифр. Например, число 359 изображалось в два этажа:

На верхнем этаже две точки и три линии — цифра 17, означающая в этой позиции единицы высшего разряда — семнадцать двадцаток (340), а на нижнем этаже — цифра 19.

17 * 20 + 19 = 359

Средневековая Европа. Упадок культуры и знаний в европейских странах, наступивший вслед за крушением Западной Римской империи, длился несколько веков. Первые столетия этой тёмной эры отмечены утратой культуры земледелия, резким спадом торговли и ремёсел, нескончаемыми войнами и почти полным забвением прошлых достижений. К счастью, преемственность знания поддержали арабы. Множество трактатов Александрийской и других школ было переведено на арабский язык, в мусульманских странах появились талантливые учёные, и их труды, вместе с работами Евклида, Архимеда, Диофанта и прочих греческих математиков, в должный срок стали доступны европейцам. Правда, в Европе нашлись и свои подражатели грекам.

Самым известным из них был римский государственный деятель Аниций Манлий Северин Боэций (480–524), автор «Основ арифметики» и других математических трактатов. Следующая значимая фигура на небосклоне европейской науки появилась спустя ещё двести лет. Леонардо Пизанский (1170–1250), прозванный Фибоначчи («сын Боначчо»), происходил из рода купцов — его семья обитала в Алжире. В качестве купца Фибоначчи странствовал по Востоку, основательно изучив арабскую математику. Возвратившись, он написал свою знаменитую «Книгу абака» («Liber Abaci», 1202), а затем — «Практика геометрии» («Practica geometriae», 1220), в которых собраны знания, полученные им во время путешествий. Фибоначчи являлся убеждённым сторонником использования арабских цифр, и его «Книга абака» стала первым в Европе математическим трактатом, где изложение ведётся с помощью этой новой счётной системы (подробнее см. Альфред Реньи. Числа Фибоначчи).

Лука Пачоли (1445–1517) составил энциклопедический труд «Сумма арифметики, геометрии, учения о пропорциях и отношениях», содержащий полное изложение известных к тому времени математических дисциплин. Книга была опубликована в Венеции в 1494 г. Пачоли написал её не на латыни, а на итальянском языке, с использованием арабских цифр. Это окончательно ввело в оборот индийско-арабскую счётную систему, ибо Пачоли пользовался среди математиков огромным авторитетом. Пачоли также первым изложил основы бухгалтерской двойной записи (см. Лука Пачоли. Трактат о счетах и записях).

В трактате Пачоли рассматривались уравнения второй и третьей степеней, но относительно последних его вывод был пессимистичен. Он писал, что для решения кубических уравнений «искусством алгебры ещё не дан способ». Сципион дель Ферро, профессор университета в Болонье, нашёл решение, но не опубликовал его. И только в 1539 году секрет дель Ферро узнал миланский профессор Джероламо Кардано, который опубликовал решение в книге «Великое искусство» (см. Джироламо Кардано. О моей жизни).

На рубеже XVI и XVII веков появился исключительно важный метод, упростивший систему вычислений. Это были логарифмы, которые ввёл в обиход Джон Непер. Это выдающееся достижение можно считать границей, разделяющей математику Средневековья и математику Нового времени, первыми героями которой стали Галилей, Декарт, Паскаль, Ньютон и Лейбниц.

Глава 2. Такие непростые числа

Ноль и бесконечность. По мнению немецкого историка Эберхарда Кноблоха, «лишь у индийцев впервые в истории человечества появляется ноль как математический символ, используемый в счётных операциях». В 711 году арабы вторглись в Испанию и завоевали почти всю её территорию. В 712 году они захватили часть Индии и покорили Синд — земли в низовьях Инда. Там они познакомились с принятой индийцами системой счисления и переняли её. С тех пор и стали говорить об «арабских цифрах». Проблемы, связанные с нулём, до сих пор дают о себе знать. 1 января 2000 года миллиарды людей встретили новое тысячелетие. Удивительно, как много людей не понимают, что третье тысячелетие и XXI век начались 1 января 2001 года!

Бесконечность – математическое понятие, которому нет аналога в физической реальности. Математическая связь ноля и бесконечности тоже была известна индийским математикам: «Количество, делённое на ноль, становится дробью, знаменатель которой равен нолю. Эту дробь называют бесконечностью».

Огромный вклад в исследование бесконечности внёс немецкий учёный Георг Кантор. Он считал, что бесконечность не только существует, но и в полном смысле постижима человеком (подробнее см. Чарльз Петцольд. Читаем Тьюринга, глава 2. Иррациональные и трансцендентные числа). Знак бесконечности (∞) ввёл в 1655 году английский математик Джон Валлис.

 «Особенные» числа. Натуральные числа возникают естественным образом при счёте предметов: 1, 2, 3… Натуральные — потому что ими обозначались реальные неделимые объекты: люди, животные, вещи. Немецкий математик Л. Кронекер (1823–1891) говорил: «Бог создал натуральные числа, всё остальное — дело рук человеческих».

Простыми называются числа, которые делятся только на единицу и на самих себя. Евклиду принадлежит теорема, изложенная в книге IX «Начал»: существует бесконечное множество простых чисел. Доказательство укладывается в одну фразу: если бы имелось ограниченное количество простых чисел, то можно было бы их все перемножить и, прибавив единицу, получить новое число, которое с гарантией не делится ни на одно простое, что невозможно.

Исторически первым расширением понятия о числе является присоединение к множеству натуральных чисел множества дробных чисел. В Древнем Риме была интересная система дробей. Она основывалась на делении единицы массы — асса. В ходу было 18 различных дробей, например, симис — половина асса; унция — двенадцатая часть асса. Кстати, и наше странное слово «скрупулёзно» происходит от римского названия 1/288 части асса — «скрупулус».

Лишь со временем практика измерений и вычислений показала, что проще и удобнее пользоваться десятичными дробями.

Как ни странно, проценты изобрели римляне, десятичной системой счёта не пользовавшиеся. Так как слова «на сто» звучали по-латыни pro centum, сотую часть и стали называть «процентом». В некоторых случаях применяют и более мелкие, тысячные доли, так называемые промилле (от латинского pro mille — «на тысячу», обозначается символом «‰»). В промиллях измеряют уровень солёности морской воды, уровень содержания алкоголя в крови человека, уклон железнодорожного пути.

Древнегреческие математики пользовались только целыми и дробными положительными числами. Эти числа и получили название «рациональных» (от латинского ratio — отношение). Иррациональные числа были найдены в пифагорейской школе при попытке соизмерить диагональ квадрата с его стороной. Иррациональные числа нельзя выразить простой дробью.

В 1545 году Джироламо Кардано предложил ввести числа «новой природы». Он показал, что система уравнений, не имеющая решений во множестве действительных чисел, имеет решения с числами отрицательными, находящимися под квадратным корнем. Рафаэль Бомбелли в своей «Алгебре» вводит последовательную теорию мнимых и комплексных чисел. Комплексные числа — числа вида x + iy, где x и y — вещественные числа, i — мнимая единица (величина, для которой выполняется равенство: i² = –1).

Термин «мнимые числа» ввёл в 1637 году французский математик и философ Рене Декарт, а в 1777 году Леонард Эйлер предложил использовать первую букву французского слова imaginaire (мнимый) для обозначения мнимого числа. Этот символ (i) вошёл во всеобщее употребление благодаря Карлу Фридриху Гауссу. Он же первым предложил изображать комплексное число z = a + ib точкой M(a, b) на координатной плоскости. Позднее оказалось, что ещё удобнее изображать число не точкой, а вектором OM, идущим в эту точку из начала координат. При таком толковании сложению и вычитанию комплексных чисел соответствуют такие же операции над векторами.

Безусловно, самая древняя из мировых констант — число π. Так, буквой греческого алфавита «π», обозначается математическая константа, равная отношению длины окружности к длине её диаметра. π — иррациональное число, то есть его значение не может быть точно выражено в виде дроби m/n, где m и n — целые числа. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим.

Глава 3. Такие простые знаки

Знаки для арифметических операций впервые появились в III веке у Диофанта Александрийского. Правда, эти знаки не были похожими на те, которыми мы пользуемся сейчас. Вплоть до XV века в мире почти не было постоянных общепринятых арифметических знаков. Знак умножения «косой крест» (×) впервые ввёл английский математик Уильям Оутред. Он же придумал умножение столбиком, знакомое нам со школьной скамьи. Позднее, в 1698 году, великий немецкий математик Готфрид Вильгельм Лейбниц ввёл знак умножения «•». Делить числа люди научились гораздо позже, чем умножать. Лейбниц для обозначения деления предпочитал двоеточие (:).

Знак равенства первым применил Диофант Александрийский, но он использовал для этого букву «i» (от греческого isoс — «равный»). Знак равенства в современной форме (только значительно длиннее), в виде двух параллельных штрихов (=), ввёл английский математик Роберт Рекорд (1557). В континентальной Европе знак «=» был введён Лейбницем.

Первую попытку ввести некий порядок в систему обозначения алгебраических величин предпринял Франсуа Виет. Знаменитая теорема, устанавливающая связь коэффициентов многочлена второй степени с его корнями, была обнародована в 1591 году. Теперь она носит имя Виета. Теорема Виета стала ныне самым знаменитым утверждением школьной алгебры.

Правда, у самого Виета математическая запись алгебраических выражений всё ещё мало похожа на ту, что мы используем сейчас. Например, уравнение в современной записи х³ + bx = d Виет формулировал так: F cubus + D planum aequatur D solido. Здесь ещё, как мы видим, довольно много слов, но ясно, что они уже играют роль будущих символов. Честь придания алгебре современного вида принадлежит Рене Декарту. Он обозначил неизвестные последними буквами латинского алфавита (x, y, z), а произвольные данные величины — начальными буквами (a, b, c). Ему же принадлежит нынешняя запись степени.

На рубеже XVI и XVII веков появился исключительно важный метод, упростивший систему вычислений. Это были логарифмы, которые ввёл в обиход Джон Непер, шотландский аристократ, богослов и математик-любитель, опубликовавший в 1614 году в Эдинбурге трактат «Описание удивительного канона логарифмов». С их помощью достигалось значительное упрощение вычислительных операций: умножение превращалось в сложение, деление — в вычитание, возведение в степень — в умножение, а извлечение корней — в деление. Вот иллюстрация этих замечательных свойств: log(ab) = log(a) + log(b), log(a/b) = log(a) – log(b), log(a^b) = b*log(a).

Но легко заметить: чтобы пользоваться этим превосходным способом – умножать, делить и возводить в степень многозначные числа, нужно сначала найти логарифмы этих операндов, а затем совершить обратное действие — по логарифму найти число-результат. Для этого нужна таблица логарифмов, вычисленных с хорошей точностью. Этой мыслью Непер поделился со своим почитателем и профессором Оксфорда Генри Бригсом, который и завершил работу после смерти Непера. Он усовершенствовал таблицы логарифмов, приняв за логарифм единицы ноль, а за логарифм десяти — единицу. В 1617 году Генри Бригс опубликовал первую восьмизначную таблицу логарифмов.

В современных терминах логарифм — это показатель степени. Логарифм 100 по основанию 10 равен 2, так как 100 = 10². Фактически идея логарифма — идея полезного кода, которая переводит одни числа в другие.

Глава 4. Вычислительная техника: от абака до компьютера

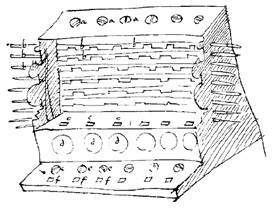
В разных странах существовало несколько видов абака: древнеегипетский (заимствованный греками), римский (рис. 6), китайский (суаньпань), японский (соробан).

Рис. 6. Реконструкция римского абака. Романо-германский центральный музей, г. Майн, Германия. Оригинал, сделанный из бронзы, находится в Национальной библиотеке Франции, Париж

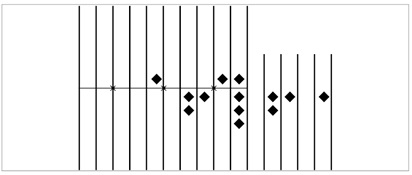
На острове Саламин в 1846 г. был найден мраморный абак, предназначенный для денежных расчётов, с пометкой столбцов, указывающей на их соответствие определённому количеству монет. Длинные столбцы, если отсчитывать их справа налево, обозначали единицы, десятки, сотни, тысячи и десятки тысяч драхм, а затем — такие же разряды, но уже талантов. Короткие столбцы обозначали обол и его доли: обол, 1/2, 1/4 и 1/8 обола. Десять длинных столбцов пересекает линия; камешек, размещённый ниже линии, соответствует одной счётной единице, а размещённые выше — пяти единицам (рис. 7). Таким образом, денежная сумма, представленная на чертеже абака, составляет 302 158 драхм, 2 обола, 1/2 обола и 1/8 обола. Следует учесть, что камешек над чертой слева обозначает пять талантов, то есть триста тысяч драхм.

Рис. 7. Чертёж абака, найденного на Соломине

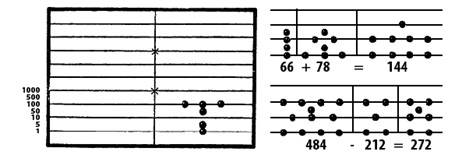
В средневековой Европе древний пятеричный счёт получил распространение в виде так называемого «счёта на линиях». Ряды на счётных таблицах всегда располагались горизонтально и счисление велось снизу вверх, от младших разрядов к старшим (рис. 8).

Рис. 8. Пример сложения и вычитания при «счёте на линиях» (из книги Я. И. Перельмана «Занимательная арифметика. Загадки и диковинки в мире чисел», М., Детгиз, 1954). Слева на счётном поле выложено число 356. Справа показано сложение (вверху) и вычитание (внизу)

Руководства для «счёта на линиях» продолжали появляться ещё долго после того, как уже широко начал входить в употребление счёт пером, т. е. наш обычный счёт. Учебники арифметики XVI в. часто противопоставляют или сопоставляют оба способа производства арифметических действий и в тексте, и в иллюстрациях.

Русские счёты — тот же абак, но с одним существенным отличием: в них применена десятичная система счисления. Возможно, по этой причине счёты применялись даже в XX столетии. Многие обороты нашей речи свидетельствуют о том, что счёты на Руси употребляются с очень давних пор: «сбрасывать со счёта», «сводить счёты», «прикидывать», «накидка», «скидка», «скостить» и много аналогичных выражений в народном языке появилось в результате пользования счётами в течение долгого времени. Как и само название «счёты», эти обороты с трудом и только приблизительно могут быть переведены на языки народов Западной Европы, никогда не знавших счётов с костяшками на прутьях.

Следующий прорыв в технике вычислений связан с появлением аналогового счётного устройства — логарифмической линейки. После того, как было осознано значение логарифмов и появились первые их таблицы, следующий шаг сделал валлийский математик и астроном Эдмунд Гюнтер (1620).

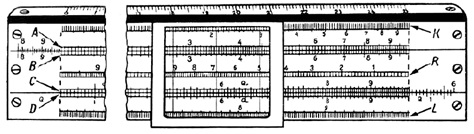
В 1654 году англичанин Роберт Биссакер предложил конструкцию прямоугольной логарифмической линейки, общий вид которой сохранился до нашего времени. Устройство состояло из трёх планок длиной около 60 см. Две внешние планки удерживались вместе металлической оправой, а третья (движок) скользила между ними. Каждой шкале на неподвижных планках соответствовала такая же на движке. Шкалы имелись на обеих сторонах линейки (рис. 9).

Рис. 9. Шкала логарифмической линейки конца XX века

Механические счётные приборы. Как научные, так и практические задачи требовали механизации вычислительных процессов. Вычислительное устройство Шиккарда позволяло работать с шестью значащими цифрами и выполнять четыре арифметических действия. Конструкция Шиккарда базировалась на системе цевочных счётчиков-колёс. С помощью таких механических элементов переносились значения разрядов — так, счётчик десятков срабатывал после полного оборота колёсика для единиц (рис. 10).

Рис. 10. Эскиз «вычислительных часов», сделанный Вильгельмом Шиккардом в письме к своему другу Иоганну Кеплеру, 25 февраля 1624 г.

Суммирующая машина, созданная Блезом Паскалем, оставила более заметный след в истории (около 1645 г.). Блез трудился над нею пять лет и с помощью лучших мастеров Руана изготовил около полусотни «счётных колёс» в разных вариантах, добился «королевских привилегий» (заменявших в те времена патент) и наладил серийное производство. Благодаря этому до наших дней дошли восемь экземпляров его устройства.

Значительным продвижением вперёд стала счётная машина, созданная великим математиком Готфридом Лейбницем лет через тридцать после «паскалева колеса». Сделанные Лейбницем усовершенствования использовались в серийных счётных машинах, первая из которых была сконструирована Шарлем Ксавье Тома де Кольмаром в 1818 г. А 1822 год стал годом рождения счётного машиностроения — в собственных мастерских в Париже де Кольмар начинает производство арифмометров.

Создатель первой механической вычислительной машины Чарлз Бэббидж родился в 1791 году на берегу Темзы в Уолфорте, графство Суррей. Бэббидж изобрёл мысленную машину — огромный блестящий агрегат из меди и сплава олова и свинца, — состоящую из тысячи дисков и роторов, зубцов и шестерёнок, изготовленных с величайшей точностью. Всю свою жизнь Бэббидж совершенствовал эту машину, которая так никогда и не была закончена (подробнее см. Джеймс Глик. Информация. История. Теория. Поток).

В 1842 г. Бэббидж познакомился с Адой Лавлейс. В единственной опубликованной статье Ады приведена первая в мировой истории компьютерная программа, написанная на подобном ассемблеру языке машины Бэббиджа. В этой программе вычисляются числа Бернулли (как пример возможностей машины), но кроме того Ада Лавлейс высказывает мысль о том, что новый способ обработки информации положит начало научной революции.

Ада Лавлейс была права: создание и использование компьютеров явилось революцией во многих отраслях знания и породило новые науки, кибернетику и информатику. Возникновение этих наук связано с именем ещё одного английского учёного XIX века, Джорджа Буля, который стал предтечей математической логики. Созданный им логический аппарат, названный булевой алгеброй, веком позже объединили с двоичной системой счисления, и этот плодотворный симбиоз стал основой для разработки электронного компьютера. В 1847 г. Буль опубликовал статью «Математический анализ логики», а позже, в 1854 г., вышел его капитальный труд под длинным названием «Исследование законов мышления, на которых основываются математические теории логики и вероятностей».

Простая логика содержит два элемента: 0 («ложь») и 1 («истина») и две операции: «∧» («и») и «∨» («или»). Логика подчиняется правилам булевой алгебры (подробнее см. Булева логика: критерии И, ИЛИ).

Клод Шеннон представил в 1938 г. свою докторскую диссертацию. В этой работе, положившей начало теории информации, были связаны воедино двоичная численная система, булева алгебра и реализация вычислительных процессов в виде электрических схем.

Работу Ады Лавлейс столетие спустя продолжил Алан Тьюринг. В 1950 году он опубликовал знаменитую статью «Может ли машина мыслить?». В разделе «Возражения леди Лавлейс» он детально разобрал научное наследие Ады Лавлейс. Программисты до сих пор используют термины, введённые леди Лавлейс. Например, «рабочие ячейки», «цикл» и некоторые другие. Алан Тьюринг стал отцом современного компьютера. Он создал идеальный мысленный компьютер — идею компьютера. Тьюринг разрабатывает несколько базовых концепций информатики — «подпрограмма», «библиотека программного обеспечения», «микропрограммирование» (подробнее о жизни Тюринга см. Эндрю Ходжес. Игра в имитацию; о классической работе Тьюринга см. Чарльз Петцольд. Читаем Тьюринга).

В 1940-х годах появились первые счётные электронные машины на основе цифровых переключателей — электронных ламп и цифровых реле. Первую простую счётную электронную машину в 1941 году создал немецкий учёный Конрад Цузе. Затем, при поддержке IBM и других корпораций, Цузе основал в Швейцарии компанию по производству вычислительной техники и в 1950 году полностью закончил машину Зет-4. На тот момент это был единственный работающий компьютер в Европе, опережавший также и американские разработки Марк-1 и УНИВАК.

Американский ЭНИАК был введён в строй в 1945 году, когда война уже закончилась. У него были предшественники — ещё в тридцатые годы Ванневар Буш проектировал в США устройства для решения дифференциальных уравнений, а другой американский инженер, Говард Эйкен, в 1939–1943 годах работал, при поддержке IBM, над электромеханическим компьютером Марк-1. Эниак находился в эксплуатации десять лет. Машина состояла из 17 тысяч электронных ламп и полутора тысяч реле. Военное ведомство США ассигновало на разработку Эниака 400 тысяч долларов, и над его созданием трудилась под руководством Экерта и Мочли команда из 50 человек. Этот электронный монстр работал в десятичной системе счисления, имел 26 метров в длину, около 3 метров в высоту и весил порядка 30 тонн.

ЭНИАК безусловно ещё не являлся универсальным компьютером, но, при всех своих недостатках, обладал приличным быстродействием — 5000 сложений и 300 умножений в секунду. К тому же во время работы устройства температура в помещении поднималась до 50 градусов Цельсия, и ходил слух, что, когда машину включают, вся Филадельфия остаётся без света, так как ЭНИАК потреблял около 160 КВт.

Фон Нейман, присоединившийся к группе изобретателей, ещё в 1945 г. опубликовал статью, в которой описывались основные компоненты вычислительной машины (процессор, память, блоки ввода/вывода) и отмечалось, что такое устройство должно работать в двоичной системе, быть электронным, а не механическим, и что команды программы должны выполняться последовательно. Эти принципы, названные «архитектурой фон Неймана», не слишком отличались от идей Бэббиджа и Цузе и легли в основу первых и всех последующих компьютеров.

Компания IBM в 1953 г. выпустила на рынок машину IBM 701. Первые УНИВАКи были приобретены Бюро переписи населения США и Пентагоном, первую IBM 701 купил атомный центр в Лос-Аламосе. Вскоре, в 1954 году, на рынке появилась машина IBM 704, которая уже была в полной мере универсальным и довольно мощным для того времени компьютером со средним быстродействием 40 000 операций в секунду. В 1960-х годах электронные лампы заменили транзисторами — полупроводниковыми переключателями, которые были надёжнее, меньше по размеру и потребляли меньше энергии. В 1965 году соучредитель компании «Интел» Гордон Мур предсказал, что мощность компьютера будет удваиваться каждые восемнадцать месяцев. И это предсказание подтвердилось настолько точно, что его стали называть законом Мура. Каким-то мистическим образом новые технологии появлялись как раз вовремя, обеспечивая точное выполнение закона Мура.

В СССР существовало порядка двадцати научных институтов и большое количество конструкторских бюро в Москве, Ленинграде, Киеве, Ереване и других городах, разработавших в пятидесятые-восьмидесятые годы не менее ста моделей ЭВМ, как универсальных, так и управляющих (в том числе — машины военного назначения). Ведущее положение среди этих организаций занимал Институт точной механики и вычислительной техники (ИТМиВТ, Москва). Генеральным конструктором этой серии ЭВМ являлся академик Сергей Алексеевич Лебедев, с которым работал большой коллектив сотрудников. М-20 являлась своего рода базовой машиной, сравнимой по мощности с IBM 704, но запущенной в производство с пятилетним отставанием от американского компьютера — в 1959 году.

По мнению экспертов, мощность полупроводниковых компьютеров достигнет своего логического насыщения к 2020 году. К этому времени точность микросхем достигнет молекулярных размеров. Закон Мура сохранит свою силу только в том случае, если к этому времени будут открыты совершенно новые компьютерные технологии. Сегодня толщина соединений в обычных схемах электронного компьютера составляет 1000 атомов. В обозримом будущем технология потребует локализовать бит информации в пределах атома вещества. И это полностью изменит вычислительную технику. Нас ждут перемены настолько радикальные, что к ним лучше заранее подготовить своё сознание.

Глава 5. Компьютеры настоящего и будущего

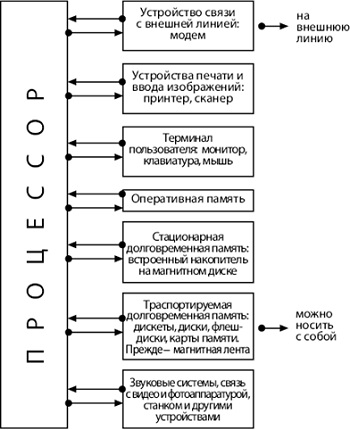
Архитектура компьютера, предложенная фон Нейманом, а до него — Чарльзом Бэббиджем, в общих чертах сохранялась довольно долго, пока её не вытеснила новая концепция общей шины (рис. 11). В этот начальный период проектирования ЭВМ перемены касались скорее дополнительных устройств, расширяющих возможности машины в части ввода/вывода информации, выхода в сеть и связи с различными агрегатами, которыми может управлять компьютер.

Рис. 11. Архитектура компьютера (архитектура фон Неймана)

Разработчики ясно понимали, что писать программы в том виде, в котором они выполняются компьютером, — самый неэффективный способ программирования. Это тормозило применение ЭВМ во всех областях, от теоретической физики до сферы управления финансами, транспортом и производством. Уже в середине 50-х годов XX века, выход был найден: применение алгоритмических языков, облегчающих программирование близких к математическому описанию задач. Первым из них стал язык Фортран (FORTRAN — FORmula TRANslation), разработка которого началась в 1954 г. компанией IBM под руководством Джона Бэкуса (1924–2007). За Фортраном последовал международный проект по созданию языка Алгол (ALGOL — ALGOrithmic Language), затем были разработаны языки Кобол, ЛИСП, ПЛ (PL-1) и т.д.

Для математического описания информационной системы нужна была понятная единица измерения. И Клод Шенон нашёл её. Единица информации есть двоичный код или двоичное цифра (binary digit), короче, бит. Шенон приводил стих из Матвея (5:37): «Но да будет слово ваше: да, да; нет, нет; а что сверх этого, то от лукавого». Бит как наименьшее возможное количество информации представляет собой количество неопределённости, возникающее при бросании монеты (подробнее см. Введение в теорию информации).

В 1989 году Джарон Ланир, один из известных деятелей киберкультуры и хакерского движения, ввёл словосочетание «виртуальная реальность». Хранение, обработка и передача данных с помощью кубитов (квантовых битов) придаст виртуальной реальности новую степень свободы. Если обычный бит может находиться в одном из двух состояний 0 или 1, то квантовая система, такая, как атом, может находиться в двух состояниях одновременно. В 1981 году Ричард Фейнман подчеркнул, что квантовый компьютер не будет машиной Тьюринга. Это будет что-то совершенно новое. Чарльз Беннет пишет: «Догадка Фейнмана состояла в том, что квантовая система в определённом смысле постоянно рассчитывает собственное будущее». Сет Ллойд, профессор Массачусетского технологического института, так иллюстрирует суть квантового компьютера: [1] «Классическое вычисление похоже на сольную партию одного музыкального инструмента — отдельные строки чистых тонов. Квантовое вычисление похоже на симфонию, состоящую из множества тонов, интерферирующих друг с другом».

Приводится краткая биография более 70 ученых, связанных с тематикой книги (с древности до наших дней).

[1] Полноценный квантовый компьютер является пока гипотетическим устройством, сама возможность построения которого связана с серьёзным развитием квантовой теории в области многих частиц и сложных экспериментов; эта работа лежит на переднем крае современной физики.