Один мой друг увлекается игрой в Fantasy Premier League (FPL), и все уши прожужжал мне про выбор игроков, и составление команды к каждому туру. В какой-то момент я сообразил, что выбор команды – это типичная задача для метода линейного программирования. Конечно, не всё так просто. Нужно, что называется, держать нос по ветру, и реагировать на тактические нюансы: травмы, ротацию игроков, две игры в туре и т.п. Но для первого приближения можно просто взять список игроков, применить имеющиеся ограничения, и найти оптимальный состав.
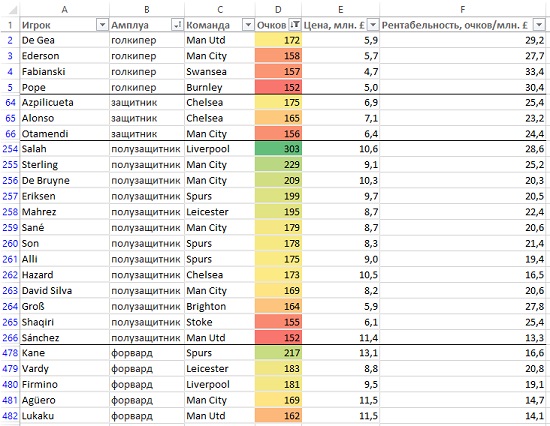
Рис. 1. Лидеры FPL сезона 2017/18 по набранным очкам
Скачать заметку в формате Word или pdf, модель в формате Excel
Общая статистика
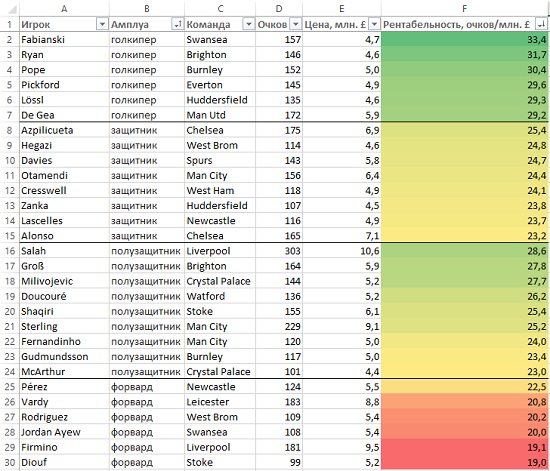
Я скачал итоги FPL сезона 2017/18, и подготовил данные для анализа. Для начала немного общей статистики. На рис. 1 показаны лидеры по амплуа, по набранным очкам. Здесь все, кто набрал в сезоне более 150 очков. Доминирование полузащитников впечатляет… Поскольку стоимость команды лимитирована 100 млн. £, возможно, еще больший интерес представляет рейтинг по рентабельности игроков = количество очков, набранное игроком за сезон, деленное на его стоимость (последняя взята на конец сезона), см. рис. 2. В таблице указаны вратари с рейтингом более 29 очком за млн. £, защитники и полузащитники с более чем 23 очками, и нападающие – более 19 очков. К одному знаменателю игроков различных амплуа привести не удалось, так как вратари существенно более рентабельны, чем защитники и полузащитники, а нападающие – полные аутсайдеры.
Рис. 2. Наиболее рентабельные игроки
Напрашиваются первые выводы: в команду следует отобрать 1 вратаря, максимальное число полузащитников, много защитников и мало нападающих.
Решение задачи линейного программирования
У меня на ПК установлена стандартная надстройка Поиск решения, поставляемая с Excel. Если вы с ней никогда не работали, но хотите разобраться, рекомендую Решение задачи линейного программирования в Excel. Если вас интересуют только выводы, вы можете пропустить технические детали.
К сожалению, установленная (бесплатная) версия надстройки допускает использование не более 200 искомых переменных. Всего в выгрузке FPL было 550 игроков, так что мне пришлось ее сократить. Я получил список из 198 игроков, исключив игроков с рейтингом менее 15, если при этом они набрали за сезон менее 80 очков. Еще раз: остались игроки, имеющие рейтинг более 15, а среди тех, у кого рейтинг менее 15, те, кто набрал 80 очков и более.
К сожалению, из-за того же ограничения в 200 переменных, я не смог включить в модель одновременный подбор, как основной команды, так и 4 запасных. Поэтому подбор запасных игроков я проводил вручную. Понятно, что среди запасных должен быть один вратарь и от 0 до 2 защитников, полузащитников и нападающих.
Модель для решения задачи линейного программирования (рис. 3) основана на списке из 198 игроков с указанием их амплуа, команды, набранных за сезон очков и стоимости на конец сезона. Также добавлена колонка Команда и Рентабельность (последняя нужна только для наглядности). В колонке Команда могут располагаться только бинарные значения – 0 или 1. Собственно первоначально я расположил в этой колонке нули, а в результате работы надстройки Поиск решения в ней появились 11 единиц для игроков, которые составили команду мечты.
Итак, модель ищет максимум для Суммы очков =СУММПРОИЗВ(D2:D199;F2:F199). При этом используется прорва ограничений. Первое – стоимость игроков основной команды =< 100 вычесть стоимость 4-х запасных. Если в качестве запасных использовать самых дешевых игроков в своем амплуа, то стоимость игроков основной команды варьируется в зависимости от расстановки в диапазоне 82,9–84,2. Следующая группа ограничений – точно заданная расстановка. Всего их семь (рис. 4). И наконец 20 ограничений, требующих чтобы от одной команды премьер-лиги было не более трех игроков.
Рис. 3. Модель для решения задачи линейного программирования; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
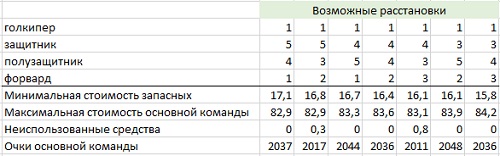
Рис. 4. Максимальная сумма очков в зависимости от расстановки
Результаты анализа
Максимальная сумма в зависимости от расстановки варьируется не очень сильно. Хотя небольшая корреляция с числом полузащитников всё же имеется. Для трех полузащитников суммы минимальны: 2011 и 2017; для 4-х – промежуточные: 2036, 2036, 2037; для пяти полузащитников – максимальные: 2044 и 2048. Также любопытно, что для расстановки с тремя полузащитниками не удается использовать все средства по максимуму, и есть небольшой остаток. Пусть вас не смущают полученные суммы, которые кажутся небольшими. Ведь они приведены без всех фишечек. Если просто удвоить очки Салаха за капитанство, то итог вырастет сразу на 303 очка. А суммы порядка 2350, пожалуй, будет достаточно для победы в большинстве лиг.
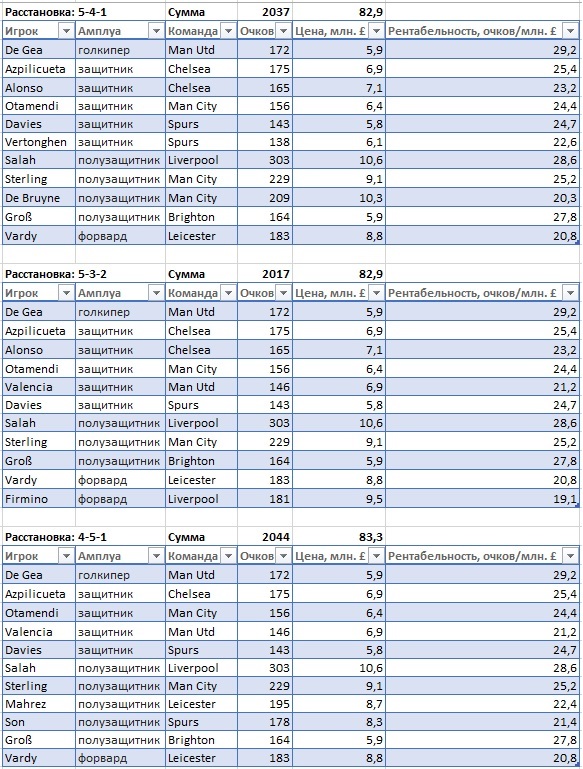
На рис. 5 приведены составы оптимальных команд при различных расстановках.
Рис. 5. Составы оптимальных команд при различных расстановках
Видно, что составы варьируются не слишком сильно, а в списке кандидатов есть свои лидеры (рис. 6). Во всех семи командах представлены: Otamendi, Sterling, Salah, Azpilicueta, Vardy. Во всех расстановках, где только один форвард, побеждает Vardy. Интересно, что лидерство De Gea не выглядит бесспорным, и его теснит Fabianski (к сожалению, Swansea покинул премьер-лигу, так что в следующем сезоне сделать ставку на Fabianski не получится). Так же до анализа казалось, что De Bruyne, Eriksen, Mahrez должны попадать в команду. Но все они уступили Groß, который хотя и набрал на 30–40 очков меньше упомянутых полузащитников, зато выиграл в цене.
Рис. 6. Число вхождений игроков в лучшие команды
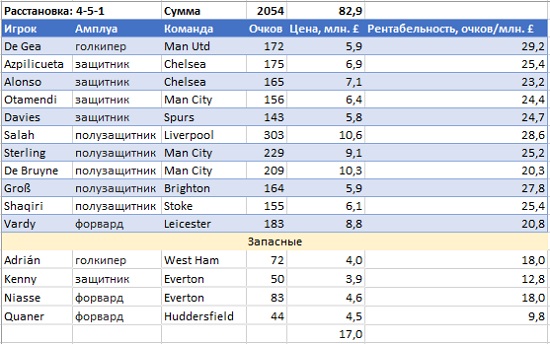
Следует отметить, что Поиск решения ведет себя не всегда понятно. Например, когда я вручную составил чуть более качественную скамейку запасных, стоимостью 17 млн. £, оптимальная команда набрала 2054 очка по сравнению с 2044 для расстановки 4-5-1 (рис. 7). К тому же остаток составил 0,1 млн. £. Я думаю, что для серьезных расчетов следует использовать более совершенное программное обеспечение.
Рис. 7. Основная команда и запасные
Дополнение от 7 июля 2020 г. Оказалось, что часть настроек в Поиске решения Excel я задал неверно. Новые настройки позволили приложению работать корректно.

Рис. 8. Настройки приложения Поиск решения: (а) первоначальные; (б) корректные



Спасибо, очень полезно.