Изучение вероятностей начинается там, где заканчивается классический курс теории вероятностей. В школе и вузе преподают частотную (комбинаторную, априорную) вероятность, или вероятность того, что определено. Эта теория редко находит применение за пределами казино. Человек устроен иначе. Мы имеем теории (мнения) по поводу всего на свете. Мы субъективно оцениваем вероятность тех или иных событий. Мы также можем изменить свое мнение при получении новых сведений. Это то, что мы делаем каждый день. Если вы встречаетесь с подругой у памятника Пушкину, вы понимаете, будет ли она вовремя, опоздает на 15 минут или полчаса. Но выйдя на площадь, и увидев 10 см свежего снега, вы обновите свои вероятности, чтобы учесть новые данные.
Новое знание = Исходные посылки + Новые данные
Предыдущая глава Оглавление Следующая глава
Скачать заметку в формате Word или pdf
Байес и Лаплас
Первым формулу, позволяющую вычислять вероятность одного события на основании знания вероятностей других событий, предложил Томас Байес – английский священник и математик, живший в XVIII веке. Единственная работа по этой теме была опубликована уже после его смерти в 1763 г. Байес предложил теорему, впоследствии названную в его честь. Однако более значительный вклад в разработку теории внес Пьер Симон Лаплас.
Байес и Лаплас перевернули подход к вероятностям с ног на голову. Обычная вероятность ведет от причин к следствиям. Если имеются различные причины, какова вероятность того или иного следствия? Байесовская вероятность отталкивается от следствия. Что-то уже произошло. Какова вероятность, что наше наблюдение проистекает из той или иной причины? Байесовский подход также называют проверкой гипотез.
Люди довольно плохо обращаются с вероятностями, и склонны впадать в две крайности:
- забывать об априорном знании (имевшемся до наблюдения), и реагировать на новости;
- не учитывать новую информацию, оставаясь в рамках своих первоначальных идей.
Теорема Байеса показывает, насколько следует изменить наше первоначальное убеждение в свете новых данных.
Как наблюдение влияет на априорное знание
Допустим, что 1% водителей садятся за руль в нетрезвом состоянии. ГИБДД предлагает использовать новый алкотестер. Если водитель нетрезв, то тестер в 98% случаев выявит это. К сожалению, если водитель трезв в 2% случаев тест даст ложное свидетельство. В ходе проверки водителя тестер выдал положительный результат. Какова вероятность того, что испытуемый действительно нетрезв? Не спишите читать дальше, попробуйте найти решение самостоятельно.
Из 1% нетрезвых водителей в 98% случаев тест даст положительный результат = 1%*98% = 0,98%. Для 99% трезвых водителей тест даст 2% положительных результатов = 99%*2% = 1,98%. Итого из 0,98% + 1,98% = 2,96% водителей с положительными результатами теста, только 0,98% – нетрезвые. Таким образом, вероятность того, что при положительном результате теста водитель действительно нетрезв составляет 0,98/2,96 = 33%. А вы думали, что 98% или около того?
Графически ситуацию можно представить следующим образом (для наглядности масштаб изменен):
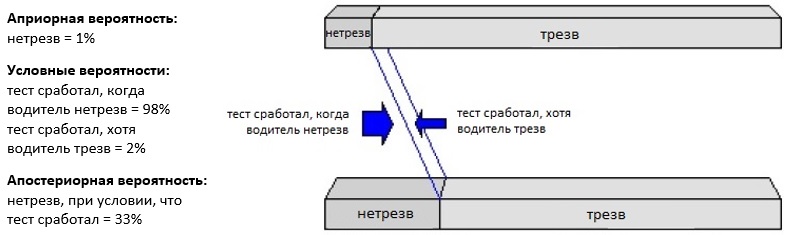
Апостериорная вероятность = априорная вероятность, скорректированная результатами теста
Скос вправо синей плоскости отражает то, как мы должны пересмотреть нашу априорную вероятность после положительной пробы. Первоначально мы обладали знанием о том, что лишь 1% водителей садятся за руль в нетрезвом состоянии. Однако проба дала положительный результат. С учетом этих новых данных вероятность того, что водитель нетрезв повысилась до 33%.
Нет ничего более практичного, чем хорошая теория
Почему так трудно научить компьютер видеть? Потому, что восприятие – не просто считывание визуальной информации, это активный контакт с миром. В голове есть представление о том, как будут выглядеть те или иные предметы. Человек сравнивает увиденное с моделями, уже существующими в голове. Чтобы компьютер мог «видеть» в него должны быть заложены эти модели.
То же верно и для компаний. Руководители должны иметь модели развития, какие-то планы и варианты. Иначе собранные наблюдения и данные не будут восприняты.
Иногда можно услышать, что существуют голые факты. Это иллюзия. Никаких чистых фактов нет. Чтобы обратить внимание на новую информацию, у нас в голове должна быть какая-то теория/идея на этот счет. Вы не замечали, как по-разному люди реагируют на одно и тоже сообщение!? Исследователи провели эксперимент: один и тот же сюжет показали палестинцам и евреям. Обе группы сделали диаметрально противоположные выводы!
Идеальный байесовский наблюдатель
Сами того не подозревая, мы являемся идеальными байесовскими наблюдателями. Эволюция встроила в мозг механизмы, корректирующие наши представления о мире на основании вновь поступающей информации. Более того, поскольку познание циклично, апостериорная вероятность предыдущего цикла будет априорной вероятностью следующего. Это позволяет нашему мозгу делать предсказания и отслеживать ошибки в них. С каждым новым циклом ошибка в предсказаниях уменьшается.
Однако в этом механизме случаются сбои. Например, в течение миллионов лет на Земле основным источником света было Солнце. Солнечный свет падает сверху. Значит вогнутость и выпуклость объектов мы определяем по расположению теней, и это прописано в нашем мозгу эволюцией:

Если вы перевернете рисунок вверх ногами, вогнутые пятнышки станут выпуклыми, а выпуклые — вогнутыми:

Современные технологии позволяют создавать множество изображений, которые мы интерпретируем неверно. Наше восприятие совмещает необработанные сигналы с нашим опытом. Наше восприятие — это предсказание того, что должно быть в окружающем нас мире.
Поиск виновного
Том Филлипс пишет, что мы часто меняем наши представления без должного обоснования, лишь на основе полученных результатов. Предположим, вы знаете, если у вас хорошая команда, то 90% проектов будут успешными, а 10% – неудачными. Если команда будет плохая, провалятся все проекты. Вы подбираете команду на новый проект… и он проваливается. Какова причина?
Предположим, вы провели этот эксперимент 100 раз. Вот какие результаты можно ожидать:

В чем причина провала проекта
Провал может быть связан как с подбором плохой команды (10-ка в первой строке) так и с неудачей хорошей команды (9-ка). Шансы почти 50 на 50. Так что будьте осторожны в своих выводах.
Байесовская революция
Байесовская математика довольно сложна, и ее широкое применение началось лишь с эрой ПК. Однако сегодня, пожалуй, это магистральное направление в науке и бизнесе. Машинное обучение, искусственный интеллект, фильтрация спама, распознавание лиц, медицинские исследования, нейросети, прогнозные модели и многое другое.
Идеи Байеса для менеджеров: https://baguzin.ru/wp/?p=6355; в конце заметки представлена подборка литература по Байесовскому подходу.
Пьер Симон Лаплас. Опыт философии теории вероятностей. – М.: Книжный дом «ЛИБРОКОМ», 2011. — 208 с. (книга впервые опубликована в 1814 г.; на старорусский язык книга переведена в 1908 г.; настоящее издание является репринтным). Конспект: https://baguzin.ru/wp/?p=16017
Крис Фрит. Мозг и душа: Как нервная деятельность формирует наш внутренний мир. – М.: Астрель: CORPUS, 2010. — 336 с. Конспект: https://baguzin.ru/wp/?p=11859
Тим Филлипс. Управление на основе данных. Как интерпретировать цифры и принимать качественные решения в бизнесе. – М.: Манн, Иванов и Фербер, 2017. – 192 с. Конспект: https://baguzin.ru/wp/?p=17283