Когда я поступил в институт (в конце 1970-х), очень популярной была игра Быки и коровы. Так совпало, что в это время я прочитал математическую новеллу Альфреда Реньи о теории информации. Я узнал, как измерять информацию, как задавать вопросы, чтобы получать максимум информации, и разработал алгоритм, позволявший отгадывать числа в среднем за 5 вопросов.
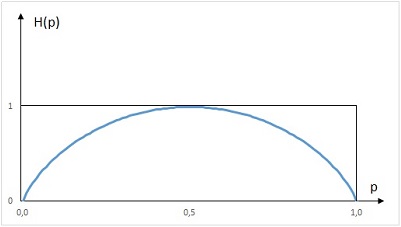
Зависимость количества информации (энтропии) от вероятности одного из двух событий
Предыдущая глава Оглавление Следующая глава
Скачать заметку в формате Word или pdf
Открытие Шеннона
Клод Шеннон во время второй мировой войны занимался криптографией в лаборатории Бела (Bell Labs). Его работы были рассекречены и опубликованы уже после войны. В них Шеннон дал несколько определений информации, и все они казались парадоксальными:
- Информация – это убыль неопределенности, которую можно измерить, сосчитав количество возможных сообщений. Если возможно лишь одно сообщение, неопределенности нет. Нет и информации. Вот почему не требуется ответ на риторический вопрос))
- Информация – это мера неожиданности. Если за буквой t (в английском языке) следует h, то передается не так много информации, потому что вероятность появления h после t высока.
- Информация – это энтропия. Это было самым странным и самым мощным определением из всех. Для физика энтропия – мера неопределенности состояния физической системы — одного из тех состояний, в которых может находиться система. Для ученого, занимающегося теорией информации, энтропия – мера неопределенности сообщения — одного сообщения из тех, которые могли появиться. Это не просто совпадение: природа дает одинаковые ответы на одинаковые вопросы.
Количество информации
Для информации и неопределенности Шеннон предложил новую единицу измерения – двоичную цифру или бит (сокращение от англ. binary digit). Бит – количество информации (неопределенности), содержащаяся в опыте, имеющем два равновероятных исхода, например, подбрасывание монеты. До опыта неопределенность составляла 1 бит, в результате опыта извлекается информация равная так же 1 бит.
Допустим случайная величина может принимать два значения, например, ответы «да» и «нет». Обозначим вероятность первого ответа p, тогда вероятность второго равна (1 – p). В этом случае энтропию случайной величины (то есть меру неопределенности, существовавшей до наблюдения), можно вычислить по формуле Шеннона:
H(p) = –p∙log2р – (1 – p)∙log2(1 – р),
На графике (см. выше) показано, как меняется энтропия при изменении р. Если вероятность равна 0 или 1, неопределенности нет, а энтропия H(p) = 0. Когда вероятность равна 0,5, энтропия максимальна H(p) = 1. Если ответ может принимать лишь два значения, то он содержит один бит информации только тогда, когда оба его значения равновероятны. Во всех остальных случаях количество информации, содержащейся в ответе, меньше одного бита. Таким образом, в игре «Быки и коровы» вопрос нужно задавать так, чтобы ответ на него давал максимальное количество информации. Для этого вопрос нужно формировать так, чтобы вероятности различных ответов были по возможности близкими. Кроме того, вопрос должен быть таким, чтобы ответ на него не содержал информацию, полученную из предыдущих вопросов.
Информация как алгоритм
Рассмотрим два двоичных числа по пятьдесят знаков каждое:
А: 01010101010101010101010101010101010101010101010101
Б: 10001010111110101110100110101000011000100111101111
Теория вероятности не дает никаких оснований считать, что строка Б более случайна, чем строка А, потому что случайный процесс может дать любую из строк. Академик Андрей Николаевич Колмогоров рассматривал бы эти строки как сообщения. Он спросил бы: «Сколько информации содержит каждая из строк?» У оператора телеграфа, посылающего сообщение А, есть способ упростить работу: он может передать «Повторить 01 двадцать пять раз». Оператору, передающему сообщение Б, придется передать каждый знак, потому что каждый знак в этом сообщении абсолютно непредсказуем; каждый знак несет один бит информации. Колмогоров предложил оценивать количество информации через длину оптимального алгоритма.
Избыточность естественных языков
Русский алфавит содержит 33 буквы и пробел. Если бы появление всех символов было равновероятным, то энтропия опыта, заключающегося в получении одной буквы составила бы Н0 = log234 = 5,09. На самом доле, появление в сообщении разных букв совсем не одинаково вероятно.

Относительная частота букв русского алфавита
С учетом частоты получим для энтропии одной буквы значение:
Н1 = – 0,175∙log20,175 – 0,0905∙log20,0905 – 0,0697∙log20,0697 – … – 0,0003∙log20,0003 = 4,35
Видно, что неравномерность появления различных букв алфавита приводит к уменьшению информации, содержащейся в одной букве, на 5,09 – 4,35 = 0,74 бит.
Более того, в осмысленном тексте последовательные буквы вовсе не независимы друг от друга. Наличие дополнительных закономерностей приводит к дальнейшему уменьшению степени неопределенности (энтропии) одной буквы. Но и это еще не всё. Знание двух предшествующих букв еще более уменьшает неопределенность опыта, состоящего в дальнейшем уменьшении НN, где N – число букв в последовательности. Разность R = 1 – НN/H0 Шеннон назвал избыточностью языка. Избыточность русского языка превышает 50%.
Не всё измеряется в битах
Следует помнить, что Шеннон решал конкретные задачи, связанные с качеством связи. Не вся информация может быть оценена в битах. Маршалл Маклюэн говорит, что письменный текст предлагает нам узкий канал коммуникации. Напротив, в устной речи лицом к лицу, оживленном жестами и прикосновениями, задействованы все чувства, а не только зрение или слух. Чем больше число задействованных чувств, тем выше вероятность передачи точной копии ментального состояния говорящего. Более того, великое художественное произведение и результат работы генератора текстов, могут измеряться одинаковым числом бит. Но ведь ясно же, что тексты информационно не равны.
Литература
Альфред Реньи. Дневник. Записки студента по теории информации // Альфред Реньи. Трилогия о математике. – М.: Мир, 1980. – С. 199–284. Конспект: https://baguzin.ru/wp/?p=2562
Разработка оптимальной стратегии игры «Быки и коровы» на основе теории информации: https://baguzin.ru/wp/?p=2574
Джеймс Глик. Информация. История. Теория. Поток. – М.: АСТ, Corpus, 2013. – 576 с. Конспект: https://baguzin.ru/wp/?p=13062
Исаак Яглом, Акива Яглом. Вероятность и информация. М.: Наука, 1973. – 512 с. Конспект: https://baguzin.ru/wp/?p=18059
А.Н. Колмогоров. Три подхода к определению понятия «количество информации» // Проблемы передачи информации. 1965, т. 1, вып. 1, стр. 3–11