Тема нелинейной динамики не оставляет меня равнодушной. С одной стороны, серьезные научные книги с большим количеством формул я всё же отклоняю, а вот популярные издания на эту тему стараюсь не пропускать. На мой взгляд, избыточная детерминированность взглядов большинства менеджеров не идет на пользу делу. Так что я вношу посильный вклад в приобщение студентов и бизнес-сообщества к идеям случайности.
На французском языке книга впервые была опубликована в 1990 г. Почему на Ozon.ru эта книга объемом 192 стр. в мягкой обложке стоит 980 руб. для меня осталось загадкой.
Ранее на эту тему мною опубликованы: Джеймс Глейк Хаос. Создание новой науки, Илья Пригожин Порядок из хаоса, Путь в синергетику. Экскурс в десяти лекциях.
Давид Рюэль. Случайность и хаос. – М.: Издательство «Регулярная и хаотическая динамика», 2001. – 192 с.
Скачать конспект (краткое содержание) в формате Word или pdf
Купить бумажную книгу в Ozon
Законы физики имеют детерминистический характер. Тем не менее, случайность может присутствовать в описании вселенной. Мы увидим, что на предсказуемость будущего накладываются суровые ограничения.
Глава 1. Случайность. Научное исследование случайности началось с анализа рулетки Блезом Паскалем, Пьером Ферма, Христианом Гюйгенсом и Якобом Бернулли. Этот анализ породил исчисление вероятностей. Центральное место в нем занимает тот факт, что при подбрасывании монетки очень большое число раз вероятность выпадения орла (или решки) приближается к 50 процентам. Таким образом, тогда как результат однократного подбрасывания монетки является совершенно неопределенным, длинный ряд подбрасываний создает почти определенный результат. Этот переход от неопределенности к почти определенности, когда мы наблюдаем длинный ряд событий или большие системы, является основной мыслью в изучении случайности.
Можно ли измерить хаотичность (случайность)? Да, например, в рамках статистической механики — области физики, созданной примерно в 1900 году австрийцем Людвигом Больцманом и американцем Дж. Уиллардом Гиббсом. Количество случайности, присутствующее в литре воздуха или килограмме свинца при определенной температуре, измеряется энтропией этого литра воздуха или килограмма свинца, и сейчас у нас есть методы точного определения энтропии веществ. С другой стороны, теория информации, созданная американским математиком Клодом Шенноном в конце 1940-х годов, позволяет нам измерить информацию сообщений (подробнее см. Введение в теорию информации).
Глава 2. Математика и физика. Отправную точку математической теории составляют несколько основных утверждений в отношении определенного количества математических объектов. Начиная с основных посылок, человек, с помощью чистой логики, пытается вывести новые утверждения, называемые теоремами. Математике свойственно глубокое единство. Она являет собой не просто набор отдельных теорий, как-то: теория множеств, топология и алгебра, — каждая из которых имеет свои собственные основные допущения; математика — это единое целое.
Цель физики — извлечь смысл из мира, нас окружающего. Обыкновенно, если вы — физик, то вы не станете пытаться понять все враз. Вы скорее будете разглядывать разные кусочки реальности по очереди. Умение перепрыгивать от одной теории к другой — важная часть занятий физикой. Физика обладает фундаментальным единством, потому что она описывает уникальную физическую вселенную, в которой мы живем. Математика своим единством обязана логической связи между различными математическими теориями. Физические же теории, напротив, не нуждаются в логической согласованности; они обладают единством, в силу того, что описывают одну и ту же физическую реальность.
Глава 3. Вероятности. Научное толкование случайности начинается, когда мы вводим вероятности. Успех любого нашего предприятия зависит от обстоятельств, одни из которых определенны, а другие — нет. Поэтому важно правильно оценивать вероятность неопределенных обстоятельств, а чтобы сделать это, нужна физическая теория вероятностей. Я настаиваю, что эта теория должна быть физической, потому что недостаточно просто иметь возможность подсчитать вероятность, нужно также уметь сравнить полученные результаты с физической реальностью на уровне операторов.
Теория вероятностей — это искусство игры с утверждениями типа prob(«А») = 0,9, что означает, что вероятность события «А» равна 90%. Событие «не А», с математической точки зрения, — представляет собой всего-навсего новый комплект символов. Событие «не А» соответствует факту, что событие «А» не происходит.
Теперь введем, помимо «А», новое событие «В». Событие «А или В» физически соответствует тому, что происходит событие «А», или происходит событие «В», или происходят оба события «А» и «В». Событие «А и В» соответствует тому, что происходят оба события «А» и «В». Теперь мы может завершить математическое представление вероятностей, перечислив три основных утверждения, или правила:
(1) prob(«не А») = 1 – prob(«A»);
(2) если «А» и «В» – взаимоисключающие события, то prob(«A или В») = prob(«A») + prob(«B»);
(3) если «А» и «В» – независимые события, то prob(«A и В») = prob(«A») x prob(«B»).
Глава 4. Лотереи и гороскопы. Когда видишь, каким успехом пользуются лотереи и гороскопы, то понимаешь, насколько поведение большинства людей отличается, в отношении вероятностей, от того, что должно было бы подсказывать здравое научное мышление. В лотерее, чем больше билетов вы покупаете, тем больше денег вы теряете; это имеет место и в более сложных лотереях, поскольку все они придуманы для того, чтобы высасывать деньги из игроков ради выгоды организатора.
Введем еще одно утверждение из исчисления вероятностей, которое представляет собой измененную формулировку правила (3), приведенного выше:
(4) если «А» и «В» независимы, то prob(«В», зная, что «А» реализуется) = prob(«B»).
Другими словами, знание того, что событие «А» реализуется, совершенно ничего не говорит нам о событии «В», и вероятность последнего события остается равной prob(«B»).
Гороскопы гораздо тоньше и интереснее лотерей, потому что в этом случае мы не в состоянии сразу увидеть роль вероятностей. Обыкновенно, гороскоп сообщает вам, что если вы — Лев, то на этой неделе планеты располагаются благоприятным для вас образом, так что вы будете удачливы в любви и играх, но если вы — Рыбы, то вы должны, чего бы вам это ни стоило, избегать полетов самолетом, сидеть дома и заботиться о своем здоровье. Астрономы и физики сказали бы, что утверждения «X — Лев» и «X будет удачлив в играх на этой неделе» — события независимые. То же самое касается и утверждений «X — Рыбы» и «X попадет в катастрофу, если на этой неделе будет путешествовать самолетом». В действительности, сложно придумать лучшие примеры событий, которые никак не связаны друг с другом и потому независимы с позиций теории вероятностей. Следовательно, мы можем применить вышеприведенное правило (4) и сделать вывод, что вероятность того, что X выиграет в лотерею, одинакова, вне зависимости от того, является X Львом или нет. Аналогичным образом, опасности путешествия самолетом для Рыб ничем не отличаются от опасностей для человека любого другого знака зодиака. В заключение добавлю: гороскопы совершенно бесполезны.
Сторонники астрологии отрицают, что два факта: «X — Лев» и «X будет удачлив в играх на этой неделе» — события независимые. Однако, наука опровергла наличие связей. Почему же иногда можно наблюдать некоторую связь? Это следствие самосбывающегося пророчества (подробнее см Р. Мертон. Самоисполняющееся пророчество. Теорема Томаса). Если наш друг X любит читать гороскопы, если он или она несколько доверчивы, то вера, что на этой неделе нам «повезет в любви», повышает нашу уверенность в себе, а потому и нашу удачу. Неизбежный вывод состоит в том, что мы зачастую принимаем иррациональные решения, основанные на случайных совпадениях, которые мы принимаем за «знамения», или предсказания.
Глава 5. Классический детерминизм. Механика Ньютона дает полностью детерминистическую картину мира: если мы знаем состояние вселенной в какое-то (произвольно выбранное) начальное время, мы должны суметь определить ее состояние в любой другой момент времени. На первый взгляд, детерминизм не оставляет места случайности. Однако, дилемма «случайность против детерминизма» — это ложная проблема. Если начальное состояние нашей системы может иметь определенное распределение вероятностей, то состояние нашей системы также будет хаотичным и в любое другое время, а ее хаотичность будет описана новым распределением вероятностей, причем последнее можно будет вывести детерминистически, используя законы механики. На практике состояние системы в начальное время никогда не известно с абсолютной точностью.
Глава 6. Игры. Полезность хаотического поведения в играх является важным замечанием как с философской, так и с практической точки зрения (по существу, мы обязаны им французу Эмилю Борелю и американцу венгерского происхождения Джону фон Нейману).
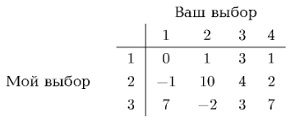
Некоторая игра определяется таблицей выплат (рис. 1).
Рис. 1. Матрица игры
У меня есть несколько выборов (скажем, 3), у вас тоже есть несколько выборов (скажем, 4), и мы делаем свой выбор независимо. Например, я выбрал 2, а вы — 4, что дает выплату в 2 доллара, которые вы должны заплатить мне. Если я выберу 3, а вы выберете 2, то выплата составит минус два доллара, т. е. я должен заплатить два доллара вам. В 1928 году Джон фон Нейман доказал, что мой максимум вашего минимума равен вашему минимуму моего максимума (это знаменитая теорема о минимаксе). Средняя выплата – эта проблема общего типа, называемого линейным программированием (подробнее см. Решение задачи линейного программирования в Excel).
Глава 7. Чувствительная зависимость от начальных условий означает, что небольшое изменение в состоянии системы при начале отсчета времени создает последующую перемену, которая экспоненциально растет во времени. В таком случае маленькая причина имеет большое следствие.
Глава 8. Адамар, Дюгем и Пуанкаре. Является ли чувствительная зависимость от начальных условий исключением или правилом среди динамических систем? Знаменитый математик Анри Пуанкаре в своей книге «Наука и метод», опубликованной в 1908 году пишет, что долгосрочная непредсказуемость примиряет случайность и детерминизм: Очень маленькая причина, которая от нас ускользает, определяет значительное следствие, которое мы не можем проигнорировать, и тогда мы говорим, что это следствие вызвано случайностью. Пуанкаре увидел несколько способов, как классическое детерминистическое описание мира может естественным образом привести к вероятностной идеализации. Одним из этих способов была чувствительная зависимость от начальных условий.
Одним из примеров Пуанкаре была метеорология, и он утверждает, что хорошо известная ненадежность прогнозов погоды вызвана чувствительностью к начальным условиям вкупе с несколько неточным знанием, которое мы обязательно имеем в отношении начальных условий. В результате этого, эволюция погоды кажется вызванной случайностью. В наше время самым поразительным моментом анализа Пуанкаре кажется его современность – циркуляция атмосферы была одним из основных объектов изучения динамических систем в последние годы.
Глава 9. Турбулентность: моды. Многие предметы, нас окружающие, начинают совершать колебания или вибрировать, когда мы по ним ударяем: маятник, металлический стержень, струну музыкального инструмента очень легко привести в периодическое движение. Такое периодическое движение является модой.
Теория Ландау-Хопфа на первый взгляд, дает удовлетворительное описание возникновения турбулентности: то, как жидкость становится турбулентной при увеличении силы, приложенной к ней извне. И все же, объяснение Ландау меня не удовлетворило, и я вместе с Флорисом Такенсом, голландским математиком, предпринял исследование, результаты которого изложил в статье «О природе турбулентности». Мы объяснили, почему, на наш взгляд, картина турбулентности, представленная Ландау, неверна, и предложили нечто другое, что содержало странные аттракторы.
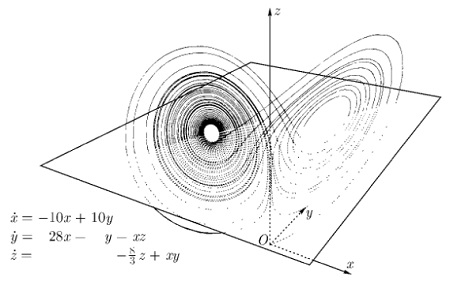
Глава 10. Турбулентность: странные аттракторы. Эдвард Лоренц — метеоролог, который работал в Массачусетском технологическом институте. Будучи метеорологом, он интересовался явлением атмосферной конвекции, которое состоит в следующем: Солнце нагревает Землю, вследствие чего низкие слои атмосферного воздуха становятся теплее и легче, чем более высокие его слои. Это вызывает движение легкого и теплого воздуха вверх, а более плотного и холодного воздуха — вниз. Эти движения и образуют конвекцию. Воздух, как и рассмотренная ранее вода, является жидкостью, поэтому его следует описывать точкой в бесконечномерном пространстве. С помощью грубого приближения Эд Лоренц заменил правильную временную эволюцию в бесконечномерном пространстве временной эволюцией в трехмерном пространстве, которую он мог изучать с помощью компьютера. Компьютер выдал объект, который изображен на рисунке 2 и в настоящее время известен как аттрактор Лоренца. Если бы начальное положение хоть чуть-чуть изменилось, то детали рисунка 2 изменились бы полностью. Общий аспект остался бы неизменным, но количество последовательных обходов правого и левого ушей стало бы совершенно другим. Так происходит потому, — как понял Лоренц, — что временная эволюция рисунка 2 обладает чувствительной зависимостью от начальных условий. Пуанкаре сделал точно такое же замечание гораздо раньше (Лоренц этого не знал).
Рис. 2. Аттрактор Лоренца
Странность аттрактора исходит из следующих признаков: во-первых, они не являются гладкими кривыми или поверхностями, но имеют «нецелую размерность» — или, как это называет Бенуа Мандельброт, — они являются фрактальными объектами (см., например, Сергей Деменок. Просто фрактал). Далее, и это еще более важно, движение на странном аттракторе выказывает чувствительную зависимость от начальных условий. И наконец, при том, что странные аттракторы имеют лишь конечную размерность, временной анализ частот выявляет континуум частот.
Глава 11. Хаос: новая парадигма. Сначала несколько, а потом много физиков и математиков начали работать над странными аттракторами и чувствительной зависимостью от начальных условий. Была признана важность идей Эдварда Лоренца. Возникла новая парадигма, которая получила имя — хаос, — данное ей Джимом Йорке, прикладным математиком, работающим в университете Мэриленда. То, что мы сейчас называем хаосом, является временной эволюцией с чувствительной зависимостью от начальных условий.
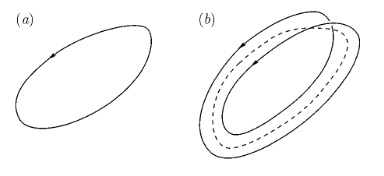
На фоне теории хаоса, благодаря своей особой красоте и значимости, особенным образом выделяется один результат — каскад удвоений периода, открытый Фейгенбаумом. При изменении сил, действующих на физическую динамическую систему, часто можно наблюдать удвоение периода (рис. 3). Периодическая орбита заменяется другой, близкой ей, но такой, что для возвращения в исходную точку необходимо обойти эту орбиту дважды. Таким образом, время, необходимое для возвращения в исходную точку, — называемое периодом — примерно удваивается.
Рис. 3. Удвоение периода: (а) проекция периодической орбиты; (б) эта орбита заменяется другой, которая примерно в два раза длиннее.
Интересно, что удвоение периода может происходить снова и снова (рис. 4).
Рис. 4. Каскад удвоений периода. При изменении сил, приложенных к системе, удвоения периода происходят при значениях, обозначенных A1, А2, A3,…, скапливающихся в А∞
На горизонтальной оси отложены силы, приложенные к системе, а точки, в которых происходят последовательные удвоения периода, — это A1, А2, A3, …; они скапливаются в точке, обозначенной А∞. Посмотрим теперь на интервалы А1А2, А2А3, А3А4, А4А5, и т.д. Они имеют свойство, что их последовательные отношения остаются почти постоянными:
Точнее, имеет место следующая замечательная формула:
Один интересный аспект каскада удвоений периода состоит в том, что когда вы заметите его в ходе эксперимента, то не спутаете ни с чем другим. Кроме того, известно, что за каскадом (справа от А∞ на рисунке 4) существует хаос. Следовательно, наблюдение каскада Фейгенбаума в гидродинамике является особенно убедительным доказательством того, что моды должны уступить хаосу.
Через несколько лет после всего, что я только что описал, хаос вошел в моду, и по этой теме начали организовывать международные конференции. Затем хаос удостоили титула нелинейной науки и для его изучения начали создавать различные институты. Появились новые научные журналы, которые целиком и полностью посвящались нелинейной науке.
Глава 12. Хаос: последствия. Количественные изучения хаоса в системе требуют количественного понимания динамики этой системы. Это понимание часто основано на хорошем знании основных уравнений эволюции, которые можно точно проинтегрировать с помощью компьютера. В биологии, а также в гуманитарных науках мы не знаем основных уравнений движения (модели, которые качественно согласуются с данными, недостаточно хороши). Вследствие этого сложно получить длинный временной ряд с хорошей точностью, да и динамика обыкновенно является не простой. Более того, во многих случаях (экология, экономика, социальные науки) основные уравнения эволюции, чем бы они ни были, медленно изменяются со временем (система «обучается»). Для таких систем влияние хаоса остается в настоящее время на уровне скорее научной философии, нежели количественной науки.
Глава 13. Экономика. Учебники по экономике главным образом занимаются равновесными ситуациями между экономическими агентами, обладающими идеальным предвидением. Эти учебники могут создать у вас впечатление, что роль законодателей и правительственных чиновников состоит исключительно в том, чтобы найти и реализовать равновесие, которое будет особенно благоприятно для сообщества. Однако примеры хаоса в физике учат нас тому, что определенные динамические ситуации создают не равновесие, а скорее хаотическую, непредсказуемую временную эволюцию. Законодательные и правительственные чиновники, таким образом, сталкиваются с возможностью того, что их решения, целью которых является создание лучшего равновесия, на самом деле приведут к бурным и непредсказуемым флуктуациям, следствия которых могут оказать катастрофическими. Сложность современной экономики способствует именно такому хаотическому поведению, а наше теоретическое понимание в этой области остается весьма ограниченным.
Глава 14. Исторические эволюции. Идеи хаоса наиболее естественным образом применяются в отношении временных эволюций с «вечным возвратом». Это временные эволюции систем, которые снова и снова возвращаются практически к тем же ситуациям. Другими словами, если система в определенное время находится в определенном состоянии, она произвольно вернется почти в то же самое состояние в более позднее время. Вечный возврат можно наблюдать в умеренно сложных системах, но не в очень сложных.
Если мы теперь посмотрим на сложный мир, который нас окружает, на эволюцию жизни, на историю человечества, то нам не стоит ожидать вечного возврата. Вечный возврат будет применим к частным аспектам мира, к малым подсистемам, но не к глобальной картине. Глобальная картина следует однонаправленному историческому развитию, для которого на данный момент полезной математической идеализации у нас нет.
История систематически создает непредсказуемые события с важными долгосрочными следствиями. Приведем пример. Все известные живые организмы связаны друг с другом и разделяют, в сущности, один и тот же генетический код. Если говорить конкретно, то генетическая информация записана как последовательность символов (или «баз»), которые являются элементами четырехбуквенного алфавита, и каждая группа трех последовательных баз является кодом (в принципе) для данного «кирпичика» протеина (т.е. аминокислоты). Кодирование от базовых триплетов до двадцати различных аминокислот происходит произвольно. Если бы жизнь развивалась независимо на другой планете, то никто не стал бы ожидать, что она использует тот же самый генетический код. В процессе эволюции, из- за мутаций и естественного отбора, структура живых организмов претерпела существенные изменения, но генетический код является настолько основным, что остался, в сущности, тем же на всех уровнях: от бактерий до человека. Видимо, еще тогда, когда жизнь делала свои первые неуверенные шаги, произошла эволюция генетического кода. Когда на определенном этапе развилась эффективная система, она уничтожила всех своих соперников и осталась одна.
Глава 15. Кванты: концептуальная основа. Великий философский интерес квантово-механического описания мира состоит в том, что существенную роль в этом описании играет случайность. Вернер Гейзенберг в 1926 году доказал, что m Δx Δv ≥ h/4π, где m — масса частицы, Δx – неопределенность в положении частицы, Δv – неопределенность в скорости частицы, h — очень маленькая величина, которая называется постоянной Планка. Вышеприведенное неравенство — это знаменитое соотношение неопределенностей Гейзенберга. Оно отчетливо демонстрирует вероятностный характер квантовой механики.
Глава 16. Кванты: счет состояний. Энтропия (Н) измеряет количество хаотичности, присутствующей в системе и может быть измерена, как логарифм числа состояний: Н = k*log(число состояний), где k – коэффициент пропорциональности.
Глава 17. Энтропия. Второй закон термодинамики: в каждом физическом процессе энтропия остается постоянной или увеличивается, и если она увеличивается, то процесс необратим. В чем же смысл энтропии? Почему она всегда увеличивается и никогда не уменьшается? Именно эти проблемы и пытался решить Больцман.
Глава 21. Информация. Длина сообщения указывает на содержащееся в нем количество информации. Если ваше сообщение записано на английском языке, вы можете сжать его, пропуская гласные, и сообщение, как правило, остается понятным. Это означает, что письменный английский язык избыточен.
Ссылаясь на то, что мы уже говорили об энтропии, мы также могли бы записать
количество информации = К*log(количество разрешенных посланий).
Количество информации обыкновенно выражается в двоичных разрядах или битах. Это означает, что вы переводите сообщение в алфавит, содержащий две «буквы»: 0 и 1, а затем измеряете его длину.
Сообщение можно сжать, если оно является избыточным, но информация не сжимается.
Определение информации было создано после определения энтропии, измеряющей количество хаотичности, присутствующей в системе. Почему информация должна измеряться хаотичностью? Просто потому, что, выбирая одно сообщение в классе всех возможных, вы рассеиваете хаотичность, присутствующую в этом классе.
Глава 22. Сложность, алгоритмическая. Информация стала одной из наиболее успешных концепций современной науки. Помимо всего прочего, информация позволяет нам подойти к проблеме сложности. Некоторая сущность является сложной, если она заключает в себе какую-то информацию, которую сложно получить. Существуют такие концепции сложности, которые можно развить с помощью чисто математических предпосылок – концепция алгоритмической сложности.
Британский математик Алан Тьюринг изобрел и точно описал компьютер, который хорошо подходит для теоретического изучения алгоритмов. Машина Тьюринга имеет конечное число внутренних состояний: несколько так называемых активных состояний и одно состояние остановки.
Алгоритм представляет собой нечто, что можно реализовать на компьютере, причем мы можем воспользоваться даже очень примитивным типом компьютера, который называется машиной Тьюринга. При наличии конкретной задачи ее можно выполнить с помощью эффективных или неэффективных алгоритмов, в зависимости от того, сколько циклов машины Тьюринга потребуется для получения ответа. Тогда алгоритмическая сложность задачи зависит от наличия эффективных алгоритмов ее решения (подробнее см. Чарльз Петцольд. Читаем Тьюринга).
Глава 23. Сложность и теорема Гёделя. В 1931 году логик Курт Гедель, австриец по национальности, опубликовал то, что, вероятно, являет собой единственный наиболее глубокий концептуальный результат, полученный человечеством в двадцатом веке. Чтобы понять открытие Геделя, следует знать, что великая мечта всех математиков — основать математику на четко определенных правилах вывода и конечном числе абсолютно явных фундаментальных утверждений, называемых аксиомами. Пиком великой мечты математиков была надежда на то, чтобы для каждого имеющего смысл утверждения о целых числах систематическим образом можно было бы решить, является оно истинным или ложным.
Гедель показал, что если установить правила вывода и любое конечное число аксиом, то существуют имеющие смысл утверждения, которые нельзя ни доказать, ни опровергнуть. Точнее, допустим, что аксиомы, принятые для целых чисел, являются непротиворечивыми, т. е. допустим, что, применяя правила вывода, вы никогда не сможете доказать ни то, что утверждение является истинным, ни то, что оно является ложным. Кроме того, существуют истинные свойства целых чисел3, которые невозможно вывести из аксиом. И если принять любое такое свойство в качестве новой аксиомы, то останутся другие недоказуемые свойства.
Открытие теоремы о неполноте привело к прогрессивному изменению описания математики. Ранее существовала великая надежда на то, что некоторый конечный набор истинных утверждений (называемых аксиомами) образует базис, из которого можно будет выводить все истинные утверждения о целых числах. Теперь нам известно, что набор всех свойств целых чисел (т. е. набор всех истинных утверждений о них) не имеет конечного базиса.
Глава 25. Интеллект. Наш мозг и интеллект имеют основу, состоящую из аппарата приспособлений, точно приспособленного к выживанию в окружающей среде определенного типа. Совсем недавно к этим основным навыкам мозга эволюция добавила некоторые функции более высокого порядка, действующие очень гибко. Наличие этих более высоких функций оказалось безусловно полезным, вследствие чего их развитию поспособствовала естественная эволюция.
Глава 26. Эпилог: наука. Случайность и хаотичность кажутся не особенно обещающими темами для точного исследования, и многие ранние ученые фактически их избегали. И тем не менее, сейчас они играют центральную роль в нашем понимании природы вещей.
Математиками, как и физиками, движет сильное очарование. Исследование в математике трудно и болезненно для интеллекта, даже если оно удачно, и вы не стали бы заниматься им, не испытывая очень сильного к тому побуждения.

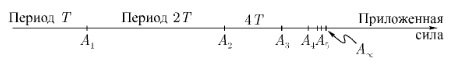
Уведомление: simpleNewz - Путь воина RSS Feed
Ждем, кто первый придумает теорию для связи квантового уровня (и принципа неопределенности) с макро-уровнем. Пока нету :)))
Спасибо за обзор.