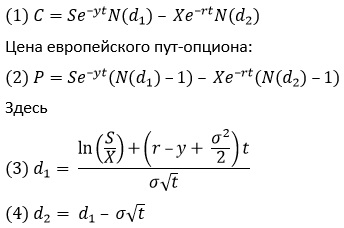В начале 70-х годов прошлого века экономисты Фишер Блэк, Майрон Шоулз и Роберт Мертон вывели формулу ценообразования опционов Блэка–Шоулза, которая позволяет получить оценку европейских колл- и пут-опционов. За свою работу Шоулз и Мертон были удостоены Нобелевской премии по экономике в 1997 г. (Блэк умер до 1997 г., а Нобелевская премия не присуждается посмертно.) Их научный труд произвел революцию в области корпоративных финансов. В данной заметке приведены основные положения этой важной научной работы, а также показано, как рассчитать стоимость опциона с помощью Excel.[1]
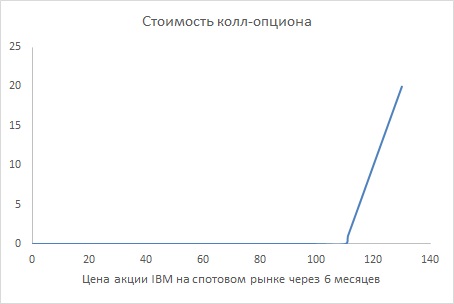
Рис. 1. Стоимость колл-опциона
Скачать заметку в формате Word или pdf, примеры в формате Excel
Основные сведения об опционах
Колл-опцион дает владельцу опциона право купить акцию (или иной актив, например, валюту) по цене исполнения. Пут-опцион дает владельцу опциона право продать акцию по цене исполнения.
Американский опцион может быть исполнен не позднее даты, известной как дата исполнения (часто называемой датой истечения срока действия опциона). Европейский опцион может быть исполнен только в последний день срока его действия.
Давайте рассмотрим итоги сделки по приобретению шестимесячного европейского колл-опциона на акции IBM с ценой исполнения 110 долларов. Пусть P — это курс акции IBM через шесть месяцев. Выигрыш от колл-опциона на эти акции составит 0 долларов, если P < 110 (зачем исполнять опцион, если цена акций на спотовом рынке ниже цены исполнения!?), и (P – 110) долларов, если P > 110. Если значение P больше 110 долларов, владелец может исполнить опцион, купив акцию за 110 долларов и немедленно продав ее на спотовом рынке за P долларов, и тем самым получить прибыль (P – 110) долларов. На рис. 1 представлен выигрыш по этому колл-опциону. Выигрыш можно записать как формулу в Excel =МАКС(0;Р-110). Если Р ≤ 110, говорят опцион не в деньгах.
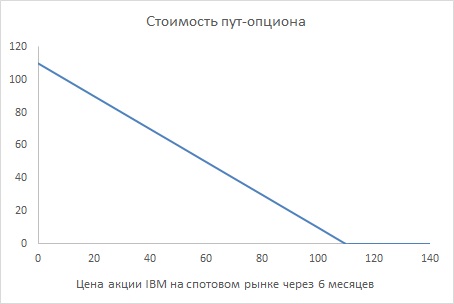
Ситуация с пут-опциона противоположна (рис. 2). Выигрыш по пут-опциону составит 0 долларов, если P > 110, и (110 – Р) долларов, если P < 110. Для значений P меньше 110 долларов владелец опциона может купить акцию за P долларов и немедленно продать ее за 110 долларов, реализуя опцион. Это принесет прибыль (110 – P) долларов. Если P больше 110 долларов, покупать акцию за P долларов и продавать за 110 долларов невыгодно, так что владелец не исполнит пут-опцион. Формула выигрыша =МАКС(0;110-Р).
Рис. 2. Стоимость пут-опциона
Параметры, определяющие цену опциона
При создании модели ценообразования Блэк, Шоулз и Мертон показали, что цена опциона зависит от следующих параметров:
- Текущая цена акции (или иного актива).
- Цена исполнения опциона.
- Время (в годах) до истечения срока действия опциона (называемое сроком опциона).
- Процентная ставка (в год с учетом сложных процентов) на безрисковые инвестиции (как правило, в казначейские векселя) в течение всего срока инвестирования. Например, если трехмесячные казначейские векселя приносят 5% дохода, безрисковая ставка вычисляется как ln(1 + 0,05). (Взятие логарифма преобразует простую процентную ставку в ставку с учетом сложных процентов.) Сложные проценты означают, что в каждый момент времени проценты приносят проценты.
- Годовая ставка (в процентах от курса акции), по которой выплачиваются дивиденды. Если акция приносит каждый год 2% своей стоимости в качестве дивидендов, норма дивидендов составляет 0,02.
- Волатильность акции (измеряемая в годовом исчислении). Годовая волатильность акции, например, 30% означает, что (приближенно) стандартное отклонение относительного годичного изменения курса акции составит примерно 30%. Во времена интернет-пузыря в конце 1990-х годов волатильность акций многих интернет-компаний превышала 100%. Этот важный параметр можно вычислить двумя способами.
В формуле ценообразования Блэка–Шоулза курс акции должен соответствовать логарифмически нормальному распределению.
Оценка волатильности акции на основе исторических данных
Для оценки исторической волатильности акции необходимо выполнить следующие шаги:
- Определить прибыль (убыток) по акции за несколько лет.
- Определить для каждого месяца ln(1 + прибыль).
- Определить стандартное отклонение для ln(1 + прибыль). Это вычисление дает ежемесячную волатильность.
- Умножить ежемесячную волатильность на для преобразования ежемесячной волатильности в годовую.
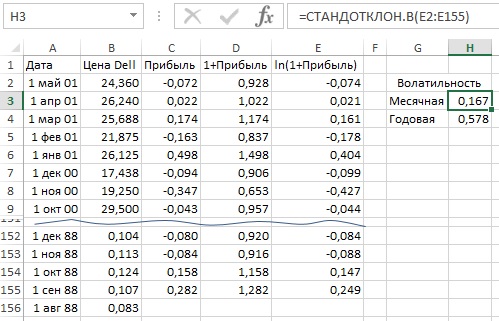
На рис. 3 приведены данные ежемесячной стоимости акций компании Dell за период с августа 1988 г. по май 2001 г. Прибыль равна разности цен за две соседние даты. Ежемесячная волатильность в ячейке Н3 определена по формуле =СТАНДОТКЛОН.В(E2:E155). (Если вам интересно в чем различие между двумя формулами Excel: СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г, см. здесь.) В ячейке Н4 используется формула =КОРЕНЬ(12)*H3. Годовая волатильность акций Dell составляет 57,8%.
Рис. 3. Вычисление исторической волатильности стоимости акций Dell
Формулу Блэка–Шоулза в Excel
Цена европейского колл-опциона вычисляется по формуле:
N(x) — вероятность того, что нормальная случайная величина со средним значением 0 и стандартным отклонением σ=1, меньше или равна x. Например, N(-1) = 0,16, N(0) = 0,5, N(1) = 0,84 и N(1,96) = 0,975. Нормальная случайная величина со средним значением 0 и стандартным отклонением 1 называется нормированной случайной величиной, распределенной по нормальному закону. Нормальное интегральное распределение в Microsoft Excel вычисляет функция НОРМ.СТ.РАСП. Формула =НОРМ.СТ.РАСП(x;ИСТИНА) возвращает вероятность того, что нормированная случайная величина, распределенная по нормальному закону, меньше или равна х. Например, формула =НОРМ.СТ.РАСП(-1;ИСТИНА), дает в результате 0,16. Это значение показывает, что нормальная случайная величина со средним значением 0 и стандартным отклонением 1 с вероятностью 16% примет значение менее -1.
S — текущий курс акции; t — срок опциона (в годах); X — цена исполнения; r — годовая безрисковая ставка (предполагается, что эта ставка постоянно вычисляется с учетом сложных процентов); σ — годовая волатильность акции; y — процент от стоимости акции, выплачиваемый в качестве дивидендов.
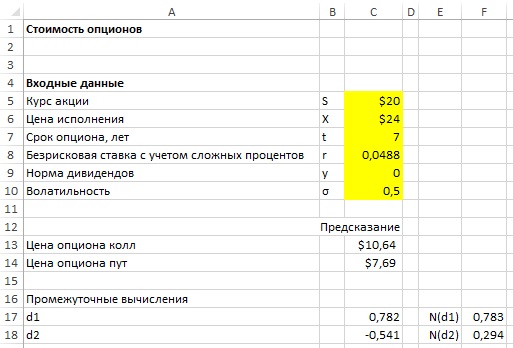
На рис. 4 находится шаблон, который вычисляет цену для европейских колл- и пут-опционов. Введите значения параметров в ячейки С5:С10 и получите цену европейского колл-опциона в С13, а цену европейского пут-опциона в С14. В качестве примера предположим, что акция Cisco сегодня продается за 20 долларов и вы выпустили семилетний европейский колл-опцион. Пусть годовая волатильность акции Cisco равна 50%, и безрисковая ставка в течение семилетнего периода исчисляется исходя из 5% в год. С учетом сложных процентов она преобразуется в ln(1+0,05) = 0,0488. Компания Cisco не выплачивает дивиденды, так что годовая норма дивидендов равна 0. Цена колл-опциона составляет 10,64 долл. Семилетний пут-опцион с ценой исполнения 24 доллара будет стоить 7,69 долларов.
Рис. 4. Определение цены европейских колл- и пут-опционов
Чувствительность стоимости опционов к росту основных параметров
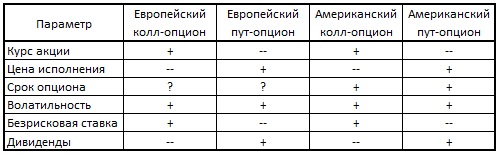
Как правило, влияние изменения входных параметра на цену колл- или пут- опциона соответствует указанному на рис. 5.
Рис. 5. Влияние роста входных параметров на стоимость опционов
Повышение сегодняшнего курса акции всегда повышает цену колл-опциона и снижает цену пут-опциона.
Повышение цены исполнения всегда повышает цену пут-опциона и снижает цену колл-опциона.
Увеличение срока опциона всегда повышает цену американского опциона. В случае выплаты дивидендов увеличение срока опциона может или повысить, или понизить цену европейского опциона.
Увеличение волатильности всегда повышает цену опциона.
Повышение безрисковой ставки повышает цену колл-опциона, поскольку более высокие ставки имеют тенденцию к увеличению темпов роста курса акции (что хорошо для колл-опциона). Эта ситуация отменяет тот факт, что в результате более высокой процентной ставки выигрыш по опциону уменьшается. Повышение безрисковой ставки всегда понижает цену пут-опциона, поскольку более высокие темпы роста курса акции, как правило, наносят ущерб пут-опциону, и будущий выигрыш по пут-опциону уменьшается. Как и в предыдущем случае, при этом предполагается, что процентные ставки не влияют на текущие курсы акций, однако это не так.
Дивиденды, как правило, снижают темпы роста курса акции, поэтому увеличенные дивиденды снижают цену колл-опциона и повышают цену пут-опциона.
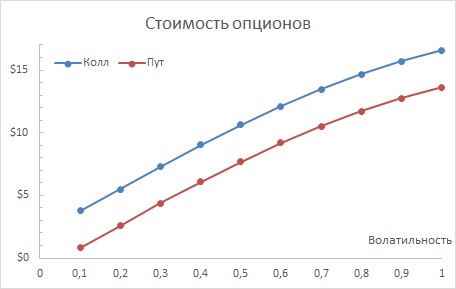
Конкретное влияние изменения параметров на цену колл- и пут-опционов можно исследовать с помощью таблицы данных (рис. 6), см. также Анализ чувствительности в Excel (анализ «что–если», таблицы данных).
Рис. 6. Анализ чувствительности опционов от волатильности
Оценка волатильности акции по формуле Блэка–Шоулза
Выше было показано, как на основе исторических данных оценить годовую волатильность акций. Проблема с оценкой исторической волатильности состоит в том, что анализ выполняется на основе прошлого. А в действительности требуется оценить волатильность акций на основе ожиданий. Подход на основе подразумеваемой волатильности просто оценивает волатильность акции как значение волатильности, при котором цена по формуле Блэка–Шоулза соответствует рыночной цене опциона. Иными словами, подразумеваемая волатильность получает значение волатильности, вытекающее из рыночной цены опциона.
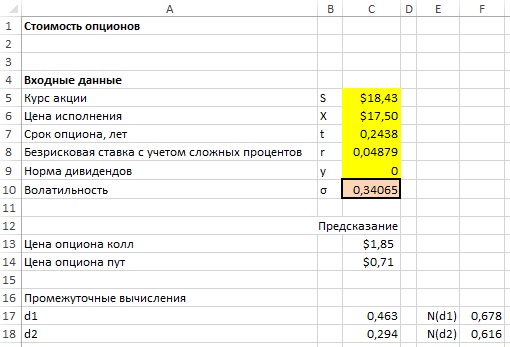
Для вычисления подразумеваемой волатильности можно воспользоваться инструментом Подбор параметра и описанными ранее входными параметрами (см. рис. 4). 22 июля 2003 г. акция Cisco продавалась за 18,43 долларов. В октябре 2003 г. колл-опцион с ценой исполнения 17,50 долларов продавался за 1,85 долларов. Срок действия этого опциона истекал 18 октября (через 89 дней в будущем). Таким образом, срок действия опциона составляет 89/365 = 0,2438 лет. Предположительно, Cisco не выплачивает дивиденды. Пусть ставка для казначейских векселей составляет 5%, и соответствующая безрисковая ставка равна ln(1 + 0,05) = 0,04879. Для определения волатильности акции Cisco, которая подразумевается ценой опциона, введите в ячейки B5:B10 (рис. 7) релевантные параметры.
Рис. 7. Вычисление волатильности акции Cisco согласно подразумеваемой волатильности
Далее в диалоговом окне Подбор параметра (Меню Данные –> Анализ «что-если»), показанном на рис. 8, определите волатильность (значение в ячейке B10), при которой цена опциона (формула в С13) достигает значения 1,85 долларов.
Как показано на рис. 7, этот опцион подразумевает годовую волатильность для Cisco в размере 34%.
Рис. 8. Настройки в диалоговом окне Подбор параметра
На сайте http://www.ivolatility.com/ и http://www.ivolatility.ru/ предоставляются оценки волатильности любой акции, как исторические, так и подразумеваемые.
Реальные опционы
Ценообразование опционов может повлиять на повышение эффективности долгосрочных инвестиций компании или на процесс принятия финансовых решений. Использование ценообразования опционов для оценки фактических инвестиционных проектов называется реальными опционами. Идею реальных опционов приписывают Джуди Левен, в прошлом финансовому директору компании Merck. По существу, реальные опционы позволяют назначить явную цену для управленческой гибкости, которую часто упускают из вида при традиционном составлении плана долгосрочных инвестиций. Рассмотрим два примера.
Пусть вы являетесь владельцем нефтяной скважины. Сегодня наиболее правдоподобное предположение о стоимости нефти в скважине — 50 млн. долларов. Через 5 лет (оставаясь владельцем скважины) вам предстоит принять решение о разработке нефтяной скважины, которая обойдется вам в 70 млн. долларов. Бизнесмен с сомнительной репутацией готов купить скважину сегодня за 10 млн. долларов. Следует ли продать скважину?
Безусловно, цена нефти через 5 лет может вырасти. Даже если предположить, что цена нефти будет расти на 5% в год, через 5 лет нефть будет стоить 63,81 млн долларов. Традиционный план долгосрочного инвестирования предполагает, что нефть обесценится, поскольку стоимость ее разработки превышает стоимость нефти в скважине. Но не торопитесь — через 5 лет цена нефти в скважине будет другой, т.к. многие вещи (такие как мировая цена на нефть) могут измениться. Существует вероятность, что через 5 лет нефть будет стоить не меньше 70 млн. долларов. Если через 5 лет нефть будет стоить 80 млн. долларов, разработка скважины через пять лет принесет 10 млн долларов.
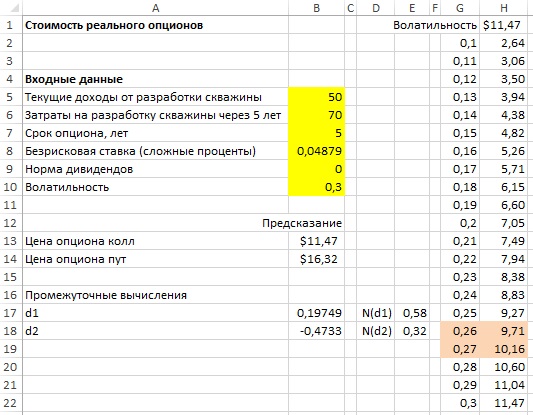
По сути, вы владеете пятилетним европейским колл-опционом на эту скважину, т.к. выигрыш от скважины через 5 лет такой же, как выигрыш по европейскому колл-опциону с курсом акции 50 млн. долларов, ценой исполнения 70 млн. долларов и сроком опциона 5 лет. Можно предположить, что годовая волатильность подобна волатильности акции типичной нефтяной компании (например, 30%). Если использовать безрисковую ставку 4,879%, можно определить, что цена такого колл- опциона составляет 11,47 млн. долларов (рис. 9). Из этого следует, что вы не должны продавать скважину за 10 млн. долларов.
Рис. 9. Реальный опцион на нефтяную скважину
Конечно, фактическая волатильность для этой нефтяной скважины неизвестна. По этой причине с помощью таблицы данных с одним входом определим, как цена опциона зависит от оценки волатильности (см. рис. 9). Как видно из таблицы, пока волатильность скважины составляет, по меньшей мере, 27%, опцион на нефтяную скважину стоит более 10 млн. долларов.
В качестве второго примера рассмотрим биотехнологическую компанию по производству лекарств, разрабатывающую лекарственный препарат для фармацевтической фирмы. В биотехнологической компании в настоящее время предполагают, что цена разрабатываемого препарата составляет 50 млн. долларов. Безусловно, цена лекарственного препарата со временем может понизиться. Для защиты от резкого падения цены биотехнологической компании требуется, чтобы препарат через 5 лет имел гарантированную цену 50 млн. долларов. Если страховая компания собирается подписать такое обязательство, какая справедливая цена должна быть назначена?
По существу, биотехнологическая компания запрашивает платеж в 1 млн. долларов для каждого миллиона долларов, на который цена препарата упадет ниже уровня 50 млн. долларов, через 5 лет. Это эквивалентно пятилетнему пут-опциону на цену лекарственного препарата. Предположим, что ставка по казначейскому векселю составляет 5% и годовая волатильность для акций сопоставимых компаний равна 40% (рис. 10), тогда цена этого опциона — 10,51 млн. долларов. Такой тип опциона часто называют опционом на отказ от проекта, но он эквивалентен пут-опциону. (На рис. 10 таблица данных показывает, как цена опциона отказа от проекта зависит от предполагаемой волатильности, составляющей 30–45% от цены лекарственного препарата.)
Рис. 10. Вычисление стоимости пут-опциона отказа от проекта
[1] Заметка написана на основе материалов из книги Уэйн Л. Винстон. Microsoft Excel 2013. Анализ данных и бизнес-моделирование, глава 78.