Мы привыкли думать, что являемся рациональными существами. Что мы делаем рациональный выбор на основе фактов и логических построений. Но, даже если отбросить влияние эмоций, наши решения всё равно будут далеки от рациональных. Казалось бы, если А лучше В, а В лучше С, то А должно быть лучше С. В настоящей статье авторы показывают, что это не всегда так. Нобелевский лауреат Даниэль Канеман известен российским читателям по книгам Канеман, Словик, Тверски. Принятие решений в неопределенности: Правила и предубеждения и Даниэль Канеман. Думай медленно… решай быстро.
Психологический журнал. – 2003. – Т. 24. — № 4. — С. 31-42. [1]
Скачать заметку в формате Word или pdf
Принятие решений является, возможно, одним из основных видов деятельности, характерных для живых существ. Поэтому попытка понять, объяснить и предсказать поведение делающего выбор индивида стала главной задачей поведенческих и социальных наук. При изучении решений возникают как нормативные вопросы, так и задачи описания процессов. Нормативный анализ используется при исследовании природы рациональности и логики процесса принятия решений. Описательный анализ, напротив, рассматривает человеческие убеждения и предпочтения таковыми, какие они есть в реальности, а не какими они должны быть. Конфликт между нормативным и описательным взглядами определяет многое в исследованиях решений и выбора.
Выбор в условиях риска
Мы представим подход к анализу выбора в условиях риска, который выводит многие гипотезы, исходя из психофизического анализа ценности и вероятности. Психофизика – это наука о взаимоотношениях между физическими величинами, такими, как длина или деньги, и их психологическими эквивалентами – воспринимаемой длиной или полезностью.
Психофизический подход к процессу принятия решений восходит к выдающемуся эссе Даниила Бернулли, опубликованному в 1738 году (см. библиографию в конце статьи), в котором он пытается объяснить, почему люди в основном не склонны к риску и почему неприятие риска снижается с увеличением богатства. Чтобы проиллюстрировать несклонность к риску и анализ Бернулли, рассмотрим выбор между проектом, в котором игрок выигрывает $1000 с вероятностью 85% (и с вероятностью 15% не выигрывает ничего), и альтернативой получения $800 наверняка. Подавляющее большинство людей предпочитают уверенность игре, хотя последняя имеет более высокий (в математическом выражении) ожидаемый результат: 0,85*$1000 + 0,15*$0 = $850. Предпочтение гарантированного выигрыша служит примером проявления несклонности к риску. Вообще говоря, предпочтение гарантированного результата участию в игре с большим или таким же ожидаемым выигрышем называется несклонностью к риску, а отказ от гарантированного результата в пользу игры с равным или даже более низким ожидаемым выигрышем – склонностью к риску (рис. 1).
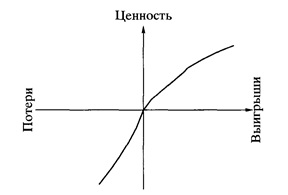
Рис. 1. Гипотетическая функция ценности.
Бернулли полагал, что люди оценивают возможные варианты исходов игры не на основе ожидаемого денежного результата, а на основе ожидаемой субъективной ценности этих результатов. Чтобы объяснить несклонность к риску в рамках данной системы взглядов, Бернулли предлагал рассматривать субъективную ценность, или полезность, как вогнутую функцию денежного дохода. Такая функция предполагает, что различие полезностей, например, между выигрышами $200 и $100 намного больше, чем разница полезностей между выигрышами $1200 и $1100. Из вогнутости следует, что субъективная ценность, приписываемая выигрышу в $800, больше стоимости ожидаемого с вероятностью 80% выигрыша в $1000. Следовательно, вогнутость функции полезности обусловливает несклонность к риску – предпочтение гарантированного выигрыша в $800 над вероятностью в 80% выиграть $1000, хотя оба варианта характеризуются одинаковыми ожиданиями.
Подобное обобщение в равной степени применимо и к потерям. Разница в субъективной ценности между потерями в $200 и $100 проявляется сильнее, нежели разница в субъективной ценности между потерями в $1200 и $1100. Когда функции ценности для выигрышей и для потерь объединены вместе, мы получаем S-образную функцию наподобие той, что представлена на рис. 1.
Функция ценности, изображенная на рис. 1, во-первых, вогнута в области выигрышей и выпукла в области потерь, и во-вторых, значительно более крутая для потерь, чем для выигрышей. Последнее качество, которое мы назовем несклонностью к риску, означает, что нежелательность потери $Х больше, чем привлекательность выигрыша $Х. Несклонность к риску объясняет нежелание людей держать пари на исход подбрасывания монеты при равных ставках: привлекательность возможного выигрыша оказывается недостаточной, чтобы компенсировать неприятие возможных потерь. Так, большинство опрошенных студентов отказывались поставить $10 на орел или решку, если им обещали выигрыш менее $30.
Предположение о несклонности к риску сыграло центральную роль в экономической теории. Однако, так же как вогнутость функции ценности в области выигрышей влечет за собой несклонность к риску, выпуклость функции ценности в области потерь – склонность к нему. Действительно, склонность к риску – это устойчивый эффект, особенно когда вероятность потерь значительна. Рассмотрим, к примеру, ситуацию, в которой индивид вынужден выбирать между вариантом потерять $1000 с вероятностью 85% (и с вероятностью 15% не потерять ничего) и вариантом потерять $800 наверняка. Большинство людей в данном случае демонстрируют предпочтение игры, а не неизбежной потери. Это выбор, подтверждающий склонность к риску, так как ожидание проигрыша ($850) являет собой худшую альтернативу ожиданиям гарантированных потерь (–$800). Правильно ли быть несклонным к риску в области выигрышей и склонным к риску в области потерь? Мы можем видеть, что S-образная функция ценности имеет некоторые нормативно недопустимые следствия.
Можно сказать, что современная теория принятия решений восходит к новаторской работе фон Неймана и Моргенштерна. Их аксиомы включают транзитивность (если А предпочитается В и В предпочитается С, то А предпочитается С) и замещение (если А предпочитается В, то, при прочих равных условиях, «А и С» предпочитаются «В и С»). Нормативный и описательный статусы аксиом рационального выбора являлись предметом всесторонних дискуссий. В частности, существуют убедительные свидетельства того, что люди часто не подчиняются аксиоме замещения; это обусловливает значительные разногласия по поводу нормативных достоинств этих аксиом. Тем не менее, в каждом исследовании рационального присутствуют два принципа: доминирования и инвариантности. Принцип доминирования утверждает: если ожидание А, как минимум, не хуже ожидания В в любом аспекте, и лучше ожидания В, как минимум, в одном аспекте, то ожидание А предпочитается ожиданию В. Принцип инвариантности требует, чтобы порядок предпочтений между различными ожиданиями не зависел от способа их описания. Далее мы покажем, что требование инвариантности, каким бы элементарным и очевидным оно ни казалось, обычно не может быть удовлетворено.
Рамочные эффекты при оценке результатов
Ожидания характеризуются возможными результатами и вероятностями их получения. Тем не менее, один и тот же выбор может быть обусловлен и описан различными способами. Например, возможные результаты игры могут быть описаны или как выгоды, или как потери. Инвариантность требует, чтобы такие изменения в описании результатов не изменяли порядок предпочтений. В двух следующих примерах показано, каким образом это требование может нарушаться. (В круглых скобках указано процентное соотношение тех, кто выбрал определенный вариант ответа.)
Пример 1. Представьте, что Соединенные Штаты готовятся к вспышке необычной азиатской болезни, которая, как ожидается, убьет 600 человек. Были предложены две альтернативные программы борьбы с этой болезнью. Предположим, что точные научные оценки последствий данных программ следующие. Если будет проводиться программа А, то удастся спасти 200 человек (72% респондентов предпочли этот вариант). Если же будет проводиться программа В, то с вероятностью 33,3% будут спасены все и с вероятностью 66,6% не выживет никто (28%). Как и ожидалось, в распределении предпочтений обнаружена несклонность к риску: подавляющее число респондентов предпочло сохранение 200 жизней наверняка, а не 600 жизней с вероятностью 1/3.
Пример 2. После аналогичного вступления, говорится, что если будет принята программа С, то 400 человек умрет (22%). Если же будет принята программа D, то с вероятностью 1/3 не погибнет никто, а с вероятностью 2/3 умрут 600 человек (78%). Как и ожидалось, при подаче информации в терминах потерь, люди демонстрируют склонность к риску, высказываясь в пользу рискового решения (вариант D), а не в пользу гарантированной потери 400 жизней. Действительно, во втором варианте проявляется большая склонность к риску, чем несклонность к нему в первом.
Следующие два примера выявляют предпочтения, которые противоречат аксиоме доминирования рационального выбора.
Пример 3. Существует выбор между:
- Е. 25% с вероятностью выиграть $240 и 75% с вероятностью потерять $750 (0%)
- F. 25% с вероятностью выиграть $250 и 75% с вероятностью потерять $750 (100%) Видно, что вариант F доминирует над вариантом Е. Действительно, все респонденты таким образом осуществили свой выбор.
Пример 4. Представьте, что вы столкнулись с необходимостью принять одновременно два решения. Сначала рассмотрите оба решения, а потом укажите то из них, которое вы предпочитаете.
Решение (i). Сделайте выбор между:
- A. гарантированным выигрышем в $240 (84%)
- B. 25%-ной вероятностью получить $1000 и 75%-ной вероятностью не получить ничего (16%)
Решение (ii). Сделайте выбор между:
- С. гарантированными потерями в $750 (13%)
- D. 75%-ной вероятностью потерять $1000 и 25%-ной вероятностью не потерять ничего (87%)
73% респондентов выбрали совместно ответы А и D, тогда как ответы В и С предпочли лишь 3% опрошенных. Но ведь варианты А и D в совокупности есть не что иное, как вариант Е в примере 3. Следовательно, рамочные эффекты и S-образная функция ценности объясняют нарушение требования доминирования в случае одновременно принимающихся решений.
Логика этих результатов обескураживает: инвариантность нормативно необходима, интуитивно отвергаема и психологически непредставима. Например, чтобы добиться инвариантности студентам экономических специальностей предлагают рассматривать каждую проблему, сопряженную с принятием решений, в терминах общей стоимости, а не в терминах выигрышей и потерь. Обеспечение стандартного представления проблемы оказывается куда более сложным в других случаях, таких, как безопасность, здоровье или качество жизни. Следует ли нам давать советы людям о том, как оценивать последствия государственной политики в области здравоохранения (см. примеры 1 и 2) – в показателях общей смертности, смертности от болезней или числа смертей, вызванных рассматриваемой болезнью?
Итак, нельзя ожидать сохранения инвариантности фреймов, а уверенность в определенном выборе не означает, что такой же выбор будет сделан при других условиях. И мы поэтому положительно оцениваем практику предумышленного изменения фреймов в повторяющихся ситуациях принятия решений с целью измерения силы предпочтений.
Психофизика возможностей
До настоящего времени наше обсуждение имело в основе правило Бернулли, в соответствии с которым ценность или полезность ожидаемого результата получается суммированием полезностей возможных исходов, взвешенных по своим вероятностям. Чтобы проверить это предположение, снова обратимся к психофизической интуиции. Устанавливая ценность статус-кво равной нулю, представим себе денежный приз, скажем, в $300 и установим его ценность равной единице. А теперь допустим, что вам вручили лишь лотерейный билет с единственным призом в $300. Каким образом меняется ценность билета как функция от вероятности выигрыша приза? Не принимая во внимание полезность самой азартной игры, ценность ожидаемых результатов такого рода должна варьироваться от 0 (когда шанс выиграть равен нулю) до 1 (когда выигрыш в $300 гарантирован).
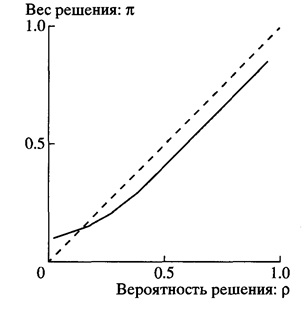
Интуиция предполагает, что ценность билета есть нелинейная функция от вероятности выигрыша, что объясняется правилом ожидаемой полезности. В частности, повышение с 0% до 5% имеет больший эффект, чем повышение с 30% до 35%, который, в свою очередь, оказывается меньше чем повышение с 95% до 100%. Эти размышления позволяют сделать предположение о существовании эффекта границы категорий, изменения от невозможности к возможности, от возможности к определенности оказывают большее влияние, чем изменения в середине интервала. Эта гипотеза проиллюстрирована с помощью кривой, изображенной на рис. 2, которая представляет удельный вес события как функцию от его зафиксированной численно вероятности. Наиболее существенной особенностью рис. 2 является то, что вес решений находится в регрессионной зависимости от вероятностей. За исключением окрестности конечных точек, увеличение вероятности выигрыша на 0,05 увеличивает ценность проекта на менее, чем на 5% от стоимости всего приза.
Рис. 2. Гипотетическая весовая функция
На рис. 2 вес решений меньше соответствующих вероятностей на большей части области определения функции. Недооцененность средних и высоких значений вероятностей по сравнению с гарантированным результатом выражается в несклонности к риску в играх с положительным исходом, снижая их привлекательность. Этот же эффект находит свое выражение в склонности к риску в играх с отрицательным исходом. Низкие значения вероятности имеют, однако, большие весовые коэффициенты, а очень малые вероятности либо слишком переоцениваются, либо игнорируются полностью, делая вес решений крайне нестабильным в этой области значений.
Придание большего веса малым значениям вероятностей изменяет описанные выше паттерны: оно повышает ценность общих планов и усиливает неприятие малой вероятности большой потери. Следовательно, люди чаще склонны к риску, имея дело с маловероятными выигрышами, и не склонны к нему в случаях с маловероятными потерями. Таким образом, весовые характеристики решений могут оказаться полезными в объяснении привлекательности как лотерейных билетов, так и политики страхования.
Нелинейность функции весов решений неизбежно приводит к нарушениям инвариантности.
Пример 5. Рассмотрим двухпериодную игру. В первом периоде вероятность закончить игру с нулевым выигрышем равна 75%, а вероятность перейти во второй период равна 25%. Если вы дойдете до него, то будете выбирать между:
- А. Заведомым выигрышем в $30 (74%)
- В. 80%-ной вероятностью выиграть $45 (26%)
Ваш выбор должен быть сделан до начала игры, то есть до того, как станет известен результат первого периода. Пожалуйста, укажите выбранный вами вариант.
Пример 6. Какой из следующих вариантов вы предпочитаете?
- С. Выиграть $30 с вероятностью 25% (42%).
- D. Выиграть $45 с вероятностью 20% (58%).
Поскольку шанс перейти на следующий уровень в проблеме 5 только один из четырех, вариант А дает возможность выиграть $30 с вероятностью 0,25, а вариант В – с вероятностью равной 0,25*0,80 = 0,20 выиграть $45.
Примеры 5 и 6, таким образом, идентичны в показателях вероятностей и результатов. Тем не менее, в обоих вариантах предпочтения различны: явное большинство выбирает шанс выиграть меньшее количество в примере 5, несмотря на то, что большинство идет другим путем в примере 6.
Мы считаем провал инвариантности результатом взаимодействия двух факторов: фреймов вероятностных ситуаций и нелинейности весовых значений решений. Точнее, мы предполагаем: в примере 5 люди игнорируют первый период, который приводит к такому же результату вне зависимости от принятого решения, и сосредоточивают свое внимание на том, что произойдет, если они дойдут до второго этапа игры. Тогда, конечно, они получают гарантированный выигрыш в случае, если выбирают вариант А, и с вероятностью 80% – выигрыш при выборе игры. На самом деле, последовательный выбор практически идентичен выбору между гарантированным выигрышем в $30 и вероятностью 85% выиграть $45. Так как гарантия выигрыша имеет больший вес по сравнению с событиями, имеющими среднюю или высокую вероятность (см. рис. 2); вариант, способный привести к выигрышу $30, более заманчив в условиях последовательного выбора. Мы характеризуем это явление как эффект псевдоопределенности, потому что событие, которое на самом деле характеризуется неопределенностью, имеет такой же вес, как если бы исход его был определен.
Рис. 2 подсказывает, что люди сильно недооценивают снижение вероятности риска по сравнению с полным его устранением. Действительно, было показано, что условная вакцина, снижающая вероятность заболевания с 20% до 10%, менее привлекательна, если характеризуется как эффективная в половине случаев, чем если она представлена как полностью эффективная против одного из двух оригинальных равновозможных штаммов вируса.
Эффекты формулировок
Примеры 1 и 2 иллюстрируют эффект формулировки, где изменение фразы с жизни сохраняются на жизни теряются заметно меняет предпочтения от несклонности к риску к его предпочтению. Эффекты формулировок возникают случайно, когда никто не догадывается о воздействии фрейма на конечное решение. Однако они могут быть использованы намеренно для регулирования относительной привлекательности вариантов. Например, Ричард Талер заметил, что лоббисты кредитных карточек настаивают на том, чтобы любая разница в ценах между покупкой за наличные или по карточке метилась как скидка, а не как доплата (см. Ричард Талер. Nudge. Архитектура выбора). Два ценника представляют различие в ценах: в одном случае как выигрыш, в другом как потерю, неявно исходя из того, какая – заниженная или завышенная – цена была взята в качестве базовой. Так как проигрыш обычно преувеличивается больше, чем выигрыш, покупатели скорее откажутся от скидки, чем согласятся на доплату. Как и следовало ожидать, попытки использовать фреймы наблюдаются и на рынке, и на политической арене.
Трансакции и торговля
Наша теория рационального выбора многим обязана работам Ричарда Талера. Следующий пример, знакомит нас с правилами, регулирующими процесс реконструкции рациональных представлений и иллюстрирующими обусловленность оценки трансакций вогнутостью функции ценности.
Пример 7. Предположим, вы собираетесь приобрести куртку за $125 и калькулятор за $15. Продавец калькуляторов сообщил: тот, который вы желаете купить, в другом филиале универсама, расположенном в 20 минутах езды, стоит $10. Поедете ли вы в другой магазин?
Этот пример связан с задачей оценки приемлемости выбора, в ходе которого необходимо сравнить связанные с поездкой неудобства с финансовым выигрышем. Фреймами данного выбора могут быть: минимальный, тематический или объясняющий расчет. Минимальный расчет включает лишь оценку разницы между двумя возможными вариантами выбора, не уделяя внимания деталям. При минимальном расчете фрейм связанного с поездкой в другой магазин преимущества – это выигрыш $5. Тематический расчет соотносит последствия возможных вариантов выбора с оценочным уровнем, определяемым из контекста, в рамках которого происходит принятие решения. В данном примере соответствующей темой является покупка калькулятора, поэтому фрейм выгоды от путешествия – снижение цены с $15 до $10. Так как потенциальная выгода связана лишь с калькулятором, цена куртки не учитывается в тематическом расчете. Цена куртки, так же как и другие расходы, может быть включена в более общий объясняющий счет, в котором экономия может быть оценена относительно, скажем, месячных трат.
Формулировка задачи может показаться нейтральной по отношения к принятию вида расчета – минимального, тематического или объясняющего. Однако можно предположить, что люди спонтанно фреймируют свои решения понятиями тематического расчета, которые в данном контексте играют роль правильных форм восприятия и базовых категорий познания. Тематическая постановка вопроса в связи с вогнутостью функции ценности подразумевает, что готовность ехать в другой магазин ради экономии $5 на покупке калькулятора должна обратно зависеть от цены калькулятора и не зависеть от цены куртки. Чтобы проверить это предположение, мы сконструировали другую версию примера, в котором цены двух товаров были взаимозависимы. Цена калькулятора в первом магазине была $125 и $120 в другом филиале, а цена куртки была установлена в $15. Как и предполагалось, соотношения респондентов, которые ответили, что совершат поездку в другой магазин, резко отличались в этих двух примерах. Результаты показали: 68% респондентов желали бы поехать в другой магазин, чтобы сэкономить $5 на калькуляторе стоимостью $15, но только 29% были готовы поехать в другой магазин, чтобы сэкономить $5 на калькуляторе стоимостью $125. Эти результаты подтверждают выводы, получаемые в концепции тематического расчета, тогда как в терминах как минимального, так и объясняющего расчета обе версии идентичны.
Важность тематического расчета для описания поведения потребителя подтверждается наблюдением: стандартное отклонение цен на определенный продукт в магазинах города в целом пропорционально средней цене данного продукта. С тех пор, как колебания цен определенно зависят от попыток потребителей найти лучшую покупку, покупатели вряд ли согласятся прилагать дополнительные усилия, чтобы сэкономить $15 на 150-долларовой покупке, чем $5 – на 50-долларовой.
Тематическая организация рационального мышления ведет к тому, что люди чаще оценивают выигрыши и потери в относительных, нежели в абсолютных показателях. Это приводит к большим различиям в относительных расходах на другие вещи, такие, например, как телефонные звонки, сделанные с целью найти удачную покупку или готовность ехать далеко, чтобы ее заполучить. Большинство покупателей обнаружат, что легче принять решение о покупке автомобильной стереосистемы или персидского ковра в контексте решения о покупке автомобиля или дома, чем по отдельности. Эти наблюдения, очевидно, противоречат традиционной рациональной теории поведения потребителя, которая предполагает инвариантность и не признает эффекты, обусловленные типами мысленных расчетов.
Пример 8. Предположим, что вы решили посмотреть пьесу и заплатили за входной билет $10. Когда вы вошли в театр, то обнаружили: билет потерян. Место не было отмечено, и билет не может быть возвращен. Заплатите ли вы $10 за другой билет? Да (46%) Нет (54%).
Пример 9. Предположим, что вы решили посмотреть пьесу, билет на которую стоит $10. Когда вы вошли в театр, то обнаружили: потеряна банкнота в $10. А в этом случае вы заплатите $10 за билет? Да (88%) Нет (12%).
Различия в ответах респондентов на эти вопросы интригуют. Почему так много людей не готовы тратить $10, потеряв билет, хотя они охотно потратят такое же количество денег, потеряв эквивалентную сумму наличных? Мы объясняли различия тематической организацией рационального мышления. Поход в театр рассматривается как трансакция, в которой стоимость билета обменивается на возможность посмотреть пьесу. Покупка второго билета увеличивает расходы на просмотр до уровня, который многие респонденты находят неприемлемым. Потеря денег, напротив, не учитывается в расходах на театр, это лишь заставляет индивида почувствовать себя несколько стесненным в средствах.
Довольно интересный эффект наблюдался, когда две версии этого примера предлагались одним и тем же людям. Желание заменить потерянный билет значительно возрастало, когда этому варианту предшествовала версия о потерянных деньгах. Напротив, готовность купить билет после потери денег не претерпела изменений после предварительного ознакомления с другим вариантом примера. Это сопоставление наводит субъекта на мысль, что имеет смысл считать потерянный билет утраченными деньгами, но не наоборот.
Нормативный статус эффектов, обусловленных типами мысленных расчетов, находится под вопросом. Уместно такое возражение: альтернативные версии примеров с калькулятором и билетом различаются также и по существу. В частности, экономия $5 при покупке стоимостью $15 может доставить большее удовольствие, чем при покупке большей стоимости; да и повторная оплата билета может раздражать сильнее, чем потеря $10 наличными. Сожаление, раздражение и самоудовлетворение также могут быть обусловлены фреймами.
Потери и затраты
Многие проблемы принятия решений приобретают форму выбора между сохранением статус-кво и принятием альтернативы, которая в каких-то отношениях полезна, а в других – имеет недостатки. Преимущества альтернативных вариантов могут быть оценены как выигрыши, а их недостатки – как потери. Так как потери переживаются сильнее, чем выигрыши, лицо, принимающее решение, более тяготеет к сохранению статус-кво.
Для того, чтобы описать нерасположенность людей расставаться с собственностью, являющейся частью их начального запаса, Талер ввел термин эффект начального запаса. В том случае, когда отказ от части собственности более неприятен, чем удовольствие от приобретения такой же ценности, цены покупки будут заметно ниже цен продажи. Исходя из этого, самая высокая цена, которую индивид заплатит за актив, будет ниже цены, которую запросит этот же индивид за отказ от актива, однажды приобретенного. Эти результаты были представлены как вызов традиционной экономической теории, в которой цены покупки и продажи совпадают, если не принимать во внимание трансакционные затраты и эффект богатства. Несклонность к потерям делает стабильность более предпочтительной, чем изменения. Комбинация приспосабливаемости и несклонности к потерям предохраняет от сожаления и зависти, уменьшая привлекательность упущенных альтернатив и начальных запасов других индивидов.
Выбор между гарантированными потерями и риском больших потерь может быть фреймом страховки. В таких случаях несогласованность в оценке затрат-потерь может вести к нарушению инвариантности.
Пример 10. Согласитесь ли вы участвовать в игре, в которой с вероятностью 10% выпадает выигрыш $95 и с вероятностью 90% – потеря $5?
Пример 11. Согласны ли вы заплатить $5 за участие в лотерее, в которой с вероятностью 10% выпадает выигрыш $100 и с вероятностью 90% – проигрыш?
Несмотря на то, что эти две задачи предлагают два объективно идентичных варианта выбора, 55% респондентов выражают различные предпочтения. Рассмотрение $5 в качестве платежа делает игру более приемлемой, чем представление этой суммы как потери. Субъективное состояние индивида может быть улучшено, если негативный исход будет восприниматься скорее, как затраты, нежели, как и потери. Возможность подобного психологического манипулирования объясняет такую форму парадоксального поведения как эффект необратимых потерь. Талер приводит пример человека, у которого развилась форма болезни, известная нам как теннисный локоть (воспаление капсулы локтевого сустава, вызванное игрой в теннис), вскоре после того, как он заплатил членский взнос в теннисный клуб. Он испытывал жуткую боль, но продолжал играть в теннис, чтобы не пропали его инвестиции. Предполагая, что человек не может играть, если он не оплатил членский взнос, зададим вопрос: как игра с острым ощущением боли может улучшить положение человека? Подобная игра, мы полагаем, позволяет оценивать членский взнос как затраты. Если же человек вынужден прекратить играть, ему придется признать взнос необратимыми потерями, что может оказаться менее предпочтительным, чем игра с болью.
Заключение
Для обычного принимающего решения лица соответствие между ожидаемой и получаемой ценностью далеко от идеального. Например, люди, заказавшие обед и будучи зверски голодными, осознают: они допустили большую ошибку после пятой перемены блюд на столе. Обычное несоответствие ценностей решения и опыта создает дополнительные элементы неопределенности во многих задачах принятия решений.
Фреймы исходов нередко индуцируют ценности, не находящие аналогов в реальном опыте. Например, фрейм расходов как необратимых затрат или как цены страхования, вероятно, может повлиять на реальный исход. В подобных случаях оценка исходов в контексте принимаемых решений поможет не только предугадывать происходящее, но и формировать его.
Список литературы на русском языке
Даниил Бернулли. Опыт новой теории измерения жребия // Вехи экономической мысли. Т. 1. Теория потребительского поведения и спроса. –– СПб.: Экономическая школа, 1993. — С. 11–27.
Ричард Г. Талер. Умственная бухгалтерия – это серьезно // Горизонты когнитивной психологии. – М.: Языки славянских культур, РГГУ, 2012. – С. 289–302.
Ричард Г. Талер. От Homo economicus к Homo sapiens // ЛОГОС #1(97)2014. – С. 141–154
Нейман Дж. фон, Моргенштерн О. Теория игр и экономическое поведение. — М.: Наука, 1970. – 708 с.
[1] Первоначально статья опубликована в American Psychologist. 1984 г., vol. 39, No. 4, pp. 341–350