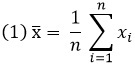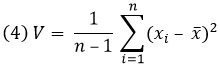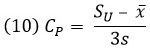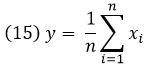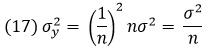В книге японских авторов рассказывается о массовом обучении персонала промышленных предприятий методам анализа дефектов и совершенствования технологий. Книга рассчитана на практическое овладение универсальными методами контроля качества и регулирования технологических процессов: построение кривых Парето, диаграмм причин и результатов и диаграмм рассеивания, гистограмм, контрольных карт. Материал изложен просто, ясно, не требует специальной математической подготовки. Книга развеивает миф о том, что статистические методы повышения качества способны освоить только сотрудники с высшим образование.
Хитосе Кумэ. Статистические методы повышения качества. – М.: Финансы и статистика, 1990. – 304 с.
Скачать конспект (краткое содержание) в формате Word или pdf, примеры в формате Excel
Купить книгу в Ozon (на момент выхода заметки книги в наличии не было)
Глава 1. ВВЕДЕНИЕ
Почему наряду с бездефектными изделиями изготавливаются дефектные? Причины этого заключаются в изменениях материалов, наладки станков, приемов работы и методов проверки. Если бы не было перечисленных изменений, все изделия были бы идентичными, а их качество оставалось бы неизменным. Изменчивость – причина выпуска дефектных изделий. Если попытаться ее уменьшить, их число, несомненно, сократится.
Все бесчисленные возможные причины делятся на две группы. К первой относится небольшое число причин, которые оказывают существенное воздействие. Вторую группу составляет большое число причин, оказывающих тем не менее незначительное. Этот принцип, именуемый принципом Парето, применим во многих случаях (подробнее см. далее главу 3). В первую очередь следует найти существенно важные причины, вызывающие появление дефектных изделий, и, после того как они будут четко выявлены, устранить их.
Процедура поиска причин появления дефектных изделий среди многочисленных факторов называется диагнозом процесса.
Взгляд на вещи сквозь призму статистики и статистические методы наиболее эффективные средства объективного наблюдения. Важно не столько знание самих статистических методов, сколько сознательное желание использовать их.
Глава 2. КАК ПОЛУЧАТЬ ИНФОРМАЦИЮ
Прежде чем начать собирать данные, надо решить, что вы будете с ними делать. Цели сбора данных в процессе контроля качества состоят в следующем: контроль и регулирование производственного процесса; анализ отклонений от установленных требований; контроль продукции. Любые собираемые данные имеют свое назначение, и после того, как информация собрана, нужно начать с нею работать.
Если вы хотите понять, каким образом два разных работника допускают дефекты, то надо брать раздельные выборки. Разделение группы данных на несколько подгрупп по определенному признаку называется расслоением, или стратификацией. Если нужно узнать, есть ли зависимость между значениями двух показателей, данные следует собирать парами. Когда есть парные данные, их можно проанализировать с помощью диаграмм рассеивания.
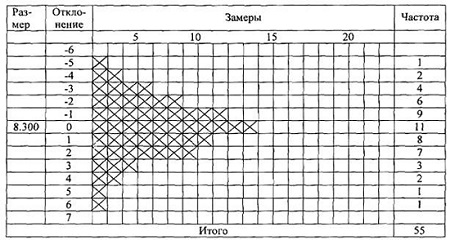
Важно в процессе сбора тщательно упорядочить данные, чтобы облегчить их последующую обработку. Контрольный листок – бумажный бланк, на котором заранее напечатаны контролируемые параметры, с тем чтобы можно было легко и точно записать данные измерений. Его главное назначение двояко: облегчить процесс сбора данных; автоматически упорядочить данные для облегчения их дальнейшего использования (рис. 1). (Сегодня – спустя 30 лет после выхода книги на английском языке – данные часто создаются внутри информационных систем, и более актуальным становится их обработка. Хотя иногда и приходится прилагать усилия для сбора данных. – Прим. Багузина.)
Рис. 1. Контрольный листок для регистрации распределения измеряемого параметра в ходе производственного процесса
Можно наложить контрольный листок на диаграмму причин и результатов (о последней подробнее см. главу 4). Такие диаграммы вычерчиваются заранее, и когда становится ясна причина или условия допущения дефекта, то у соответствующей стрелочки делается пометка. По этой диаграмме можно сразу определить, устранению каких причин важно отдавать предпочтение.
Глава 3. АНАЛИЗ ПАРЕТО
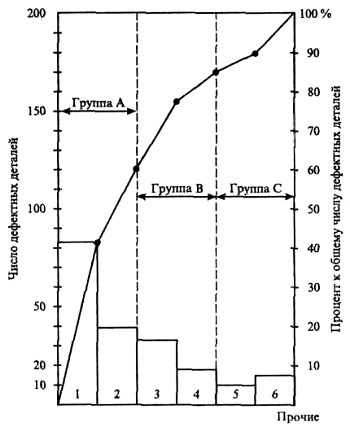
Доктор Д.М. Джуран применил диаграмму Парето в сфере контроля качества для классификации проблем качества на немногочисленные существенно важные и многочисленные несущественные, и назвал этот метод анализом Парето (рис. 2; как построить диаграмму Парето см. АВС-анализ и принцип Парето для бизнеса). Нежелательно, чтобы группа «прочие» факторы составляла большой процент. Если такое происходит, значит объекты наблюдения расклассифицированы неправильно и слишком много объектов попало в одну группу.
Рис. 2. Диаграмма Парето по видам дефектов
Дополнение от 30 ноября 2016 г. В версии Excel 2016 появились несколько типов новых диаграмм, которые широко применяются в менеджменте качества: диаграмма Парето, «ящик с усами», частотная гистограмма. Подробнее см. Новые диаграммы в Excel 2016
Глава 4. ДИАГРАММЫ ПРИЧИН И РЕЗУЛЬТАТОВ
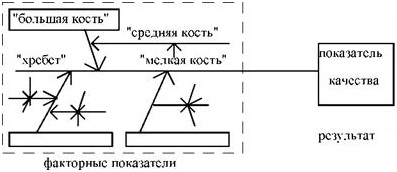
Результат процесса зависит от многочисленных факторов, между которыми существуют отношения типа причина результат. Диаграмма причин и результатов средство, позволяющее выразить эти отношения в простой и доступной форме. В 1953 г. профессор Токийского университета Каору Исикава, обсуждая проблему качества на одном заводе, суммировал мнение инженеров в форме диаграммы причин и результатов. Считается, что тогда этот подход был применен впервые. В японском промышленном стандарте дано следующее определение: диаграмма причин и результатов – диаграмма, которая показывает отношение между показателем качества и воздействующими на него факторами (рис. 3).
Рис. 3. Структура диаграммы причин и результатов (диаграмма «рыбий скелет»)
При построении диаграммы причин и результатов начните с выбора одного показателя качества и напишите его в середине правого края чистого листа бумаги. Слева направо проведите прямую линию («хребет»), а записанный показатель заключите в прямоугольник. Продолжайте наполнение диаграммы, идя от общих к частным причинам.
Постройте столько диаграмм причин и результатов, сколько показателей вы хотите исследовать. Выберите такие показатели качества и такие факторы, которые можно измерить. Установите важность каждой причины на основе объективных значений или данных. Использование диаграммы Парето в сочетании с диаграммой причин и результатов особенно полезно.
Глава 5. ГИСТОГРАММЫ
Вся совокупность рассматриваемых объектов называется генеральной совокупностью (популяцией). Один или несколько элементов, взятых из генеральной совокупности для получения информации о ней, называется выборкой. Данные, полученные на основе анализа выборки, служат основой для решений о генеральной совокупности. Организуя множество данных в гистограмму, мы можем получить о совокупности объективное представление.
В Excel есть несколько возможностей, позволяющих быстро изучить частотные закономерности: функция ЧАСТОТА (подробнее см. Функция массива ЧАСТОТА) и сводные таблицы (подробнее см. Группировка данных сводной таблицы в Excel 2013, раздел Группировка числовых полей).
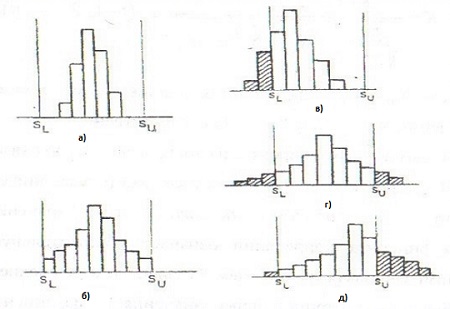
Если имеется допуск, то нанесите на гистограмму линии его границ, дабы сравнить распределение с этими границами. Тогда вы увидите, хорошо ли располагается гистограмма внутри границ (рис. 4).
Рис. 4. Гистограммы и границы поля допуска
Когда гистограмма удовлетворяет допуску, возможно, что: а) поддержание существующего состояния это все, что требуется, поскольку гистограмма вполне соответствует допускам; б) допуски удовлетворяются, но нет никакого запаса. Поэтому было бы лучше сократить разброс до меньшего значения. Когда гистограмма не удовлетворяет допуску, возможно, что: в) необходимо добиться смещения среднего ближе к центру поля допуска; г) потребуются действия, направленные на снижение вариации; д) одновременно потребуются меры, описанные в пунктах в) и г).
Типичной мерой для представления центра данных выборки служит среднее арифметическое:
но для генеральной совокупности среднее определяется (для дискретных значений):
или (для непрерывных значений):
где Р(х) – вероятность, a f(x) – плотность распределения случайной величины х.
Величина х̅ – среднее арифметическое полученных данных, она называется выборочным средним. Величина μ – среднее арифметическое всего множества, которое мы рассматриваем, она называется генеральным средним.
Дисперсия и стандартное отклонение принадлежат к мерам, используемым для выражения степени концентрации данных относительно их центра. Когда у нас есть n отдельных значений х1, x2, …, хn, их дисперсия дается выражением
а стандартное отклонение
Дисперсия генеральной совокупности получается из формулы
или
а стандартное отклонение, которое представляет собой корень квадратный из дисперсии, обозначается через σ.
Величины V и s – значения, получаемые из имеющихся данных, они называются выборочной дисперсией и выборочным стандартным отклонением соответственно. Величины σ2 и σ – значения, относящиеся к генеральной совокупности, их называют генеральной дисперсией и генеральным стандартным отклонением соответственно (подробнее о различии см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?).
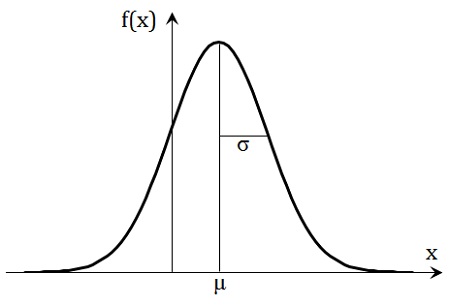
Есть множество видов распределений, но самое типичное из них нормальное распределение (рис. 5; подробнее см. Нормальное распределение. Построение графика в Excel. Концепция шести сигм).
Рис. 5. Нормальное распределение и его параметры (этот график построен в приложенном файле Excel)
Математически эту кривую можно представить следующим образом:
Вероятность того, что случайная величина х из распределения N(μ, σ2) окажется в пределах μ ± uσ показана на рис. 6. Теоретически нормальная переменная х может принимать любое значение от –∞ до +∞. Но из рисунка видно, что уже для u = 3 вероятность составит 99,7%. Это означает, что на практике мы можем пренебречь шансами, что х окажется за пределами u ± Зσ. Этот факт представляет собой важное правило нормального распределения, называемое правилом трех сигм. Оно служит основанием для определения контрольных пределов в контрольных картах.
Когда выясняется, что гистограмма следует нормальному распределению, часто предпринимается исследование воспроизводимости процесса. Оно важно при оценке того, сможет ли процесс пересечь границы поля допуска или нет. Если допустить, что процесс имеет нормальное распределение, то можно сразу же определить процент дефектов, оказавшихся за данными границами допуска при данных параметрах (μ, σ). Но более полезно оценить процесс с помощью индекса воспроизводимости процесса – СP.
При двусторонних границах допуска (верхней – SU и нижней – SL):
При односторонних границах допуска (либо SU, либо SL):
или
А вот как оценивается процесс с помощью СP:
1) 1,33 ≤ СP – вполне удовлетворительно;
2) 1,00 ≤ СP < 1,33 – адекватно;
3) Ср < 1,00 – неадекватно.
Глава 6. ДИАГРАММЫ РАССЕИВАНИЯ
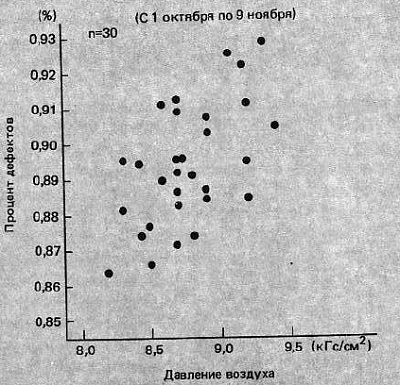
Для изучения зависимостей между двумя переменными, такими, как скорость токарного станка и размер детали или концентрация и удельный вес, мы можем воспользоваться так называемой диаграммой рассеивания (рис. 6).
Рис. 6. Диаграмма рассеивания для давления сжатого воздуха и процента дефектов
Точно так же, как по гистограмме можно распознать форму распределения, по диаграмме рассеивания можно представить себе общее распределение пар. Степень корреляции можно выразить количественно с помощью коэффициента корреляции (подробнее см. Ковариация и коэффициент корреляции).
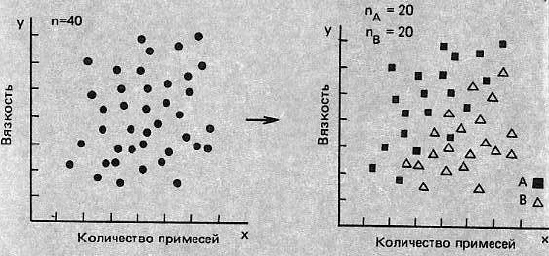
Метод суждения о существовании корреляции с помощью построения диаграмм рассеивания и вычисления коэффициента корреляции, называется корреляционным анализом. На рис. 7 слева, где данные двух компаний А и В объединены и обезличены, кажется, что корреляции не должно быть, но стоит только выделить компании и корреляция сразу проявляется (рис. 7 справа). Если есть какой-нибудь стратифицирующий фактор, то после разделения данных на отдельные слои и обозначения их разными цветами или символами мы можем получить жизненно важную информацию.
Рис. 7. Расслоение на диаграмме рассеивания
Даже если коэффициент корреляции высок, это совсем не обязательно указывает на причинно-следственную связь. Корреляция такого рода называется ложной корреляцией.
Если у пары переменных выявлена корреляция, можно построить линейную зависимость одной переменной от другой: у = α + βx. Такая прямая обычно называется линией регрессии, где у – отклик (зависимая переменная), а х объясняющая (независимая) переменная, фактор. Кроме того, α – называется константой (свободным членом) и β – коэффициентом регрессии (угловым коэффициентом). Количественный подход к представлению связи между х и у, отыскиваемой в виде линии регрессии, называется регрессионным анализом (подробнее см. Простая линейная регрессия).
Глава 7. КОНТРОЛЬНЫЕ КАРТЫ
Впервые контрольные карты были предложены в 1924 г. Уолтером Шухартом, работавшим в Bell Telephone Laboratories, с намерением исключить необычную вариацию, отделяя вариации, которые обусловлены определенными причинами, от тех, что обусловлены случайными причинами. Всякая контрольная карта состоит из центральной линии, пары контрольных пределов, по одному над и под центральной линией, и значений характеристики (показателя качества), нанесенных на карту для представления состояния процесса. Если все эти значения оказываются внутри контрольных пределов, не проявляя каких бы то ни было тенденций, то процесс рассматривается как находящийся в контролируемом состоянии. Если же, напротив, они попадут за контрольные пределы или примут какую-нибудь необычную форму, то процесс считается вышедшим из-под контроля.
Для такой вариации есть различные причины, которые можно разделить на следующие два вида. Случайная причина. Вариация, обусловленная случайными причинами, неизбежно встречается в любом процессе, даже если технологическая операция проводится с использованием стандартных сырья и методов. В настоящее время исключение случайных причин непрактично технически и экономически. Определенная причина. Вариация, обусловленная определенной причиной, означает, что существуют факторы, допускающие изучение. Этих воздействий можно избежать и нельзя упускать такую возможность: бывают случаи, когда изменения вызваны несоблюдением стандартов (подробнее о теории и практике контрольных карт см. Дональд Уилер, Дэвид Чамберс. Статистическое управление процессами; шаблон и формулы для Excel – см. Пример построения контрольной карты Шухарта в Excel).
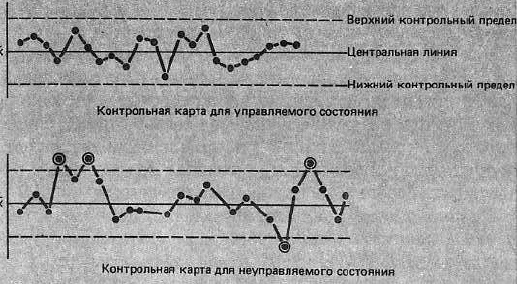
Рис. 8. Примеры контрольных карт
Что важнее всего в процессе управления, так это точное понимание положения объекта управления с помощью чтения контрольной карты и быстрое осуществление подходящих действий, как только в объекте обнаружится что-нибудь необычное. Контролируемое состояние объекта – это такое состояние, когда процесс стабилен, а его среднее и разброс не меняются. Находится ли процесс в данном состоянии или нет, определяется по контрольной карте на основании следующих критериев.
- Выход за контрольные пределы. Точки, которые лежат вне контрольных пределов.
- Серия – это проявление такого состояния, когда точки, хотя и не вышли за контрольные границы, но демонстрируют определенные закономерности (подробнее см. Контрольные карты Шухарта. Правила определения отсутствия управляемости).
- неизменно оказываются по одну сторону от средней линии; число таких точек называется длиной серии.
Разбиение на подгруппы наиболее важная часть подготовки контрольной карты, определяющая ее работоспособность. Неподходящий способ разбиения дает бесполезную карту (подробнее см. Рациональная группировка данных при построении контрольной карты Шухарта).
Вариация данных делится на внутригрупповую и межгрупповую. Межгрупповая вариация – это та вариация, которая проявляется в каждой подгруппе и обнаруживается в значении R̅ на R-карте. С другой стороны, межгрупповая вариация – это как раз то, что проявляется между подгруппами и выявляется в распределении точек х̅ на х̅-карте.
Когда одна и та же продукция производится на нескольких станках или несколькими рабочими, собираемые данные лучше классифицировать в соответствии с этими станками или рабочими, т.е. чтобы можно было анализировать различия между станками или рабочими. Цель расслоения заключается в выявлении различий в средних значениях и вариациях между разными классами и в измерении этих различий, если они проявятся.
Если для анализа какого-либо вопроса используются контрольные карты, то они, как правило, применяются не отдельно, а вместе с гистограммами (массу примеров вы найдете в У. Эдвардс Деминг. Выход из кризиса: Новая парадигма управления людьми, системами и процессами). Надо группировать данные таким образом, чтобы сделать внутригрупповую вариацию настолько случайной, насколько это возможно, превращая вариацию, обусловленную проявлениями процесса в межгрупповую вариацию.
Когда в состоянии процесса обнаруживаются технические изменения, контрольные линии надо пересматривать. Для введения процесса в целом в контролируемое состояние прежде всего следует представить себе вклад факторов в флуктуацию процесса и избегать ненормальных изменений этих факторов. А чтобы этого достигнуть, нужна стандартизация технологических приемов и методов.
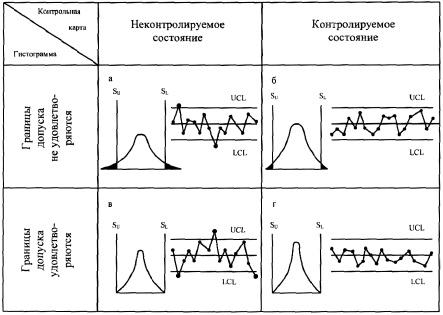
Даже если процесс и находится в контролируемом состоянии, все равно может производиться некондиционная продукция и наоборот. Расстояние между контрольными пределами определяется вариацией, обусловленной случайными причинами. Границы поля допуска, напротив, выбираются в зависимости от требований потребителя или пользователя (рис. 9).
Рис. 9. Сравнение контрольных карт с границами допуска
Вы, вероятно, встретитесь с одним из следующих случаев (см. буквенные обозначения на рис. 9):
- процесс в неконтролируемом состоянии, а значит, производится брак;
- процесс в контролируемом состоянии, но тем не менее брак есть;
- процесс в неконтролируемом состоянии, но брака нет;
- процесс в контролируемом состоянии, а значит, брака нет.
Глава 8. АДДИТИВНОСТЬ ДИСПЕРСИЙ
Если x1, х2, …, хn – независимые случайные величины и их средние и дисперсии соответственно равны µ1, µ2, …, µn и σ1, σ2, …, σn, то математическое ожидание и дисперсия их алгебраической суммы
(12) y = a1x1 + a2x2 + … + anxn
составят:
(13) µy = a1µ1 + a2µ2 + … + anµn
и
В последней формуле, поскольку складываются квадраты коэффициентов, дисперсия получается суммой, даже если в выражение входят разности случайных величин. Это свойство называется аддитивностью дисперсий.
Если измерения суть выборки одного размера из генеральной совокупности со средним µ и генеральной дисперсией σ2, то, положив в формулах (12)–(14) a1 = a2 = … = an = 1/n, получим:
(16) µy = µ
Это и есть хорошо известные формулы для распределения выборочного среднего.
При работе с выборками присутствуют ошибки двух видов. Один из них называется ошибкой выборки и встречается, когда из партии берется выборка, а другой называется ошибкой измерений и возникает в процессе анализа.
Если измерения повторялись n раз, дисперсия среднего значения умножается на 1/n. Однако если ошибки возникают на отдельных стадиях, то компоненты дисперсии уменьшаются по-разному в зависимости от того, на какой стадии сделаны повторения. Ошибки можно разделить на две категории: смещения и вариации. Тогда как вариация уменьшается при повторении измерений, смещения остаются неизменными, сколько ни повторяй наблюдения, и усреднение не ведет к их уменьшению (о смещенной и несмещенной оценке см. подробнее СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?).
Аддитивность дисперсий хорошо служит, пока случайные величины взаимно независимы. Если х и у зависимы с коэффициентом корреляции –1 ≤ ρ ≤ 1, то
Если детали выбираются случайно и соединяются, дисперсия сумм и разностей их размеров всегда будет равна сумме дисперсий всех деталей, поскольку имеет место аддитивность дисперсий, и эта общая дисперсия должна быть всегда больше, чем дисперсии отдельных размеров. Традиционный путь снижения общей дисперсии изделий заключается в снижении дисперсий отдельных деталей. Если, однако, для данной продукции по технологическим причинам это слишком трудно сделать, то приходится вместо случайного выбора деталей прибегать к подбору наиболее подходящих «партнеров».
В промышленности часто имеет место массовое производство одного и того же вида продукции. Надо стремиться обеспечивать минимум вариации показателей качества такой продукции, и достижение этого одна из главных задач контроля качества. Вариации показателей качества обусловлены изменениями большого числа факторов, влияющих на эти показатели. Могут встретиться многообразные сочетания следующих четырех элементов:
- вариации в материалах;
- вариации в станках и оборудовании;
- вариации в людях и методах (рабочие и методы работы);
- вариации в измерениях.
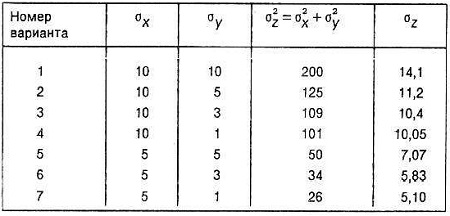
Из теоремы об аддитивности дисперсий мы можем вывести следующий важный закон: «Для уменьшения общей дисперсии снижайте наибольшую дисперсию» (рис. 10).
Рис. 10. Уменьшение наибольшей дисперсии для снижения общей дисперсии
Видно, что при переходе от варианта 2 к варианту 4, когда σy сокращается на 4 единицы, суммарная дисперсия σz сокращается всего лишь на 1,15. В тоже время при переходе от варианта 2 к варианту 5, когда σx сокращается на 5 единиц, суммарная дисперсия σz сокращается на 4,15.
Глава 9. ВВЕДЕНИЕ В ТЕОРИЮ СТАТИСТИЧЕСКОГО ВЫВОДА
Если первые 8 глав были посвящены сугубо практическим вопросам, то обнаружить такую девятую главу мне было довольно странно. На мой взгляд, эта теоретическая часть не соответствует духу книги, и, пожалуй, противоречит словам авторов, что прочитать книгу может человек без специальной математической подготовки. Поэтому подробное изложение этой главы я вынес в отдельную заметку – см. Введение в теорию статистического вывода. Также могу рекомендовать: Проверка гипотез: одновыборочные критерии и Фишер. Статистический вывод. — Прим. Багузина.
Глава 10. ЗАМКНУТЫЙ ЦИКЛ УПРАВЛЕНИЯ КАЧЕСТВОМ
Управление качеством это процедура решения проблем. Она представляет собой замкнутый цикл. Решение проблемы осуществляется в ходе следующих семи этапов:
- Поиск проблемы: выявление конкретной проблемы.
- Наблюдения: вникание в суть проблемы.
- Анализ: отыскание главных причин.
- Проведение мероприятий: осуществление действий по устранению причин.
- Проверка: подтверждение эффективности действий.
- Стандартизация: постоянное устранение причин.
- Окончание работы: оценка действий и планирование дальнейшей работы.
Эпилог. ФАКТЫ
Главные причины трудностей, возникающих на производстве, ложные представления и ошибочные действия. Каждый считает, что именно он знает факты, а на самом деле не знает никто. Это напоминает историю о слепцах, которые ощупывали слона. Бесконечные обсуждения не устраняют трудностей. Факты не всегда можно описать словами. Измеряйте!
Человека, который долгое время занимается какой-нибудь одной работой, мы называем опытным. Опытный человек накопил большие знания о своем деле. Но знания бывают верными и неверными. Проблема состоит в том, что он не знает, что верно, а что ошибочно. Настоящий эксперт – это такой опытный человек, который постоянно соотносит свои знания с фактами, проверяет их и вносит поправки.
Кэнко-хоси: «…рассказы низкородных людей особенно насыщены поражающими слух происшествиями. Мудрый человек удивительных историй не рассказывает».