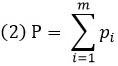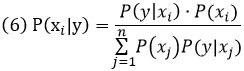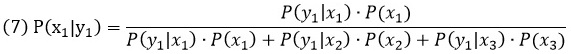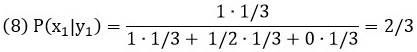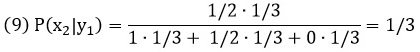В книге выдающегося французского математика, физика и астронома Пьера Лапласа (1749–1827) представлено популярное изложение основ теории вероятностей и ее приложений. Совершенно без формул дается свод почти всех главных вопросов этой теории; приводятся общие принципы исчисления вероятностей, описываются аналитические методы и законы вероятностей. Особое внимание в работе уделяется приложению теории вероятностей к различным вопросам жизни, большинство которых, по мнению Лапласа, есть не что иное, как задачи теории вероятностей. Рассматривается приложение этой теории к натуральной философии и нравственным наукам; исследуется вероятность свидетельских показаний и судебных приговоров, анализируются результаты выборов и решения собраний с точки зрения теории вероятностей, затрагивается вопрос об иллюзиях в оценке вероятностей. Работа широко цитируется в современной литературе. Я решил оставить русский перевод 1908-го года, и снабдить его комментариями.
Пьер Симон Лаплас. Опыт философии теории вероятностей. – М.: Книжный дом «ЛИБРОКОМ», 2011. — 208 с. (книга впервые опубликована в 1814 г.; на старорусский язык книга переведена в 1908 г.; настоящее издание является репринтным).
Скачать конспект (краткое содержание) в формате Word или pdf
Купить книгу на Ozon
О вѣроятности
Всякое имѣющее мѣсто явленіе связано съ предшествующимъ на основаніи того очевиднаго принципа, что какое-либо явленіе не можетъ возникнуть безъ производящей его причины. Эта аксіома, извѣстная подъ именемъ «принципа достаточнаго основанія». Мы должны разсматривать настоящее состояніе вселенной какъ слѣдствіе ея предыдущаго состоянія и какъ причину послѣдующаго.
Далее следует одно из самых широко цитируемых выражений, в котором Лаплас выступает, как сторонник детерминизма
Умъ, которому были бы извѣстны для какого-либо даннаго момента всѣ силы, одушевляющія природу, и относительное положеніе всѣхъ ея составныхъ частей, еслибы вдобавокъ онъ оказался достаточно обширнымъ, чтобы подчинить эти данныя анализу, обнялъ бы въ одной формулѣ движенія величайшихъ тѣлъ вселенной наравнѣ съ движеніями легчайшихъ атомовъ: не осталось бы ничего, что было бы для него недостовѣрно, и будущее, также какъ и прошедшее, предстало бы передъ его взоромъ.
Теорія случайностей состоитъ въ томъ, чтобы свести всѣ однородныя явленія къ извѣстному числу равно возможныхъ случаевъ, т.-е. такихъ, существованіе которыхъ для насъ было бы одинаково неопредѣленно, и опредѣлить число случаевъ, благопріятствующихъ явленію, вѣроятность котораго отыскивается. Отношеніе этого числа къ числу всѣхъ возможныхъ случаевъ и есть мѣра этой вѣроятности, которая такимъ образомъ ие что иное, какъ дробь, числитель которой есть число всѣхъ благопріятныхъ случаенъ, а знаменатель—число всѣхъ возможныхъ случаевъ.
Общіе принципы исчисленія вѣроятностей
I-ый принципъ. Вѣроятность – есть отношеніе числа случаевъ благопріятствующихъ къ числу всѣхъ возможныхъ случаевъ.
где m – благоприятные исходы, n – все исходы; для случая, когда вероятности всех исходов равны.
II-ой принципъ. При этомъ различные случаи предполагаются равно возможными. Если же это не такъ, то сперва опредѣляютъ ихъ соотвѣтственныя возможности, точная оцѣнка которыхъ является однимъ изъ самыхъ деликатныхъ пунктовъ теоріи случайностей. Тогда вѣроятность будетъ суммою возможностей каждаго благопріятнаго случая.
где i – благоприятные исходы, pi – вероятность i-го благоприятного исхода; m – число благоприятных исходов; для случая, когда вероятности исходов не равны.
III-ій принципъ. Если событія независимы одно отъ другого, вѣроятность существованія ихъ совмѣстности есть произведеніе ихъ частныхъ вѣроятностей.
Вероятность наступления двух независимых событий равно произведению их вероятностей:
где Р(х,у) – вероятность одновременного наступления событий х и у, Р(х) – вероятность наступления события х, Р(у) – вероятность наступления события у.
IV-ый принципъ. Если два событія находятся въ зависимости другъ отъ друга, вѣроятность сложнаго событія есть произведеніе вѣроятности перваго событія на вѣроятность того, что, когда оно совершилось, совершится и второе.
Вероятность одновременного наступления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло:
где Р(х,у) – вероятность одновременного наступления событий х и у, Р(х) – вероятность наступления события х, Р(у) – вероятность наступления события у, Р(у|х) – условная вероятность наступления события у при условии, что событие х наступило, Р(х|у) – условная вероятность наступления события х при условии, что событие у наступило.
Ѵ-ый принципъ. Если вычислить а priori вѣроятность совершившагося событія и вѣроятность событія, состоящаго изъ этого перваго и изъ другого, которое ожидается, то вторая вѣроятность, дѣленная на первую, будетъ вѣроятностью ожидаемаго событія, выведенною изъ наблюденнаго событія.
Дается определение условной вероятности, которое может быть выведено из (4)
VI-ой принципъ. Каждая изъ причинъ, которой можетъ быть приписано наблюденное событіе, тѣмъ болѣе правдоподобна, чѣмъ болѣе вѣроятно, что при существованіи этой причины событіе будетъ имѣть мѣсто; вѣроятность существованія какой-либо изъ этихъ причинъ равна, слѣдовательно, дроби, числитель которой есть вѣроятность событія, вытекающая изъ этой причины, а знаменатель есть сумма подобныхъ вѣроятностей, относящихся ко всѣмъ причинамъ; если эти различныя причины, разсматриваемыя а priori, не одинаково вѣроятны, то вмѣсто вѣроятности событія, вытекающей изъ каждой причины, слѣдуетъ взять произведеніе этой вѣроятности на вѣроятность самой причины. Это основной принципъ той отрасли анализа случайностей, которая занимается переходамъ отъ событій къ причинамъ.
А это уже теорема Байеса! В общем виде, как она сформулирована выше у Лапласа, она имеет вид:
На мой взгляд, обычный человек, впервые сталкиваясь с теоремой Байеса, как правило остается в недоумении – теорема обескураживает, а ее смысл прячется за формулами. Я довольно много читал о теореме Байеса, и с каждым разом мне казалось, что я понимаю ее всё лучше и лучше. Я даже написал довольно большую заметку, обобщив свои наблюдения (подробнее см. Идеи Байеса для менеджеров). И вот, читая Лапласа, я продвинулся еще на шаг в понимании сути теоремы. А помогла мне вот эта фраза:
Это основной принципъ той отрасли анализа случайностей, которая занимается переходамъ отъ событій къ причинамъ.
Не от причин к событиям, а наоборот. Вопрос звучит не «в чем причина события?», а «каковы закономерности, что они привели к появлению такого (а не иного) события?» (см. также Формула Байеса)
Представьте, что у вас есть три гипотезы. Например, в урне могут быть, либо два белых шара, либо один белый и один черный, либо два черных. Все гипотезы равновероятны. Или на языке Байеса: априорная вероятность каждой гипотезы = 1/3. Вы проводите эксперимент, и вытаскиваете один шар. И его цвет – белый. Наступило событие, которое изменяет вероятности первоначальных гипотез. Без какой-либо теоремы Байеса очевидно, что теперь вероятность гипотезы о двух черных шарах = 0. А вот как подсчитать вероятности двух оставшихся гипотез!? В терминологии Байеса вероятности гипотез после наступления события называются апостериорными.
Что делает теорема Байеса? Она дает возможность на основании априорных вероятностей гипотез и вероятностей наступления событий, подсчитать апостериорные вероятности гипотез. Первоначально мы имели три гипотезы. То, что мы вытащили белый шар, позволило нам полностью исключить одну гипотезу (оба шара – черные), но интуитивно кажется, что из двух оставшихся гипотез более вероятно, что оба шара белые. Проверим это с помощью теоремы Байеса. Для нашего случая (три гипотезы и два события) она принимает вид:
х – случайная величина (гипотеза), принимающая значения: х1 – два белых, х2 – один белый, один черный; х3 – два черных; у – случайная величина (событие; появление шара), принимающая значения: у1 – вытащен белый шар и у2 – вытащен чёрный шар; р(х1) – вероятность первой гипотезы до вытаскивания шара (априорная вероятность) = 1/3; р(х2) – вероятность второй гипотезы до вытаскивания шара = 1/3; р(х3) – вероятность третьей гипотезы до вытаскивания шара = 1/3; р(у1|х1) – вероятность вытащить белый шар, в случае, если верна первая гипотеза (шары белые) = 1; р(у1|х2) – вероятность вытащить белый шар, в случае, если верна вторая гипотеза (один шар белый, второй – черный) = ½; р(у1|х3) – вероятность вытащить белый шар, в случае, если верна третья гипотеза (оба черных) = 0; и, наконец, то, что мы ищем – р(х1|у1) – вероятность того, что верна первая гипотеза (оба шара белых), при условии, что мы вытащили белый шар. Вот она кульминация: не от причины к событию, а от события к прояснению первоначальной гипотезы.
Вероятность того, что верна вторая гипотеза (один шар белый, второй – черный), при условии, что мы вытащили белый шар:
VII-ой принципъ. Вѣроятность будущаго событія есть сумма произведеній вѣроятности каждой причины, выведенной изъ наблюденнаго событія, на вѣроятность того, что при существованіи этой причины будущее событіе будетъ имѣть мѣсто.
А это знаменатель в теореме Байеса. Применительно к изложенному выше примеру, вероятность вытащить белый шар есть сумма произведений: вытащить белый, если верна первая гипотеза на вероятность первой гипотезы + вытащить белый, если верна вторая гипотеза на вероятность второй гипотезы + вытащить белый, если верна третья гипотеза на вероятность третьей гипотезы:
Представимъ себѣ урну, содержащую только два шара, каждый изъ которыхъ пусть будетъ бѣлымъ или чернымъ. Вынимаютъ одинъ изъ этихъ шаровъ, который кладутъ затѣмъ обратно въ урну, чтобы приступить къ новому тиражу. Предположимъ, что при первыхъ двухъ тиражахъ появились бѣлые шары; спрашивается, какова вѣроятность новаго появленія бѣлаго шара при третьемъ тиражѣ.
Продолжим пример выше. В урне два шара, либо оба белых, либо один белый и один черный, либо два черных. Мы вынули белый шар и вернули его обратно. Во второй попытке опять вынули белый, и вернули его в урну. Спрашивается, какова вероятность, что и третий раз мы вытащим белый шар?
Если верна первая гипотеза, вероятность вытащить два белых подряд P(y1│x1) = 1. Если верна вторая гипотеза, вероятность вытащить два белых подряд P(y1│x2) = ¼. Если верна третья гипотеза P(y1│x3) = 0. Всего 5/4 разных шансов. Причем вероятность первой гипотезы = 1:5/4 = 4/5, а вероятность второй гипотезы = 1/4:5/4 = 1/5. С другой стороны, если верна первая гипотеза вероятность вытащить белый шар в третьем раунде = 1. Если верна вторая гипотеза вероятность вытащить белый шар в третьем раунде = ½. Итого, вероятность вытащить белый шар в третий раз = 1*4/5 + 1/5*1/2 = 9/10.
Объ ожиданіи
Математическое ожиданіе равна произведенію ожидаемой суммы на вѣроятность ея полученія.
VIII-ой принципъ. Если выгода зависитъ отъ многихъ событій, то, беря сумму произведеній вѣроятности каждаго событія на благо, связанное съ его наступленіемъ, мы получимъ эту выгоду.
IX-ый принципъ. Имѣя рядъ вѣроятныхъ событій, изъ которыхъ одни приносятъ прибыль, а другія убытокъ, мы узнаемъ выгоду, которая изъ нихъ послѣдуетъ, составляя сумму произведеній вѣроятности каждаго благопріятнаго событія на приносимую имъ прибыль и отнимая отъ этой суммы сумму произведеній вѣроятности каждаго неблагопріятнаго событія на связанный съ нимъ убытокъ. Если вторая сумма превосходитъ первую, то прибыль обращается въ убытокъ, а надежда въ страхъ.
Слѣдующій вопрос очень занимал геометровъ. Павелъ играетъ въ крестъ и рѣшетку съ условіемъ, что онъ получаетъ два франка, если у него выпадетъ крестъ при первомъ бросаніи, четыре франка, если онъ выпадетъ лишь при второмъ бросаніи, восемь франковъ, если онъ выпадетъ лишь при третьемъ и т.д. Его ставка въ игрѣ должна быть, согласно восьмому принципу, равна числу бросаній; такъ что, если партія продолжается до безконечности, то его ставка должна быть безконечною. Между тѣмъ ни одинъ разумный человѣкъ не пожелалъ бы поставить въ этой игрѣ даже умѣренную сумму, пятьдесятъ франковъ, напр. Откуда происходитъ эта разница между результатомъ исчисленія и указаніями здраваго смысла? Скоро узнали, что она зависитъ отъ того, что нравственная выгода, доставляемая намъ какимъ-либо благомъ, не пропорціональна этому благу, и что она зависитъ отъ тысячи обстоятельствъ, часто съ трудомъ поддающихся опредѣленію, самымъ общимъ и важнымъ изъ которыхъ является однако состояніе. Слѣдуетъ поэтому отличать въ ожидаемомъ благѣ его абсолютную цѣнность отъ цѣнности относительной: эта послѣдняя зависитъ отъ мотивовъ, заставляющихъ желать его, въ то время какъ первая отъ этого независима. Нельзя дать общаго принципа для оцѣнки этой относительной цѣнности. Вотъ однако принципъ, предложенный Даніиломъ Бернулли, и могущій быть полезнымъ во многихъ случаяхъ.
Х-ый принципъ. Относительная цѣнность безконечно малой суммы равна ея цѣнности абсолютной, дѣленной на все имущество заинтересованнаго лица. Здѣсь предполагается, что всякій человѣкъ имѣетъ какое-либо имущество, цѣнность котораго ни въ какомъ случаѣ не можетъ предполагаться равною нулю. Въ самомъ дѣлѣ, даже тотъ, кто ничѣмъ не обладаетъ, все же придаетъ произведенію своихъ трудовъ и своихъ надеждъ цѣнность, по крайней мѣрѣ равную тому, что какъ разъ необходимо, чтобы жить.
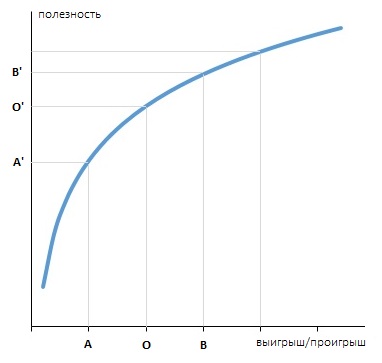
Это, так называемый, принцип убывающей полезности (рис. 1).
Рис.1. Принцип убывающей полезности
Если вы владеете состоянием О, то выигрыш ОВ и проигрыш ОА фактически равны, но ощущаемая вами их полезность О’B’ и O’A’ различаются. Причем полезность выигрыша меньше полезности (вреда) проигрыша. Этим законом, в частности, объясняется не склонность людей к риску. Стремление выиграть не столь велико, как боязнь потерь. Подробнее см. Даниил Бернулли. Опыт новой теории измерения жребия.
О неизвѣстныхъ неравенствахъ, которыя могутъ существовать между шансами, предполагаемыми равными
Неравенства этого рода оказываютъ значительное вліяніе, заслуживающее особаго вниманія, на результаты исчисленія вѣроятностей. Разсмотримъ игру въ крестъ и рѣшетку и предположимъ, что обѣ стороны монеты выпадаютъ съ одинаковою легкостью; тогда вѣроятность выпаденія креста при первомъ бросаніи равна 1/2, а вѣроятность его выпаденія два раза подъ рядъ равна 1/4. Но, если въ монетѣ существуетъ неравенство, заставляющее одну изъ сторонъ выпадать преимущественно передъ другой, и неизвѣстно, которой сторонѣ благопріятствуетъ это неравенство, то вѣроятность выпаденія креста при первомъ бросаніи будетъ все еще 1/2, потому что при нашемъ незнаніи стороны, которой благопріятствуетъ это неравенство, вѣроятность простого событія настолько же увеличивается, если это неравенство ей благопріятствуетъ, насколько она уменьшается, если неравенство ей не благопріятствуетъ.
Но при томъ же незнаніи вѣроятность выпаденія креста два раза подъ рядъ увеличивается. Въ самомъ дѣлѣ, эта вѣроятность является вѣроятностью выпаденія креста при первомъ бросаніи, умноженною на вѣроятность того, что послѣ выпаденія при первомъ бросаніи онъ выпадетъ при второмъ; но выпаденіе его при первомъ бросаніи даетъ поводъ думать, что неравенство монеты ему благопріятствуетъ; значитъ неизвѣстное неравенство увеличиваетъ въ такомъ случаѣ вѣроятность выпаденія креста при второмъ бросаніи; оно увеличиваетъ, слѣдовательно, произведеніе обѣихъ вѣроятностей.
Для того, чтобы подвергнуть этотъ вопросъ исчисленію, предположимъ, что это неравенство увеличиваетъ на одну двадцатую вѣроятность простого событія, которому оно благопріятствуетъ. Если это событіе есть выпаденіе креста, вѣроятность его будетъ равна 1/2 плюсъ 1/20 или 11/20, а вѣроятность его двукратнаго выпаденія сряду будетъ равна квадрату 11/20, или 121/400. Если благопріятствуемое событіе есть выпаденіе рѣшетки, то вѣроятность креста будетъ равна 1/2 минусъ 1/20 или 9/20, вѣроятность его двукратнаго выпаденія сряду будетъ равна 81/400. Такъ какъ нѣтъ никакого основанія думать напередъ, что неравенство благопріятствуетъ одному изъ этихъ событій преимущественно передъ другимъ, то ясно, что для нахожденія вѣроятности сложнаго событія—крестъ крестъ, надо сложить обѣ предшествующія вѣроятности и взять половину ихъ суммы, что даетъ 101/400 для этой вѣроятности, превышающей 1/4 на 1/400 или на квадратъ приращенія 1/20, на которое неравенство увеличиваетъ возможность благопріятствуемаго имъ событія.
Подобнымъ же образомъ вѣроятность выпаденія рѣшетка рѣшетка равна 101/400, но каждая изъ вѣроятностей выпаденія крестъ рѣшетка или рѣшетка крестъ равна только 99/400, ибо сумма этихъ четырехъ вѣроятностей должна равняться достовѣрности или единицѣ. Такимъ образомъ обыкновенно оказывается, что постоянныя и неизвѣстныя причины, которыя благопріятствуютъ простымъ событіямъ, считающимся равно возможными, всегда увеличиваютъ вѣроятность повторенія одного и того же простого событія.
О законахъ вѣроятности, вытекающихъ изъ неопредѣленнаго увеличенія числа событій
Въ кругу непостоянныхъ и неизвѣстныхъ причинъ, которыя мы разумѣемъ подъ именемъ случая и которыя дѣлаютъ ходъ событій непостояннымъ и неправильнымъ, по мѣрѣ увеличенія ихъ числа возникаетъ замѣтная, поразительная правильность, которая кажется зависящей отъ преднамѣренности и которую считали доказательствомъ Провидѣнія. Но, размышляя объ этомъ, мы скоро убѣждаемся, что эта правильность есть не что иное какъ раскрытіе соотвѣтственныхъ возможностей простыхъ событій, которыя должны случаться чаще, когда они болѣе вѣроятны.
Отсюда вытекаетъ слѣдующая теорема знаменитого геометра Якова Бернулли: «Вѣроятность того, что отношеніе числа изъятыхъ бѣлыхъ шаровъ къ числу всѣхъ вышедшихъ шаровъ не уклонится, сверхъ даннаго интервала, отъ отношенія числа содержащихся въ урнѣ бѣлыхъ шаровъ къ числу всѣхъ шаровъ, неопредѣленно приближается къ достовѣрности при неопредѣленномъ увеличеніи числа событій, какъ бы малъ ни былъ предполагаемый интервалъ».
Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая. На этом свойстве основаны методы оценки вероятности на основе анализа конечной выборки. Наглядным примером является прогноз результатов выборов на основе опроса выборки избирателей.
Это обстоятельство дѣлаетъ прибыль отъ лотерей такою же вѣрною, какъ продукты земледѣлія въ виду того, что шансы, которые онѣ представляютъ себѣ, обезпечиваютъ имъ выгоду при большомъ числѣ ставокъ.
Если примѣнить эту теорему къ отношенію рожденій мальчиковъ къ рожденіямъ дѣвочекъ, наблюдавшемуся въ различныхъ странахъ Европы, то окажется, что это отношеніе, повсюду приблизительно равное отношенію 22 къ 21, указываетъ съ крайнею вѣроятностью на большую легкость рожденій мальчиковъ.
Современная демография подтверждает эту статистику. См., например, Почему чаще рождаются мальчики.
Приложеніе теоріи вѣроятностей къ натуральной философіи
Явленія природы сопровождаются по большей части столькими посторонними обстоятельствами, вліяніе многочисленныхъ возмущающихъ причинъ настолько къ нимъ примѣшивается, что становится очень труднымъ познавать ихъ. Достигнуть этого можно только повторнымъ наблюденіемъ и опытомъ, чтобы постороннія вліянія взаимно уничтожались, и средніе результаты сдѣлали бы очевидными эти явленія и ихъ различные элементы. Съ помощью теоріи вѣроятностей опредѣляютъ затѣмъ самые подходящіе (выгодные) средніе результаты, или такіе, которые оставляютъ всего менѣе мѣста ошибкѣ. Правило сводится къ тому, чтобы сдѣлать minimum’омъ сумму квадратовъ ошибокъ наблюденій.
Сегодня это правило известно, как метод наименьших квадратов. См., например, Простая линейная регрессия и Анализ временных рядов.
При разсмотрѣніи вѣроятностей узналъ я также причину вѣкового ур-ія луны. Новѣйшія наблюденія этого свѣтила, будучи сравнены съ прежними затменіями, указали астрономамъ на ускореніе въ движеніи луны; но геометры, и особенно Лагранжъ, послѣ безуспѣшнаго исканія членовъ, oтъ которыхъ зависитъ это ускореніе, въ возмущеніяхъ, испытываемыхъ этимъ движеніемъ, отбросили это ускореніе. Внимательное разсмотрѣніе старыхъ и новѣйшихъ наблюденій, а также промежуточныхъ затменій, наблюдавшихся арабами, показало мнѣ, что указанія на него имѣютъ большую вѣроятность. Съ этой точки зрѣнія я снова разсмотрѣлъ лунную теорію, и я нашелъ, что вѣковое ур-іе луны происходитъ отъ дѣйствія солнца на этого спутника въ связи съ вѣковымъ измѣненіемъ эксцентриситета земной орбиты, а это меня привело къ открытію вѣковыхъ ур-ій движеній узловъ и перигелія лунной орбиты, ур-ій, о которыхъ и не подозрѣвали астрономы. Весьма замѣчательное соотвѣтствіе этой теоріи со всѣми древними и новѣйшими наблюденіями сдѣлали ее въ высшей степени очевидной.
Современные методы с использованием ЭВМ позволили уточнить теорию Лапласа. См., например, Теория движения Луны.
Я обращусь теперь къ разсмотрѣнію земли и жидкостей, покрывающихъ ее. Явленіемъ, могущимъ пролить больше всего свѣта на правильность ея пластовъ, оказывается измѣненіе тяжести на ея поверхности. Это измѣненіе опредѣляется либо посредствомъ перенесенія въ разныя мѣста одного и того же маятника, при чемъ считаютъ число его колебаній въ извѣстный промежутокъ времени; либо непосредственнымъ измѣреніемъ длины секунднаго маятника. Опыты эти легки и могутъ быть теперь чрезвычайно точны. Если земля представляетъ эллипсоидъ вращенія, то ея сжатіе 1/272. Слѣдовательно, будетъ больше четырехъ тысячъ шансовъ противъ одного за то, что сжатіе земли меньше этой дроби. Милліоны милліардовъ шансовъ противъ одного будутъ за то, что оно меньше того, которое соотвѣтствуетъ однородности земли.
По современным данным сжатие Земли оценивается в 1/298.
По предложенію Академіи Наукъ въ началѣ прошлаго столѣтія были произведены въ Брестѣ наблюденія надъ приливомъ и отливомъ, продолжавшіяся въ теченіе’шести лѣтъ подъ рядъ. Тамъ дѣйствительно замѣчается большая правильность. Пораженный этой правильностью, я обратился къ правительству съ просьбой повелѣть произвести въ Брестѣ новый рядъ наблюденій въ продолженіе всего періода движенія узловъ лунной орбиты, что и было исполнено. Эти наблюденія начались съ перваго іюня 1806-го года и съ того времени продолжаются безъ перерыва до сихъ поръ. Они представили мнѣ слишкомъ благопріятный случай примѣнить мои формулы вѣроятности къ одному изъ величайшихъ явленій природы. Я нашелъ, что они съ большой вѣроятностью устанавливали законы высотъ и промежутковъ между приливами и отливами въ зависимости отъ фазъ луны, временъ года и разстояній луны и солнца до земли.
Мы такъ далеки отъ знанія всѣхъ силъ природы и ихъ различныхъ проявленій, что было бы мало научно отрицать явленія, только потому что они необъяснимы при современномъ состояніи нашихъ знаній. Мы должны только изслѣдовать ихъ съ тѣмъ большими вниманіемъ и тщательностью, чѣмъ намъ кажется труднѣе допустить ихъ; здѣсь — то становится необходимымъ исчисленіе вѣроятностей для того, чтобы опредѣлить до какихъ поръ слѣдуетъ умножать наблюденія или опыты, чтобы получить въ пользу обнаруживающихся въ нихъ силъ вѣроятность, которая одержала бы верхъ надъ тѣми основаніями, на которыхъ ихъ все-таки можно бы не признавать.
Исчисленіе вѣроятностей позволяетъ оцѣнить достоинство и недостатки методовъ, примѣняемыхъ въ наукахъ, основанныхъ на догадкахъ. Такъ, чтобы узнать, который изъ вошедшихъ въ употребленіе методовъ лѣченія какой-либо болѣзни является наилучшимъ, достаточно испытать каждый изъ нихъ на одномъ и томъ же числѣ больныхъ при совершенно сходныхъ условіяхъ; преимущество самаго выгоднаго метода будетъ обнаруживаться все болѣе и болѣе, по мѣрѣ того какъ это число будетъ возрастать; а исчисленіе даетъ намъ соотвѣтственную вѣроятность его преимущества и отношеніе, выражающее предпочтительность его въ сравненіи съ остальными.
Примѣненіе исчисленія вѣроятностей къ нравственнымъ наукамъ
Мы только что убѣдились въ выгодѣ, предоставляемой анализомъ вѣроятностей при изысканіи законовъ естественныхъ явленій, причины которыхъ неизвѣстны или же слишкомъ сложны для того, чтобы дѣйствія ихъ могли быть подчинены вычисленію. То же самое относится почти ко всѣмъ объектамъ нравственныхъ наукъ. Столько причинъ непредвидѣнныхъ, или скрытыхъ, или неподдающихся оцѣнкѣ вліяетъ на человѣческія учрежденія, что судить о ихъ слѣдствіяхъ а priori невозможно.
Не будемъ противополагать безполезнаго и часто опаснаго сопротивленія неизбѣжнымъ слѣдствіямъ прогресса просвѣщенія, но будемъ измѣнять лишь крайне осторожно наши учрежденія и обычаи, къ которымъ мы давно уже примѣнились. Мы хорошо знаемъ по опыту прошлаго неудобства, которыя они представляютъ, но мы не знаемъ, какъ велико будетъ зло, которое можетъ причинить ихъ измѣненіе.
О вѣроятности свидѣтельскихъ показаній
Въ виду того, что большая часть нашихъ сужденій основана на вѣроятности свидѣтельскихъ показаній, очень важнымъ является подчинить ее исчисленію.
Предположимъ, что урна содержитъ 999 черныхъ шаровъ и одинъ бѣлый, и что по изъятіи изъ нея одного шара свидѣтель этого изъятія объявляетъ, что вынутъ бѣлый шаръ. Положимъ, что намъ извѣстно по опыту, что свидѣтель этотъ обманываетъ одинъ разъ изъ десяти, такъ что вѣроятность его свидѣтельства 9/10. Первая гипотеза – свидѣтель правдив, вторая гипотеза – свидѣтель обманываетъ. Вѣроятность наблюденнаго событія, опредѣленная а priori при первой гипотезѣ, равняется 1/1000*9/10 = 9/10000. Но при предположеніи, что свидѣтель обманываетъ, бѣлый шаръ не вышелъ, и вѣроятность этого случая равна 999/1000. Надо умножить ее на вѣроятность 1/10 обмана, что даетъ 999/10000 для вѣроятности наблюденнаго событія при второй гипотезѣ.
Всего 9 + 999 = 1008 вариантов. Вѣроятность первой гипотезы и выхода бѣлаго шара равнялась бы 9/1008, а вѣроятность второй гипотезы и выхода чернаго шара 999/1008. Мы видимъ, какъ возрастаетъ вѣроятность обмана по мѣрѣ того, какъ самый фактъ становится болѣе необычайнымъ.
Нѣкоторые авторы утверждали противное, основываясь на томъ, что, такъ какъ форма необычайнаго факта совершенно подобна формѣ обычнаго, то одни и тѣ же мотивы должны насъ побуждать вѣрить свидѣтелю одинаково, утверждаетъ ли онъ, что тотъ или что другой изъ этихъ фактовъ имѣлъ мѣсто. Простой здравый смыслъ опровергаетъ столь странное утвержденіе; но исчисленіе вѣроятностей, подтверждая указанія здраваго смысла, еще болѣе оцѣниваетъ правдоподобность свидѣтельствъ о необычайныхъ фактахъ.
Здѣсь является умѣстнымъ изслѣдовать знаменитый аргументъ Паскаля, который англійскимъ математикомъ Крэгомъ былъ облеченъ въ геометрическую форму. Нѣсколько свидѣтелей показываютъ, что само Божество имъ повѣдало, что, согласившись съ извѣстною вещью, можно наслаждаться не одною или двумя, но безконечнымъ множествомъ счастливыхъ жизней. Какъ бы мала ни была вѣроятность свидѣтельскихъ показаній, если только она не безконечно мала, очевидно, что выгода тѣхъ, кто соглашается съ этимъ предписаніемъ, безконечно велика, потому что она является произведеніемъ этой вѣроятности на безконечное благо: поэтому нельзя и колебаться, доставить ли себѣ эту выгоду.
Это известное пари Паскаля — предложенный математиком и философом Блезом Паскалем аргумент для демонстрации рациональности религиозной веры. Текст аргументации является фрагментом размышлений, содержащихся в разделе VIII «Разумнее верить, чем не верить в то, чему учит христианская религия» посмертно изданной работы «Мысли о религии и других предметах». Паскаль рассуждал: «Бог есть или нет. На которую сторону мы склонимся? Разум тут ничего решить не может. На что вы будете ставить? Для поиска ответа Паскаль предположил, что шансы существования или отсутствия Бога примерно равны или, по крайней мере, что вероятность существования Бога больше нуля. Тогда возможны два варианта:
- Жить без веры крайне опасно, так как возможный «проигрыш» в случае существования Бога бесконечно велик — вечные муки. Если же Бог не существует, то цена «выигрыша» невелика — безверие нам ничего не даёт и от нас ничего не требует. Реальным выигрышем атеистического выбора будет некоторая экономия средств и времени, так как не будет религиозных обрядов.
- Жить по канонам веры неопасно, хотя и чуть более затруднительно из-за постов, всяческих ограничений, обрядов и связанных с этим затрат средств и времени. Цена «проигрыша» в случае отсутствия Бога невелика — затраты на обряды и усилия на праведную жизнь. Зато возможный «выигрыш» в случае существования Бога бесконечно велик — спасение души, вечная жизнь.
Какова же оценка рассматриваемых вариантов? При умножении пусть даже большой вероятности, что Бога нет, на небольшую ценность приза получается величина возможно и большая, но всегда конечная. При умножении любой ненулевой, даже очень маленькой, вероятности того, что Бог окажет человеку милость за его добродетельное поведение, на бесконечно большую ценность приза получается бесконечно большая величина.
Чтобы понять аргументъ Паскаля, достаточно представить нумерами урны всѣ возможныя числа счастливыхъ жизней, отчего число этихъ нумеровъ становится безконечнымъ, и замѣтить, что, если свидѣтели обманываютъ, то самымъ выгоднымъ для нихъ является обѣщать вѣчное блаженство, чтобы аккредитовать свою ложь. Выраженіе вѣроятности ихъ показанія становится тогда безконечно малымъ. Послѣ умноженія ея на безконечное число обѣщанныхъ счастливыхъ жизней, безконечность пропадаетъ въ произведеніи, выражающемъ выгоду, которая вытекаетъ изъ этого обѣщанія, что и разбиваетъ аргументъ Паскаля.
О вѣроятности судебныхъ приговоровъ
Безъ сомнѣнія, судьямъ нужны, чтобы осудить обвиняемаго, самыя сильныя доказательства его преступленія; но нравственное доказательство есть всегда только вѣроятность, и опытъ слишкомъ хорошо показалъ, какія ошибки возможны въ уголовныхъ приговорахъ, даже тѣхъ, которые кажутся самыми справедливыми. Возможность исправлять эти ошибки есть самый основательный аргументъ философовъ, желавшихъ отмѣны смертной казни.
Въ спеціальныхъ судахъ, гдѣ пяти голосовъ изъ восьми достаточно для осужденія обвиняемаго, вѣроятность ошибки, которой можно опасаться относительно мягкости приговора, равна 65/256, или выше 1/4. Величина этой дроби ужасна; однако отчасти примиряющимъ должно являться то соображеніе, что чаще всего судья, который оправдываетъ обвиняемаго, не смотритъ на него какъ на невиннаго: онъ только объявляетъ, что противъ обвиняемаго нѣтъ уликъ, достаточныхъ для его осужденія.
Въ судѣ присяжныхъ изъ двѣнадцати членовъ, при большинствѣ, требуемомъ для осужденія, въ восемь голосовъ изъ двѣнадцати, вѣроятность ошибки, которой можно опасаться, равна 1093/8192, или немного болѣе одной восьмой. Вѣроятность рѣшеній слишкомъ слаба въ нашихъ судахъ присяжныхъ, и, по моему мнѣнію, для достаточнаго огражденія невиновности, слѣдуетъ требовать по крайней мѣрѣ большинства девяти голосовъ изъ двѣнадцати.
О выгодахъ предоставляемыхъ учрежденіями, основанными на вѣроятности событій
Страхованія морскія, отъ пожаровъ и отъ бури и вообще всѣ установленія этого рода исчисляются на основаніи тѣхъ же принциповъ. Купецъ имѣетъ на морѣ суда и желаетъ застраховать ихъ стоимость и стоимость ихъ груза отъ опасностей, которымъ они могутъ подвергнуться; съ этою цѣлью онъ вручаетъ извѣстную сумму какому-либо обществу, которое отвѣчаетъ согласно оцѣнкѣ за стоимость его груза и судовъ. Отношеніе этой стоимости къ суммѣ, которую слѣдуетъ заплатить въ качествѣ преміи страхованія, зависитъ отъ опасностей, которымъ подвергаются суда, и можетъ быть оцѣнено не иначе, какъ посредствомъ многочисленныхъ наблюденій надъ судьбою судовъ, отправившихся изъ порта по тому же назначенію.
Если бы застрахованныя лица платили страховому обществу только сумму, указанную исчисленіемъ вѣроятностей, то это общество не могло бы нести расходовъ, связанныхъ съ его учрежденіемъ; необходимо поэтому, чтобы они платили болѣе высокую премію страхованія. Но какова въ такомъ случаѣ ихъ выгода? Здѣсь становится необходимымъ разсмотрѣніе нравственной невыгоды, связанной съ неизвѣстностью. Понятно, что если самая справедливая игра становится невыгодной, потому что игрокъ мѣняетъ вѣрную ставку на невѣрный выигрышъ, страхованіе, въ которомъ невѣрное мѣняется на вѣрное, должно быть выгодно.
Товарищества взаимнаго страхованія, когда они состоятъ изъ очень большого числа лицъ, выгоднѣе для страхователей, чѣмъ страховыя общества, которыя изъ-за получаемой ими прибыли нравственную выгоду предоставляютъ всегда меньшую математической.
Объ иллюзіяхъ въ оцѣнкѣ вѣроятностей
Умъ имѣетъ свои иллюзіи, какъ чувство зрѣнія; и подобно тому, какъ осязаніе исправляетъ эти послѣднія, разсужденіе и исчисленіе исправляютъ первыя.
Урна содержитъ четыре шара черныхъ или бѣлыхъ, которые однако не всѣ одного цвѣта. Вынули одинъ изъ шаровъ, бѣлаго цвѣта, и положили его обратно въ урну, чтобы приступить снова къ подобному же тиражу. Спрашивается вѣроятность того, что при четырехъ слѣдующихъ тиражахъ будутъ появляться только черные шары.
Если бы число бѣлыхъ и черныхъ шаровъ было одинаково, эта вѣроятность была бы четвертою степенью вѣроятности 1/2 изъятія чернаго шара при каждомъ тиражѣ; слѣдовательно она равнялась бы 1/16. Но изъятіе бѣлаго шара при первомъ тиражѣ указываетъ на преобладаніе числа бѣлыхъ шаровъ въ урнѣ; ибо, если предположить, что въ урнѣ три бѣлыхъ шара и одинъ черный, то вѣроятность изъятія изъ нея бѣлаго шара равна 3/4; она равна 2/4, если предположить что въ ней два бѣлыхъ шара и два черныхъ; наконецъ она сводится къ 1/4, если предположить, что въ урнѣ три черныхъ шара и одинъ бѣлый. Согласно принципу вѣроятности причинъ, извлеченной изъ опыта, вѣроятности этихъ трехъ предположеній относятся между собою какъ количества 3/4, 2/4, 1/4; слѣдовательно, онѣ равны 3/6, 2/6, 1/6.
Такимъ образомъ пять шансовъ противъ одного за то, что число черныхъ шаровъ уступаетъ или, самое большее, равно числу бѣлыхъ. Кажется, судя по изъятію бѣлаго шара при первомъ тиражѣ что вѣроятность изъятія подрядъ четырехъ черныхъ шаровъ должна была бы быть меньше, чѣмъ въ случаѣ равенства обоихъ цвѣтовъ, или менѣе одной шестнадцатой. Между тѣмъ этого нѣтъ и помощью очень простого вычисленія находимъ, что эта вѣроятность больше одной четырнадцатой. Въ самомъ дѣлѣ она была бы равна четвертой степени 1/4, 2/4, 3/4 при первомъ, второмъ и третьемъ предыдущихъ предположеніяхъ относительно цвѣта шаровъ въ урнѣ. При умноженіи соотвѣтственно каждой степени на вѣроятность соотвѣтствующаго предположенія, или на 3/6, 2/6 и 1/6, сумма произведеній будетъ вѣроятностью изъятія подрядъ четырехъ черныхъ шаровъ. Такимъ образомъ имѣемъ для этой вѣроятности 29/384 дробь, большую, чѣмъ 1/14.
Это противорѣчіе объясняется, если примемъ во вниманіе, что указаніе перваго тиража на преобладаніе бѣлыхъ шаровъ надъ черными вовсе не исключаетъ преобладанія черныхъ шаровъ надъ бѣлыми, — преобладанія, исключаемаго предположеніемъ равенства того и другого цвѣта. А это преобладаніе, хотя мало правдоподобное, должно сдѣлать вѣроятность появленія подрядъ даннаго числа черныхъ шаровъ большею, чѣмъ при послѣднемъ предположеніи, если данное число значительно; и мы видимъ, что такъ и будетъ начиная съ четырехъ.
Внутренніе образы не являются дѣйствіями одной только причины; они вытекаютъ либо изъ впечатлѣній, полученныхъ одновременно однимъ и тѣмъ же, или различными органами чувствъ, либо изъ внутреннихъ впечатлѣній, вызванныхъ памятью. Взаимное вліяніе этихъ впечатлѣній является психологическимъ принципомъ, богатымъ послѣдствіями.
Пусть наблюдатель, находящійся въ совершенной темнотѣ, видитъ два свѣтящихся шара одного и того же діаметра на разныхъ разстояніяхъ: они покажутся ему неодинаковой величины. Ихъ внутренніе образы будутъ пропорціональны соотвѣтствующимъ изображеніямъ, запечатлѣвшимся на сѣтчаткѣ. Но если, по прекращеніи темноты, онъ увидитъ одновременно съ шарами все промежуточное пространство, то это зрѣлище увеличиваетъ внутренній образъ болѣе удаленнаго шара и дѣлаетъ его почти равнымъ образу другого шара.
Подробнее об оптических иллюзиях см. Марк Чангизи. Революция в зрении: что, как и почему мы видим.
Различные способы приближенія къ достовѣрности
Индукція, аналогія гипотезъ, основанныхъ на фактахъ и безпрестанно повѣряемыхъ новыми наблюденіями, счастливый природный тактъ, подкрѣпленный частымъ сравниваніемъ ихъ указаній съ опытомъ, — таковы главныя средства достиженія истины.
Анализъ и натуральная философія обязана своими важнѣйшими открытіями тому плодотворному методу, который называется индукціей. Однако одной индукціи, позволяющей открывать общіе принципы наукъ, не достаточно, для того чтобы установить ихъ въ точности. Ихъ нужно еще подтверждать доказательствами или окончательнымъ испытаніемъ, ибо исторія наукъ указываетъ намъ, что индукція приводила иногда къ неточнымъ результатамъ (о развенчании индукции, как научного метода см. Карл Поппер. Объективное знание. Эволюционный подход).
Аналогія основывается на вѣроятности того, что сходныя вещи происходятъ отъ однородныхъ причинъ и имѣютъ одинаковыя слѣдствія. Чѣмъ совершеннѣе подобіе, тѣмъ болѣе увеличивается эта вѣроятность. Такъ, мы, не сомнѣваясь, рѣшаемъ, что существа, надѣленныя одними и тѣми же органами, выполняя одно и то же, испытываютъ одинаковыя ощущенія и движимы одинаковыми желаніями. Вѣроятность того, что животныя, приближающіяся къ намъ по своимъ органамъ, имѣютъ ощущенія аналогичныя нашимъ, хотя и меньше вѣроят-ности, которая относится къ особямъ нашего рода, но все еще чрезвычайно велика, и потребовалось все вліяніе религіозныхъ предразсудковъ, чтобы заставить нѣкоторыхъ философовъ думать, что животныя — простые автоматы.
Историческій очеркъ исчисленія вѣроятностей
Уже давно были опредѣлены въ самыхъ простыхъ играхъ отношенія статочностей благопріятствующихъ и неблагопріятствующихъ игрокамъ: ставки и пари устанавливались сообразно этимъ отношеніямъ. Но до Паскаля и Фермата никто еще не далъ принциповъ и методовъ для подчиненія этого предмета исчисленію и не рѣшалъ хоть сколько-нибудь сложныхъ вопросовъ этого рода. Этимъ двумъ великимъ геометрамъ слѣдуетъ поэтому приписать первые элементы науки о вѣроятностяхъ (см. Альфред Реньи. Письма о вероятности: письма Паскаля к Ферма).
Гюйгенсъ собралъ различныя уже рѣшенныя задачи и прибавилъ къ нимъ еще новыя въ маленькомъ трактатѣ, первомъ, который появился объ этомъ предметѣ и который озаглавленъ: De Ratiociniis in ludo aleae (О расчётах в азартных играх).
Галлей въ Англіи примѣнили исчисленіе къ вѣроятностямъ человѣческой жизни, и Галлей опубликовалъ для этой цѣли первую таблицу смертности. Около того же времени Яковъ Бернулли предложилъ геометрамъ различныя задачи о вѣроятностяхъ, рѣшенія которыхъ онъ затѣмъ далъ. Онъ написалъ, наконецъ, свою прекрасную работу, озаглавленную „conjectandi» (предположения), которая появилась лишь спустя семь лѣтъ послѣ его смерти, произошедшей въ 1706 году.
Монмортъ и Моавръ выпустили два трактата объ исчисленіи вѣроятностей.
Бэйесъ (Bayes) въ Transactions phllisophiques 1763 года искалъ непосредственно вѣроятность того, что возможности, указанныя уже произведенными опытами, заключаются въ данныхъ предѣлахъ, и онъ достигъ своего способомъ тонкимъ и очень остроумнымъ, хотя и немного запутаннымъ. Этотъ предметъ примыкаетъ къ теоріи вѣроятностей причинъ и будущихъ событій, выведенной изъ наблюденныхъ событій.
Одно изъ самыхъ интересныхъ примѣненій исчисленія вѣроятностей касается среднихъ значеній, которыя слѣдуетъ выбирать изъ результатовъ наблюденій. Многіе геометры этимъ занимались, а Лагранжъ опубликовалъ въ Mémoires de Turin прекрасный методъ для опредѣленія этихъ среднихъ, когда законъ ошибокъ наблюденій извѣстенъ.
Похоже, речь о проверке гипотезы и оценке среднего генеральной совокупности, когда дисперсия известна (подробнее см. Введение в теорию статистического вывода).